Abstract
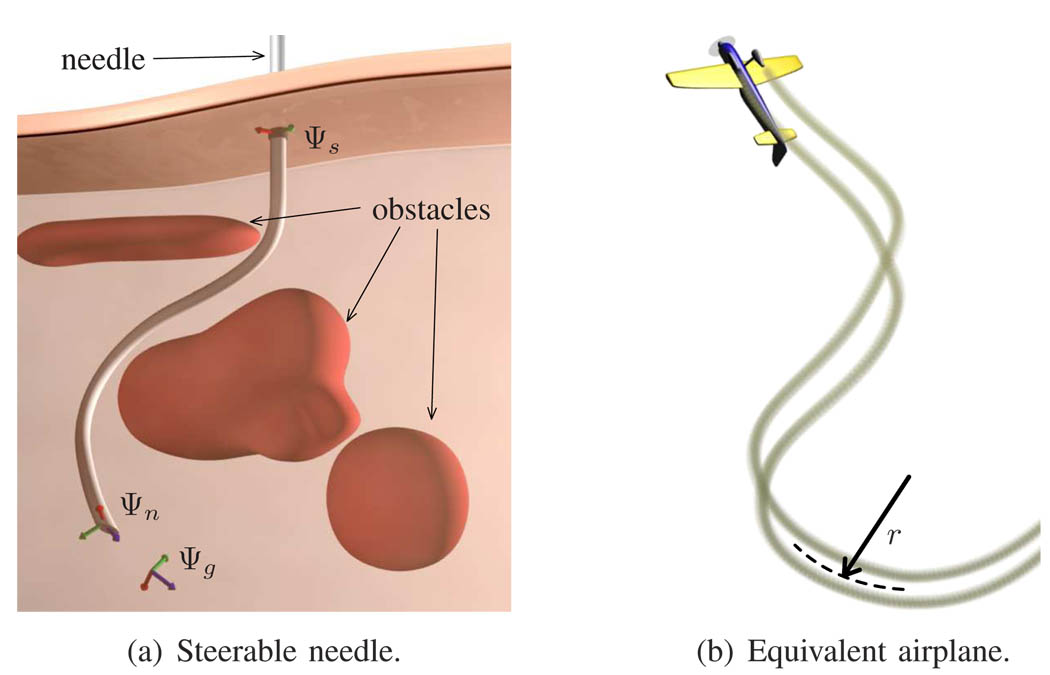
Steerable needles can be used in medical applications to reach targets behind sensitive or impenetrable areas. The kinematics of a steerable needle are nonholonomic and, in 2D, equivalent to a Dubins car with constant radius of curvature. In 3D, the needle can be interpreted as an airplane with constant speed and pitch rate, zero yaw, and controllable roll angle.
We present a constant-time motion planning algorithm for steerable needles based on explicit geometric inverse kinematics similar to the classic Paden-Kahan subproblems. Reachability and path competitivity are analyzed using analytic comparisons with shortest path solutions for the Dubins car (for 2D) and numerical simulations (for 3D). We also present an algorithm for local path adaptation using null-space results from redundant manipulator theory. Finally, we discuss several ways to use and extend the inverse kinematics solution to generate needle paths that avoid obstacles.
I. INTRODUCTION
Steering needles through soft tissue has the potential to enable physicians to reach targets behind sensitive or impenetrable areas. We focus on a subclass of flexible needles that provide steerability due to asymmetric forces acting at the needle tip, for example due to a beveled surface (Webster, Okamura, Cowan, Chirikjian, Goldberg & Alterovitz 2006) or a kink near the end of the needle (Engh et al. 2006). By rotating the needle at the base, the orientation of the tip can be changed and hence the trajectory of the needle can be controlled. Other needle steering approaches have also been developed, including symmetric flexible needles controlled by applying asymmetric forces at the base (DiMaio & Salcudean 2005), not at the tip. For the purposes of this paper, we refer to asymmetric flexible needles (based on beveled tips or kinks) simply as steerable needles. The extra mobility of steerable needles over rigid needles can be harnessed in medical applications such as brachytherapy (Alterovitz et al. 2005) and brain surgery (Engh et al. 2006) to reach difficult targets.
Experimental studies (Webster et al. 2005) show that the motion of steerable needles can be approximated as having a constant radius of curvature that is independent of insertion speed. The control inputs for the needle are the insertion speed and rotation (roll) angle, although for motion planning (the topic of this paper) insertion speed is often not important. The rotation angle is then the only real control input and trajectories can be parameterized by insertion depth. A steerable needle (Fig. 1a) is thus kinematically equivalent to an airplane with fixed speed and pitch rate, zero yaw, and controllable roll rate (Fig. 1b).
Fig. 1.
Model setup of a steerable needle and a kinematically equivalent airplane with fixed speed and pitch rate, zero yaw, and controllable roll rate.
Motion planning for steerable needles is an important problem and has been studied in several ways in literature. Most studies focus on planar motion, for which the control input reduces to switching between curve-left and curve-right. Alterovitz et al. present a roadmap-based motion planning framework that explicitly incorporates motion uncertainty and computes the path that is most likely to succeed (Alterovitz et al. 2005, Alterovitz et al. 2007, Alterovitz & Goldberg 2008, Alterovitz et al. 2008). Minhas et al. (2007) show planning based on fast duty cycle spinning of the needle, effectively removing the limitation of a fixed-radius path but requiring continuous angular control input. Kallem & Cowan (2007) introduce a controller that stabilizes the needle motion to a plane, allowing practical implementation of planar motion planning methods.
The first 3D motion planning algorithm was introduced by Park et al. (2005, 2008) and used diffusion of a stochastic differential equation to generate a family of solution paths. The authors also describe several extensions to avoid obstacles. Duindam et al. (2008) presented a second 3D motion planning algorithm that uses fast numerical optimization of a cost function to compute feasible needle paths in 3D environments with obstacles.
This paper presents a different solution to the 3D motion planning problem for steerable needles, based on inverse kinematics. We propose a new geometry-based algorithm inspired by the Paden-Kahan subproblems in traditional inverse kinematics algorithms (Murray et al. 1994). Just as the Paden-Kahan subproblems, our algorithm (Section III) can be fully described in geometric terms of intersecting lines, planes, and circles, and computing the solution simply requires a few trigonometric functions. We analyze reachability and competitivity of the solution (Section IV) using analytic comparison to the Dubins car solution (Dubins 1957) and numerical simulations. We also present a method to locally adapt needle paths using null-motions (Section V).
The proposed motion planning algorithms find feasible needle paths very quickly and provide some capability for obstacle avoidance. As the current accuracy of medical data is limited, these algorithms may be sufficient by themselves, but we envision them being part of more general global motion planning systems for more complex environments with obstacles, as discussed in Section VI.
II. PROBLEM STATEMENT AND MODELING ASSUMPTIONS
A. Model parameters and assumptions
Throughout this paper, we only consider the idealized kinematics of the needle in a static and rigid (non-deforming) environment. We assume that the motion of the needle is fully determined by the motion of the needle tip, that the motion of the needle tip is instantaneously along a perfect circle of constant radius r, and that rotations of the base are instantly transmitted to rotations of the tip. Experimental results (Webster et al. 2005) show that needle materials can be chosen such that the needle indeed moves along an arc of approximately constant radius, but the effects of tissue inhomogeneity, friction, and needle torsion can be significant and will require compensation (Kallem & Cowan 2007) in practical applications. The assumption of rigidity is strong but necessary to reduce complexity. We consider the presented method for path planning as a tool to compute an initial solution that may be locally adapted and optimized to account for deformations. Tissue deformation for planar needle motion planning has been studied for rigid needles (Alterovitz et al. 2003) and recently for control using external tissue manipulation (Torabi et al. 2009).
Under the previous assumptions, the motion of the needle is determined kinematically by two control inputs: the insertion velocity, denoted v, and the tip rotation velocity, denoted ω. We present the kinematics model for general v(t) but remove this redundant degree of freedom in the next section.
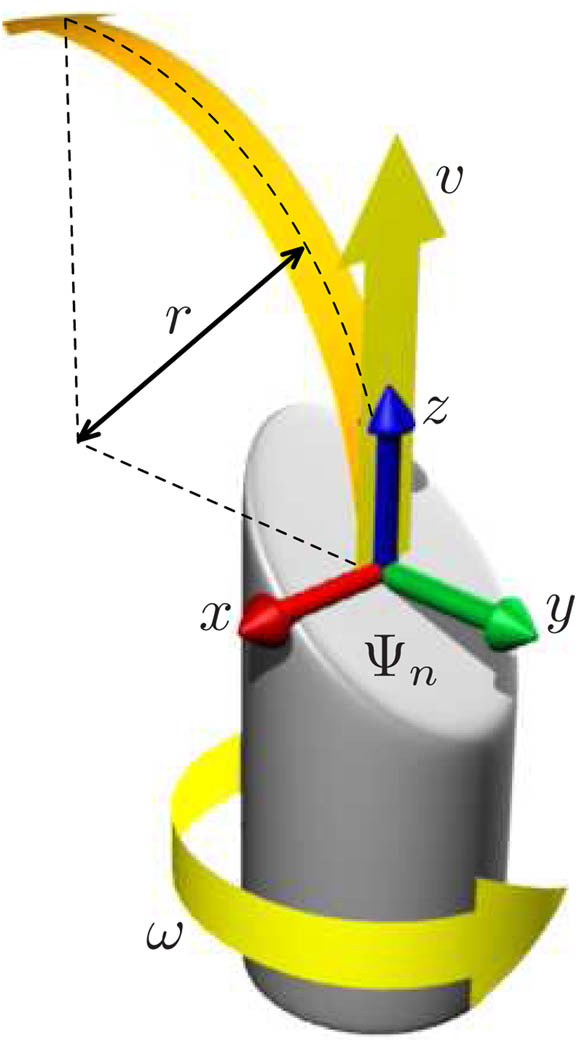
Fig. 2 illustrates the model setup. We rigidly attach a coordinate frame Ψn to the tip of the needle, with axes aligned as in the figure, such that the z-axis is the direction of forward motion v and needle orientation ω, and the beveled tip causes the needle to rotate instantaneously around a line parallel to the x-axis and passing through the point (0, −r, 0).
Fig. 2.
Choice of coordinates and reference frame Ψn at the needle tip. Control input ω generates a rotation around z, while control input v generates a circular motion around an axis parallel to x and passing through (0, −r, 0).
Following standard robotics literature (Murray et al. 1994), the position and orientation of the needle tip relative to a reference frame Ψs can be described compactly by a 4 × 4 matrix gsn(t) ∈ SE(3) of the form
| (1) |
with Rsn ∈ SO(3) the rotation matrix describing the relative orientation, and psn ∈ T (3) the vector describing the relative position of frames Ψs and Ψn.
The instantaneous linear and angular velocities of the needle are described by a twist vsn ∈ se(3) which in body coordinates Ψn takes the convenient form
| (2) |
in equivalent vector and matrix notation. The twist relates to gsn as
| (3) |
This kinematic model is the same as the unicycle model by Webster, Kim, Cowan, Chirikjian & Okamura (2006). When the twist is constant, (3) becomes a linear ordinary differential equation (ODE) that can be integrated as
| (4) |
for which a relatively simple analytic expression exists (Murray et al. 1994). In the path planning algorithms, we construct paths for which is piecewise constant and compute the resulting transformation using this efficient analytic expression.
B. Problem statement
The objective of the motion planning algorithms in this paper is to find feasible paths between given start and goal configurations in the absence of obstacles1. More precisely, the inputs to the algorithm are an initial needle pose gstart G SE(3) and a desired needle pose ggoal ∈ SE(3). The outputs of the algorithm are control functions v(·) and ω(·) and a finite end time 0 ≤ T < ∞, such that the solution gsn(·) of the differential equation (3) with gsn(0) = gstart satisfies gsn(T) = ggoal. If no feasible path can be found, the algorithm returns failure.
The kinematics equations (2) and (3) are invariant to time scaling, in the sense that the path traced out by the needle does not change if the control inputs v(·) and ω(·) are scaled by the same (possibly time-varying) factor. Therefore, we can simplify the motion planning problem by assuming without loss of generality that v(·) ≡ 1, which is equivalent to parameterization by insertion depth (Kallem & Cowan 2007, Duindam et al. 2008). The insertion time T thus represents the total path length since . A pure rotation, i.e. motion with non-zero ω and zero v, can be represented by a Dirac pulse in the signal ω with magnitude equal to the desired total angle of rotation. These impulses and the general choice v ≡ 1 are used only for compact representation of the path; in practical execution of a given solution path, the speed of insertion can be changed such that the motion is safe, while impulsive rotations should obviously be executed by stopping insertion (v = 0) and slowly rotating the needle until the desired angle.
Although motion planning is based on connecting general 3D poses (both position and orientation), solving a difference in initial or final roll angle is trivial as this degree of freedom is directly controlled through ω(·). So although the inputs to the algorithm are general elements of SE(3), we often mainly focus on path planning between given start and goal position and direction of the needle, i.e. only considering the z-axis of Ψn. Given a solution from the start position and direction to the goal position and direction, the full motion plan from a start pose to a goal pose follows directly by adding the required pure rotations as Dirac impulses in ω at the beginning and end of this solution. We discuss the difference in the number of degrees of freedom in the control solution vs. the configuration space in Section III-B.
III. PATH PLANNING USING INVERSE KINEMATICS
We present two motion planning solutions based on inverse kinematics, one for the planar (2D) case and one for the general spatial (3D) case. The motion planning problem is considered planar if the start position ps, start direction zs, goal position pg, and goal direction zg are all in the same plane.
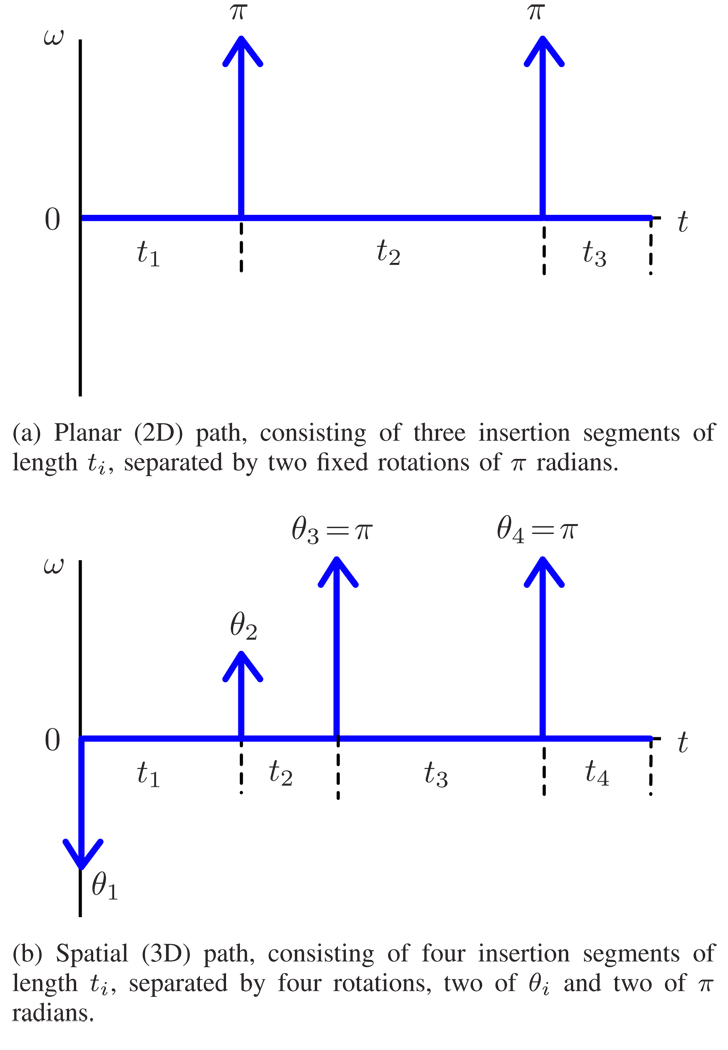
In both inverse kinematics solutions, we look for a control input function ω(·) of a very specific form, namely a function that is zero everywhere except for a fixed number of Dirac impulses (two in the planar case, four in the spatial case, see Fig. 3). Geometrically, this means that we look for trajectories that are concatenations of a fixed number of circular segments with radius r: the needle moves along a circle when ω = 0, and instantaneously changes direction at the time instants that ω is a Dirac impulse. Furthermore, the magnitudes of the Dirac impulses in the planar case are constrained to be exactly π, corresponding to a change in direction between curve-left and curve-right. We also choose a spatial solution for which the last two impulsive rotations are π, making the last three segments of the spatial path co-planar as well.
Fig. 3.
Structure of the solution ω(·) for the 2D and 3D planning problems.
The specific choices in the structure of ω(·) result in geometrically intuitive solutions that are relatively straightforward to compute. The simplicity of the proposed solutions comes at the cost of not necessarily being optimal in terms of path length or required control effort. Earlier work (Duindam et al. 2008) studied methods to find needle trajectories by numerically optimizing a particular given cost function expressing the desired balance between control effort, path length, and other costs. The solution paths discussed in the present paper could be used as initial guess for these optimization algorithms and thus be (locally) adapted to have lower cost.
A. Inverse kinematics in 2D
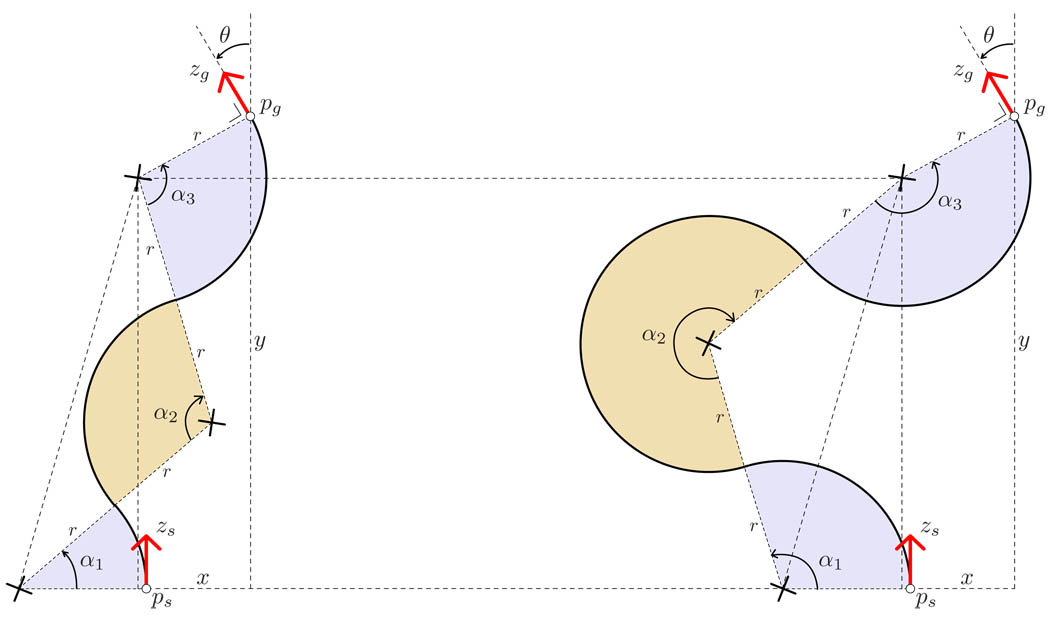
We first consider the planar path planning problem with ω(·) as in Fig. 3a. For simplicity, we only consider relatively short-distance planning problems for which a solution with three consecutive circular segments exists; the approach can be extended for longer paths by adding additional circular segments. The relative position of the start and goal are described by two displacements x and y, their relative orientation by a single angle θ. The purpose of the path planning algorithm is to find the three insertion depths t1,t2,t3 describing a feasible needle path from start to goal. Note that the needle travels a distance ti = rαi when moving along a circle of radius r for αi radians, and hence we can equivalently look for the three angles αi in Fig. 4. These should be such that if we start at ps in the direction zs heading left, move rα1 forward, turn π, move rα2 forward, turn π, and move rα3 forward, we arrive exactly at the desired goal pose. The mirrored case starting with a right turn can be computed similarly.
Fig. 4.
Two geometric solutions for the same planar inverse kinematics problem, both using sequential curve-left, curve-right, curve-left motions.
We can solve for the angles αi by looking at the setup in Fig. 4 and realizing that the three centers of rotation (marked by × in the figure) form a triangle with known edge lengths. Using the cosine rule for this triangle, we can write
| (5) |
This equation has two solutions for α2, which correspond to the two paths shown in Fig. 4. With α2 known, the other two angles follow uniquely as
| (6) |
| (7) |
with atan2 the inverse tangent function solved over all four quadrants. Since the needle can only move forward, angles must be chosen as αi ∈ [0,2π). The required insertion distances ti follow immediately as ti = rαi.
B. Inverse kinematics in 3D
Now consider the 3D inverse kinematics problem of connecting two general poses in SE(3) by a valid needle path. We propose one solution using eight consecutive insert and turn motions as shown in Fig. 3b; an explicit geometric solution using fewer motions is still an open problem.
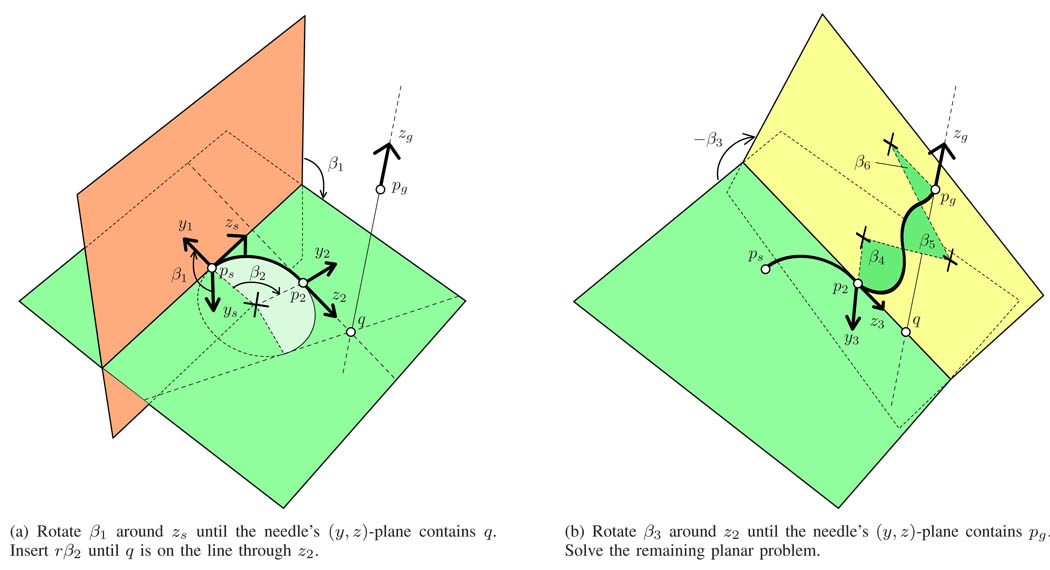
The geometry of this solution is illustrated in Fig. 5. The problem is split into two parts: first, the needle is turned and inserted such that its instantaneous line of motion (the instantaneous direction of the needle) intersects the line describing the goal position and direction. Second, the remaining planar problem is solved using the solution from Section III-A.
Fig. 5.
Geometric derivation of an inverse kinematic solution on SE(3). The point q may be chosen anywhere along the line through pg in the direction zg, although not all choices may generate a solution path. The planar IK algorithm is used to find the values of (β4,5,6.
More precisely, we first choose any point q on the line defined by pg and zg. This point q will be the intersection point of the two lines defining the remaining planar problem. With q defined, the needle is first rotated by θ1 = β1 until its (y, z)-plane contains q. The required angle β1 satisfies
| (8) |
which has two solutions β1 that differ by π.
Second, the insertion distance t1 = rβ2 is solved such that the line through the needle tip in the direction z2 contains the point q. If q is outside the circle describing the needle motion along β2, two solutions exist, with z2 either pointing towards (as in the figure) or away from q. These solutions are
| (9) |
with qv := q − ps + ry1. No solution exists if q is inside the circle (|qv | < r).
Third, the needle is rotated by θ2 = β3 until pg (and hence the whole line through q and pg) is contained in the needle’s (y,z)-plane:
| (10) |
which again gives two solutions that differ by π. The remaining angles β4, β5, β6 (corresponding to the time segments t2,t3,t4) can then be solved using the 2D planner from Section III-A.
In this algorithm, we have the following degrees of freedom to choose a solution. First is the choice of the point q: this can be anywhere on the line containing pg and zg, which means varying q generates a one-dimensional subspace of possible inverse kinematics solutions. Second, we can choose one of two possible solutions βi for each of the four angles in equations (8–10) and (5), resulting in 24 possible combinations. Not all of these choices may give feasible paths for a given start and end pose, and it is also not directly obvious which choice will result in the ‘best’ path between the two poses. Nevertheless, since the inverse kinematics equations can be computed very quickly, one can simply compute all combinations for a number of choices of q and pick the best solution, with ‘best’ defined, for example, using a cost function.
The inverse kinematics solution describes a path consisting of four insertions (translations) and four rotations, a control space with eight degrees of freedom as shown in Fig. 3b. Two degrees of freedom (θ3 and θ4) are constrained to be exactly π, and one additional degree of freedom is constrained through the choice of the point q. The remaining five degrees of freedom are exactly sufficient to describe any relative position and direction between the start and goal needle configuration; the final roll angle of the needle is not prescribed and hence the space of relative configurations is five-dimensional. We could even consider the space of relative configurations to be four-dimensional if we discard the initial roll angle, but this is merely a matter of calling β1 either a control action or an initialization step. In Section V, we relax the constraints on the control space and show how the shape of the needle path can be adapted using the resulting extra degrees of freedom.
IV. REACHABILITY AND COMPETITIVITY
To evaluate the quality of the paths generated by the presented inverse kinematics (IK) solutions, we study the set of reachable needle poses and competitivity (Icking & Klein 1995, Gabriely & Rimon 2005) of the computed solutions. Competitivity in this case refers to the path length of the computed solution; it has no relation to competitivity in the sense of computational speed (the IK algorithms run in constant time).
A. Reachability and competitivity in 2D
Consider first the solution to the planar problem as described in Section III-A. The algorithm will clearly only find a solution if the right-hand side of (5) has norm less than or equal to one, or geometrically, if the centers of the circles tangent to the start and goal poses are no farther than 4r apart. This condition defines the set of reachable relative needle poses.
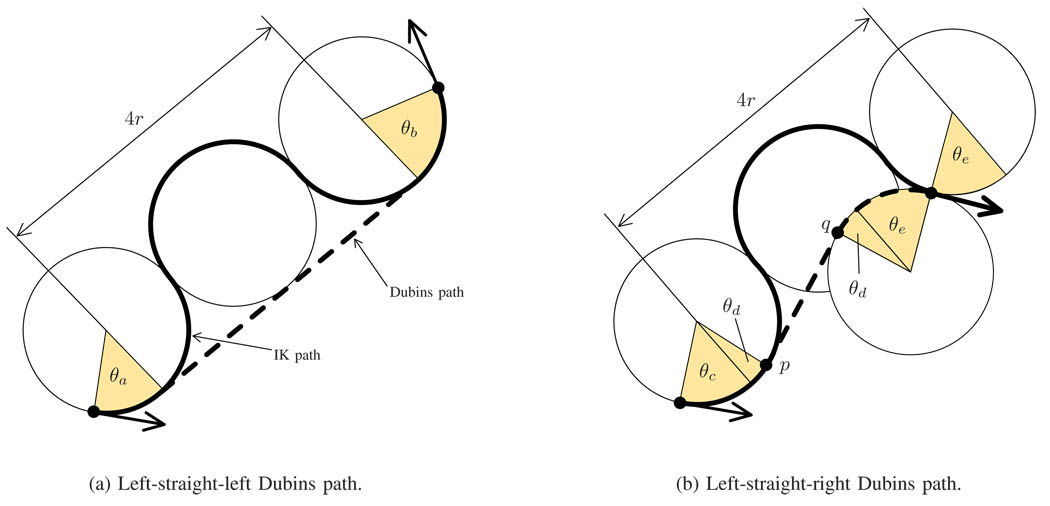
To describe competitivity of the algorithm for these reachable poses, we compare the IK solutions to the trajectories generated by allowing an infinite number of direction changes. In that case, a trajectory can be generated with an arbitrary radius of curvature larger than or equal to r, by asymmetrically cycling between curve-left and curve-right and taking the limit of this cycling frequency to infinity, similar to the idea used by Minhas et al. (2007). This means that in the limit, the needle can behave like a Dubins car (Dubins 1957) with minimum radius of curvature r.
The optimal path for a Dubins car is known to consist of two circular arcs with radius r connected by another circular arc or a straight line (Dubins 1957). For a given start and end pose, the IK solution only differs from the Dubins path if the connecting segment for the Dubins path is a straight line; the IK solution will still contain a (sub-optimal) circular arc. Furthermore, the Dubins path may start and end with circular arcs in the same direction or in opposite directions (Fig. 6), whereas the IK solution always starts and ends with a turn in the same direction. It is intuitively clear that the largest difference in path length occurs at the border of the reachable space where the three circles of the IK solution are aligned; if the circles are not aligned, one of the two solution paths is relatively ‘more straight’ and hence shorter, as illustrated in Fig. 4. In the first case (Fig. 6a), the maximum ratio of the path lengths is
| (11) |
For the second case (Fig. 6b), we can compute the length of the straight-line segment q – p as
| (12) |
from which we find that the maximum path length ratio equals
| (13) |
The degree of competitivity of the 2D IK solution is hence approximately 1.63. Note that this is a bound on the competitivity that does not take into account the number of direction changes; the medical benefit of a shorter needle path (less tissue cutting) may very well be outweighed if this requires a large number of direction changes (180° rotations) with associated amounts of friction forces on the tissue surrounding the needle path. In addition, from a planning and control point of view, direction changes increase uncertainty in the state estimate and complexity in the control algorithm (Reed 2008, Reed et al. 2008).
Fig. 6.
Paths generated by the 2D inverse kinematics algorithm compared to the optimal paths for a Dubins car. The worst-case scenario occurs when the three circles defining the IK solution are farthest apart and the straight-line segment of the optimal Dubins path provides the best ‘short-cut’.
B. Reachability and competitivity in 3D
Continuing with the 3D IK solution from Section III-B, we present a reachability and competitivity analysis based on numerical simulation. Formal geometric proofs and bounds of the algorithm are subject of future research; at this point we do not have a good approximation for the optimal path and simply compare the IK solutions to the Euclidean distance between the start and goal positions. Future work could compare the presented solution to the paths generated by the method of Park et al. (2008). We take q = pg throughout the analysis; different choices give qualitatively similar results.
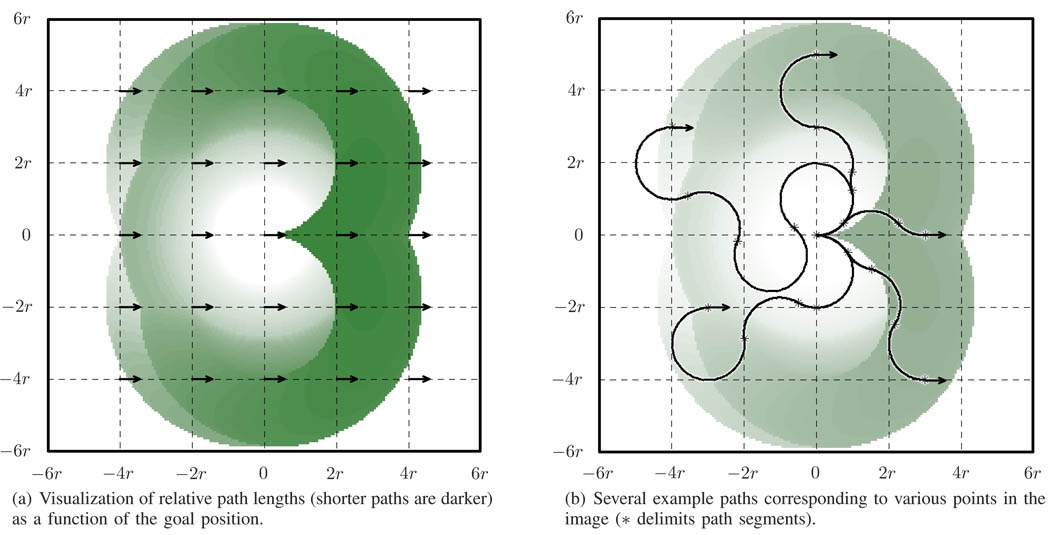
First consider Fig. 7. This illustrates the lengths of the IK trajectories starting at the center of the figure and ending at goal positions in the plane of the figure, with start and goal directions equal and pointing to the right. The brightness of each pixel indicates the length of the IK path divided by the Euclidean distance between the start and goal locations: dark colors represent small ratios (good paths) while light colors represent large ratios (bad paths). Fig. 7b illustrates several examples of solution trajectories.
Fig. 7.
Reachability and relative path lengths obtained using the inverse kinematics algorithm. The algorithm tries to find a path from the center of the image to each pixel in the image, with both start and goal direction aimed to the right.
A set of reachable states shows up in the figure as the ‘figure-eight’ around the start location. Points outside this shape cannot be reached for the given goal direction. The figure also shows a distinction between poses that can be reached with reasonably short curves (darker region) and poses that require significantly longer paths (lighter region). This distinction is sharp in the area in front of the needle (right side of the figure) but is more diffuse for poses on the sides of the needle (top and bottom of the figure). If we consider competitivity in an informal way, meaning whether the algorithm can generated paths of reasonable lengths, we can say that the algorithm is competitive in the darker region of the figure; relative poses that are in the lighter region may be reachable, but the paths are so unwieldy that they are of little practical use in our brachytherapy application.
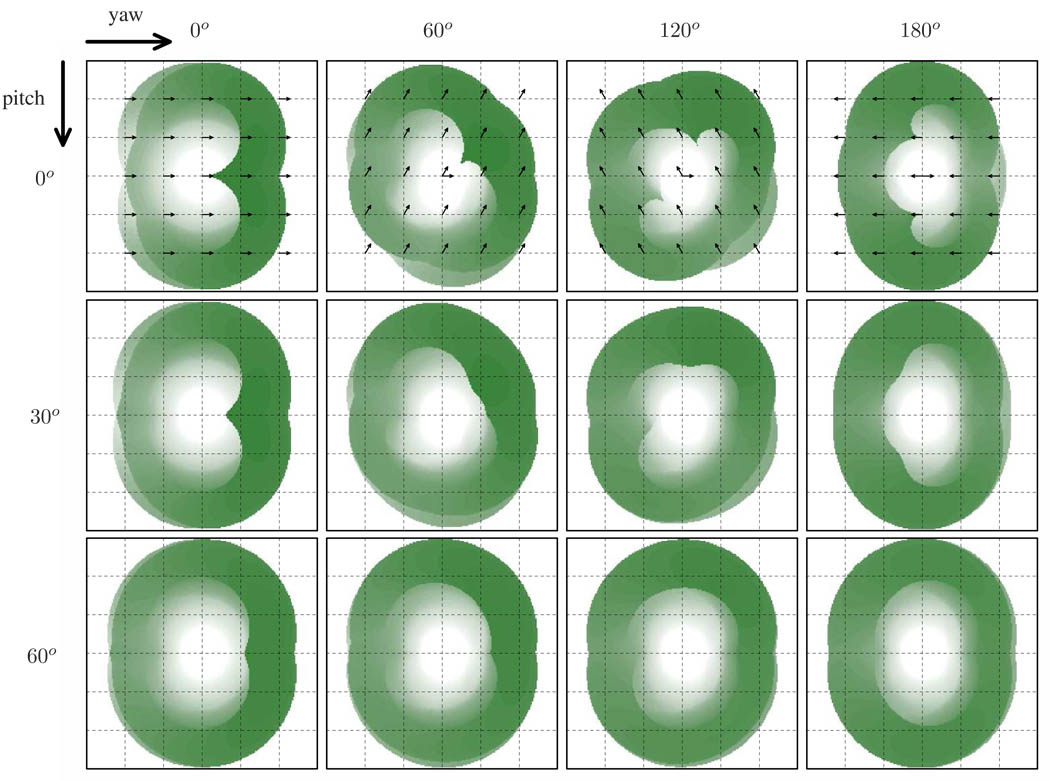
Fig. 8 shows additional plots generated by varying the two remaining degrees of freedom in placing the goal pose: the in-plane yaw angle and out-of-plane pitch angle (the inverse kinematics solution is invariant to roll about the initial and final needle directions).
Fig. 8.
Reachability and relative path lengths as in Fig. 7 for various relative yaw and pitch angles for the goal pose. Grid lines are 2r units apart.
The figure shows that as the goal direction is turned away from the straight-ahead case (change in yaw), the set of reachable and competitive paths rotates in the same direction while maintaining a roughly similar shape. As the goal direction is rotated out of plane (change in pitch), the competitive paths near the starting pose disappear until only poses at a significant distance (three to five times the radius of curvature) are competitive.
In the three-dimensional case, it remains a difficult task to precisely characterize the set of poses that can be reached with a reasonably short path. Comparing the solutions to the Euclidean distance provides some insight but no global bound on the solutions: competitivity measures are unbounded when comparing to the Euclidean distance, since for infinitely close but non-collinear needle orientations the path length of the IK solution remains finite while the Euclidean distance converges to zero.
To use the inverse kinematics planner as a local planner in global roadmap-based planning methods such as the Probabilistic Roadmap method (Kavraki et al. 1996), it is important to characterize the set of goal poses that are reachable from a given needle pose. Numerical simulations such as those shown in Fig. 8 can be used to construct an approximation of the set of goal poses that can be reached with a competitive path (with ‘competitive’ in the informal meaning of ‘reasonably short path’). This set can be used as the definition of ‘neighborhood’, i.e. those needle poses that are likely to be connectible and can become edges in the roadmap if they do not intersect obstacles.
V. PATH ADAPTATION USING NULL-MOTIONS
The presented inverse kinematics solution can be computed very quickly but is generally not the optimal solution in the sense of avoiding obstacles or minimizing path length or required control effort. Earlier work considered path planning as a pure numerical optimization problem (Duindam et al. 2008), but in this section we show how sub-optimal paths such as those generated by the IK planner can be locally optimized and adjusted using null-motions.
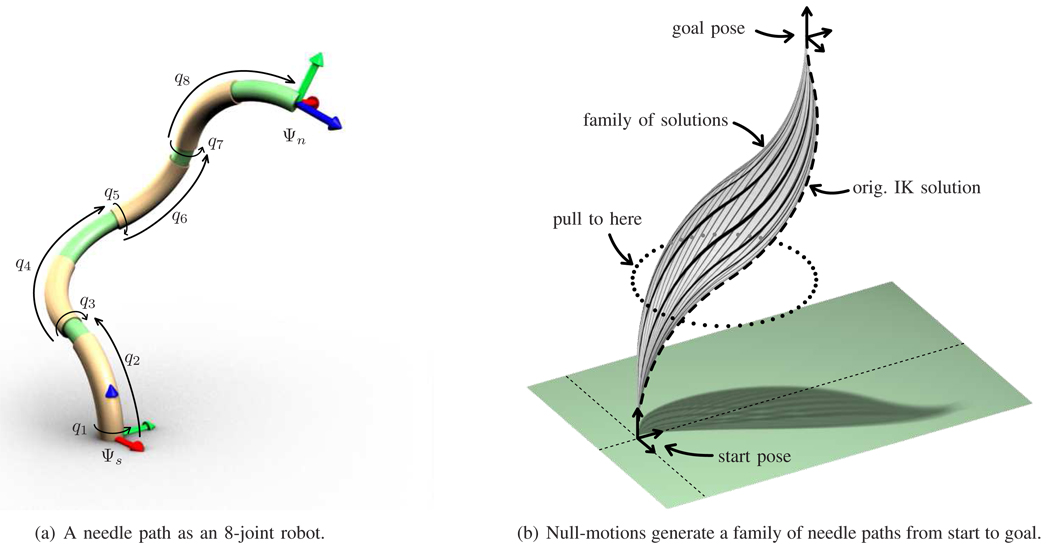
Consider an IK solution between two general 3D needle poses. By construction, this solution describes a path from start to goal consisting of eight consecutive turning and insertion control actions. We can think of this path as a redundant serial robot manipulator arm with eight joints (Fig. 9a). Since the relative pose of the goal is given by six parameters, standard robotics theory (Murray et al. 1994) tells us that the robot has a two-dimensional space of null-motions2, provided it is not at a singularity. If the joints are moved in this null-motion space, the shape of the robot (i.e. the shape of the needle path) will change without changing the pose of the end effector (i.e. the needle tip).
Fig. 9.
Representation of a needle path as a robot with eight joints, and how null motions can be used to generate a family of solution curves.
The set of null motions is described by the null space of the geometric Jacobian J(q) ∈ ℝ6×8 of the robot, which relates the spatial twist to the joint velocities q̇ as (Murray et al. 1994). Given the Jacobian, we can change the shape of the path by changing the joint angles in such a way that q̇ ∈ Null(J(q)) at all times.
Fig. 9b shows an example of how one inverse kinematics solution can be locally transformed in this way into a family of solution curves. Intuitively, this set of curves was generated by starting from the IK solution indicated in the figure (the dashed line), and ‘pulling’ on the curve from several points laid out in a circle, while holding the start and end pose of the needle fixed. More precisely, we model the robot as a viscous system with damping in each joint that counteracts applied forces, and write the governing equations as
| (14) |
| (15) |
with Fi the wrench (Murray et al. 1994) corresponding to the (known) externally applied pulling force, Ji(q) the Jacobian of link i at which Fi is applied, λ the required constraint wrench acting at the tip to constrain its motion, and B(q) > 0 the symmetric positive-definite inverse damping matrix that relates the joint torques τ to the joint velocities as q̇ = B(q)τ. The first equation relates the total torque (due to external forces Fi and λ) to the change in the joint angles, the second equation describes the end point constraint that should be satisfied. Note that these equations do not relate to any actual physical needle motions and only represent a mathematical procedure.
Substituting (14) into (15), solving for λ, and substituting back into (14) results in an unconstrained equation for q̇ that no longer contains λ:
| (16) |
This ODE describes the evolution of q under the influence of an external wrench Fi and tip constraint Jq̇ = 0. It has a unique solution if B is invertible and J has full rank (no singularity). Equation (16) projects the velocity due to the wrench Fi along the columns of BJT onto the null space of J. The matrix B(q) defines a metric on the space of torques that can be chosen in any appropriate way, e.g. as a function that drives the system away from configurations that are singular or contain negative-length path segments.
For the example of Fig. 9b, we chose B diagonal with Bjj(q) → 0 as qj → 0 for all joints j describing insertion path segments, thus avoiding negative-length path segments. We applied a linear force in the middle of the kinematic chain (link 5), directed toward one of the dots, and integrated (16) over time to obtain the pod-shaped family of needle paths shown in the figure.
This method of path adaptation can be used in fully automated motion planning (e.g. to perform gradient descent on some cost function with penalty costs for obstacle penetration) with changes in q constrained to be null motions. More directly, in interactive (computer-assisted) motion planning systems, it can provide the user with an intuitive path adjustment tool similar to the control points on a spline curve that can be moved to change its local shape. Although there is no guarantee this approach will always work, it provides the user with an additional tool to construct suitable needle paths.
VI. EXTENSIONS FOR OBSTACLE AVOIDANCE
The inverse-kinematics based motion planning algorithm quickly computes feasible needle paths and allows the user to focus on specifying higher-level objectives in terms of start and goal needle poses. Indeed, the main motivation and reason for computer-assistance in this motion planning problem is the degree of under-actuation and nonholonomicity, which can be dealt with using the presented approach.
Nevertheless, the algorithms provide no guarantees for a solution or a structured incremental way to search for other trajectories in case of failure due to obstacles or other complications. The only possibilities are to choose different parameter settings or, for the null-motion based method, to try applying external forces at a different point or in a different direction.
This section briefly discusses four ways in which the described planning algorithms can be used and extended to produce needle paths that avoid obstacles. Some can be implemented directly; others are the subject of ongoing research.
First, the inverse kinematics solutions have a number of free parameters that can be chosen to maximize obstacle avoidance. In the planar case, this merely amounts to choosing the left or right solution in Fig. 4 and whether to start curve-left or curve-right. The spatial solution, however, not only provides four such binary choices (sixteen combinations), but in addition allows the point q to be chosen anywhere on a line (though not all choices may result in a solution path). This choice defines two planes in which the spatial solution path will be contained, and we hence the solution path will be free if we choose q such that these two planes do not intersect obstacles. This is clearly a conservative strategy since the actual needle path will only reside in a small part of the planes.
A second way to implement obstacle avoidance is to use optimization-based planning (Duindam et al. 2008), in which obstacle penetration is associated with a penalty cost, and the motion planning algorithm implicitly avoids obstacles by minimizing the cost. One of the open problems in this optimization-based scheme is the choice of a good initial estimate for the optimal solution, since the optimization problem is nonlinear and non-convex. The inverse kinematics solutions presented in this paper may serve as good initial estimates for the optimization routine, since they already achieve the goal of connecting the start state to the goal state. The optimization can then locally adapt the solution paths as to avoid obstacles.
Third, the inverse kinematics solutions can be used as a component in global planning methods that can avoid obstacles. In motion planning techniques such as PRM (Probabilistic Roadmaps, see Kavraki et al. (1996)) and related techniques such as RRT (Rapidly-Exploring Random Trees, LaValle (1998)) and SMR (Stochastic Motion Roadmaps, Alterovitz et al. (2007)), possible paths for a system are explored by sampling from the free configuration space and connecting these samples using a fast so-called local planner. In the case of steerable needles, the presented inverse kinematics solution could be used as a local planner, as it can quickly compute a feasible trajectory between nearby configuration states. This is the subject of ongoing research, some preliminary results are described by Xu et al. (2008).
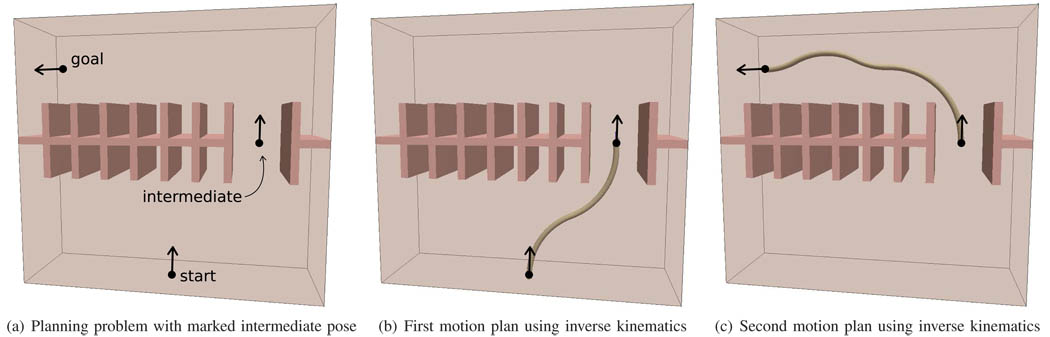
Finally, a fourth way to use the inverse kinematics solutions in obstacle avoidance schemes is to rely partially on user input. When it comes to global motion planning, computers are severely limited in cognitive abilities and can require large amounts of computation power and time to solve problems that are easy for humans. Consider for instance the motion planning problem of Fig. 10a: for the reader it is instantly clear that any feasible path should pass near the intermediate point marked in the figure, but computer-based planners may take significant amounts of computation time to ‘realize’ this, or they may not be able to find a feasible solution at all.
Fig. 10.
Difficult motion planning problems with complex obstacles can be solved using semi-automated planning. The algorithm is provided with an intermediate pose, a ‘way point’ that separates the global motion planning problem into two relatively straight-forward local motion planning problems.
One way to solve this problem is to combine human cognitive abilities for global planning with computer power for local planning. This idea is similar to the concept of ‘many-worlds browsing’ (Twigg & James 2007), in which the user assists an optimization algorithm and interactively and intuitively constrains the vast search space of possible solutions. For our motion planning system, if a human path planner indicates the desired intermediate point as in Fig. 10a, automatic motion planning algorithms can be applied to solve the resulting two subpaths. Finding a path from the start location to the intermediate location is trivial, as is finding a path from the intermediate location to the goal. Figs. 10b and 10c show the resulting subpaths obtained using the inverse kinematics planner; comparable results are obtained when using the direct numerical optimization approach described by Duindam et al. (2008). For this example, the algorithms are not sensitive to the exact position and orientation of the intermediate pose, but the approach could be extended to iterate over several intermediate poses near the one indicated.
VII. CONCLUSIONS AND FUTURE WORK
This paper presents constant-time geometrically motivated motion planning algorithms for steerable needles and airplanes with constant speed and pitch rate, zero yaw, and controllable roll. The first algorithm uses inverse kinematics to explicitly compute feasible paths in 3D, the second uses null-motions to adapt paths to avoid obstacles or achieve other objectives.
As briefly discussed, these algorithms can be used as components in larger more general motion planning schemes, possibly using limited user-input to guide automatic local planning. In future work, we plan to explore this direction and use the IK algorithm as a local planner in (autonomous) roadmap-based algorithms. Recent results using Rapidly-Exploring Random Trees (Xu et al. 2008) are encouraging, although computation requirements are still several orders of magnitude larger than with direct optimization-based algorithms (Duindam et al. 2008).
Another main future direction of our research is to find a systematic way to include uncertainty during motion planning and control (Hauser et al. 2009). Our application of steerable needles contains several sources of uncertainty, including needle motion uncertainty, tissue flexibility and friction, and sensing inaccuracies. These uncertainties should be taken into account in the motion planning stage, as discussed and implemented for the 2D case in previous work (Alterovitz et al. 2007). The presented fast local motion planning algorithm can be used to quickly test connectivity and iteratively study the effect of perturbations.
Finally, reachability and competitivity analyses were presented for the 2D and 3D inverse kinematics algorithms. Future work will be aimed at reducing the number of control parameters to six (or five when discarding final roll) to match the intrinsic dimension of the control problem. We also plan to extend the analysis of the current 3D algorithm to provide bounds on the competitivity compared to the optimal shortest-path solution. A promising direction is the comparison with paths generated by the approach of Park et al. (2008). The results from these analyses may also prove useful for roadmap-based motion planning and help define ‘neighborhood’ of states: a static asymmetric relation that describes what configurations are reachable from a certain configuration via a reasonably short path (in the absence of obstacles). This extra structure would hopefully reduce the required number of function calls to the local planner.
ACKNOWLEDGMENTS
This work is supported in part by the National Institutes of Health under grants R01 EB006435 and F32 CA124138 and by the Netherlands Organization for Scientific Research. We thank Professors Okamura, Chirikjian, Cowan, and Taylor from Johns Hopkins university for the helpful comments and suggestions, and Prof. Cowan for the idea of using null-motions for path adaptation. We also thank Jean Pouliot and I-Chow Joe Hsu from the University of California, San Francisco.
Footnotes
Section VI discusses several ways to use and extend the presented algorithm to environments with obstacles.
The method can be directly extended to the case where we only consider the final (and initial) needle direction, leaving the roll angle unconstrained. This results in five (four) parameters describing the relative configuration and hence a three-dimensional (four-dimensional) space of null-motions.
Contributor Information
Vincent Duindam, Email: v.duindam@ieee.org.
Jijie Xu, Email: jijie.xu@rit.edu.
Ron Alterovitz, Email: ron@cs.unc.edu.
Shankar Sastry, Email: sastry@coe.berkeley.edu.
Ken Goldberg, Email: goldberg@berkeley.edu.
REFERENCES
- Alterovitz R, Branicky M, Goldberg K. Motion planning under uncertainty for image-guided medical needle steering. International Journal of Robotics Research. 2008;27(11–12):1361–1374. doi: 10.1177/0278364908097661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alterovitz R, Goldberg K. Motion Planning in Medicine: Optimization and Simulation Algorithms for Image-Guided Procedures, Vol. 50 of Springer Tracts in Advanced Robotics (STAR) Springer; 2008. [Google Scholar]
- Alterovitz R, Goldberg K, Okamura A. Planning for steerable bevel-tip needle insertion through 2D soft tissue with obstacles; Proceedings of the IEEE International Conference on Robotics and Automation; 2005. pp. 1640–1645. [Google Scholar]
- Alterovitz R, Goldberg K, Pouliot J, Taschereau R, Hsu I. Sensorless planning for medical needle insertion procedures; Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems; 2003. pp. 3337–3343. [Google Scholar]
- Alterovitz R, Siméon T, Goldberg K. The stochastic motion roadmap: A sampling framework for planning with Markov motion uncertainty; Proceedings of Robotics: Science and Systems; 2007. [Google Scholar]
- DiMaio SP, Salcudean SE. Needle steering and motion planning in soft tissues. IEEE Transactions on Biomedical Engineering. 2005;52(6):965–974. doi: 10.1109/TBME.2005.846734. [DOI] [PubMed] [Google Scholar]
- Dubins LE. On curves of minimal length with a constraint on average curvature, and with prescribed initial and terminal positions and tangents. American Journal of Mathematics. 1957;79(3):497–516. [Google Scholar]
- Duindam V, Alterovitz R, Sastry S, Goldberg K. Screw-based motion planning for bevel-tip flexible needles in 3D environments with obstacles; Proceedings of the IEEE International Conference on Robotics and Automation; 2008. pp. 2483–2488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engh JA, Podnar G, Kondziolka D, Riviere CN. Toward effective needle steering in brain tissue; Proc. 28th Annu. Intl. Conf. IEEE Eng. Med. Biol. Soc; 2006. pp. 559–562. [DOI] [PubMed] [Google Scholar]
- Gabriely Y, Rimon E. Algorithmic Foundations of Robotics VI, Vol. 17 of STAR. Springer-Verlag; 2005. chapter Competitive Complexity of Mobile Robot On Line Motion Planning Problems; pp. 155–170. [Google Scholar]
- Hauser K, Alterovitz R, Chentanez N, Okamura A, Goldberg K. Feedback control for steering needles through 3D deformable tissue using helical paths; Proceedings of Robotics: Science and Systems; 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Icking C, Klein R. Modelling and Planning for Sensor Based Intelligent Robot Systems. 1995. Competitive strategies for autonomous systems; pp. 23–40. [Google Scholar]
- Kallem V, Cowan NJ. Image-guided control of flexible bevel-tip needles; Proceedings of the IEEE International Conference on Robotics and Automation; 2007. pp. 3015–3020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kavraki LE, Švestka P, Latombe JC, Overmars MH. Probabilistic roadmaps for path planning in high-dimensional configuration spaces. IEEE Transactions on Robotics and Automation. 1996;12(4):566–580. [Google Scholar]
- LaValle SM. Rapidly-exploring random trees: A new tool for path planning. Computer Science Department, Iowa State University; Technical Report TR 98-11. 1998
- Minhas DS, Engh JA, Fenske MM, Riviere CN. Modeling of needle steering via duty-cycled spinning; Proceedings of the International Conference of the IEEE EMBS Cité Internationale; 2007. pp. 2756–2759. [DOI] [PubMed] [Google Scholar]
- Murray RM, Li Z, Sastry SS. A Mathematical Introduction to Robotic Manipulation. CRC Press; 1994. [Google Scholar]
- Park W, Kim JS, Zhou Y, Cowan NJ, Okamura AM, Chirikjian GS. Diffusion-based motion planning for a nonholonomic flexible needle model; Proceedings of the IEEE International Conference on Robotics and Automation; 2005. pp. 4611–4616. [Google Scholar]
- Park W, Liu Y, Zhou Y, Moses M, Chirikjian GS. Kinematic state estimation and motion planning for stochastic nonholonomic systems using the exponential map. Robotica. 2008;26:419–434. doi: 10.1017/S0263574708004475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reed KB. Compensating for torsion windup in steerable needles; Proceedings of the IEEE/RAS-EMBS International Conference on Biomedical Robotics and Biomechatronics; 2008. pp. 936–941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reed KB, Kallem V, Alterovitz R, Goldberg K, Okamura AM, Cowan NJ. Integrated planning and image-guided control for planar needle steering; Proceedings of the IEEE/RAS-EMBS International Conference on Biomedical Robotics and Biomechatronics; 2008. pp. 819–824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torabi M, Hauser K, Alterovitz R, Duindam V, Goldberg K. Guiding medical needles using single-point tissue manipulation; Proceedings of the IEEE International Conference on Robotics and Automation; 2009. pp. 2705–2710. [Google Scholar]
- Twigg CD, James DL. Many-worlds browsing for control of multibody dynamics. ACM Transactions on Graphics (SIGGRAPH 2007) 2007;26(3) [Google Scholar]
- Webster RJ, Kim JS, Cowan NJ, Chirikjian GS, Okamura AM. Nonholonomic modeling of needle steering. International Journal of Robotics Research. 2006;5/6:509–525. [Google Scholar]
- Webster RJ, Memisevic J, Okamura AM. Design considerations for robotic needle steering; Proceedings of the IEEE International Conference on Robotics and Automation; 2005. pp. 3588–3594. [Google Scholar]
- Webster RJ, Okamura AM, Cowan NJ, Chirikjian GS, Goldberg K, Alterovitz R. Distal bevel-tip needle control device and algorithm. US patent pending 11/436,995. 2006
- Xu J, Duindam V, Alterovitz R, Goldberg K. Motion planning for steerable needles in 3D environments with obstacles using rapidly-exploring random trees and backchaining; Proceedings of the IEEE Conference on Automation Science and Engineering; 2008. pp. 41–46. [Google Scholar]