Order parameters for macromolecules: Application to multiscale simulation

A Singharoy; S Cheluvaraja; P Ortoleva

doi:10.1063/1.3524532

. 2011 Jan 24;134(4):044104. doi: 10.1063/1.3524532

Order parameters for macromolecules: Application to multiscale simulation

A Singharoy ¹, S Cheluvaraja ¹, P Ortoleva ^1,^a)

PMCID: PMC3045216 PMID: 21280684

Abstract

Order parameters (OPs) characterizing the nanoscale features of macromolecules are presented. They are generated in a general fashion so that they do not need to be redesigned with each new application. They evolve on time scales much longer than 10⁻¹⁴ s typical for individual atomic collisions∕vibrations. The list of OPs can be automatically increased, and completeness can be determined via a correlation analysis. They serve as the basis of a multiscale analysis that starts with the N-atom Liouville equation and yields rigorous Smoluchowski∕Langevin equations of stochastic OP dynamics. Such OPs and the multiscale analysis imply computational algorithms that we demonstrate in an application to ribonucleic acid structural dynamics for 50 ns.

INTRODUCTION

A multiscale framework for simulating the dynamics of macromolecules is developed. Their dynamics is divided into high frequency atomic vibrations and slow (coherent) large-spatial-scale conformational changes. A set of order parameters (OPs) is introduced to describe the coherent, overall structural changes while the small amplitude and high frequency atomic fluctuations are described by an equilibrium distribution following from entropy maximization constrained to instantaneous values of the OPs. In effect, OPs as conceived here filter out the high frequency atomistic fluctuations. These concepts are put on a firm mathematical basis via a multiscale analysis of the Liouville equation. The result of the latter analysis is a set of Langevin equations, all factors within which are related to an interatomic force field. This yields a force-field based multiscale algorithm that allows for all-atom simulation of macromolecular structural transitions with high CPU efficiency. We believe this computational approach will be of great value in fundamental and applied studies of the dynamics of macromolecules and their interactions with their microenvironment.

OPs characterize the state of organization of a system. As used here they describe the overall structure of a macromolecule. The objective of introducing OPs has been dimensionality reduction, i.e., to arrive at a practical computational algorithm for large systems and to understand the salient features of the structure∕dynamics of nanoscale assemblies.¹ They are related to the underlying all-atom description, enabling a unified treatment based on the Newtonian Liouville equation.²^,³ The present objective is to analyze a set of OPs, showing that they facilitate a complete analysis of macromolecular dynamics.

Given that the OPs evolve much slower than the 10⁻¹⁴s time scale of atomistic collisions∕vibrations, the latter have sufficient time to arrive at a quasiequilibrium consistent with the instantaneous state of the OPs. The OPs modify the probability distribution of atomistic configurations, which, in turn, determines the diffusions and thermal-average forces mediating OP dynamics. In this view, macromolecular structural dynamics follows from the coupling of processes across multiple scales in space and time.²^,³^,⁴^,⁵^,⁶^,⁷^,⁸^,⁹^,¹⁰^,¹¹ The result of the multiscale analysis of the Newtonian Liouville equation is a set of Langevin equations of stochastic OP dynamics. If the set of OPs is incomplete (i.e., their dynamics is coupled to that of other slowly changing variables), then they satisfy equations involving time delays (i.e., memory effects) as resulting from traditional projection operator analysis.¹² In contrast, the formal multiscale analysis presented here does not involve these memory effects because of the time scale separation enabled by the OPs.

A practical property of macromolecular OPs is that their construction be automatable. This has two implications: (1) the description can readily be enriched if it is found to be incomplete and (2) the tedious process of inventing new OPs for each macromolecule is avoided. The OPs must capture key features of the free-energy landscape in order to be complete dynamically. In this way, they capture key pathways for structural transitions and associated energy barriers. Earlier choices for OP-like variables include principal component analysis (PCA) modes to identify collective behaviors in macromolecular systems,¹³^,¹⁴^,¹⁵ dihedral angles,¹⁶^,¹⁷ curvilinear coordinates to characterize macromolecular folding and coiling,¹⁸ bead models wherein a peptide or nucleotide is represented by a bead which interacts with others via a phenomenological force, and spatial coarse-grained models.¹⁹^,²⁰^,²¹ These approaches suffer from one or more of the following difficulties: (1) characteristic variables are not slowly varying in time; (2) macromolecular twist is not readily accounted for; (3) their internal dynamics, and hence inelasticity of their collisions is neglected; and (4) the forces involved must be calibrated for most new applications. In contrast as discussed in Secs. 2, 3, these difficulties are overcome in the present approach.

However, PCA has been successfully used to study protein folding. The PCA modes (involving collective degrees of freedom) probe the global motions of proteins in an “essential” subspace.²²^,²³ Dihedral PCA (dPCA) has been suggested to naturally provide a correct separation of internal and overall motions.¹⁶ Free-energy landscapes of several small molecules including protein and ribonucleic acid (RNA) hairpin have been analyzed using dPCA. However, it has been commented that dPCA produces distortions on the free-energy surface that can lead to artificial energy barriers and minima.²⁴ One of the simulation methods based on PCA is essential dynamics sampling (EDS). Here the PCA modes are used to guide the macromolecular dynamics. This method has been successfully used to study the folding path of cytochrome c over hundreds of ps. But the principal components vary significantly during large transformations and hence need to be carefully changed from those of the starting structure.¹³^,²² Another problem with EDS is the prerequisite of PCA modes that require up to several nanoseconds of molecular dynamics (MD) run. For big systems, this becomes computationally expensive.²¹ Improvements to EDS have been made via a technique called amplified collective motion. However normal modes derived from this model via an anisotropic network¹³ may not be consistent with all-atom models, especially if the structure undergoes severe deformation. Direct essential dynamics (DED) on the other hand uses the most active collective mode and a weak force to jump out of energy minima as discussed and reviewed in Ref. 13. This has been demonstrated on a 15 amino acid S-peptide where DED trajectories overcame local minima and energy barriers and folded the protein faster than conventional MD. Stock et al. developed a multidimensional Langevin model of biomolecules where dPCA modes are used to determine slow, large amplitude motions.¹⁶ This has been used to model tri- and hepta-alanine structural transitions. The methodology stresses on the large dimensionality of the model essential for timescale separation.¹⁷ Similar ideas arise from our multiscale analysis developed in Sec. 3 and other papers.²⁵^,²⁶ However, to accurately generate the stochastic driving field for the Langevin equation, long time MD data is required to calculate the PCA modes. For example, a 100 ns trajectory is required as an input for subsequent analysis of tri-alanine. “Scrambled” data from replica MD is suggested to suffice. These would again make calculations expensive for large systems that exhibit timescale separation. A variational coarse-graining approach was used to locate the coarse-grain (CG) sites on centers of masses of various collections of atoms identified via PCA or normal mode analysis based on the C_α atoms of each residue.²⁰ However, a simulation method has not yet been implemented using this CG representation. In order to account for considerable far-from equilibrium structures, a nonlinear dimensionality reduction free-energy profiling scheme based on the isometric mapping algorithm isomap has been developed and demonstrated on Src homology three protein using MD simulations.²⁷ Another coarse-graining approach is the rigid region decomposition model.²⁸ This has been implemented via algorithms like framework rigidity optimized dynamic algorithm and rigid cluster normal mode analysis to investigate protein mobility.²⁸

In this study, we have several objectives to be achieved by introducing OPs: (1) provide a set of OPs for macromolecules that capture the essence of macromolecular structural dynamics (Sec. 2), (2) provide an efficient computational algorithm to simulate structural dynamics (Sec. 3), and (3) demonstrate the applicability of our OPs to the multiscale algorithm of Sec. 3 via viral RNA simulations (Sec. 4).

MACROMOLECULAR OPs

A key element of the multiscale analysis of a macromolecule is the identification of OPs that describe its nanoscale features. A central property of an OP is that it evolves slowly. Slow OP dynamics emerges in several ways including

inertia associated with the coherent dynamics of many atoms evolving simultaneously;
migration over long distances;
stochastic forces that tend to cancel; and
species population levels as in chemical kinetics or self-assembly, which involve many units, only a few of which change on the atomic timescale.

OPs considered here relate macromolecular features to a reference structure (e.g., from x-ray crystallography). They are introduced via (1) a transformation warping space⁶ and (2) maximizing their information content to relate them to the atomistic configurations.⁷ Consider OPs constructed by embedding the system in a volume V_S. Basis functions $U_{k} (\binom{⇀}{r})$ for a triplet of labeling indices k are introduced. If computations are carried out using periodic boundary conditions to simulate a large system (e.g., to minimize boundary effects and to handle Coulomb forces), periodic basis functions (Fourier modes) can be used. Other possible basis functions would be spherical harmonics when the system is embedded in a spherical volume. More generally, as is familiar in quantum theory or hydrodynamics, the basis functions used are chosen for convenience to reflect the overall geometry of the system and the conditions imposed at the boundary. Furthermore the basis functions should be free of unphysical features (e.g., poles). In the present study, we found Legendre polynomials to be convenient for simulating systems with closed boundaries of rectangular geometry.⁴^,⁶^,⁸^,⁹

In our approach, points $\binom{⇀}{r}$ within the system are considered to be a displacement of original points ${\binom{⇀}{r}}^{0}$ .⁶ A set of vector OPs ${\binom{⇀}{Φ}}_{k}$ are constructed as follows. The macromolecule deforms in 3D space such that a point $\binom{⇀}{r}$ is displaced from an original point ${\binom{⇀}{r}}^{0}$ . Deformation of space taking any ${\binom{⇀}{r}}^{0}$ to $\binom{⇀}{r}$ is continuous and is used to introduce OPs ${\binom{⇀}{Φ}}_{k}$ via

\binom{⇀}{r} = \sum_{k} U_{k} ({\binom{⇀}{r}}^{0}) {\binom{⇀}{Φ}}_{k} .

(2.1)

As the ${\binom{⇀}{Φ}}_{k}$ change, space is deformed, and so does the macromolecule embedded in it. The objective is to ensure that the dynamics of the ${\binom{⇀}{Φ}}_{k}$ reflects the physics of the macromolecule and that the deformation captures key aspects of the atomic-scale details of the structure. In this way, the ${\binom{⇀}{Φ}}_{k}$ constitutes a set of vector OPs if they are slowly varying in time (see below).

Let the i^th atom in the macromolecule (i = 1, …, N) be moved from its original position ${\binom{⇀}{r}}_{i}^{0}$ via the above deformation by evolving the ${\binom{⇀}{Φ}}_{k}$ and correcting for atomic-scale details as follows. Given a finite truncation of the k sum in Eq. 2.1, for e.g., choosing N_OP number of OPs, there will be some residual displacement (denoted ${\binom{⇀}{σ}}_{i}$ ) for each atom in addition to the coherent deformation generated by the k sum:

{\binom{⇀}{r}}_{i} = \sum_{k} {\binom{⇀}{Φ}}_{k} U_{k} ({\binom{⇀}{r}}_{i}^{0}) + {\binom{⇀}{σ}}_{i} .

(2.2)

To maximize the information content of the OPs, the magnitude of the ${\binom{⇀}{σ}}_{i}$ can be minimized by the choice of basis functions and the number of terms in the k sum. Conversely, imposing a permissible size threshold for the residuals allows one to determine the number of terms to include in the k sum.

To start the multiscale analysis, the ${\binom{⇀}{Φ}}_{k}$ must be expressed in terms of the fundamental variables ${\binom{⇀}{r}}_{i}$ . To arrive at this relationship, we minimize the mass-weighted square residual $(m_{1} σ_{1}^{2} + \dots m_{N} σ_{N}^{2})$ with respect to the ${\binom{⇀}{Φ}}_{k}$ , where m_i is the mass of atom i. This implies

\begin{matrix} \sum_{k^{'}} B_{{k k}^{'}} {\binom{⇀}{Φ}}_{k^{'}} = \sum_{i = 1}^{N} m_{i} U_{k} ({\binom{⇀}{r}}_{i}^{0}) {\binom{⇀}{r}}_{i}, \\ B_{{k k}^{'}} = \sum_{i = 1}^{N} m_{i} U_{k} ({\binom{⇀}{r}}_{i}^{0}) U_{k^{'}} ({\binom{⇀}{r}}_{i}^{0}) . \end{matrix}

(2.3)

Thus, the OPs can be computed in terms of the atomic positions by solving Eq. 2.3. For convenience, we choose the basis functions U_k to be mass weighted orthogonal. In that case, the B-matrix equation (II.3) is diagonal. We view $U_{k} ({\binom{⇀}{r}}_{i}^{0})$ as the ith component of an N-dimensional vector for an N-atom macromolecule. There are N_OPN-dimensional vectors, each labeled by its k value. Orthogonalization of these vectors is carried out using a Gram–Schmidt procedure. In the above notation, k is a set of integers (each of which can be 0,1…); with this, Φ_100X is the X component of the OP ${\binom{⇀}{Φ}}_{100}$ that weights the U₁₀₀ contribution in Eq. 2.2 after the latter has been subjected to Gram–Schmidt orthogonalization. In our implementation, before orthogonalization U_{_{k 1}_{k 2}_{k 3}} is a product of Legendre polynomials of order k₁, k₂, k₃ for the X, Y, Z components of ${\binom{⇀}{r}}_{i}^{0}$ respectively. The orthogonalization scheme preserves the physical nature of the three fundamental OPs (100X, 010Y, 001Z) because they are always chosen to be the first three members of the basis.⁴ For other OPs, the k labeling corresponds to the original $U_{k} ({\binom{⇀}{r}}_{i}^{0})$ from which each orthogonal vector was constructed via the Gram–Schmidt procedure.

Mass-weighted orthonormality of the basis functions implies that B_kk^′ is 0 for k≠k^′ . With this

\begin{matrix} {\binom{⇀}{Φ}}_{k} = \frac{\sum_{i = 1}^{N} m_{i} U_{k} ({\binom{⇀}{r}}_{i}^{0}) {\binom{⇀}{r}}_{i}}{{\tilde{μ}}_{k}}, {\tilde{μ}}_{k} = \sum_{i = 1}^{N} m_{i} {\{U_{k} ({\binom{⇀}{r}}_{i}^{0})\}}^{2} . \end{matrix}

(2.4)

Thus for a given set of atomic positions the corresponding OPs are uniquely defined.

Next consider the timescale of OP dynamics. The Liouville operator is defined $L = - \sum_{i = 1}^{N} {\binom{⇀}{p}}_{i} ∕ m_{i} \cdot \partial ∕ \partial {\binom{⇀}{r}}_{i} + {\binom{⇀}{F}}_{i} \cdot \partial ∕ \partial {\binom{⇀}{p}}_{i}$ , where ${\binom{⇀}{p}}_{i}$ and ${\binom{⇀}{F}}_{i}$ are the momentum of, and net force on atom i. Given Eq. 2.4, one may compute dΦ∕dt as −LΦ, where Φ(Γ) is a set of OPs ${\binom{⇀}{Φ}}_{k}$ . With this

\begin{matrix} \frac{d {\binom{⇀}{Φ}}_{k}}{d t} = \frac{{\binom{⇀}{\tilde{Π}}}_{k}}{{\tilde{μ}}_{k}}, \\ {\binom{⇀}{\tilde{Π}}}_{k} = \sum_{i = 1}^{N} U_{k} ({\binom{⇀}{r}}_{i}^{0}) {\binom{⇀}{p}}_{i} . \end{matrix}

(2.5)

Inclusion of m_i in developing Eq. 2.3 gives ${\binom{⇀}{Φ}}_{k}$ the character of a generalized center-of-mass-like (CM) variable. In fact, if U_k is a constant then ${\binom{⇀}{Φ}}_{k}$ is proportional to the CM. While the ${\binom{⇀}{Φ}}_{k}$ are given in terms of a sum of N-atomic displacements, many terms of which have similar directions due to the smooth variation of U_k with respect to ${\binom{⇀}{r}}_{i}^{0}$ , the momenta ${\binom{⇀}{\tilde{Π}}}_{k}$ are given by a sum of atomic momenta, which tend to cancel near equilibrium. Hence the thermal average of ${\binom{⇀}{\tilde{Π}}}_{k}$ is small and thus the ${\binom{⇀}{Φ}}_{k}$ tends to evolve slowly.

First consider the dynamics of the CM, i.e., ${\binom{⇀}{Φ}}_{000}$ . From Eq. 2.5, ${\binom{⇀}{Φ}}_{000}$ satisfies $d {\binom{⇀}{Φ}}_{000} ∕ d t = {\binom{⇀}{Π}}_{000} ∕ M$ , where ${\tilde{μ}}_{000} = M$ is the total mass of the macromolecule. Since M is large, ${\binom{⇀}{Φ}}_{000}$ evolves slowly relative to the time scale of atomic collision∕vibration. This suggests that ${\binom{⇀}{Φ}}_{000}$ satisfies a key criterion to be an OP and serves as the starting point of a multiscale analysis.

To reveal the time scale on which the OPs evolve, it is convenient to define the smallness parameter ε = m∕M, where m is a typical atomic mass. For any of the ${\binom{⇀}{Φ}}_{k}$ , letting ${\binom{⇀}{v}}_{i}$ be the velocity of particle i, the definition of ε and Eq. 2.5 yields

\begin{matrix} \frac{d {\binom{⇀}{Φ}}_{k}}{d t} & = & \frac{\sum_{i = 1}^{N} U_{k} ({\binom{⇀}{r}}_{i}^{0}) {\binom{⇀}{p}}_{i}}{{\tilde{μ}}_{k}} = \frac{\sum_{i = 1}^{N} U_{k} ({\binom{⇀}{r}}_{i}^{0}) m_{i} {\binom{⇀}{v}}_{i}}{{\tilde{μ}}_{k}} \\ = \frac{\sum_{i = 1}^{N} U_{k} ({\binom{⇀}{r}}_{i}^{0}) m {\hat{m}}_{i} {\binom{⇀}{v}}_{i}}{M μ_{k}} = ε \frac{\sum_{i = 1}^{N} U_{k} ({\binom{⇀}{r}}_{i}^{0}) {\hat{m}}_{i} {\binom{⇀}{v}}_{i}}{μ_{k}} = ε \frac{{\binom{⇀}{Π}}_{k}}{μ_{k}}, \end{matrix}

(2.6)

where $μ_{k} = {\tilde{μ}}_{k} ∕ M$ and ${\hat{m}}_{i} = m_{i} ∕ m$ .

Thus ${\binom{⇀}{Φ}}_{k}$ changes at a rate O(ε) under the assumption that the atomic momenta tend to cancel as is consistent with the quasiequilibrium probability distribution $\hat{ρ}$ below. Special initial conditions could make the rate of OP change scale differently; examples of such conditions include an initial density discontinuity (leading to a shockwave), injection of the macromolecule at a high velocity or a sudden jump in temperature. Under these conditions, the slowness of motion within our reduced dimensionality framework (OPs) and all the resulting advantages (e.g., calculating thermal-average forces) is lost. Therefore, for any class of initial conditions, the slow rate of OP dynamics must be confirmed before applying the multiscale ideas developed in Sec. 3. In this study we demonstrate the applicability of the ε-scaling for typical conditions underlying macromolecular behavior (Sec. 4).

A simple case of the ${\binom{⇀}{r}}_{i}, {\binom{⇀}{Φ}}_{k}$ relationship suggests how it captures rigid rotation. Take U_k ,k=100,010,001 to be x⁰, y⁰, and z⁰, respectively. Then neglecting the residuals, Eq. 2.2 becomes $x_{i} = Φ_{100 x} x_{i}^{0} + Φ_{010 x} y_{i}^{0} + Φ_{001 x} z_{i}^{0}$ , and similar for y_i and z_i (where x_i ,_yi ,_zi are the three Cartesian components of ${\binom{⇀}{r}}_{i}$ vector). The relationship can be written in the tensorial form ${\binom{⇀}{r}}_{i} = \begin{matrix} ⇀ \\ ⇀ \\ Φ \end{matrix} {\binom{⇀ 0}{r}}_{i}$ . It is seen that for a special case (i.e., where the tensor $\begin{matrix} ⇀ \\ ⇀ \\ Φ \end{matrix}$ is a rotation matrix), ${\binom{⇀}{Φ}}_{k}$ constitute a length preserving rotation about the CM if ${\binom{⇀}{r}}_{i}$ is relative to the CM. More generally, for the above three basis functions, the ${\binom{⇀}{r}}_{i} - {\binom{⇀}{Φ}}_{k}$ relationship corresponds to a mixed rotation, extension∕compression. In fact the OPs defined here constitute a strain tensor thereby accounting for elastic deformations. In addition, our multiscale formulation (Sec. 3) is all-atom and hence captures internal friction effects via the force field. Therefore, the theory accounts for both elastic and viscous effects. As discussed in the original paper, where the present OPs (denoted “global co-ordinates” there) were introduced,⁶ the higher order OPs specifically second and third order capture twisting, bending, and more complex deformations. Such OPs were shown to capture polyalanine folding from a linear to a globular state. In another work, the OPs were shown to capture nucleation and front propagation in a virus capsid.⁸ While it is not trivial to interpret all the deformations associated with the higher order polynomial-defined OPs, it is the generality of our multiscale approach (Sec. 3) that accounts for all their dynamics. Ultimately the interpretation of the OPs is embodied in the description of the phenomenon itself, e.g., macromolecular structural transition. A commonplace example is hydrodynamics wherein one does not always interpret the meaning of each Fourier density mode, but rather speaks in terms of phenomena such as propagating waves or viscous boundary layers. Additional properties of the OPs are discussed in Appendix A.

The set Φ of OPs have technical advantages that greatly facilitate theoretical analyses. Consider an extended set Φ_ex of OP and OP-like variables, notably the ${\binom{⇀}{Φ}}_{k}$ for k in the list of OPs plus similarly defined variables ${\binom{⇀}{Φ}}_{k res}$ for k not in the OP list. Thus we write

{\binom{⇀}{r}}_{i} = \sum_{k} OP {\binom{⇀}{Φ}}_{k} U_{k} ({\binom{⇀}{r}}_{i}^{0}) + \sum_{k} res {\binom{⇀}{Φ}}_{kres} U_{k} ({\binom{⇀}{r}}_{i}^{0}) .

(2.7)

This relation maps the 3N configuration variables r onto Φ_ex , also a 3N-dimensional space. Expression (2.7) for ${\binom{⇀}{r}}_{i}$ in terms of Φ and Φ_res provides a way to generate ensembles of ${\binom{⇀}{Φ}}_{k}$ -constrained configurations by randomly varying the ${\binom{⇀}{Φ}}_{k res} .$ An expression for ${\binom{⇀}{σ}}_{i}$ in terms of Φ_res is obtained by comparing Eqs. 2.2, 2.7. However, generating ensembles by randomly varying the ${\binom{⇀}{σ}}_{i}$ typically leads to very high-energy configurations. This difficulty is readily avoided as long as ${\binom{⇀}{σ}}_{i}$ is chosen by constraining ${\binom{⇀}{Φ}}_{k res}$ for higher order k to small values.⁴ The lower $k - {\binom{⇀}{Φ}}_{k res}$ do provide major structural variations by moving atoms in the ensemble with a measure of coherence, avoiding near-atom overlap. Thus ${\binom{⇀}{Φ}}_{k res}$ provides a way to generate rich ensembles at fixed Φ and with modest energies (and hence Boltzmann relevance). In practice, a “hybrid” sampling method, wherein short MD runs are performed starting with configurations from the ${\binom{⇀}{Φ}}_{k res}$ -generated sample is used to enrich fluctuations about the constant set of OPs Φ.⁴ All these properties are critical for the practical implementation of a multiscale molecular dynamics∕order parameter extrapolation (MD∕OPX) approach⁷ and more recently a fully self-consistent multiscale approach and software SIMNANOWORLD^™.⁴ Implementation of the former is based on the philosophy of equation-free multiscale approach.³⁰ In this, the absence of macroscopic equations of motion is overcome by extrapolating OPs over large time intervals using short bursts of MD simulation. In contrast, SIMNANOWORLD computations are guided by the Langevin equation for OPs (III.9). Its development is closer to the theme of the heterogeneous multiscale modeling,³¹ in the sense, maximum knowledge (or ignorance) on the various scales in the system is utilized in deriving the quasi-equilibium probability density.

Note, even though the OPs are defined in terms of atoms in the macromolecule, multiscale analysis developed in Sec. 3 accounts for both the macromolecule and the medium, allowing simulation of the entire system. Since the OPs evolve on a long timescale, their dynamics filters out the high frequency atomistic fluctuations (residuals). Thus the slowly evolving OPs can be projected over large intervals in time. These timesteps are appreciably larger than simple MD timesteps and, therefore, efficiently probe the long time behavior of a macromolecule. As the above OPs are generated in an automated fashion, the set may be expanded by increasing the range of the k sum. As discussed in Sec. 3, this addresses the difficulty that arises when a limited set of OPs couples to other slow variables.

MULTISCALE THEORY AND COMPUTATION

In this section, we use the OPs considered above and the Liouville equation to derive equations for the stochastic dynamics of a macromolecule. The analysis starts by writing the Liouville equation for the N-atom probability density Υ, i.e., ∂Υ∕∂Υ∂t=LΥ∂t=LΥ for Liouville operator L. Υ depends on the set of 6N positions and momenta Γ and time t.

Multiscale analysis starts with a transformation of the N-atom probability density from the Υ(Γ,t) formulation to one that makes the multiple ways on which Υ depends on Γ, t more explicit. This involves introduction of a set of OPs Φ(Γ) (i.e., ${\binom{⇀}{Φ}}_{k}$ of Sec. 2 for all k on the list of OPs) that depends on Γ and which are shown to evolve on a time scale much greater than that of individual atomic collisions∕vibrations.

First we write Υ in a form that makes the dependence on Γ and t of various types explicit:

Υ (Γ, t) = ρ \{Γ_{0} (Γ), Φ (Υ), t_{0} (t), t (t); ε\} .

(3.1)

Thus we make an ansatz that reformulated probability density ρ depends on the N-atom state Γ both directly (i.e., via Γ₀ (Γ)=Γ) and, via a set of OPs Φ(Γ), indirectly. Similarly,ρ depends on the sequence of times $t_{0} (t), t_{1} (t), t_{2} (t), ... = t_{0} (t), \underset{̲}{t} (t),$ where t_n (t)=εⁿt. The times t_n for n > 0 are introduced to account for the slower behaviors in ρ; while t₀ accounts for processes on the fast timescale (i.e., t₀ changes by one unit when 10⁻¹⁴ s elapse). ε is a small parameter as defined in Sec. 2. The ε dependence of ρ and scaling of time are justified later in this section.

In adopting this perspective, Φ is not a set of additional independent dynamical variables; rather, its appearance in ρ is a place holder for a special dependence of ρ on Γ that underlies the slow temporal dynamics of ρ. A simple example that elucidates our ansatz is the function f(x)=exp^−εx sin(x). We restate f(x) as f(x₀ ,x₁ ) where x₀ =x and x₁ =εx. In making this transformation, we do not add any independent variable to the description, rather we make the discrete dependencies on x explicit. It is shown below that the dual dependence of ρ on Γ can be constructed if ε is sufficiently small. An equation of stochastic OP dynamics that preserves the feedback between the atomistic and nanoscale variables⁴ is now obtained via a multiscale perturbation analysis for a classical N-atom system.

In the following, we use the above framework to derive an equation for the OP probability distribution. One finds that LΦ naturally reveals a small parameter ε, i.e., $d {\binom{⇀}{Φ}}_{k} ∕ d t = ε ({\binom{⇀}{Π}}_{k} ∕ μ_{k})$ (Sec. 2). Starting with Eq. 3.1, the Liouville equation for Υ and the chain rule, one obtains the multiscale Liouville equation (Appendix B),

\sum_{n = 0}^{\infty} ε^{n} \frac{\partial ρ}{\partial t_{n}} = (L_{0} + ε L_{1}) ρ .

(3.2)

Many authors (see Refs. ⁹^,³²^,³³ for reviews) have analyzed such equations in the small ε limit. Equation (III.2) is solved perturbatively via a Taylor expansion in ε. As shown in Appendix B and,²⁵L₀ involves partial derivatives with respect to Γ₀ at constant Φ [when operating on ρ in the multiscale form (3.1)], and conversely for L₁ . With this L₀and_{L 1} take the forms

L_{0} = - \sum_{i = 1}^{N} \frac{{\binom{⇀}{p}}_{i}}{m_{i}} \cdot \frac{\partial}{\partial {\binom{⇀}{r}}_{i}} + {\binom{⇀}{F}}_{i} \cdot \frac{\partial}{\partial {\binom{⇀}{p}}_{i}}

(3.3)

L_{1} = - \sum_{k} \frac{Π}{μ_{k}} \cdot \frac{\partial}{\partial Φ} .

(3.4)

Note that L₀ and L₁ operate in the space of functions that depend explicitly on variables Γ₀ and Φ; Π signifies a set of ${\binom{⇀}{Π}}_{k}$ and subscripts 0 on ${\binom{⇀}{r}}_{i}$ and ${\binom{⇀}{p}}_{i}$ in Eq. 3.3 are henceforth dropped because of the simple Γ₀ (Γ)=Γ dependence of ρ. While the space of functions on which L₀ and _{L 1} operates is composed of 6N+_{N OP} variables (the 6N atomic positions and momenta Γ₀ plus the N_OP OPs Φ), the formalism does not assume that the variables are dynamically independent. Rather, from Eq. 3.2, one determines the dependence of ρ on Γ₀ and Φ, but ultimately through Eq. 3.1 how Υ depends on Γ. Hence Eqs. 3.2, 3.3, 3.4 do not imply that Γ₀ and Φ are independent dynamical variables but, in accordance with Eq. 3.1 the equations track the multiple space and time dependencies of Υ. Therefore, there are still 6N dynamical variables as the OPs do not evolve independently of the 6N atomic positions and momenta. Equations (2.4) and (2.6) show the explicit dependencies of atomic and coarse-grained quantities. In contrast, one could introduce collective modes as new dynamical variables in addition to the 6N atomic positions and momenta Γ. However, this approach carries the burden of eliminating selective position and momentum variables to keep the number (6N) of degrees of freedom fixed. In summary, to uncloak the explicit space-time dependencies of the N-particle density Υ, we make use of 6N+N_OP variables of which N_OP are not independent of the remainder [with dependencies defined via Eqs. 2.4, 2.6]. As no additional independent variables are added to the description of the N-atom system, Υ still remains a function of the 6N dynamical variables. Furthermore, the O(ε) scaling of the Liouville equation is a natural consequence of the slowness of OPs. This justifies a perturbative solution and hence the ε dependence of the N-atom probability density. With this, the N-atom probability density is constructed as $ρ = \sum_{n = 0}^{\infty} ε^{n} ρ_{n}$ . Putting the perturbation expansion for ρ into Eq. 3.2 and analyzing different orders in ε (discussed in details in Appendices SI, SII, and SIII (Ref. ³⁵), the Smoluchowski equation for the coarse-grained probability distribution $\tilde{W}$ is obtained,

\frac{\partial \tilde{W}}{\partial τ} = \sum_{k k^{'}} \frac{\partial}{\partial {\binom{⇀}{Φ}}_{k}} [{\begin{matrix} ⇀ \\ ⇀ \\ D \end{matrix}}_{k k^{'}} [\frac{\partial}{\partial {\binom{⇀}{Φ}}_{k^{'}}} - β {\binom{⇀}{f}}_{k^{'}}] \tilde{W}] .

(3.5)

The diffusivity factors ${\begin{matrix} ⇀ \\ ⇀ \\ D \end{matrix}}_{k k}$ are related to the correlation function of time derivatives of OPs via

\begin{matrix} ⇀ \\ ⇀ \\ D \end{matrix} = \frac{1}{μ_{k} μ_{k^{'}}} \int_{- \infty}^{0} d t_{0}^{'} 〈{\binom{⇀}{Π}}_{k} e^{- L_{0} t_{0^{'}}} {\binom{⇀}{Π}}_{k^{'}}〉,

(3.6)

where ${\binom{⇀}{Π}}_{k}$ is defined in terms of the OP time derivatives via Eqs. 2.5, 2.6. In constructing the correlation functions the initial data is at fixed Φ; since Φ does not change appreciably during the period in which the correlation function is appreciable, ${\begin{matrix} ⇀ \\ ⇀ \\ D \end{matrix}}_{k k^{'}}$ depends on Φ.

The thermal-average force ${\vec{f}}_{k}$ is given by

{\binom{⇀}{f}}_{k} = - \frac{\partial F}{\partial {\binom{⇀}{Φ}}_{k}} = 〈{\binom{⇀}{f}}_{k}^{m *}〉,

(3.7)

for Φ constrained Helmholtz free-energy F, where

F = - \frac{1}{β} \ln Q (Φ, β),

(3.8)

Q(Φ, β) is the partition function associated with $\hat{ρ}$ [Appendices SI, SII, and SIII (Ref. ³⁵)], and ${\binom{⇀}{f}}_{k}^{m *} = \sum_{i = 1}^{N} U_{k} ({\binom{⇀}{r}}_{i}^{0}) {\binom{⇀}{F}}_{i}^{*}$ is the “OP force.” Details of Eq. 3.7 derivation are provided in Appendix C.

Equivalent to Eq. 3.5 is an ensemble of OP time courses generated by the Langevin equations

\frac{\partial {\binom{⇀}{Φ}}_{k}}{\partial τ} = β \sum_{k^{'}} [{\begin{matrix} ⇀ \\ ⇀ \\ D \end{matrix}}_{k k^{'}} {\binom{⇀}{f}}_{k^{'}}] + {\binom{⇀}{ξ}}_{k} .

(3.9)

The coherent part of the evolution is determined by the product of the diffusion factors and the thermal-average forces; the stochastic evolution is determined by the random force ${\binom{⇀}{ξ}}_{k}$ . The latter is constrained by requiring the integral of its autocorrelation function to be proportional to the diffusion coefficient.

The expression for diffusion factors provided above involves an integration of the correlation function over all time. However, if the correlation function decays on a long time scale (i.e., on that comparable to OP evolution), the above Smoluchowski equation would be replaced by one that is nonlocal in time. This would suggest that the set of OPs couples to other slow variables. Since the OPs are generated automatically (as described in Sec. 2), new slow variables can be added in a straightforward way to make the existing set Φ complete, e.g., eliminate the long-time tail. Completing the set of OPs modifies the operator L₀ [and hence the velocity correlation of Eq. 3.6] as the latter involves derivatives with respect to Γ₀ at constant Φ. This modifies the diffusion factor, affecting dynamics of the OPs on the free-energy surface they define. Such an operator is automatically accounted for via standard MD codes when the correlation time of OP velocities is short relative to the timescale of OP evolution. Thus the long-time behavior of correlation functions provides a completeness criterion for the set of OPs and, thereby, a self-consistency check for the theory and computations.

Another self-consistency check is related to refreshing of the reference structure r⁰ . Our simulations begin with the energy-minimized and thermally equilibrated x-ray crystallographic or other all-atom structure as the reference structure. As the system evolves in time, the resulting deformation may increase some of the residuals. This may reflect the need for a new reference structure. The reference structure transition point is chosen when the maximum residual for a structure in the constant OP ensemble becomes comparable with its root mean square deviation (RMSD) from the initial reference structure ${[| {\binom{⇀}{r}}_{1} - {\binom{⇀}{r}}_{1} 0 |^{2} + \dots {| {\binom{⇀}{r}}_{N} - {\binom{⇀}{r}}_{N} 0 |}^{2} ∕ N]}^{1 ∕ 2}$ , i.e., when some local change in a structure reaches the order of an overall deformation [Fig. S1 in Ref. 35]. The increase in residual may indicate the presence of coherent motions that are not accounted for by the set of OPs initially chosen. If the emerging modes couple to the previously defined set of OPs, long-time OP velocity autocorrelation tails are also expected. The remedy for this difficulty is to increase the number of OPs considered, a process greatly facilitated by the automated generation of OPs (Sec. 2). Increase in the residuals may indicate the presence of an improbable fluctuation in the MD generated part of the finite ensemble used for a practical computation. This increase is generally minimized via the low $k - {\binom{⇀}{Φ}}_{k res}$ sampling and, for the thermal-average forces, via the Boltzmann factor (structures with larger values of ${\binom{⇀}{Φ}}_{k res}$ for higher order k tend to be high in energy as suggested in Fig. S2 in Ref. 35). However, for these cases, a simple reference structure renewal would suffice to account for the resulting motions, and additional OPs are not required.

As stressed above, new OPs should be added in order to redefine the constant OP ensemble (i.e., to eliminate the long-time tails of the correlation functions) and to account for the systematic growth of residuals that is not accounted for via re-referencing. In principle, a simple addition of higher order OPs to the set of existing ones, till the complete elimination of the long-time correlation tail would suffice. However, this might include some unnecessarily high frequency modes as OPs. As a result, the Langevin timestep must be reduced, affecting the efficiency of multiscale simulation. Efficiency can be restored by optimal choice of the OPs to be added. For example, one could carry out a ns conventional MD run and use the resulting configuration time courses to rank the omitted OPs according to their average rate of change. Variables that qualify as OPs are slow and coherent, whereas residuals (that are described by ${\binom{⇀}{Φ}}_{k res}$ ) are highly fluctuating with mean close to zero (Sec. 4). The former are added, one at a time, to the list of existing OPs and new ensembles are generated by sampling the remaining variables. This is repeated till the residuals become reasonably small and the long-time tail in the autocorrelation function is eliminated. This procedure allows for addition of only slow variables and hence consideration of high frequency modes as OPs is avoided. Such a procedure is also used in selecting OPs to start the SIMNANOWORLD simulations.

Multiscale analysis provides a numerical simulation approach implied by the feedback between nano and atomic scale variables.⁴ As ${\binom{⇀}{f}}_{k}$ and ${\begin{matrix} ⇀ \\ ⇀ \\ D \end{matrix}}_{k k^{'}}$ are OP-dependent, they must be computed at each Langevin timestep to account for the interscale feedback. A finite Langevin timestep Δt advancement takes the OPs from time t to a time t + Δt via Eq. 3.9. Thermal forces ${\binom{⇀}{f}}_{k}$ are efficiently computed via an ensemble∕Monte Carlo integration method enabled by the nature of our OPs.⁴ Atomic forces obtained from the residual generated OP constrained ensemble (Sec. 2) are used to calculate the OP force ${\binom{⇀}{f}}_{k}^{m}$ . Monte Carlo integration averaging of ${\binom{⇀}{f}}_{k}^{m}$ over the ensemble is carried out to obtain the thermal ( $\hat{ρ}$ ) average force ${\binom{⇀}{f}}_{k}$ . Hence the free-energy driving force is obtained via the all-atom probability density $\hat{ρ} (Γ_{0}, Φ)$ , capturing the cross talk between the OPs and individual atomic degrees of freedom. Since $\hat{ρ} (Γ_{0}, Φ)$ reflects the OP constrained ensemble, the 6N atomic degrees are consistent with the state of the OPs. Note, the definition of ${\binom{⇀}{f}}_{k}$ as OP derivative of free-energy Eq. 3.7, and ${\begin{matrix} ⇀ \\ ⇀ \\ D \end{matrix}}_{k k^{'}}$ as time integral of OP velocity autocorrelation function Eq. 3.6 is independent of the linearity in the r − Φ relationship. This implies that the multiscale analysis developed can be applied to any complete set of slow variables provided the O(ε) time scaling, and Newton’s laws of motion hold for their dynamics. As mentioned in Appendix A, Secs. 2, 4, the present OPs form a set of slow variables that has suitable properties to serve as a basis of our approach. Other sets of slow variables can also be used as long as all criteria of OPs dynamics are satisfied.

Adiabatic schemes have been successfully implemented to perform approximate quantum dynamics simulations³⁶^,³⁷ and Car-Parrinello type ab initio quantum dynamics.³⁸ The latter belongs to a family of extended Lagrangian approaches wherein the time scales of faster and slower degrees of freedom are adjusted to ensure the adiabatic propagation of the former in response to motions in the latter. This adjustment is achieved via attributing fictitious masses and kinetic energy to the faster modes.³⁸^,³⁹ For many atom systems, a free-energy profiling scheme, adiabatic free-energy dynamics (AFED) based on an adiabatic partitioning of the slow and fast variables have been developed.⁴⁰ The AFED allows for application of higher temperature for the slow variables facilitating rare events sampling and high mass leading to an adiabatic decoupling.⁴⁰ Therefore, the separation of timescale between those of OPs versus atomic dynamics Eq. 2.6, the relatively high OP masses ${\tilde{μ}}_{k}$ ,⁴¹ and the role of average forces [Eqs. 11, 12, and 13 in Ref. 38, Eq. 3.7 in the present paper and elsewhere¹²^,⁴²) for driving the slow variables across the free-energy landscape suggests implementation of an adiabatic dynamics algorithm for thermal-average force calculations. Unlike explicit variable transformation in AFED, extended phase space approaches like temperature accelerated molecular dynamics (TAMD)⁴³ are also used for simultaneous propagation of slow and fast degrees of freedom. Solving the resulting equations of motion in the extended phase space is equivalent to solving Eq. 3.9. This bypasses explicit averaging. Another related approach, driven adiabatic free-energy dynamics (d-AFED) employs explicit masses and dynamics closer to that of AFED in formulating TAMD.⁴⁴ This allows direct generation of multidimensional free-energy surfaces for complex systems from the probability distribution function of the extended phase-space variables. Even though an adiabatic decoupling appears naturally in our analysis by the O(ε) scaling of the Liouville operator, the relative efficiency of an adiabatic relaxation scheme versus the present residual-generated sampling scheme remains to be determined. In particular the present scheme requires the development of a rich ensemble of atomistic configurations at each Langevin timestep, while the adiabatic scheme requires coevolution of the slow and many [O(N)] fast variables. This issue is of critical importance for the efficiency of the simulation of systems involving 10⁵ or more atoms. However, in analogy to AFED, using higher temperature for propagating the slower variables (OPs here) would yield an algorithm for the simulation of rare-events phenomenon. This is further discussed in Sec. 5.

The diffusion factors are computed via the correlation functions of Eq. 3.6 using short MD runs. The latter is allowed because the correlation times in these functions are much shorter than the characteristic timescale of OP evolution (Sec. 4). All factors in the OP dynamics equation (III.9) are computed from the interatomic force field via Monte Carlo integration and MD. Thus the only element of the calibration in constructing the thermal-average forces and diffusions is through the existing force fields (e.g., CHARMM or AMBER). At each Langevin timestep, the updated OPs are used to generate the atomistic configurations of the macromolecule; then the host medium is introduced via a resolvation module⁴⁵ and the entire system is thermalized. An ensemble of such equilibrated atomistic configurations is used to generate the thermal-average forces and diffusions. The latter factors are used to update the OPs completing one cycle of the Langevin timesteping. A simple description of steps involved in the SIMNANOWORLD simulation workflow is included in the supplementary material as Appendix SIV in Ref. 35.

In the present approach the OPs are defined over the macromolecule. However, like for the atomic configurations of the macromolecule, water, and ion are accounted for via the quasiequilibrium ensemble (i.e., the configuration of the water and ions rapidly explores a quasiequilibrium ensemble at each stage of the OP dynamics). This assumption holds only when water∕ion equilibrate on a timescale much smaller than that of OPs. Similar resolvation scheme has been used with OPs in simulating virus capsid expansion in Na⁺ and Ca²⁺ solutions.⁴⁵ Therefore, fluctuations from water and ions modulate the residuals generated within the MD part of the constant OP sampling and hence affect the thermal-average force. This is the rationale behind not including the water and ions in the definition of the OPs. If slow hydrodynamic modes are found to be of interest, these atoms can be included in the definition of the OPs. Ions when tightly bound to the macromolecule are considered a part of OPs. After every Langevin timestep, an ion accessible surface is constructed and ions close to the surface are tracked during the MD ensemble enrichment calculation. Those with appreciable residence time within the surface are included in the definition of the OPs henceforth.

The notion of water and ion dynamics being much faster than a set of slow modes is similar to that used in normal mode Langevin (NML).⁴⁶ If these fast modes correspond to the coordinated motion of just a few atoms, then there is no clear separation in their time scale from that of single atom vibrations. Thus such fast modes cannot be described by Langevin dynamics unless memory kernels are used.¹² However, NML identifies the modes by diagonalizing a Hessian matrix and fully relaxes (overdamps) the high frequency modes near their energy minimum (respecting the subspace of low frequency normal modes). In the limit of large damping coefficient, this is equivalent to using Brownian dynamics to propagate high frequency modes. In contrast, for our approach rapidly fluctuating variables are allowed to explore a representative ensemble of configurations. For our purposes, using the overdamped value of the fast variables to construct an all-atom configuration and using that configuration to compute the OP force neglects the difference between the OP forces as a function of the average configuration versus the average of the OP force over an ensemble of atomic configurations. Hence, overdamping of fast modes is avoided. Furthermore, the NML approach would become computationally expensive for the N of O (10⁶) atom systems of interest here. In contrast, our approach avoids the need to diagonalize a large Hessian matrix, a feature that follows directly from the explicit formulation of our order parameters via Eqs. 2.2, 2.4. Finally our OPs are essentially normal modes in that they are linear combinations of atomic positions and furthermore are slowly varying. However, our equations of motion are highly nonlinear in the OPs and are dissipative. Thus, unlike for normal mode analysis, our formulation can account for states that are far from a free-energy minimizing structure.

For some choice of initial data, the O(ε) contribution to $\tilde{W} (Φ, t)$ can have short timescale dependence (e.g., due to a shock wave). Under this condition our basic assumption of the lowest order quasiequilibrium behavior is violated as the O(ε) scaling of the OP motion is disturbed (Sec. 2). Thus the theory breaks down. In such a case one expects Fokker–Planck behavior. The present formulation can be generalized to accommodate such inertial effects.³⁴ However, for the macromolecular phenomena considered here this class of initial data is ignored.

NUMERICAL SIMULATIONS

A study was undertaken to assess the viability of the OPs of Sec. 2 as a basis of a multiscale algorithm for simulating macromolecules. An evaluation of other variables in this context is also obtained. Comparisons with traditional MD were made to determine the accuracy and efficiency of the method. All multiscale simulations were done using the SIMNANOWORLD software⁴^,⁵ that is based on the OPs of Sec. 2 and the multiscale analysis of Sec. 3. The CHARMM22∕27 force-field and NAMD are incorporated in SIMNANOWORLD as part of the computation of the thermal-average forces and diffusion factors for our OPs.

The demonstration system was the RNA of Satellite Tobacco Mosaic Virus (STMV).⁴⁷ This molecule contains 949 nucleotides. The initial state of the system was that believed to be at equilibrium when the RNA resided with the associated proteins within the STMV capsid. Evolution followed after the capsid was removed instantaneously. The host medium was 0.3M NaCl solution and the temperature was 300 K. The system was placed within a cube and NVT conditions were applied. Details of the NAMD settings are given in Table 1. SIMNANOWORLD simulations were done in these conditions (and not those used in other studies⁴⁷) as more dramatic structural changes occur because the RNA is more stabilized by Mg²⁺ than by Na⁺.⁴⁸ This is because Na⁺ is expected to be diffusively bound to RNA⁴⁸ where as Mg²⁺ remains tightly bound. The structure used to initialize the simulation was generously provided by Prof. K. Schulten; the same structure was used in Ref. 47.

Table 1.

Input parameters for the NAMD and SIMNANOWORLD simulations.

Parameter	Values
Temperature	300 K
Langevin damping	5
Timestep	1 fs
Full-Elect Frequency	2 fs
Non-bonded Frequency	1 fs
Box size	145 Å × 145 Å × 145 Å^a or 162 Å × 162 Å × 162 Å^b
Force-field parameter	par_all27_prot_na.prm
1—4 scaling	1.0
Switch dist	10.0 Å
Cutoff	12.0 Å
Pair list dist	20.0 Å
Steps per cycle	2
Rigid bond	Water

Open in a new tab

Box for free RNA simulation for 3 ns.

Box for free RNA simulation from 3–50 ns and protein-bound RNA.

As mentioned in Sec. 2, in the following we examine the slowness in rate of change of a typical OP (001Z) to ensure its applicability within our multiscale framework. The one considered in particular exhibits properties of dilation∕extension about the Z-axis. The time evolution of this OP is compared to other variables only to validate that some of the latter are not suitable as slow variables for the purpose of our multiscale analysis. If the fluctuations in these variables probe short space-time events then they are expected to be accounted for by the quasiequilibrium ensemble, otherwise larger space-time events are accounted for by one or more of our OPs. Appropriateness of these other variables for specific problems have been discussed in the literature cited below and is only included here to distinguish them from our OPs.

Consider some other variables commonly used to characterize macromolecules, denoted “structural parameters”(SPs) here and compare their dynamics with that of the OPs of Sec. 2. The SPs analyzed in this paper are different types of dihedrals and their cosines,⁴⁹^,⁵⁰ radius of gyration, end-to-end distances,⁵⁰ and typical components of the unit vectors along the bonds connecting monomers.⁵¹ We designate these SPs: SP₁, SP₂, SP_3, and SP_4, respectively. Each of them was calculated over a 1 ns MD trajectory for the RNA under conditions mentioned above. Their time evolutions are plotted in Fig. S3 in Ref. 35. We calculated the moving averages over a window of 50 ps to filter out the coherent part of the variations from the fluctuations (λ). Details on λ computation are provided in Appendix D. The coherent and fluctuating parts of SP variations are plotted in Fig. S4 in Ref. 35. The dihedrals γ, δ, and ε defined according to Fig. 1a in Ref. 17 were chosen for this comparison. The time evolution of these depends on their location in the back bone. δ fluctuates the least due to geometric constraints imposed by a five membered ring.¹⁷ In contrast, those not associated with the backbone fluctuate even more than γ or ε. Fluctuations of variables characterizing the overall size of the macromolecule, like SP₂ or SP₃, are much smaller. For SP_4, fluctuations are maximum and are also sensitive to bond location.

Figure 1.

Download video file^{(79.6MB, mpg)}

Open in a new tab

(a) Ten OP velocity autocorrelation function time-courses for 001Z starting from same initial conditions but different initial velocity random seeds. (b) A Boltzmann average OP velocity autocorrelation function time-course showing the absence of a long-time tail, and hence the lack of coupling to other slow variables not included in the set of OPs. Decay trend similar to a single MD derived autocorrelation function of Fig. S8 (enhanced online) .

We compared the time evolution of these SPs to that of the OPs from Sec. 2. In Fig. S5 in Ref. 35 the coherent and fluctuating parts are shown for the same 50 ps window. Fluctuations in SP₁ and SP₄ are several orders of magnitude higher in amplitude than those for OPs, and∕or their characteristic time scale is much shorter. Hence they do not evolve slowly and cannot serve as a basis of our multiscale analysis. Finally SP₂ and SP₃ are suitable as OPs but do not readily enable the generation of SP ensembles as they are a subset of a more general set of OPs.⁶ This presents difficulties in computing thermal-average forces and diffusion factors needed for a multiscale analysis. In contrast, our OPs are automatically generated and, therefore, the set Φ can be augmented for systems of higher complexity. Furthermore, the end-to-end distance and radius of gyration are accounted for via our more general OPs (shown below). Another OP like variable often found in literature²⁷ is the number of macromolecular hydrogen bonds. Later in this section we show that our OPs also account for these slow variables.

As system size increases the OPs become better filters of the high frequency fluctuations. To validate this, we simulated hepta-alanine with 8000 water molecules in a cubic box of side 44 Å under settings mentioned in Table 1. Fluctuations in OPs for larger systems are found to be much smaller than those of smaller ones [i.e., the same OP shows amplified fluctuations as the system is changed from RNA to hepta-alanine (Fig. S6 in Ref. 35)]. Figure S7 in Ref. 35 compares the moving averages in lower and higher order OPs for RNA and hepta-alanine. Distinct differences in length scales allow better separation of the lower order OPs from those of the higher ones in the RNA. This facilitates filtering of the low and high frequency modes. For smaller systems like hepta-alanine, the length scale separation diminishes. Thus OPs cannot facilitate filtering of high frequency fluctuations, and consequently the implementation of multiscale analysis becomes inefficient.

The choice of OPs depends on the characteristics of the system of interest. This can be understood a priori via analyzing OP evolution for short MD trajectories and observing the decay in the OP velocity autocorrelation functions. It is found most efficient for the present problem to only use four OPs (i.e., the center of mass and three corresponding to overall extension–dilatation). To verify completeness of this set of OPs for the present problem, we plot the OP velocity autocorrelation functions for a window of 1 ps in Fig. S8 in Ref. 35. The correlation decays sharply on a time scale much shorter than that of OP evolution (i.e., the OPs were constant over the time of autocorrelation decay). The decay zone is followed by a fluctuating phase that reflects insufficient statistics for constructing long-time correlation function behavior. To illustrate this, we plot several autocorrelation functions for 1 ps trajectories with identical starting structure, initial conditions but different random seeds for generating initial velocities [Fig. 1a]. In principle, an average of such single MD simulation derived correlation functions is required to compute the diffusion factors. However, using only the early part of a single MD correlation function (wherein the most statics are accumulated) was found to suffice [Fig. 1b]. Furthermore, the correlation analysis validates the completeness of the set of OPs as there is no long-time tail behavior in the correlation functions.

Omission of a slow variable that couples with the existing set can lead to a long-time correlation tail. To validate this, we redid the correlation calculation without the 100X OP. This leads to a long-time tail in the velocity autocorrelation function for the 001Z and 010Y OPs (Fig. S9 in Ref. 35). In general terms, the deformational behavior in a given Cartesian direction is driven by forces that depend on the OPs in all directions. Therefore, a missing OP will create an ensemble of atomic configurations that reflect its absence, which in turn is expressed in slower behavior of the retained OP velocities, and hence the associated autocorrelation functions. Simultaneously, the ensemble had a major population of structures with very high residuals (∼10 Å) also signaling omission of a slow mode. Therefore, the diffusion calculation indicates the absence of a key slow variable that can be optimally added to the existing set via the procedure of Sec. 3. Due to orthogonality of our basis functions, the cross-correlation functions between different OPs are several orders of magnitude smaller than the autocorrelation functions; this implies that the OPs are not coupled through the diffusion factors but only through the OP dependence of the thermal-average forces. This greatly simplifies the construction of the random forces as they are related to the diffusion matrix.

Constructing higher order OPs from an MD run via Eq. 2.4 shows that they are highly fluctuating and, therefore, not appropriate as OPs in the sense used here (Fig. S10 in Ref. 35). Rather they are accounted for via the quasiequilibrium probability density (i.e., in the ensemble used to calculate averages). As presented earlier,⁴ the ensemble of atomistic configurations is generated via Eq. 2.2. The residuals ( ${\binom{⇀}{σ}}_{i}$ ) are generated by a formula similar in structure to that used to obtain the atomic positions but the sum over basis functions does not include those associated with the OPs (Sec. 2).⁴

Addition of OPs to a pre-existing set is needed in various cases. If the system is changed, for e.g., if it is composed of multiple macromolecules then more OPs are required to form a complete set. The added OPs probe complex intermacromolecular motions. New OPs could also be added in a dynamic fashion in the course of a simulation to account for types of motions absent initially. As mentioned above, the appearance of long-time tails in the correlation functions later in a simulation is a key indicator of the need to augment the set of OPs.

To assess the accuracy of the multiscale OP dynamics comparisons were carried out with conventional MD simulations for trajectories of 10 ns. On removal of the viral capsid, the RNA is no longer constrained and tends to expand. Following initial expansion the RNA shrinks, and finally fluctuates among a range of distinct atomistic states of similar energy. Figure 2a shows the radius of gyration obtained with MD and SIMNANOWORLD, while Fig. 2b shows the progress of the RMSD from the initial structure as a function of time; agreement of the radius, and the RMSD between MD and the multiscale simulation is excellent. Figure S11 in Ref. 35 shows the overall and pentameric structural alignment⁵² of the MD and the SIMNANOWORLD generated RNA structures at the end of 10 ns. We further plot OP time courses from the final 5 ns of conventional MD and SIMNANOWORLD [Fig. 2c]. These results show that both the structures in Fig. S11 in Ref. 35 are essentially a part of similar OP ensembles having similar overall characteristics and confirm that multiscale simulation is generating configurations consistent with the same value of the OPs that arise in MD. However, it is inappropriate to compare our predictions with that of a single MD since the former corresponds to an ensemble of MD simulations (see below). Significantly, the multiscale simulations capture the overall structural dynamics, which is often the main interest. However, the atomistic configurations are also accounted for via the quasiequilibrium distribution. This illustrates that radius of gyration and end-to-end distance (as mentioned above) is accounted for by our OPs (Fig. S12 in Ref. 35). Figure S13 in Ref. 35 shows the potential energy for the multiscale simulations. It fluctuates about a constant value. Energies show identical trend and are within a percent of those from the MD run. Figure 2d is the same as Fig. S13 in Ref. 35 but without the water–water and water–ion interactions. This shows that the RNA gains stability as the potential energy gradually decreases. Energies from the MD and SIMNANOWORLD generated trajectories show excellent agreement in trend as well as in magnitudes. The observed difference is within limits of those from multiple MD or SIMNANOWORLD runs starting from the same initial structure with different initial velocities. As another basis of comparison, time evolutions of the number of intramacromolecular hydrogen bonds for both methods are shown [Fig. 2e]. Hydrogen bonds are defined solely on the basis of geometric parameters (bond angle: 20^°; bond-length: 3.8 Å) between donors and acceptors. Initial expansion reduced the number of these bonds (primarily the ones involved in the RNA tertiary structure). The number of bonds decreased less rapidly in the later part of the trajectories when expansion ceased. A detailed account of the various types of hydrogen bonds will be given below.

Figure 2.

Download video file^{(28.2MB, mpg)}

Open in a new tab

Time evolution of the (a) radius of gyration via conventional MD (blue) and SIMNANOWORLD (red), (b) RMSD from the 0 ns structure to that after 10 ns for conventional MD (blue) and SIMNANOWORLD (red) simulations, (c) OPs 010Y (MD [blue]; SIMNANOWORLD[orange]), 100X (MD[mauve]; SIMNANOWORLD[red]) and 001Z (MD[deep-blue]; SIMNANOWORLD[green]) showing the OP-equivalence of SIMNANOWORLD and conventional MD, (d) RNA potential energy via MD (red) and SIMNANOWORLD (blue), (e) number of nucleic acid–nucleic acid hydrogen bonds via MD (blue) and SIMNANOWORLD (red) (enhanced online) .

An obvious advantage of multiscaling is the potential to use timesteps of tens or hundreds of ps or greater (in contrast to the 10⁻¹⁵ s of conventional MD or 0.2–1 ps for the Langevin PCA approach¹⁶^,¹⁷). For relatively slow processes in large systems, the speed-up over conventional MD is significant. To assess the efficiency of our approach, 128 processors were used. During the initial transient, 40 ps timesteps were used. To accommodate the initial expansion and account for the structural anisotropy (Fig. S14 in Ref. 35) the RNA was resolvated in a bigger box (Table 1) after the first 3 ns. Post initial transient, Langevin evolution was executed using 150 ps timesteps, reflecting the longer characteristic time for this phase. In this slower evolution regime (probed till 50 ns for the study) efficiency becomes 11 fold. However comparison with a single MD run is not appropriate since SIMNANOWORLD correspond to ensemble MD. In this study a single SIMNANOWORLD simulation corresponds to an ensemble of 168 traditional MD runs. While for each MD run the OP time course is essentially the same as that predicted by SIMNANOWORLD, the detailed atomistic configuration varies dramatically among members of the ensemble. This factor of 168 comes from the sample size used in the Monte Carlo integration to compute the thermal-average forces. Finally, a single MD run may not be representative of an ensemble of possible time courses, which, in contrast is automatically overcome in our approach. If the finer short timescale structural transition is of interest they can be pursued by either shorter timescale traditional MD runs or by including more OPs (although this will decrease the minimum characteristic time of OP dynamics (Fig. S10 in Ref. 35) and, therefore, reduce the efficiency of multiscale simulations). Unlike the Langevin PCA model¹⁶ where single or multiple ns MDs are used to generate input, here only short ps MDs are required to generate a constant OP ensemble and thereby equivalent trajectory ensemble. Selecting OPs for running the multiscale simulation requires an initial analysis of their time trends over 1 ps—1 ns timescale. However, this analysis need not be repeated in the course of simulations until the emergence of new OPs, thereby restoring efficiency of the multiscale simulation.

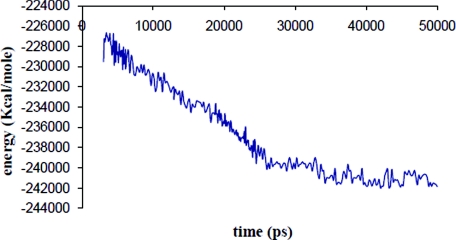
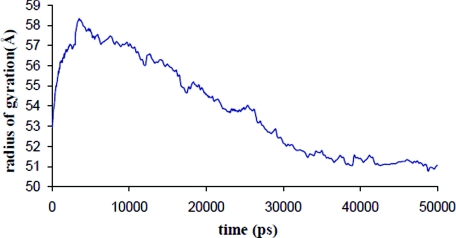
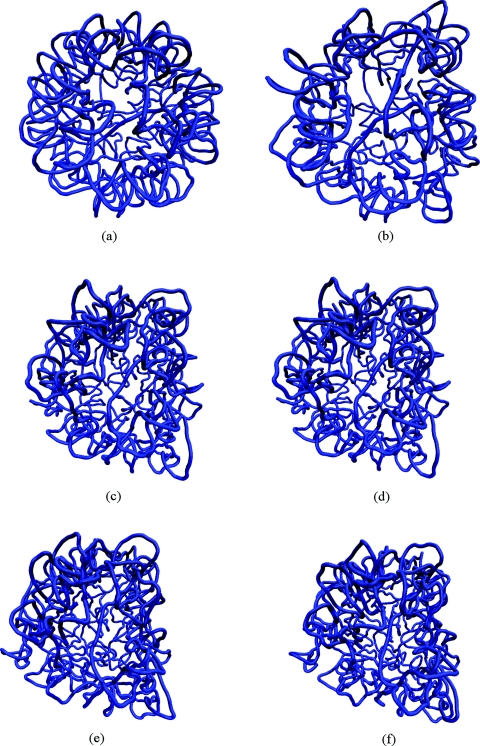
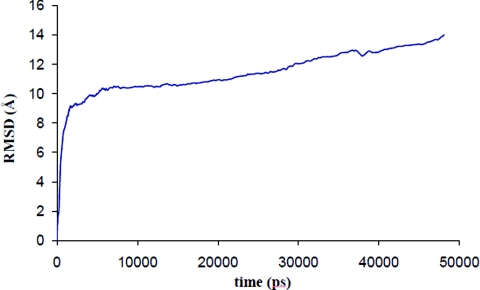
Making use of the above efficiency, we probed the long-time behavior of the RNA with SIMNANOWORLD. In Fig. 3 we plot potential energy versus time for the RNA. The energy decreases and fluctuates about a minimum. The radius of gyration is plotted for the 50 ns trajectory in Fig. 4. Following rapid initial expansion, RNA gradually shrinks for 30 ns before reaching a dynamic equilibrium wherein it fluctuates about 50 Å. These overall changes in shape and size are tracked by our OPs (Fig. S15 in Ref. 35). Their values also gradually decrease before flattening out. However, the magnitude of the three OPs is different, probing different extents of deformation along the three Cartesian axes. This is consistent with the fact that even though overall shape and size follow simple trends (reflected in Fig. 4), the anisotropy in the system leads to a symmetry breaking which is tracked by our OPs and the constant OP ensemble. Figure 5 validates that the initial symmetry is completely lost in the course of the simulation. In the final structure (after 50 ns) the tertiary structure of the RNA is highly disrupted, though secondary structure still remained. The latter is in agreement with experiments that suggest free RNA can possess some secondary structure.⁵² Figure 6 shows the RMSD over the entire 50 ns trajectory. RMSD shows a rapid increase followed by a gradual one. In Fig. S16 in Ref. 35 we plot RMSD versus energy for the final 20 ns of our trajectory. The increase in RMSD signifies that even though the energy, overall shape and size (OPs) change negligibly, there are local (noncoherent) changes that are accounted for by the constant OP ensemble (i.e., fluctuations in the higher order OPs). Thus SIMNANOWORLD captures the exploration of multiple isoenergetic configurations by the RNA.

Time evolution of the RNA potential energy via 50 ns SIMNANOWORLD simulation.

Time evolution of the RNA radius of gyration via 50 ns SIMNANOWORLD simulation.

RNA structure snapshots at (a) 0 ns, (b) 10 ns, (c) 20 ns, (d) 30 ns, (e) 40 ns, and (f) 50 ns.

As in Fig. 2b but for a total simulation time of 50 ns.

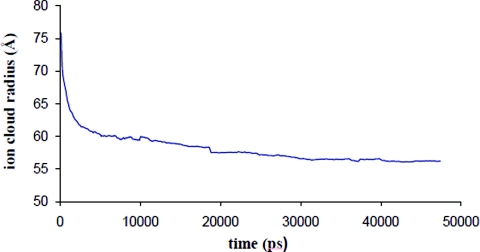
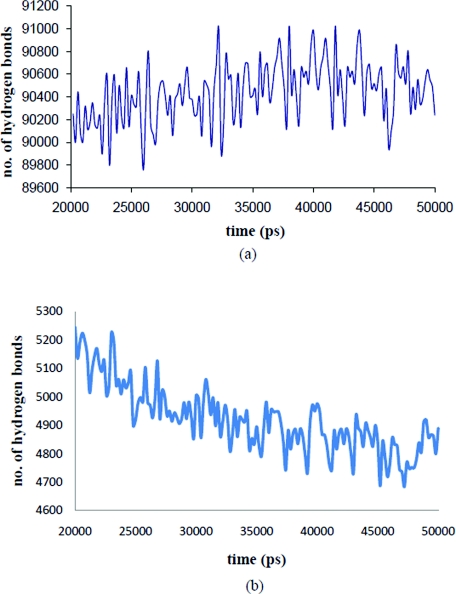
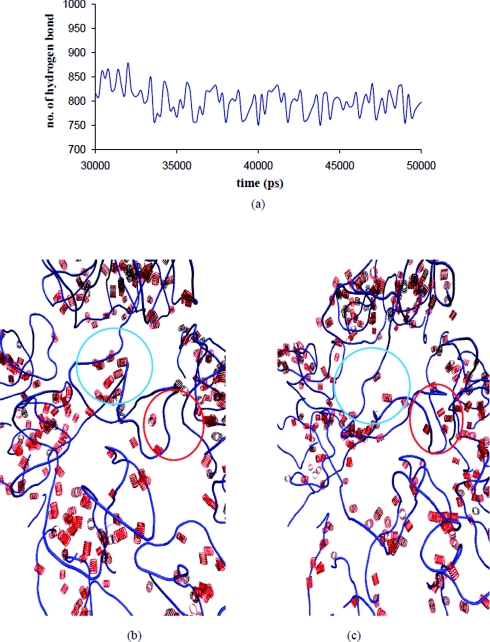
The gradual shrinkage of RNA is explained on the basis of ion shielding effects. Figure 7 shows the radius of the ion cloud decreases with time. Thus the ion cloud concentrates and distributes about the RNA (Fig. 7 and movie 1 in the supplementary material), shielding the electrostatic repulsion between similarly charged nucleic acid residues in the RNA, causing them to come closer. When the cloud is removed similarly charged groups mutually repel and the RNA expands instead of shrinking. To confirm the above physical picture, the structure at the end of 20 ns was deionized and a further 7.5 ns simulation was carried out in aqueous solvent. The expansion due to electrostatic repulsion is reflected in the radius of gyration and OP changes over this simulation (Fig. S17 in Ref. 35 and movie 2 in supplementary material). Note, since we use 1:1 electrolyte the ions are diffusively bound. Therefore, they exchange positions unlike for tightly bound ions such as Mg²⁺, justifying their inclusion as a part of the ensemble and not as an OP. Even though the ions are not included in an OP calculation, their rapid quasiequilibrium redistribution accompanying structural changes in the OP defined macromolecule at each Langevin timestep correctly accounts for the ion cloud around the RNA. Closely related to the distribution of ions is the distribution of water and hydrogen bonds. The total number of hydrogen bonds remains constant throughout the 50 ns simulation. However, the number of nucleic acid–water hydrogen bond decreases, while those for water–water hydrogen bonds increases, conserving the total number of bonds (Fig. 8). This phenomenon is consistent with mobile ion screening induced RNA shrinkage. As the RNA shrinks, water from the inner RNA cavity is expelled, thereby increasing the number of bulk water–water interactions. These shifts in sodium ion population, coordinated with hydrogen bond rearrangement, guide the system to the final structure. There is also a redistribution of internucleotide hydrogen bonds as the RNA samples isoenergetic configurations in the final 20 ns. However, the total number of nucleic acid–nucleic acid hydrogen bonds is conserved (Fig. 9).

Time evolution of mobile ion (Na⁺) cloud radius over 50 ns.

Time evolution of the water–water (a) and nucleic acid–water (b) hydrogen bonds for simulated RNA dynamics during the final 30 ns of the Fig. 5 simulation.

(a) Time evolution of the number of nucleic acid–nucleic acid hydrogen bonds for the final 20 ns of the Fig. 5 simulation. [(b), (c)] Shift in hydrogen bonds from blue encircled to the red encircled region.

While coherent structural dynamics are tracked by changes in the OPs, additional high frequency macromolecular motions are captured by the residual modified∕MD generated ensemble. These high frequency modes capture small-timescale local alterations, over and above the OP mediated deformations in the RNA, and consequent effects on atom scale features like the hydrogen bond distribution. However, other complex and∕or slow modes like bending or twisting can arise in the course of the RNA dynamics and affect the hydrogen bonds. As stressed above, emergence of new modes can be captured by our OPs and are signaled by our self-consistency checks. Within the simulated period of time (50 ns), we have not come across any long-time velocity autocorrelation tail or a significant population of high residual structures signifying absence of additional slow modes. A plausible explanation is that in viral RNAs it is possible that the bending modes leading to an unfolding transition appear much later in the time course (>50 ns) of structural evolution or secondary structure disruption occurs at a temperature much higher than 300K.⁵³^,⁵⁴ Another possibility is the sampling limitation of our implementation. RNA unfolding has often been modeled using higher temperature sampling techniques like replica exchange MD.⁵⁵^,⁵⁶ Such sampling techniques can take into account contributions from rare events and prevent entrapment of a structure in deep potential wells. Therefore, they efficiently probe unfolding conformations. Our approach has not yet been modified to take into account the above and, therefore, can suffer from problems of rare event sampling as does conventional MD. However most of the simulation results in this paper are independent of such events as they deal with reaching the energy minima rather than being entrapped in one. Starting from the last few ns of the reported simulation during which the system tends to equilibrate, application of rare event sampling techniques becomes useful in taking the system away from the obtained minima by sampling other free-energy basins. Comments on other efficient sampling techniques are included in Sec. 5.

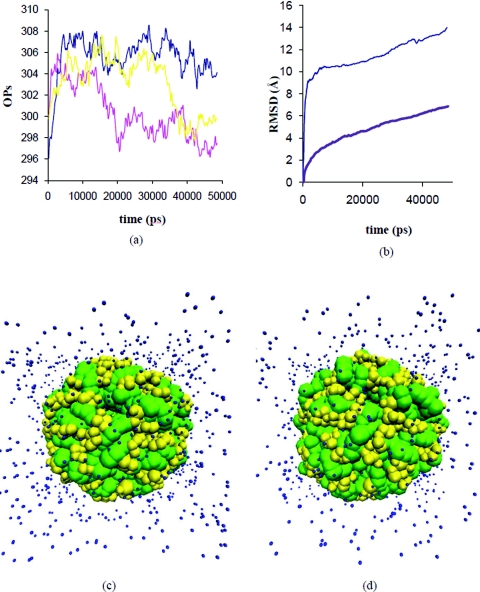
We did a control experiment to compare the deformation in the free RNA versus that in protein encapsulated RNA. We redid the simulation using identical physical conditions (temperature, salinity) and software settings for the RNA core of STMV. The RNA core is composed of capsid protein strands (residue 2–27) complexed with the RNA.⁵⁷ This complex is found to be stable with a radius distribution of ∼50 Å. The added protein segments complex with the RNA, reducing the degrees of freedom. The structure was energy minimized and thermally equilibrated before starting the multiscale simulation. Time evolution of the OPs, RMSD and structures for this simulation are shown in Fig. 10. Figure 10b also shows the RMSD for free RNA. RMSD of RNA in the bound state is much less than in the free state. Unlike the previous case where the difference in the OPs was large, here the difference is small and their change is slower; this suggests the preservation of the symmetry originally imposed by the capsid. Thus changes in the protein RNA complex are much less than those of free RNA. This longer characteristic time allows more efficient application of OP dynamics as now timesteps of the order of 250 ps are possible. This implies that SIMNANOWORLD is 16 times faster than a single conventional MD for the present problem.

Time evolution of the Ops (a) RMSD (b) and structure [(c),(d)] for the protein bound RNA in 0.3 M NaCl solution at 300K showing the restriction on RNA motion imposed by the proteins.

CONCLUSIONS

An efficient multiscale algorithm that probes the dynamics of macromolecules using OPs is demonstrated and validated. The OPs are shown to be slowly varying and hence are well suited as a basis of our multiscale algorithm. Completeness of a set of OPs is determined by the shortness of correlation times relative to the characteristic time of OP evolution. Automated construction of order parameters enables efficient augmentation of the set of OPs to address incompleteness. SIMNANOWORLD results show excellent agreement with those from a conventional MD run. SIMNANOWORLD efficiency increases for larger systems undergoing slow transformations, as these allow significant length and timescale separation for the OPs to filter out the high frequency fluctuations from the coherent dynamics. Thus OP mediated coarse graining of the free-energy landscape allows for a Langevin timestep of a few hundred ps (10⁵ times greater than conventional MD). SIMNANOWORLD predictions correspond to an ensemble of MD trajectories and hence are more statistically significant than results from a single MD run. Multiscale simulation via the OP description is found to capture significant structural details like ion screening, hydrogen bond rearrangement, and symmetry breaking transitions.

The approach presented has been successful for phenomenon that does not involve high barrier-crossing events. However, this does not imply that our approach is lacking in the basic physical framework; rather it implies that simulating very high barrier-crossing events is computationally challenging.⁵⁵ Note, as OPs coarse grain the free-energy landscape, some of the low energy barriers are naturally addressed. A number of authors have presented approaches for simulating rare barrier crossing events and corresponding applications to free-energy profiling. An incomplete list includes umbrella sampling,⁵⁸ thermodynamic integration,⁵⁹^,⁶⁰^,⁶¹ metadynamics,⁶²^,⁶³ and adiabatic molecular dynamics.⁴⁰ More recently, a multiscale conformation space exploration scheme is developed and applied to proteins.⁶⁴ These methods can be used to complement the present approach to address rare events and hence explicitly construct the free-energy landscape. In this direction, potential modifications of our approach are as follows: (i) In analogy to metadynamics, sequential free-energy basin discovery can be implemented via a memory dependent thermal force averaging that minimizes the forces which would have driven the systems to basins already discovered in an earlier step. With this, each sequential elimination simulation is guaranteed to find a new basin. (ii) In analogy with, Ref. 65 our procedure can be run at a set of high temperatures, for each of which the first passage time between two basins of interest is computed. This high temperature data can be fit to an Arrhenius-type law and the results are extrapolated down to the temperature of interest. This yields an approximation to the rate of crossing high free-energy barriers. Such modifications were not required in the current simulations as in these we aimed to probe the most likely pathways along the free-energy surface and not rare events.

Recently, schemes like reconstruction algorithm for coarse-grained structures⁶⁶ have been developed for constructing low-energy all-atom protein structures form configurations with only C_α atoms. In the present context, this could facilitate SIMNANOWORLD simulations starting from low resolution structures (e.g., electron cryomicroscopic models⁶⁷) via reconstructing all-atom input structures. A higher order Langevin solver shall be incorporated into the SIMNANOWORLD implementation. This will utilize data from multiple time intervals thereby increasing the accuracy of the coherent part of the Langevin dynamics and over-all CPU efficiency. In summary, we show that our OP-multiscale computational approach is ideally suited for studying structural dynamics in large macromolecules and macromolecular complexes.

ACKNOWLEDGMENTS

We appreciate efforts of the JCP editor and reviewers whose suggestions greatly improved the manuscript. We thank Professor Srini Iyengar for fruitful discussions on extended Lagrangian approaches. This project was supported in part by the National Science Foundation (Collaborative Research in Chemistry program), National Institutes of Health (NIBIB), Department of Energy (Office of Basic Science), METAcyt through the Center of Cell and Virus Theory, and Indiana University College of Arts and Sciences.

APPENDIX A: LINEAR RELATIONSHIP BETWEEN OPS AND POSITIONS

The relationship between ${\binom{⇀}{Φ}}_{k}$ and ${\binom{⇀}{r}}_{i}$ is taken here to be linear. This ensures that ${\binom{⇀}{r}}_{i}$ has a unique value for a given set of ${\binom{⇀}{Φ}}_{k}$ and residuals Eq. 2.2. Should this not be the case then, as Newton’s equations evolve r, the system could spontaneously transition to another state of order without a change of microstate. By similar arguments application of $\sum_{k^{'}} B_{k k'} {\binom{⇀}{Φ}}_{k^{'}} = \sum_{i = 1}^{N} m_{i} U_{k} ({\binom{⇀}{r}}_{i}^{0}) \binom{⇀}{g} ({\binom{⇀}{r}}_{i})$ , where $\binom{⇀}{g}$ is a function of ${\binom{⇀}{r}}_{i}$ , may not always be suitable. This would have been implied by replacing Eq. 2.2 with $\binom{⇀}{g} ({\binom{⇀}{r}}_{i}) = \sum_{k} {\binom{⇀}{Φ}}_{k} U_{k} ({\binom{⇀}{r}}_{i}^{0}) + {\binom{⇀}{σ}}_{i} .$ If $\binom{⇀}{g}$ is linear in ${\binom{⇀}{r}}_{i}$ , then the unique relation between ${\binom{⇀}{Φ}}_{k}$ , residuals and ${\binom{⇀}{r}}_{i}$ holds, allowing for the multiscale analysis of Sec. III. However, if $\binom{⇀}{g}$ is a nonlinear function of ${\binom{⇀}{r}}_{i}$ then this uniqueness could be lost; multiple solutions for ${\binom{⇀}{r}}_{i}$ could exist for a given set of ${\binom{⇀}{Φ}}_{k}$ and residuals. This could create situations wherein an initial r state evolves to multiple states allowed by the nonlinearity of $\binom{⇀}{g}$ . Newtonian mechanics prohibits this dynamical bifurcation of states (i.e., simultaneous evolution of one state into multiple ones); hence, in the present OP construction formalism, inclusion of a nonlinear function $\binom{⇀}{g}$ could lead to unphysical results if uniqueness of the r − Φ relationship is violated. Other transformations can be designed that allow for nonlinear combinations of r without violating this uniqueness. However, this was not pursued here. The suggested bifurcation of states should not be confused with the multiplicity of atomic configurations that arise due to ${\binom{⇀}{σ}}_{i}$ sampling (Sec. II). The present formulation does not imply that our OP dynamics is linear, i.e., the thermal-average forces driving OP dynamics in general are related to the OPs in a highly nonlinear fashion. This nonlinearity is critical in simulating far-from equilibrium structures.²⁷

In the above context, relationship (2.4) is the origin of the unique value of ${\binom{⇀}{Φ}}_{k}$ for a given set of ${\binom{⇀}{r}}_{i}$ . While r implies ${\binom{⇀}{Φ}}_{k}$ uniquely, the converse is not true, i.e., there is an ensemble of r for given Φ. This stems from the fact that a theory with N_OP (≪N) OPs cannot predict 3N atomic co-ordinates uniquely; this is the motivation for adding the residuals to Eq. 2.1 and generating an ensemble of atomic configurations consistent with the OPs in Eq. 2.2. In particular, N ${\binom{⇀}{r}}_{i}$ cannot be uniquely expressed in terms of N_OP ${\binom{⇀}{Φ}}_{k}$ from Eqs. 2.3 or 2.4. Therefore, the r − Φ relationship is not one-to-one, as it should not be.

Generation of atomic ensemble consistent with coarse-grained variables has been discussed in other multiscale approaches.²⁹ However, in these approaches the dynamics of all atoms was not accounted for, leading to issues in treating diffusion and long range electrostatics.²⁹ One suggested way of overcoming this is to couple the atomistic and coarse-grained representations via the boundary conditions.²⁹ This has been implemented by parameterization of a coarse-grained model with MD simulation data, and demonstrated on transmembrane proteins.²⁹ In contrast, the present approach accounts for the all-atom configurations via a quasiequilibrium probability distribution, which evolves adiabatically with the OPs. Viscoelastic effects in the dynamics of the macromolecule are accounted via thermal-average forces and diffusion coefficients (Secs. II and III).

APPENDIX B: DERIVATION OF THE MULTISCALE LIOUVILLE OPERATOR

Here we derive the multiscale Liouville operator of Eq. 3.2 using the ansatz Eq. 3.1 and the chain rule, starting from the classical Liouville operator L. With this, the contribution to Lρ from particle i is given by

\begin{matrix} - \frac{{\binom{⇀}{p}}_{i}}{m_{i}} \cdot \frac{\partial ρ}{\partial {\binom{⇀}{r}}_{i}} - {\binom{⇀}{F}}_{i} \cdot \frac{\partial ρ}{\partial {\binom{⇀}{p}}_{i}} - \sum_{α, α^{'}, k} \frac{p_{i α}}{m_{i}} (\frac{\partial Φ_{α^{'}}}{\partial r_{i α}}) {(\frac{\partial ρ}{\partial Φ_{α^{'}}})}_{Γ = Γ_{0},} \end{matrix}

(B1)

where α and α^′ signifies Cartesian components of the position∕momentum and OPs respectively.

The first two terms in Eq. B1 are the ith contribution to L₀ . Extending the above to N particles,

L_{0} = - \sum_{i = 1}^{N} \{\frac{{\binom{⇀}{p}}_{i}}{m_{i}} \cdot \frac{\partial}{\partial {\binom{⇀}{r}}_{i}} + {\binom{⇀}{F}}_{i} \cdot \frac{\partial}{\partial {\binom{⇀}{p}}_{i}}\} .

(B2)

Furthermore considering the third term of Eq. B1, the ${\binom{⇀}{Φ}}_{k} - \binom{⇀}{r}$ relationship (II.4), and the definition of μ_k (II.6) yields

L_{1} = \sum_{k} \frac{{\binom{⇀}{Π}}_{k}}{μ_{k}} {(\frac{\partial ρ}{\partial {\binom{⇀}{Φ}}_{k}})}_{Γ = Γ_{0}} .

(B3)

This justifies the form of Liouville operator in Eq. 3.2 through Eq. 3.4.

APPENDIX C: THERMAL-AVERAGE FORCES AS FREE-ENERGY GRADIENTS

By definition the αth Cartesian component of the thermal-average force is given by

\begin{matrix} f_{k α} = - \frac{\partial F}{\partial Φ_{k α}} = \frac{1}{β Q (β, Φ)} \frac{\partial}{\partial Φ_{k α}} \int ω d Γ^{*} Δ (Φ - Φ^{*}) e^{- β H^{*}}, \end{matrix}

(C1)

where Φ^* is the set of the first N_OP components of $Φ_{ex}^{*}$ (i.e.,Φ_ex evaluated at Γ^* ); ω and Δ are defined in Appendix SII and references therein. The contribution $\tilde{Q}$ from the r^* integration of Eq. C1 is given by

\tilde{Q} = \int ω d^{3} r^{*} Δ (Φ - Φ^{*}) e^{- β H^{*}} .

(C2)

As Φ does not affect the momentum contribution to the Q-integral in deriving the thermal-average forces, we proceed with the analysis of $\partial \tilde{Q} ∕ \partial Φ_{k α}$ .

Note, the thermal averaging involves integration over all positions and momenta Γ^* which are consistent with a given value of Φ as imposed through the △ factor. In taking the derivative of the integral with respect to Φ_kα , in concept, one calculates the integral at two closely lying Φ_kα values and divides the difference by the increment in Φ_kα ; at all stages of this conceptual calculation, H is taken to be a function of Γ^* and not Φ^* directly. This implies the L₁H=0 condition encountered in the course of constructing the multiple dependencies of ρ₀ is not violated.

Taking the derivative inside the integral in Eq. C1, and using the fact that △ only depends on the difference (Φ−Φ^* ), one obtains

\frac{\partial \tilde{Q}}{\partial Φ_{k α}} = - \int ω d^{3} r^{*} \frac{\partial Δ (Φ - Φ^{*})}{\partial Φ_{k α}^{*}} e^{- β H^{*}} .

(C3)

Using Eq. 2.7 and the chain-rule yields

\begin{matrix} \frac{\partial \tilde{Q}}{\partial Φ_{k α}} & = & - \int ω d^{3} r^{*} \sum_{α^{'} = 1}^{3} \sum_{i = 1}^{N} \frac{\partial ▵ (Φ - Φ^{*})}{\partial r_{i α^{'}}^{*}} \frac{\partial r_{i α^{'}}^{*}}{\partial Φ_{k α}^{*}} e^{- β H^{*}} \\ = & - \int ω d^{3} r^{*} \sum_{α^{'} = 1}^{3} \sum_{i = 1}^{N} δ_{α α^{'}} U_{k} ({\binom{⇀}{r}}_{i}^{0}) \frac{\partial ▵ (Φ - Φ^{*})}{\partial r_{i α^{'}}^{*}} e^{- β H^{*}}, \end{matrix}

(C4)

where Kronecker delta δ_α^α′ arises since $\partial r_{i α'}^{*} ∕ \partial Φ_{k α}^{*}$ is zero if α ≠ α′. Integration by parts of Eq. C4, and simplification of the expression yield

\frac{1}{β} \frac{\partial \tilde{Q}}{\partial Φ_{k α}} = \int ω d^{3} r^{*} Δ (Φ - Φ^{*}) f_{k α}^{m *} e^{- β H^{*}},

(C5)

where $f_{k α}^{m *} = \sum_{i} U_{k} ({\binom{⇀}{r}}_{i}^{0}) F_{i α}^{*}$ , for $F_{i α}^{*} = - \partial V^{*} / \partial r_{i α}^{*}$ . Here $V^{*} = V ({\binom{⇀}{r}}_{1}^{*}, {\binom{⇀}{r}}_{2}^{*} \dots {\binom{⇀}{r}}_{N}^{*})$ is the N-atom potential evaluated at r^* .

Reinstating vector notation, integrating over the momenta, and dividing both sides by Q yields

{\binom{⇀}{f}}_{k} = \frac{1}{Q} \int ω d Γ^{*} ▵ (Φ - Φ^{*}) {\binom{⇀}{f}}_{k}^{m *} e^{- β H^{*}} = 〈{\binom{⇀}{f}}_{k}^{m *}〉 .

(C6)

This validates Eq. 3.7 and also shows how the interatomic forces ${\binom{⇀}{F}}_{i}$ influence ${\binom{⇀}{f}}_{k}$ through the N-atom potential in H. On arriving at Eq. C6, all the position dependence of H is relegated to r^* . Therefore, the condition L₁H=0 is sustained.

APPENDIX D: λ COMPUTATION

Fluctuations λ in SPs is calculated using $λ (S P_{j}, t_{i}) = (\sqrt{\sum_{i = 0}^{N_{f} - 1} {[S P_{j} (t_{i}) - ⟨ S P_{j} ⟩]}^{2}} ∕ N_{f}) ∕ S P_{j, \max} (t_{i}); j = 1, \dots 4$ , where t_i is the ith time, N_f is the total number of MD time frames used for the moving averages, ⟨S_Pj⟩ is the moving average (over 50 ps), and S_Pj,max is the maximum absolute value of the SP within the range of SPs sampled for the moving average calculation. Fluctuations are defined about a moving absolute maxima rather than a moving average to avoid singularities for zero moving averages. The normalization makes λ dimensionless. Thus λ can be compared between different SPs and OPs.

References

Williamson J. R., Nat. Chem. Biol. 4, 458 (2008). 10.1038/nchembio.102 [DOI] [PubMed] [Google Scholar]
Ortoleva P., J. Phys. Chem. B 109, 21258 (2005). 10.1021/jp051381b [DOI] [PubMed] [Google Scholar]
Ortoleva P., Adhangale P., Cheluvaraja S., Fontus M. W. A., and Shreif Z., IEEE Eng. Med. Biol. Mag. 28, 70 (2009). 10.1109/MEMB.2009.932389 [DOI] [PubMed] [Google Scholar]
Cheluvaraja S. and Ortoleva P., J. Chem. Phys. 132, 075102 (2010). 10.1063/1.3316793 [DOI] [PMC free article] [PubMed] [Google Scholar]
Cheluvaraja S., Roy A., and Ortoleva P., “Roadmap for SimNanoworld^™ an all-atom nanosystem simulator. In preparation, 2011 (unpublished).
Jaqaman K. and Ortoleva P. J., J. Comput. Chem. 23, 484 (2002). 10.1002/jcc.10040 [DOI] [PubMed] [Google Scholar]
Miao Y. and Ortoleva P., J. Comput. Chem. 30, 423 (2009). 10.1002/jcc.21071 [DOI] [PMC free article] [PubMed] [Google Scholar]
Miao Y. and Ortoleva P., Biopolymers 93, 61 (2010). 10.1002/bip.21299 [DOI] [PubMed] [Google Scholar]
Pankavich S., Miao Y., Ortoleva J., Shreif Z., and Ortoleva P., J. Chem. Phys. 128, 234908 (2008). 10.1063/1.2931572 [DOI] [PMC free article] [PubMed] [Google Scholar]
Pankavich S., Shreif Z., Miao Y., and Ortoleva P., J. Chem. Phys. 130, 194115 (2009). 10.1063/1.3134683 [DOI] [PubMed] [Google Scholar]
Shreif Z., Adhangale P., Cheluvaraja S., Perera R., Kuhn R. J., and Ortoleva P., Sci. Model. Simul. 15, 363 (2008). 10.1007/s10820-008-9101-5 [DOI] [Google Scholar]
Zwanzig R., Nonequilibrium Statistical Mechanics (Oxford University Press, New York, 2001). [Google Scholar]
Chen C. and Xiao Y., Biophys. J. 88, 3276 (2005). 10.1529/biophysj.104.046904 [DOI] [PMC free article] [PubMed] [Google Scholar]
Hayward S., Kitao A., and Berendsen H. J. C., Proteins: Struct., Funct., Bioinf. 27, 425 (1997). [DOI] [PubMed] [Google Scholar]
Hayward S., Kitao A., and Go N., Proteins: Struct., Funct., Genet. 23, 177 (1995). 10.1002/prot.340230207 [DOI] [PubMed] [Google Scholar]
Altis A., Nguyen P. H., Hegger R., and Stock G., J. Chem. Phys. 126, 2444111 (2007). 10.1063/1.2746330 [DOI] [PubMed] [Google Scholar]
Riccardi L., Nguyen P. H., and Stock G., J. Phys. Chem. B 113, 16660 (2009). 10.1021/jp9076036 [DOI] [PubMed] [Google Scholar]
Shreif Z. and Ortoleva P., J. Stat. Phys. 130, 669 (2008). 10.1007/s10955-007-9452-4 [DOI] [Google Scholar]
Arkhipov A., Freddolino P. L., and Schulten K., Structure 14, 1767 (2006). 10.1016/j.str.2006.10.003 [DOI] [PubMed] [Google Scholar]
Zhang Z., Pfaendtner J., Grafmüller A., and Voth G. A., Biophys. J. 97, 2327 (2009). 10.1016/j.bpj.2009.08.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
Zhang Z., Lu L., Noid W. G., Krishna V., Pfaendtner J., and Voth G. A., Biophys. J. 95, 5073 (2008). 10.1529/biophysj.108.139626 [DOI] [PMC free article] [PubMed] [Google Scholar]
Amadei A., Linssen A. B. M., and Berendsen H. J. C., Proteins: Struct., Funct., Bioinf. 17, 412 (1993). 10.1002/prot.340170408 [DOI] [PubMed] [Google Scholar]
Maisuradze G. G. and Leitner D. M., Proteins: Struct., Funct., Bioinf. 67, 569 (2007). 10.1002/prot.21344 [DOI] [PubMed] [Google Scholar]
Hinsen K., Proteins: Struct., Funct., Bioinf. 64, 795 (2006). 10.1002/prot.20900 [DOI] [PubMed] [Google Scholar]
Miao Y. and Ortoleva P., J. Chem. Phys. 125, 44901 (2006). 10.1063/1.2218838 [DOI] [PubMed] [Google Scholar]
Miao Y. and Ortoleva P. J., J. Chem. Phys. 125, 214901 (2006). 10.1063/1.2400858 [DOI] [PubMed] [Google Scholar]
Das P., Moll M., Stamati H., Kavraki L. E., and Clementi C., Proc. Natl. Acad. Sci. U.S.A. 103, 9885 (2006). 10.1073/pnas.0603553103 [DOI] [PMC free article] [PubMed] [Google Scholar]
Gohlke H. and Thorpe M. F., Biophys. J. 91, 2115 (2006). 10.1529/biophysj.106.083568 [DOI] [PMC free article] [PubMed] [Google Scholar]
Kevrekidis Y. G., Gear C. W., and Hummer G., AIChE J. 50, 1346 (2004). 10.1002/aic.10106 [DOI] [Google Scholar]
Weinan E., Engquist B., Li X., Ren W., and Vanden-Eijnden E., Comm. Comp. Phys. 2, 367 (2007). [Google Scholar]
Izvekov S. and Voth G. A., J. Phys. Chem. B 109, 2469 (2005). 10.1021/jp044629q [DOI] [PubMed] [Google Scholar]
Izvekov S. and Voth G. A., J. Chem. Phys. 123, 134105 (2005). 10.1063/1.2038787 [DOI] [PubMed] [Google Scholar]
See Supplementary Material at http://dx.doi.org/10.1063/1.3524532 for appendices SI, SII, SIII, SIV, and Figs. S1–S17.
Cao J. and Martyna G. J., J. Chem. Phys. 104, 2028 (1996). 10.1063/1.470959 [DOI] [Google Scholar]
Marx D., Tuckerman M. E., and Martyna G. J., Comput. Phys. Commun. 118, 166 (1999). 10.1016/S0010-4655(99)00208-8 [DOI] [Google Scholar]
Car R. and Parrinello M., Phys. Rev. Lett. 55, 2471 (1985). 10.1103/PhysRevLett.55.2471 [DOI] [PubMed] [Google Scholar]
Iyengar S. S., Schlegel H. B., Millam J. M., Voth G. A., Scuseria G. E., and Frisch M. J., J. Chem. Phys. 115, 10291 (2001). 10.1063/1.1416876 [DOI] [Google Scholar]
Rosso L., Minary P., Zhu Z., and Tuckerman M. E., J. Chem. Phys. 116, 4389 (2002). 10.1063/1.1448491 [DOI] [Google Scholar]
Pankavich S. and Ortoleva P., J. Math. Phys. 51, 063303 (2010). 10.1063/1.3420578 [DOI] [PMC free article] [PubMed] [Google Scholar]
Deutch J. M. and Oppenheim I., Faraday Discuss. Chem. Soc. 83, 1 (1987). 10.1039/dc9878300001 [DOI] [Google Scholar]
Maragliano L. and Vanden-Eijnden E., Chem. Phys. Lett. 426, 168 (2006). 10.1016/j.cplett.2006.05.062 [DOI] [Google Scholar]
Abrams J. B. and Tuckerman M. E., J. Phys. Chem. B 112, 15742 (2008). 10.1021/jp805039u [DOI] [PubMed] [Google Scholar]
Miao Y. and Ortoleva P., J. Phys. Chem. B 114, 11181 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
Sweet C. R., Petrone P., Pande V. S., and Izaguirre J. A., J. Chem. Phys. 128, 145101 (2008). 10.1063/1.2883966 [DOI] [PMC free article] [PubMed] [Google Scholar]
Pankavich S., Shreif Z., and Ortoleva P., Phys. A 387, 4053 (2008). 10.1016/j.physa.2008.03.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
Freddolino P. L., Arkhipov A. S., Larson S. B., McPherson A., and Schulten K., Structure 14, 437 (2006). 10.1016/j.str.2005.11.014 [DOI] [PubMed] [Google Scholar]
Singharoy A., Yesnik A., and Ortoleva P., J. Chem. Phys. 132, 174112 (2010). 10.1063/1.3424771 [DOI] [PMC free article] [PubMed] [Google Scholar]
Ginder J. M. and Epstein A. J., Phys. Rev. B 41, 10674 (1990). 10.1103/PhysRevB.41.10674 [DOI] [PubMed] [Google Scholar]
Severin M. and Inganas O., Europhys. Lett. 25, 347 (1994). 10.1209/0295-5075/25/5/006 [DOI] [Google Scholar]
Ivanov V. A., Stukan M. R., Müller M., Paul W., and Binder K., J. Chem. Phys. 118, 10333 (2003). 10.1063/1.1572812 [DOI] [Google Scholar]
Schneemann A., Annu. Rev. Microbiol. 60, 51 (2006). 10.1146/annurev.micro.60.080805.142304 [DOI] [PubMed] [Google Scholar]
Lin M. M., Meinhold L., Shorokhov D., and Zewail A. H., Phys. Chem. Chem. Phys. 10, 4227 (2008). 10.1039/b804675c [DOI] [PMC free article] [PubMed] [Google Scholar]
Sorin E. J., Engelhardt M. A., Herschlag D., and Pande V. S., J. Mol. Biol. 317, 493 (2002). 10.1006/jmbi.2002.5447 [DOI] [PubMed] [Google Scholar]
Sugita Y. and Okamoto Y., Chem. Phys. Lett. 314, 141 (1999). 10.1016/S0009-2614(99)01123-9 [DOI] [Google Scholar]
Villa A., Widjajakusuma E., and Stock G., J. Phys. Chem. B 112, 134 (2008). 10.1021/jp0764337 [DOI] [PubMed] [Google Scholar]
Day J., Kuznetsov Y. G., Larson S. B., Greenwood A., and McPherson A., Biophys. J. 80, 2364 (2001). 10.1016/S0006-3495(01)76206-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
Torrie G. M. and Valleau J. P., J. Comput. Phys. 23, 187 (1977). 10.1016/0021-9991(77)90121-8 [DOI] [Google Scholar]
Kirkwood J. G., J. Chem. Phys. 3, 300 (1935). 10.1063/1.1749657 [DOI] [Google Scholar]
Carter E. A., Ciccotti G., Hynes J. T., and Kapral R., Chem. Phys. Lett. 156, 472 (1989). 10.1016/S0009-2614(89)87314-2 [DOI] [Google Scholar]
Fleurat-Lessard P. and Zeigler T., J. Chem. Phys. 123, 084101 (2005). 10.1063/1.1948367 [DOI] [PubMed] [Google Scholar]
Laio A. and Parinello M., Proc. Natl. Acad. Sci. U.S.A. 99, 12562 (2002). 10.1073/pnas.202427399 [DOI] [PMC free article] [PubMed] [Google Scholar]
Ianuzzi M., Laio A., and Parinello M., Phys. Rev. Lett. 90, 238302 (2003). 10.1103/PhysRevLett.90.238302 [DOI] [PubMed] [Google Scholar]
Shehu A., Kavraki L. E., and Clementi C., Proteins: Struct., Funct., Genet. 76, 837 (2009). 10.1002/prot.22390 [DOI] [PMC free article] [PubMed] [Google Scholar]
Pande V. S. and Rokhsar D. S., Proc. Natl. Acad. Sci. U.S.A. 96, 9062 (1999). 10.1073/pnas.96.16.9062 [DOI] [PMC free article] [PubMed] [Google Scholar]
Heath A. P., Kavraki L. E., and Clementi C., Proteins: Struct., Funct., Genet. 68, 646 (2007). 10.1002/prot.21371 [DOI] [PubMed] [Google Scholar]
Modis Y., Trus B. L., and Harrison S. C., EMBO J. 21, 4754 (2002). 10.1093/emboj/cdf494 [DOI] [PMC free article] [PubMed] [Google Scholar]
Ayton G. S. and Voth G. A., J. Struct. Biol. 157, 570 (2007). 10.1016/j.jsb.2006.10.020 [DOI] [PubMed] [Google Scholar]

[c1] Williamson J. R., Nat. Chem. Biol. 4, 458 (2008). 10.1038/nchembio.102 [DOI] [PubMed] [Google Scholar]

[c2] Ortoleva P., J. Phys. Chem. B 109, 21258 (2005). 10.1021/jp051381b [DOI] [PubMed] [Google Scholar]

[c3] Ortoleva P., Adhangale P., Cheluvaraja S., Fontus M. W. A., and Shreif Z., IEEE Eng. Med. Biol. Mag. 28, 70 (2009). 10.1109/MEMB.2009.932389 [DOI] [PubMed] [Google Scholar]

[c4] Cheluvaraja S. and Ortoleva P., J. Chem. Phys. 132, 075102 (2010). 10.1063/1.3316793 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c5] Cheluvaraja S., Roy A., and Ortoleva P., “Roadmap for SimNanoworld^™ an all-atom nanosystem simulator. In preparation, 2011 (unpublished).

[c6] Jaqaman K. and Ortoleva P. J., J. Comput. Chem. 23, 484 (2002). 10.1002/jcc.10040 [DOI] [PubMed] [Google Scholar]

[c7] Miao Y. and Ortoleva P., J. Comput. Chem. 30, 423 (2009). 10.1002/jcc.21071 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c8] Miao Y. and Ortoleva P., Biopolymers 93, 61 (2010). 10.1002/bip.21299 [DOI] [PubMed] [Google Scholar]

[c9] Pankavich S., Miao Y., Ortoleva J., Shreif Z., and Ortoleva P., J. Chem. Phys. 128, 234908 (2008). 10.1063/1.2931572 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c10] Pankavich S., Shreif Z., Miao Y., and Ortoleva P., J. Chem. Phys. 130, 194115 (2009). 10.1063/1.3134683 [DOI] [PubMed] [Google Scholar]

[c11] Shreif Z., Adhangale P., Cheluvaraja S., Perera R., Kuhn R. J., and Ortoleva P., Sci. Model. Simul. 15, 363 (2008). 10.1007/s10820-008-9101-5 [DOI] [Google Scholar]

[c12] Zwanzig R., Nonequilibrium Statistical Mechanics (Oxford University Press, New York, 2001). [Google Scholar]

[c13] Chen C. and Xiao Y., Biophys. J. 88, 3276 (2005). 10.1529/biophysj.104.046904 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c14] Hayward S., Kitao A., and Berendsen H. J. C., Proteins: Struct., Funct., Bioinf. 27, 425 (1997). [DOI] [PubMed] [Google Scholar]

[c15] Hayward S., Kitao A., and Go N., Proteins: Struct., Funct., Genet. 23, 177 (1995). 10.1002/prot.340230207 [DOI] [PubMed] [Google Scholar]

[c16] Altis A., Nguyen P. H., Hegger R., and Stock G., J. Chem. Phys. 126, 2444111 (2007). 10.1063/1.2746330 [DOI] [PubMed] [Google Scholar]

[c17] Riccardi L., Nguyen P. H., and Stock G., J. Phys. Chem. B 113, 16660 (2009). 10.1021/jp9076036 [DOI] [PubMed] [Google Scholar]

[c18] Shreif Z. and Ortoleva P., J. Stat. Phys. 130, 669 (2008). 10.1007/s10955-007-9452-4 [DOI] [Google Scholar]

[c19] Arkhipov A., Freddolino P. L., and Schulten K., Structure 14, 1767 (2006). 10.1016/j.str.2006.10.003 [DOI] [PubMed] [Google Scholar]

[c20] Zhang Z., Pfaendtner J., Grafmüller A., and Voth G. A., Biophys. J. 97, 2327 (2009). 10.1016/j.bpj.2009.08.007 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c21] Zhang Z., Lu L., Noid W. G., Krishna V., Pfaendtner J., and Voth G. A., Biophys. J. 95, 5073 (2008). 10.1529/biophysj.108.139626 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c22] Amadei A., Linssen A. B. M., and Berendsen H. J. C., Proteins: Struct., Funct., Bioinf. 17, 412 (1993). 10.1002/prot.340170408 [DOI] [PubMed] [Google Scholar]

[c23] Maisuradze G. G. and Leitner D. M., Proteins: Struct., Funct., Bioinf. 67, 569 (2007). 10.1002/prot.21344 [DOI] [PubMed] [Google Scholar]

[c24] Hinsen K., Proteins: Struct., Funct., Bioinf. 64, 795 (2006). 10.1002/prot.20900 [DOI] [PubMed] [Google Scholar]

[c25] Miao Y. and Ortoleva P., J. Chem. Phys. 125, 44901 (2006). 10.1063/1.2218838 [DOI] [PubMed] [Google Scholar]

[c26] Miao Y. and Ortoleva P. J., J. Chem. Phys. 125, 214901 (2006). 10.1063/1.2400858 [DOI] [PubMed] [Google Scholar]

[c27] Das P., Moll M., Stamati H., Kavraki L. E., and Clementi C., Proc. Natl. Acad. Sci. U.S.A. 103, 9885 (2006). 10.1073/pnas.0603553103 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c28] Gohlke H. and Thorpe M. F., Biophys. J. 91, 2115 (2006). 10.1529/biophysj.106.083568 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c30] Kevrekidis Y. G., Gear C. W., and Hummer G., AIChE J. 50, 1346 (2004). 10.1002/aic.10106 [DOI] [Google Scholar]

[c31] Weinan E., Engquist B., Li X., Ren W., and Vanden-Eijnden E., Comm. Comp. Phys. 2, 367 (2007). [Google Scholar]

[c32] Izvekov S. and Voth G. A., J. Phys. Chem. B 109, 2469 (2005). 10.1021/jp044629q [DOI] [PubMed] [Google Scholar]

[c33] Izvekov S. and Voth G. A., J. Chem. Phys. 123, 134105 (2005). 10.1063/1.2038787 [DOI] [PubMed] [Google Scholar]

[c35] See Supplementary Material at http://dx.doi.org/10.1063/1.3524532 for appendices SI, SII, SIII, SIV, and Figs. S1–S17.

[c36] Cao J. and Martyna G. J., J. Chem. Phys. 104, 2028 (1996). 10.1063/1.470959 [DOI] [Google Scholar]

[c37] Marx D., Tuckerman M. E., and Martyna G. J., Comput. Phys. Commun. 118, 166 (1999). 10.1016/S0010-4655(99)00208-8 [DOI] [Google Scholar]

[c38] Car R. and Parrinello M., Phys. Rev. Lett. 55, 2471 (1985). 10.1103/PhysRevLett.55.2471 [DOI] [PubMed] [Google Scholar]

[c39] Iyengar S. S., Schlegel H. B., Millam J. M., Voth G. A., Scuseria G. E., and Frisch M. J., J. Chem. Phys. 115, 10291 (2001). 10.1063/1.1416876 [DOI] [Google Scholar]

[c40] Rosso L., Minary P., Zhu Z., and Tuckerman M. E., J. Chem. Phys. 116, 4389 (2002). 10.1063/1.1448491 [DOI] [Google Scholar]

[c41] Pankavich S. and Ortoleva P., J. Math. Phys. 51, 063303 (2010). 10.1063/1.3420578 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c42] Deutch J. M. and Oppenheim I., Faraday Discuss. Chem. Soc. 83, 1 (1987). 10.1039/dc9878300001 [DOI] [Google Scholar]

[c43] Maragliano L. and Vanden-Eijnden E., Chem. Phys. Lett. 426, 168 (2006). 10.1016/j.cplett.2006.05.062 [DOI] [Google Scholar]

[c44] Abrams J. B. and Tuckerman M. E., J. Phys. Chem. B 112, 15742 (2008). 10.1021/jp805039u [DOI] [PubMed] [Google Scholar]

[c45] Miao Y. and Ortoleva P., J. Phys. Chem. B 114, 11181 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]

[c46] Sweet C. R., Petrone P., Pande V. S., and Izaguirre J. A., J. Chem. Phys. 128, 145101 (2008). 10.1063/1.2883966 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c34] Pankavich S., Shreif Z., and Ortoleva P., Phys. A 387, 4053 (2008). 10.1016/j.physa.2008.03.008 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c47] Freddolino P. L., Arkhipov A. S., Larson S. B., McPherson A., and Schulten K., Structure 14, 437 (2006). 10.1016/j.str.2005.11.014 [DOI] [PubMed] [Google Scholar]

[c48] Singharoy A., Yesnik A., and Ortoleva P., J. Chem. Phys. 132, 174112 (2010). 10.1063/1.3424771 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c49] Ginder J. M. and Epstein A. J., Phys. Rev. B 41, 10674 (1990). 10.1103/PhysRevB.41.10674 [DOI] [PubMed] [Google Scholar]

[c50] Severin M. and Inganas O., Europhys. Lett. 25, 347 (1994). 10.1209/0295-5075/25/5/006 [DOI] [Google Scholar]

[c51] Ivanov V. A., Stukan M. R., Müller M., Paul W., and Binder K., J. Chem. Phys. 118, 10333 (2003). 10.1063/1.1572812 [DOI] [Google Scholar]

[c52] Schneemann A., Annu. Rev. Microbiol. 60, 51 (2006). 10.1146/annurev.micro.60.080805.142304 [DOI] [PubMed] [Google Scholar]

[c53] Lin M. M., Meinhold L., Shorokhov D., and Zewail A. H., Phys. Chem. Chem. Phys. 10, 4227 (2008). 10.1039/b804675c [DOI] [PMC free article] [PubMed] [Google Scholar]

[c54] Sorin E. J., Engelhardt M. A., Herschlag D., and Pande V. S., J. Mol. Biol. 317, 493 (2002). 10.1006/jmbi.2002.5447 [DOI] [PubMed] [Google Scholar]

[c55] Sugita Y. and Okamoto Y., Chem. Phys. Lett. 314, 141 (1999). 10.1016/S0009-2614(99)01123-9 [DOI] [Google Scholar]

[c56] Villa A., Widjajakusuma E., and Stock G., J. Phys. Chem. B 112, 134 (2008). 10.1021/jp0764337 [DOI] [PubMed] [Google Scholar]

[c57] Day J., Kuznetsov Y. G., Larson S. B., Greenwood A., and McPherson A., Biophys. J. 80, 2364 (2001). 10.1016/S0006-3495(01)76206-6 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c58] Torrie G. M. and Valleau J. P., J. Comput. Phys. 23, 187 (1977). 10.1016/0021-9991(77)90121-8 [DOI] [Google Scholar]

[c59] Kirkwood J. G., J. Chem. Phys. 3, 300 (1935). 10.1063/1.1749657 [DOI] [Google Scholar]

[c60] Carter E. A., Ciccotti G., Hynes J. T., and Kapral R., Chem. Phys. Lett. 156, 472 (1989). 10.1016/S0009-2614(89)87314-2 [DOI] [Google Scholar]

[c61] Fleurat-Lessard P. and Zeigler T., J. Chem. Phys. 123, 084101 (2005). 10.1063/1.1948367 [DOI] [PubMed] [Google Scholar]

[c62] Laio A. and Parinello M., Proc. Natl. Acad. Sci. U.S.A. 99, 12562 (2002). 10.1073/pnas.202427399 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c63] Ianuzzi M., Laio A., and Parinello M., Phys. Rev. Lett. 90, 238302 (2003). 10.1103/PhysRevLett.90.238302 [DOI] [PubMed] [Google Scholar]

[c64] Shehu A., Kavraki L. E., and Clementi C., Proteins: Struct., Funct., Genet. 76, 837 (2009). 10.1002/prot.22390 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c65] Pande V. S. and Rokhsar D. S., Proc. Natl. Acad. Sci. U.S.A. 96, 9062 (1999). 10.1073/pnas.96.16.9062 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c66] Heath A. P., Kavraki L. E., and Clementi C., Proteins: Struct., Funct., Genet. 68, 646 (2007). 10.1002/prot.21371 [DOI] [PubMed] [Google Scholar]

[c67] Modis Y., Trus B. L., and Harrison S. C., EMBO J. 21, 4754 (2002). 10.1093/emboj/cdf494 [DOI] [PMC free article] [PubMed] [Google Scholar]

[c29] Ayton G. S. and Voth G. A., J. Struct. Biol. 157, 570 (2007). 10.1016/j.jsb.2006.10.020 [DOI] [PubMed] [Google Scholar]

PERMALINK

Order parameters for macromolecules: Application to multiscale simulation

A Singharoy

S Cheluvaraja

P Ortoleva

Abstract

INTRODUCTION

MACROMOLECULAR OPs

MULTISCALE THEORY AND COMPUTATION