Ionic solvation studied by image-charge reaction field method

Abstract

In a preceding paper [J. Chem. Phys. 131, 154103 (2009)], we introduced a new, hybrid explicit∕implicit method to treat electrostatic interactions in computer simulations, and tested its performance for liquid water. In this paper, we report further tests of this method, termed the image-charge solvation model (ICSM), in simulations of ions solvated in water. We find that our model can faithfully reproduce known solvation properties of sodium and chloride ions. The charging free energy of a single sodium ion is in excellent agreement with the estimates by other electrostatics methods, while offering much lower finite-size errors. Similarly, the potentials of mean force computed for Na–Cl, Na–Na, and Cl–Cl pairs closely reproduce those reported previously. Collectively, our results demonstrate the superior accuracy of the proposed ICSM method for simulations of mixed media.

INTRODUCTION

Electrostatic interactions play a central role in computer simulations of condensed-matter media. The treatment of these interactions in simulations of biological molecules solvated in water¹ is of particular importance. Among many available approaches to such systems, one group of methods replaces explicit water molecules with a dielectric continuum, thereby reducing the total number of degrees of freedom. In the interest of computational efficiency, these methods, termed implicit solvents,^{2, 3} sacrifice the accuracy. A number of flaws, including the description of salt bridges⁴ and the treatment of boundaries between solvent and solute^{5, 6} are known for implicit solvents, all associated with the continuum approximation. Although much effort was recently put into improving implicit models,⁷ not all outstanding issues have been resolved. In particular, the implicit description of solvent–solvent correlations remains problematic.⁸

Alternative explicit solvation schemes are more accurate in terms of solvent description, however, they suffer from a number of other shortcomings. One source of error is the truncation of electrostatic interactions beyond certain cut-off distance.^{1, 9, 10} Due to their long-range nature, truncated Coulomb forces have been shown to lead to severe artifacts in simulations of liquids,^{11, 12} solvated ions,^{13, 14, 15, 16} ion pairs,^{17, 18, 19, 20, 21, 22} and biomolecules.^{23, 24, 25, 26} Methods considering interactions among all pairs of charges on an infinite lattice created by the periodic replication of the original system throughout space are designed to remedy the truncation problem.^{27, 28, 29, 30, 31, 32} However, these lattice-sum methods introduce an error associated with the periodicity of the simulated system. For instance, a solute in an infinite bath of solvent becomes an infinite lattice of solute images, all of which interact with one another. The effects of periodicity-induced artifacts in computer simulations are little understood at present.^{33, 34, 35} Using the continuum approximation, Hünenberger et al. have investigated the causes of these effects in generic solutes placed in a bath of solvent.^{33, 36, 37} Three factors emerged from these studies as most important: (i) a solvent of low dielectric permittivity, (ii) a solute cavity of non-negligible size compared to the unit cell size, and (iii) a solute bearing a large overall charge.

In a recent paper,³⁸ we introduced a hybrid solvation model that combines the strengths of the implicit and explicit solvent representations. The model contains a central spherical cavity in which a solute molecule and some solvent are treated explicitly, thus removing the continuum approximation near the solute. The cavity is surrounded by a continuum dielectric medium that generates reaction fields acting on the explicit part. The electrostatic potential experienced by the solute is thus devoid of periodicity artifacts. The reaction fields are computed efficiently using the image-charge method and the fast multipole expansion technique,^{39, 40} developed by our group previously.^{41, 42, 43} Our method, termed image-charge solvation method (ICSM), had been tested in simulations of liquid water,³⁸ where many structural, static, and dynamic properties were seen to be identical to those obtained by the lattice-sum methods for sufficiently large boxes.

In this paper, we investigate the performance of the ICSM in simulations of ions solvated in water. Aside from being a convenient test system, ions in aqueous solutions are critical for many processes in chemistry and biology.^{44, 45, 46, 47, 48} First, we consider one sodium ion and compute its charging free energy ΔG_cg for varying size of the simulation box L. After applying corrections accounting for finite-size effects, ΔG_cg obtained by the ICSM method is found in excellent agreement with the lattice-sum and a variety of other methods reported earlier.⁴⁹ Importantly, the required finite-size corrections are much lower than those in alternative techniques, demonstrating advantages of our method. Next, we compute the potential of mean force (PMF) for the pairs of Na – Cl , Na-Na, and Cl-Cl ions, and again find an excellent agreement with the lattice-sum simulations. For the first pair, this finding confirms the superior accuracy of our method. For the last two pairs, our results demonstrate that the lattice-sum simulations are not affected by the periodicity artifacts to any significant degree. This is an important conclusion as the theoretical basis for performing the lattice-sum simulations of charged systems is not very clear. The empirical rule of thumb has been that such systems need to be neutralized by the addition of counterions.^{35, 50} These counterions, however, may have adverse effects on simulations, especially those involving proteins.^{51, 52, 53} Our tests show that counterions used in the lattice-sum simulations do not have a strong effect on the interactions between the same-charge Na and Cl ions in water.

The paper is organized as follows. First we briefly describe the ICSM method as well as give details of our simulations. Next, we validate our model in the computation of charging free energy of ion solvation, within which the effects of box size and location of the ion are discussed. The PMFs for the three simple ion pairs are computed and compared with those from the lattice-sum method. The effect of counterions is also discussed. Finally, conclusions are given.

METHODS AND MODELS

The image-charge solvation model

Our model was described in detail previously.³⁸ Here, we provide a brief outline of its most important features, for the sake of consistency. The central component is the computation of Φ_RF , the reaction field (RF) for a single charge q placed at position r_s inside a spherical cavity with radius a and dielectric permittivity ε_i embedded in an infinite solvent of dielectric permittivity ε_o , as shown in Fig. 1a. The RF potential at any point r inside the cavity can be approximated by a series over image charges $q_m^{\prime }$ located outside the spherical cavity:

$${\Phi }_{\mathrm{RF}}\left(\mathbf{r}\right)\approx \frac{q_K^{\prime }}{4\pi {\epsilon }_i\left|\mathbf{r}-{\mathbf{r}}_K\right|}+\sum _{m=2}^{N_i}\frac{q_m^{\prime }}{4\pi {\epsilon }_i\left|\mathbf{r}-{\mathbf{r}}_m\right|},$$ (1)

where r_K =a² ∕r_s , q_K =γaq∕r_s , $q_K^{\prime }=q_K+q_1^{\prime }=(1+{\omega }_1{\epsilon }_i∕2{\epsilon }_o)q_K,$ γ=(ε_i −ε_o )∕(ε_i +ε_o ), and

$$\begin{array}{c}\hfill q_m^{\prime }=\frac{{\epsilon }_i({\epsilon }_i-{\epsilon }_o)}{2{\epsilon }_o({\epsilon }_i+{\epsilon }_o)}\frac{{\omega }_m{r}_m}{a}q,r_m=r_K{\left(\frac{2}{1-s_m}\right)}^{1+{\epsilon }_i∕{\epsilon }_o}.\end{array}$$ (2)

The quantities ${\{{\omega }_m,s_m\}}_{m=1}^{N_i}$ are the weights and points of the Gauss–Radau quadrature⁴¹ that depend on the number of images N_i . This number controls the accuracy of the multiple-image approximation: the greater the N_i , the higher the accuracy. In the limit of ε_o →∞, only one image survives, $q_K^{\prime }=q_K$ at the location r_K , which is equivalent to the classical Kelvin image for a conductor in the electrostatics theory,³⁸ hence the notations.

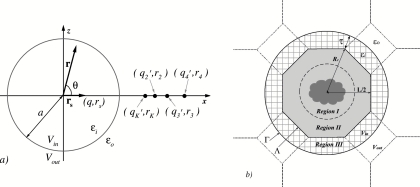
Figure 1.

(a) An illustration of how the multiple-image method is applied to compute the reaction field in a spherical cavity V _in embedded in the solvent bath V _out . The radius of the sphere is a, the dielectric permittivity inside the sphere is ε_i , and that outside of it is ε_o . The polarization of the solvent V _out by the source charge q at position r_s results in the reaction field Φ_RF (r,θ) that is approximated by the potential created by auxiliary charges, referred to as image charges, $q_K^{\prime }$, $q_i^{\prime }$, i ⩾ 2, located at positions r_K , r_i , i ⩾ 2, respectively. (b) A schematic representation of the ICSM model. The truncated octahedron simulation box Λ is placed inside a spherical cavity with radius R_c . The sphere, together with the buffer layer of depth τ, forms a larger cavity Γ. Shown as hatched area is Region III which consists of charges with radius less than R_c +τ that are nearest periodic images of Λ. Particles in Λ that have images in Γ make up Region II. The remaining, nonimaged particles in the simulation box form Region I, indicated as a broken line.

The spherical cavity is integrated with the molecular dynamics method into a computational model explained in Fig. 1b. Shown in this figure is the xz plane cross section of a truncated octahedron (TO) simulation box built from a cube of length L, which along with the buffer layer of thickness τ forms the inside of the spherical cavity. Water molecules in the buffer layer are periodically imaged from the main simulation box, shown in the figure as “Region II.” The unimaged part of the box, marked as “Region I,” forms the productive region of the simulation cell in which a solute molecule can be placed. Its size varies among box geometries and for the TO boxes stands at $d=L(\sqrt{3}-\sqrt{5}∕2)-2\tau =0.61L-2\tau$. No cut-offs are employed for the Coulomb interactions of the charges within the central sphere R_c +τ. Reaction fields generated by all charges in Regions I, II, and III are applied to particles in the TO simulation box.

The electrostatic forces acting on charges within the main simulation box are computed using the image-charge reaction method, and therefore are almost free of periodicity artifacts. Other nonbonded interactions, such as dispersion forces, are computed using the standard periodic boundary conditions with the nearest-image convention.⁹ In total, there are three adjustable parameters in our model: L—size of the simulation box, τ—thickness of the buffer layer, and N_i —the number of image charges. We have determined previously³⁸ that a minimal N_i =1 is adequate for solutions with a high dielectric constant such as water and, therefore, this value was used throughout this work. Parameters τ and L were allowed to vary.

Computational details

All molecular dynamics simulations by the ICSM method were performed by an in-house software, written specifically for this project. The parameters of the fast multipole method code were set as discussed previously.³⁸ The positions and velocities of particles were propagated according to an implementation of the velocity Verlet algorithm, coupled with the Nosé–Hoover thermostat, by Jang and Voth.⁵⁴ The algorithm labeled VV1 in the original paper was employed. The covalent bond lengths of water molecules were constrained according to the noniterative matrix method.^{55, 56} The van der Waals interactions were modeled by the Lennard-Jones potential which was truncated at 10 Å. The location of the oxygen atoms was used to measure the distance from one molecule to another. The integration time step was set to 2 fs. The simulations were performed under constant temperature conditions at T = 300 K and the thermostat’s coupling constant was 0.05 ps. The trajectories were recorded every 0.2 ps for subsequent analysis.

Charging free energy simulations

The conditions of the charging free energy simulations were chosen to match those of Kastenholz and Hünenberger.⁵⁷ The simple-point charge (SPC)⁵⁸ water model and Berendsen’s Na ⁺ ion parameters were used.¹⁵ The total number density was ρ=33.43 nm ⁻³ (the number density corresponding to water density of 1 g cm ⁻³ ) and the simulations were run at a constant volume. The relative permittivity was set to 66.6, as appropriate for the SPC water model. For the charging process, 11 charge states were considered with the increment of 0.1, starting with 0 and ending at 1. Three box sizes L = 30, 45, and 60 Å, with the same buffer layer τ = 6 Å, were used to test the box size effect. To test the dependence on the location of charge, simulations with five different positions along the x axis of the simulation box were performed for L = 60 Å box. In total, 77 MD simulations, 500 ps each, were carried out in this study.

Potential of mean force simulations

PMFs are computed by the ICSM for three pairs of ions: Na ⁺ – Cl ⁻, Na ⁺ – Na ⁺, and Cl ⁻ – Cl ⁻ . The TIP3P⁵⁹ all-atom model is used for water, that of Aaqvist⁶⁰ for the sodium ion and the model of Chandrasekhar et al.⁶¹ for the chloride ion. The dielectric constant was set to 80 in the PMF calculations.

The PMFs were generated by employing the umbrella sampling technique⁶² in conjunction with the weighted histogram analysis method.^{63, 64} The umbrella potentials were applied along the z coordinate with one ion fixed and the other ion allowed to move freely in one direction. The force constants are set at 2000 kJ ∕ mol ∕ nm ² . Twelve windows were considered, each applied with a 1 Å step starting at the separation between the ions of 3 Å. In each window, 0.1 ns of equilibration periods was followed by 4 ns of productive simulations in which data were collected. Various initial positions were considered, as explained in the main text. The simulation time was determined in repeat independent runs as minimal time required for convergence, as explained previously.⁶⁵ Two different box sizes, L = 30 and 45 Å, were used. Buffer layer thickness of 4 Å is applied to the smaller box, and 6 Å to the larger box.

Reference particle-mesh Ewald simulations

The particle-mesh Ewald (PME) technique⁶⁶ was first used to generate initial configurations for the ICSM method. Runs of 200 ps under constant temperature and pressure were performed in GROMACS program package ^{67, 68} to achieve equilibration. A weak coupling to an external heat bath (coupling time constant τ_T =0.1 ps , target temperature T₀ =300 K) and a weak coupling barostat (time constant τ_p =0.5 ps , target pressure P₀ =1 atm ) were applied. Covalent bonds of TIP3P water molecules were constrained using SETTLE procedure⁶⁹ with a relative tolerance of 10⁻⁴ . Once equilibrated, the system was then cut into different TO boxes with desired sizes. This was followed by replacing two water molecules by two desired ions at the preselected positions. PME simulations were also used to compute reference PMF curves. The ions were solvated in a rectangular box of dimensions 4.5×4.5×4.5 nm ³ (denoted as 45 Å box). The other parameters were as stated above. Two PME simulations were conducted for the Na-Na system to test the effect of counterions on the PMF. In the first, two added chloride ions were fixed at the corners of the simulation box. In the second, the ions were allowed to move freely. The duration of these simulations was 4 ns, as in other PMF calculations.

RESULTS AND DISCUSSION

Free energy of ionic solvation

The free energy of ionic solvation, or charging free energy ΔG _cg , describes the amount of work required to increase adiabatically the charge of an ion from zero to its actual value. This quantity is directly relevant to modeling of a number of processes in chemistry and biology where a change in the charge state occurs, including electron transfer and pKa calculations in proteins.^{70, 71}

Computing ΔG_cg from computer simulations

Given that the Hamiltonians of the initial state—uncharged ion, and the final state—fully charged ion, are known and can be readily transformed into one another, computing ΔG _cg in computer simulations is seemingly an easy problem. Indeed, one can simply use either the thermodynamic integration or the free energy perturbation techniques⁹ to calculate ΔG _cg as an integral over the ion charge q. Early such attempts,⁷² however, revealed inconsistent results that strongly depend on the cut-off radius employed in the simulations. Although it was possible to rationalize the cut-off dependence on the basis of continuum electrostatics,⁷³ the early tests revealed that large corrections exist in ionic solvation energy obtained in computer simulations.^{73, 74, 75, 76} These corrections are associated with the finite size of the simulation box and apply to all electrostatics schemes, including the ICSM,³⁸ finite droplet models,^{70, 77, 78, 79} lattice-sum methods,²⁷ or reaction-field approaches.⁸⁰ In the past 20 years, extensive research efforts identified four main sources that contribute to the finite-size corrections: (1) cut-off distances in the straight truncation method,^{73, 76, 81} (2) boundary conditions, which can be periodic, a finite simulation box, or some combination, thereof,^{70, 82, 83} (3) finite-size and periodicity effects,^{73, 76, 84} and (4) the way in which potential at the ion site is computed: based on molecular or atomic positions.^{85, 86} In 2006, Kastenholz and Hünenberger reported a systematic theoretical study of various correction terms for a number of electrostatics schemes.⁵⁷ They found that the magnitude of the correction differs significantly from one method to another. From the practical standpoint, a method that is least affected by corrections is preferable. For a sodium ion solvated in water, different electrostatics methods with different parameters yielded consistent charging free energy ΔG _cg =−480 kJ∕mol.⁴⁹ Here, we use this number as reference to examine the quality of the ICSM method. We show that a consistent ΔG _cg can be obtained across a range of computation-box sizes as well as for various locations of the ion inside the simulation box. Uniformity across the box and convergence with the box size are the two most important properties expected of a successful electrostatics scheme.

Dependence on the size of the simulation box

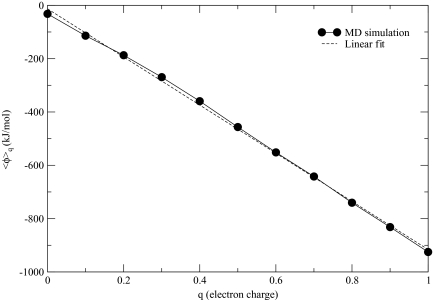
The charging free energy of a sodium ion was computed by the thermodynamic integration $\Delta G_{\mathrm{cg}}={\int }_0^q{⟨\varphi ⟩}_q$ dq, where ϕ denotes the potential at the location of the ion and ⟨⋯⟩_q stands for the average at the charge state q. Three box sizes were used, L = 30, 45, and 60 Å, with the same buffer layer of τ = 6 Å. More computational details are discussed in Sec. II. Figure 2 shows the average potential obtained in the charging simulations with L = 60 Å. With the molecule-based truncation, ⟨ϕ⟩_q should be zero⁴⁹ at q = 0 for sufficiently high temperatures. Our data with ⟨ϕ⟩ = −32 kJ∕mol and a standard deviation of 45 kJ∕mol is close to that limit, indicating that finite-temperature effects are low, in accordance with the earlier conclusions.⁴⁹ Also shown in Fig. 2 is a linear fit to ⟨ϕ⟩_q . The linear dependence is characteristic of the continuum electrostatics models. It is seen to be only approximate for q < 0.4 in our explicit solvent model. When integrated, the curve shown in Fig. 2 yields $\Delta G_{\mathrm{cg}}^s=-465$ kJ∕mol, where superscript s indicates that the free energy was obtained directly in charging simulations. Similar data were collected in the other two simulations. The resulting solvation energies, compiled in Table 1, show that $\Delta G_{\mathrm{cg}}^s$ changes by ∼20 kJ∕mol when L is varied between 30 and 60 Å. With increasing box size, $\Delta G_{\mathrm{cg}}^s$ converges toward the reference value of −480 kJ∕mol.⁴⁹ The residual error is small, declining from 35 kJ∕mol for the smallest box to 15 kJ∕mol for the largest box, but measurable. It arises because of the finite-size effects, which affect any electrostatics method.

Figure 2.

Average potential at the ion site observed in the thermodynamic integration simulations for L = 60 Å. Shown as a broken line is the linear fit of the numerical data. Linear approximation, appropriate for continuum models, is not very accurate for small q.

Table 1.

Electrostatic solvation energy ΔG_cg (in kJ∕mol) of a sodium ion in water obtained in this work in simulation boxes of different sizes L. Finite-size corrections ΔG_c are evaluated separately from the charging free energy $\Delta G_{\mathrm{cg}}^s$ computed directly in the simulations (explained in the text).

L ( Å)	$\Delta G_{\mathrm{cg}}^s$	ΔGc	ΔGcg
30	−445	−64	−509
45	−457	−33	−490
60	−465	−20	−485

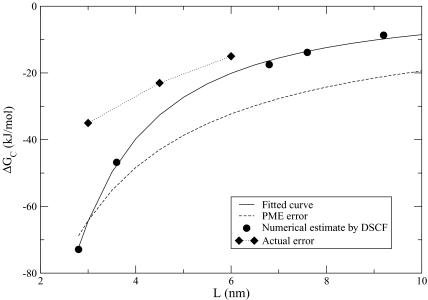
In the terminology of Kastenholz and Hünenberger,⁴⁹ three types of finite-size corrections, A, B, and C, need to be considered in charging free energy calculations of ions. Corrections of type A compensate for non-Coulombic forms of the electrostatic forces and clearly do not apply in our model. There are two C-type corrections. The first accounts for the choice of the summation rule for which the potential at the ionic site is evaluated. It can be based on atomic positions or a molecular position with multiple interpretations. The molecular position based on the oxygen atom in water molecules was shown to be the proper choice for Coulombic (unmodified) electrostatic interactions.⁵⁷ We show in the Appendix that with the current method of separating charges into explicit and implicit parts of our model, this correction is zero. The second C-type correction is employed whenever a vacuum-liquid interface is present. It represents contributions, which are temperature-dependent, from the potential jump at the interface. Since we simulate ions in homogeneous liquid and the “liquid” regions occupy both explicit and implicit parts of our model, there is no interface involved and, therefore, no corrections to be applied. Finally, corrections of type B account for the finite-size and periodicity effects which both apply to our model. The latter arise because certain parts of the main simulation box are imaged within the spherical cavity as described in Fig. 1b. The former enter through the dependence on the size of the sphere R_c , and thus the size of the simulation box L. As explained in the Appendix, we estimate the type B corrections using continuum electrostatics models.^{87, 88} Note that the finite-size and periodicity effects cannot be distinguished in these calculations and, therefore, are treated as one term ΔG_c . Our estimates yield an empirical relationship ΔG_c =−408∕L^ν kJ∕mol, where ν = 1.68 and L is measured in nm. The correction is shown in Table 1 and plotted in Fig. 3. As expected, it declines with L, dropping from −64 kJ∕mol for L = 30 Å to −20 kJ∕mol for L = 60 Å. Importantly, the rate of the decline is very rapid. It is almost twice as large as for the lattice-sum method, whose finite-size corrections decrease with L as O(1∕L ^ν ) where ν = 1. When plotted in one graph, see Fig. 3, the PME is seen to generate much larger errors than the ICSM method. The advantage of the latter increases with L, where it produces errors reduced at least twofold for L> 70 Å.

Figure 3.

Finite-size correction ΔG_c to the charging free energy of a sodium ion in water, estimated in this work for the ICSM model using the self-consistent field method. (Refs. ⁸⁷ and ⁸⁸) For comparison, the finite-size correction of the PME method, ΔG_B , (Ref. ⁴⁹) and the actual error, computed as −480 kJ∕mol-$\Delta G_{\mathrm{cg}}^s$, are also shown.

With the predicted values of ΔG_c , the corrected free energy falls within the computational uncertainty, which we estimate to be at least 10 kJ∕mol, of the reference value −480 kJ∕mol⁴⁹ for all considered simulation boxes except the smallest one. We attribute this discrepancy to the limitation of the continuum approximation we used in computing ΔG_c . We showed in our previous work³⁸ that boxes with L = 30 Å or less have not crossed into the macroscopic regime yet. This is revealed in nonuniform dielectric constant ε and in ε deviating from the bulk value. A recent work by Hassan⁸ also showed that ε varies on length scales that are almost identical to ours.³⁸ With the distance-dependent and carefully parameterized ε, it perhaps would be possible to lower the correction value from the current −64 kJ∕mol closer to the actual −35 kJ∕mol. But such computations would be highly system-specific and, in general, do not seem worthwhile pursuing compared to the simpler alternative of increasing L. We concluded that with the present methodology, the correction for our model cannot be predicted reliably for L ⩽ 30 Å.

Dependence on the location of the ion

Although there is no translational invariance in our model, unlike in other electrostatics methods under periodic boundary conditions, the central, productive part of the simulation cell is supposed to be uniform in all physical properties. To test whether this applies to the ionic solvation energy, the location of the sodium ion was varied across the simulation box and ΔG _cg was recalculated.

With the center of the simulation box set at the origin, five different locations along the x axis were chosen. The distances to the origin for each location (denoted as R) in L = 60 Å simulation were set at 0.0, 6.0, 12.0, 18.0, and 24.0 Å. The first three locations fall within the productive region of the simulation box, whose size is 24.6 Å, while the last two are in Region “II” which is imaged to the buffer layer, see Fig. 1b. The values for $\Delta G_{\mathrm{cg}}^s$ obtained for the different locations are listed in Table 2. The free energy remains constant, from −465 to −468 kJ∕mol, when the ion is in the productive region R < 12 Å, or close to the boundary of that region, R = 18 Å. For ions far outside of the productive part, $\Delta G_{\mathrm{cg}}^s$ begins to rise, reaching −459 kJ∕mol for R = 24 Å. The deviation from the central location is expected since multiple ions are considered in the imaged part of the simulation box. But its magnitude is surprisingly small, reaching only about 6 kJ∕mol for R = 24 Å. This figure is well within the statistical error of our estimate. Collectively, our data lead to the following conclusion: the charging free energy is uniform with high accuracy within the productive part of the simulation box.

Table 2.

Charging free energy $\Delta G_{\mathrm{cg}}^s$ computed for different ion locations in the 60 Å simulation box.

Distance to origin (Å)	$\Delta G_{\mathrm{cg}}^s$ (kJ∕mol)
0	−465
6.0	−468
12.0	−467
18.0	−468
24.0	−459

Potential of mean force of ion pairs

To test correlations between the charged particles solvated in water, we computed PMF, G(r), for three pairs of ions: Na–Cl, Na – Na , and Cl–Cl. Representing effective interactions between ions, the PMFs have a profound influence on many simulated properties, including biochemical reaction rates and structure, and dynamics of biomolecules.^{44, 45, 46, 47, 48} Several simulations were performed for the same pair of ions to establish reproducibility. The error estimates that follow from these repeat simulations are 0.2 kcal∕mol. More computational details are given in Sec. II.

Pair of unlike charges

First we consider the Na – Cl pair. This system has been studied multiple times previously, using multiple force fields and electrostatics schemes.^{65, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99} We found in our previous study⁶⁵ that the range over which interesting physical features appear in the PMF is not more than 10 Å. This puts a lower bound on the size of the productive region of the simulation box at 0.61L − 2τ ⩾ 10 Å. Combined with the optimal value of τ = 6 Å determined earlier,³⁸ this relationship limits the size of the simulation box to L ⩾ 36 Å. For the smaller box L = 30 Å, we were forced to reduce the thickness of the buffer layer to 4 Å. The optimal τ was used in the larger box L = 45 Å.

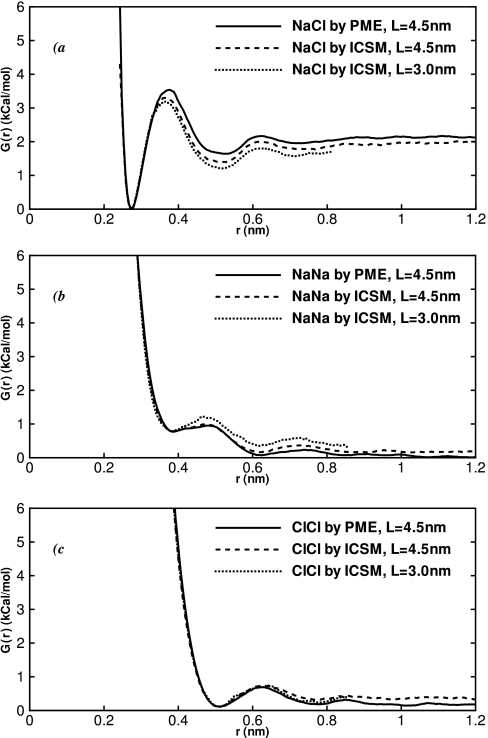
The PMF generated by the ICSM in the box with L = 45 Å is shown in Fig. 4a, along with the reference PMF calculated by the PME method.⁶⁶ The two curves agree with each other and with our earlier simulations⁶⁵ within the statistical uncertainty. They share a shape typical for many ionic and neutral small solutes. The most important features are (i) a global minimum at r ≈ 2.7 Å corresponding to close contact configuration (CCM), (ii) a solvent-separated minimum (SSM) at r ≈ 3.7 Å, and (iii) a prominent free energy barrier in between the two. A second, smaller, solvent-separated minimum also appears. The SSM is approximately 1.7 kcal∕mol higher in free energy than the CCM, indicating that the latter is the more stable configuration. A transition from the SSM to CCM configuration requires overcoming a 1.9 kcal∕mol barrier. The energy required to bring the two ions together, or the association or binding energy, is ≈2.0 kcal∕mol.

Figure 4.

PMF computed in this work for (a) Na – Cl pair of ions, (b) Na – Na pair, and (c) Cl–Cl pair using the PME and ICSM electrostatics methods. The two methods are seen in good agreement for all three types of ions and for different sizes of the simulation box. The curves were made to overlap at the first minimum.

The PMF obtained in the smaller L = 30 Å box, shown in Fig. 4a, is qualitatively similar to those of the PME and the larger L = 45 Å box simulations. But the quantitative characteristics of the extrema, summarized in Table 3 for all three curves, seem to be different. The height of the first maximum, for instance, is 3.2 kcal∕mol in the L = 30 Å box and 3.5 kcal∕mol in the PME simulation. The difference of 0.3 kcal∕mol is outside the estimated 0.2 kcal∕mol error. The PMF of the larger L = 45 Å box, on the other hand, is within 0.2 kcal∕mol of the reference PME curve throughout the full range of covered distances, including the first maximum. It is clear, therefore, that small finite-size artifacts exist in our PMF curve obtained in the small L = 30 Å box simulation. This conclusion is in line with our earlier assertion³⁸ that boxes of this size cannot be used to model the bulk properties of water effectively.

Table 3.

Comparison of the extrema of the PMFs for monovalent ion pairs in water.

		First minimum		First maximum		Second minimum
Ion types	Simulations	r ( Å)	G(r)(kcal∕mol)	r ( Å)	G(r)(kcal∕mol)	r ( Å)	G(r)(kcal∕mol)
	PME (45 Å)	2.73	0.0	3.77	3.53	5.23	1.64
Na – Cl	ICSM (45 Å)	2.73	0.0	3.72	3.30	5.27	1.39
	ICSM (30 Å)	2.71	0.0	3.68	3.20	5.18	1.20
	PME (45 Å)	3.88	0.78	4.83	1.06	6.38	0.15
Na – Na	ICSM (45 Å)	3.86	0.78	4.77	0.95	6.23	0.07
	ICSM (30 Å)	3.86	0.78	4.66	1.23	6.14	0.35
	PME (45 Å)	5.08	0.12	6.28	0.70	7.73	0.19
Cl–Cl	ICSM (45 Å)	5.08	0.12	6.27	0.69	7.63	0.19
	ICSM (30 Å)	5.08	0.12	6.47	0.73	7.79	0.23

Pairs of like charges

As in the Na – Cl pair, we see excellent agreement between the ICSM and the PME methods for the PMF of Na – Na and Cl–Cl pairs, as shown in Figs. 4b, 4c. Qualitatively, the PMFs of the same-charge ions are similar to that of the opposite-charge pair, Na – Cl , in having two minima and one maximum. The minima in the cations case are located at r = 3.7 Å and r = 6.1 Å. Our examination and those of others^{100, 101} show that in the configuration corresponding to the first minimum the water molecules do not intercalate between the ions but rather serve as a bridge between them. This minimum, thus, is equivalent to CCM in the Na – Cl curve. In the second minimum, water freely passes between the two ions and we, therefore, ascribe it to SSM. Both minima are unstable compared to the dissociated state of the ions. The CCM is destabilized by a larger amount, approximately −0.96 kcal∕mol. Our Na – Na PMFs are qualitatively similar to those published previously.^{18, 20, 100, 102, 103, 104} For instance, Guàrdia et al.¹⁰⁰ and Lyubartsev et al.^{102, 103, 104} reported the first minimum at ≈3.8 Å and the second minimum at ≈6.0 Å, in agreement with our predictions.

The first minimum in the PMF of the anionic Cl–Cl pair occurs at r = 5.08 Å. Its meaning is similar to that of CCM in the Na – Na pair, but now water molecules form hydrogen bonds with the ions, instead of bridging them by oxygens.¹⁰⁰ The second minimum appears at r = 7.73 Å and corresponds to the SSM conformations. As seen in Fig. 4c, the bound states of the Cl–Cl pair have almost the same free energy as the dissociated states. But extrapolations beyond 12 Å using the limiting q ² ∕εr dependence clearly show that the bound states are unstable. The shape of the Cl–Cl PMF in water remained controversial for some time. Using the reference intraction-site model (RISM) integral equation, Pettit and Rossky¹⁷ first reported a deep minimum in PMF at r = 3.4 Å, corresponding to a tightly bound chloride dimer. The existence of the dimer was subsequently confirmed by the same group in MD simulations using cut-off electrostatics schemes.¹⁸ Around the same time, Yu and Karplus¹⁰⁵ pointed out that the integral-equation calculations can be very sensitive to the approximations employed in them, leading to the appearance or disappearance of extrema in PMFs. Subsequent work by Hummer et al.⁹⁵ showed in direct comparison between the MD and RISM calculations that the close-contact minimum appears because of the flaws in the latter. Similarly, Guàrdia et al.¹⁰⁰ suggested that the minimum seen in the MD simulations¹⁸ can be attributed to a faulty electrostatics scheme. Backed up by other theoretical¹⁰⁶ and some experimental evidence,^{95, 100} it is now accepted that the first minimum in the Cl–Cl should occur around 5 Å, not around 3.4 Å as suggested earlier.¹⁷ Our simulations support this conjecture.

The effect of the simulation box size on PMFs is noticeable but small, as shown in Figs. 4b, 4c and in Table 3. The magnitude of the deviation of the PMFs obtained in the L = 30 Å box from their PME counterparts is less than or equal to 0.2 kcal∕mol everywhere. It is, therefore, impossible to determine whether these differences are statistically meaningful. The small-size artifacts for the like-charged ions seem to be less severe than those observed in the opposite-charge Na – Cl system.

Effect of counterions

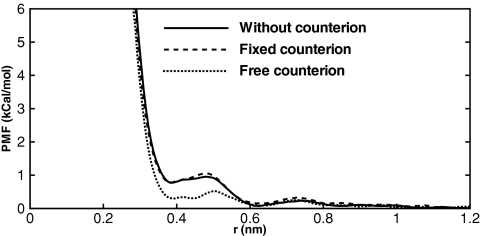
In this work, we compute the reference PMFs with the help of the PME method,⁶⁶ which is considered one of the most accurate electrostatics schemes currently available. Yet even this method has its limitations. One controversial issue concerns conducting PME simulations for non-neutral systems. In addition to the corrections to the charging free energy, as discussed above, such simulations require special handling in other circumstances, for instance under constant pressure.⁸⁴ In its conventional formulation,⁹ PME assumes uniform neutralizing background for net-charged systems. The effect of this background on the simulated properties is poorly understood. This uncertainty has led to the empirical rule of thumb recommending neutralization of charged systems by the addition of counterions.^{35, 50} Apart from the purely conceptual question of how different the two neutralization models are (the uniform background and explicit counterions), and which of them is more “correct,” adding counterions may create a technical problem associated with their slow equilibration. Because of their low demixing rate, added counterions in simulations of solvated proteins, for instance, are known to lead to hysteresis and strong dependence on the initial placement of the ions.^{51, 52, 53} In light of these difficulties, it makes sense to compare directly the two neutralization methods for a simple solvation problem, such as interionic PMF.

We showed in the preceding section that the PMFs computed for the Na – Cl pair by the ICSM are largely free of finite-size artifacts. Since the validity of this method does not depend on the total charge of the simulated system, there is no reason to doubt its accuracy for the same-charge Na – Na and Cl–Cl pairs. We therefore can use their PMFs as a reference in our analysis of the effect of counterions in the PME simulations. To test this effect we added two Cl anions to the Na – Na simulations and fixed their positions at two corners of the simulation box. The resulting PMF, shown in Fig. 5, is indistinguishable from those obtained without counterions. We therefore conclude that both neutralizing schemes perform correctly and equally well. Releasing the ions and conducting simulations over the same amount of time as without counterions (convergence time for PMFs) can test the effects of counterions equilibration. The PMFs obtained in this way are also shown in Fig. 5. Clear differences with the converged PMFs emerge, suggesting that the method using free counterions for neutralization should be avoided.

Figure 5.

Potentials of mean force computed for the Na – Na ion pair in PME simulations. The total charge in the simulations without counterions is neutralized by uniform charge background. This has the same effect as explicit counterions fixed in space. Free counterions are seen to lead to markedly different PMFs. The simulations were performed in a L = 45 Å box. The free energy curves were made to overlap at r = 1.2 nm.

CONCLUSIONS

In this paper, we tested the performance of the new electrostatics solvation model ICSM, introduced by us earlier,³⁸ in simulations of ions solvated in water. Two aspects of the ion solvation were examined: (i) charging free energy and (ii) potentials of the mean force among ions. These applications have implications for how the ICSM can be used to model biological molecules. For each task, our simulations lead to the following conclusions:

1. When corrected for finite-size effects, the ICSM reproduces well the ionic solvation energy of charging. This application is directly relevant for the free energy evaluation of the charged and neutral forms of ionizable amino acids, as in pKa estimates and charge-transfer reactions in proteins. Another potential application is force-field parameterization for numerical solvers of the Poisson–Boltzmann equation.^{107, 108, 109, 110} Although computing corrections to ΔG _cg is relatively easy for a simple ionic solute, it may become more of a challenge for a solute with arbitrary shape, such as a protein. In that case, methods that need smaller corrections would be seen as more advantageous. Using the sodium ion as a benchmark, below we attempt to assess the performance of different electrostatics schemes as applied to more general solutes. Table 4 displays the charging free energy $\Delta G_{\mathrm{cg}}^s$ computed by a number of common electrostatics methods, including the ICSM and the lattice-sums. The ICSM data are shown in the smallest box examined, L = 30 Å, with maximum possible finite-size effects. The data of the PME and straight cut-off method (CM) are shown in a comparable box with the side of 31.3 Å.⁴⁹ For the PME, the correction associated with the P-type summation was added since it is almost constant for all simulation boxes. The CM data are shown for the maximum allowed cut-off distance of 14 Å. For comparison, we also computed $\Delta G_{\mathrm{cg}}^s$ by the spherical solvent boundary potential model (SSBP)⁷⁰ using a cavity of 15 Å radius. The simulations were performed by CHARMM¹¹¹ with the setup as published previously.⁷⁰ Additionally, the data for a finite water droplet of comparable size, 18 Å radius, is also included.⁴⁹

   In absolute numbers, the ICSM works better than any other method we examined. Its error of 35 kJ∕mol is slightly lower than the 38 kJ∕mol error of the close second CM method. The two methods differ in reaction field and finite-size contributions to the free energy. The former apparently offers a better balance of neglected terms. Furthermore, the straight cut-off method has other significant flaws that erode its performance. For instance, it is known to produce unphysical correlations among ions solvated in water.^{21, 65} It is very likely that this method will predict wrong solvation energy as well when two or more ions are considered. As we showed in the preceding sections, no such limitation exists in the ICSM.

   Next in performance comes the PME and the finite droplet model, which both offer a 50–60 kJ∕mol error in ΔG _cg . The main source of artifacts in the PME method is the periodicity of the electrostatic potential. In the ICSM, it is the finite size of the simulation box, and to a lesser extent periodic replication of some parts of the simulated system. We see in Fig. 3 that these two effects behave differently with increasing L. The ICSM is much less affected by the finite-size effects, especially for a large L, demonstrating a clear advantage in accuracy. The finite droplet models^{78, 79} are strongly affected by surface effects, which in addition to the usual finite-size correction require a correction associated with the crossing of the vacuum-liquid boundary. The latter is model-specific and, importantly, grows with the size of the simulation box. As a consequence, the uncorrected $\Delta G_{\mathrm{cg}}^s$ deteriorate with the system size,⁴⁹ so that no convergence is observed. This is unlike the ICSM, whose free energy rapidly converges to the reference value.

   With the −388 kJ∕mol solvation energy, the SSBP is seen to perform worst for the given test. This method is similar to the ICSM in spirit, but differs from it in two important aspects. First, the ICSM does not create a vacuum layer at the boundary between the explicit and implicit solvents. The layer is present due to technical reasons but its effect on $\Delta G_{\mathrm{cg}}^s$ is non-negligible. A simple continuum-based calculation for a common SSBP setup with the 10 Å cavity radius and 2.4 Å layer thickness⁷⁰ leads to up to 10 kJ∕mol error in $\Delta G_{\mathrm{cg}}^s$. Second, the reaction field in the SSBP is computed using the Kirkwood series, while the image-charge approximation is employed in the ICSM. We showed in our previous work⁴¹ that the image approximation is more than an order of magnitude faster at comparable accuracy. The consequence is that an increasingly large number of terms are needed in the Kirkwood series to achieve convergence in $\Delta G_{\mathrm{cg}}^s$ for off-center ion locations. Our tests show that a 5 Å ion displacement in the simulations with 15 Kirkwood terms shown in Table 4 leads to a 8 kJ∕mol lower solvation free energy. Uncorrected $\Delta G_{\mathrm{cg}}^s$ computed by the ICSM are virtually invariant across the productive part of the simulation cell. The corrections to the SSBP free energy come from the vacuum-liquid potential jump, which results from the water molecules near interfaces developing positional and orientational preferences different from the bulk, and from the finite-size effects. It is not feasible at the moment to evaluate the relative importance of these two corrections because of the lack of suitable expressions for them. Expressions are available for the vacuum correction for planar and spherical interfaces,^{49, 57} but they cannot be employed directly in the SSBP since this method applies additional angle-dependent interfacial potential. The finite-size corrections could, in principle, be evaluated by the dielectric self-consistent field (DSCF) method^{87, 88} used for the ICSM.

   In summary, a comparative analysis of the methods presented in Table 4 show that the ICSM is the least affected by finite-size effects electrostatics method. We therefore argue that it is most suitable for computing the uncorrected charging solvation energy for solutes of arbitrary shape and charge distribution.

2. In addition to single ions, the ICSM is seen to perform well for pairs of ions. Correlations that exist between two ions in solvent, described quantitatively by the potential of mean force, are properly reproduced regardless of whether the ions are bearing the same or opposite charges. The proper balance of electrostatic solvation forces across interparticle distances is important in protein modeling for predicting the stability of salt-bridged conformations or for ion binding. That the validity of the ICSM does not depend on the charge of the solute allowed us to gain insights into how the PME method is used in the context of net-charged protein models. In particular, we find that adding immobile counterions has no effect on the PMF of same-charge ions. At the same time, poor equilibration may drastically alter the PMF when the counterions are released. We therefore conclude that counterions should be avoided in simulations of proteins, if they are known to have no functional role.

Table 4.

Comparison of charging free energy $\Delta G_{\mathrm{cg}}^s$ of sodium ion computed in this work by the ICSM and SSBP model (Ref. ⁷⁰) with the values reported for systems of comparable dimensions by PME, straight cut-off method and finite-drop model (Ref. ⁴⁹).

Method∕model	$\Delta G_{\mathrm{cg}}^s$ (kJ∕mol)
ICSM (30 Å box)	−445
PME with P-type correction (Ref. 49) (31.3 Å box)	−420
Straight cut-off with Rc =14 Å (Ref. 49) (31.3 Å box)	−442
Finite droplet (Ref. 49) (18 Å radius)	−429
SSBP (15 Å radius)	−388
Reference value (Ref. 49)	−480

The main motivation for developing the ICSM was to eliminate the artifacts of lattice-sum methods associated with the periodicity of electrostatic potentials. The calculations performed here show that this goal has been largely achieved. The demonstrated ability of the ICSM to suppress the periodicity artifacts makes it an ideal tool for examining other systems∕conditions in which these artifacts may play a role. Previous work by Hünenberger et al.^{33, 36, 37} has identified two other potential factors: (i) a solvent of low dielectric permittivity and (ii) a solute cavity of non-negligible size compared to the unit cell size. The significance of these effects will be examined by the ICSM in our future work.

APPENDIX: CORRECTIONS TO THE SOLVATION ENERGY OF AN ION IN THE ICSM

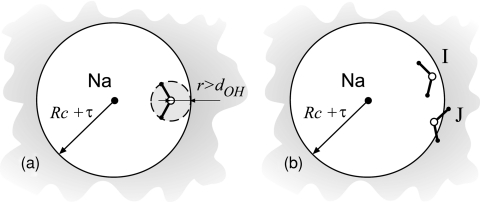
We use the terminology of Kastenholz and Hünenberger,⁵⁷ who identified three types of corrections in computer estimates of the charging solvation energy, to analyze the results of our simulations. The corrections of type A account for non-Coulombic forms of electrostatic interactions and do not apply in our model. The second C-type correction is applied when water-vacuum interface is present. As we explained in the main text, there is no such interface in our model and, therefore, the correction does not apply. The first type-C correction is introduced to explain the difference between the so-called P- and M-type truncations of electrostatic interactions. The first truncation type sums up interactions between the water molecules according to the interparticle distances of their constituent atoms. Referred to as atom-based, this truncation is applied whenever an interatomic distance exceeds a certain predefined value. The M-type truncation, on the other hand, operates on distances between groups of charges, such as those in a water molecule. It is applied when the centers of two groups are beyond a cut-off distance. When applied to the ionic charging free energy problem, the two truncation types produce different potentials at the site of the ion Φ. Introducing an auxiliary state of the simulated water in which orientations of all water molecules are completely disordered, the so-called orientational disorder limit (ODL), Kastenholz and Hünenberger⁴⁹, ⁵⁷ have shown that the P-summation leads to a nonzero potential Φ_ODL , and thus nonvanishing ΔG _cg . Since liquids in the ODL limit cannot be polarized, the nonzero ΔG _cg signals inconsistency of this summation scheme. The M-type truncation based on the location of the oxygen atom in water molecules, on the other hand, produces no spurious potential at the ionic site in the ODL limit and is, therefore, deemed appropriate for the ΔG _cg calculations. Whether the second type-C correction applies to the ICSM or not depends on how all the charges present in the system are divided into explicit and implicit regions. Figure 6 shows two possible M-type schemes. In scheme (a), only the water molecules whose oxygen atoms are at least a distance d _OH away from the boundary of the central sphere, see Fig. 1, are included in the explicit part. Here d _OH is the length of the oxygen–hydrogen bond. As Fig. 6a explains, all water molecules are allowed to rotate, guaranteeing that there will be no spurious potential in the ODL limit. An alternative scheme (b) sorts molecules according to the positions of all three of their atoms. If the whole molecule is within a cut-off, as in example I in Fig. 6b, it is included in the explicit part. The water molecules are not split in this scheme, making it an M-type. In the orientational disorder limit, however, not all potential created by waters close to the boundary will be compensated. For instance, configuration J is needed to balance the effect of configuration I but is missing because its hydrogen atoms are beyond cut-off. As a result, a nonzero potential arises at the central ion location. We estimated this potential to be close to 39 kJ∕mol for the current system. If scheme (b) is used to compute ΔG _c by the ICSM, the C-type correction needs to be applied. In the present work, we use the scheme shown in Fig. 6a, so no correction is necessary.

Figure 6.

Two alternative schemes for the separation of all charges in the ICSM into explicit and implicit regions. In scheme (a), only water molecules whose oxygen atom is more than the length of the hydrogen-oxygen bond, d_OH , away from the sphere boundary are included in the explicit part. This choice allows for free rotation of waters near the boundary. In scheme (b), water molecules whose all three atoms, as in example I, are within R_c +τ are included in the explicit part. Example J shows that not all waters in this scheme are allowed to rotate. As a consequence, this scheme will create a nonzero potential at the site of the sodium ion in the orientational disorder limit.⁵⁷ In the terminology of Kastenholz and Hünenberger (Ref. ⁵⁷) such potentials lead to the first C-type correction.

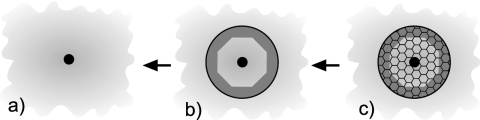
The final correction type B accounts for the error introduced by the finite size of the simulated system. As in previous studies (Refs. ⁴⁹, ⁵⁷, and references therein), we estimate it using a continuum electrostatics approach. The corrections in our method have two origins: (a) finite size of the central dielectric sphere and (b) periodicity within the sphere. The first effect relates to the applicability of continuum approximation to finite systems. And the second effect arises because certain regions in the main simulation cell are periodically imaged, see Fig. 1b. To estimate how much solvation energy is associated with these two effects, we consider continuum analogs of our atomic system as shown in Fig. 7. The reference system, Fig. 7a, is an ion immersed in an infinite bath of dielectric medium with permittivity ε. The solvation energy of that system is given by the Born model, $\Delta G_{\mathrm{Born}}=-\frac{q^2}{2R_I}(1-1∕\epsilon )$, where R_I is the radius of the ion. In our simulations, part of that continuum, the central sphere, is treated explicitly, with certain areas of the main simulation cell periodically imaged, as shown in Fig. 7b by shading. The free energy difference between systems in Figs. 7a, 7b is the correction needed to obtain a size-independent estimate of the solvation energy.

Figure 7.

Succession of models that allowed us to compute finite-size corrections to the ionic solvation energy ΔG_c .

To estimate the solvation energy of system (b), we use the DSCF method.⁸⁷, ⁸⁸ Within this method, the continuum domain Ω occupied by the studied system is divided into a number of smaller space-filling objects Ω_i , each of which is located at a radius vector ${\vec{r}}_i$ from the center and is assigned a dipole moment ${\vec{\mu }}_i$. We use truncated octahedron boxes to perform space discretization, as is schematically illustrated in Fig. 7c. Within the DSCF, the dipole moment at each ${\vec{r}}_i$ is related to the total electric field at that point, ${\vec{E}}_i$, through linear constitutive laws. This results in a closed system of equations for the dipoles:⁸⁷, ⁸⁸

$${\vec{\mu }}_i=\frac{3}{4\pi }\frac{{\epsilon }_i-1}{{\epsilon }_i+2}\Delta V({\vec{E}}_0+{\vec{E}}_d),$$ (A1)

where ε_i is the dielectric permittivity at point ${\vec{r}}_i$, ΔV is the volume of Ω_i , ${\vec{E}}_0$ is the electric field created by the explicit charges present in the system, and ${\vec{E}}_d$ is the electric field created by dipoles other than the ith. In our setup, ${\vec{E}}_0=q∕r_i^3{\vec{r}}_i$ is the field of a point charge at the center of the sphere. The dipole field ${\vec{E}}_d$ contains contributions ${\sum }_{j\ne i}{\vec{E}}_j^d$ from other dipoles within Ω, where ${\vec{E}}_j^d=-{\vec{\mu }}_j∕|{\vec{r}}_{ij}{|}^3+3\left({\vec{\mu }}_j{\vec{r}}_{ij}\right)∕|{\vec{r}}_{ij}{|}^5{\vec{r}}_{ij}$ and ${\vec{r}}_{ij}={\vec{r}}_i-{\vec{r}}_j$. Additionally, the reaction field created by these dipoles, as well as the central charge which is zero due to symmetry, must be added, ${\sum }_j{\vec{E}}_j^{\prime }$. To compute these latter contributions, we need expressions for the reaction field created by a point dipole inside a dielectric cavity.

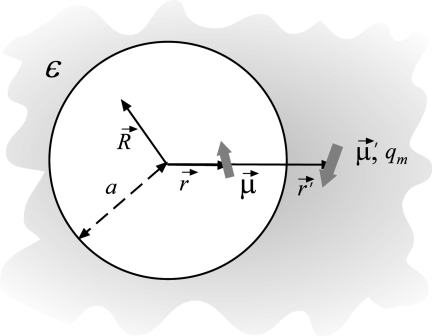
These expressions are derived by analogy with the image approximations for the reaction field of point charges. As explained in Fig. 8, let us assume that we limit ourselves to one image only. The reaction field at point $\vec{R}$, $\varphi \left(\vec{R}\right)$, created by a finite dipole made up of a charge −q placed at location $\vec{r}-\vec{l}∕2$ and another charge q placed at $\vec{r}+\vec{l}∕2$, with the dipole moment $\vec{\mu }=q\vec{l}$, can be computed exactly. This potential can then be expanded around the location of the source dipole $\vec{r}$, leading to a series in powers of $\vec{l}$ and its components. In the point-dipole limit, where $|\vec{l}|\to 0$ while $\vec{\mu }$ is kept constant, only two terms in the series survive: one is the electric field created by a charge ${\displaystyle q_m=-\gamma \left(a∕r\right)\left(\vec{r}\vec{\mu }\right)∕r^2}$ placed at the location of the first charge-image ${\displaystyle {\vec{r}}^{\prime }={\left(a∕r\right)}^2\vec{r}}$, while the other is the field created by a dipole ${\displaystyle {\vec{\mu }}^{\prime }=\gamma {\left(a∕r\right)}^3\vec{\mu }+{\left(a∕r\right)}^{2}2q_m\vec{r}}$ placed at the same location. Here γ=(1−ε)∕(1+ε) and other notations are explained in Fig. 8. It is seen that the generalization of the image-charge approach to dipoles is not straightforward. In addition to image dipoles, which one would expect, also image charges need to be considered. The latter vanish, however, when $\vec{\mu }$ is perpendicular to the radius vector of the dipole, $\vec{r}$.

Figure 8.

Cartoon illustrating how the reaction field Φ _RF is created by a point dipole placed in a vacuum cavity embedded in a dielectric continuum. An image charge q_m as well as an image dipole ${\vec{\mu }}^{\prime }$ are required to compute Φ_RF anywhere inside the cavity.

In the one-image approximation, the dipolar reaction field at location ${\vec{r}}_i$ is ${\sum }_j{\vec{E}}_j^{\prime }$, where ${\vec{E}}_j^{\prime }=-{\vec{\mu }}_j^{\prime }∕|{\vec{r}}_{ij}^{\prime }{|}^3+3\left({\vec{\mu }}_j^{\prime }{\vec{r}}_{ij}^{\prime }\right)∕|{\vec{r}}_{ij}^{\prime }{|}^5{\vec{r}}_{ij}^{\prime }+q_{m,j}∕|{\vec{r}}_{ij}^{\prime }{|}^3{\vec{r}}_{ij}^{\prime }$ and ${\vec{r}}_{ij}^{\prime }={\vec{r}}_i-{\vec{r}}_j^{\prime }$. All primed properties refer to image dipoles as explained above and in Fig. 8. Similar expressions can be derived for multi-image approximations. However, we limit ourselves to one image only in this paper, as this approximation was seen adequate previously.³⁸ With the expressions linking electric fields and dipole moments, ${\vec{E}}_d={\sum }_{j\ne i}{\vec{E}}_j^d+{\sum }_j{\vec{E}}_j^{\prime }$, Eq. A1 can be solved iteratively (setting uniform dielectric constant ε_i =ε) to generate dipole distributions ${\vec{\mu }}_i$ for any charge of the ion q. The fields created by these dipoles then can be summed up to produce the electrostatic potential at q and thus the solvation energy.

We implemented the above algorithm numerically by dividing the interior inside the central sphere of radius R_c +τ into small truncated octahedral boxes with the side L_B =L∕N_g , where L is the size of the main simulation box and N_g is the number of grid points in one dimension. Five sizes, L = 28, 36, 68, 76, and 92 Å were considered with the size of the ion set at R_I =2 Å. The number of grid points N_g was then chosen such that L_B =R_I . Dipole moments in the periodically imaged parts, see Fig. 7b, were replicated from equivalent dipoles within the main simulation box. The discretization of the space necessarily produces an error. The solvation energy of the system in Fig. 7c, ΔG_N , will, therefore, be different from the energy for Fig. 7b. To test the magnitude of this error, we increased N_g twofold, so that L_B =R_I ∕2, and recalculated ΔG_N . The results changed by less than 10 kJ∕molso we take this number as an estimate of the numerical error in our calculations. Finally, to minimize the discretization error in ΔG_N , a discrete version of system in Fig. 7a is needed. Solving the DSCF equations for an infinite system is not possible, however. We therefore obtain its solvation energy, ΔG _Born , by extrapolation from system (c). Fitting ΔG_N as a function of L to the template A+B∕L ^ν returns A = −299 kJ∕mol, B = 408, and ν = 1.68, where L is measured in nm. We therefore can identify A with the Born solvation energy ΔG_Born of the discretized system, which produces a 12% error compared to the −342 kJ∕molenergy of the continuum model. The finite-size correction is estimated as the difference ΔG _Born −ΔG_N , resulting in ΔG_c =−408∕L^1.68 kJ/mol. Figure 3 shows that the agreement between the actual data points and the fitted curve is very good. The correction decays to the level of statistical uncertainty for L ⩾ 80 Å, allowing the ICSM to estimate the solvation energy for such systems error-free.