Determining the View of Chest Radiographs

Abstract

Automatic identification of frontal (posteroanterior/anteroposterior) vs. lateral chest radiographs is an important preprocessing step in computer-assisted diagnosis, content-based image retrieval, as well as picture archiving and communication systems. Here, a new approach is presented. After the radiographs are reduced substantially in size, several distance measures are applied for nearest-neighbor classification. Leaving-one-out experiments were performed based on 1,867 radiographs from clinical routine. For comparison to existing approaches, subsets of 430 and 5 training images are also considered. The overall best correctness of 99.7% is obtained for feature images of 32 × 32 pixels, the tangent distance, and a 5-nearest-neighbor classification scheme. Applying the normalized cross correlation function, correctness yields still 99.6% and 99.3% for feature images of 32 × 32 and 8 × 8 pixel, respectively. Remaining errors are caused by image altering pathologies, metal artifacts, or other interferences with routine conditions. The proposed algorithm outperforms existing but sophisticated approaches and is easily implemented at the same time.

ALTHOUGH MODERN IMAGING MODALITIES such as computed tomography or magnetic resonance imaging increase in number while many types of conventional x-ray examinations decrease, the upright or supine chest radiograph is still by far the most common x-ray taken, accounting for at least one third of all examinations in a typical radiology department.¹ However, the reading of chest radiographs is extremely challenging, even for specialists and therefore is a wide area of research for computer-aided diagnosis (CAD). In particular, the segmentation of lung fields or the rib cage, as well as local analysis such as nodule detection, are the most frequently studied problems in automatic image processing of chest radiographs.² To implement a CAD system into the clinical environment, it is important to correctly identify the orientation of image acquisition, ie, posteroanterior (PA) or anteroposterior (AP) versus lateral view,^3,4 as well as top-down, left-right, and mirroring.^5,6,7 These are also essential preprocessing steps for data handling in picture archiving and communication systems (PACS) and content-based image retrieval (CBIR).⁸

Pietka and Huang⁵ presented an automatic three-step procedure that determined the image orientations of computed radiography chest images and rotated them in steps of 90 degrees into a standard position for viewing by radiologists. Based on horizontal and vertical pixel profiles, the orientation of the spine within the images was detected and the upper extremities were located. Finally, the lungs were extracted and compared to decide whether the image was flipped. Based on a set of 976 images, a rate of 95.4% correctly orientated radiographs was reported. To simplify this approach and to make it suitable for hardware implementation, Evanoff and McNeill⁷ applied linear regression to only two orthogonal profiles. Then, the edge of the heart was located to make sure that the image is not displayed as a mirror image. However, only 90.4% correctness was reported based on a data set of only 115 chest images. A more sophisticated approach proposed by Boone et al⁶ extracted feature data from 1,000 digitized chest radiographs to train a neural network for orientation correction. Based on another set of 1,000 images which had not been seen during training, 99.4% were correctly rotated, but the overall correctness including mirroring was only 88.8%. Harreld et al³ also applied neural networks to identify the view position of chest radiographs and reported an accuracy of 98.7%. However, the design of neural networks is sophisticated, their training requires a large number of examples, and also, it is desirable to develop more accurate methods for the identification of correct views of chest radiographs.

Recently, Arimura et al⁴ have proposed an advanced computerized method by using a template matching technique for correctly identifying either PA or lateral views. They applied it to a large database of approximately 48,000 PA and 16,000 lateral chest radiographs. In particular, 24 templates were generated by the summation of, in total, 464 reference images, which had been manually selected and combined. A two-step scheme was applied. If the difference between the two largest correlation coefficients with three PA and two lateral templates was above a certain threshold, the second step was applied to distinguish small and large patients and to classify the radiograph based on another 11 to 19 particular templates. Although an accuracy of 99.99% was reported, the manual generation of such a large number of templates is cumbersome, time-consuming and, most crucial, it is highly observer-dependent. Therefore, the technique of Arimura et al is difficult to reproduce and to apply to other PACS or CBIR environments.

In this article, we present a simpler method based on the nearest-neighbor (NN) classifier resulting in almost equal accuracy rates but with greater computational efficiency and full automation.

MATERIALS AND METHODS

Our approach to the identification of the view position of chest radiographs is embedded in a system for content-based image retrieval in medical applications (IRMA).⁸ IRMA is a distributed system using a central relational database that stores administrative information about distributed objects (image data, methods of computation, and features resulting from method processing) and query processing to control distributed computing on all IRMA workstations.⁹

Image Data

The IRMA database is used as reference for this study. Currently, it holds 1,867 chest radiographs that have been selected arbitrarily from clinical routine in a radiology department of a 1,500+- bed hospital. In particular, 1,266 radiographs in posteroanterior/anteroposterior (PA/AP) view and 601 images in lateral view position are available. Scanned at a resolution of 300 dpi with 8 bit quantization, the size of radiographs ranges between 2,000 and 4,000 pixels in both the x- and y-directions. The non-lateral images can be differentiated into plain images of upright patients, supine images of critically ill patients from intensive care units, and pediatric images in both suspended and lying positions (Fig 1). Because it is representative of a large radiological department, the database contains material of all grades of image quality: (i) regular images with decent contrast and no severe pathology; (ii) medium-grade images with low contrast and/or partial technical defects, eg, collimation errors, over-/under-exposure; and (iii) poor quality images with metal artifacts, grave technical problems, and/or severe pathologies with significant image changes.

Figure 1.

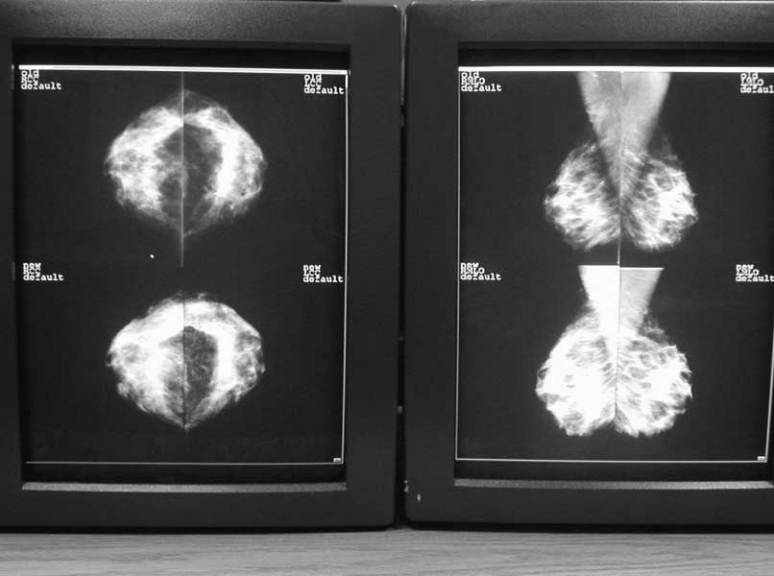
The chest radiographs within the IRMA database are used as references: (a) high-contrast PA view from an adult patient; (b) and (c) supine AP view from intensive care units of an adult and an infant patient, respectively; (d) and (e) lateral views of adult patients in upright position, also high contrasted.

Size Reduction

Automatic categorization of PA/AP and lateral view positions is achieved in two steps. First, the image is substantially reduced in size. Regardless of the initial aspect ratio, a maximal-sized squared intermediate image is obtained by linear interpolation, where the number of pixels in the x and y directions is the next smaller power of two. Integrating adjacent pixels, a feature image of size h × h is generated (Fig 2).

Figure 2.

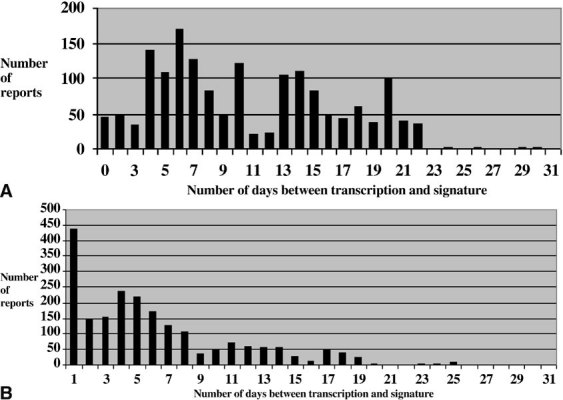
The h × h-sized feature images (h = 64, 32, 16, 8, 4, 2, 1) were obtained from the upper left PA/AP chest radiograph.

Distance Measures

To determine the similarity between a reference image r(x,y) and the sample radiograph under investigation s(x,y) a distance measure is required. Because of its mathematical simplicity, the Euclidean distance

is frequently applied to accomplish such a task. However, D_E is affected by differences in the general illumination of the images to be compared. In other words, the Euclidean distance becomes large if the x-ray dose is changed but the patient imaged and the imaging geometry are maintained between the acquisition of r and s. Therefore, the empirical correlation coefficient, which is also referred to as the normalized crosscorrelation coefficient or cross covariance coefficient,

is applied, where

and

denote the means of r and s, respectively. To compensate translations within the radiographs, the maximum of the covariance function D_F (m,n) is determined by

where m and n denote the integer shift between the feature images r and s. The integer d denotes the maximal displacement, which is chosen to depend linearly on the size h of the feature images

where ⌊·⌋ denotes the truncation to the next lower integer value. Note that (2) results from (3) for the special case of d = 0. Hence, D_F ≡ D_V if h < 8.

Although shifts in the x and y directions are handled in (3), other global transforms such as scaling, rotation, or axis deformation may occur in chest radiographs. In 1993, Simard et al¹⁰ proposed an invariant distance measure called tangent distance. A transformation t(r,α) of an image r(x,y), which depends on L parameters α ∈ ℜ^L (eg, the scaling factor and the rotation angle), typically leads to nonlinear, difficult to handle alterations in pattern space. The set of all transformed patterns is a manifold of, at most, dimension L in pattern space. The distance between two patterns can now be defined as the minimum distance between their respective manifolds, being truly invariant with respect to the L regarded transforms. However, computation of this distance is a hard nonlinear optimization problem and, in general, the manifolds do not have an analytic expression. Therefore, small transforms of the pattern r(x,y) are approximated by a linear tangent subspace to the manifold at the point r(x,y). The subspace is obtained by adding to r(x,y) a linear combination of the vectors v_l(x, y), l = 1,...,L that are the partial derivatives of t(r,α) with respect to α_l and span the tangent subspace. The tangent distance D_T is then defined as the minimum distance between the tangent subspaces of reference r(x,y) and observation s(x,y) (two-sided tangent distance). In the experiments, only one of the two subspaces was considered (one-sided tangent distance):

This distance can be computed efficiently as the minimization is easily solved by standard linear algebra techniques, and it is invariant to small amounts of the transformations considered. Simard et al proved D_T to be especially effective for the task of handwritten character recognition.¹⁰ In addition, it has been shown in a previous study that D_T outperforms many other techniques when applied to the classification of radiographs.¹¹ Optimal results were obtained when the tangent distance was combined with an image-distortion model that compensates for local image alterations, eg, caused by noise, pathologies, varying collimator fields, or changing positions of the scribor in a radiograph.¹¹ Therefore, we applied this extended D_T to distinguish PA/AP and lateral views of chest radiographs. In our experiments, L = 7 was chosen, modeling affine transforms and contrast variations.

Classification

Instead of computing the distance to a template obtained from the summation of references, as proposed by Arimura et al,⁴ a k-nearest neighbor (k-NN) classification scheme is used. In other words, D_E, D_V, D_F, or D_T is computed to all references, and the k most similar references are determined. The classifier then chooses the class with most examples within this set of k-NN. With respect to a previous investigation,¹² we set k = 5. Based on the entire set of 1,867 radiographs, leaving-one-out experiments were performed. All images were successively selected for testing, and the training is done with the remaining 1,866 radiographs. The number of errors is counted over all 1,867 experiments.

Simulation of Arimura’s Method

To compare the classification results to the approach of Arimura et al⁴ three PA/AP radiographs representing the classes (i) to (iii) mentioned before and two lateral reference images of different chest width were selected (Fig 1). They were reduced in size applying the method described earlier. This approximates the first step in Arimura et al,⁴ where, however, the 5 templates where obtained from summation of 430 references (230 frontal images and 200 lateral images). Because the addition of instances is suitable to increase the signal-to-noise ratio only if geometric transforms such as translations or rotations do not occur, the quality of classification improves when the similarities of an image to be classified are individually computed to all of the references. This fact has also been verified experimentally in a previous study.¹² Therefore, we did not attempt to reproduce the second step of Arimura’s scheme. Instead, we arbitrarily selected 230 frontal and 200 lateral radiographs for training, and the remaining images were used for testing.

RESULTS

The complete results of this study for all distance measures and reference sets are summarized in Table 1. The experiments based on 1,867 and 430 references were executed using a 5-NN classifier, while those referring to 5 reference images were based on a 1-NN classifier.

Table 1.

Results of automatic detection algorithm for identifying the view of chest radiographs

		Pixel Size of Feature image
Distance Measure	Number of References	64 × 64	32 × 32	16 × 16	8 × 8	4 × 4	2 × 2	1 × 1
DE	1,867	98.66	98.66	98.72	98.66	98.86	94.80	81.41
	430	98.77	98.77	98.93	98.82	98.82	94.54	81.90
	5	90.52	90.79	90.09	89.56	87.47	992.98	84.52
DV	1,867	99.20	99.20	99.09	99.14	98.39	91.64	67.81
	430	98.77	98.72	98.66	98.55	97.00	91.12	67.54
	5	96.63	96.52	95.82	95.82	90.31	90.47	67.76
Df	1,867	99.46	99.57	99.25	99.25	98.39	—	—
	430	98.93	99.04	98.93	98.39	97.00	—	—
	5	96.89	96.84	96.79	95.45	90.31	—	—
Dr	1,867	99.62	99.68	99.46	98.55	94.06	—	—
	430	99.25	99.25	99.20	97.97	94.86	—	—
	5	95.02	96.14	96.47	87.63	87.63	—	—

Euclidean Distance

The overall best correctness is 98.9%, resulting from a feature image of 16 × 16 pixels (256 feature values) and 430 reference images. However, the quality of leaving-one-out experiments is only slightly lower. Referring to only 5 prototypes, only 90% correctness is obtained. The worst correctness of 81.4% is obtained with the mean gray value of the radiographs (1 × 1 pixel size or 1 feature value) and leaving-one-out experiments. This correctness is still above the theoretical threshold of 67.8% for this experiment based on 601 lateral and 1,266 PA/AP radiographs, indicating a significant difference in the mean gray value of each group.

Correlation Coefficient

The use of the empirical correlation coefficient D_V as a distance measure was suggested by Arimura et al.⁴ In this case, the overall best performance is 99.2%, obtained with leaving-one-out experiments based on 32 × 32 pixel feature images (1,024 feature values). It is remarkable that the correctness as compared to the Euclidean distance is significantly improved for the 5-prototypes method, where performance reaches 96.6% for the largest size of feature images. Because D_V is independent of the mean gray value, the worst classification of about 67.8% is obtained for all methods with 1 × 1 pixel size. Note that this corresponds exactly to the theoretical threshold of this experiment.

Correlation Function

Determining the maximum of the correlation function compensates horizontal and vertical shifts of the thorax position within the chest radiographs. Hence, further improvement is obtained in almost all experiments. Because the displacement is adapted to the size of the reduced image, experiments for smallest image sizes were skipped. The best correctness is 99.6% using the 5-NN classification scheme based on 32 × 32-sized feature images. This means that eight images were misclassified (Fig 3). Reducing the number of feature components to 64 (8 × 8-sized feature images), the correctness is still 99.3%. Referring to only 430 prototypes, still a correctness of about 99% is obtained for 32 × 32-sized feature images.

Figure 3.

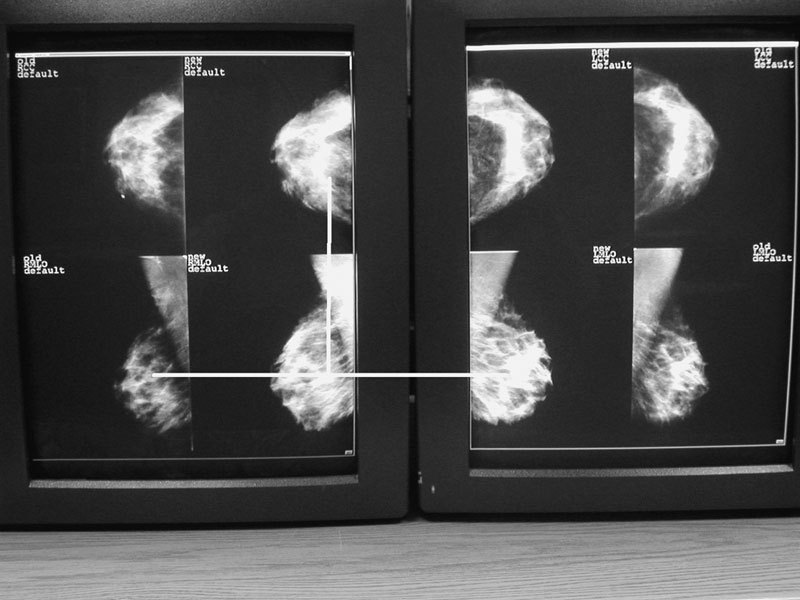
Eight images were misclassified using the correlation function and 32 × 32-sized feature images.

Tangent Distance

The tangent distance compensates for intensity differences and small global transformations such as rotation, scaling, shearing, and translations, while the image distortion model compensates for small local transforms like noise or changing scribor positions.¹¹ Hence, further improvement in accuracy is obtained. Especially for large numbers of references and a sufficient size of the feature images, the tangent distance D_T outperforms the correlation function D_F. For instance, a 99.3% correctness is obtained with 32 × 32-sized feature images, whereas that obtained with the covariance function is only 98.5%. The best correctness of 99.7% is obtained with 32 × 32-sized feature images and the 5-NN classifier.

Computing Times

Although the leaving-one-out experiments for large image sizes are time consuming, the classification of a single item is reasonably fast for all methods. For a feature image with 16 × 16 pixels, runtimes are about 0.005 s, 0.02 s, 1.7 s, and 2.0 s for D_E, D_V, D_F, and D_T, respectively. However, increasing the image size increases the runtime, especially for the covariance function-based method, because here, also d is increased. For a 32 × 32-sized template, classification based on D_F and D_T takes about 22.5 s and 7.0 s, respectively. All time measurements were obtained on a regular Pentium III PC with 1 GHz clock running under Linux. All programs are compiled with GNU C++ 2.95 with standard optimization.

DISCUSSION

Automatic differentiation between PA/AP and lateral views of chest radiographs is an important step for several image processing tasks. A recent approach is based on manual selection and combination of radiographs for template generation. We have shown that this task can be fully automated and substantially simplified if the maximum of the normalized correlation function is used directly for classification. Based on 1,867 reference images from the IRMA database, a sufficient precision of 99.3% is obtained for 8 × 8-sized radiographs using 5-NN classification. Applying 32 × 32-sized feature images, the correctness increases to 99.6%. Figure 3 displays the eight radiographs misclassified using the correlation function. All images show severe pathologies, metal devices, or other artifacts such as a frame from misalignment during the scanning process. However, this also proves the IRMA database to be representative of routine applications. Figure 4 displays the five nearest neighbors of one of the misclassified images from Figure 3. Clearly, the rotation of the radiographs before scanning is the reason for misclassification.

Figure 4.

Misclassified image (4a) and its five nearest neighbors ordered by increasing distance (4b–f).

Arimura et al have suggested a 16 × 16 pixel template.⁴ Because a 32 × 32-sized feature image was found to be optimal, but sufficient accuracy can be obtained using 8 × 8-sized images, this result is supported by the more detailed data analysis presented here.

Although the impact of the covariance function is remarkable with respect to the covariance coefficient, the classification correctness obtained with the tangent distance further improves the overall results only slightly. For 32 × 32 pixel features, 99.7% correctness were obtained. This indicates that the compensation of chest position already accounts for most of the affine transformations in chest radiographs and that compensation of the remaining affine transformation components and local distortions has only a small additional positive effect. For sizes of 8 × 8 pixels and smaller, the tangent distance leads to less accuracy of the classifier. This is not surprising, as the effective dimensionality of the feature vector is reduced implicitly by the dimensionality of the tangent subspace (eg, a 6-dimensional subspace for affine transformations). If this reduction is large with respect to the image size (eg, ratio 6/(4 × 4) = 37.5%), then important information may be lost; by comparison, the effect usually is beneficial for larger image sizes (eg, ratio 6/(64 × 64) = 0.15%).

As a result of the local image distortion model within the tangent distance, misclassified images from correlation method and tangent distance do not correspond. Hence, a combination of both distances further improves the overall correctness. In particular, the 32 × 32-sized feature images result in six and eight errors for the tangent distance and the Euclidean distance, respectively. However, only two errors are in common. Using a 10-NN classifier and deciding for the lateral group with lower a-priori probability on equal voting halves the error rate. More sophisticated combinations of both measures will be investigated in the future.

CONCLUSIONS

The IRMA framework enables the validation of numerous image-processing algorithms on a large data set.⁸ Here, it was employed to evaluate and simplify the method proposed by Arimura et al⁴ for automatic detection of the view of chest radiographs. With the normalized cross correlation function as distance measure, the correctness of classification is 99.6%. However, the approach presented here does not need any manual selection of reference images for template generation. Because the detection of the view position and orientation of radiographs is an important preprocessing step for CAD,² PACS,¹³ and CBIR,⁸ numerous applications might benefit from the simple approach presented here.