Analyzing the components of the free-energy landscape in a calcium selective ion channel by Widom’s particle insertion method

Abstract

The selectivity filter of the L-type calcium channel works as a Ca^{2 +} binding site with a very large affinity for Ca^{2 +} versus Na⁺. Ca^{2 +} replaces half of the Na⁺ ions in the filter even when these ions are present in 1 μM and 30 mM concentrations in the bath, respectively. The energetics of this strong selectivity is analyzed in this paper. We use Widom’s particle insertion method to compute the space-dependent profiles of excess chemical potential in our grand canonical Monte Carlo simulations. These profiles define the free-energy landscape for the various ions. Following Gillespie [Biophys. J. 94, 1169 (2008)], the difference of the excess chemical potentials for the two competing ions defines the advantage that one of the ions has over the other in the competition for space in the crowded selectivity filter. These advantages depend on ionic bath concentrations: the ion that is present in the bath in larger quantity (Na⁺) has the “number” advantage which is balanced by the free-energy advantage of the other ion (Ca^{2 +}). The excess chemical potentials are decomposed into hard sphere exclusion and electrostatic components. The electrostatic terms correspond to interactions with the mean electric field produced by ions and induced charges as well to ionic correlations beyond the mean field description. Dielectrics are needed to produce micromolar Ca^{2 +} versus Na⁺ selectivity in the L-type channel. We study the behavior of these terms with changes in bath concentrations of ions, charges, and diameters of ions, as well as geometrical parameters such as radius of the pore and the dielectric constant of the protein. Ion selectivity in calcium binding proteins probably has a similar mechanism.

INTRODUCTION

The selectivity filter of calcium (Ca) channels, especially the highly Ca^{2 +} selective L-type Ca channel, is thought to have a high-affinity binding site for cations.¹ The filter, at appropriate pH, is rich in negatively charged carboxyl groups similar to the binding sites of Ca^{2 +}-binding proteins. Point mutation experiments show that the filter contains four negative charges that make the filter selective for Ca^{2 +} over monovalent cations. The energetics of this selectivity is the main concern of this paper. We compute the components of the equilibrium free-energy landscape of various ions as a function of Ca^{2 +} concentration in the bath to understand how each component contributes to selectivity.

The calculation of free-energy of binding of a ligand to a receptor has drawn considerable attention in the last decades.² Though the theoretical background of free-energy calculations has been known for some time,^{3, 4} their practical use became possible with the appearance of fast computers. After the development of the first simulation methods for free-energy calculations,^{5, 6, 7, 8, 9, 10, 11, 12} application to biomolecular systems started in the middle of the 1980s.^{13, 14, 15, 16, 17, 18} Most free-energy calculations focus on relative free-energy differences between states 1 and 2. This difference is formally given by Zwanzig’s formula:⁴

$$\Delta G=G\left(2\right)-G\left(1\right)=-kT\ln {〈\exp \left(-\Delta U∕kT\right)〉}_1,$$ (1)

where k is Boltzmann’s constant, T is the absolute temperature, ΔU is the energy difference between configurations of the two states, and the 〈⋅⋅⋅〉₁ denotes an ensemble average in state 1. Zwanzig introduced this procedure as a perturbation method, where state 2 is a small perturbation to state 1. Therefore, it is called the free-energy perturbation (FEP) method. In practical biological applications states 1 and 2 can be far from each other, so the difference is usually computed by an integration through small steps between states 1 and 2.

In the case of Ca channels, we are interested in the binding free-energy of a given ionic species i in the selectivity filter from a bath of given ionic concentrations:

$$\Delta G_i=G_i\left(\mathrm{filter}\right)-G_i\left(\mathrm{B}\right),$$ (2)

where B denotes “bath.” The free-energy G_i(B) can be obtained from Eq. 1 assuming that state 1 is the bath electrolyte and that state 2 is produced by adding an ion to the bath electrolyte:

$$G_i\left(\mathrm{B}\right)=-kT\ln {〈\exp \left(-\Delta U^{\mathrm{B}}∕kT\right)〉}_{\mathrm{B}}$$ (3)

and similarly for G_i(filter). This equation formally corresponds to Widom’s particle insertion method,⁵ in which a “ghost” particle is added to the system at uniformly distributed random locations; the energy cost of this insertion is calculated; and the Boltzmann factor is averaged in a simulation sampled over the system without the inserted particle. (That is why it is called a ghost particle.) Widom’s method estimates the excess chemical potential (EXCP) that describes the influence of intermolecular interactions beyond the ideal gas approximation:

$${\mu }_i={\mu }_i^{\mathrm{TOT}}-kT\ln {\Lambda }_i^3=kT\ln c_i\left(\mathbf{r}\right)+{\mu }_i^{\mathrm{EX}}\left(\mathbf{r}\right),$$ (4)

where μ_i is the configurational chemical potential, ${\Lambda }_i=h∕\sqrt{2\pi m_{i}kT}$ is the thermal de Broglie wavelength, h is Planck’s constant, m_i is the mass of the ion, c_i(r) is the possibly space-dependent density (we call it concentration from now on) profile, and ${\mu }_i^{\mathrm{EX}}\left(\mathbf{r}\right)$ is the possibly space-dependent EXCP. The free-energy G_i(B) then corresponds to the EXCP of the ion ${\mu }_i^{\mathrm{EX}}\left(\mathrm{B}\right)$. The free-energy difference then reduces to the calculation of the difference of EXCPs:

$$\Delta G_i=\Delta {\mu }_i^{\mathrm{EX}}={\mu }_i^{\mathrm{EX}}\left(\mathrm{filter}\right)-{\mu }_i^{\mathrm{EX}}\left(\mathrm{B}\right).$$ (5)

Three very important aspects of ion binding in ion channels must be emphasized.

1. The EXCP is strongly space dependent in an ion channel and can change steeply over a wide range. The concentration c_i(r) necessarily changes steeply over a wide range too. Ca^{2 +} ions, for example, can have a large density in the filter (on the order of 10 M), while their concentration can be less than 10⁻⁶ M in the bath (for example, in biological cells). This variation must be mirrored by ${\mu }_i^{\mathrm{EX}}\left(\mathbf{r}\right)$ because μ_i is constant in equilibrium [see Eq. 4]. Therefore, the binding free-energy cannot be characterized simply by a number: one must calculate an EXCP profile $\Delta {\mu }_i^{\mathrm{EX}}\left(\mathbf{r}\right)$ (free-energy landscape) in order to properly describe the energetics of ion binding. Anything that changes the landscape will change the binding free-energy. Rate constants derived from that free-energy are widely used to characterize ion binding to enzymes¹⁹ and their cousin,²⁰ ion channels.²¹ Binding constants cannot be constant if free-energy profiles vary.

2. The other, often overlooked, property of binding free-energies is that they usually depend strongly on the ionic concentrations (e.g., of Ca^{2 +} and Na⁺) in the bath. In molecular dynamics (MD) simulations, the binding free-energy is usually computed at infinite dilution^{22, 23, 24} with little attention paid to the fact that experimental measurements are usually reported over a wide range of concentrations and compositions of the bathing solutions. The ionic composition of the filter (and consequently, the EXCP) changes as the composition of that bath is changed. In the L-type Ca channel, for example, Ca^{2 +} gradually replaces Na⁺ in the selectivity filter as the concentration of Ca^{2 +} is increased in the bath from 0 to millimolar. Therefore, EXCP profiles should be reported as functions of bath electrolyte composition so that simulations can connect to experiments.

3. Third, the structure of the binding site alone is not enough to characterize the conductance properties of the channel. (In this work, we define the binding site as the region of the selectivity filter, where the local concentration is very large.) As we have pointed out previously,^{25, 26, 27, 28, 29} regions outside the binding site, where the ionic concentrations are very small (depletion zones), are equally important in determining the permeation properties of the channel (as they are in determining properties of transistors³⁰). We can look at the permeation pathway as resistors in series, where a slice of the channel along the axis corresponds to a resistor. If the concentration is depleted in such a slice, the resistance in that slice is large. Consequently, the resistance of the whole channel becomes large too. The depletion zones are reflected in the EXCP profiles. The energetics of the EXCP profiles then provides useful information about the formation of depletion zones and the conductance properties of the channel. This is especially important because the current flowing through the channel at various bath concentrations is the primary experimental variable to compare with simulations or theories and also responsible for many biological functions.

The Widom method is frequently overlooked in biomolecular simulations probably because particle insertion is inefficient in dense systems with the explicit water usually used in simulations of biological systems. In this work, we use a simple implicit-water model for the Ca channel that has been successful in qualitatively reproducing experimental data such as the micromolar Ca^{2 +} block of Na⁺ current and other mole fraction effects in mixtures of various ions in the L-type Ca channel.^{27, 28, 31, 32, 33, 34} In our reduced channel model, the terminal groups of the four glutamate side chains (EEEE) are treated as mobile structural ions, and the polarization properties in the channel are tuned by adjusting the dielectric constant of the channel protein.³¹ Competition of ions for space in the highly charged and crowded selectivity filter is the main driving force behind this selectivity, called the charge-space competition (CSC) mechanism.^{35, 36}

In this study, this reduced channel model is studied using equilibrium grand canonical Monte Carlo (GCMC) simulations^{31, 37, 38, 39} and the EXCP profiles are computed with Widom’s particle insertion method^{5, 9} (see the Appendix). Following the recipe of Gillespie,⁴⁰ we decompose the EXCP into various terms (volume exclusion, electrostatic term due to ions, electrostatic term due to dielectrics, and a self-term due to the dielectric barrier) and study how these components contribute to selectivity. Using a model of the ryanodine receptor (RyR) calcium channel that both reproduces and predicts experimental data, Gillespie⁴⁰ showed that RyR selects Ca^{2 +} over monovalent cations because Ca^{2 +} ions are screened (coordinated) better by the four aspartates of the selectivity filter. The RyR model does not include dielectric interfaces, which we have shown gives the L-type calcium channel substantially larger Ca^{2 +} affinity than RyR.³¹ This paper builds on the work of Gillespie, not only by including dielectric interfaces, but also by analyzing the effect of changing the pore geometry on the energetic components of selectivity.

MODEL

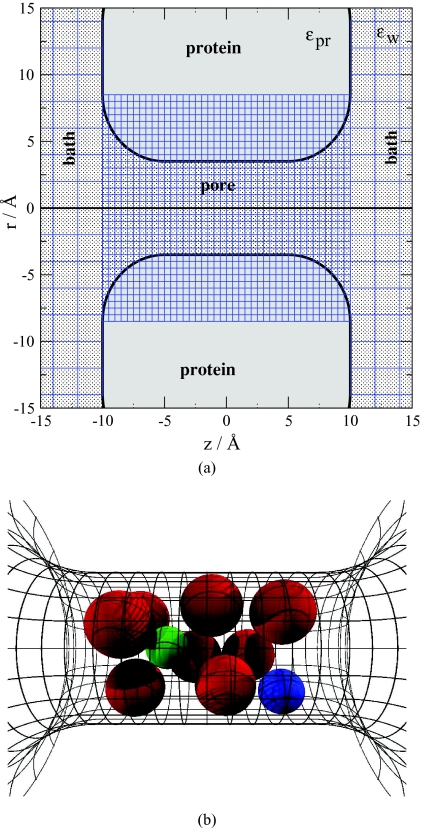
In our model, most of the atomic structure of the calcium channel is reduced to a coarse-grained geometry [Fig. 1a]. The channel protein is represented as a continuum solid with dielectric coefficient ϵ_pr. The three-dimensional body of the protein is obtained by rotating the thick line in Fig. 1a about the r = 0 axis. The protein, thus, forms an aqueous pore that connects the two baths. Water in the baths and pore is described as an implicit solvent that is a continuum dielectrics with uniform dielectric coefficient ϵ_w = 80. The central cylindrical part of the pore (with radius R = 3.5 − 4.5 Å and length 10 Å) forms the selectivity filter that includes the only atoms of the protein that are treated explicitly. These atoms are eight half-charged “oxygen ions” O^1∕2− [Fig. 1b, red spheres], representing the charged terminal groups of the four glutamate residues of the EEEE locus. The structural oxygen ions are confined to the selectivity filter (their centers are in the region r ⩽ R − 1.4 Å, |z| ⩽ 3.6 Å), but they can move freely inside the filter. The oxygen ions “coordinate” counter ions as particles of a confined liquid; their arrangement in Fig. 1b represents one snapshot of the millions of configurations sampled during a simulation.

Figure 1.

Model of ion channel, membrane, and electrolyte. The three-dimensional geometry (B) is obtained by rotating the two-dimensional shape shown in panel a around the z-axis. The simulation cell is much larger than shown in the figure. The blue lines represent the grid over which the EXCP profiles are computed. The grid is finer inside the channel (width 0.5 Å), while it is coarser outside the channel (width 2 Å). The selectivity filter (|z| < 5 Å) contains eight half-charged oxygen ions O^{1∕2 −} (red spheres in panel b). Green and blue spheres represent Na⁺ and Ca^{2 +} ions, respectively. For the radii of the ions, the Pauling radii are used: 0.6, 0.95, 1.33, 0.99, 1.35, 1.81, and 1.4 Å for Li⁺, Na⁺, K⁺, Ca^{2 +}, Ba^{2 +}, Cl⁻, and O^{1∕2 −}, respectively.

The ions are modeled as charged hard spheres with crystal radii (see caption of Fig. 1). The intermolecular energy terms due to screened Coulomb potentials and interactions with polarization charges induced on the dielectric boundaries [the boundary of the protein and the electrolyte, thick line in Fig. 1a] are described in Sec. 3A. Ions are restricted to the aqueous space of the model and cannot overlap with hard walls in the system. Figure 1 shows only the small central region of the simulation cell. The entire simulation cell is a cylinder with typical dimensions of radius 40 Å and length 180 Å. The channel is embedded in a membrane region that excludes ions by hard walls as described before.³¹

COMPUTATION OF THE CHEMICAL POTENTIAL TERMS

In the particle insertion method developed by Widom^{5, 9} we work with the following operation:

$$\mathcal{W}\left(U\left(\mathbf{r}\right)\right)=-kT\ln 〈e^{-U\left(\mathbf{r}\right)∕kT}〉,$$ (6)

where an ion is inserted in a small ΔV volume around position r. Its interaction energy with the system is denoted by U(r), and the brackets denote grand canonical (GC) ensemble average. Widom developed the formula in the canonical ensemble.⁹ Following his treatment, we show in the Appendix that the same formula applies when we simulate the whole system in the GC ensemble. The quantity W(U) depends on position through U(r), namely, on the position where we insert the test particle.

Energy terms

Separating the chemical potential into different terms is based on a separation of the energy of the system into different terms. The ion–ion (denoted by II) interaction energy between a ghost ion of species i inserted at position r and all the existing ions in the system is

$$U_i^{\mathrm{II}}\left(\mathbf{r}\right)=\sum _{\alpha }{z}_i{z}_{\alpha }{\psi }^{\mathrm{II}}(\mathbf{r},{\mathbf{r}}_{\alpha }),$$ (7)

where z_i is the valence of the inserted ghost ion, the index α runs over all the existing ions in the system, z_α is the valence of the αth ion, and

$${\psi }^{\mathrm{II}}(\mathbf{r},\mathbf{s})={\displaystyle \frac{1}{2}}{\displaystyle \frac{e^2}{4\pi {ϵ}_0|\mathbf{r}-\mathbf{s}|}}\left({\displaystyle \frac{1}{ϵ\left(\mathbf{r}\right)}}+{\displaystyle \frac{1}{ϵ\left(\mathbf{s}\right)}}\right)$$ (8)

is the interaction energy between two ions with unit valences at positions r and s, ϵ(r) is the dielectric constant at position r, e is the electronic charge, and ϵ₀ is the permittivity of vacuum.

The ion–dielectric (denoted by ID) interaction energy between the inserted ion and the polarization charge induced on the dielectric boundary B by all the other existing ions is

$$U_i^{\mathrm{ID}}\left(\mathbf{r}\right)=\frac{1}{2}e{z}_i\sum _{\alpha }{z}_{\alpha }{\psi }^{\mathrm{ID}}(\mathbf{r},{\mathbf{r}}_{\alpha }),$$ (9)

where

$${\psi }^{\mathrm{ID}}(\mathbf{r},\mathbf{s})={\displaystyle \frac{e}{4\pi {ϵ}_0}}{\int }_{\mathcal{B}}{\displaystyle \frac{h(\mathbf{s},{\mathbf{r}}^{\prime })}{|\mathbf{r}-{\mathbf{r}}^{\prime }|}}d{\mathbf{r}}^{\prime }$$ (10)

is the potential from the polarization charge at position r. h(s, r′) is the polarization charge at r′ induced by a unit charge (z_α = 1) placed at position s (and vice versa).

The interaction energy between the inserted ion and the polarization charge induced on B by the ion itself is

$$U_i^{\mathrm{SELF}}\left(\mathbf{r}\right)=\frac{1}{2}{z}_i^{2}e{\psi }^{\mathrm{SELF}}\left(\mathbf{r}\right),$$ (11)

where

$${\psi }^{\mathrm{SELF}}\left(\mathbf{r}\right)={\psi }^{\mathrm{ID}}(\mathbf{r},\mathbf{r})$$ (12)

is the potential from the polarization charge at position r.

The ions are modeled as charged hard spheres (HS). The HS energy $U_i^{\mathrm{HS}}$ is zero if the inserted ion does not overlap with any other existing particles and infinite otherwise.

The total energy change of the system produced by inserting an ion of species i is

$$U_i\left(\mathbf{r}\right)=U_i^{\mathrm{HS}}\left(\mathbf{r}\right)+U_i^{\mathrm{II}}\left(\mathbf{r}\right)+U_i^{\mathrm{ID}}\left(\mathbf{r}\right)+U_i^{\mathrm{SELF}}\left(\mathbf{r}\right).$$ (13)

The EXCP of an ionic species i inserted at position r can be determined from

$$\begin{array}{c}\hfill {\mu }_i^{\mathrm{EX}}\left(\mathbf{r}\right)=\mathcal{W}\left(U_i^{\mathrm{HS}}\left(\mathbf{r}\right)+U_i^{\mathrm{II}}\left(\mathbf{r}\right)+U_i^{\mathrm{ID}}\left(\mathbf{r}\right)+U_i^{\mathrm{SELF}}\left(\mathbf{r}\right)\right).\end{array}$$ (14)

Note that the interior of the protein and the membrane excludes ions; therefore, another potential term should be included in Eq. 13: an external potential $U_i^{\mathrm{WALL}}\left(\mathbf{r}\right)$, which is infinite whenever an ion of species i overlaps with these regions or any hard wall in the system and zero otherwise. Therefore, rigorously, Eq. 4 should be supplemented with a corresponding chemical potential term ${\mu }_i^{\mathrm{WALL}}\left(\mathbf{r}\right)$. Because we will show profiles averaged over the ion-accessible area, where ${\mu }_i^{\mathrm{WALL}}\left(\mathbf{r}\right)=0$ (see Sec. 4B), this issue is not relevant from the point of view of our discussion.

The components of the excess chemical potential

Now, we separate the EXCP into different terms. Such a separation is straightforward for the energy, but we have to apply such a separation with extra care in the case of the chemical potential. Any separation of the EXCP corresponding to a separation of the energy is necessarily not unique. In this paper, we propose a possible separation that is physically well based and helps to understand the energetics of selectivity, but it is not unique.

The chemical potential of an ionic species in an ideal solution is commonly defined as

$${\mu }_i^{\mathrm{id}.\mathrm{sol}.}=kT\ln c_i+z_{i}e\overline{\phi },$$ (15)

where $\overline{\phi }$ is the mean electrical potential in the solution. In this approximation, the EX term is just the interaction with the mean potential and the ions are treated as point charges.

Using this analogy, we can define a mean field (MF) term of the EXCP. In fact, we can define various MF terms depending on what the source of the potential is. The mean potential from the ions in the system is computed as

$${\overline{\phi }}^{\mathrm{II}}\left(\mathbf{r}\right)=〈\sum _{\alpha }{z}_{\alpha }{\psi }^{\mathrm{II}}(\mathbf{r},{\mathbf{r}}_{\alpha })〉.$$ (16)

The potential from the polarization charge induced by these ions is

$${\overline{\phi }}^{\mathrm{ID}}\left(\mathbf{r}\right)=\frac{1}{2}〈\sum _{\alpha }{z}_{\alpha }{\psi }^{\mathrm{ID}}(\mathbf{r},{\mathbf{r}}_{\alpha })〉.$$ (17)

The third term is the potential from the polarization charge of an inserted ion at the position where the ion was inserted:

$${\overline{\phi }}^{\mathrm{SELF}}\left(\mathbf{r}\right)=\frac{1}{2}〈{\psi }^{\mathrm{SELF}}\left(\mathbf{r}\right)〉=\frac{1}{2}{\psi }^{\mathrm{SELF}}\left(\mathbf{r}\right).$$ (18)

The mean potentials are computed in the simulation by inserting test charges in various positions, the corresponding potential terms are computed at these positions, and the results are averaged over numerous insertions. This is expressed by the brackets in the above equations. The corresponding MF terms of the chemical potential then are defined as

$${\mu }_i^{\mathrm{MFI}}\left(\mathbf{r}\right)=z_i{\overline{\phi }}^{\mathrm{II}}\left(\mathbf{r}\right),$$ (19)

$${\mu }_i^{\mathrm{MFD}}\left(\mathbf{r}\right)=z_{i}e{\overline{\phi }}^{\mathrm{ID}}\left(\mathbf{r}\right),$$ (20)

$${\mu }_i^{\mathrm{SELF}}\left(\mathbf{r}\right)=z_i^{2}e{\overline{\phi }}^{\mathrm{SELF}}\left(\mathbf{r}\right).$$ (21)

In an ideal solution the ions are point charges. Here, we often deal with concentrated solutions that are not at all ideal. Ions have a finite size. Therefore, we would like to have a term in the EXCP that describes the HS exclusion of ions. We define this term by inserting particles that have the same diameter as the corresponding ion, but no charge. This means that we include only the $U_i^{\mathrm{HS}}$ term in Eq. 6. The HS component of the chemical potential, thus, is defined as

$${\mu }_i^{\mathrm{HS}}\left(\mathbf{r}\right)=\mathcal{W}\left(U_i^{\mathrm{HS}}\left(\mathbf{r}\right)\right).$$ (22)

If we subtract the HS term and the MF terms from the total EXCP, what remains corresponds to the electrostatic correlations between ions “beyond mean field” [denoted by SC for “screening”]:

$$\begin{array}{ccc}& & {\mu }_i^{\mathrm{SC}}\left(\mathbf{r}\right)={\mu }_i^{\mathrm{EX}}\left(\mathbf{r}\right)-\left[{\mu }_i^{\mathrm{HS}}\left(\mathbf{r}\right)+{\mu }_i^{\mathrm{MFI}}\left(\mathbf{r}\right)\right.\hfill \\ & & \left.+{\mu }_i^{\mathrm{MFD}}\left(\mathbf{r}\right)+{\mu }_i^{\mathrm{SELF}}\left(\mathbf{r}\right)\right].\hfill \end{array}$$ (23)

We can see a pattern if we write this equation this way:

$$\begin{array}{ccc}\hfill {\mu }_i^{\mathrm{SC}}\left(\mathbf{r}\right)=& & \mathcal{W}\left[U_i^{\mathrm{HS}}\left(\mathbf{r}\right)+U_i^{\mathrm{II}}\left(\mathbf{r}\right)+U_i^{\mathrm{ID}}\left(\mathbf{r}\right)+U_i^{\mathrm{SELF}}\left(\mathbf{r}\right)\right]\hfill \\ & & -\left[{\mu }_i^{\mathrm{HS}}\left(\mathbf{r}\right)+{\mu }_i^{\mathrm{MFI}}\left(\mathbf{r}\right)+{\mu }_i^{\mathrm{MFD}}\left(\mathbf{r}\right)+{\mu }_i^{\mathrm{SELF}}\left(\mathbf{r}\right)\right].\hfill \end{array}$$ (24)

We have similar contributions in the first and the second term on the right-hand side. In the first term (the Widom evaluation of the EXCP) we compute the energies corresponding to the HS, II, ID, and SELF terms and sample all the cross correlations between these terms. The second term also contains these contributions, but in a mean field way. We subtract these from the total, so the SC term expresses all the electrostatic correlations that are not included in the MF treatment. Because many studies still use MF theories such as Poisson–Boltzmann theory or its generalization to nonequilibrium (Poisson–Nernst–Planck), it is particularly useful to explicitly evaluate this term in order to show its importance. The SC term measures the error in mean field theories.

The next step is the separation of the correlation effects corresponding to ions and induced charges in the SC term. Formally,

$${\mu }_i^{\mathrm{SC}}\mathbf{r}={\mu }_i^{\mathrm{SCI}}\mathbf{r}+{\mu }_i^{\mathrm{SCD}}\mathbf{r},$$ (25)

where the superscripts SCI and SCD indicate ionic and dielectric correlations, respectively. If, in the Widom method, we insert ions in the system, but exclude the dielectrics, we can estimate a term that contains only the ionic correlations and excludes all terms involving dielectrics: $\mathcal{W}\left(U_i^{\mathrm{HS}}\left(\mathbf{r}\right)+U_i^{\mathrm{II}}\left(\mathbf{r}\right)\right)$. If we follow the pattern in Eq. 24 and subtract the corresponding MF term, we obtain the SCI term as a leftover:

$$\begin{array}{ccc}\hfill {\mu }_i^{\mathrm{SCI}}\left(\mathbf{r}\right)=& & \mathcal{W}\left(U_i^{\mathrm{HS}}\left(\mathbf{r}\right)+U_i^{\mathrm{II}}\left(\mathbf{r}\right)\right)-\left[{\mu }_i^{\mathrm{HS}}\left(\mathbf{r}\right)+{\mu }_i^{\mathrm{MFI}}\left(\mathbf{r}\right)\right].\hfill \end{array}$$ (26)

The SCD is then what is leftover; it is obtained simply from Eq. 25. All these terms can be illustrated as

$$\begin{array}{c}\hfill \stackrel{{\displaystyle \mathrm{EX}}}{\overbrace{\mathrm{HS}+{\underbrace{\mathrm{MFI}+\mathrm{SCI}}}_{{\displaystyle \mathrm{ION}}}+{\underbrace{\mathrm{MFD}+\mathrm{SELF}+\mathrm{SCD}}}_{{\displaystyle \mathrm{DIEL}}}}}.\end{array}$$ (27)

Energetics of ion selectivity

Because the system is in equilibrium, the chemical potential is the same in the bath and in the channel:

$$\begin{array}{ccc}\hfill {\mu }_i& =& kT\ln c_i\left(\mathrm{B}\right)+{\mu }_i^{\mathrm{EX}}\left(\mathrm{B}\right)\hfill \\ & =& kT\ln c_i\left(\mathbf{r}\right)+{\mu }_i^{\mathrm{EX}}\left(\mathbf{r}\right).\hfill \end{array}$$ (28)

The EXCP in the bulk (${\mu }_i^{\mathrm{EX}}\left(\mathrm{B}\right)$) that corresponds to prescribed ionic concentrations c_i(B) is calculated using the adaptive-GCMC (A-GCMC) method of Malasics and Boda.^{41, 42} If we define the difference [see Eq. 5]

$$\Delta {\mu }_i^{\mathrm{EX}}\left(\mathbf{r}\right)={\mu }_i^{\mathrm{EX}}\left(\mathbf{r}\right)-{\mu }_i^{\mathrm{EX}}\left(\mathrm{B}\right),$$ (29)

we obtain

$$\Delta {\mu }_i^{\mathrm{EX}}\left(\mathbf{r}\right)=kT\ln \left({\displaystyle \frac{c_i\left(\mathbf{r}\right)}{c_i\left(\mathrm{B}\right)}}\right).$$ (30)

This equation makes it possible to check the consistency of our calculations because the two sides of the equation are computed differently in the simulation. The left-hand side is computed using Widom’s particle insertion, which is an additional sampling procedure “on top” of the normal GCMC simulation. The right-hand side (the concentration) is computed in the GCMC simulation in the usual way as an ensemble average. Although, the EXCP could be calculated from the GCMC simulation without the Widom sampling, the particle insertions are necessary to compute the components of the EXCP.

We can define the differences between the channel and the bulk (B) not only for the excess term, but also for every term introduced above:

$$\Delta {\mu }_i^{\mathrm{HS}}\left(\mathbf{r}\right)={\mu }_i^{\mathrm{HS}}\left(\mathbf{r}\right)-{\mu }_i^{\mathrm{HS}}\left(\mathrm{B}\right),$$ (31)

$$\Delta {\mu }_i^{\mathrm{MFI}}\left(\mathbf{r}\right)={\mu }_i^{\mathrm{MFI}}\left(\mathbf{r}\right)-{\mu }_i^{\mathrm{MFI}}\left(\mathrm{B}\right),$$ (32)

$$\Delta {\mu }_i^{\mathrm{MFD}}\left(\mathbf{r}\right)={\mu }_i^{\mathrm{MFD}}\left(\mathbf{r}\right)-{\mu }_i^{\mathrm{MFD}}\left(\mathrm{B}\right),$$ (33)

$$\Delta {\mu }_i^{\mathrm{SELF}}\left(\mathbf{r}\right)={\mu }_i^{\mathrm{SELF}}\left(\mathbf{r}\right)-{\mu }_i^{\mathrm{SELF}}\left(\mathrm{B}\right),$$ (34)

$$\Delta {\mu }_i^{\mathrm{SCI}}\left(\mathbf{r}\right)={\mu }_i^{\mathrm{SCI}}\left(\mathbf{r}\right)-{\mu }_i^{\mathrm{SCI}}\left(\mathrm{B}\right),$$ (35)

$$\Delta {\mu }_i^{\mathrm{SCD}}\left(\mathbf{r}\right)={\mu }_i^{\mathrm{SCD}}\left(\mathbf{r}\right)-{\mu }_i^{\mathrm{SCD}}\left(\mathrm{B}\right),$$ (36)

$$\Delta {\mu }_i^{\mathrm{SC}}\left(\mathbf{r}\right)={\mu }_i^{\mathrm{SC}}\left(\mathbf{r}\right)-{\mu }_i^{\mathrm{SC}}\left(\mathrm{B}\right).$$ (37)

The ${\mu }_i^{\mathrm{MFI}}\left(\mathrm{B}\right)$, ${\mu }_i^{\mathrm{MFD}}\left(\mathrm{B}\right)$, and ${\mu }_i^{\mathrm{SELF}}\left(\mathrm{B}\right)$ terms are zero because the corresponding mean potentials (${\overline{\phi }}^{\mathrm{II}}\left(\mathbf{r}\right)$, ${\overline{\phi }}^{\mathrm{ID}}\left(\mathbf{r}\right)$, and ${\overline{\phi }}^{\mathrm{SELF}}\left(\mathbf{r}\right)$) are defined to be zero in the bulk. The sum of the differences for the HS, MFI, MFD, SELF, SCI, and SCD terms is the difference of the excess term. Let us now summarize all these differences for Na⁺ and Ca^{2 +} and express the differences of differences:

$$\Delta \Delta {\mu }^{\mathrm{HS}}\left(\mathbf{r}\right)=\Delta {\mu }_{{\mathrm{Na}}^{+}}^{\mathrm{HS}}\left(\mathbf{r}\right)-\Delta {\mu }_{{\mathrm{Ca}}^{2+}}^{\mathrm{HS}}\left(\mathbf{r}\right),$$ (38)

$$\Delta \Delta {\mu }^{\mathrm{MFI}}\left(\mathbf{r}\right)=\Delta {\mu }_{{\mathrm{Na}}^{+}}^{\mathrm{MFI}}\left(\mathbf{r}\right)-\Delta {\mu }_{{\mathrm{Ca}}^{2+}}^{\mathrm{MFI}}\left(\mathbf{r}\right),$$ (39)

$$\Delta \Delta {\mu }^{\mathrm{MFD}}\left(\mathbf{r}\right)=\Delta {\mu }_{{\mathrm{Na}}^{+}}^{\mathrm{MFD}}\left(\mathbf{r}\right)-\Delta {\mu }_{{\mathrm{Ca}}^{2+}}^{\mathrm{MFD}}\left(\mathbf{r}\right),$$ (40)

$$\Delta \Delta {\mu }^{\mathrm{SELF}}\left(\mathbf{r}\right)=\Delta {\mu }_{{\mathrm{Na}}^{+}}^{\mathrm{SELF}}\left(\mathbf{r}\right)-\Delta {\mu }_{{\mathrm{Ca}}^{2+}}^{\mathrm{SELF}}\left(\mathbf{r}\right),$$ (41)

$$\Delta \Delta {\mu }^{\mathrm{SCI}}\left(\mathbf{r}\right)=\Delta {\mu }_{{\mathrm{Na}}^{+}}^{\mathrm{SCI}}\left(\mathbf{r}\right)-\Delta {\mu }_{{\mathrm{Ca}}^{2+}}^{\mathrm{SCI}}\left(\mathbf{r}\right),$$ (42)

$$\Delta \Delta {\mu }^{\mathrm{SCD}}\left(\mathbf{r}\right)=\Delta {\mu }_{{\mathrm{Na}}^{+}}^{\mathrm{SCD}}\left(\mathbf{r}\right)-\Delta {\mu }_{{\mathrm{Ca}}^{2+}}^{\mathrm{SCD}}\left(\mathbf{r}\right),$$ (43)

$$\Delta \Delta {\mu }^{\mathrm{SC}}\left(\mathbf{r}\right)=\Delta {\mu }_{{\mathrm{Na}}^{+}}^{\mathrm{SC}}\left(\mathbf{r}\right)-\Delta {\mu }_{{\mathrm{Ca}}^{2+}}^{\mathrm{SC}}\left(\mathbf{r}\right).$$ (44)

Following Gillespie,⁴⁰ these terms are called “advantages” because a positive value of any of them favors Ca^{2 +} binding (accumulating) by increasing Ca^{2 +} concentration. Using Eq. 29 and these terms, we obtain

$$\ln \left({\displaystyle \frac{c_{{\mathrm{Ca}}^{2+}}\left(\mathbf{r}\right)}{c_{{\mathrm{Na}}^{+}}\left(\mathbf{r}\right)}}\right)=\ln \left({\displaystyle \frac{c_{{\mathrm{Ca}}^{2+}}\left(\mathrm{B}\right)}{c_{{\mathrm{Na}}^{+}}\left(\mathrm{B}\right)}}\right)+{\displaystyle \frac{\Delta \Delta {\mu }^{\mathrm{EX}}\left(\mathbf{r}\right)}{kT}},$$ (45)

where

$$\begin{array}{ccc}\hfill \Delta \Delta {\mu }^{\mathrm{EX}}\left(\mathbf{r}\right)=& & \Delta \Delta {\mu }^{\mathrm{HS}}\left(\mathbf{r}\right)+\Delta \Delta {\mu }^{\mathrm{MFI}}\left(\mathbf{r}\right)+\Delta \Delta {\mu }^{\mathrm{MFD}}\left(\mathbf{r}\right)\hfill \\ & & +\Delta \Delta {\mu }^{\mathrm{SELF}}\left(\mathbf{r}\right)+\Delta \Delta {\mu }^{\mathrm{SCI}}\left(\mathbf{r}\right)+\Delta \Delta {\mu }^{\mathrm{SCD}}\left(\mathbf{r}\right).\hfill \end{array}$$ (46)

In Eq. 45, the left-hand side is called “binding selectivity” because it expresses the degree to which Ca^{2 +} is favored over Na⁺ at location r. The corresponding term on the right-hand side with the bulk concentrations is called “number advantage” because it expresses the advantage that one ionic species has from outnumbering the other ionic species in the bulk. If $\Delta \Delta {\mu }_i^{\mathrm{EX}}\left(\mathbf{r}\right)$ were zero, the channel would not be selective at all. The ratio of ion concentrations would be the same in the channel as in the bulk. The energetic advantage terms on the right-hand side of Eq. 46 describe to what degree each term contributes to the binding affinity of Ca^{2 +} over Na⁺, i.e., how each term contributes to this selectivity.

METHODS

Grand canonical Monte Carlo simulations

MC simulations using Metropolis sampling are performed in the GC ensemble.^{31, 37, 38, 39} This ensemble, as described before,^{31, 33} is especially suitable to simulate the small ionic concentrations typical of Ca channels (for example, 1 μM Ca^{2 +} versus 30 mM Na⁺). MC moves include (1) small displacement from the old position (for sampling regions with large densities; this is the only kind of attempt used for the oxygen ions in the selectivity filter); (2) changes to a new position selected randomly from a uniform distribution anywhere in the cell (used for sampling regions with gaslike densities such as in the baths); (3) moving a particle from a position in the selectivity filter to a position in the baths, or vice versa; this move prefers particle exchanges between certain subvolumes and thus the acceptance test includes the subvolume ratio to prevent statistical bias;⁴³ (4) insertion∕deletion of individual ions (chemical potentials of individual ions are determined by the A-GCMC method of Malasics and Boda⁴²); (5) insertion∕deletion of a neutral group of ions (e.g., Na⁺+Cl⁻ or Ca^{2 +}+2Cl⁻); (6) particle insertions or deletions analogous to (5) but involving subvolumes of the simulation cell that we want to sample more intensely (in particular, the selectivity filter).³³ Only cation insertions or deletions are applied in these subvolumes, Cl⁻ ions are still inserted∕deleted into∕from the whole simulation cell. These attempts are applied randomly with predefined probabilities. Changing these probabilities does not change the final result; it only influences the speed with which the simulation converges to the final result. The typical length of a GCMC simulation is 5 × 10⁸ sampled configurations (attempts).

The acceptance tests for new particle configurations involve the total electrostatic energy of the system, as described in Sec. 3A. Computation of the energy terms involving dielectrics ($U_i^{\mathrm{ID}}\left(\mathbf{r}\right)$ and $U_i^{\mathrm{SELF}}\left(\mathbf{r}\right)$) assumes the computation of the polarization surface charge h(r, s) induced on the dielectric boundaries. We compute the polarization charge using a boundary element method that we have called “induced charge computation”.^{31, 44} The Poisson equation with boundary conditions is transformed into an integral equation and solved by surface discretization. For a given dielectric geometry, the coefficient matrix produced by the discretized integral equation does not depend on the ion configuration. It is inverted at the beginning of the simulation and used repeatedly (millions of times) during the simulation to determine h(r, s). Vectors of discretized induced charge for varied ion configurations are computed thereafter by a matrix–vector multiplication.

Numerical implementation of the Widom sampling

To compute the space-dependent EXCP profiles with Widom’s particle insertion method^{5, 9} (see the Appendix) we have constructed a two-dimensional grid shown in Fig. 1a. Because the system is rotationally symmetric, we defined the subvolumes described in the Appendix as a function of only two variables z and r. In the channel we used squares of width 0.5 Å, while outside the channel near the channel entrances we used squares of width 2 Å. These squares correspond to rings in three dimensions. In the two baths, we used large cylinders far from the hard walls of the system. We inserted test particles into these rings with equal probabilities. Thus, we insert particles into the rings in proportion to their cross sectional area in the (r, z)-plane instead of their volume.

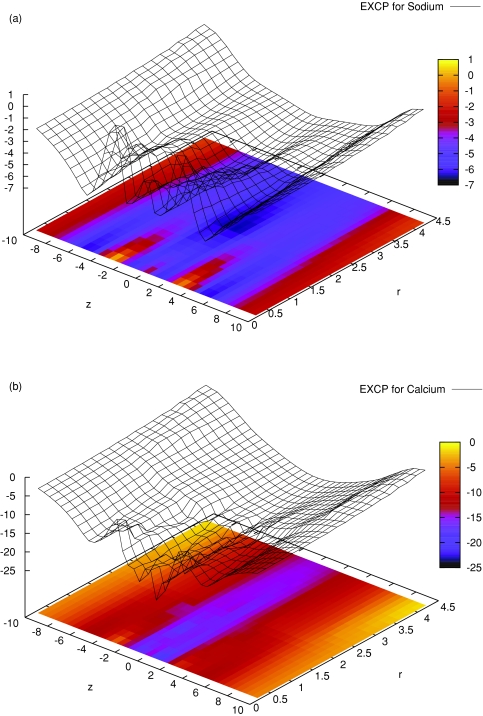
Figure 2 shows $\Delta {\mu }_{{\mathrm{Na}}^{+}}^{\mathrm{EX}}(z,r)$ (part a) and $\Delta {\mu }_{{\mathrm{Ca}}^{2+}}^{\mathrm{EX}}(z,r)$ (part b) for the state point that we use as an example throughout our paper: R = 3.5 Å, ϵ_pr = 10, c _{Na ⁺}(B)=30 mM, c _{Ca ²⁺}(B)=1 μM. This is the case that corresponds to the IC50 of the experiment of Almers and McCleskey:^{45, 46} 1 μM Ca^{2 +} reduces the current of 30 mM Na⁺ to half of that measured in the absence of Ca^{2 +}. As we have pointed out,²⁷ our model with the geometrical parameters used in this paper and protein dielectric coefficient ϵ_pr = 10 is able to reproduce this experimental result. At these bath concentrations, the filter binds about the same amount of Na⁺ and Ca^{2 +}, the amount of Na⁺ being half of that bound if Ca^{2 +} is not present in the baths. Therefore, Na⁺ current is half the current in the absence of Ca^{2 +}. Ca^{2 +} ions do not carry significant current in the case shown in Fig. 2, because depletion zones are formed at the filter entrances in the density profile of Ca^{2 +}. We have previously used the integrated Nernst–Planck equation to quantify how these depletion zones form high-resistance elements along the ionic pathway in a simplified situation.²⁷ Peaks in Fig. 2 correspond to these depletion zones [where c_i(r) is small, ${\mu }_i^{\mathrm{EX}}\left(\mathbf{r}\right)$ is large]. The ridges at |z| ≈ 5 Å represent these depletion zones, while the valley in the center of the filter represents the binding site for the ions.

Figure 2.

Free-energy landscapes: the excess chemical potential profiles (in units of kT) for Na⁺ (top) and Ca^{2 +} (bottom) as functions of the z and r coordinates for c _{Ca ²⁺}(B)=10⁻⁶ M, c _{Na ⁺}(B)=30 mM, R = 3.5 Å, and ϵ_pr = 10.

Because it is quite difficult to distill relevant information from such landscapes and because we are primarily interested in the behavior of the system along the ionic pathway, we average these profiles over the r-dimension:

$$\Delta \overline{{\mu }_i^{\mathrm{EX}}}\left(z\right)={\displaystyle \frac{2}{R_{\min }^2}}{\int }_0^{R_{\min }}r\Delta {\mu }_i^{\mathrm{EX}}(z,r)dr.$$ (47)

Similar expressions apply for all the other chemical potential terms. When averaging, one must be careful. We need to average the profiles for Na⁺ and Ca^{2 +} over the same range of r in order to compute the difference $\Delta \Delta \overline{{\mu }^{\mathrm{EX}}}\left(z\right)=\Delta \overline{{\mu }_{{\mathrm{Na}}^{+}}^{\mathrm{EX}}}\left(z\right)-\Delta \overline{{\mu }_{{\mathrm{Ca}}^{2+}}^{\mathrm{EX}}}\left(z\right)$ properly. The range over which we average is the range that is accessible to the center of the largest ion: R_min = R − R_{largest ion}. In this way we can compare EXCPs for the two ions over a cross section that both ions occupy. We will drop the overline from now on to simplify the notation.

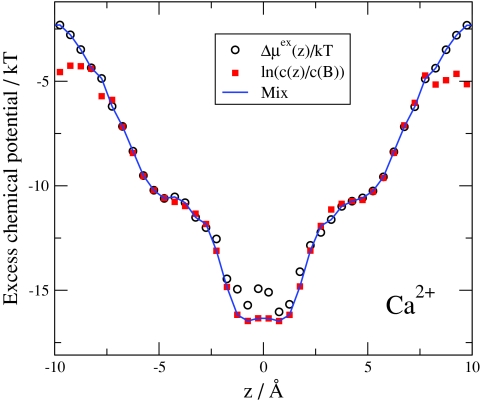
Equation 30 makes it possible to check the self-consistency of our simulations. Figure 3 shows both the profile $\Delta {\mu }_{{\mathrm{Ca}}^{2+}}^{\mathrm{EX}}\left(z\right)∕kT$ and the profile ln[c _{Ca ²⁺}(z)∕c _{Ca ²⁺}(B)]. It is apparent that in regions of small Ca^{2 +} concentrations (outside the central binding site) the Widom sampling works better. In these regions, sampling of Ca^{2 +} concentration can be poor. In some volume elements, Ca^{2 +} concentration can be zero; therefore, the logarithm diverges making the average over the cross section in Eq. 47 diverge too. The Widom sampling, on the other hand, can be poor in regions of large concentrations because particle insertion is problematic in high-density regions. Therefore, we mix a $\Delta {\mu }_{{\mathrm{Ca}}^{2+}}^{\mathrm{EX}}\left(z\right)∕kT$ profile from these two functions. We define a central region where we use ln (c_i(r)) (|z| = 3 Å in Fig. 3). We define another region outside the central region where we use Widom sampling to obtain $\Delta {\mu }_i^{\mathrm{EX}}\left(\mathbf{r}\right)$. The profiles shown from now on are mixed in this way. The two kinds of profiles are practically identical for Na⁺ ions (data not shown), because sampling is much better for Na⁺ than for Ca^{2 +}.

Figure 3.

Check of consistency on the basis of Eq. 29. The final EXCP profile is mixed from $\Delta {\mu }_i^{\mathrm{EX}}\left(z\right)∕kT$ and ln [c_i(z)∕c_i(B)]. The latter is used in the region |z| ≈ 3 Å, the former is outside this region. The figure is for the same state point as in Fig. 2.

RESULTS

We will present our results using the point (R = 3.5 Å, ϵ_pr = 10, c _{Na ⁺}(B)=30 mM, c _{Ca ²⁺}(B)=1 μM) as a reference point. Then, we will show the effects of changing c _{Ca ²⁺}(B), ϵ_pr, filter radius (R), and the radius of the monovalent cation on the chemical potential profiles.

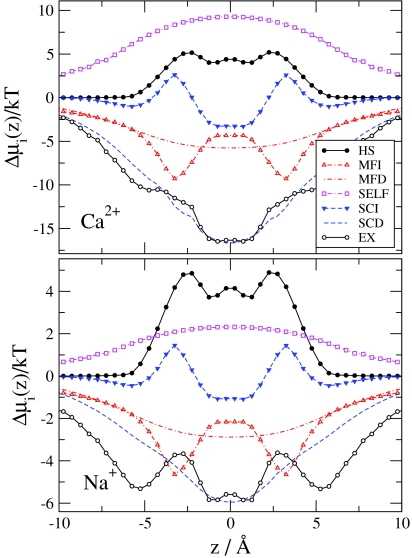
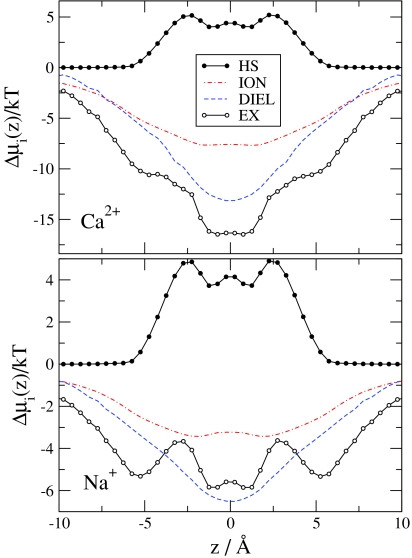
Figure 4 shows the chemical potential terms (compared to bulk) introduced in Eqs. 31, 32, 33, 34, 35, 36, 37. The EX term is much deeper for Ca^{2 +} than for Na⁺, but this difference is necessary to overcome the large number advantage of Na⁺ over Ca^{2 +}. The EX term is the sum of all the other terms shown in Fig. 4. This division shows how this large (free) energetic advantage for Ca^{2 +} decomposes into different contributions, which we describe in detail below.

Figure 4.

Chemical potential terms (relative to bulk) for Ca^{2 +} (top panel) and Na⁺ (bottom panel) as functions of z for the same state point as in Fig. 2. The MFI, SCI, MFD, SCD, and SELF electrostatic terms are shown.

The HS term describes the free-energy that is necessary to insert a neutral hard sphere (with the same diameter as the corresponding ion) into the system. This term is repulsive and has similar magnitude for Ca^{2 +} and Na⁺ because these two ions have similar size. The HS profiles have large peaks more or less where the oxygen concentration profiles have peaks (|z| = 3.6 Å), namely, where the probability that an inserted particle overlaps a particle already in the system is the largest.

The SELF term is the consequence of a dielectric penalty of an ion passing through the channel; it measures the interaction of the ion with the polarization charge induced by the ion itself.^{47, 48} This term is positive for both ions because the ions induce repulsive charge on the dielectric interface. This dielectric penalty is four times larger for Ca^{2 +} than for Na⁺.

The MF terms describe the interaction of an inserted ion with the mean electrostatic potential. The mean electrostatic potential is averaged over the millions of sampled configurations and is related to the average ionic concentration profiles (and, thus, to the EXCP profiles) through Poisson’s equation. Thus, the MF terms describe the channel’s ability to attract cations electrostatically in an average manner. The mean potential is negative because the channel is not charge neutral (it is net negative): cations are unable to neutralize the oxygen ions perfectly because the channel is narrow and crowded. The balancing charge is outside the channel.

The MF terms can be split into the MFI and MFD terms depending on the source of the potential (MFI from ions and MFD from dielectric induced charge). The MFI profiles follow the variation in the profile of the ionic charges, ∑_iz_iec_i(r). Peaks in oxygen ion profiles produce minima in the MFI profiles. The MFD profile follows the variation of the induced charge on the dielectric interface: the induced charge is negative in the filter (because the net charge of the filter is negative) and it changes smoothly going outward from the center of the channel (see Fig. 11 of Boda et al.³¹). The induced charge is positive on the outer surface of the protein. Although the net amount of induced charge is zero on the whole surface of the protein due to Gauss’s law, the mean potential it produces (MFD) inside the channel is negative. The MFI and MFD terms have similar magnitude at this value of the protein dielectric constant. The MFI and MFD terms together (MF term) overcome the repulsive SELF term, but the electrostatic terms beyond the MF terms (SC) are crucial to produce the deep excess terms resulting in the strong Ca^{2 +} versus Na⁺ selectivity.

The SC terms describe electrostatic correlations beyond the MF terms. Formally, they can be interpreted by the difference

$$-kT\ln 〈e^{-\psi ∕kT}〉-〈\psi 〉,$$ (48)

where ψ denotes some kind of energy in the system. (Note that this equation is a simplification for pedagogical purposes. The exact computation of the SC terms is given in Sec. 3B.) In particular, the SCI term is related to the ability of the local surrounding electrolyte to screen the charge of the ion inserted into a given position in the system. (This screening should not be confused with screening by water, which is represented by the dielectric coefficient.)

The difference between the MFI and SCI terms can be illustrated by the example of bulk electrolytes. In a bulk electrolyte, the MFI term is zero because the average electric potential is zero, while the EXCP is equal to the sum of the HS and SCI terms. The SCI term is then the electrostatic part of the EXCP that describes the deviation from ideality. This term is commonly (and approximately) described by the textbook theory of Debye and Hückel (this theory ignores the HS term and thus is in error under many important conditions).

To understand the SCD term, first we consider the MFD term which represents the potential from the average induced charge [second term in Eq. 48]. The induced charge, however, varies as ions change positions in the channel during MC sampling. A successfully inserted (no overlap) test ion will then experience the potential of the induced charge of a given ionic configuration. Different successfully inserted ions will experience different forces. The average over all these configurations is computed by the Widom sampling [first term in Eq. 48]. The difference of these two terms defines the SCD term.

The SCI term in Fig. 4 has a nonmonotonic behavior. It has a positive maximum where the MFI profile has a minimum. At these positions it is more difficult for the surrounding ions to screen the inserted ion compared to the average. The SCD term can be very different from the mean (MFD) as seen in Fig. 4: the SCD term is deeper (more attractive) than the MFD term under the given conditions. Note that the effect of the charge induced by the inserted test ion itself is not included in the SCD term, that is the SELF term.

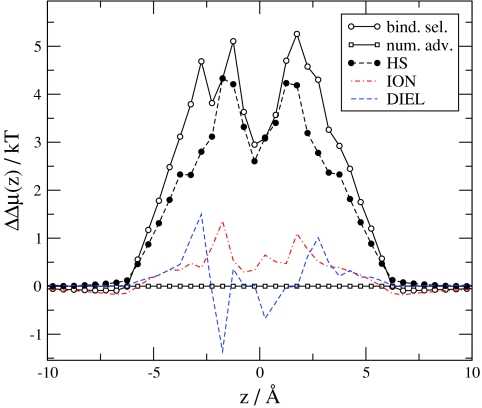
Different insight can be gained if we separate the EXCP into components corresponding to interactions with ions (ION=MFI+SCI) and to interactions with induced charge (DIEL=SELF+MFD+SCD), see Eq. 27. The results are shown in Fig. 5. Interestingly, the ION term is a nonoscillating function of z (apart from the one minimum), while its components (MFI and SCI) are oscillating. The DIEL term is also nonoscillating. Figure 5 shows that at this value of ϵ_pr the DIEL term is even deeper than the ION term. The ions occupy positions in the filter with higher probability with which they minimize free-energy. The number of such configurations is limited. Therefore, the SCI term has its limitations in drawing more ions into the filter. It is the DIEL term that has a large additional attractive effect, if ϵ_pr is small.

Figure 5.

Chemical potential terms (relative to bulk) for Ca^{2 +} (top panel) and Na⁺ (bottom panel) as functions of z for the same state point as in Fig. 2. The ION and DIEL electrostatic terms are shown.

Figure 5 gives the impression that it is the HS term and volume exclusion effects between ions that produce the oscillatory behavior of the EXCP and thus the peaks in the ionic profiles. This impression is false, however, because large density has its consequences not only directly in the HS term, but also indirectly in the electrostatic terms. The cations try to find positions between the oxygens with the best possible screening. Together with the effects of confinement from the pore wall and the oxygen ions, this results in layering in the density profiles. The oscillations in the SCI and MFI profiles reflect this phenomenon.

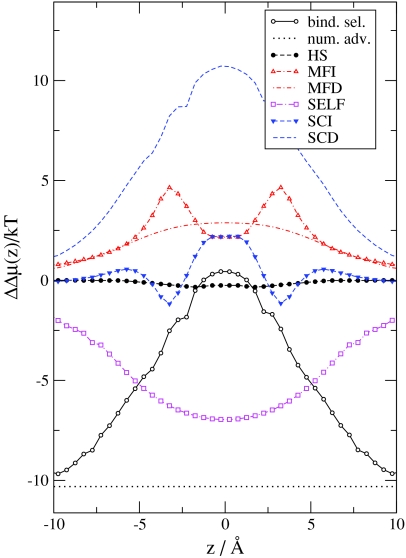
In the next step, we take the differences of the Δμ_i(z) functions shown in Fig. 4 [Eqs. 38, 39, 40, 41, 42, 43, 44] and express binding selectivity and the advantages stemming from the different terms [Eq. 46]. Figure 6 shows these ΔΔμ(z) functions. The number advantage favors Na⁺ over Ca^{2 +} because there is much more Na⁺ in the bulk than Ca^{2 +} (ln (10⁻⁶∕0.03) = −10.3, a constant). This expresses the higher probability of Na⁺ ions diffusing in the vicinity of the channel relative to Ca^{2 +}. The binding selectivity curve equals the number advantage curve in the baths outside the channel. Inside the channel, however, the binding selectivity curve increases and in the binding site (center) of the selectivity filter it is positive, meaning that this site favors Ca^{2 +} over Na⁺ under the given conditions. To overcome the large number disadvantage, a large EXCP advantage (ΔΔμ^EX(z)) is needed for Ca^{2 +}.

Figure 6.

Binding selectivity of Ca^{2 +} over Na⁺ and various advantage terms [from Eqs. 44, 45] as functions of z for the same state point as in Fig. 2. The MFI, SCI, MFD, SCD, and SELF electrostatic terms are shown.

Figure 6 shows how this advantage splits into different terms. The HS advantage is close to zero because the size of the two ions is very similar. Both the MFI and MFD terms favor Ca^{2 +}, as expected, because the double charge of Ca^{2 +} has double the interaction energy with the MF potentials (${\overline{\phi }}^{\mathrm{II}}\left(z\right)$ and ${\overline{\phi }}^{\mathrm{ID}}\left(z\right)$) compared to Na⁺. The most favorable term for Ca^{2 +} is the SCD term. The SCD term is so large that it (together with the MFI, MFD, and SCI terms) can overcome the unfavorable SELF term. The self-term is the only term that is very unfavorable for Ca^{2 +} because Ca^{2 +} has four times the interaction energy with its own repulsive induced charge than Na⁺ does.

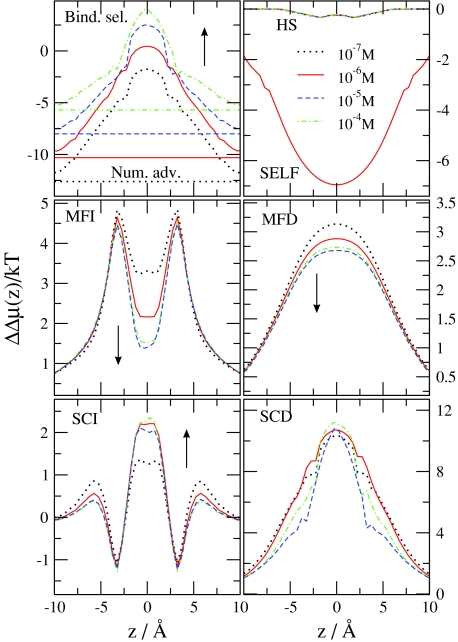
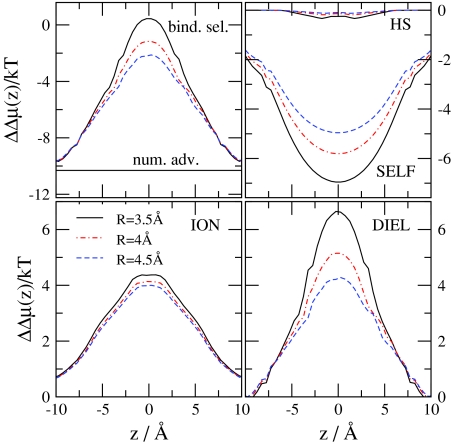
Next, we analyze the effect of various parameters on ion selectivity and the role of the different advantage terms in the change of selectivity. First, we consider the Ca^{2 +} titration experiment performed by Almers and McCleskey^{45, 46} and change c _{Ca ²⁺}(B) in the fixed 30 mM Na⁺ background. Figure 7 shows the various advantage terms for different values of the bulk Ca^{2 +} concentration. (Note that different advantage terms will be shown for different problems in Figs. 7891011 depending on which term is more important for a given case.) The basic conclusions are similar to those drawn by Gillespie⁴⁰ for the RyR Ca channel in a similar experiment. Binding selectivity increases (becomes more favorable for Ca^{2 +}) as c _{Ca ²⁺}(B) increases (the Na⁺ number advantage decreases). The MFI and MFD terms decrease with increasing c _{Ca ²⁺}(B) because the channel becomes more charge neutral; Ca^{2 +} ions are more efficient in neutralizing the oxygen ions. Therefore, the decrease of the MF terms is the main reason of the saturation of selectivity at large Ca^{2 +} concentrations. The SCI and SCD terms change less with increasing c _{Ca ²⁺}(B), while the HS and the SELF term do not change at all.

Figure 7.

Binding selectivity of Ca^{2 +} over Na⁺ and various advantage terms as functions of z for the indicated values of c _{Ca ²⁺}(B) M. The other variables are held fixed: c _{Na ⁺}(B)=30 mM, R = 3.5 Å, and ϵ_pr = 10. The MFI, SCI, MFD, SCD, and SELF electrostatic terms are shown. Arrows indicate the direction in which Ca^{2 +} concentration increases.

Figure 8.

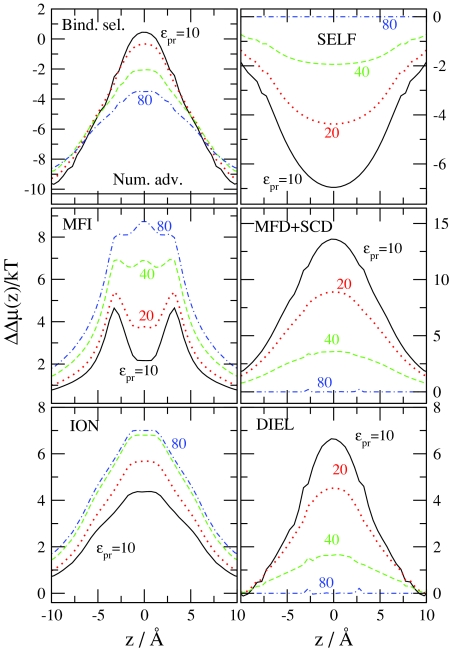
Binding selectivity of Ca^{2 +} over Na⁺ and various advantage terms as functions of z for the indicated values of ϵ_pr. The other variables are held fixed: c _{Ca ²⁺}(B)=10⁻⁶ M, c _{Na ⁺}(B)=30 mM, and R = 3.5 Å. The MFI, MFD+SCD, SELF, ION, and DIEL electrostatic terms are shown.

Figure 9.

Binding selectivity of Ca^{2 +} over Na⁺ and various advantage terms as functions of z for the indicated values of R. The other variables are held fixed: c _{Ca ²⁺}(B)=10⁻⁶ M, c _{Na ⁺}(B)=30 mM, and ϵ_pr = 10. The SELF, ION, and DIEL electrostatic terms are shown.

Figure 10.

Binding selectivity of Ca^{2 +} over Na⁺ and various advantage terms as functions of z for the indicated monovalent cations. The other variables are held fixed: c _{Ca ²⁺}(B)=10⁻⁶ M, c₊(B) = 30 mM, R = 3.5 Å, and ϵ_pr = 10. The SELF, ION, and DIEL electrostatic terms are shown.

Figure 11.

Binding selectivity of Ca^{2 +} over Ba⁺ and various advantage terms as functions of z for c _{Ca ²⁺}(B)=c _{Ba ²⁺}(B)=50 mM, R = 3.5 Å, and ϵ_pr = 10. The ION and DIEL electrostatic terms are shown.

The Ca^{2 +} versus Na⁺ selectivity of the model channel can be characterized by the Ca^{2 +} concentration at which the number of Na⁺ ions in the filter is half of that in the absence of Ca^{2 +}. As we have shown before,^{27, 28, 34} this value coincides with the IC50 value with which selectivity is characterized in experiments.

In a series of publications,^{27, 28, 31, 32, 34} we have shown that the shape of the titration curves (average number of Ca^{2 +} and Na⁺ ions in the filter as functions of log₁₀[c _{Ca ²⁺}(B)]) is similar in different conditions: Ca^{2 +} gradually replaces Na⁺ in the filter as c _{Ca ²⁺}(B) is increased. The titration curves differ, however, in their position along the abscissa; namely, at which c _{Ca ²⁺}(B) this replacement occurs. The titration curves are shifted whenever we change the radius of the filter (Fig. 2 of Ref. 32); the length of the filter (Fig. 6 of Ref. 34); the dielectric coefficient of the protein (Fig. 8 of Ref. 31); the concentration of the background Na⁺ (Fig. 6 of Ref. 28); the radius of the monovalent cation [Fig. 7(a) of Ref. 28)]; or the radius of the divalent cation [Fig. 7(b) of Ref. 28)]. Changing any of these parameters changes the energetics of the competition between the two cations, and, consequently selectivity. The CSC mechanism states that the selectivity filter favors Ca^{2 +} because it is more efficient at balancing the charge of the oxygen ions than Na⁺. It provides twice the charge in the same excluded volume. In this picture, the fact that the filter is crowded has a special significance. All the parameters listed in the preceding paragraph influence the ionic density in the filter somehow, and, thus, they influence the strength of the competition between cations for the limited amount of space available in the filter. The radius and length of the filter, for example, change the volume of the filter, and, thus, ionic density. The smaller dielectric coefficient of the protein acts to attracts more cations into the filter thus making it more crowded.

Excluded volume obviously is a dominant feature of selectivity filters. Thus, it may seem counter intuitive that Ca^{2 +} versus Na⁺ selectivity does not depend on the HS term very much. This is because the HS terms express the direct effect of the steric exclusion of the ions on their abilities to find space in the filter. If two ions have the same size, these direct effects are the same. The crowded nature of the selectivity filter, however, has a profound indirect effect on the electrostatic parts of the EXCP. Because the filter is crowded, ions have difficulty finding space in it. The filter, therefore, is never charge neutral; due to confinement and limited space, cations within the filter can only partially balance the negative oxygen ions. Some of the balancing charge is outside the filter. The resulting negative filter produces a free-energy well for the cations. In this large-density negatively charged environment, many-body ionic correlations are very important, as shown by the SC terms.

Figure 8 shows the dependence of our results on the protein dielectric coefficient, ϵ_pr, relative to the reference condition of R = 3.5 Å, c _{Na ⁺}(B)=30 mM, c _{Ca ²⁺}(B)=1 μM. Because the bulk concentrations are fixed, the number advantage is the same for all values of ϵ_pr. Binding selectivity, however, increases (the channel becomes more Ca^{2 +} selective) as ϵ_pr decreases from 80. The ION term decreases with decreasing ϵ_pr. The principal source of this decrease is the MFI term. When ϵ_pr is small, more cations are attracted into the channel as discussed in our previous work.³¹ The energetic explanation is that it takes energy to polarize the dielectric boundaries so the system is trying to minimize the induced charge. This is possible only by making the channel more charge neutral by attracting more cations into it. Because the channel is closer to charge neutrality at small ϵ_pr, the MFI advantage decreases with decreasing ϵ_pr.

The term that increasingly favors Ca^{2 +} with decreasing ϵ_pr is, of course, the DIEL term. Although the SELF term favors Na⁺ with decreasing ϵ_pr, the other two dielectric terms (MFD and SCD) increasingly favor Ca^{2 +} with decreasing ϵ_pr. This result is expected because the induced charges are larger when the difference between the dielectric coefficients on the two sides of the dielectric interface is larger.

If we keep ϵ_pr = 10 constant and change the radius of the filter, R, instead, we obtain the results shown in Fig. 9. Binding selectivity increases as R decreases. The ION term changes only a little with changing R; the DIEL term, on the other hand, changes a lot. Apparently, the value of ϵ_pr is the first order determinant of the number of cations attracted into the filter. The value of ϵ_pr determines the degree of charge neutrality of the filter, which, in turn, determines the MFI term. The ions seem to coordinate to get efficient screening even when R is small. The important term that determines selectivity with changing R is the DIEL term. In a more narrow pore ions are closer to the pore wall on average. Therefore, the induced charge is larger and the potential produced by it in the filter is also larger. The low dielectrics surrounding the pore focuses field lines, making the total field density in the filter larger. The filter with a smaller radius focuses the field lines even more strongly. These findings are in agreement with Fig. 3 of Boda et al.³² which shows that Ca^{2 +} versus Na⁺ selectivity is more sensitive to R when ϵ_pr = 10 than in the case when ϵ_pr = 80.

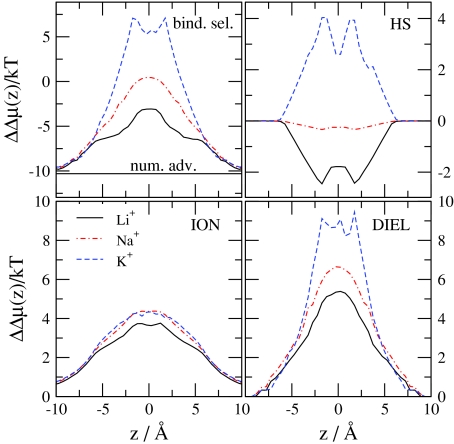
If we change the size of the monovalent ion (by switching ion type to Li⁺, Na⁺, and K⁺, using the corresponding Pauling radii), we obtain the results shown in Fig. 10. Ca^{2 +} binding selectivity increases as the radius of the monovalent ion increases. One of the important terms is the HS term that increases considerably as the radius of the monovalent ion increases. Ca^{2 +} can compete more efficiently for space with the larger monovalent cations. The other important term is the DIEL term, which has the same behavior. The induced charges are smaller for the larger ions because ion centers (where charges are) are farther from the dielectric boundary. Larger positive ions, therefore, induce less positive induced charge, leaving the total induced charge more negative. More negative induced charge favors the binding of Ca^{2 +} as we described above.

Figure 11 shows the results for the competition of two cations of the same charge but different size. The bath concentration of both Ca^{2 +} and Ba^{2 +} is the same (50 mM), so the numerical advantage of Ca^{2 +} over Ba^{2 +} is zero. The HS term is the main source of the large binding selectivity of the smaller Ca^{2 +} over the larger Ba^{2 +}, while the electrostatic terms are of little importance in this case.

SUMMARY

We have analyzed the energetics of selectivity for a reduced model of the L-type calcium channel in terms of various components of the EXCP. These components included those due to volume exclusion (HS) and various electrostatic terms. The electrostatic terms included the MF terms due to interactions with the average field of ions and induced charges. The terms beyond the MF terms are due to many-body correlations between ions (SCI), as well as between ions and induced charges (SCD). These correlations are crucial in the case of calcium channels, where the ionic density in the selectivity filter is very large and everything interacts with everything else strongly.

Polarization, in particular, plays an important role in the behavior of the selectivity filter of the L-type calcium channel. It makes the electric field in the filter stronger and, thus, it makes the competition between the cations stronger. In this competition, multivalent and smaller ions have the advantage in the highly charged and crowded selectivity filter. This is consistent with experimental data on both L-type and RyR calcium channels.

Even in our very reduced model of the channel we encountered a complex picture. Different terms played different roles depending on which variable was changed: bath ion concentrations, ion charges, ion radii, pore radius, or protein dielectric coefficient. It is important to emphasize that this complexity is an automatic consequence of our model and an output of our calculations. All the terms we computed must have analogs in more detailed models of the protein and electrolyte. Therefore, it is likely that this rich behavior will be present not only in real calcium channels, but also in other carboxylate-rich binding sites like those of calcium binding proteins (e.g., calmodulin) and chelators [e.g., ethylenediamine tetra-acetic acid (EDTA), ethylene glycol tetraacetic acid (EGTA)].

APPENDIX: COMPUTATION OF THE EXCESS CHEMICAL POTENTIAL PROFILE IN AN INHOMOGENEOUS SYSTEM USING WIDOM’S METHOD IN THE GRAND CANONICAL ENSEMBLE

Let us assume that we have a large simulation cell of volume V at temperature T where the thermodynamic state is set by fixing the chemical potentials of the components ${\mu }_i^{\mathrm{TOT}}$. The system can be inhomogeneous with external forces (walls, electric field, etc.) acting on the particles. This means that the concentration and the EXCP can be position dependent.

We introduce the formalism for a pure fluid of spherical particles; the extension for mixtures and nonspherical particles is straightforward. The grand partition function is

$$\begin{array}{ccc}\hfill \Xi =& & \sum _N{\displaystyle \frac{e^{\beta {\mu }^{\mathrm{TOT}}N}}{{\Lambda }^{3N}N!}}{\int }_V\cdots {\int }_{V}d{\mathbf{r}}_1\cdots d{\mathbf{r}}_N\hfill \\ & & \exp \left[-\beta U_N({\mathbf{r}}_1\cdots {\mathbf{r}}_N)\right],\hfill \end{array}$$ (A1)

where β = 1∕kT. The one-particle density is

$$\begin{array}{ccc}\hfill \rho \left(\mathbf{r}\right)& & =〈N\delta (\mathbf{r}-{\mathbf{r}}_N)〉\hfill \\ & & ={\displaystyle \frac{1}{\Xi }}\sum _N{\displaystyle \frac{e^{\beta {\mu }^{\mathrm{TOT}}N}}{{\Lambda }^{3N}(N-1)!}}{\int }_V\cdots {\int }_{V}d{\mathbf{r}}_1\cdots d{\mathbf{r}}_{N-1}\hfill \\ & & \exp \left[-\beta U_N({\mathbf{r}}_1\cdots {\mathbf{r}}_{N-1},\mathbf{r})\right].\hfill \end{array}$$ (A2)

Treating the Nth particle as a perturbation (ghost particle), the energy splits into two terms:

$$U_N({\mathbf{r}}_1\cdots \mathbf{r})=U_{N-1}({\mathbf{r}}_1\cdots {\mathbf{r}}_{N-1})+\Delta U_N({\mathbf{r}}_1\cdots \mathbf{r}).$$ (A3)

Therefore,

$$\begin{array}{ccc}\hfill \rho \left(\mathbf{r}\right)& =& {\displaystyle \frac{e^{\beta \mu }}{{\Lambda }^3}}{\displaystyle \frac{1}{\Xi }}\sum _N{\displaystyle \frac{e^{\beta {\mu }^{\mathrm{TOT}}(N-1)}}{{\Lambda }^{3(N-1)}(N-1)!}}\hfill \\ & & \times {\int }_V\cdots {\int }_{V}d{\mathbf{r}}_1\cdots d{\mathbf{r}}_{N-1}{e}^{-\beta \Delta U_N}{e}^{-\beta U_{N-1}}\hfill \\ & =& {\displaystyle \frac{e^{\beta \mu }}{{\Lambda }^3}}〈e^{-\beta \Delta U_N\left(\mathbf{r}\right)}〉.\hfill \end{array}$$ (A4)

On the right-hand side, we find the GC ensemble average of exp [ − βΔU_N(r)], where the Nth particle acts as a test particle added to a (N − 1)-particle system at position r. Expressing μ, we obtain

$$\begin{array}{ccc}\hfill \mu =& & kT\ln {\Lambda }^3+kT\ln \rho \left(\mathbf{r}\right)\hfill \\ & & -kT\ln 〈\exp \left[-\beta \Delta U_N\left(\mathbf{r}\right)\right]〉.\hfill \end{array}$$ (A5)

This equation corresponds to Eq. 4. Therefore, the space-dependent EXCP can be computed by inserting test particles at position r of the full GC system.

In practice, we insert particles into a small subvolume around position r uniformly and average over many such insertions. This subvolume must be small enough that the concentration and the EXCP can be assumed constant in this subvolume. At the same time, the subvolume must be large enough for adequate sampling. The subvolume is open, so particles can enter and leave all the time during thermal motion. In this respect, the subvolume is related to the small system grand canonical ensemble.⁴⁹