Protein folding in a reverse micelle environment: The role of confinement and dehydration

Abstract

Characterization of the molecular interactions that stabilize the folded state of proteins including hydrogen bond formation, solvation, molecular crowding, and interaction with membrane environments is a fundamental goal of theoretical biophysics. Inspired by recent experimental studies by Gai and co-workers, we have used molecular dynamics simulations to explore the structure and dynamics of the alanine-rich AKA₂ peptide in bulk solution and in a reverse micelle environment. The simulated structure of the reverse micelle shows substantial deviations from a spherical geometry. The AKA₂ peptide is observed to (1) remain in a helical conformation within a spherically constrained reverse micelle and (2) partially unfold when simulated in an unconstrained reverse micelle environment, in agreement with experiment. While aqueous solvation is found to stabilize the N- and C-termini random coil portions of the peptide, the helical core region is stabilized by significant interaction between the nonpolar surface of the helix and the aliphatic chains of the AOT surfactant. The results suggest an important role for nonpolar peptide–surfactant and peptide–lipid interactions in stabilizing helical geometries of peptides in reverse micelle environments.

INTRODUCTION

Dramatic progress has been made in the experimental observation^{1, 2, 3, 4, 5, 6} and simulation of protein folding using minimal coarse-grained^{7, 9, 10, 11} and atomistic models.^{12, 13, 14, 15, 16} As a result, a general understanding of the time scale and mechanism of protein folding has been developed, including how the kinetics may be related to characteristics of the protein’s free energy landscape. That work has led to the identification of a number of fundamental principles that relate the importance of microscopic interactions, including hydrogen bond formation, solvation, desolvation, molecular crowding, formation of native contacts, and the possible role of non-native interactions in the protein folding pathway and stabilization of the protein’s native state structure.

Observations of protein folding and aggregation in reverse micelles

Reverse micelle (RM) assemblies, consisting of oil∕detergent∕water ternary complexes, play an important role in biochemistry.¹⁷ The detergent, also known as a surfactant, is an amphiphilic molecule composed of a hydrophilic head group and hydrophobic tail group.^{18, 19, 20} The head groups of the surfactant molecules aggregate around a polar water core, while the hydrophobic tails extend out into the nonpolar solvent. RMs are often assumed to have a spherical shape and their size is directly proportional to the water-to-surfactant ratio (w₀ = [H₂O]∕[surfactant]) or water loading.²¹ When the number of surfactant molecules is above the critical micelle concentration (CMC), reverse micelles will spontaneously form in solution. By manipulating the water loading, one can vary the radius of the RM and the number of water molecules accessible to the peptide. The use of a reverse micelle to confine the peptides provides a tunable confinement geometry that can be used to adjust the total ratio of peptides to water in the encapsulation of peptides in the micellar water core.

Recently, Gai and co-workers studied the effect of hydration on alanine-rich peptides where the sequence is periodically punctuated by charged lysine residues (ACE-YGAKAAAA-(KAAAA)_nG-NH₂ where n = 1 and 3), known to exhibit increased helical content with backbone dehydration, by incorporating them into AOT∕H₂O∕isooctane RMs. Far-UV circular dichroism (CD) spectroscopy indicated that the peptides have partial helical structure in the RM environment, whereas they are unstructured in bulk water.²² In a related study, Gai and co-workers used IR spectroscopy of the amide I^′ vibrational transitions to track the degree of hydration of two alanine-rich peptides, AKA₂ and AKA₆ (ACE-YGAKAAAA-(KAAAA)_nG-NH₂ where n = 2 and 6, respectively), in AOT∕;D₂O∕isooctane RMs as a function of water loading and temperature. The AKA_n + RM complexes produced two overlapping amide I^′ transitions centered at 1634 and 1650 cm⁻¹, indicating that the peptide backbone is helical and is also partially hydrated and partially dehydrated in the RM environment. The observed temperature dependence indicates that for small RM water loadings (w₀ = 6 and 10) at a certain onset temperature, the peptides produced amide I^′ transitions characteristic of aggregates rich in antiparallel β-sheets. These features were not observed when the same analysis was performed on the peptides in bulk D₂O nor in RMs with higher water loading values (w₀ = 20). This suggests that it is the degree of hydration that promotes peptide aggregation, rather than the increasing temperature (which may help the peptide overcome a desolvation barrier).²³

The nature of a reverse micelle environment in peptide confinement

There has been an increasing interest in understanding the shape and dynamics of RMs and the unique properties of their water cores.²⁴ The structure of RMs has been studied with experimental techniques including fluorescence,^{25, 26, 27} NMR,^{28, 29, 30} IR,^{31, 32, 33} and small-angle neutron scattering (SANS)∕small-angle x-ray scattering (SAXS).^{34, 35, 36, 37, 38, 39} Scattering studies provide limited insight into the size distribution of the RMs as well as the degree of shape fluctuations. In considering the use of RMs as a confining environment for the study of peptide folding and aggregation, it is important to consider the possible role of RM shape fluctuations in any interpretation of the thermodynamics or kinetics of folding and aggregation. Moreover, accurate scattering experiments may provide insight into changes in the size distribution and shape fluctuations induced by the addition of peptide to the solution of RMs, even when the number of RMs occupied by the peptide represents a small fraction of the overall RM population.

Computational methods have been employed to gain an atomic-level understanding of the properties and dynamics of the RM and its water core.^{24, 40, 41, 42} Marchi and co-workers used explicit molecular dynamics (MD) simulations to study the structure and dynamics of an AOT∕H₂O∕isooctane RM assembly.⁴⁰ They found that the RMs did not retain a spherical shape. Instead, substantial deformations from a spherical geometry were observed.⁴⁰ In a later study, Marchi and co-workers incorporated an octaalanine (A₈) peptide into the AOT∕H₂O∕isooctane RM.⁴³ The size and shape of the RM was observed to be only slightly affected by the presence of the peptide. However, they observed a substantial slowing down of the translational motion of the water in the smaller RM (w₀ = 5). Moreover, the diminished availability of water enhanced intramolecular peptide hydrogen bonds acting to preserve the peptide’s initial helical structure. No significant slowing down was observed for the water dynamics in the RM with w₀ = 6. In the larger system, the peptide’s helical structure was not conserved.⁴³

More recently, dynamics of water confined in an AOT RM environment has been found to exhibit extreme “glassy” behavior with a stretched exponential decay and characteristic exponent of β = 0.2. The IR spectra for water computed from those simulations, where the RMs exhibited nonspherical geometries, were found to be in good agreement with experiment.^{44, 45} Finally, Tian and Garcia⁴⁶ employed molecular dynamics simulations to study the self-assembly of AOT∕water RMs (w₀ = 6 and 11) in isooctane. The RM systems included one helical AK4 (${\mathrm{NH}}_3^{+}$-YG(AKAAA)₄AG-COO⁻) peptide. After encapsulation by the RM, the helical peptide remained at the water∕AOT∕isooctane interface such that the peptide and AOT head groups shared coordinated water molecules, and the entropy loss of the water is reduced.⁴⁶

Our study employs MD calculations to simulate systems approximating those examined by Gai and co-workers, with a focus on elucidating the structure and dynamics of the AOT RM with and without peptide. Our goal is to acquire an atomic-level understanding of the effect that the RM environment (w₀ = 6) has on the conformational folding equilibrium of the alanine-based peptide, AKA₂ (ACE-YGAKAAAA-(KAAAA)_nG-NH₂ where n = 2). The study is designed to address a number of questions related to micelle structure and fluctuations as well as the nature of the AKA₂ peptide conformational structure and dynamics in bulk water and in a RM environment. How do we characterize the RM structure and fluctuations? How do we characterize the structure of the peptide within the RM environment? How is the peptide conformational equilibrium influenced by the constraints imposed by the RM environment relative to its structure in bulk solvent? Is the peptide primarily solvated within the RM or are there significant interactions between the AOT and the peptide? Our simulation results address each of these questions and provide important insights essential to the interpretation of experimental studies of the peptide’s structure and dynamics in the RM environment.

METHODS

RM simulations were performed where the overall geometry was (1) restrained to retain the overall spherical shape of the RM water droplet by imposing a harmonic restraining force to the charged head groups of the AOT surfactant molecules, or (2) unrestrained. In the restrained simulations, the AOT head groups were maintained within a spherical annulus of radius ranging from 13 to 15 Å. Four separate RM simulations were performed including (1) restrained RM, (2) unrestrained RM, (3) AKA₂ peptide in a restrained RM environment, and (4) AKA₂ peptide in an unrestrained RM environment. All simulations performed on the AOT∕H₂O∕isooctane assembly included sodium counter ions to ensure overall electroneutrality. The initial helical configuration of the AKA₂ peptide in each system was generated using the CHARMM32 package with the CHARMM27 all atom force field.⁴⁷ No CMAP correction was used. The TIP3 water model was used and force field parameters for the AOT and isooctane were taken from Abel et al.⁴⁰ The parameters for the size of the RM and the number of surfactant and water molecules were based on the work of Amararene et al.³⁴ For reference, two AKA₂ peptides were simulated in a bulk water environment. To test the sensitivity of the results on the specific force field used, complementary simulations were performed using the GROMOS96 53a6 force field and the GROMACS (Ref. ⁴⁸) simulation program resulting in similar ranges of average elliptical radii and radius of gyration explored. This consensus check suggests that these results are robust for the system studied.

Equilibration and production runs were performed with NAMD.⁴⁹ Details regarding the initial conditions, equilibration, and production runs are provided in the supplemental information.⁵⁰ Simulation details are summarized in Table 1. The simulation of two AKA₂ peptides in bulk solvent was also run with NAMD.⁴⁹ The peptides were solvated with TIP3 water in a truncated octahedron with periodic boundary conditions. The system was then equilibrated for 800 ps at constant pressure and temperature. After equilibration, the system was simulated for 50 ns with an NVT ensemble at 300 K using Langevin dynamics to control the temperature and Ewald sums to evaluate electrostatics.

Table 1.

Summary of simulation details for the composition and duration of peptide and reverse micelle simulations, including water loading (w₀), number of AOT molecules (n_AOT), number of sodium counterions (n_counterions), number of water molecules (n_H2O), number of isooctane molecules (n_iso), and production run time in nanoseconds (t (ns)).

System	w0	nAOT	ncounterions	nH2O	niso	t (ns)
Restrained RM	6	80	80 Na+	474	1542	50
Unrestrained RM	6	80	80 Na+	474	1542	50
AKA2 + restrained RM	6	80	77 Na+	474	1542	50
AKA2 + unrestrained RM	6	80	77 Na+	474	1542	50
AKA2 + bulk solvent	n∕a	n∕a	6 Cl−	3968	n∕a	50

Radial pair distribution functions (PDFs; Ref. 51) for the water droplets of the final structures of the restrained and unrestrained RM simulations were calculated in order to characterize the simulated RM structures. The PDFs for the water in each restrained RM were fit to a Gaussian, and the PDFs for the water in each unrestrained RM were fit to the sum of two Gaussians.

RESULTS

Simulations of the reverse micelle for water loading of w₀ = 6 were carried out (1) in the presence and absence of spherical restraints and (2) with and without AKA₂ peptide. The results of the peptide simulations were compared with standard results for the AKA₂ peptide in bulk aqueous solution.

The reverse micelle shows substantial deviations from spherical geometry

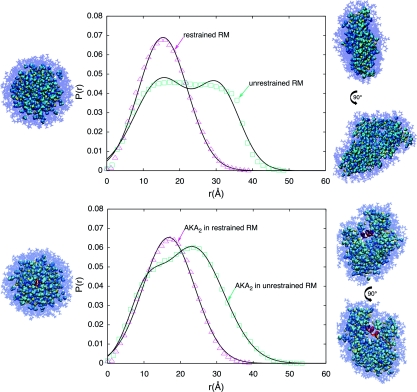
The structure of the reverse micelle was analyzed visually, through evaluation of the radius of gyration and ellipticity parameters, and through the computation of the PDF associated with the RM water core. The final snapshot for the restrained micelle and two views of the final snapshot for the unrestrained RM are shown in Fig. 1 along with the corresponding PDF of each water droplet. These representative structures demonstrate the strong deviations from spherical geometry observed in our simulations of the RM with water loading at w₀ = 6. The distorted Gaussian shape of the unrestrained RM is similar to that observed by Yano et al.³⁹ for reverse micelles with small w₀ values.

Figure 1.

Radial pair distribution functions (PDF) computed for the reverse micelle water core for the instantaneous final structures of the RM only (top) and the RM including AKA₂ (bottom) simulations. The pink triangles and green boxes represent data points calculated from the trajectories. The solid black lines are the Gaussian functions fit to the data. Final snapshots of the reverse micelle assembly from each dynamics trajectory are shown for the restrained RM systems (left) and unrestrained systems (right). The transparent stick model represents the AOT surfactant molecules (blue), while the space-filling model represents the water (cyan), and sodium counterions (yellow).

The unrestrained RM is commonly found in geometries that are best described as toroidal or disclike. It is not uncommon to see the unrestrained water droplet assume a toroidal shape with a center formed by a concentration of nonpolar aliphatic tails of the AOT molecules. The AOT tails are observed to interact with and stabilize a “pinch” in the RM surface. These substantial deviations from spherical structures lead to distinct signatures in the distribution functions. For toroidal structures, the distribution function shows two clear peaks while those of spherical RMs are unimodal.

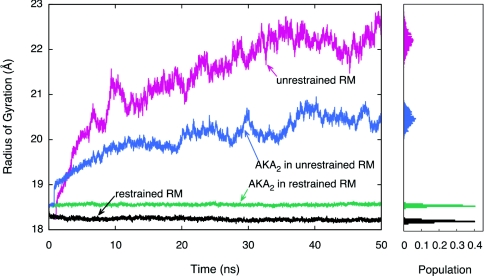
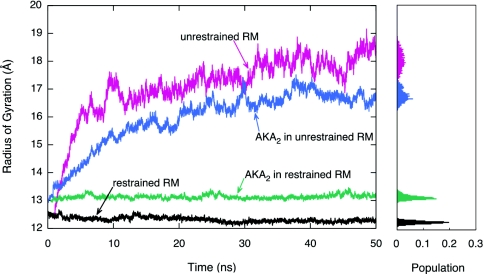
As an additional order parameter for the characterization of structural fluctuations in the RMs, the radii of gyration for the full RM assemblies and the RM water cores are shown in Figs. 23 (data shown here are for CHARMM simulations only). The radius of gyration values for the last 15 ns of the simulations are projected in the histograms on the right in each figure. An analysis of these plots demonstrates that the deviation from the initial shape and size of the unrestrained RMs is established within the first few nanoseconds. It is also interesting to note that the radius of gyration of the restrained RM with the AKA₂ is slightly larger than that of the restrained RM with no peptide. Upon insertion of the peptide into the RM, the RM expands to accommodate the larger volume in its interior. The opposite is seen for the unrestrained RM systems, as the RM with no peptide has a higher radius of gyration indicating that it becomes much more disclike than the RM with the AKA₂.

Figure 2.

Radius of gyration versus time plot for the full reverse micelle assemblies of the restrained RM (black), unrestrained RM (red), restrained RM with AKA₂ peptide (green), and unrestrained RM with AKA₂ peptide (blue) systems. The histogram to the right shows the population of radius of gyration values for the last 15 ns of simulation.

Figure 3.

Radius of gyration versus time plot for the water droplet of the restrained RM (black), unrestrained RM (red), restrained RM with AKA₂ peptide (green), and unrestrained RM with AKA₂ peptide (blue) systems. The histogram to the right shows the population of radius of gyration values for the last 15 ns of simulation.

The average radius of gyration values over the last 15 ns of simulation (R_RM, R_wat) and their associated standard deviations (σ_RM, σ_wat, respectively) were also computed for all CHARMM and GROMACS simulations. These data are shown in Table 2 along with initial ($R_{\mathrm{RM}}^i$, $R_{\mathrm{wat}}^i$), final ($R_{\mathrm{RM}}^f$, $R_{\mathrm{wat}}^f$), and overall averages ($R_{\mathrm{RM}}^{\mathrm{avg}}$, $R_{\mathrm{wat}}^{\mathrm{avg}}$) of the radii of gyration. The average radii of gyration for the last 15 ns of simulation are larger for the unrestrained RM systems (for both the full RM and the water core). The standard deviations have the same trend, although less pronounced for the GROMACS systems. This further indicates that the unrestrained RMs deviate from a spherical shape, whereas the size and shape of the spherically restrained RM systems remain relatively constant throughout the simulation.

Table 2.

Characteristics of distributions of the radius of gyration of the full reverse micelle assemblies and the radius of gyration of the water cores, where (R_RM), (R_wat), σ_RM, and σ_wat are the averages and standard deviations over the last 15 ns of the trajectories. $R_{\mathrm{RM}}^i$, $R_{\mathrm{wat}}^i$ and $R_{\mathrm{RM}}^{\mathrm{avg}}$, $R_{\mathrm{wat}}^{\mathrm{avg}}$ and $R_{\mathrm{RM}}^f$, $R_{\mathrm{wat}}^f$ are the radii of gyration for the initial configurations, averages of the entire trajectories, and final snapshots, respectively.

System	$R_{\mathrm{RM}}^i$	$R_{\mathrm{RM}}^{\mathrm{avg}}$	$R_{\mathrm{RM}}^f$	RRM	σRM	$R_{\mathrm{wat}}^i$	$R_{\mathrm{wat}}^{\mathrm{avg}}$	$R_{\mathrm{wat}}^f$	Rwat	σwat
CHARMM restrained RM	18.6	18.2	18.2	18.2	0.02	12.6	12.3	12.2	12.3	0.05
CHARMM unrestrained RM	18.3	21.4	22.3	22.2	0.23	12.4	17.1	18.4	18.0	0.34
CHARMM AKA2 + restrained RM	18.6	18.6	18.6	18.6	0.02	13.0	13.1	13.2	13.2	0.08
CHARMM AKA2 + unrestrained RM	18.5	20.0	20.4	20.5	0.16	13.0	15.9	16.7	16.7	0.23
GROMACS AKA2 + restrained RM	18.6	18.6	18.6	18.6	0.03	13.8	15.2	15.5	15.4	0.08
GROMACS AKA2 + unrestrained RM	18.6	19.7	19.7	19.8	0.07	13.8	17.5	18.0	17.8	0.09

A similar trend is seen in observations of the degree of hydration, defined as the number of water molecules within 4 Å of the central SO₃ moiety of the AOT head groups (N_AOT, σ_AOT) and the sodium counterions (N_Na, σ_Na), as shown in Table 3. Upon removing the spherical restraints on the RM structure, a significant increase in the degree of hydration of the AOT head groups and, to a lesser extent, the sodium counterions is observed. This suggests that the deviation of size and shape of the unrestrained RM is driven by the reorganization of water molecules hydrating the AOT head groups and sodium counterions. A more detailed description is available in the Supplemental Information.⁵⁰

Table 3.

Characteristics of distributions of the hydration of AOT head groups (N_AOT), and ion association distances (N_Na) and their associated standard deviations (σ_AOT, σ_Na).

System	NAOT	σAOT	NNa	σNa
Restrained RM	324	5.2	301	9.2
Unrestrained RM	385	11.5	334	10.8
AKA2 + restrained RM	342	4.6	307	8.2
AKA2 + unrestrained RM	377	12.2	318	12.9

Average elliptical radii values calculated for all RM systems are shown in Table 4. Results obtained for the CHARMM and GROMACS simulations of the RMs with the AKA₂ peptides are almost the same for the restrained systems. In the unrestrained systems, the numbers suggest that CHARMM RM is flatter than the GROMACS RM, but both lose the initial spherical geometry. In all cases, the values for the restrained RMs are lower than for the unrestrained RMs further emphasizing that the restrained RMs maintain their spherical shape while the unrestrained RMs do not. Our values are comparable to those obtained by Pieniazek et al. whose elliptical radii averages also suggest that unrestrained RMs of similar water loadings deviate from their initial spherical shape.⁴⁵

Table 4.

Average elliptical radii (〈a〉, 〈b〉, and 〈c〉) for RM simulations in CHARMM and GROMACS.

System	〈a〉	〈b〉	〈c〉
CHARMMrestrained RM	14.8 ± 0.04	14.9 ± 0.04	15.0 ± 0.04
CHARMMunrestrained RM	14.2 ± 0.70	17.6 ± 1.34	20.1 ± 1.21
CHARMMAKA2 + restrained RM	15.1 ± 0.03	15.1 ± 0.21	15.3 ± 0.03
CHARMMAKA2 + unrestrained RM	15.0 ± 0.33	16.6 ± 0.58	17.4 ± 0.63
GROMACSAKA2 + restrained RM	15.1 ± 0.04	15.2 ± 0.03	15.4 ± 0.04
GROMACSAKA2 + unrestrained RM	15.1 ± 0.10	15.6 ± 0.13	17.6 ± 0.35

Different structures of the AKA₂ peptide are observed in the bulk solvent, restrained RM, and unrestrained RM environments

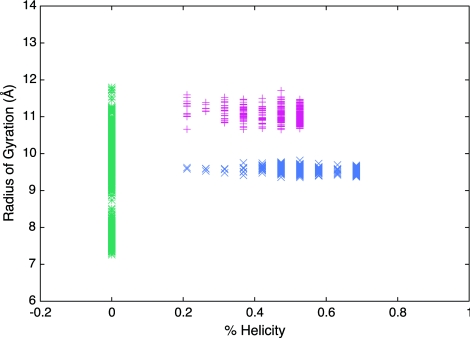
The root mean square deviations (RMSD) of the AKA₂ peptide backbone were calculated as a way to quantify the structural changes of the peptide in the three different systems: bulk solvent, restrained RM, and unrestrained RM. Analysis of the RMSD versus time plot⁵⁰ shows that the AKA₂ peptides in bulk water deviate significantly from their original structures and have large fluctuations in their RMSDs. In contrast, the AKA₂ peptides in the RMs show much less deviation from their initial values, and the smaller fluctuations in RMSD indicate the peptide backbones are constrained, especially in the case of the AKA₂ in the restrained RM. The radius of gyration versus percent helicity plot (see Fig. 4) reinforces the finding that AKA₂ peptides in bulk are no longer helical by the end of the simulation and that the peptide in the restrained RM has more helical character (and a smaller radius of gyration) than the peptide in the unrestrained RM.

Figure 4.

Radius of gyration of the peptide versus percent helicity plot for the last 5 ns (45–50 ns) of the simulation of AKA₂ in bulk water (green stars), restrained RM (blue Xs), and unrestrained RM (red crosses) environments. The results indicate that the peptides in bulk water do not retain their initial helical structure. The peptide in the restrained RM remains mostly helical and has a lower radius of gyration than the peptide in the unrestrained RM, which is slightly less helical.

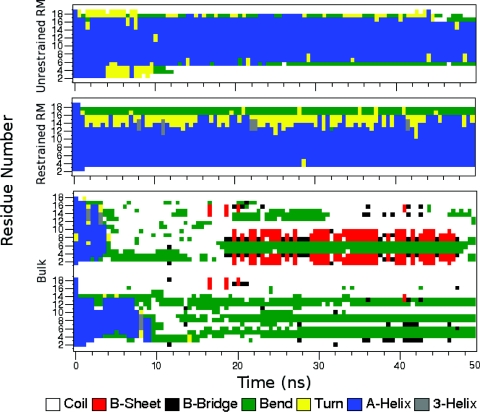
The progression of change in secondary structure for each CHARMM system is shown clearly in Fig. 5. The AKA₂ peptides in both restrained and unrestrained reverse micelles clearly maintain their helicity in the core residues of the peptide throughout the simulation, while the peptides in bulk water lose all their helicity within the first 10 ns. Results for the GROMACS systems show the same trend.⁵⁰ The definition of helicity used in both Figs. 45 is based on Kabsch and Sander’s DSSP method.⁵²

Figure 5.

Structure of residues versus time plot. Results demonstrate that in a RM environment, the structure of AKA₂ is significantly helical as compared to its structure in bulk water. In both reverse micelles, the peptides maintain a helical core and the peptides in bulk water lose all helicity in the first 10 ns of simulation.

Partially folded peptide structure is stabilized by nonpolar interactions with AOT

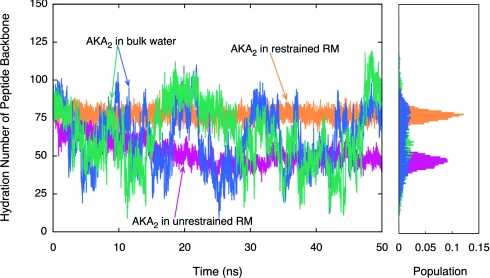
To determine how hydration affects the structure and dynamics of AKA₂, we analyzed the degree of hydration of the peptide backbone as a function of time (see Fig. 6). The hydration level of the AKA₂ peptide in a restrained RM environment is observed to be constant throughout the simulation. The AKA₂ peptides in bulk water show a significantly higher degree of hydration due to the unfolded coil state of the peptide. In the unrestrained RM environment, the hydration level of the peptide backbone decreases significantly below the value observed in bulk water.

Figure 6.

Hydration number (waters within 4 Å) of peptide backbone versus time plot. Results demonstrate that in an unrestrained RM environment, AKA₂ experiences a decrease in backbone hydration. The histogram to the right shows the population of hydration number values for the last 25 ns of simulation.

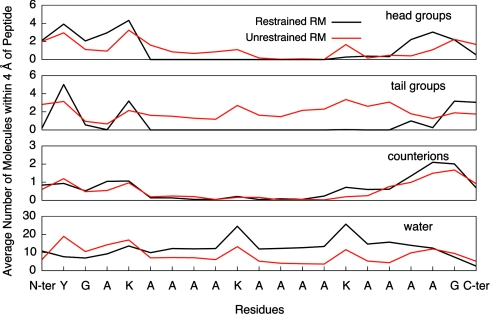
The average number of contacts of the peptide with AOT head groups, AOT tail groups, sodium counterions, and waters (see Fig. 7) show that the N- and C-terminal ends of the peptide associate with the AOT head groups and sodium counterions in both the restrained (black) and unrestrained (red) RM environments. In addition, the results show that the central portion of AKA₂ in the restrained RM environment has significant contact with water and little contact with the AOT tail groups. The opposite effect is seen in the unrestrained RM environment where the central portion of the peptide has significant contact with the AOT tail groups and little contact with water.

Figure 7.

Average contact (group within 4 Å) for AKA₂ residues with AOT head group atoms (top), AOT tail group atoms (second), sodium counterions (third), and water (bottom). The results demonstrate that in both the restrained (black curve) and unrestrained (red curve) RM environments, the N- and C-terminal ends of the peptide have significant contact with the head groups and sodium counterions. In the restrained RM environment, the central portion of the peptide has extensive contact with water, unlike the peptide in the unrestrained RM, which has significant association with the AOT tail group atoms and little contact with water.

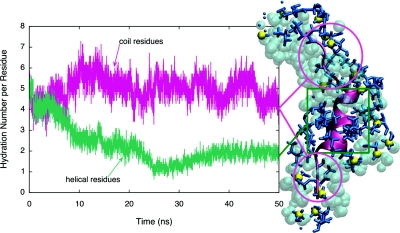
Analysis of the initial and final AKA₂ structures in the unrestrained RM environment, including atoms within 5 Å of the peptides (see Fig. 8), demonstrates that the AOT tail groups interact strongly with the central portion of the peptide. Those interactions effectively dehydrate the peptide, immersing it in a low dielectric environment, thereby stabilizing the helical peptide geometry. The degree of hydration of AKA₂ in the unrestrained RM (see Fig. 8) indicates that the helical residues are dehydrated throughout the simulation, while the hydration of the coil residues remains relatively constant.

Figure 8.

Hydration number (waters within 4 Å) per AKA₂ residue versus time in an unrestrained RM. Results demonstrate that the hydration of the helical residues (green) decreases, while hydration of the coil residues (red) remains relatively constant. The final AKA₂ structure, shown on right, includes water (cyan), AOT (blue), and sulfur atoms of AOT (yellow) within 5 Å of the peptide.

DISCUSSION

We have used MD simulations to obtain an atomic-level understanding of the structure and fluctuations of a reverse micelle assembly in the presence and absence of the alanine-rich AKA₂ peptide. As had been observed in earlier simulations by Abel et al.^{40, 43} and Brodskaya and Mudzhikova⁸, substantial deviations from spherical geometries are observed for the unrestrained reverse micelle and are found to be an essential feature of the RM solvation environment.

RM environment stabilizes peptide helix formation at w₀ = 6

In simulations of the AKA₂ peptide in a spherically restrained reverse micelle environment, the peptide maintained most of its initial helical structure for the course of the simulation and demonstrated relatively small structural fluctuations. In simulations of the AKA₂ peptide in bulk water solution, the peptide was found to adopt random coil conformations and demonstrate large structural fluctuations. In contrast, simulations of the AKA₂ peptide in an unrestrained RM resulted in a partially folded peptide with a random coil structure in the N- and C-terminal regions and a helical structure in the core region. These results are in qualitative agreement with the experimental observations of Mukherjee et al.^{22, 23} Importantly, we observe that the partially folded peptide structure is stabilized by (1) strong solvation of the unfolded, coil structure in the N- and C-terminal regions and (2) substantial interaction with the aliphatic tail groups of the surfactant molecules that stabilize the helical core region. Similar interactions were seen in the MD simulations of the AK4 peptide in a self-assembling RM environment performed by Tian and Garcia.⁴⁶ It was observed that the AK4 peptide remained helical throughout the simulation, and once the RM encapsulation occurred, the peptide interacted mainly with the AOT head and tail groups. The peptide backbone had some interaction with water, but significantly less in bulk water.

Our simulations support the conclusion of Mukherjee et al.^{22, 23} that the AKA₂ peptide is partially helical and partially dehydrated in the RM environment. Importantly, our simulations indicate that the dehydration of the peptide is driven by direct interactions between the peptide and the nonpolar AOT tail groups, in addition to the limited availability of water.

Interpretations of water loading and limitations of spherical RM models

Our simulations of the structure and dynamics of RMs with a water loading of w₀ = 6 suggest that there are substantial deviations from the assumed spherical geometry employed in the pioneering simulations of Faeder and Ladanyi.^{53, 54} More recent work^{8, 45} suggests that reverse micelles are less spherical than originally presumed. The simulations reported here represent a single monodisperse interpretation of the water loading of w₀ = 6, with 474 water molecules and 80 AOT molecules. In a RM solution, the water loading represents the bulk ratio of water to AOT molecules. The actual size of a RM may vary somewhat from that number due to (1) thermal fluctuations inducing polydispersity in the [water]∕[AOT] ratio in an ensemble of spherical RMs and (2) deviations from a spherical geometry that may vary the ratio of interior volume (related to the number of water molecules) to surface area (defined by the number of AOT head groups and the surface area per head group). It is the latter effect that would appear to represent the most significant contribution to variations in the most probable RM size for a given water loading, particularly for smaller loadings such as w₀ = 6.

Will different interpretations of the number of AOT molecules corresponding to w₀ = 6 affect our results in a significant way? Based on prior simulations of the interpretation of various water loading ratios, the number of AOT molecules for solutions with w₀ = 5 and w₀ = 7 would lead to an estimate of 76 AOT molecules for w₀ = 6. The simulations of Abel et al.⁴⁰ employed an AOT count of 82 for a RM of w₀ = 7, a value that is 10% lower than the estimate based on the interpretation of SAXS experiments.³⁴ We consistently observe that each AOT head group supports a solvation shell of five water molecules. We conjecture that the strong solvation of the AOT head groups depletes the number of free water molecules in the RM interior. The effect of enhancing the “skin” of the RM relative to its “load” increases the propensity of the RM to pucker, leading to the observed “pinched” toroidal geometries. Additional exploratory simulations with slight variations in the [water]∕[AOT] ratio were carried out and indicate that small variations of 3 to 4 in the number of AOT molecules used in our interpretation of w₀ = 6 will not change this behavior in a significant way.

Deviations from a spherical geometry allow for significant enhancements in the hydration of the AOT head groups. As such, nonspherical RMs are expected to have a larger fraction of water molecules associated with the first solvation shell of the AOT–water interface, leading to (1) a reduction in the number of free water molecules in the RM interior and (2) an increase in the surface area per AOT head group. That effect leads to a decreased average mobility of water in the nonspherical micelles relative to the idealized spherical geometries. Most significantly, the extensive recruitment of water to the AOT head groups and sodium counterions lowers the activity of water molecules in the RM interior, making the water less available to solvate peptides dissolved in the RM.

It would be interesting to observe peptides in reverse micelles made with surfactants other than AOT. Wand and co-workers have spent time considering the effects of different surfactants.^{55, 56, 57} They used reverse micelles to encapsulate proteins with high structural fidelity using a combination of anionic (AOT) and cationic (CTAB: cetyltrimethylammonium bromide) surfactants.⁵⁶ In addition to Wand’s approach, the use of nonionic surfactants [Igepal⁵⁸ or Brij-30 (Ref. ⁵⁹)] would allow us to compare differences in RM geometry, peptide secondary structure, and peptide interaction with water and surfactant.

Considerations for peptide folding in larger reverse micelles

Our simulations of the structure and dynamics of the AKA₂ peptide in a reverse micelle environment have been restricted to the RM with a water loading of w₀ = 6. Experimentally, Gai and co-workers have explored RMs with water loadings as large as w₀ = 20.²³ Experimental findings suggest that larger RMs are more likely to maintain a spherical geometry than RMs with smaller water loadings.³⁹

The solvation of the peptide in a more spherical RM environment should influence the overall ensemble of coil, partially helical, and fully helical peptide conformations. Our simulations indicate that for w₀ = 6, deformations in the RM allow for the partial nonpolar solvation of the core region of the AKA₂ peptide, stabilizing the local helical peptide geometry. With increasing water loading, we expect that the activity of water will increase, allowing for more complete solvation of the peptide and relative stabilization of the coil states. In the limit that the RM is very large, we expect the peptide conformational equilibrium to resemble that of the peptide in bulk aqueous solvent where it exists predominately in a coil geometry.

Connection to protein folding near a membrane interface

Early computational studies, including those of melittin^{60, 61} and alamethicin^{62, 63} in lipid bilayers, have provided insight into the role of a water–membrane interface in stabilizing the folded state of amphipathic helical proteins. By breaking the symmetry of the bulk solvent, peptides with a sequence that supports a folded state having a nonpolar face and a polar face have been known to associate with a membrane interface stabilizing the helical conformation both (1) at the interface (relative to bulk solution) and (2) in the helical conformation (relative to the disordered coil state). Similar driving forces are at play for peptide folding in a RM environment.