In Situ Parameter Identification of Optimal Density-Elastic Modulus Relationships in Subject-Specific Finite Element Models of the Proximal Femur

Abstract

Quantitative computed tomography based finite element analysis of the femur is currently being investigated as a method for non-invasive stiffness and strength predictions of the proximal femur. The specific objective of this study was to determine better conversion relationships from QCT-derived bone density to elastic modulus, in order to achieve accurate predictions of the overall femoral stiffness in a fall-on-the-hip loading configuration. Twenty-two femurs were scanned, segmented and meshed for finite element analysis. The elastic moduli of the elements were assigned according to the average density in the element. The femurs were then tested to fracture and force-displacement data was collected to calculate femoral stiffness. Using a training set of nine femurs, finite element analyses were performed and the parameters of the density-elastic modulus relationship were iteratively adjusted to obtain optimal stiffness predictions in a least-squares sense. The results were then validated on the remaining 13 femurs. Our novel procedure resulted in parameter identification of both power and sigmoid functions for density-elastic modulus conversion for this specific loading scenario. Our in situ estimated power law achieved improved predictions compared to published power laws, and the sigmoid function yielded even smaller prediction errors. In the future, these results will be used to further improve the femoral strength predictions of our finite element models.

Introduction

Osteoporosis-related proximal femur fractures impose a major public health risk for the elderly, as they lead to high rates of disability and complications [1,2]. The majority of femoral fractures are sustained as a result of a lateral fall on the hip [3]. Noninvasive femoral strength evaluation methods are valuable tools for diagnosing osteoporosis, monitoring treatment, and facilitating drug developments. Among those, dual-energy X-ray absorptiometry (DXA), which quantifies areal bone mineral density (aBMD), is the current clinical standard to assess bone strength and diagnose osteoporosis [4]. However, DXA is a two-dimensional (2D) imaging modality, which does not account for femur geometry and bone mineral variations in three dimensions, and can only moderately predict femoral stiffness and strength. Strength evaluations based on three-dimensional (3D) imaging modalities such as quantitative computed tomography (QCT), in particular with the aid of finite element analysis, have the potential to overcome these shortcomings and produce more accurate results than aBMD alone [5].

Three dimensional (3D) finite element meshes can be constructed from QCT images of femurs to account for femur geometry, and material properties such as elastic modulus can be assigned to each element based on the image grayscale to account for spatial variations in bone mineral density [6]. QCT-based finite element analysis (QCT/FEA) is currently extensively investigated for non-invasive assessment of fracture load, type, and location [7-11]. In the QCT/FEA method, bone density is obtained from the QCT grayscale using a calibration phantom present in the scan, and the modulus of elasticity is subsequently derived from the bone density using empirical equations. However, the conversion of the bone mineral density to elastic modulus greatly influences the accuracy of the QCT/FEA prediction [12]. Various power law equations, obtained from uniaxial testing of small bone coupons with a range of densities have been previously used to describe the elasticity-density relationship in QCT/FEA models [13-15]. However, significant differences exist between reported equations [16]. In addition, they may not be accurate for femoral stiffness predictions when applied to whole bone subject-specific finite element models. Furthermore, a limitation of reported material tests on bone coupons is that the bone samples were cut from whole femurs. This prevented the measurements to be performed under conditions that are as close to the in vivo state as possible, namely an intact proximal femur. Thus, quasi-statically measured mechanical properties may not reflect the in vivo mechanical properties of the bone in a fall-on-the-hip loading orientation, with loading rates that reflect a fall from standing height. In this paper, we propose a novel technique to identify the parameters of the density-elastic modulus relation based on mechanical tests conducted on intact proximal human cadaveric femurs. First, QCT images of the femurs were used to generate 3D finite element meshes in which the element material properties were assigned based on the QCT image grayscale of the voxels contained in each element. A linear analysis was performed to obtain the QCT/FEA predicted overall bone stiffness. The cadaveric femurs were then tested to failure in a fall-on-the-hip configuration to obtain stiffness and strength measurements. The parameters of the equation describing the density-elastic modulus relationship were estimated by systematically adjusting the parameters of this relationship such that the QCT/FEA stiffness prediction matched the values obtained by the measurements in a least-squares sense. In addition to the previously used power laws, we adopted a sigmoid function to describe the density-elastic modulus relationship. The resulting equations were further validated on a separate set of femurs.

Materials and Methods

Femur preparation

Twenty-two human cadaveric femurs were obtained (Musculoskeletal Transplant Foundation, Edison, NJ) from 6 male and 16 female donors, age 66 ± 8 years (range 57 to 93 years) in fresh frozen condition. The femurs were preserved in frozen condition before the specimen preparation to maintain the in vivo mechanical properties. X-ray scans were used to confirm the absence of any fractures or tumors prior to the scanning and testing. Measurements of aBMD were obtained using a GE Lunar iDXA system (GE Healthcare Inc., Waukesha, WI), and six femurs were classified as normal, 10 as osteopenic, and six as osteoporotic based on the criteria determined by the World Health Organization [17].

Soft tissues were removed from each cadaveric femur, and the distal end of the femur was cut and removed such that the remaining proximal femur had a length of 250 mm. About 100 mm of the distal end of the shaft was embedded into a polymethylmethacrylate (PMMA) filled block container using an in-house designed potting holder. The holder maintained the femoral neck rotation at 15° angle. The femur specimens were kept moist during the preparation process and until the mechanical testing.

Mechanical testing

The mechanical testing was conducted within three hours after the frozen femur specimens were thawed. The thawed specimens were kept moist at room temperature prior to the testing. An in-house designed fixture was used in conjunction with a standard mechanical testing machine (MTS, Minneapolis, MN) to test the femurs to fracture. The fixture held the femur specimen in a fall-on-the-hip loading configuration (Figure 1): the PMMA block was inserted into the fixture and clamped such that the shaft was at a 10° angle with respect to the y-axis, and the femur was allowed to rotate about the x-axis to mimic knee rotation. A multi-axis load cell (JR3, Woodland, CA) inserted in between the PMMA block and the rotation point was used to measure three force and three moment components in the shaft. Two aluminum cups were in contact with the femoral head and the greater trochanter; the cup connected to the greater trochanter was filled with PMMA to distribute the load over a larger contact area. Each cup was attached to a single-axis load cell (Transducer Techniques, Temecula, CA) to measure the reaction forces in the vertical direction. The load cell at the femoral head was attached to the hydraulic ram through linear bearings to provide near frictionless displacement in the xy-plane.

Figure 1.

Photograph of the experimental setup. The distal end of the femur was potted in a block of dental cement and clamped in a fixture. The fixture was initially placed at an angle of 10° with respect to the y-axis, and could rotate about the x-axis. The trochanter was fixed to a cup with dental cement, which was connected to a load cell fixed to a metal frame. The femoral head was placed underneath an aluminum cup with curved surface. This cup was connected to a load cell which could move in the x and y directions using low-friction linear bearings.

The hydraulic ram moved at a velocity of 100 mm s^-1, which is believed to result in bone deformation rates representative of a fall-on-the-hip condition [27, 31] Maximum ram displacement was set to 25 mm, and was sufficient to fracture all femur specimens. The overall femoral stiffness (K, [N mm^-1]) was obtained by plotting the vertical load at the greater trochanter against the femoral head displacement. A line was fitted to the linear-elastic section of this force-displacement curve, and K was derived as the slope of the line (Figure 2).

Figure 2.

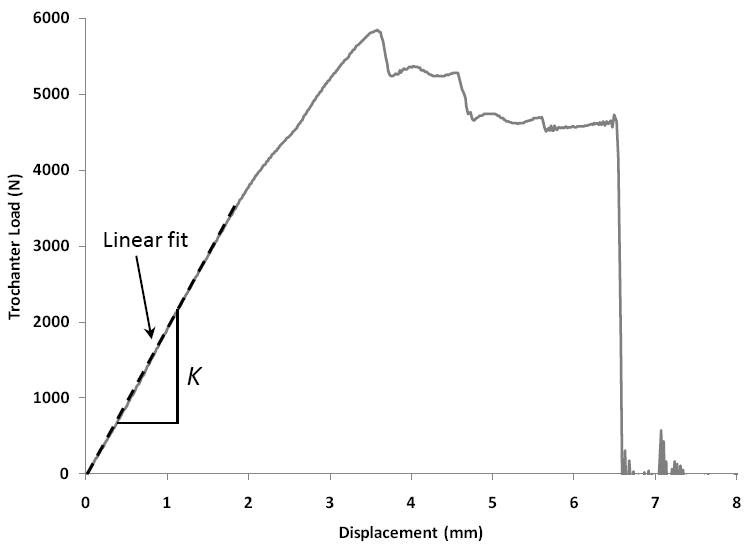
Representative force-displacement curve of a femur with normal aBMD. Trochanter load is plotted versus femoral head displacement. The slope of the linear elastic part of the curve is measured as the overall femoral stiffness.

QCT images

Before mechanical testing, we acquired quantitative QCT images of the femurs. Before each scan, a single femur was placed in a fixture and aligned with the scanner axis such that the femur was oriented in the same way as it was during mechanical testing. No pelvic bone or contralateral femur was presented during the scanning. Two aluminum rods (11.5 mm in length and 2.5 mm in diameter) were placed 75 mm apart in this fixture and corresponded to the axis of rotation of the fixture used in mechanical testing. These rods served as markers to register the QCT images to the physical coordinate system in the MTS machine.

A calibration phantom (Midways, Inc., San Francisco, CA) containing five rods of different reference materials was scanned along with each femur to convert QCT Hounsfield numbers (HU) to equivalent K₂HPO₄ density (ρ_K2HPO4). QCT scans were obtained using on a Siemens Somatom Definition scanner (Siemens, Malvern, PA) and the X-ray source was operated at 120 kVp and 216 mA. Both the femur and the calibration phantom were scanned in air at room temperature. The acquired images had a field-of-view dependent in-plane resolution of approximately 0.30 to 0.45 mm and a slice thickness of 0.4 mm. The QCT scans were reconstructed using a kernel that resulted in improved representation of cortical geometry and detailed distribution of trabecular density. The calibration parameters were practically constant among scans. By assuming the ash density (ρ_ash) was identical to ρ_K2HPO4, the QCT number in each voxel was converted to ρ_ash using the linear relationship:

$${\rho }_{\mathrm{ash}}={\rho }_{\mathrm{K}2\mathrm{HPO}4}=­9·{10}^{­3}+7·{10}^{­4}·\mathrm{HU}$$ (1)

The QCT images were then segmented such that only the bone tissue was selected for FE mesh generation. Mimics (Materialise, Ann Arbor, MI) was used to perform the segmentation. An initial automatic segmentation across the entire image volume was obtained using a threshold of 300 HU; the initial segmentation was then manually edited to ensure accuracy and to exclude any soft tissue at the surface of the femur.

Finite element mesh generation

Using Mimics, a 3D triangular surface mesh was generated from the segmented QCT image volume. To prepare for finite element mesh generation, the surface mesh was smoothed using Laplacian smoothing and the maximum edge length was adjusted to control the mesh density. To investigate convergence of the QCT/FEA-predicted stiffness, uniform surface meshes with 1.5, 2.5, and 5.0 mm edge length were produced. In addition, a ‘smart mesh’ with non-uniform edge length was constructed: maximum edge length was 2.0 mm in the head, neck, and trochanter region, 3.0 mm in the subtrochanteric region, and 4.0 mm in the rest of the shaft.

The advancing front mesh generation module in ICEM CFD (ANSYS, Canonsburg, PA) was used to generate 10-node tetrahedral volume meshes for the femurs. Uniform surface meshes were converted into uniform volume meshes with the same edge length. However, an expansion factor of 1.3 was used for the smart mesh, such that elements in the trabecular region had longer edge lengths (up to approximately 5.0 mm in the neck and trochanter) than the elements in the cortical shell (Figure 3).

Figure 3.

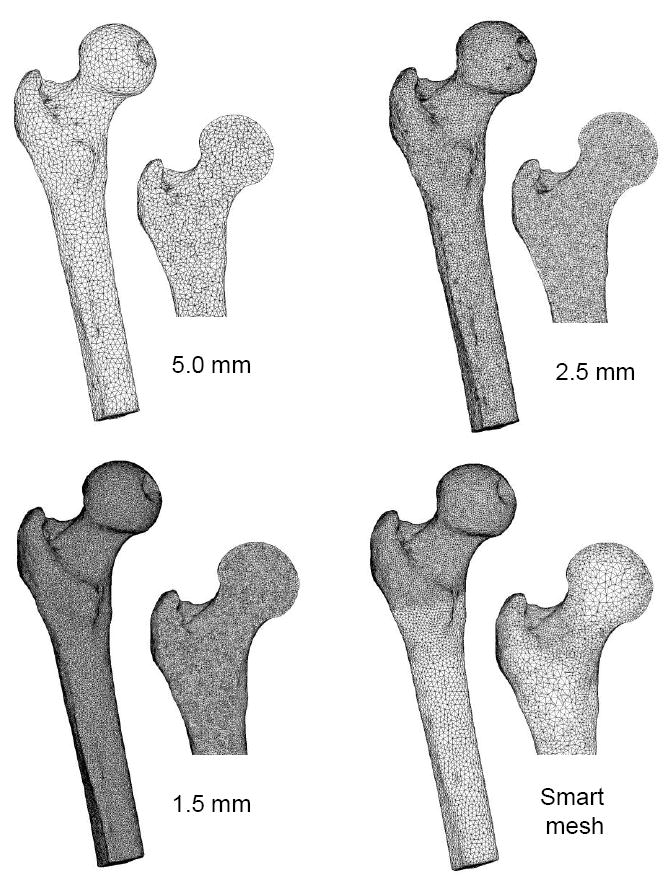
Surface and cut planes of finite element meshes used in the convergence analysis. Three uniform meshes with different maximum element edge lengths were used, and a smart mesh was developed with finer elements in the head/neck/trochanter region and coarser elements in the shaft. Moreover, the smart mesh contained smaller elements at the cortical shell and larger elements in the trabecular region.

Density-elastic modulus relationship

The finite element meshes were imported into Mimics to calculate the average HU number over each tetrahedral element. The HU numbers were next converted to ash density (ρ_ash) based on the phantom calibration data. The densities were then grouped into 22 equally sized material bins, with the exception of the first bin, which was assigned a very small density of ρ_ash = 0.01 g cm^-3 to avoid conversion of negative HU values to unphysical negative densities.

Isotropic elastic modulus (E) for each material was calculated from the ash density. Most previously published relationships were based on the power function

$$E=a{\rho }_{\mathit{ash}}^b,$$ (2)

where parameters a and b are determined based on experimental data. First, we evaluated the applicability of three previously published power laws, as follows:

$$E=14664{\rho }_{\mathit{ash}}^{1.49}[13],$$ (3a)

$$E=10500{\rho }_{\mathit{ash}}^{2.29}[14],\mathrm{and}$$ (3b)

$$E=17546{\rho }_{\mathit{ash}}^3[15]$$ (3c)

Equations 3a and 3c were converted from apparent density (ρ_app) to ash density assuming ρ_ash / ρ_app = 0.6 [18,19]. In addition, to arrive at Eq. 3c, we assumed a strain rate of 1.0 s^-1, which is in agreement with our deformation rate of 100 mm s^-1 in femurs approximately 100 mm from greater trochanter to head. Subsequently, we estimated parameters a and b based on data obtained during our proximal femur mechanical tests, using a combination of FEA and parameter identification techniques (Parameter estimation section below).

We have also used a sigmoid function as an alternative model for the ρ_ash to E relationship, using the Gompertz curve [20]:

$$E=E_{\max }{e}^{{\mathit{ae}}^{b{\rho }_{\mathit{ash}}}},$$ (4)

where E_max is the asymptotic value of the elastic modulus, and a and b are negative growth rates. This function has one additional parameter compared to the power law. To make the parameter estimation more feasible, we fixed E_max at either 15, 20, or 25 GPa. These values were based on the wide range of previously reported values for the cortical tissue elastic modulus [21-24]. Parameters a and b were determined using parameter identification (Parameter identification section below). In addition to Young’s modulus, a constant Poisson’s ratio of 0.3 was assigned to each material bin.

Finite element analysis

The finite element mesh and material assignments were imported into ANSYS (ANSYS, Canonsburg, PA). The axis of rotation, mimicking rotation about the knee, corresponded to the aluminum rods in the QCT scan. A single node was added to the imported FE mesh to model the rotation point, and rigid beams were used to connect the distal end of the shaft to the rotation node. Boundary conditions were set up to mimic the mechanical testing in the fall-on-the-hip configuration (Figure 4).

Figure 4.

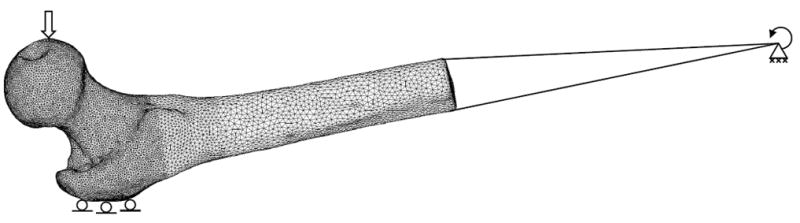
Boundary conditions were applied to the finite element model to mimic a fall on the side. A vertical force was applied to the femoral head and vertical displacements were set to zero at the greater trochanter. The distal end of the femur was connected with beams to a rotation point. At the rotation point, only rotation about the x-axis was allowed; the other five degrees of freedom were set to zero.

To model contact at the femur head, a force of 300 N in the z-direction was distributed over a small area (approximately 500 nodes) on the surface of the femoral head. To model contact at the greater trochanter, displacement in the vertical direction (z-axis) was prohibited but free movement in the horizontal plane (xy-plane) was allowed for about 1000 nodes on part of the surface of the greater trochanter. The node defining the axis of rotation (parallel to x-axis, Figure 1) was assigned zero displacement conditions in all three directions, and rotations about the y and z-axes were set to zero. Rotation about the x-axis was unrestricted.

A static linear elastic analysis was performed using ANSYS to calculate the femoral head displacement in the z-direction and the resulting reaction force on the greater trochanter. We defined the predicted overall stiffness (K̂ ) of the femur specimen as

$$\widehat{K}=\frac{F_T}{u_H},$$ (5)

where F_T is the calculated reaction force on the greater trochanter, and u_H is the calculated femoral head displacement. For each femur, the calculations used 2 cores of a 32 processor Sun Fire X4600 Linux server with 256 Gbytes of internal memory.

Parameter identification

The 22 femur specimens were divided into two groups: nine femurs were used to estimate the best set of parameters of the density-elastic modulus relationship models, and the remaining 13 femurs were used as a validation set. The nine femurs for modeling consisted of three normal, three osteopenic, and three osteoporotic femurs, whereas the validation group consisted of three normal, seven osteopenic, and three osteoporotic femurs. To estimate the parameters we used optimization techniques to iteratively update the parameters such that the predicted femur stiffness K̂ from the finite element analysis matched the measured bone stiffness K obtained from mechanical testing. First, we defined an error metric to quantify the discrepancy between the predicted and measured quantities:

$$\mathrm{Error}=\sqrt{\frac{1}{n}{{\sum }_{i=1}^n\left(\frac{K_i-{\widehat{K}}_i}{K_i}\right)}^2},$$ (6)

where n is the number of femur specimen used for modeling, K_i is the measured stiffness of the i^th femur in the modeling set and K̂_i is the FEA predicted stiffness. Subsequently, the Nelder-Mead simplex search algorithm in the optimization toolbox of MATLAB (The Mathworks Inc., Natick, MA) was used to minimize the error function. For each error function evaluation step, the parameters of the density-elastic modulus relationship were updated, material properties were reassigned, and ANSYS was invoked by MATLAB to perform linear elastic analyses to predict the stiffness values for the nine femurs in the modeling set. The optimization was terminated when the change in error function was below 10^-9. For validation purposes, finite element analyses of the 13 validation femurs were then performed using the parameters estimated before on the other nine femurs. The error for the validation set was also evaluated using Eq. 6.

Results

Femur specimens

All 22 femurs were tested to fracture. Even though there was a statistically significant difference in donor age between the two groups (p = 0.03), aBMD values and measured stiffness values were not significantly different (p > 0.05), as shown in Table 1.

Table 1.

Age, areal bone mineral density (aBMD) and stiffness of the estimation and validation group

	Estimation group (n=9)		Validation group (n=13)
	Mean ± SD	Range	Mean ± SD	Range
Age (years)	70 ± 10	62-93	63 ± 4*	57-69
aBMD (g cm-2)	0.78 ± 0.19	0.47-1.02	0.79 ± 0.13	0.56-0.93
Stiffness (N mm-1)	1573 ± 479	922-2350	1694 ± 482	1016-2417

Finite element mesh convergence

The four meshes with different element edge lengths were generated for all nine femurs in the training group. The average number of elements was 58,000 ± 13,000 for the 5.0 mm meshes, 510,000 ± 100,000 for the 2.5 mm meshes, and 2,000,000 ± 500,000 for the 1.5 mm meshes. The number of elements in the smart meshes (360,000 ± 60,000) was about 5.6 times lower than the number of elements in the 1.5 mm meshes. The 1.5 mm uniform meshes produced convergent results by FEA and were used to calculate the degree of convergence of the other meshes. For the convergence study, the density-elastic modulus power law previously determined by Morgan et al. [13] was used (Eq. 3a). Using the finest mesh (1.5 mm edge length), a linear elastic analysis took on average four hours. The computations took on average 30 minutes using the 2.5 mm meshes, 15 minutes using the smart meshes, and 5 minutes using the 5 mm meshes. The absolute relative error compared to the convergent 1.5 mm meshes was calculated as a measure of convergence (Figure 5). The coarser 5.0 mm meshes produced inaccurate stiffness predictions, with errors exceeding 20%. Meshes with maximum edge length of 2.5 mm produced stiffness predictions within 10% of the converged values for normal and osteopenic femurs; however, the errors were more than 15% for osteoporotic femurs. The smart meshes with about 10 times less nodes than the finest mesh, resulted in stiffness predictions within 6% of the converged results. Thus, these meshes offered a good balance between accuracy and computational performance, and were therefore used in the parameter identification studies.

Figure 5.

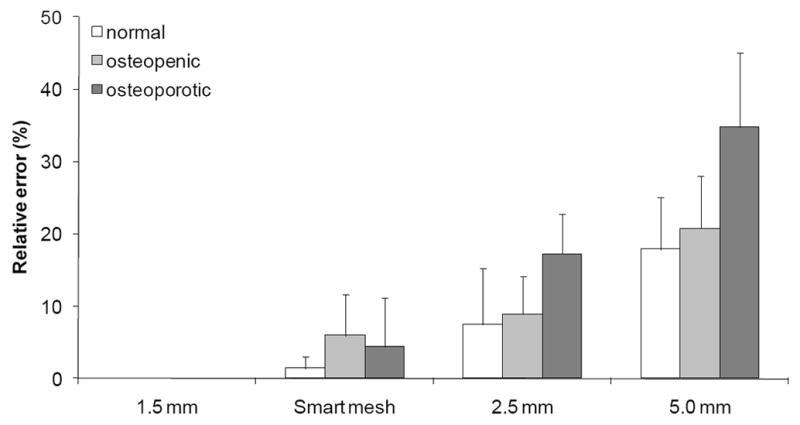
Results of the mesh convergence study. Mean ± SD of the errors relative to the 1.5 mm meshes are plotted for the nine femurs in the training group for the smart mesh, 2.5 mm mesh, and the 5.0 mm mesh.

Comparison of stiffness estimation using previously published power laws and experimental data

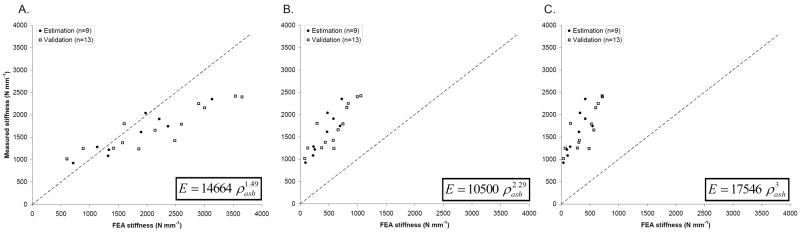
As a baseline, we used the smart meshes to compute the femoral stiffness based on three existing density-elastic modulus relationships in Eq. 3a-c. To indicate the degree of fit with experimental data, we plotted the measured stiffness against the FE predicted stiffness for the entire set of 22 femurs (Figure 6). The errors between predicted and measured stiffness values were calculated according to Eq. 6 (Table 2). The power laws published by Keller (1994) and by Carter and Hayes (1977) resulted in considerable underestimations of the experimentally measured stiffness. The power law proposed by Morgan et al. (2003) produced the best match to the measured stiffness, although it tended to overestimate the stiffness for femurs with stiffness values above ~2000 N mm^-1. As the goal of QCT/FEA is to directly provide physical values, the coefficients of determination (R²) were calculated with respect to the line y = x, without applying any additional linear regression models (Table 2). This resulted in low, in most cases even negative values for R² for the previously published power laws, confirming the poor fits with y = x observed in Figure 6.

Figure 6.

Measured vs. FEA predicted overall femoral stiffness using density-elastic modulus relationships previously published by (A) Morgan et al. (2003), (B) Keller (1994) and (C) Carter and Hayes (1977). For consistency, we differentiated between the estimation (solid circles) and validation (open squares) groups used in the parameter estimation procedure developed in this paper.

Table 2.

Prediction errors and coefficient of determination (R²) relative in the estimation and validation groups for the 3 existing power laws, and for the power law and sigmoid function estimated using our parameter identification method. Prediction errors were calculated according to Eq. 6 and range from 0 to 1. R² was calculated relative to y = x and can therefore become negative.

Density-elastic modulus relation	Reference	Estimation group (n=9)		Validation group (n=13)
		Prediction Error	R2 with y = x	Prediction Error	R2 with y = x
$E=14664{\rho }_{\mathit{ash}}^{1.49}$	Morgan et al. (2003)	0.22	0.30	0.40	-1.40
$E=10500{\rho }_{\mathit{ash}}^{2.29}$	Keller (1994)	0.76	-5.75	0.68	-4.97
$E=17546{\rho }_{\mathit{ash}}^3$	Carter and Hayes (1977)	0.85	-7.63	0.78	-6.93
$E=8050{\rho }_{\mathit{ash}}^{1.16}$	This study	0.14	0.80	0.21	0.50
$E=15000e^{-4.91e^{-2.63{\rho }_{\mathit{ash}}}}$	This study	0.10	0.88	0.17	0.71
$E=20000e^{-5.19e^{-2.30{\rho }_{\mathit{ash}}}}$	This study	0.09	0.90	0.17	0.69
$E=25000e^{-5.40e^{-2.10{\rho }_{\mathit{ash}}}}$	This study	0.09	0.91	0.17	0.69

Parameter estimation using a power law

Eq. 3a was used as the starting point for the parameter identification, as it produced the most accurate results with an error of 0.22 for the estimation group. The parameter estimation procedure converged after 62 iterations (14 hours computation time), with the major decrease in the error function obtained within the first 20 iterations (Figure 7). The final value of the objective function was 0.14, and the following power law was obtained:

$$E=8050{\rho }_{\mathit{ash}}^{1.16}$$ (7)

Figure 7.

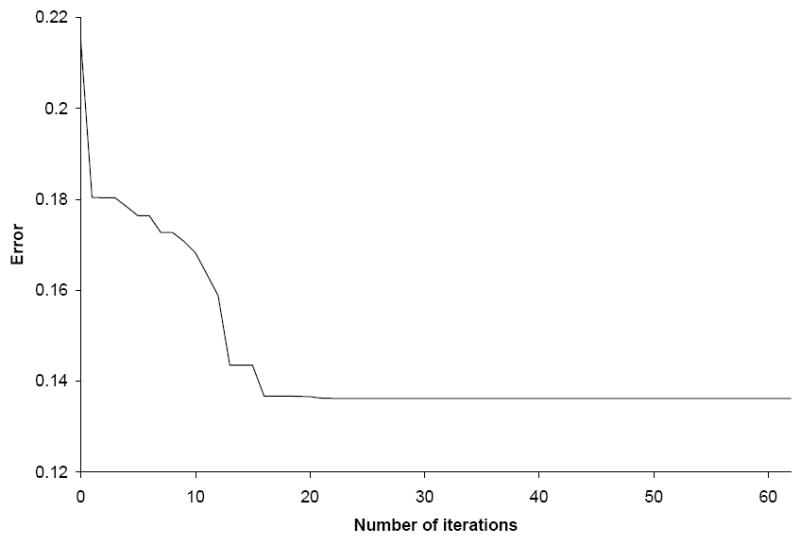
Convergence of the error between FEA prediction and experimental measurements (Eq. 6) during the parameter estimation procedure for the power law. After 62 iterations, the change in the objective function was below 10^-9.

To test its robustness, the estimated power law was used to determine the prediction errors in the validation femur set, resulting in a validation error of 0.21 (Figure 8A), also much lower than the error observed using Morgan’s law (Eq. 3a), which was 0.40. Thus, the new power law (Figure 8A) showed a significantly improved fit between measured and predicted femoral stiffness for both the estimation and validation sets (Table 2). A high R² value of 0.80 was found for the best fit power law in the training group, and a moderate R² = 0.50 in the validation group.

Figure 8.

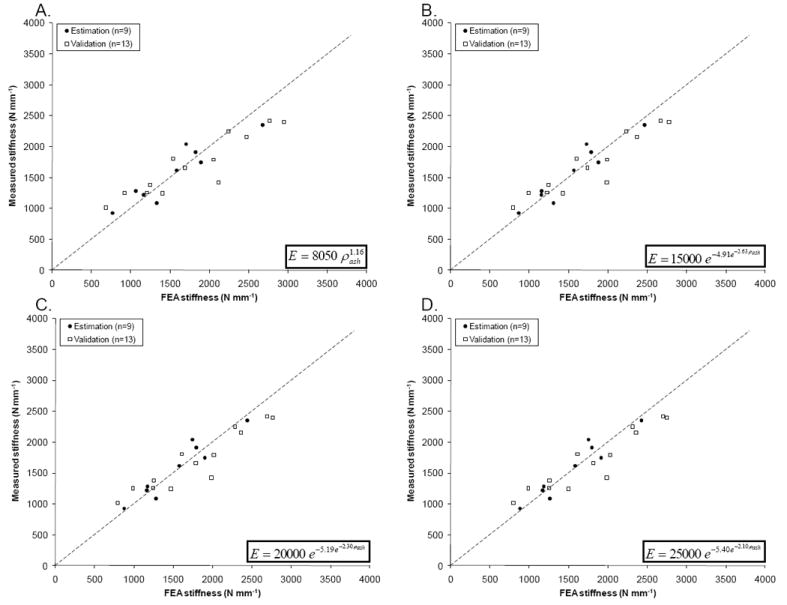
Measured vs. predicted stiffness for the estimation and the validation groups, based on the optimized power law (A), and sigmoid functions with E_max = 15 GPa (B), 20 GPa (C) and 25 GPa (D).

Parameter estimation using a sigmoid function

We explored a novel density-elastic modulus relationship law, using a sigmoid function, in an attempt to further enhance the accuracy of the femoral stiffness prediction. Parameter identification on the nine femurs of the estimation set was used to estimate the growth rates of three sigmoid functions with maximum cortical elastic modulus of E_max = 15, 20 or 25 GPa. The initial guess of the parameters was obtained by trial-and-error. Convergence of the estimation procedure resulted in estimation errors of 0.10 when E_max = 15 GPa and 0.09 when E_max = 20 or 25 GPa. The estimated sigmoid functions (Table 2) were then used to predict stiffness for the validation set (Figure 8B, C and D), resulting in validation errors of 0.17 for all three estimations (Table 2). Compared to the estimated power law, all three estimated sigmoid functions showed further improvement in stiffness predictions of the validation set, particularly at higher and lower stiffness, where the power law performed less accurately (Figure 8A). Moreover, the fit between FEA predictions and measurements is much tighter compared to the previously published laws. The R² value for the validation set increased from negative values when using the previously published laws to R² ranging from 0.69 to 0.71 for the three sigmoid functions (Table 2), a vast improvement over all estimations using power equations.

Discussion and Conclusion

In this study, we used a novel process to determine the parameters of the density-elastic modulus relationship for use in subject-specific finite element models of femoral stiffness. The in situ parameter estimation was based on fitting the predicted stiffness of QCT/FEA models to experimentally measured stiffness obtained during fracture tests on ex vivo human cadaveric femurs with a wide range of bone mineral densities. The results were validated on a separate data set. This method significantly improved the prediction of femoral stiffness using subject-specific finite elements. In addition, we developed a novel sigmoid equation for the density-elastic modulus relationship, which enhanced the predictive power even further, making it better than that of any power equation. In our future work, we will use these optimal density-elastic modulus equations to improve the prediction of our subject-specific finite element models of femoral fracture strength.

Published power laws

Previously published power laws for conversion of bone ash density to elastic modulus have been based on tests of small coupons of bone with varying densities. We studied the applicability of three existing power laws (Figure 9A) that were used before in various finite element studies of femoral strength [7,8,25]. These equations proposed by Keller (1994) and Carter and Hayes (1977) were obtained based on axial compressive mechanical tests of both cortical and cancellous bone spanning a broad density range. Applied to our proximal femur fracture tests, these equations underestimated the femoral stiffness by a factor of about 2.5 to 3. Morgan et al. (2003) studied the modulus in trabecular bone samples taken from various sites of the femur over a wide range of apparent densities using an on-axis loading protocol. Although cortical bone was not included in this study, their power law for femoral neck samples allowed for reasonably good extrapolation to cortical bone, as was previously shown in other FEA studies [12]. Among all literature data, we also found this particular equation to yield the best stiffness predictions for our femur fracture tests, most likely because it predicts higher elastic moduli in the trabecular region (ρ_ash ≈ 0.05 to 0.5 g cm^-3) than Eqs. 3b and c. However, Eq. 3a resulted in overestimation of the stiffness in femurs with higher stiffness, presumably due to the extrapolation to cortical bone densities that were not included in the original study. Thus, we found that these empirical density-elastic modulus equations obtained from on-axis compressive tests on small bone samples cannot be used to accurately predict the stiffness of femurs using subject-specific finite element models of femurs in fall-on-the-hip loading conditions.

Figure 9.

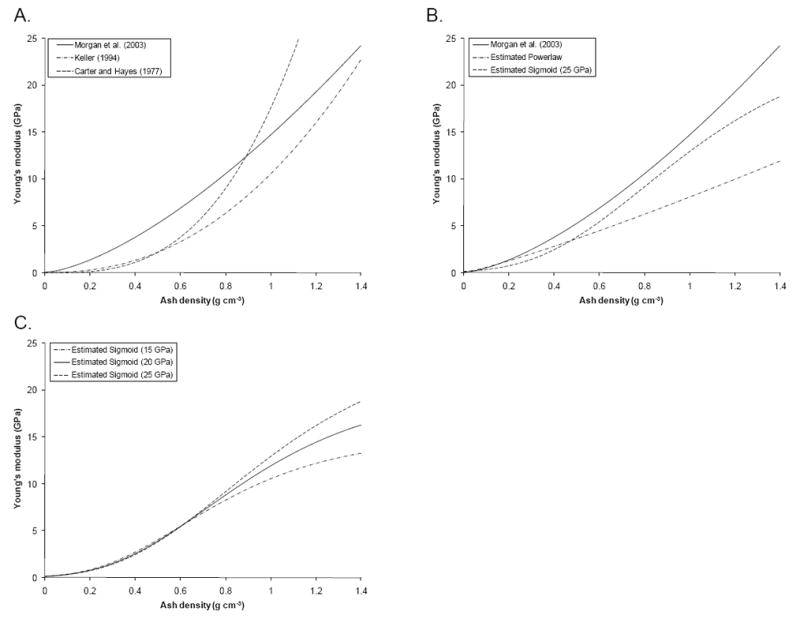
Elastic (Young’s) modulus-density relationships for (A) three previously published power laws, (B) the estimated power law and sigmoid function with E_max = 25 GPa, and (C) all three estimated sigmoid functions.

In situ parameter identification

During a fall on the hip, compression is mainly experienced in the superior neck region, whereas the inferior neck is generally under tension [26]. The rates of bone deformation are higher during a lateral fall than the quasi-static rates applied during mechanical tests of small bone samples reported in the literature [27]. In contrast, we developed a novel process for in situ estimation of the density-elastic modulus relationship. The parameters of the relationship were iteratively adjusted to obtain the best agreement between the measured and predicted overall femoral stiffness. Although parameter identification has been previously applied to biological problems where the solution of the underlying mathematical models can be obtained quickly [28], its application to subject-specific finite element models of the proximal femur has been limited due to (1) the complexity of the QCT/FEA process, (2) the high requirements in terms of computational power and memory for solving FE models with large numbers of degrees of freedom, and (3) the limited number of available experimental data on stiffness and fracture loads in femurs using fall-on-the-hip loading. We have overcome these issues by automating the material property assignments and the application of boundary conditions required for FEA, such that the ANSYS FE solver could be configured and executed from within the parameter identification routine programmed in MATLAB. Furthermore, we developed a non-uniform meshing strategy that allowed for fast computation of accurate results, and used a powerful multi-processor computational server with a large amount of memory to simultaneously conduct multiple finite element analyses for parameter identification. Finally, we acquired stiffness data from fracture tests of 22 femurs covering a broad range of bone mineral densities. Also, our method allowed for the estimation of the density-elastic modulus relationship using test data from femurs in a fall-on-the-hip loading condition, which we believe is more accurate and clinically relevant for use in subject-specific finite element models of proximal femur fracture risk than relationships obtained using mechanical tests on small bone samples.

Estimated power and sigmoid functions

Our best power law fit was $E=8050{\rho }_{\mathit{ash}}^{1.16}$, which resulted in a significant decrease in prediction error when compared to any of the published power laws we investigated. The exponent of our estimated power law, b = 1.16, falls within the wide range of exponents reported in the literature: linear relationships (i.e., power of 1.0) have been published [29], as well as power laws with exponents up to 3.0 [15]. The large inter-study differences found in reported density-elastic modulus relationships are most likely caused by the different experimental testing techniques used to characterize small bone coupons [16]. Our method allowed for determining the density-elastic modulus without cutting bone samples from the femur, and considered the abnormal loading rate and bone orientation observed during a fall on the hip.

Although our estimated power law improved the FE stiffness prediction considerably when compared to published power laws, we found that the FE prediction had a slight tendency to overestimate stiffness, especially for femurs with higher stiffness. In an attempt to develop a more robust method to assign elastic modulus, we replaced the power law by a Gompertz growth sigmoid function. Using our parameter identification scheme, we then estimated the two growth rates of the sigmoid function, and obtained a density-elastic modulus relationship that exhibited a plateau in the Young’s modulus at higher densities (Figures 9B and C). Using the sigmoid function, the FEA stiffness prediction improved even further, such that the overestimation of stiffness was considerably reduced. Hence, a sigmoid function should be considered as a good alternative for density-elastic modulus relationship in subject-specific finite element models.

Meshing strategy

Since nonlinear parameter identification requires multiple iterations to compute the objective function, we developed a modeling strategy that realized accurate, converged results in a relatively short amount of time. To achieve this, we first conducted a mesh convergence study with uniform meshes of three different densities. Convergence of the uniform meshes was achieved using a maximum element edge length of 1.5 mm, however, this high quality mesh contained an average of two million elements, requiring a few hours per analysis, rendering them impractical. Therefore, we developed a smart mesh strategy that used small elements at the cortex in the head/neck/trochanter area and coarser elements in the trabecular region and the shaft. In the proximal region, the cortex can be thin, especially in osteoporotic bones, but has a major contribution to femur stiffness and strength. It was critical to model the cortical bone using smaller elements to accurately resolve the geometrical shape of the femur, and to minimize spatial averaging of the local elastic modulus of the cortex with the elastic properties of soft tissues and less dense trabecular bone near the cortex. Using these non-uniform ‘smart’ meshes, we achieved a high accuracy with ten times less degrees of freedom than the 1.5 mm meshes but comparable accuracy, thus reducing the parameter identification time.

Potential Limitations

Our proposed in situ parameter estimation procedure had several limitations. First, both FEA and experiments were mimicking fall-on-the-hip loading conditions, since lateral falls are the major cause of hip fractures in the elderly. Therefore, our optimized density-elastic modulus relationship is specific for a fall-on-the-hip loading condition, and we do not expect the same level of accuracy when applying the current results to other loading conditions (e.g. stance or walking loading conditions) or other anatomical sites (e.g. spine). However, it should be pointed out that the same methodology could be readily applied to other loading conditions and anatomical locations, as long as experimental data is available for the parameter estimation.

The femur specimens in this study were scanned in air, with a slice thickness smaller than is generally used under clinical conditions. The presence of surrounding tissues (e.g. soft tissues and pelvic bone) and larger slice thickness in real patient scans will affect the accuracy of the direct translation of the reported findings. Tanck et al. showed that scanning the femurs in air, in water or with tissue and pelvic bone results in differences as high as 15% in BMD values obtained from QCT scans [36]. The differences in HU values in QCT images under different scan conditions could be caused by the beam-hardening artifact, which could be effectively reduced using correction algorithms [30]. Future studies using scan condition that mimic the patient scan could facilitate the translation to clinical application.

It is known that density-modulus relationships are site-dependent [12], but our estimation procedure did not account for any spatial variations in the ρ_ash to E relationships. This has likely caused the estimated relations to be biased towards the regions with the most influence on femoral stiffness. Incorporating site-specific relations (e.g., for neck, trochanter and shaft) may improve the prediction results, but will also require the determination of more parameters, potentially with reduced reliability of the estimated values.

The micro-scale features of bone, such as the degree of collagen crosslinking, osteon density, or the presence of microcracks have major impacts on fracture toughness [32-33]. Recently, micro-mechanical approaches were used to derive the bone material properties by modeling the micro-scale structures of bone [34-35]. These detailed models incorporate pore fluid pressures, poroelastic properties as well as anisotropy, but require more computation time and validation with micro- or nano-CT. The image resolution of our clinical CT scanner (~300 μm) did not allow us to capture nano- and micro-scale features of the bone, and therefore we assumed that within a single finite element, the material was homogeneous and isotropic.

Any viscoelastic behavior could potentially be captured in a different material model that incorporates strain rate, e.g. a Kelvin-Voigt viscoelastic model. Using a more complex model may improve the accuracy of the finite element simulation, but will increase computation time and requires additional parameters to be estimated for the strain-rate dependent part. The optimization process proposed in this work requires solving the finite element problem multiple times. Therefore, we have restricted the current simulations to a linear elastic material model, such that the computational time is ‘manageable’ (about 10 hours on a powerful computational server). In our case, some of the viscoelastic effects may have been captured by the sigmoid function instead. Robust estimation of the strain-rate dependent parameters of a viscoelastic model likely requires additional experimental data, where the femurs are loaded at a different (e.g. slower than 100 mm s^-1) rate. This is certainly a possibility in future studies.

Some errors in the FEA stiffness predictions may have resulted from the segmentations of the QCT images, which required manual interaction to carefully exclude all soft tissues on the femur surface, without excluding any cortical bone. In future studies, we intend to study the reproducibility of the segmentation process using multiple operators.

In conclusion, we developed a novel method to estimate the density-elastic modulus relationship using cadaveric fracture tests to improve the overall femoral stiffness prediction of subject-specific finite element models. In addition, we developed a novel sigmoid function for the density-elastic modulus relationship that resulted in a more robust estimation of femoral strength. Future work will incorporate a bone damage model into the FEA models for femoral strength prediction, and will use experimental data and a similar parameter identification method to estimate the parameters of this damage model. After full validation using clinical fracture data to assess predictive power, these relatively inexpensive and noninvasive finite element models could be used for accurate quantitative assessment of femoral fracture risk, and to aid clinicians in a timely identification of patients at high risk for osteoporosis and the monitoring of treatment efficacy.