A Mathematical Model of Tumour and Blood pHe Regulation: The ${\mathrm{HCO}}_3^{-}∕{\mathrm{CO}}_2$ Buffering System

Abstract

Malignant tumours are characterised by a low, acidic extracellular pH (pHe) which facilitates invasion and metastasis. Previous research has proposed the potential benefits of manipulating systemic pHe, and recent experiments have highlighted the potential for buffer therapy to raise tumour pHe, prevent metastases, and prolong survival in laboratory mice. To examine the physiological regulation of tumour buffering and investigate how perturbations of the buffering system (via metabolic/respiratory disorders or changes in parameters) can alter tumour and blood pHe, we develop a simple compartmentalised ordinary differential equation model of pHe regulation by the ${\mathrm{HCO}}_3^{-}∕{\mathrm{CO}}_2$ buffering system. An approximate analytical solution is constructed and used to carry out a sensitivity analysis, where we identify key parameters that regulate tumour pHe in both humans and mice. From this analysis, we suggest promising alternative and combination therapies, and identify specific patient groups which may show an enhanced response to buffer therapy. In addition, numerical simulations are performed, validating the model against well-known metabolic/respiratory disorders and predicting how these disorders could change tumour pHe.

1. Introduction

Malignant tumours consume significantly higher amounts of glucose than corresponding normal tissues or benign tumours [1, 2]. This increased glucose uptake is observed even in the presence of adequate levels of oxygen, a phenomenon referred to as aerobic glycolysis. The use of aerobic glycolysis by cancer cells was characterised as early as the 1930s and named the Warburg effect [3, 4]. The inefficiency of this type of metabolism significantly contributes to the observed increased glucose uptake and a subsequently increased acid load.

Upregulated aerobic glycolysis is a hallmark of malignant cancers [1]. The high level of glycolysis results in increased production of H⁺ ions, leading to an acidification of the tumour microenvironment. This has been well documented by experiments showing that solid tumour extracellular pH (pHe) is commonly 0.5-1 units lower than normal tissue (tumour pHe of 6.5-7 versus a normal tissue pHe of 7.4) [5, 6, 7].

Despite the early discovery of the Warburg effect, little is understood about the reasons why malignant tumours consistently upregulate the use of aerobic glycolysis. In a series of papers, Gatenby et al. hypothesised that tumour acidification confers an advantage to the tumour cells, by producing a harsh environment in the peritumoural soft tissues as acid is transported along concentration gradients from the tumour in adjacent normal regions. This results in normal cell death, extracellular matrix degradation, increased angiogenesis and disordered immune response facilitating tumour invasion [8, 4, 1, 9, 10, 2]. This ‘acid mediated invasion hypothesis’ is supported by experiments which have shown that normal cells proliferate optimally at a pHe of 7.4, with a steep decrease in proliferative ability below 7.1, while tumour cells obtain an optimal proliferation rate at pHe 6.8, which correlates with the slightly acidic environment found in invasive tumours [9].

The ‘acid-mediated invasion hypothesis’ leads to the prediction that neutralising the acidic tumour pHe will inhibit invasion and, subsequently, spontaneous metastasis, which has been explored in a recent set of experiments [11]. To test this prediction, Robey et al. implanted highly metastatic human breast cancer cells in the mammary fat pad of severe combined immunodeficient mice. Oral administration of sodium bicarbonate (which acts as a buffer to resist changes in pHe) raised primary tumour pHe, reduced the number and size of metastases, and prolonged survival [11]. More generally, Gatenby and Gawlinski [4] propose that manipulation of systemic pHe (either through acidification or alkalinisation) could reduce tumour growth by perturbing the system from the optimal pHe for tumour proliferation.

To examine how manipulation of the systemic buffering system can alter tumour pHe, we develop a simple but realistic model of tumour pHe regulation via the ${\mathrm{HCO}}_3^{-}∕{\mathrm{CO}}_2$ system, including the effects of physiological control of blood buffering, which is detailed in Section 2. With this model, we explore model behaviour by constructing an asymptotic approximation (Section 2.2) and subsequently perform a sensitivity analysis to ascertain the key parameters regulating tumour pHe, and identify which of those parameters can be altered with minimal effect on blood pHe regulation (Section 3.4). Additionally, we model respiratory and metabolic disordered states, comparing blood pHe predictions to known data, and predicting the resulting effect on tumour pHe (Section 3.1).

2. Mathematical Model

2.1. Model formulation and construction

To produce a basic model of blood and tumour buffering we first develop a simple model of the main extracellular buffering system, the ${\mathrm{HCO}}_3^{-}∕{\mathrm{CO}}_2$ system, along with the physiological regulation of this system. The aim is to develop a simple model of pHe at the tumour and blood compartment scale which accurately models the physiological regulation of tumour and blood pHe. Although as a first approximation, we compare the behaviour of our model to known human data. Any additional buffering from intrinsic non-motile buffers (such as proteins, amino acids, and phosphates) operate on a faster scale than the ${\mathrm{HCO}}_3^{-}∕{\mathrm{CO}}_2$ buffer. As there is little to no movement of intrinsic buffers between compartments, we assume this contribution in the tumour tissue is constant and implicitly incorporated in the tumour proton production parameter. Furthermore, our model tracks arterial blood delivery to the tumour, which has haemoglobin in the oxygen-bound form with low proton carrying capacity. Consequently, it is reasonable to assume only a small proportion of blood delivered to hypoxic areas of the tumour will contain the deoxygenated form of haemoglobin which can bind protons. This hypoxic subcompartment would be low in bicarbonate, high in CO₂, and likely have poor flow and connectivity to the vascular network, and therefore would likely reduce the potential efficacy of any buffer delivery to that region. Subsequently, our model could be extended to include additional buffering components at different spatial and temporal scales. Hence, we consider a two-compartment model, simulating the blood and tumour tissue, incorporating the bicarbonate-carbon dioxide system. Crucially, the model also includes the physiological regulation of the bicarbonate system through ventilation and kidney filtration. In this respect, our model can be seen as an extension of the work of [12], and our analysis will show that inclusion of these effects can significantly affect model predictions. As we are interested in average tumour pHe and not pHe differences within the tumour, we neglect fine scale spatial variations in tumour acid production. Hence, we can subsequently ignore regional variation in oxygen levels and consumption as considered in previous models [12] and assume an average acid production rate. Furthermore, as tumour cells exhibiting the glycolytic phenotype rely on glycolysis even in the presence of oxygen, the local oxygen concentration should not significantly alter acid production.

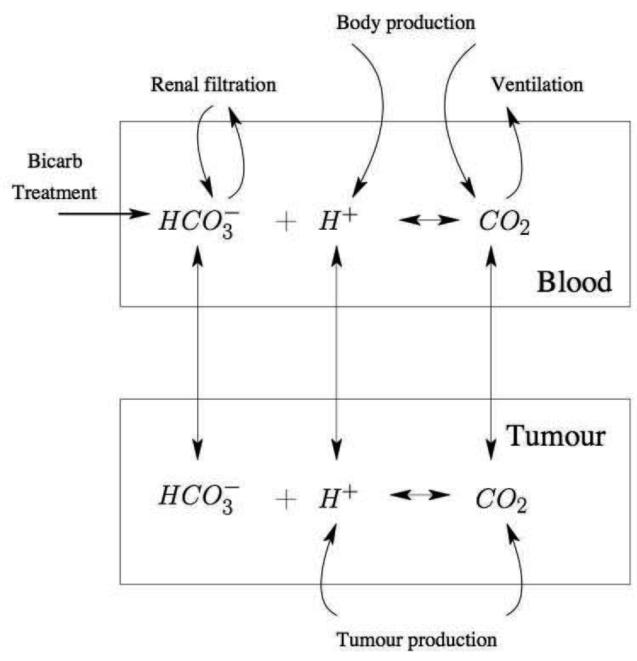
The schematic for the mathematical model is shown in Figure 1. We have that B_t,b represents the concentration of bicarbonate per volume in the tumour and blood respectively, in units of moles/litre. H_t,b represents the volumetric concentration of free protons within the tumour and blood respectively, in units of moles/litre. C_t,b represents the concentration of carbon dioxide for the tumour and blood respectively, in units of moles/litre. Note that as we are modelling extracellular pH, we model the levels of ions in the tumour interstitial fluid surrounding the cells, and neglect the intracellular pH of the tumour cells themselves.

Figure 1.

Schematic of the systemic buffering model presented in Equations (2)-(7). The two compartments, blood and tumour, are linked through the vascular transfer of protons and buffering components such as carbon dioxide (CO₂) and bicarbonate (HCO₃). In the blood, various physiological systems such as ventilation and renal filtration tightly regulate the buffering system.

Each equation includes a term describing the chemical buffering reactions of the ${\mathit{HCO}}_3^{-}∕{\mathit{CO}}_2$ system, which proceeds as follows:

$${\mathit{HCO}}_3^{-}+H^{+}\underset{k_2}{\overset{k_1}{\rightleftharpoons }}{\mathit{CO}}_2+H_{2}O$$ (1)

The first two terms in each equation describe this chemical buffering reaction, with k₂ and k₁ the reaction rate constants. This reaction is accelerated by the presence of the enzyme carbonic anhydrase (CA), the activity of which varies depending on the isozyme type. In our model, we include the action of carbonic anhydrase in both the blood and tumour by increasing the rate constants of the reaction to reflect this acceleration. The fastest acceleration occurs in the blood, where CA II in red blood cells can accelerate the hydration reaction 50,000 to 1,000,000 fold over the uncatalyzed rate at human body temperature [13]. Tumour associated carbonic anhydrases include CA II and CA IX [14], and the activity of CA IX has recently been found to be as high as CA II [15]. Hence, we assume for simplicity that the catalytic rates in the blood and tumour tissue are equal. Further, the asymptotic analysis indicates that the model is robust to changes of several orders of magnitude of these parameters (provided the pK_a, and hence ratio of the kinetic parameters, remains equal), as this will only alter the fast reaction timescale as the solution relaxes to the intermediate and slow solutions.

The equations also include a vascular exchange term of the respective ion or molecule between the blood and the tumour. Hence, γ₁, γ₂, γ₃ are the vessel fluxes for bicarbonate, lactate, and carbon dioxide respectively. The vessel fluxes are calculated by γ_i = V AD × P_i where V AD is the vessel length per tumour cross section area (in cm/cm²), and P_i is the vessel permeability (in cm/s) for the respective ion or molecule [16]. In order to ensure conservation of total quantities of H⁺, CO₂ and ${\mathit{HCO}}_3^{-}$ during the vascular exchange process from the tumour to the blood, we multiply γ_i by v_T, where v_T = V_tumour/V_blood, where V_tumour is the volume of the tumour and V_blood is the volume of blood. Although tumour volume varies over time, the timescale of tumour growth is much slower than the pHe regulation dynamics examined in this model, and we therefore assume tumour size is constant. Furthermore, the sensitivity analysis in Section 3.4 indicates the system is not sensitive to this parameter.

The first three equations capture the tumour dynamics, and will be discussed in turn below.

$$\frac{d{B}_t}{dt}=\stackrel{\text{chemical reactions}}{\overbrace{k_2{C}_t-k_1{B}_t{H}_t}}+\stackrel{\text{vascular exchange}}{\overbrace{{\gamma }_1(B_b-B_t)}}.$$ (2)

Equation 2 describes the bicarbonate dynamics in the tumour. As there is no direct production or consumption of ${\mathit{HCO}}_3^{-}$ in the tumour, this equation only includes chemical reaction terms and vascular exchange of ${\mathit{HCO}}_3^{-}$ between the blood and the tumour, where γ₁ is the vessel flux rate for bicarbonate.

$$\frac{d{H}_t}{dt}=\stackrel{\text{chemical reactions}}{\overbrace{k_2{C}_t-k_1{B}_t{H}_t}}+\stackrel{\text{tumour production}}{\overbrace{{\varphi }_1}}-\stackrel{\text{vascular exchange}}{\overbrace{{\gamma }_2(H_t-H_b)}}.$$ (3)

Equation 3 models the tumour H⁺ concentration. The third term, ϕ₁, is the net production of H⁺ per unit volume of the tumour through aerobic glycolysis, implicitly incorporating the fixed contribution of minor additional non-motile tissue buffering components which act on a faster timescale than the other reactions detailed. It is this production term that is generally higher than normal tissue due to the upregulation of glycolysis in malignant tumours. The final term is the vascular exchange, where γ₂ is the vessel flux rate for lactate as protons move in association with lactate to maintain electroneutrality.

$$\frac{d{C}_t}{dt}=\stackrel{\text{chemical reactions}}{\overbrace{k_1{B}_t{H}_t-k_2{C}_t}}+\stackrel{\text{tumour production}}{\overbrace{{\varphi }_5}}-\stackrel{\text{vascular exchange}}{\overbrace{{\gamma }_3(C_t-C_b)}}.$$ (4)

Equation 4 represents the tumour CO₂ dynamics. The third term, ϕ₅, represents the tumour production of CO₂ from cellular metabolism.

The last three equations capture the blood dynamics, and will be presented in turn. Firstly:

$$\frac{d{B}_b}{dt}=\stackrel{\text{chemical reactions}}{\overbrace{k_2{C}_b-k_1{B}_b{H}_b}}+\stackrel{\text{kidney filtration}}{\overbrace{{\varphi }_2{C}_b-{\lambda }_1{B}_b}}+\stackrel{\text{treatment}}{\overbrace{{\theta }_1}}-\stackrel{\text{vascular exchange}}{\overbrace{{\gamma }_1{v}_T(B_b-B_t)}}.$$ (5)

This equation describes the blood ${\mathit{HCO}}_3^{-}$. The third and fourth terms are standard representations used to model the complex process of renal filtration and reabsorption of bicarbonate [17, 18]. The details of this system can be found in the Appendix A. Briefly, an increase in blood CO₂ results in more conversion of CO₂ into ${\mathrm{HCO}}_3^{-}$ and H⁺ inside the kidney nephrons, elevated levels of acid secretion into the bladder, and increased absorption of ${\mathrm{HCO}}_3^{-}$ into the bloodstream. If CO₂ levels are stable (through ventilation), then any increases in ${\mathrm{HCO}}_3^{-}$ result in an increased rate of renal bicarbonate filtration (and subsequent loss in the urine). Here, ϕ₂ is the acid secretion rate, and λ₁ is the bicarbonate filtration rate. The fifth term, θ₁, is the bicarbonate treatment term used in the Robey et al. [11] study we examine in the sensitivity section.

$$\frac{d{H}_b}{dt}=\stackrel{\text{chemical reactions}}{\overbrace{k_2{C}_b-k_1{B}_b{H}_b}}+\stackrel{\text{body production}}{\overbrace{{\varphi }_3}}+\stackrel{\text{vascular exchange}}{\overbrace{{\gamma }_2{v}_T(H_t-H_b)}}.$$ (6)

Equation 6 models the blood H⁺ dynamics. The first two terms in Equation 6 represent the bicarbonate buffering reaction kinetics in the blood. The third term represents the net contribution of protons from the rest of the body tissues (except for the tumour) after the contribution of non-motile tissue buffers.

$$\frac{d{C}_b}{dt}=\stackrel{\text{chemical reactions}}{\overbrace{k_1{B}_b{H}_b-k_2{C}_b}}+\stackrel{\text{body production}}{\overbrace{{\varphi }_4}}-\stackrel{\text{ventilation}}{\overbrace{{\lambda }_2{C}_{b}f\left(C_b\right)}}+\stackrel{\text{vascular exchange}}{\overbrace{{\gamma }_3{v}_T(C_t-C_b)}}.$$ (7)

Equation 7 models the blood CO₂ concentration. The third term is the CO₂ source from the normal body tissues; here ϕ₄ represents the rate of CO₂ entry into the bloodstream from the normal tissue.

The fourth term in Equation 7 represents the regulation of blood CO₂ levels by respiration, where CO₂ lost through ventilation is proportional to the product of the ventilation rate, f(C_b), and the CO₂ concentration. The function for ventilation we use is:

$$f\left(C_b\right)=\{\begin{array}{cc}{V}_{\mathit{min}}\hfill & \text{if}f\left(C_b\right)<V_{\mathit{min}},\hfill \\ V_{\text{slope}}{C}_b-V_{\text{intercept}}\hfill & \text{if}{V}_{\mathit{min}}<f\left(C_b\right)<V_{\mathit{max}},\hfill \\ V_{\mathit{max}}\hfill & \text{if}f\left(C_b\right)>V_{\mathit{max}}.\hfill \end{array}\phantom{\}}$$ (8)

Note the linearity over a range with minimum and maximum thresholds [19]. Although the specific form of this term is a simplification of the complex dynamics surrounding ventilation, it is an appropriate approximation for the purposes of our model. The experimental ventilation response to blood CO₂ has been well quantified in both humans and mice and used to derive biological values for the ventilation parameters [20, 21, 22].

The initial conditions are C_b(0) = c₀, C_t(0) = c₀, B_b(0) = b₀, B_t(0) = b₀, H_b(0) = h₀, and H_t(0) = h₀. We choose c₀, b₀, and h₀ to be the standard blood values of CO₂, ${\mathit{HCO}}_3^{-}$, and H⁺ respectively. This allows a clear visualisation of H⁺ and CO₂ accumulation in the tumour, and subsequent depletion of ${\mathit{HCO}}_3^{-}$. Furthermore, as tumours can develop in many types of tissue with different metabolic rates, the baseline tissue values are likely to vary, but as there is only one steady-state the initial conditions do not affect the long-term behaviour of the system and are not a focus of this study.

In order to nondimensionalise our model, we use the rescaling τ = k₂t, b₀b_t = B_t, c₀c_t = C_t, h₀h_t = H_t, b₀b_b = B_b, c₀c_b = C_b, and h₀h_b = H_b to obtain the system,

$$\frac{d{b}_t}{d\tau }={\delta }_1(c_t-{\alpha }_2{b}_t{h}_t)+{\Gamma }_1(b_b-b_t)$$ (9)

$$\frac{d{h}_t}{d\tau }={\delta }_3(c_t-{\alpha }_2{b}_t{h}_t)+{\Phi }_1-{\Gamma }_2(h_t-h_b)$$ (10)

$$\frac{d{c}_t}{d\tau }=-(c_t-{\alpha }_2{b}_t{h}_t)+{\Phi }_5-{\Gamma }_3(c_t-c_b)$$ (11)

$$\frac{d{b}_b}{d\tau }={\delta }_1(c_b-{\alpha }_2{b}_b{h}_b)+{\Phi }_2{c}_b-{\xi }_1{b}_b+{ϴ}_1-{\Gamma }_1{v}_T(b_b-b_t)$$ (12)

$$\frac{d{h}_b}{d\tau }={\delta }_3(c_b-{\alpha }_2{b}_b{h}_b)+{\Phi }_3+{\Gamma }_2{v}_T(h_t-h_b)$$ (13)

$$\frac{d{c}_b}{d\tau }=-(c_b-{\alpha }_2{b}_b{h}_b)+{\Phi }_4-{\xi }_3\left(c_b\right)c_b+{\Gamma }_3{v}_T(c_t-c_b),$$ (14)

with ${\delta }_1=\frac{c_0}{b_0}$, ${\alpha }_2=\frac{k_1{h}_0{b}_0}{k_2{c}_0}$, ${\Gamma }_1=\frac{{\gamma }_1}{k_2}$, ${\delta }_3=\frac{c_0}{h_0}$, ${\Phi }_1=\frac{{\varphi }_1}{k_2{h}_0}$, ${\Gamma }_2=\frac{{\gamma }_2}{k_2}$, ${\Gamma }_3=\frac{{\gamma }_3}{k_2}$, ${\Phi }_2=\frac{{\varphi }_2{c}_0}{k_2{b}_0}$, ${\xi }_1=\frac{{\lambda }_1}{k_2}$, ${ϴ}_1=\frac{{\theta }_1}{k_2{b}_0}$, ${\Phi }_3=\frac{{\varphi }_3}{k_2{h}_0}$, ${\Phi }_4=\frac{{\varphi }_4}{k_2{c}_0}$, ${\Phi }_5=\frac{{\varphi }_5}{k_2{c}_0}$. Additionally, the nondimensionalised ventilation function is now:

$${\xi }_3\left(c_b\right)=\{\begin{array}{cc}{\Delta }_{\mathit{min}}\hfill & \text{if}{\xi }_3\left(c_b\right)<{\Delta }_{\mathit{min}},\hfill \\ {\Delta }_1{c}_b-{\Delta }_2\hfill & \text{if}{\Delta }_{\mathit{min}}<{\xi }_3\left(c_b\right)<{\Delta }_{\mathit{max}},\hfill \\ {\Delta }_{\mathit{max}}\hfill & \text{if}{\xi }_3\left(c_b\right)>{\Delta }_{\mathit{max}},\hfill \end{array}\phantom{\}}$$ (15)

with ${\Delta }_{\mathit{min}}=\frac{{\lambda }_2}{k_2}{V}_{\mathit{min}}$, ${\Delta }_1=\frac{{\lambda }_2}{k_2}{V}_{\text{slope}}{c}_0$, and ${\Delta }_{\mathit{max}}=\frac{{\lambda }_2}{k_2}{V}_{\mathit{max}}$.

The initial conditions become:

$$c_b\left(0\right)=1,c_t\left(0\right)=1,b_b\left(0\right)=1,b_t\left(0\right)=1,h_b\left(0\right)=1,\text{and}{h}_t\left(0\right)=1.$$ (16)

From the calculations detailed in Appendix A, the full parameter sets for a laboratory mouse and human are shown in Table 1. The nondimensionalised values for a mouse and human are shown in Table 2.

Table 1.

Mouse and human parameter values and sources. Details of the extraction and calculation of the parameters can be found in Appendix A. All citations of The Jackson Laboratory are in reference to the Mouse Tumor Biology Database (MTB), Mouse Genome Informatics, The Jackson Laboratory, Bar Harbor, Maine. The MTB is a database of laboratory mouse strain measurements of phenotypic and genotypic data [56]. The database is located at http://tumor.informatics.jax.org.

Name	Mouse	Human	Units	Source (M: mouse, H: Human)
h 0	3.98 × 10−8	3.98 × 10−8	mol/L	M:[35, 36] H: [18]
b 0	2.4 × 10−2	2.4 × 10−2	mol/L	M:[35, 36] H:[18]
c 0	1.2 × 10−3	1.2 × 10−3	mol/L	M:[35, 36] H:[18]
P 1	3.4 × 10−5	3.4 × 10−5	cm/s	[16, 37]
P 2	1.2 × 10−4	1.2 × 10−4	cm/s	[9]
P 3	1 × 10−3	1 × 10−3	cm/s	[38, 39]
V AD	20	20	cm/cm 2	[40, 41, 42]
vT	0.1	0.01	– –	M: [11, 43] H:[44, 43]
ϕ 1	7.8 × 10−6	7.8 × 10−6	mol/L/s	fit to [11], within the range from [45, 9]
ϕ 4	3.7 × 10−5	3 × 10−6	mol/L/s	M:[46, 35, 36] H: [46]
ϕ 2	6.16 × 10−2	1.14 × 10−2	1/s	M:[47] H: [17, 18]
ϕ 3	1.5 × 10−6	1.2 × 10−6	mol/L/s	M: [45, 35] H: [45, 17]
ϕ 5	2 × 10−7	2.5 × 10−7	mol/L/s	M: [46, 35] H:[46, 17]
λ 1	3 × 10−3	5.2 × 10−4	1/s	M:[48, 49] H: [18, 50, 51, 52]
λ 2	102	0.042	1/L	M:[53] H: [17, 18]
k 2	2.73 × 104	2.73 × 104	1/s	[13, 14, 15]
k 1	3.437 × 1010	3.437 × 1010	L/mol × s	from pKa in [17, 54]
Vslope	0.34	1.1 × 103	L2/mol × s	M:[22] H:[20, 21]
Vmax	5.5 × 10−4	1	L/s	M:[22] H:[20, 21]
Vmin	1.4 × 10−4	0.02	L/s	M:[22] H:[20, 21]
Vintercept	9.4 × 10−5	1.237	L/s	M:[22] H:[20, 21]
θ 1	7.6 × 10−6	6 × 10−7	mol/L × s	M: [11] H: [11, 55]

Table 2.

Mouse and human nondimensionalised parameter values.

Name	Mouse	Human
δ 1	5.0 × 10−2	5.0 × 10−2
Γ 1	2.5 × 10−8	2.5 × 10−8
δ 3	3.02 × 104	3.02 × 104
φ 1	7.17 × 10−3	7.17 × 10−3
Γ 2	8.79 × 10−8	8.79 × 10−8
α 2	1.0	1.0
φ 5	6.11 × 10−9	7.63 × 10−9
Γ 3	7.32 × 10−7	7.32 × 10−7
φ 2	1.13 × 10−7	2.11 × 10−8
ξ 1	1.10 × 10−7	1.90 × 10−8
Θ 1	1.16 × 10−8	9.16 × 10−10
vT Γ 1	2.5 × 10−9	2.5 × 10−9
φ 3	1.28 × 10−3	1.1 × 10−3
vT Γ 2	8.79 × 10−9	8.79 × 10−9
φ 4	1.13 × 10−6	9.16 × 10−8
vT Γ 3	7.32 × 10−8	7.32 × 10−8
Δ min	5.23 × 10−7	3.08 × 10−8
Δ 1	1.52 × 10−6	2.03 × 10−6
Δ 2	3.51 × 10−7	1.9 × 10−6
Δ max	2.05 × 10−6	1.54 × 10−6

2.2. Asymptotic simplification of the model

In this section we will construct a uniformly valid asymptotic approximation. This analytical solution is used to understand the general model behaviour and key parameter groupings. It is also used to perform a sensitivity analysis in Section 3.4 in order to examine which parameters have a large effect on tumour pHe. Potential treatments are then suggested which relate to the important parameters indicated by the sensitivity analysis.

Preliminary numerical simulations, as well as the wide variation in parameter values spanning several orders of magnitude, indicate different timescales in our solution. There are three characteristic timescales for our system. The inner, or fastest, is the timescale on which the reaction dynamics take place (k₁ and k₂ in Equations (2)-(7)). This is on the order of milliseconds. Then, there is an intermediate timescale where proton production takes place, on the order of seconds (ϕ₁ and ϕ₃ in Equations (3) and (6)). This intersects with a slower, outer solution which takes into account the rest of the physiology (kidney filtration, ventilation, etc), and occurs on the scale of minutes to hours (ϕ₂, λ₁, λ₂ in Equations (5) and (7)). With this in mind, let us first examine the inner, fast solution.

2.2.1. Fast timescale dynamics

From our biological knowledge of the system, we know that the chemical reaction equations occur on the order of nano- to milliseconds, and are much faster than the other processes in our system. Furthermore, we can see that the parameter δ₃ is several orders of magnitude larger than any other, indicating that the h_t,b equations will vary on the fast timescale (which is verified by proceeding with a standard asymptotic analysis). Thus we anticipate that chemical reactions will dominate the fast dynamics. To proceed, we define ∈ = 10⁻³, whereupon Equations (2)-(7) rescale to:

$$\frac{d{b}_t}{d\tau }={\delta }_1(c_t-{\alpha }_2{b}_t{h}_t)+{∊}^2{\widehat{\Gamma }}_1(b_b-b_t)$$ (17)

$$\frac{d{h}_t}{d\tau }={\delta }_3(c_t-{\alpha }_2{b}_t{h}_t)+∊{\widehat{\Phi }}_1-{∊}^2{\widehat{\Gamma }}_2(h_t-h_b)$$ (18)

$$\frac{d{c}_t}{d\tau }=-(c_t-{\alpha }_2{b}_t{h}_t)+{∊}^2{\widehat{\Phi }}_5-{∊}^2{\widehat{\Gamma }}_3(c_t-c_b)$$ (19)

$$\frac{d{b}_b}{d\tau }={\delta }_1(c_b-{\alpha }_2{b}_b{h}_b)+{∊}^2{\widehat{\Phi }}_2{c}_b-{∊}^2{\widehat{\xi }}_1{b}_b+{∊}^2{\widehat{ϴ}}_1-{∊}^2{\widehat{\Gamma }}_1{v}_T(b_b-b_t)$$ (20)

$$\frac{d{h}_b}{d\tau }={\delta }_3(c_b-{\alpha }_2{b}_b{h}_b)+∊{\widehat{\Phi }}_3+{∊}^2{\widehat{\Gamma }}_2{v}_T(h_t-h_b)$$ (21)

$$\frac{d{c}_b}{d\tau }=-(c_b-{\alpha }_2{b}_b{h}_b)+{∊}^2{\widehat{\Phi }}_4-{∊}^2{\widehat{\xi }}_3\left(c_b\right)c_b+{∊}^2{\widehat{ϴ}}_3{v}_T(c_t-c_b),$$ (22)

where ${\delta }_1=\frac{c_0}{b_0}$, ${\alpha }_2=\frac{k_1{h}_0{b}_0}{k_2{c}_0}$, ${\widehat{\Gamma }}_1=\frac{{\gamma }_1}{{∊}^2{k}_2}$, ${\delta }_3=\frac{c_0}{h_0}$, ${\widehat{\Phi }}_1=\frac{{\varphi }_1}{∊k_2{h}_0}$, ${\widehat{\Gamma }}_2=\frac{{\gamma }_2}{{∊}^2{k}_2}$, ${\widehat{\Gamma }}_3=\frac{{\gamma }_3}{{∊}^2{k}_2}$, ${\widehat{\Phi }}_2=\frac{{\varphi }_2{c}_0}{{∊}^2{k}_2{b}_0}$, ${\widehat{\xi }}_1=\frac{{\lambda }_1}{{∊}^2{k}_2}$, ${\widehat{ϴ}}_1=\frac{{\theta }_1}{{∊}^2{k}_2{b}_0}$, ${\widehat{\Phi }}_3=\frac{{\varphi }_3}{∊k_2{h}_0}$, ${\widehat{\Phi }}_4=\frac{{\varphi }_4}{{∊}^2{k}_2{c}_0}$, $\widehat{\xi }\left(c_b\right)=\frac{{\lambda }_2}{{∊}^2{k}_2}f\left(c_b\right)$.

The ventilation function becomes:

$${\widehat{\xi }}_3\left(c_b\right)=\{\begin{array}{cc}{\widehat{\Delta }}_{\mathit{min}}\hfill & \text{if}{\xi }_3\left(c_b\right)<{\widehat{\Delta }}_{\mathit{min}},\hfill \\ {\widehat{\Delta }}_1{c}_b-{\widehat{\Delta }}_2\hfill & \text{if}{\widehat{\Delta }}_{\mathit{min}}<{\widehat{\xi }}_3\left(c_b\right)<{\widehat{\Delta }}_{\mathit{max}},\hfill \\ {\widehat{\Delta }}_{\mathit{max}}\hfill & \text{if}{\widehat{\xi }}_3\left(c_b\right)>{\widehat{\Delta }}_{\mathit{max}},\hfill \end{array}\phantom{\}}$$ (23)

with ${\widehat{\Delta }}_{\mathit{min}}=\frac{{\lambda }_2}{{∊}^2{k}_2}{V}_{\mathit{min}}$, ${\widehat{\Delta }}_1=\frac{{\lambda }_2}{{∊}^2{k}_2}{V}_{\text{slope}}{C}_0$, ${\widehat{\Delta }}_2=\frac{{\lambda }_2}{{∊}^2{k}_2}{V}_{\text{intercept}}$, and ${\widehat{\Delta }}_{\mathit{max}}=\frac{{\lambda }_2}{{∊}^2{k}_2}{V}_{\mathit{max}}$.

Note that we can decouple the reaction dynamics by making the following substitution: u₁ = b_t + δ₁c_t, u₂ = b_b + δ₁c_b, v₁ = h_t + δ₃c_t, v₂ = h_b + δ₃c_b. With these substitutions, Equations (17)-(22) become:

$$\begin{array}{cc}\hfill \frac{d{u}_1}{d\tau }& ={∊}^2{\widehat{\Gamma }}_1\left(u_2-\frac{{\delta }_1}{{\delta }_3}{v}_2+\frac{{\delta }_1}{{\delta }_3}{h}_b-u_1+\frac{{\delta }_1}{{\delta }_3}{v}_1-\frac{{\delta }_1}{{\delta }_3}{h}_t\right)+{\delta }_1{∊}^2{\widehat{\Phi }}_5\hfill \\ \hfill & -{∊}^2\frac{{\delta }_1}{{\delta }_3}{\widehat{\Gamma }}_3\left(v_1-h_t-v_2+h_b\right)\hfill \end{array}$$ (24)

$$\frac{d{v}_1}{d\tau }=∊{\widehat{\Phi }}_1-{∊}^2{\widehat{\Gamma }}_2(h_t-h_b)+{\delta }_3{∊}^2{\widehat{\Phi }}_5-{∊}^2{\widehat{\Gamma }}_3\left(v_1-h_t-v_2+h_b\right)$$

$$\frac{d{h}_t}{d\tau }=v_1-h_t-{\alpha }_2{h}_t({\delta }_3{u}_1-{\delta }_1{v}_1+{\delta }_1{h}_t)+∊{\widehat{\Phi }}_1-{∊}^2{\widehat{\Gamma }}_2(h_t-h_b)$$ (26)

$$\begin{array}{cc}\hfill \frac{d{u}_2}{d\tau }=& {∊}^2{\widehat{\Phi }}_2\left(\frac{1}{{\delta }_3}(v_2-h_b)\right)-{∊}^2{\widehat{\xi }}_1\left(u_2-\frac{{\delta }_1}{{\delta }_3}{v}_2+\frac{{\delta }_1}{{\delta }_3}{h}_b\right)+{∊}^2{\widehat{ϴ}}_1\hfill \\ \hfill -& {∊}^2{\widehat{\Gamma }}_1{v}_T\left(u_2-\frac{{\delta }_1}{{\delta }_3}{v}_2+\frac{{\delta }_1}{{\delta }_3}{h}_b-u_1+\frac{{\delta }_1}{{\delta }_3}{v}_1-\frac{{\delta }_1}{{\delta }_3}{h}_t\right)+{\delta }_1{∊}^2{\widehat{\Phi }}_4\hfill \\ \hfill -& {∊}^2\frac{{\delta }_1}{{\delta }_3}(v_2-h_b){\widehat{\xi }}_3\left(\frac{1}{{\delta }_3}(v_2-h_b)\right)+{∊}^2\frac{{\delta }_1}{{\delta }_3}{\widehat{\Gamma }}_3{v}_T\left(v_1-h_t-v_2+h_b\right)\hfill \end{array}$$ (27)

$$\begin{array}{cc}\hfill \frac{d{v}_2}{d\tau }& =∊{\widehat{\Phi }}_3+{∊}^2{\widehat{\Gamma }}_2{v}_T(h_t-h_b)+{\delta }_3{∊}^2{\widehat{\Phi }}_4-{∊}^2(v_2-h_b){\widehat{\xi }}_3\left(\frac{1}{{\delta }_3}(v_2-h_b)\right)\hfill \\ \hfill & +{∊}^2{\widehat{\Gamma }}_3{v}_T(v_1-h_t-v_2+h_b)\hfill \end{array}$$ (28)

$$\frac{d{h}_b}{d\tau }=v_2-h_b-{\alpha }_2{h}_b({\delta }_3{u}_2-{\delta }_1{v}_2+{\delta }_1{h}_b)+∊{\widehat{\Phi }}_3+{∊}^2{\widehat{\Gamma }}_2{v}_T(h_t-h_b).$$ (29)

Our new variables v_1,2 are not scaled to order 1, in fact, they are O( δ₃)=O(10⁴). However, the advantage is that the leading order equations then simplify on noting the size of v_1,2, yielding at leading order:

$$\frac{d{u}_1}{d\tau }=\frac{d{v}_1}{d\tau }=0$$ (30)

$$\frac{d{h}_t}{d\tau }=v_1-h_t-{\alpha }_2{h}_t({\delta }_3{u}_1-{\delta }_1{v}_1+{\delta }_1{h}_t)$$ (31)

$$\frac{d{u}_2}{d\tau }=\frac{d{v}_2}{d\tau }=0$$ (32)

$$\frac{d{h}_b}{d\tau }=v_2-h_b-{\alpha }_2{h}_b({\delta }_3{u}_2-{\delta }_1{v}_2+{\delta }_1{h}_b).$$ (33)

From these equations, we can see that u₁, v₁, u₂ and v₂ are constant, respectively denoted A₁, A₂, A₃, and A₄, and hence,

$$\frac{d{h}_t}{d\tau }=-{\alpha }_2{\delta }_1{h}_t^2+(-1-{\delta }_3{\alpha }_2{A}_1+{\delta }_1{\alpha }_2{A}_2)h_t+A_2$$ (34)

$$\frac{d{h}_b}{d\tau }=-{\alpha }_2{\delta }_1{h}_b^2+(-1-{\delta }_3{\alpha }_2{A}_3+{\delta }_1{\alpha }_2{A}_4)h_b+A_4.$$ (35)

These equations have one positive, stable steady state given by

$${\tilde{h}}_{t+}=\frac{(-1-{\delta }_3{\alpha }_2{A}_1+{\delta }_1{\alpha }_2{A}_2)+\sqrt{{(-1-{\delta }_3{\alpha }_2{A}_1+{\delta }_1{\alpha }_2{A}_2)}^2+4{\alpha }_2{\delta }_1{A}_2}}{2{\alpha }_2{\delta }_1}$$ (36)

$${\tilde{h}}_{b+}=\frac{(-1-{\delta }_3{\alpha }_2{A}_3+{\delta }_1{\alpha }_2{A}_4)+\sqrt{{(-1-{\delta }_3{\alpha }_2{A}_3+{\delta }_1{\alpha }_2{A}_4)}^2+4{\alpha }_2{\delta }_1{A}_4}}{2{\alpha }_2{\delta }_1}$$ (37)

Therefore, in our original variables, the solution, which we will denote as W_fast, follows these equations:

$$\frac{d{h}_t}{d\tau }=-{\alpha }_2{\delta }_1{h}_t^2+(-1-{\delta }_3{\alpha }_2{A}_1+{\delta }_1{\alpha }_2{A}_2)h_t+A_2$$ (38)

$$\frac{d{h}_b}{d\tau }=-{\alpha }_2{\delta }_1{h}_b^2+(-1-{\delta }_3{\alpha }_2{A}_3+{\delta }_1{\alpha }_2{A}_4)h_b+A_4$$ (39)

$$c_t=\frac{1}{{\delta }_3}(A_2-h_t)$$ (40)

$$c_b=\frac{1}{{\delta }_3}(A_4-h_b)$$ (41)

$$b_t=A_1-\frac{{\delta }_1}{{\delta }_3}{A}_2+\frac{{\delta }_1}{{\delta }_3}{h}_t$$ (42)

$$b_b=A_3-\frac{{\delta }_1}{{\delta }_3}{A}_4+\frac{{\delta }_1}{{\delta }_3}{h}_b.$$ (43)

In general, the model dynamics of interest on the intermediate and slow timescales are insensitive to the timescales of the fast reactions (providing the fast reactions remain fast). Hence, altering the specific kinetic parameters (but keeping the pK_a, and hence the ratio of these parameters, equal) does not alter the system behaviour on the timescales of interest.

2.2.2. Intermediate timescale dynamics

To examine the intermediate timescale dynamics, let us rescale time, so τ₂ = ∈τ. We have, at leading order, again noting that our variables v_1,2 are not scaled to order 1, but instead O(δ₃)=O(10⁴),

$$\frac{d{u}_1}{d{\tau }_2}=0$$ (44)

$$\frac{d{v}_1}{d{\tau }_2}={\widehat{\Phi }}_1+{\delta }_3∊{\widehat{\Phi }}_5-∊{\widehat{\Gamma }}_3(v_1-v_2)$$ (45)

$$0=-{\alpha }_2{\delta }_1{h}_t^2+(-1-{\delta }_3{\alpha }_2{u}_1+{\delta }_1{\alpha }_2{v}_1)h_t+v_1$$ (46)

$$\frac{d{u}_2}{d{\tau }_2}=0$$ (47)

$$\frac{d{v}_2}{d{\tau }_2}={\widehat{\Phi }}_3+{\delta }_3∊{\widehat{\Phi }}_4-∊\left(\frac{{\widehat{\Delta }}_1}{{\delta }_3}{v}_2^2-{\widehat{\Delta }}_2{v}_2\right)+∊{\widehat{\Gamma }}_3{v}_T(v_1-v_2)$$ (48)

$$0=-{\alpha }_2{\delta }_1{h}_b^2+(-1-{\delta }_3{\alpha }_2{u}_2+{\delta }_1{\alpha }_2{v}_2)h_b+v_2.$$ (49)

Thus we can see immediately that u₁ and u₂ are constant as previously and respectively denoted by A₁ and A₃. Further, h_t and h_b are at their slow dynamics steady states, given by Equations (36) and (37).

Hence, we are left with only two ODEs, Equations (45) and (48), where the initial conditions for v₁ and v₂ are the equilibrium values from the fast solution, A₂ and A₄, respectively.

Here we can see that the positive equilibrium solutions are:

$${\tilde{v}}_2=\frac{∊{\delta }_3{\widehat{\Delta }}_2+{\delta }_3\sqrt{{∊}^2{\widehat{\Delta }}_2^2+4∊\frac{{\widehat{\Delta }}_1}{{\delta }_3}({\widehat{\Phi }}_3+{\delta }_3∊{\widehat{\Phi }}_4+v_T{\widehat{\Phi }}_1+{\delta }_3∊{\widehat{\Phi }}_5{v}_T)}}{2∊{\widehat{\Delta }}_1}$$ (50)

$${\tilde{v}}_1=\frac{∊{\delta }_3{\widehat{\Delta }}_2+{\delta }_3\sqrt{{∊}^2{\widehat{\Delta }}_2^2+4∊\frac{{\widehat{\Delta }}_1}{{\delta }_3}({\widehat{\Phi }}_3+{\delta }_3∊{\widehat{\Phi }}_4+v_T{\widehat{\Phi }}_1+{\delta }_3∊{\widehat{\Phi }}_5{v}_T)}}{2∊{\widehat{\Delta }}_1}+\frac{1}{∊{\widehat{\Gamma }}_3}\left({\widehat{\Phi }}_1+{\delta }_3∊{\widehat{\Phi }}_5\right),$$ (51)

where standard linear analysis shows this steady state is stable.

Changing back into our original variables so we can compare our approximate analytical solution to our numerical simulations, the solutions (which we will denote as W_intermediate) satisfy these equations:

$$h_{t+}=\frac{(-1-{\delta }_3{\alpha }_2{A}_1+{\delta }_1{\alpha }_2{v}_1)+\sqrt{{(-1-{\delta }_3{\alpha }_2{A}_1+{\delta }_1{\alpha }_2{v}_1)}^2+4{\alpha }_2{\delta }_1{v}_1}}{2{\alpha }_2{\delta }_1}$$ (52)

$$h_{b+}=\frac{(-1-{\delta }_3{\alpha }_2{A}_3+{\delta }_1{\alpha }_2{v}_2)+\sqrt{{(-1-{\delta }_3{\alpha }_2{A}_3+{\delta }_1{\alpha }_2{v}_2)}^2+4{\alpha }_2{\delta }_1{v}_2}}{2{\alpha }_2{\delta }_1}$$ (53)

$$c_t=\frac{1}{{\delta }_3}(v_1-h_t),c_b=\frac{1}{{\delta }_3}(v_2-h_b)$$ (54)

$$b_t=A_1-\frac{{\delta }_1}{{\delta }_3}(v_1-h_t),b_b=A_3-\frac{{\delta }_1}{{\delta }_3}(v_2-h_b)$$ (55)

where v₁ and v₂ are determined by the solution to Equations (45) and (48).

2.2.3. Slow timescale dynamics

The final, slow timescale, is where the physiological responses such as ventilation and kidney excretion take effect. To examine the slow dynamics, let us rescale time, defining τ₃ = ∈²τ. Once again we note that v_1,2 are O(δ₃)=O(10⁴), hence we consider each term in turn when approximating to leading order. Thus we have at leading order,

$$\frac{d{u}_1}{d{\tau }_3}={\widehat{\Gamma }}_1\left(u_2-\frac{{\delta }_1}{{\delta }_3}{v}_2-u_1+\frac{{\delta }_1}{{\delta }_3}{v}_1\right)+{\delta }_1{\widehat{\Phi }}_5-{\widehat{\Gamma }}_3\frac{{\delta }_1}{{\delta }_3}(v_1-v_2)$$ (56)

$$0={\widehat{\Phi }}_1+{\delta }_3∊{\widehat{\Phi }}_5-∊{\widehat{\Gamma }}_3(v_1-v_2)$$ (57)

$$0=-{\alpha }_2{\delta }_1{h}_t^2+(-1-{\delta }_3{\alpha }_2{u}_1+{\delta }_1{\alpha }_2{v}_1)h_t+v_1$$ (58)

$$\begin{array}{cc}\hfill \frac{d{u}_2}{d{\tau }_3}=& \frac{{\widehat{\Phi }}_2}{{\delta }_3}{v}_2-{\widehat{\xi }}_1\left(u_2-\frac{{\delta }_1}{{\delta }_3}{v}_3\right)+{\widehat{ϴ}}_1-{\widehat{\Gamma }}_1{v}_T\left(u_2-\frac{{\delta }_1}{{\delta }_3}{v}_2-u_1+\frac{{\delta }_1}{{\delta }_3}{v}_1\right)\hfill \\ \hfill +& {\delta }_1{\widehat{\Phi }}_4-\frac{{\delta }_1{\widehat{\Delta }}_1}{{\delta }_3^2}{v}_2^2+\frac{{\delta }_1{\widehat{\Delta }}_2}{{\delta }_3}{v}_2+{\widehat{\Gamma }}_3{v}_T\frac{{\delta }_1}{{\delta }_3}(v_1-v_2)\hfill \end{array}$$ (59)

$$0={\widehat{\Phi }}_3+{\delta }_3∊{\widehat{\Phi }}_4-∊(\frac{{\widehat{\Delta }}_1}{{\delta }_3}{v}_2^2-{\widehat{\Delta }}_2{v}_2)+∊{\widehat{\Gamma }}_3{v}_T(v_1-v_2)$$ (60)

$$0=-{\alpha }_2{\delta }_1{h}_b^2+(-1-{\delta }_3{\alpha }_2{u}_2+{\delta }_1{\alpha }_2{v}_2)h_b+v_2.$$ (61)

The initial conditions are the intermediate timescale equilibrium values for u_1,2 (denoted A₁ and A₃). As these equations are linear in u₁ and u₂, they can be solved explicitly. The equilibrium values, which are both positive with our parameters, are

$${\tilde{u}}_2=\frac{1}{{\widehat{\xi }}_1}\left(\frac{{\widehat{\Phi }}_2}{{\delta }_3}{v}_2+\frac{{\widehat{\xi }}_1{\delta }_1}{{\delta }_3}{v}_2+{\widehat{ϴ}}_1+{\delta }_1{v}_T{\widehat{\Phi }}_5+{\delta }_1{\widehat{\Phi }}_4-\frac{{\delta }_1{\widehat{\Delta }}_1}{{\delta }_3^2}{v}_2^2+\frac{{\delta }_1{\widehat{\Delta }}_2}{{\delta }_3}{v}_2\right)$$ (62)

$${\tilde{u}}_1={\tilde{u}}_2-\frac{{\delta }_1}{{\delta }_3}{v}_2+\frac{{\delta }_1}{{\delta }_3}{v}_1+\frac{1}{{\widehat{\Gamma }}_1}\left({\delta }_1{\widehat{\Phi }}_4-\frac{{\delta }_1{\widehat{\Gamma }}_3}{{\delta }_3}[v_1-v_2]\right).$$ (63)

Standard linear analysis shows that this equilibrium point is a linearly stable node.

Changing back into our original variables in order to calculate and compare our approximate analytical solution to our numerical solution, the slow solutions (which we will denote as W_slow), follow these equations,

$$h_t=\frac{(-1-{\delta }_3{\alpha }_2{u}_1+{\delta }_1{\alpha }_2{v}_1)+\sqrt{{(-1-{\delta }_3{\alpha }_2{u}_1+{\delta }_1{\alpha }_2{v}_1)}^2+4{\alpha }_2{\delta }_1{v}_1}}{2{\alpha }_2{\delta }_1}$$ (64)

$$h_b=\frac{(-1-{\delta }_3{\alpha }_2{u}_2+{\delta }_1{\alpha }_2{v}_2)+\sqrt{{(-1-{\delta }_3{\alpha }_2{u}_2+{\delta }_1{\alpha }_2{v}_2)}^2+4{\alpha }_2{\delta }_1{v}_2}}{2{\alpha }_2{\delta }_1}$$ (65)

$$c_t=\frac{1}{{\delta }_3}(v_1-h_t)$$ (66)

$$c_b=\frac{1}{{\delta }_3}(v_2-h_b)$$ (67)

$$b_t=u_1-\frac{{\delta }_1}{{\delta }_3}(v_1-h_t)$$ (68)

$$b_b=u_2-\frac{{\delta }_1}{{\delta }_3}(v_2-h_b),$$ (69)

where v_1,2 and h_t,b are defined by the algebraic Equations (57), (58) (60), (61) and u_1,2 are the solutions to the ODEs in Equations (56) and (59). The explicit large time asymptote, steady state, solutions can be readily found, yielding the steady state solutions in our original variables:

$${\tilde{h}}_t=\frac{(-1-{\delta }_3{\alpha }_2{\tilde{u}}_1+{\delta }_1{\alpha }_2{v}_1)+\sqrt{{(-1-{\delta }_3{\alpha }_2{\tilde{u}}_1+{\delta }_1{\alpha }_2{v}_1)}^2+4{\alpha }_2{\delta }_1{v}_1}}{2{\alpha }_2{\delta }_1}$$ (70)

$${\tilde{h}}_b=\frac{(-1-{\delta }_3{\alpha }_2{\tilde{u}}_2+{\delta }_1{\alpha }_2{v}_2)+\sqrt{{(-1-{\delta }_3{\alpha }_2{\tilde{u}}_2+{\delta }_1{\alpha }_2{v}_2)}^2+4{\alpha }_2{\delta }_1{v}_2}}{2{\alpha }_2{\delta }_1}$$ (71)

$${\tilde{c}}_t=\frac{1}{{\delta }_3}(v_1-{\tilde{h}}_t)$$ (72)

$${\tilde{c}}_b=\frac{1}{{\delta }_3}(v_2-{\tilde{h}}_b)$$ (73)

$${\tilde{b}}_t={\tilde{u}}_1-\frac{{\delta }_1}{{\delta }_3}(v_1-{\tilde{h}}_t)$$ (74)

$${\tilde{b}}_b={\tilde{u}}_2-\frac{{\delta }_1}{{\delta }_3}(v_2-{\tilde{h}}_b),$$ (75)

where v₁ and v₂ are the steady state solutions from the intermediate timescale in Equation (50) and (51) respectively. Also, ${\tilde{u}}_1$ and ${\tilde{u}}_2$ are the steady state solutions of Equations (56) and (59).

By extracting the leading order terms with our chosen parameters, we find,

$${\tilde{h}}_t=\frac{\left(\frac{{\delta }_3{\widehat{\Delta }}_2}{{\widehat{\Delta }}_1}+\frac{{\widehat{\Phi }}_1}{∊{\widehat{\Gamma }}_3}\right)}{{\delta }_3{\alpha }_2\left(\frac{{\widehat{\Phi }}_2{\widehat{\Delta }}_2}{{\widehat{\xi }}_1{\widehat{\Delta }}_1}-\frac{{\delta }_1{\widehat{\Phi }}_1}{{\widehat{\Gamma }}_1{\delta }_3∊}\right)}+O\left(\frac{1}{{\delta }_3}\right)$$ (76)

From Equation (76) we can see that to leading order, ${\tilde{h}}_t$ is proportional to $\widehat{\xi }$ and inversely proportional to α₂, ${\widehat{\Gamma }}_3$, ${\widehat{\Gamma }}_1$ and ${\widehat{\Phi }}_2$. Therefore, lowering the glomerular filtration rate (ξ₁) will lower H⁺ levels in the tumour. Conversely, raising the acid secretion rate (φ₂), carbon dioxide vessel permeability (Γ₃), or bicarbonate vessel permeability (Γ₁) will lower tumour H⁺. This expression can tell us about how groups of parameters affect the long time steady-state, and allows us to identify the most important ones. However, quantification of the relative importance with this expression is difficult, so we will proceed with a formal sensitivity analysis in Section 3.4 after we construct the uniformly valid solution.

2.2.4. Uniformly valid solution

It is now straightforward to construct an approximate uniformly valid solution using our fast, intermediate, and slow solutions from above. This uniform solution has the form:

$$W_{\text{uniform}}=W_{\text{fast}}+W_{\text{intermediate}}+W_{\text{slow}}-{\tilde{W}}_{\text{fast}}-{\tilde{W}}_{\text{intermediate}}$$ (77)

where ${\tilde{W}}_{\text{fast},\text{intermediate}}$ are the quasi-steady state solutions to the W_fast and W_intermediate equations, respectively.

2.2.5. Sensitivity analysis

It is important to identify how sensitive the system is to the chosen parameter values. Most importantly, we would like to be able to predict treatments targeting the parameters that have the most pronounced effect on raising tumour pHe. In particular, we are most interested in the parameters which have the greatest effect in lowering the steady state tumour pHe, as well as how the treatment term can affect the pHe of the tumour and the blood. Also, as parameter variations exist naturally between patients, if the system is particularly sensitive to a given parameter it would be important to highlight this system behaviour. As noted, the previously derived analytical approximation can tell us about how groups of parameters affect the long time steady-state, but it is difficult to quantify the relative importance of each individual parameter contribution. Hence, analytical sensitivity values can provide this added information.

One way of examining the effect of a parameter, p, on one of our steady state variables, V, is to calculate a sensitivity coefficent. This can be defined as

$$S_{V,p}=\frac{p}{V}\frac{\partial V}{\partial p}.$$ (78)

The calculation of this sensitivity coefficient, S, tells us what effect a percentage change in the parameter, p, has on the variable, V. If ǀSǀ > 1, a percent change in p produces a larger percent change in V, and thus p has a strong effect on V.

The analytical value of the sensitivity coefficient was calculated in Maple, and the parameter values were then substituted to obtain the numerical value.

2.2.6. Description of numerical methods

The model equations (9)-(14) were solved using the Matlab stiff ODE solver ode15s, a variable order multistep solver. A stiff solver is necessary due to the multiple timescales in this system, with rapid transient movement of the reaction kinetics, and then slowly varying long transients. Initial conditions were used as in (16) and parameters from Table 1. The simulations were run until τ = 1 × 10¹⁰ to ensure steady state is reached.

3. Results

3.1. Model Validation: Comparison of respiratory/metabolic disorders to observed blood pHe

In this section we present a set of numerical simulations of Equations (9)-(14) to confirm that the model produces qualitatively and quantitatively reasonable and accurate results.

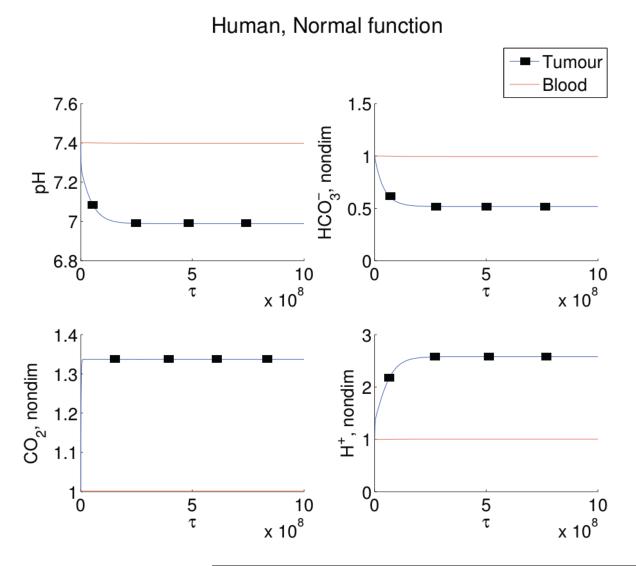
In order to confirm that the mathematical model correctly simulates blood pHe, we examine the accuracy of the model in a variety of clinical situations which we can compare to data. In the unperturbed system, the blood pHe equilibriates at the normal blood value of 7.4 (see Figure 2), with blood carbon dioxide and bicarbonate concentrations also at their normal values (nondimensionalised to 1).

Figure 2.

Simulations of Equations (9)-(14) for human blood (red line) and tumour (blue line with squares) values of pHe (top left), ${\mathit{HCO}}_3^{-}$ (top right), CO₂ (bottom left), and H⁺ (bottom right) levels, with no metabolic or respiratory disorder, and no bicarbonate treatment. Note the blood pHe remains at 7.4, with normal levels of ${\mathit{HCO}}_3^{-}$ and CO₂. By contrast, the tumour has a lowered pHe to 7.0, with elevated CO₂ and low ${\mathit{HCO}}_3^{-}$ levels. The numerical simulations are run with initial conditions (16) and parameters as in Table 1 but with θ₁ = 0. Note that τ of 10⁹ corresponds to a dimensional time of approximately 10 hours.

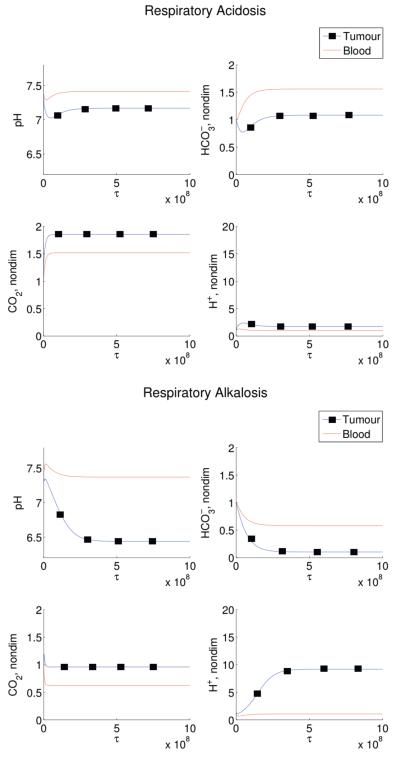
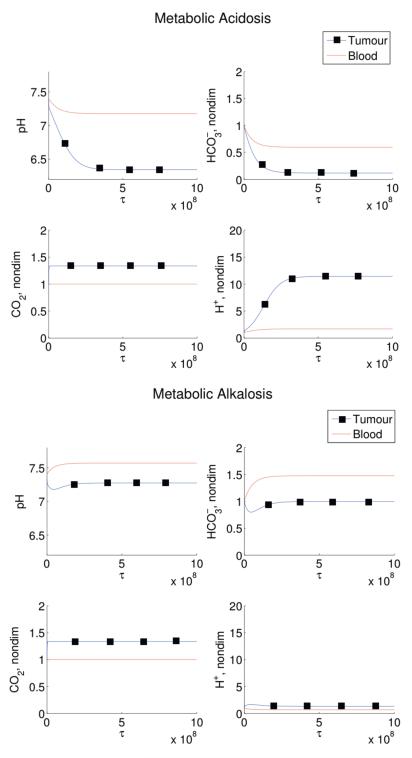
Four disordered states are then simulated: respiratory alkalosis, metabolic alkalosis, respiratory acidosis, and metabolic alkalosis. In our simulations, the respiratory disorders are induced by fixing the ventilation rate, ξ₃(c_b), at higher or lower values than normal, thereby changing the blood CO₂ levels. Metabolic disorders are induced by altering the blood ${\mathit{HCO}}_3^{-}$ levels by the addition or removal of bicarbonate (θ₁). These results are shown in Figures 3 and 4. For the respiratory disturbance scenarios, in agreement with experiments which induce patients to hyperventilate or hypoventilate, the ventilation rate is fixed and varied to produce either acidosis or alkalosis. Initially, change in ventilation rate causes a change in blood CO₂, which immediately alters the ${\mathit{HCO}}_3^{-}$ and H⁺ levels. After a few hours the effects of the renal compensation are visible, with the amount of reabsorbed bicarbonate changing to compensate and push the pHe back to normal. Both of these simulated disorders match the correct clinically predicted pHe and compensation timescale [17]. Simulations of metabolic disorders (acidosis or alkalosis) as a result of persistent administration of bicarbonate (due to bicarbonate loading) or loss of bicarbonate (for example, through vomiting) predict no respiratory compensation, hence blood pHe levels do not return to normal.

Figure 3.

Simulated respiratory disorders in humans. Induced respiratory acidosis (left panels) and induced respiratory alkalosis (right panels). In both situations, there is an initial blood pHe alteration due to the respiratory disturbance. However, after a few hours, the effect of renal compensation is visible, pushing the pHe back to normal and resulting in altered bicarbonate and carbon dioxide levels. In this simulation, Equations (9)-(14) are solved with initial conditions (16) and parameters as in Table 1 except the change in ξ₃(c_b) (ξ₃(c_b)=7.7 × 10⁻⁸ for respiratory acidosis, ξ₃(c_b)=2.3 × 10⁻⁷ for respiratory alkalosis), and with θ₁ = 0. Note that τ of 10⁹ corresponds to a dimensional time of ≈ 10 hours.

Figure 4.

Simulated metabolic disorders in humans. Results are shown for induced metabolic acidosis (left panels) and induced metabolic alkalosis (right panels). Elevations (reductions) in blood pHe result in subsequent increases (decreases) in tumour pHe. Additionally, acidification of the bloodstream can cause substantial reductions in tumour pHe, potentially to toxic levels for tumour cells. In this simulation, Equations (9)-(14) are solved with initial conditions (16) and parameters as in Table 1 except with θ₁ = −5 × 10⁻⁶ in metabolic acidosis and θ₁ = 4 × 10⁻⁶ in metabolic alkalosis.

To compare our results more rigorously with clinical data on acid/base disturbances, a standard buffer curve of the blood pHe is constructed. This is accomplished by inducing a respiratory or metabolic disturbance into the model (as described above), and tracking blood pHe prior to renal compensation. Although in these simulations we are primarily interested in the blood dynamics, the full coupled model is simulated (blood and tumour). This is reasonable as the tumour of our simulated size has a negligible effect on blood dynamics (results not shown, but the model sensitivity is calculated in Section 3.4).

The simulated results and clinical buffer curves for humans are shown in Figure 5. The mathematical model performs well, particularly in predicting the response to metabolic disorders, and also in our range of interest (a normal blood of pHe 7.35-7.45). For example, the pHe changes caused by altering the amount of bicarbonate in the blood (for example, by changing θ₁ as is done in the simulations, or by impaired renal function which could affect φ₂ or ξ₁) are shown by the red squares. The resulting curve follows a contour line of constant pCO₂ at 40mmHg, the normal level, as tight regulation of ventilation prevents any change in CO₂ levels. As this model is primarily interested in the effect of adding bicarbonate in this way, the accuracy of the simulations is encouraging.

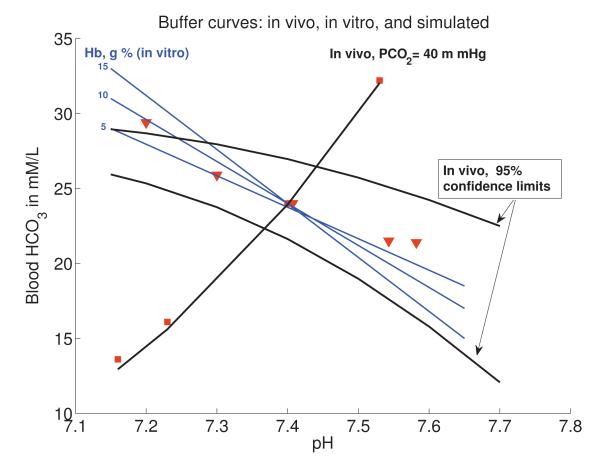
Figure 5.

Human buffer curve comparison between in vitro, in vivo, and calculated with our model. Blue lines represent in vitro curves of blood containing varying amounts of haemoglobin. Dark black lines are the in vivo observed ranges in values for a normal human. Red squares and triangles represent calculated values when Equations (9)-(14) are solved with initial conditions (16) and parameters as in Table 1 but with varying ξ₃ to simulate impaired ventilation, and varying θ₁ to simulate ingestion or loss of bicarbonate. Red squares represent inducing a metabolic disturbance by varying ${\mathit{HCO}}_3^{-}$ (θ₁) with a constant pCO₂ level (40 mm Hg). The accuracy of the mathematical model, particularly with regards to metabolic alkalosis, is encouraging. Red triangles represent the effect of varying CO₂ through disordered ventilation. These data points were obtained by fixing ventilation rate, ξ₃, at several values, running the simulations as in Figure 3, and taking the blood CO₂, ${\mathit{HCO}}_3^{-}$, and pHe values prior to renal compensation consistent with experiments. Although this model does not focus on respiratory disturbances, it still provides a good fit to data in this region, particularly in the region of interest where blood pHe is in the normal and safe region of 7.35-7.45. In vitro and in vivo data adapted with permission from The University of Chicago Press (Figures 17 and 18 in [18]).

Alternatively, the pHe changes caused by altering the CO₂ levels by fixing the ventilation rate, ξ₃(c_b) (clinically induced via rebreathing CO₂ or hyperventilating), follow the red triangles. As shown in the previous section, respiratory disturbances immediately alter blood pHe and bicarbonate levels. Eventually, renal compensation occurs (both clinically and in our simulation), which is not shown in this gure as the in vivo studies were performed on a short timescale before compensation could occur. Again, the model performs well, despite the approximations to the CO₂/ventilation term, falling well within the 95% confidence limits of the data within the biological pHe range we are examining (7.35-7.45). Only at very low pHe is there a deviation from the predicted buffer line, which is acceptable particularly as the model is developed specifically to examine metabolic alkalosis (possibly induced by the bicarbonate treatment), not acidosis.

3.2. Model prediction: Effect of respiratory/metabolic disorders on tumour pHe

Simulations of respiratory and metabolic disorders indicate that these disordered states can cause significant changes in tumor pHe. The model predicts tumor pHe is elevated (greater than 7.1 from a normal tumor pHe of 7.0) during the conditions of respiratory acidosis and metabolic alkalosis. During states of respiratory alkalosis and metabolic acidosis, tumor pHe can be lowered to potentially toxic levels for tumour cells (less than 6.5 from a normal tumor pHe of 7.0).

3.3. Comparison of Numerical Solutions and Asymptotic Approximations

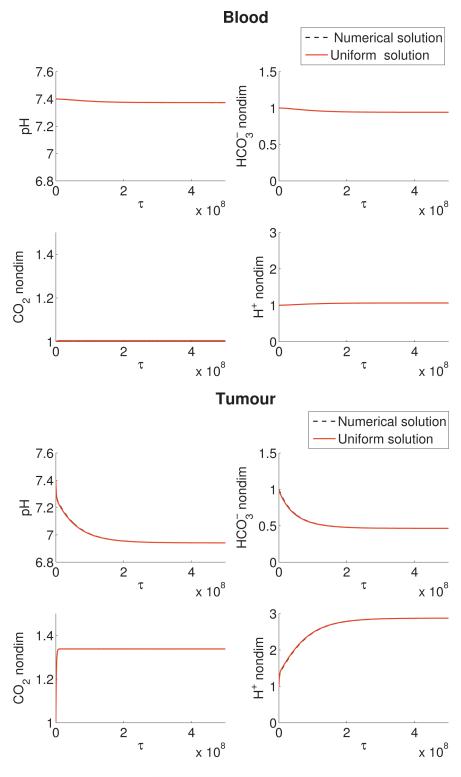
Figure 6 shows the uniform solution, Equation (77), plotted against the numerical simulation, and agreement is excellent. The numerical solution is simulated with Equations (9)-(14). For the purposes of this comparison, the numerical and analytical solutions are calculated with initial conditions (16) and parameters from Table 2 but with Θ₁ = 0.

Figure 6.

Comparison of the numerical (black dashed line) and uniform analytical approximation (red line) in the (a) blood and (b) tumour in an untreated human. The uniform analytical solution is calculated from Equation (77). The numerical solution is simulated with Equations (9)-(14). All numerical and analytical solutions are calculated with initial conditions (16) and parameters from Table 1 but with θ₁ = 0.

3.4. Modelling therapy: Sensitivity analysis

The full results of the sensitivity analysis are presented in Appendix B in Table B.3, which displays the sensitivity of all the variables to each of the parameters for both mice and humans in the untreated and treated cases. The results are similar for both cases. The human and mouse tumour H⁺ sensitivity coefficients with the largest effect on tumour pHe (selected by an absolute value greater than 1) are shown in Figure 7. In both humans and mice, the sensitivity coefficients indicate that the most important parameters affecting the tumour pHe are those involved with renal function: bicarbonate clearance and reabsorption. Targeting these processes not only raises the tumour pHe, but also increases the bicarbonate therapy efficacy (simulations not shown).

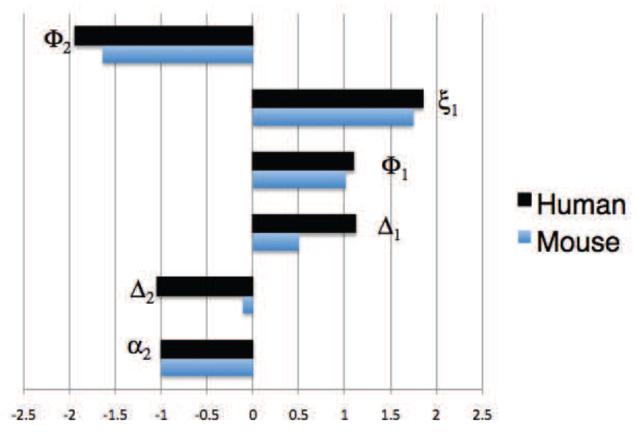
Figure 7.

Tumour H⁺ (${\widehat{h}}_t$) sensitivity coefficients (S_ht,p) with respect to parameter (p) with an absolute value greater than 1 for a treated human (black) and mouse (blue). The human tumour pHe is most sensitive to tumour proton production (φ₂), renal function parameters (ξ₁ and φ₁), ventilation parameters (Δ₁ and Δ₂), and pK_a (α₂). By comparison, the mouse is less sensitive to the parameters in general, and in particular much less sensitive to the ventilation parameters (Δ₁ and Δ₂). These coefficients were calculated with bicarbonate treatment, values as in Table 1. A table of all the sensitivity coefficients can be found in Appendix B.

Other key parameters which most significantly affect tumour pHe are ${\widehat{\Phi }}_1$, which incorporates the tumour proton production rate and the pK_a parameter ${\widehat{\alpha }}_2$. In humans, the ventilation parameters (${\widehat{\Delta }}_1$ and ${\widehat{\Delta }}_2$) are predicted to be very important, but less so in the mouse. Treatments which target renal parameters (${\widehat{\xi }}_1$ and ${\widehat{\Phi }}_2$), however, also have a strong effect on the blood pHe (see Appendix B).

As shown in the previous section, the sensitivity analysis confirms that none of the variables are sensitive to the parameter representing vascular exchange of the protons between tumour and blood, ${\widehat{\Gamma }}_2$. This suggests that the majority of the removal of protons from the tumour is accomplished via CO₂ evacuation, and not direct movement of free protons. This is reasonable because despite the high proton production of tissues, the actual concentration of free protons in the tissue is very small (several orders of magnitude lower than the respective buffering components). Therefore, by far the majority (ca. ratio of 1 in 10⁵) of protons will exit the tumour attached to a buffer.

Unsurprisingly, the parameter incorporating the kinetics of the bicarbonate reaction, ${\widehat{\alpha }}_2$, is shown as important in this analysis, as altering the ratio of the forward to back reactions (and, therefore, the pK_a of the reaction), will strongly alter the effect of the buffer.

The sensitivity of the system with respect to the parameters used for its non-dimensionalisation (for example, δ₁ and δ₃) is not considered, as these parameters do not have a natural biological interpretation. Hence, as initial conditions in the nondimensional system they do not effect the steady state values of the variables.

4. Discussion and Conclusion

This paper presents a systemic blood and tumour buffering model, which is parameterised with both mouse and human data sets. The model accurately simulates blood pHe in normal and acid/base disordered states. The simulations indicate that respiratory acidosis and metabolic alkalosis elevate tumor pHe. Conversely, respiratory alkalosis and metabolic acidosis lower tumor pHe to potentially toxic levels. These predictions confirm the hypothesis that inducing metabolic alkalosis through the chronic administration of buffers such as sodium bicarbonate can elevate tumour pHe to normal levels, which has been verified through in vivo experiments [11]. This normalisation of tumour pHe could help promote the survival and functions of the normal cells, reducing the tumour’s ability to invade. Furthermore, inducing metabolic acidosis is predicted to reduce tumour pHe from the already acidic level, potentially to levels which could be toxic to the tumour cells. Several experimental studies have shown that patients with metastatic renal cancer benefit from cytoreductive nephrectomy [23, 24, 25]. Our model supports the speculation by Gatenby and Gawlinski [4] that the observed benefits are a consequence of potential metabolic acidosis caused from the kidney removal, which could lower tumour pHe to levels toxic to the tumour cells.

In order to identify promising proton reducing targets which could prevent tumour acidity and normalise tumour pHe), a sensitivity analysis of the model was performed and indicates that the tumour pHe is most sensitive to tumour proton production and kidney filtration/reabsorption of bicarbonate. For example, the model predicts that decreasing glomerular filtration rate (GFR) leads to a rise in baseline levels of bicarbonate, and any treatment will not be filtered out as effectively. Similarly, the model predicts increasing the renal acid secretion rate would raise bicarbonate levels and significantly increase tumour pHe. However, as treatments targeting these parameters also have a significant effect on blood pHe, any therapy used to adjust kidney function should be undertaken with extreme caution.

On the other hand, altering tumour proton production, ${\widehat{\Phi }}_1$, has a signicant effect on tumour pHe, but virtually no effect on blood pHe, and therefore should be considered a safe option. Any potential therapy which could decrease proton production (such as through inhibiting glycolysis) could be used in combination with bicarbonate to an enhanced effect. Ongoing studies by our research group are currently exploring these possibilities.

There are several important extensions to this model which would improve the accuracy of the predictions. First, more detailed modelling of the contribution of other intrinsic buffering components would strengthen the quantitative predictions of the model. The incorporation of these static tissue buffers would not alter the regulation examined in this model, but do contribute to the overall buffering capacity of the tumour. We have assumed a constant buffering contribution from intrinsic buffers, implicitly included in the proton production term. However, it is likely that the intrinsic buffering capacity of the tumour is pH dependent, and thus would be an important model extension to examine. Currently, the model will most likely overestimate the effect of bicarbonate treatment on both the blood and the tissue. Nevertheless, comparing our mathematical model to in vivo data indicates this model performs well alone.

Secondly, the predictions in this model are based on the assumption that the tumours in humans will have the same vascularity as in mice, which is not necessarily valid in all cases. However, the cell lines used in the mice were human breast cancer cells, thus it is reasonable to assume the cell lines will produce the same amount of pro-angiogenic signals and therefore initiate similar vasculature. Still, the stromal responses might differ in each situation, which highlights the difficulties of using animal models (even with human cell lines) in therapy experimentation. Additionally, vascular heterogeneity within a single tumour will result in variable buffer delivery across the tumour, which will be important to study with advances in functional vessel imaging.

Thirdly, the effects of systemic alkalosis on respiration is controversial, and we have neglected the effect of H⁺ on ventilation rate for several reasons. Firstly, isolated changes in H⁺ are mainly sensed by the peripheral chemoreceptors [26], which only contribute a small amount to ventilation. Secondly, respiratory compensation to metabolic alkalosis is controversial [27, 28, 29]. Early studies indicated that there was little to no respiratory compensation in humans and dogs [27, 28]. Later studies have shown that in some human cases there is respiratory compensation, although the magnitude of compensation is highly variable, and in all cases limited [30]. Even in cases of severe metabolic alkalosis, it is extremely rare to see respiratory compensation raising pCO₂ levels above 55mmHg from the normal 40mmHg [31, 32]. There is no concrete evidence surrounding murine respiratory compensation. However, respiratory compensation to metabolic alkalosis is present in some humans. As our model system is sensitive to the ventilation term, the refinement of this term is worth further consideration.

Experimental studies undertaken by our group are currently examining the presence (or absence) of respiratory compensation in mice, which will hopefully elucidate the variability, timing, and extent of this compensation should it occur. These and other experimental results will be used to refine and develop the current model, which can further aid in developing safe and effective anti-tumour therapies.

Despite the many possible extensions, our simplified model accurately predicts acid-base regulation in the blood and tumour, and can be used to suggest the most promising parameters and processes to target in order to reduce tumour acidity and prolong survival. Novel therapies utilising exogenous buffers or other combinations can be built on this basic framework for future study. Finally, this model could be linked to other cellular models of tumour growth [33, 34], and subcellular models of tumour metabolism to provide a multiscale model linking pHe regulation with tumour invasion.