Neurofunctional model of large-scale correlates of selective attention governed by stimulus-novelty

Abstract

Multiple studies demonstrate the influence of the limbic system on the processing of sensory events and attentional guidance. But the mechanisms involved therein are yet not entirely clear. The close connection of handling incoming sensory information and memory retrieval, like in the case of habituation towards insignificant stimuli, suggests a crucial impact of the hippocampus on the direction of attention. In this paper we thus present a neurofunctional forward model of a hippocampal comparator function based on the theory of theta-regulated attention. Subsequently we integrated this comparator model into a multiscale framework for the simulation of evoked responses. The results of our simulations were compared to experimental data on electroencephalographic (EEG) correlates of habituation towards familiar stimuli using time-scale analysis. In consequence we are able to present additional evidence for limbic influences on the direction of attention driven by stimulus novelty and a systems neuroscience framework for the statements given in the theta-regulated attention hypothesis.

Introduction

Attention can be considered as a process of selecting important sensory information for higher processing while suppressing insignificant stimuli at the same time. A second important function is to assign processing resources to the attended signal stream. Crucial for this workflow is the detection of signal novelty and habituation to already known signals. In almost every environmental setting the organism is confronted with concurrent perceptual stimuli of different behavioural importance. The attenuation of indifferent perceptive events concurring to behavioural important stimuli is highly important for avoiding energy expanse and for the government of limited processing resources. The appraisal of incoming sensory information with reference to their overall novelty demands the involvement of brain structures closely related to memory. However the influence of the limbic system on the processing of sensory events and attentional guidance is not entirely clear up to now.

Mathematical forward modeling has become a valuable tool for the analysis of fundamental processes in neuroscience. The mathematical description of biological features, e.g., the characterization of neural firing mode dynamics and related (de-)synchronization processes (Wang et al. 2006; Zhang et al. 2010), allows in the simulation the adjustment and adaptation of parameters not accessible in the human experiment and thus provides the opportunity to make clear predictions on pathogenic changes in the system. Going hand in hand with an experimental evaluation of the simulated data the forward model is a promising approach to gain a deeper insight in the functional mechanisms of attentional guidance. In preliminary studies we could demonstrate an objective evaluation of attentional binding towards a repetitive acoustic event (Mai et al. 2009). We were able to show a significant loss of attention over the presentation of a stimulus that is not affecting the subject, while a stimulus that is clearly annoying is keeping a constant level of attentional binding. The loss of attention in the first case can only be explained by a “habituation” of attention due to a familiarity of the stimulus. So the claim exists for a mechanism combining attentional guidance and memory retrieval of already classified events. This claim is supported by a number of studies. The idea of the hippocampus working as a comparator device of incoming sensory events and already stored memory was proposed by many authors (Miller et al. 1988; Squire and Zola-Morgan 1988; Salzmann 1992; Grossberg and Merrill 1992; Pribram 1986). Yi et al. could demonstrate in 2005, that only selectively attended events were able to form memory traces (Yi and Chun 2005). Also various animal models showed an unsettled attentive behaviour after hippocampal lesions, compareable to the explorative behaviour in entirely new environments (Roberts et al. 1962; Glickman et al. 1970; Kim et al. 1970). A habituation towards the orienting reaction might be considered as loss of attention. Novelty thus seems to serve as its own quality for focussing attention and the conduction of behavioural schemes. Furthermore some studies gave evidence for a loss of stability in selective attention in schizophrenic patients with hippocampal lesions (Cohen et al. 1987; Oades and Sartory 1997; Grace 2000). Considering these links of unsettled attentive behaviour and impaired memory formation our goal was to demonstrate a potential impact of limbic influences on attentional information-processing.

In 1973 Hillyard could demonstrate a difference in the processing of attended and unattended stimuli at the level of late auditory evoked potentials (Hillyard et al. 1973). Especially the N1–P2 complex shows a significant difference in reaction to pure exogenous components of the auditory stimuli compared to the reaction to a willingly attended signal or rather the endogenous component arising from focussed attention. In preliminary work we were able to show a difference in the synchronization stability of the N1–P2 component in the cases of attended and unattended stimuli (Low et al. 2007).

According to Bregmans Auditory Scene Analysis (ASA) (Bregman 1999) the formation of an auditory stream is divided into two stages: The decomposition of the acoustical environment into discrete sensory elements and the subsequent recombination of those elements into a sensory stream. This stream can be seen as the spatial representation of a single sound source.

Based on the neurophysiological work of Vinogradova (2001) and the article of Kryukov (2008) we develop a computational oscillatory model of the hippocampal comparator function in this article. In subsequent steps our comparator model is integrated into a multiscale framework for the simulation of evoked responses, so we are able to compare our simulated ERPs directly to our experimental data.

Emphasis of this modeling work is clearly on the theoretical aspect of connecting two independently developed models of a hippocampal comparator function on one hand and of cortico-thalamic feedback interactions on the other hand, to a functional multiscale model of attentional guidance due to stimulus novelty. The experimental part was used to consolidate our hypothesis as we were able to predict the averaged experimental outcome in-silico. In this work we take only the processing of a single sensory stream into account. We hypothesize that the input signal originating from the medial septum (MSDB), representing this auditory stream, is nearly entirely stripped from higher properties of the actual auditory signal, but still carries information on the signals source’s spatial location and on its exogenous weight (Vinogradova 2001; Dwyer et al. 2007).

Materials and methods

Experimental setup

Subjects

Ten adults (4 female and 6 male with mean age 30 years and 11 months (standard deviation was 3 years and 9 Months) participated in this study. Normal hearing was verified by an audiogram before and immediately after the experiment to ensure no negative after effects arised from the experiment.

Data acquisition, segmentation and paradigm

Late auditory evoked potentials (LAEPs) were obtained using an acquisition system set up based on commercial devices by Guger Technologies, Austria. The system consists of an attenuator system (g.PAH), a trigger conditioner (g.TRIGbox) and an amplifier for biosignal acquisition (g.USBamp).

The EEG recordings were performed in a sound proof room. The subjects were asked to lie down and they were inquired to relax during the experiment, to keep their eyes closed, not to move and to ignore the presented stimuli. It was ensured that the subjects did not fall asleep during the experiment.

The auditory stimuli were pure tones of 1 kHz with a duration of 40 ms and constant interstimulus interval (ISI) of 1 s. We presented the stimuli at two stimulation levels of 50 dB (HL) (low) and 100 dB (HL) (high) successively with a 3 min break in between. The stimulus-presentation was counterbalanced: 50 percent of the subjects received low-intensity stimulation first, followed by high-intensity stimulation respectively vice versa for the remaining subjects. The stimuli were presented monaurally to the right ear via headphone. Electrical cross-talk was ruled out.

The responses to the individual tones were recorded using surface electrodes (Ag/AgCl) which were placed ambilateral at the mastoid (active electrodes), vertex (counter-electrode) and the forehead (ground). The impedances of all electrodes remained below 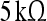in all measurements. The EEG was sampled at 512 Hz. Thousand sweeps were obtained for each stimulation level in every subject. Only the ipsilateral data was analyzed. The EEG recording was segmented into 750 ms post-stimulus sweeps and filtered using a 1–30 Hz digital filter. Sweeps containing artifacts were rejected using amplitude threshold detection (amplitude larger than 50 μV). At least 800 artifact-free sweeps of each subject were acquired for the following analysis.

Data analysis

The continuous wavelet transform (CWT) has been established as an important tool in time–frequency analysis. This analyzing method has been used in this article for investigating the loca characteristic of non-stationary signals, i.e., EEG data [see (Klein et al. 2006) and (Lachaux et al. 2002) for exemplary application].

The basis function of the CWT is the so-called mother wavelet 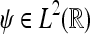. From this mother wavelet we create a family of double-indexed wavelets ψ_a,b. Let 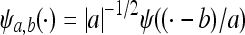, where 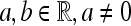. The wavelet has to satisfy the following admissibility condition: .

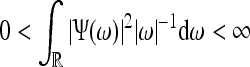Here 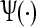is the Fourier transform of the wavelet. The CWT 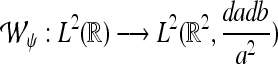of a signal 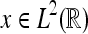with respect to the wavelet ψ is given by the inner L²–product:

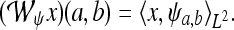1

The CWT is used to construct a time–frequency representation of our EEG-signals offering a good time and frequency localization and is thus an excellent tool for mapping the changing properties of these non-stationary signals. [See (Louis et al. 1997) for more details and an introduction to wavelets and their application]. Note that the scale parameter a can always be associated with a ‘pseudo’ frequency f_a in Hz by 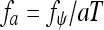, where T is the sampling period, i.e., the inverse of the sampling frequency, and f_ψ is the center frequency of the wavelet ψ (Abry 1997). From the CWT of two signals, α and β, the wavelet cross spectrum between α and β can be defined as:

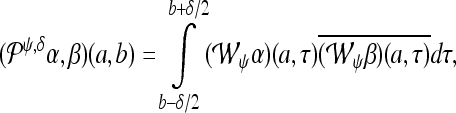2

where 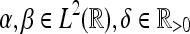. Here δ gives the window size for the calculation of wavelet coherence. Finally the wavelet coherence (Lachaux et al. 2002) of two signals (in our case a set of actual data sweeps and a reference set of sweeps), α and 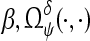is defined as

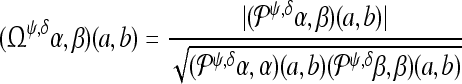3

The Schwartz inequality ensures that 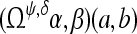takes its values between 0 and 1. This wavelet coherence increases with the correlation of the envelopes (amplitudes) between two signals as well as if their phase shows smaller variations in time (Lachaux et al. 1999).

Neurofunctional comparator model

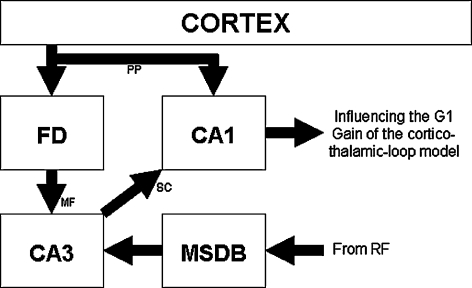
The proposed model is a modular expansion of our mathematical model for the simulation of evoked responses. Our model of the hippocampal comparator function consists of four functional structures according to the neuroanatomical data of Vinogradova et al. (2001). The medial septum (MSDB) and Fascia Dentata (FD) subunits serve as modules for the formation and evolution of the neuronal stimulus representation by feature extraction. They form two inputs to the comparator subunit CA3, which is on its part controlling the valve-element CA1. The CA1 subunit also receives input from a cortical element EC. See Fig. 1 for a symbolic model representation.

Fig. 1.

Schematic outline of the proposed module of habituation towards stimulus novelty and selective attention guidance for integration into the framework. FD Fascia Dentata, MSDB Medial Septum and Diagonal Band of Broca, SC Schaffer Collaterals, PP Perforant Path, MF Mossy Fibres, RF Reticular Formation

The MSDB subunit is directly processing the sensory stimulation. According to Vinogradova et al. (2001) we can assume the MSDB activity as stimulus dependant but stripped of every higher signal property. We consider the MSDB activity as being a direct neuronal representation of the exogenous stimulus weight. In our model the activity of the MSDB element is given by the Eqs. 4, 5 and 6 formulating the oscillating membrane potential U_mms

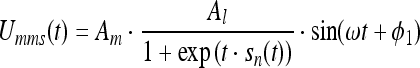4

and the gamma band bursting U_bms

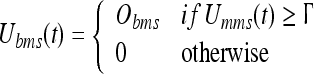5

with

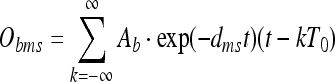6

Let T₀ be the base-period of the gamma-band oscillation and d_ms a constant in R⁺ describing the recruiting of CA3 neurons in time. Let 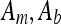and A_l be constants in R⁺ denoting amplitudes while ϕ₁ and ϕ₂ are constants in R⁺ denoting a phase shift. s_n (t) is a function in R acting as a slope-factor governing the evolving decrease in firing length. The underlying theta-band oscillation of the membranes serves us (and also might in vivo) as time and phase window. Resulting in a bursting spike neuron model as long as the membrane potential reaches a given threshold value 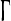. The dependence of the sigmoid damping coefficient s from the number of stimuli n represents neuronal firing habituation on the level of a functional unit by the number of stimulus presentations as demonstrated by Vinogradova et al. (2001). Also the FD subunit activity is given by a damped oscillation and superposed high frequency oscillation as shown in the equations for the membrane potential U_mfd

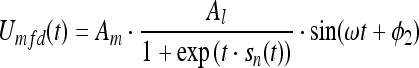7

and the gamma-band bursting U_bfd

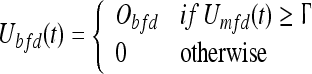8

with

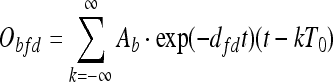9

In this FD model the damping and the phase depend on the number of stimulus presentations n. In the experimental setting the FD shows no habituation on cellular level, but a process of elongated firing—i.e. the formation of memory traces. In our model this mechanism is given by a decrease of the oscillation-damping s_n (t). In our model the phasic relation of the both oscillators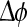

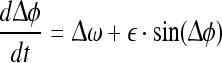10

behaves according to Adler’s equation for weakly coupled oscillators. The MSDB is acting as the actual oscillation pacemaker, while FD oscillations behave accordingly to a weakly driven oscillator. The coupling of both oscillators ε , given in (10), is assumed to be a constant in first, but might in-vivo follow a non-linear function due to synaptic plasticity. This approach is plausible as experimental data is not sufficient to evaluate the phasic behavior of the FD firing in detail. As long as CA3 neurons are not pre-recruited by FD projections they will react to MSDB input by a suppression of their tonic fire. In future this state is referred as reaction to novelty. In terms of modeling: The FD input imprints a response threshold on the CA3 subunit for a given timeframe defined by the decline of the potential d_fd given in (9). As long as the response threshold in CA3 is not higher than a given value it will react to MSDB input by a suppression of its tonic fire, putting the CA1 element into a receptive state. During this receptive state the CA1 subunit integrates the input from the entorhinal cortex (EC). If a determined number of spikes 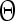arrives in a theta-band window the CA1 element reacts with a single action potential. The firing rate of CA1 F^CA1_n(t) is given by

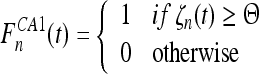11

with

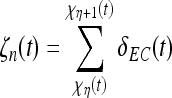12

We define a natural firing frequency of the CA1 neurons f = 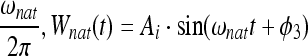in the theta band by calculating a time-window for the integration of incoming spikes. Upper and lower limit of every time window is given by the zeroes of a theta–frequency oscillation 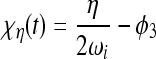. δ_EC denotes a single spike of a train of spikes originating from the EC. Let 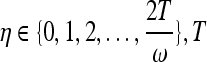denotes the duration of the CA3 reaction to novelty and t .

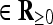Embedding into the model of corticothalamic interaction

For the integration of the CA1 firing into the model for the simulation of late evoked responses we normalize the firing rate to F^CA1_n(t)  ∈ [0,1], so that 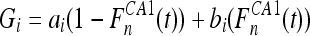takes values in the interval (Trenado et al. 2007).

In agreement with previous studies (Hoppensteadt 1991; Destexhe 2000) we adopt that stimuli of various intensities arrive in the thalamus, which trough forward and feed-forward (loop) interactions with the cortex, selects the most demanding or relevant stimuli for further processing. Also, as suggested by experimental findings (Crick 1984) that emphasized the localized enhancement and inhibition of the cortex under attentive states, we support that such a selective process can be facilitated by corticothalamic modulations, (Lachaux et al. 2002) that in terms of our model can be achieved by the transfer function (defined in the Fourier domain (k, w) by convenience)

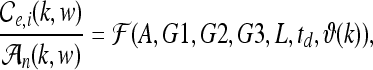13

which represents the activity between cortical (excitatory e and inhibitory i) neural populations 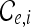and subcortical incoming auditory stimuli 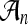. Here, 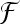is a rational function involving corticothalamic gains G1, G2, and G3 (See Fig. 2), dendritic low-pass filtering effects L, corticofugal time delays t_d, large response amplitude A, and a dispersion relation ϑ(k) describing a mean field cortical pulse-wave propagation of the average response of populations of neurons (Jirsa and Haken 1996).

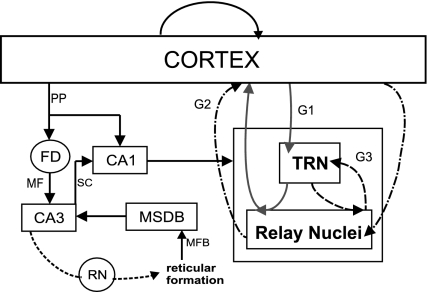
Fig. 2.

Scheme of the Multiscale Corticothalamic Model

Following (Freeman 1991) the response to an auditory stimulus A_n, by assuming that the excitatory neural population is the main source of large-scale brain activity, is given by

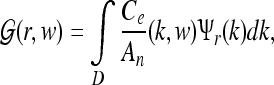14

where 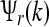is a function that incorporates physical parameters related to the auditory stimulus, D is a two dimensional finite domain (a square of side 578 mm) as an approximation of the unfolded human cortex. The brain large-scale response, in a spatio-temporal coordinate system (r, t), is thus obtained by inverse Fourier transform of the function 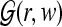. In regard to physiological mechanisms underlying gain modulation we consider the cortico-striato-thalamo-cortical loop (CSTC) (Vollenweider et al. 1999) that is represented in our model by the gains G1 and G2. The basic idea behind the CSTC loop is that the thalamus acts as a filter or gating mechanism whose capacity is controlled by cortico-striato-thalamic (CST) feedback loops, modulated by limbic influences (Carlsson and Carlsson 1990).

Parameter definition

The majority of the parameters used in the underlying algorithms are based on physiological measurements and represent average values of biological system properties. Development process was divided into two modeling steps (1. modeling cortico-thalamic interactions and 2. modeling a hippocampal comparator) and a subsequent experimental stage for the validation of the model predictions.

The neuronal field model for the simulation of late evoked responses is based on a rate of incoming excitatory and inhibitory pulses and the corresponding potential respectively. The free parameters of this model are only three gain functions, representing reenforcing and attenuating effects of cortico-thalamic and intrathalamic projections each. For a detailed description of algorithm-parameters used for modeling see (Trenado et al. 2007, 2009).

The parameters of the algorithms underlying the hippocampal comparator model are based on the experimental results of Vinogradova (2001). Here also the majority of parameters represent physiological average values. The freely adjustable parameters are the phasing of the sensory and of the memory stream as well, representing differences in neural coding for varying physical properties of the perceived stimulus. Also freely adjustable is the strength of coupling of the MSDB driving force and the driven oscillator FD, representing a hebbian memory process.

During the development process no parameter fitting of either model to experimental data was used to archive the presented results.

Results

Using our comparator module we could simulate in general the results of Vinogradova et al. (2001). We can clearly show a significant regression of the duration of the CA1 firing over the number of presented stimuli. The CA1 activity can be seen as the bridge connecting the two different scaled models. On one hand it depicts the regulating output of the comparator module to thalamic area, on the other hand the CA1 activity is the input into the modulated gain G1 of the large-scale cortico-thalamic model. Figure 3 depicts a part of our final results in the simulation: We were able to model physiological firing behaviour of the CA1 in reaction to a number of subsequently presented, uniform stimuli [please compare to physiological data in Vinogradova et al. (2001)]. The duration of the CA1 reaction diminishes with the sequential number of presented stimuli. We emphasize this part of model behaviour due to its importance in connecting two independent mathematical models.

Fig. 3.

Activity of the CA1 neurons in reaction to the 1st (1.row) to 16th (last row) stimulus. The number of subsequent stimuli is indicated on the right. The attenuation of firing behaviour in our simulation [as well as in-vivo (Vinogradova 2001)] is clearly related to the sequential number of presented stimuli. Timebase indicated on right floor is ca. 200 ms; the small arrows indicate the stimulus onset

For further processing the G1 gain of our forward model of cortico-thalamic interactions is modulated by the number of stimuli presented. The results of our simulations resemble remarkably the experimental findings related to the synchronization stability of late AEPs. Figures 4 and 5 show a contour-plot of a single-sweep matrix comparing habituated and the non-habituated stimuli on the level of late auditory evoked potentials. Every singe-sweep response is displayed as horizontal, greyscale-coded line, with dark colours representing low amplitudes, and light colours depicting high amplitudes respectively. Y-axis represents the number of subsequent stimulus presentations (thus the duration of the experiment), while X-axis depicts the temporal characteristics of the stimulus–response. The notations N1 and P2 indicate the envelope of the N1 and P2 component respectively of the evoked responses.

Fig. 4.

A stimulation with high intensity stimuli prevents the habituation to the stimulus. Depicted is a normalized contour-plot of a low-pass filtered (gaussian blur), greyscale-coded single-sweep matrix of late auditory evoked potentials. Subsequent single-sweeps are displayed from top to bottom as horizontal lines. Notations N1 and P2 indicate the envelope of the N1 and P2 component respectively of the evoked responses

Fig. 5.

Low intensity stimulation leads to a habituation to the stimulus. Depicted is a normalized contour–plot of a low–pass filtered (gaussian blur), greyscale-coded single-sweep matrix of late auditory evoked potentials. Subsequent single-sweeps are displayed from top to bottom as horizontal lines. Notations N1 and P2 indicate the envelope of the N1 and P2 component respectively of the evoked responses

Increased activity of the CA1 module, due to simulated stimulus novelty, leads to a higher synchronization stability in the artificial evoked responses, as well as a decrease in CA1 activity leads to a desynchronization. Our experimental findings confirm a significant loss in synchronization stability of the N1–P2 component of late AEPs in the case of habituation towards a familiar stimulus (Mai et al. 2009). Figures 6, 7 and 8 depict a comparison of our experimental results of the time-scale coherence of late AEPs and the results of our simulations.

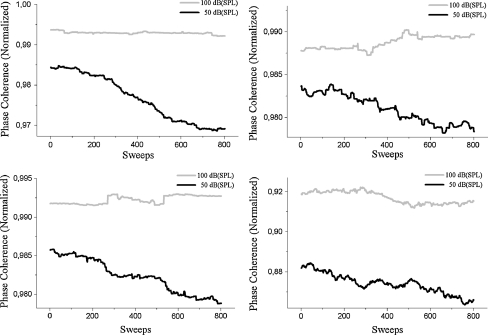
Fig. 6.

Figures show exemplary the results of the habituation experiments for four different subjects. The light grey curve depicts the normalized phase coherence over 800 stimuli for a stimulation level of 100 dB (SPL) (as described in Data analysis), the black curve indicates the same for a stimulation level of 50 dB (SPL)

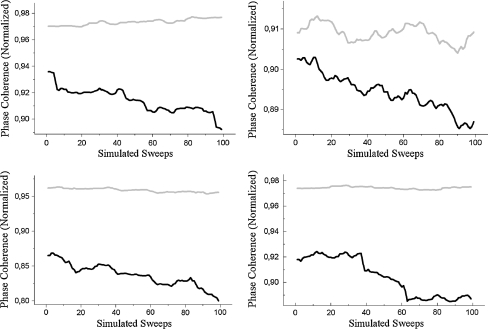
Fig. 7.

Figures show exemplary the results of four different simulations. The light grey curve depicts the normalized phase coherence over 100 erp—simulations (as described in Data analysis) for an unpleasant stimulation level, the black curve indicates normalized phase coherence for a comfortable stimulation level. Time scales are not adapted to the experimental paradigm yet

Fig. 8.

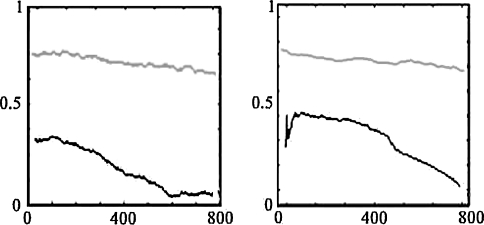
Comparison of experimental data (left) and the in-silico results (right). Both pictures show the evolution of time-scale coherence (normalized scale) over the number of stimuli presented (as described in Data analysis). The black line in both pictures depicts the loss of attention due to stimulus familiarity. The grey line depicts the binding of attentional resources on an unpleasant stimulus. We comment this behavior in the following Discussion section and in (Mai et al. 2009)

Discussion

We were able to simulate experimental data on attention and habituation using our model based on the hypothesis of hippocampus working as a comparator and Vinogradovas theta-regulated attention theory. The effects of attention and habituation on the N1–P2 components of late AEPs were reproduced. Besides the Vinogradova model there exits a different model of CA1 working as a comparator by Lisman and Grace (Lee et al. 2005a). In this hypothesis the CA3 area predicts future events on the base of associative memory, while the CA1 is the factual comparator of incoming sensory information and predicted environmental changes. Lisman and Grace state, that the locus of novelty detection in the hippocampus is not known with certainty. Latest results however suggest that the CA3 area of the hippocampus is the factual comparator. Lee et al. and Hasselmo confirmed a potential role of the CA3 in novelty detection in 2005 (Lee et al. 2005b; Hasselmo 2005). Crick stated 1984 a high importance of the thalamic reticular nucleus (TRN) for the attentional spotlight (Crick 1984). Latest publications support this hypothesis. Animal models report from impairments in the attentional orienting after TRN lesions (Weese et al. 1999) and the result of c-fos stains suggest a critical role of the TRN in attentional gating. Our results also support this hypothesis in-silico. Facing the problems of hippocampal models in comparison to experimental and behavioural data our model—in expanse—can provide satisfying results. Along with the habituation there come a number of related claims and tasks like stimulus specificity, dishabituation or simply the inability to habituate towards annoying stimuli (Kryukov 2008). In all cases we assume a shift in at least the coding phase of either the sensory stream or of the memory trace. Dishabituation occurs with changes in the signal parameters, thus in a change in the exogenous weight or spatial location, or an electrical stimulation of the reticular formation. This can be considered as a break of the original stream grouping into an entirely new stream. In our model the continous signal stream is also interrupted and the encoding of a new stream results in a new signal phase and possibly new frequency and phase coding in the MSDB subunit. The specificity, i.e. the persistence of certain stimulus responses in the core system can be explained by a classical hebbian approach.

Most interesting is the question why sometimes an inability to habituate towards certain stimuli occurs. A number of publications demonstrated the influence of the central amygdala on the dentate gyrus (Ikegaya et al. 1996; Sheth et al. 2007). An unpleasant stimulus thus might, by a co-activation of accompanying brain areas like the amygdala, prevent the habituation by a modification of the FD firing pattern. Similar to this case we hypothesize the possibility of voluntary attending insignificant stimuli. Planing areas are likely to influence also the coded pattern in the FD as well.

We did not model the appearance of concurrent auditory streams, so the feedback of the CA3 to the reticular formation (FR) via the Raphe nuclei (RN) is not included in the model yet. For further modeling purposes we consider the FR responsible for the selection of the attended stream by means of a probabilistic stream selection model presented in Trenado et al. (2007). Thus the release from tonic inhibition during the reaction to novelty can be considered as method to stabilize the attended stream against concurrent stimuli (Vinogradova et al. 2001).

Conclusion

Combining two independently developed neurofunctional models we were able to reproduce experimental results on attentional guidance due to stimulus novelty. We consider this approach as a promising method to gain deeper insights in the mechanisms underlying attentional habituation and the guidance of attention driven by stimulus novelty. Our experimental results as well as the in-silico reproduction of these results might lead to a better understanding of the effect of small neuronal groups on measurable large-scale effects, like for example the electroencephalogram.

We neglected the detailed simulation of the mechanisms involved in the formation of associative memory traces, but focussed entirely on the guidance of attention by a hippocampal comparator mechanism. As stated in the work of Manahan–Vaughan and Bikbaev (2007) a potentiation in both, STP and LTP, is associated with a transient facilitation of theta and gamma oscillations in the dentate gyrus. The subsequent steps in expanding our comparator-model will incorporate the detailed simulation of facilitation processes due to the increasing familiarity-level of repetitively presented stimuli.