Skip to main content
PMC home page
Springer logoLink to Springer
. 2010 Dec 14;40(3):317–327. doi: 10.1007/s00249-010-0649-0

The influence of topographic microstructures on the initial adhesion of L929 fibroblasts studied by single-cell force spectroscopy

Patrick Elter 1,✉, Thomas Weihe 2, Regina Lange 1, Jan Gimsa 2, Ulrich Beck 1
PMCID: PMC3045512  PMID: 21153809

Abstract

Single-cell force spectroscopy was used to investigate the initial adhesion of L929 fibroblasts onto periodically grooved titanium microstructures (height ~6 μm, groove width 20 μm). The position-dependent local adhesion strength of the cells was correlated with their rheological behavior. Spherical cells exhibited a significantly lower Young’s modulus (<1 kPa) than that reported for spread cells, and their elastic properties can roughly be explained by the Hertz model for an elastic sphere. While in contact with the planar regions of the substrate, the cells started to adapt their shape through slight ventral flattening. The process was found to be independent of the applied contact force for values between 100 and 1,000 pN. The degree of flattening correlated with the adhesion strength during the first 60 s. Adhesion strength can be described by fast exponential kinetics as 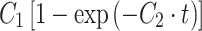Inline graphic with C 1 = 2.34 ± 0.19 nN and C 2 = 0.09 ± 0.02 s−1. A significant drop in the adhesion strength of up to 50% was found near the groove edges. The effect can be interpreted by the geometric decrease of the contact area, which indicates the inability of the fibroblasts to adapt to the shape of the substrate. Our results explain the role of the substrate’s topography in contact guidance and suggest that rheological cell properties must be considered in cell adhesion modeling.

Electronic supplementary material

The online version of this article (doi:10.1007/s00249-010-0649-0) contains supplementary material, which is available to authorized users.

Keywords: Cell adhesion, Cell elasticity, Atomic force microscopy, Hertz model

Introduction

A major task in biomaterials research is functionalization of implant surfaces to adjust their biocompatibility for specific applications. Besides numerous chemical modifications, topographic variations are frequently employed, which leads to a correlation between surface structures and the biosystem (Breme et al. 2007; Lange et al. 2007). As a prominent example, artificial hip joints and dental implants are frequently provided with stochastic surface roughness to improve osseointegration (Boyan et al. 2001). Beyond stochastic roughness modifications, well-defined microstructures can induce contact guidance and result in directed cell migration and alignment of cells along the topography (Weiss 1958; Brunette 1986; Clark et al. 1987, 1990; Lange et al. 2010). Based on this discovery, surface designs with regular microstructures such as specially contoured grooves have been proposed for a number of clinical applications, e.g., for dental implants to prevent epithelial downgrowth (Rompen and Domken 2006). However, the relationship between the surface properties and the reaction of a biological system is very complex, and modifications are still based mainly on trial and error. Therefore, a more detailed understanding of the mechanism of how biological cells interact with surface topography is in great demand.

One of the first events observed when a foreign material comes into contact with a living body is adsorption of molecules of the extracellular matrix (ECM), which forms a complex meshwork of proteoglycans, collagens, and other glycoproteins such as fibronectin and laminins (Bosman and Stamenkovic 2003). Besides unspecific interactions, the subsequent cell adhesion is mediated by specific (so-called lock-and-key) interactions between receptors of the cell and molecules of the ECM, and adhesion involves a number of cell adhesion molecules (CAMs) such as cadherins, selectins, and α/β-heterodimeric integrins (Schwartz and Ginsberg 2002; Hynes 1992; Kemmler 1992). With time, the latter often form highly organized structures such as fibrillar adhesions, focal complexes, and focal adhesions (Geiger et al. 2001). The formation of specific bonds is frequently described by a steady-state approach with an equilibrium determined by balancing the forward and reverse reactions (Bell 1978, 1981; Zhu 2000; Evans and Ritchie 1997; Dembo et al. 1988). A simple formulation for the average number of active bonds can be derived from Poisson statistics if the number of bonds is much smaller than the number of receptors and corresponding ligands. The expression can be written as (Chesla et al. 1998)

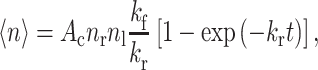graphic file with name M2.gif 1

where ‹n› is the average number of active bonds, A c is the contact area, n r and n l are the surface densities of receptors and ligands, and k f and k r are the rate constants for the forward and reverse reactions, respectively. More detailed descriptions also take the rheological properties of the cell into account, which can substantially influence cell adhesion by determining the capability of the cell to adapt its contact area to the substrate; for example, a computational multiscale approach was introduced by combining the steady-state models of CAMs with the elastic and geometric properties of the cell (N’Dri et al. 2003). However, the description of the initial cell adhesion on topographically microstructured substrates is more complex, and more details have to be considered; for instance, the contact area will depend on the topography, the cell size, and the exact location of the cell. Moreover, geometric and electrostatic effects near the edges of a topographic structure have been shown to locally affect the adsorption of ECM molecules and result in a location-dependent ligand density (Roach et al. 2006; Galli et al. 2002; Elter et al. 2010; Chen et al. 2007; Song and Chen 2007). Consequently, a detailed understanding of the influence of topography on biological cells must deal with the important question of whether the cells are primarily influenced by selective adhesion or by mechanical/rheological limitations. To elucidate this, an individual examination of the cells in their local environment is useful, and the results for cells with different sizes or positions would ideally not be mixed in surface-integral parameters.

In this study, the co-action of contact area adaptation and specific bond formation has been investigated during the initial adhesion of L929 fibroblasts on titanium microstructures. A suitable method to observe both parameters simultaneously is atomic force microscopy (AFM)-based single-cell force spectroscopy (SCFS). In a SCFS experiment, a living cell is attached to a functionalized AFM cantilever and brought into contact with a substrate (Benoit et al. 2000; Zhang et al. 2002; Benoit and Gaub 2002; Taubenberger et al. 2007; Helenius et al. 2008). After a defined contact time, the cell is retracted from the surface and the adhesion forces are derived from the vertical cantilever deflection. Employing the lateral displacement capabilities of the AFM, the local adhesion of a single cell can be compared at different positions on the substrate. L929 mouse fibroblasts are widely used for biocompatibility tests and well known for their reproducible growth rates and biological responses (ISO 1992; ISO 1997). A number of papers have shown that fibroblasts are strongly influenced by contact guidance on grooved microstructures with dimensions of micrometers in height and tens of micrometers in width (Scheideler et al. 2003; Brunette 1986). Hence, this combination represents an interesting model system for detailed analysis by SCFS. Here we have used SCFS to map the initial cell adhesion on a grooved titanium microstructure and to correlate the results with the formation of specific bonds and the rheological properties of the cell.

Materials and methods

Substrate preparation and characterization

Silicon wafer pieces (1 × 1 cm2) with thickness of 500 μm were microstructured using deep reactive-ion etching (Center for Microtechnologies ZFM, Chemnitz, Germany). A periodically grooved topography (Fig. 1a) with plateau and groove width of 20 μm and step height of ~6 μm was fabricated on the chip and sputter-coated with 50 nm titanium to provide a uniform, biocompatible (Bogner et al. 2006) surface chemistry. The dimensions of the topography were selected such that the cells and the surface structures were of similar size and were in the range where contact guidance has been observed in a number of other studies (Scheideler et al. 2003; Brunette 1986). Moreover, the length of a full topographical period perpendicular to the grooves did not exceed the lateral scanning limits of the AFM (100 × 100 μm2), and only the cell (and not the cantilever) came into contact with the substrate. Each sample had a small planar area in one corner for reference measurements. Overview images of the samples were made using field-emission scanning electron microscopy (Supra 25; Zeiss, Germany), and cross-sectional profiles were recorded by AFM (see below) in intermittent contact mode using NCH cantilevers (doped silicon, 42 N/m spring constant; NanoWorld, Neuchâtel, Switzerland).

Fig. 1.

Fig. 1

Open in a new tab

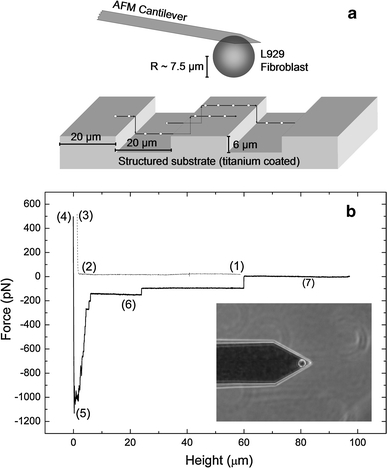
Illustration of the experiment. a Schematic setup: the adhesion strength is mapped for different positions perpendicular to the grooves on the microstructure. b Force–distance curve of an L929 fibroblast on a planar titanium substrate (10 s contact time, 500 pN contact force, 5 μm/s retraction speed). Sections (1)–(3) correspond to the approach of the cell to the substrate, while sections (4)–(7) correspond to the retraction. (1) Baseline of the free cell, (2) contact point, (3) height at the contact force, (4) reduced height after the contact period, (5) maximal adhesion strength, (6) rupture events of receptors/tethers, (7) baseline of the free cell. Inset phase-contrast image of an L929 fibroblast attached to a tipless Arrow TL-1 cantilever

Cell culture

Murine L929 fibroblasts (cat. no. CCL-1; ATCC, Rockville, MD, USA) were grown in Dulbecco’s modified Eagle’s medium (DMEM; Biochrom, Berlin, Germany) supplemented with 10% horse serum (Biochrom), l-glutamine, 100 IU/ml penicillin, and 100 μg/ml streptomycin (Biochrom) in a humidified 5% CO2 atmosphere at 37°C and were passaged every third day. Before the SCFS experiments, cells were transferred to serum-free, CO2-independent medium [DMEM containing 20 mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES)] and were detached after a period of 60 min by incubation with Accutase (PAA, Pasching, Germany). SCFS measurements were performed at 37°C in serum-free CO2-independent medium after dilution of the cells to a low concentration of ~100 cells/ml.

SCFS experiments

SCFS experiments were carried out using a Nanowizard II AFM (JPK Instruments, Berlin, Germany) mounted on top of an Axiovert 200 inverted microscope (Zeiss, Jena, Germany). The device is equipped with a special SCFS stage (CellHesion, JPK Instruments) to provide an extended z-range of 100 μm and a mini-incubator for measurements at 37°C in a closed volume (PetriDishHeater, JPK Instruments; TPP 93040 Petri dishes). The structured substrate chips were sonicated in acetone, isopropyl alcohol, 70% ethanol, and distilled water and immersed overnight in serum-containing cell medium (see above) to produce an adsorbed ECM on the surface (Kothari et al. 1995; Kurrat et al. 1998), which is comparable to common in vitro cell cultivation experiments in serum-containing medium. At the beginning of the SCFS experiments, the chips were transferred to the cell chamber while taking care that the surface of the chip always remained wet. A fresh tipless AFM cantilever (Arrow-TL1, doped silicon, 0.03 N/m spring constant; NanoWorld, Neuchâtel, Switzerland) was cleaned in 70% ethanol and distilled water and functionalized with 25 μg/ml bovine fibronectin (Sigma–Aldrich, Munich, Germany) in phosphate buffered saline (PBS: 137 mM NaCl, 2.7 mM KCl, 10 mM Na2HPO4, and 1.76 mM KH2PO4; pH 7.4) for 25 min. To convert the vertical deflection of the cantilever into units of force, the sensitivity of the optical lever and the spring constant were calibrated in situ. The optical lever was determined by fitting the slope of a force–distance curve obtained on the bottom of the Petri dish, and the spring constant was calibrated using the thermal noise method (Hutter and Bechhoefer 1993). Due to the lower noise, the second resonance peak was used with a correction factor of 0.251 (Butt and Jaschke 1995). All spring constants were found to be within the manufacturer’s specifications. The cell was captured by pressing the cantilever at constant force of 500 pN onto a round, suspended fibroblast. After 5 s, the cantilever with the attached cell was lifted from the surface, followed by a waiting period of 30 min to ensure firm adhesion. In all of the experiments in this study, the cell was approached and retracted at constant speed of 5 μm/s using the maximal pulling range (100 μm), and the system was operated in constant force mode during the contact with the substrate. Cantilever drift was compensated automatically by adjustment of the baseline in the force–distance curve before each scan, which ensured a constant contact force even after a large number of scans. After each SCFS scan, a recovery time of 60 s was allowed, and each location on the substrate was measured only once to prevent the local ECM from being altered by a previous adhesion process. The radius of each spherical fibroblast was obtained from the optical microscopy image.

Interpreting the results of SCFS experiments

A SCFS cycle consisted of three sections, which were repeated periodically: the approach of the cell to the substrate, the contact with the substrate for a defined time, and the retraction of the cell while a characteristic adhesion signature was measured. An example of the resulting force–distance curve is illustrated in Fig. 1b. Region (1) corresponds to the approach of the cell, which came into contact with the substrate at the contact point (2). Beyond this point, a further reduction of the substrate–tip distance caused an increase in the measured force, which was determined by the elastic compression of the cell and the bending of the cantilever. When a user-defined contact force (3) of a few hundred piconewtons was reached, the system remained in closed-loop mode for a preselected contact time, in either the constant force or the constant height mode. Subsequently, the cantilever with the cell was retracted, which resulted in an inversion of the force acting on the cell (4)–(5). An important parameter is the maximal strength of the cell–substrate binding, which is given by the minimum of the force–distance curve (5). With increasing distance, the detachment of individual cell receptors and tethers became visible by a step signature in the force–distance curve (5)–(7). In contrast to single-molecule force spectroscopy, a variety of receptors may be simultaneously involved in adhesion, and the related forces may result from different mechanisms; for example, rupture events with sawtooth shape at low distances are frequently assigned to mechanically stressed and ruptured receptors, which are anchored to the cell cortex. In contrast, rupture events preceded by a long plateau (up to 100 μm) are believed to originate from purely membrane-bound receptors at the tip of a nanotube, which is pulled out of the cell membrane (see Müller et al. 2009 for more detailed information about SCFS signatures). After a recovery time, the sequence (1)-(7) was repeated.

Rheological properties

The rheological cell properties were studied in detail using a single spherical fibroblast and were compared with the elastic behavior resulting from many cells. The vertical compression (distance between the contact point and the z-height at the desired contact force), the height decrease during contact (viscoelastic relaxation and beginning of cell spreading), and the associated adhesion strength of a round L929 fibroblast were observed for different contact forces in the planar region of the substrate. A total number of 40 SCFS scans (10 scans each at 100, 300, 500, and 1,000 pN) were made with a constant contact time of 20 s using a single cell. The contact point was determined manually by visually analyzing each force–distance curve (instead of extracting it from the indentation slope) to obtain model-independent values for the vertical compression. The vertical compression was corrected for cantilever bending (Lin et al. 2007) and compared with the Hertz model for an elastic sphere (Hertz 1881). Once the data matched the model, the Young’s modulus was calculated by assuming a Poisson ratio of 0.5 (Wu et al. 1998) and equal compressions of the cell on the cantilever and substrate sides. Inversely, the contact force was left constant at 500 pN and the contact time was varied over a total number of 70 SCFS scans (10 scans each at 1, 2, 5, 10, 20, 30, and 60 s) using a single cell. The distribution of the Young’s moduli for L929 fibroblasts was determined by fitting the approach/extension curves of 497 scans from 24 cells. The distribution of the cell radii was determined from 80 spherical cells using optical light microscopy. After each series of SCFS cycles, the spreading state of the cantilever-attached fibroblasts was analyzed using optical light microscopy [Fig. S1 in the Electronic Supplementary Material (ESM)], and the data were only used if the cells were still in the round state and no changes in cell shape were detected.

Influence of topography

The initial cell adhesion was investigated at different positions on the grooved titanium surface. At the beginning of the experiments, the scanning angle was adjusted to the orientation of the substrate. The cantilever was moved above the edge of the chip using the outline function of the AFM software, and the scanning angle was adjusted in 1° steps until the edge and movement were congruent. Because the grooves of the surface structure were aligned perpendicularly to the edge of the substrate, the measuring points could be oriented perpendicular to the topographic structure. A low contact force of only 250 pN and a moderate contact time of 10 s were used to ensure that the cell was not damaged by the edges of the microstructure and remained viable even after a high number of SCFS cycles. At different locations on the substrate (Fig. 1a), 10 perpendicular lines of points were measured with 32 equally spaced positions per line over a line length of 50 μm. The exact position of each data point was determined by analyzing the measured topography for each line. The positions were chosen based on the z-positions at the end of the approach curve where the contact force was reached and represent the convolution of the surface structure with the shape of the cell. The maximal adhesion strength, the number of unbinding events (i.e., the number of rupture steps in the force–distance curve), and the step height distribution of the individual rupture events were evaluated using the JPK data processing software. The adhesion strength and the associated (zeroth-order leveled) height of each line were arranged into 25 different bins depending on their topographical location perpendicular to the grooved microstructure. Each bin had a width of 1.56 μm (50 μm divided by 32 points), which corresponds to the distance between the measured points. Hence, a full period was analyzed. The measured line length (50 μm) was slightly longer than a full topographic period (40 μm), which allowed more detailed supervision of the cell during the measurements; for example, possible alterations in cell shape (e.g., cell spreading) or position (e.g., cell migration on the cantilever) on the cantilever could be detected simply from the changes in the measured height profile. Data were only used if none of these confounding effects were observed during the measurement time. Moreover, the cell was monitored after the experiments by using optical light microscopy. The cells always detached from the substrate and not from the cantilever, showing firm adhesion at the same spot on the cantilever after the experiments. Time-dependent alterations in the adhesion behavior of the fibroblasts were detected by comparing the average adhesion strengths of the plateau points for different scan lines. The fibroblasts usually exhibited a slight decrease in their average adhesion strength during the first few SCFS cycles, followed by a constant adhesion behavior for the remaining measurement time (see Fig. S2 in the ESM for a detailed discussion). It was assumed that this effect was due to the formation of a balance between worn and regenerated receptors of the cell and did not provide relevant position-dependent contributions to the results.

Simple geometric considerations

As an aid to interpreting the results, the substrate topography of a scan with a hard sphere with the same radius as the cell was calculated using a simple numerical algorithm. The sphere was triangulated with 1002 surface elements, and the contact point was calculated for each lateral position by shifting the sphere towards the substrate until one of the elements overlapped with part of the microstructured surface (see Fig. S6 in the ESM for a graphical representation). Moreover, the local contact area between a flattened sphere and the grooved microstructure was estimated. The substrate was discretized using cubic finite elements with edge length of 0.05 μm. The areas of the boundary elements that overlapped with the sphere after an additional vertical shift beyond the contact point were summed (see Fig. S7 in the ESM for a graphical representation). In this estimation, infinite stiffness of the substrate was assumed, and the lateral contraction of the cell was neglected. The value for the additional vertical shift was obtained from the measured compression of the cell.

Results and discussion

Substrate characterization

Figure 2 shows scanning electron micrographs of the microstructured substrate and the profile measured by AFM. The titanium-coated structure exhibits a well-defined periodic geometry consisting of parallel grooves with ditch and plateau width of 20.2 ± 0.3 μm and step height of 6.3 ± 0.4 μm. A stochastic nanoroughness R a of 25.2 ± 4.2 nm (10 × 10 μm2 scan area, planar region) was superimposed on the regular microstructure due to the titanium coating process and slight irregularities from the dry etching procedure. The influence of the nanoroughness on cell adhesion was assumed to be constant and position independent in this study.

Fig. 2.

Fig. 2

Open in a new tab

Characterization of the substrate structure. a SEM image at 100× magnification (100 μm scale bar). b SEM image at 1,000× magnification (10 μm scale bar). c Profile scanned with AFM (filled squares trace, open circles retrace)

Rheological properties

In the initial experiments, the rheological behavior of the fibroblasts was characterized in the planar regions of the titanium-coated substrate using SCFS. To this end, the vertical compression (the distance between the contact point and the measured height at the desired contact force in the approach curve corrected for cantilever deflection) was analyzed for different contact forces. Figure 3a presents the results for a round, cantilever-attached fibroblast with radius of 9.2 μm. The data point at 0 N was obtained by assuming that zero force will result in zero compression. With increasing contact force, the vertical compression shows a nonlinear increase, which can be explained by the Hertz model (Hertz 1881) prediction of a 2/3-power behavior for the elastic compression of a sphere between two planes. The relationship between the compression α of a hemisphere and the contact force F is given by

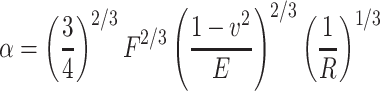graphic file with name M3.gif 2

where R is the radius of the cell, E is its Young’s modulus, and v is the Poisson ratio. We must note that the Hertz model is related to elastic materials, whereas cells are viscoelastic. The agreement of the data with the 2/3-power behavior of the Hertz model indicates that the initial compression phase of an SCFS cycle is primarily governed by elastic effects. This finding is understandable considering the high compression rate of 5 μm/s. Clearly, the resulting compression time was too short for significant viscoelastic relaxation of the cell. Neglecting the viscoelastic relaxation during compression and assuming both a Poisson ratio of 0.5 (Wu et al. 1998) and equal compression of the cellular hemispheres on the cantilever and substrate sides, the Young’s modulus can be estimated by an error-weighted linear regression of α 3/2 versus F. The resulting value of 267 ± 89 Pa is significantly lower than the data obtained for the center of spread fibroblasts (Wu et al. 1998) but is consistent with other reports on round cells (Bacabac et al. 2008; Rosenbluth et al. 2006; Guilak et al. 1999); for example, an elastic constant between 200 and 263 Pa was found for partially adherent round MLO-Y4 osteocytes, which increased to 4.3 kPa during the spreading process (Bacabac et al. 2008). The distribution of the Young’s moduli and the cell radii for multiple cells is displayed in Figs. 3b and c, respectively. Almost all of the round cells were found to have Young’s modulus below 1 kPa. Nevertheless, their elastic properties and radii differed considerably from cell to cell.

Fig. 3.

Fig. 3

Open in a new tab

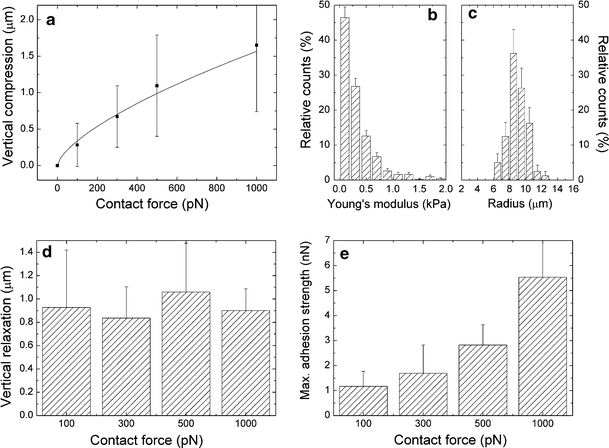
Rheological properties of L929 fibroblasts on a titanium substrate. a Vertical compression [mean ± standard deviation (SD)] for a round L929 fibroblast with radius of 9.2 μm. The line indicates the vertical compression according to the Hertz model for an elastic sphere (Eq. 2 with E = 267 Pa, v = 0.5, and R = 9.2 μm). b Distribution of the Young’s moduli (rel. counts ± Poisson error) for 24 cantilever-attached cells. c Distribution of the cell radii for 80 cells (rel. counts ± Poisson error). d Height decrease of the cell (mean ± SD, cell radius 9.2 μm) during the contact period for different contact forces. e Maximal adhesion strength (mean ± SD) for different contact forces. The results in (a), (d), and (e) originate from the same cell

Cell elasticity and cell dimensions will influence the contact area and hence the number of receptors participating in adhesion to the substrate. According to the Hertz model, the contact area between a round elastic cell and a planar substrate is proportional to the cell’s vertical compression (Puttock and Thwaite 1969). However, in our SCFS experiments we usually observed a further reduction of the tip–substrate distance during the subsequent contact period at constant force. Besides very slight contributions of cantilever drift (for silicon cantilevers), this height decrease must be ascribed to flattening of the cell by viscoelastic relaxation and an initial cell spreading phase. Cell flattening leads to a further time-dependent increase of the contact area (see Figs. S3 and S4 in the ESM for a correlation with light microscopy images). Figure 3d shows the height decrease of an L929 fibroblast during a constant contact period of 20 s for different contact forces (i.e., alterations in cell height subsequent to the initial compression phase). No significant differences were found for forces up to 1,000 pN. Hence, the height decrease appears to be independent of the contact force for the measured interval and outweighs the previous (force-dependent) compression for low contact forces. The maximal adhesion strength (Fig. 3e, 20 s contact time) rose significantly with increasing contact force. Because cell flattening during the contact period was independent of the force, this effect was obviously caused by the larger contact area that was induced in the initial compression stage.

In a different set of experiments, the contact force was left constant (500 pN) and the contact time was varied between 1 and 60 s. In these experiments, the initial vertical compression was constant, and the total height decreased with increasing contact time. In Fig. 4a, the adhesion strength (left scale) of an L929 fibroblast is compared with the height decrease (right scale) for different contact times. The adhesion strength displays a nonlinear increase and can be described during the first 60 s by an exponential convergence as 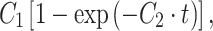Inline graphic where t is the time, C 1 is a fit parameter defining the plateau height (2.34 ± 0.19 nN), and C 2 is a time constant that determines the slope of the curve (0.09 ± 0.02 s−1). Interestingly, the total height decrease of the cell exhibits almost the same characteristics (except for a constant offset) and correlates linearly with the adhesion strength (Fig. 4b, R 2 = 0.94). A height decrease during the contact period results from a change in cell shape (see also Fig. S4 in the ESM). Consequently, the adaptation of the cell shape and the development of bonds are correlated during the first 60 s. However, note that cell adhesion forces frequently grow in a sigmoidal pattern and will increase further with contact times significantly longer than 60 s.

Fig. 4.

Fig. 4

Open in a new tab

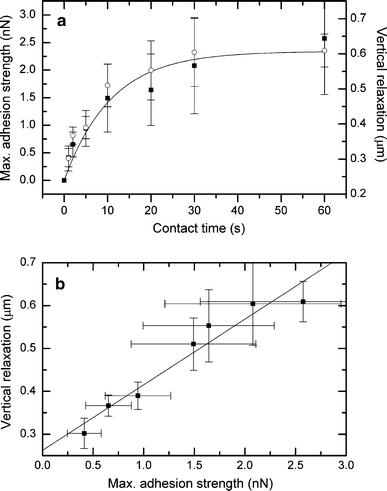
a Kinetics of initial cell adhesion of an L929 fibroblast on a planar titanium substrate (contact force 500 pN, 5 μm/s retraction speed, cell radius 7 μm). Filled squares represent the maximal adhesion strength (left ordinate, mean ± SD), and open circles denote the height decrease of the cell during the contact period (right ordinate, mean ± SD). b Correlation between the average height decrease and the average adhesion strength (mean ± SD)

Influence of topography

The influence of the topography on the initial fibroblast adhesion parameters was studied by comparing the SCFS results at different positions on the microstructured titanium surface. Figure 5 shows the schematic profile of the substrate (a), the measured topography (b), the measured adhesion strength (c), and the calculated contact area (d) at different positions perpendicular to the groove. The presented data were obtained from a spherical cell with radius of 7.5 μm using a low contact force of only 250 pN and a 10 s contact time (see “Materials and methods” for details). The topography (Fig. 5b) resulting from the measured height at the contact force of 250 pN is determined by the convolution of the microstructure with the shape of the cell. Accordingly, the groove in the center of the graph and the plateau appear narrowed and broadened, respectively, depending on the size of the cell. The solid line illustrates the calculated profile for a hard sphere with the same radius as the cell. The comparison between the calculated and the measured profiles suggests that the cell remains spheroidal despite the applied contact force. The cell exhibited only slight shape deviations near the groove flanks, where the contact area is small; hence, the local pressure was increased.

Fig. 5.

Fig. 5

Open in a new tab

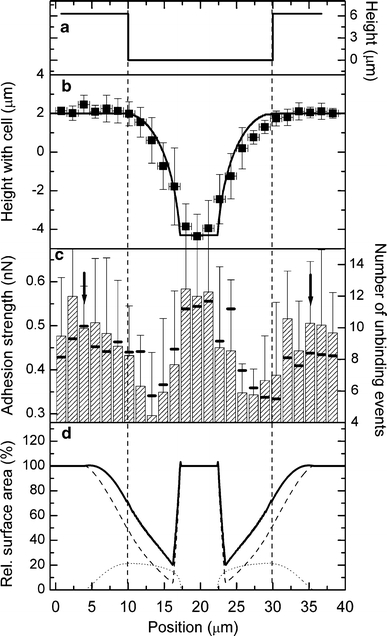
Influence of topography on initial cell adhesion. a Schematic profile of the grooved substrate. b Measured profile (mean ± SD) with a cell attached to the cantilever. The solid line represents a computer simulation for the profile of a hard sphere. c The hatched bars show the local cell adhesion (mean ± SD) of an L929 fibroblast with radius of 7.5 μm. The small black bars represent the average number of unbinding events in the force–distance curves. The contact time was 10 s, the contact force was 250 pN, and the retraction speed was 5 μm/s. The vertical arrows denote the position where parts of the contact area came into contact with the edge of the plateau. d Estimated contact area of the cell (radius 7.5 μm) from computer simulations for a vertically flattened sphere. The solid line represents the total contact area, and the dashed line is the horizontal part and the dotted line is the vertical part of the contact area

The adhesion strength (Fig. 5c, hatched bars) shows no differences between the planar regions of the plateau and the valley, but it significantly decreases near the groove flanks of the substrate (P < 0.05 for unpaired t test, normal distribution confirmed by Shapiro–Wilk test). A drop of the adhesion strength occurred according to the uncertainty of the measurements at these positions, where the computer simulations predicted a small contact area for a vertically flattened sphere (Fig. 5d, solid line). The position-dependent contact area decreases near the flanks of the groove after crossing the edge of the plateau until the cell comes into contact with the base of the groove. The agreement of the predicted positions with the decrease in the measured data indicates that the results can be interpreted by geometric/elastic effects in which the cell is less able to adapt its shape to the edge of the plateau. To establish equal contact areas at these positions, the cell deformation must be increased. Because cell deformation was found to be a time-dependent process, the contact area that develops after the same time is smaller and leads to a smaller total adhesion strength. The black bars in Fig. 5c denote the average number of unbinding events (sawtooth shape and tethers) in the force–distance curves, which also decreases near the flanks. The results point out that the reduced contact area is directly related to a decrease in the number of unbinding events. Nevertheless, the computer simulations predicted a decrease of the contact area by ~79%, whereas an adhesion drop of only ~50% was observed. This difference can be explained by the increased local pressure near the flanks (see above), which leads to higher compression and counteracts the observed decrease of the adhesion strength.

Geometric and electrostatic effects near the edges of a topographic structure may locally affect the adsorption of proteins and result in a location-dependent ligand density (Elter et al. 2010). Therefore, altered protein adsorption properties would have affected the adhesion strength only when parts of the cell came into contact with the edges, which should already be the case for the outer regions in Fig. 5c (vertical arrows). However, in these regions neither significant positive nor negative influences on cell adhesion were found.

Flattening of the cell near the edge will allow the establishment of a contact area with the side-walls of the groove (Fig. 5d, dotted line). The breaking of specific bonds in the horizontal or vertical directions may provide different contributions to the total adhesion. Therefore, the individual force–distance curves were analyzed for possible contributions from the side-walls. Figure 6 shows the force–distance curves for a position on top of a plateau with maximal horizontal contact area and for a position near the groove flanks with maximal vertical contact area. Both curves exhibit an initial peak in the retraction curve, which obviously resulted from nonspecific interactions between the cell and the substrate, as well as a rupture of the specific bonds connected to the horizontal contact area. However, a subsequent plateau with sawtooth shape was frequently observed, which was significantly extended for the positions with the maximal vertical contact area and exhibited a length which roughly corresponds to the groove depth (Fig. 6b). The results can be interpreted in two ways. First, the cell was still in contact with the side-walls for the first 1.2 s of the retraction period (5 μm/s retraction speed and 6 μm groove depth). Hence, new bonds could be formed during retraction, leading to the sawtooth shape of the curve, which was determined by additional increases of the cell–substrate interaction and the subsequent breakage of the bonds. Second, cell membranes are frequently considered to be a continuous fluid in which membrane proteins are free to move by diffusion (Zagyansky and Edidin 1976; Swaisgood and Schindler 1989; Hirata et al. 2005; Singer and Nicolson 1972) as long as no focal contacts are formed (Duband et al. 1988). When the cell was retracted in the vertical direction, the bonds to the horizontal plateaus of the substrate would be loaded almost simultaneously, whereas the receptors attached to the side-walls would be exposed to a smaller force because the lipids of the cell membrane might be able to slide around them. Hence, their full contribution to the measured adhesion strength was observed only when the respective receptors reached the leading edge of the cell: each time a receptor reached the leading edge, the cell–substrate interaction increased, followed by the subsequent rupture of the bond; this process results in the observed sawtooth structure. Figure 6c displays the local adhesion energy (area under the force–distance curve) for different positions on the grooved microstructure. The data originate from the same cell used in Fig. 5. In contrast to the maximal adhesion force, the adhesion energy is also sensitive to the tip–sample separation distance of the individual unbinding events. For positions near the groove flanks (Figure 6c, arrows) the adhesion energy decreases less than the adhesion force (Fig. 5c), which leads to a significantly broadened peak in the center of the diagram. The smaller decrease of the adhesion energy indicates a shift of some of the unbinding events to greater distances for these positions. The results support our interpretation that some unbinding events occur at greater tip–sample separations due to the contact with the side-walls and do not contribute with their full magnitude to the maximal adhesion force. Nevertheless, a missing contribution of the side-walls to the measured maximal adhesion strength cannot be the only reason for its decrease near the flanks, because the total number of unbinding events decreased near the flanks (Fig. 5c, black bars) and the contact area to the side-walls is too small to explain the full effect (only ~20% vertical contact area versus ~50% decrease of adhesion, see Fig. 5c and d). Hence, the total contact area must decrease due to the limited elasticity of the cell.

Fig. 6.

Fig. 6

Open in a new tab

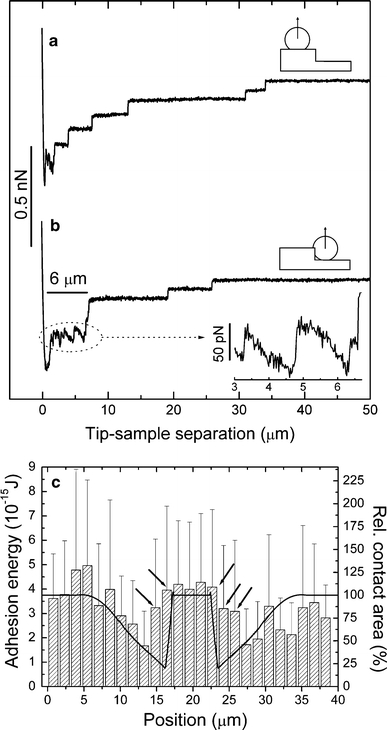
Force–distance curves of an L929 fibroblast at different positions on the microstructured substrate. The data originate from the same cell used in Fig. 5. The contact time was 10 s, the contact force was 250 pN, and the retraction speed was 5 μm/s. a Curve measured on top with primarily horizontal contact area. b Curve measured near the flanks with maximal vertical contact area. A long plateau with sawtooth shape was frequently observed for this position. Inset Magnification of the plateau. c Local adhesion energy (area under the force–distance curve) for different positions on the grooved microstructure. The groove is located in the center of the diagram (see Fig. 5b for the profile). The hatched bars show the local adhesion energy (mean ± SD, left scale); the solid line represents the calculated local contact area (right scale). The arrows denote the positions near the groove flanks where a high adhesion energy but a low adhesion force was found

Conclusions

In this study, the initial adhesion of L929 fibroblasts on periodically grooved titanium microstructures was investigated. SCFS allowed us, for the first time, to directly compare the local adhesion strength of the same cell at different positions on a topographical microstructure. It was shown that initial cell adhesion is governed by two processes: specific bond development, and contact area enlargement by cell flattening. The latter is influenced by the rheological properties of the cell, is independent of the contact force for values up to 1,000 pN, and determines the number of receptors participating in adhesion. The results of this study prove that these two processes are correlated for L929 fibroblasts, which confirms the importance of including the rheological properties in cell adhesion models. On the periodically grooved microstructure, the local cell adhesion strength significantly decreased near the groove flanks as soon as the edge of the plateau was crossed. This effect may be explained by a decrease of the contact area due to the limited elasticity of the cell. Our study suggests that it is more favorable for the fibroblasts to adapt their contact area to the planar regions of the substrate than around the sharp edge of the microstructure. No indirect influence of the edges on cell adhesion by a local impact on protein adsorption was detected. Consequently, to tailor functional microstructures on implant surfaces, the mechanical properties of the cells must be considered in relation with their local deformation. However, we only addressed initial cell adhesion. For longer contact times, the development of focal adhesion complexes, the formation of protrusions, and cell migration may have a considerable impact on cell behavior. Furthermore, the topography that a cell senses is the convolution of the substrate’s structure with its own shape. Accordingly, averaging the results from multiple cells with different radii and different elastic properties may disturb the detection of position-dependent effects. Consequently, the resolution for such experiments will always be limited.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (DOC 3668 kb) (3.6MB, doc)

Acknowledgments

We thank Dr. Torsten Müller (JPK Instruments) for helpful discussions. Funding by the Deutsche Forschungsgemeinschaft (Graduate School “Welisa” 1505/1 and project BE 2362/2-1) and the federal state of Mecklenburg-West Pomerania (V220-630-08-TFMV-F-011/V220-630-08-TFMV-F-036) is gratefully acknowledged.

Open Access

This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.

References

  1. Bacabac R, Mizuno D, Schmidt CF, MacKintosh FC, Van Loon J, Klein-Nulend J, Smit TH. Round versus flat: bone cell morphology, elasticity and mechanosensing. J Biomech. 2008;41:1590–1598. doi: 10.1016/j.jbiomech.2008.01.031. [DOI] [PubMed] [Google Scholar]
  2. Bell GI. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
  3. Bell GI. Estimate of the sticking probability for cells in uniform shear flow with adhesion caused by specific bonds. Cell Biophys. 1981;3:289–304. doi: 10.1007/BF02782629. [DOI] [PubMed] [Google Scholar]
  4. Benoit M, Gaub HE. Measuring cell adhesion forces with the atomic force microscope at the molecular level. Cells Tissues Organs. 2002;172:174–189. doi: 10.1159/000066964. [DOI] [PubMed] [Google Scholar]
  5. Benoit M, Gabriel D, Gerisch G, Gaub HE. Discrete interactions in cell adhesion measured by single-molecule force spectroscopy. Nat Cell Biol. 2000;2:313–317. doi: 10.1038/35014000. [DOI] [PubMed] [Google Scholar]
  6. Bogner E, Dominizi K, Hagl P, Bertagnolli E, Wirth M, Gabor F, Brezna W, Wanzenboeck HD. Bridging the gap–biocompatibility of microelectronic materials. Acta Biomater. 2006;2:229–237. doi: 10.1016/j.actbio.2005.10.006. [DOI] [PubMed] [Google Scholar]
  7. Bosman FT, Stamenkovic I. Functional structure and composition of the extracellular matrix. J Patheol. 2003;200:423–428. doi: 10.1002/path.1437. [DOI] [PubMed] [Google Scholar]
  8. Boyan BD, Lohmann CH, Dean DL, Sylvia VL, Cochran DL, Schwartz Z. Mechanisms involved in osteoblast response to implant surface morphology. Annu Rev Mater Res. 2001;31:357–371. doi: 10.1146/annurev.matsci.31.1.357. [DOI] [Google Scholar]
  9. Breme J, Kirkpatrick JC, Thull R (2007) Metallic biomaterial interfaces. Wieley-VCH, Weinheim, ISBN 978-3-527-31860-5
  10. Brunette DM. Fibroblasts on micro machined substrata orient hierarchically to grooves of different dimensions. Exp Cell Res. 1986;164:11–26. doi: 10.1016/0014-4827(86)90450-7. [DOI] [PubMed] [Google Scholar]
  11. Butt HJ, Jaschke M. Calculation of thermal noise in atomic force microscopy. Nanotechnology. 1995;6:1–7. doi: 10.1088/0957-4484/6/1/001. [DOI] [Google Scholar]
  12. Chen J, Mwenifumbo S, Langhammer C, McGovern JP, Li M, Beye A, Soboyejo O. Cell/surface interactions and adhesion of Ti-6Al-4 V: effects of surface texture. J Biomed Mater Res. 2007;82B:360–373. doi: 10.1002/jbm.b.30741. [DOI] [PubMed] [Google Scholar]
  13. Chesla SE, Periasamy S, Zhu C. Measuring Two-dimensional receptor-ligand binding kinetics by micropipette. Biophys J. 1998;75:1553–1572. doi: 10.1016/S0006-3495(98)74074-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Clark P, Connolly P, Curtis ASG, Dow JAT, Wilkinson CDW. Topographical control of cell behaviour. Development. 1987;99:439–448. doi: 10.1242/dev.99.3.439. [DOI] [PubMed] [Google Scholar]
  15. Clark P, Connolly P, Curtis ASG, Dow JAT, Wilkinson CDW. Topographical control of cell behaviour: II. Multiple grooved substrata. Development. 1990;108:635–644. doi: 10.1242/dev.108.4.635. [DOI] [PubMed] [Google Scholar]
  16. Dembo M, Torney DC, Saxman K, Hammer DA. The reaction-limited kinetics of membrane-to-surface adhesion and detachment. P R Soc London. 1988;B234:55–83. doi: 10.1098/rspb.1988.0038. [DOI] [PubMed] [Google Scholar]
  17. Duband JL, Nuckolls GH, Ishihara A, Hasegawa T, Yamada KM, Thiery JP, Jacobson K. Fibronectin receptor exhibits high lateral mobility in embryonic locomoting cells but is immobile in focal contacts and fibrillar streaks in stationary cells. J Cell Biol. 1988;107:1385–1396. doi: 10.1083/jcb.107.4.1385. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Elter P, Lange R, Thull R, Beck U. Protein adsorption on topographically structured surfaces: a mesoscopic computer simulation for the prediction of preferred adsorption sites. Mater Sci Forum. 2010;638–642:542–547. doi: 10.4028/www.scientific.net/MSF.638-642.542. [DOI] [Google Scholar]
  19. Evans E, Ritchie K. Dynamic strength of molecular adhesion bonds. Biophys J. 1997;72:1541–1555. doi: 10.1016/S0006-3495(97)78802-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Galli C, Collaud Coen M, Hauert R, Katanaev VL, Groning P, Schlapbach L. Creation of nanostructures to study the topographical dependency of protein adsorption. Col Surf B. 2002;26:255–267. doi: 10.1016/S0927-7765(02)00015-2. [DOI] [Google Scholar]
  21. Geiger B, Bershadsky A, Pankov R, Yamada KM. Transmembrane crosstalk between the extracellular matrix-cytoskeleton crosstalk. Nat Rev Mol Cell Biol. 2001;2:793–805. doi: 10.1038/35099066. [DOI] [PubMed] [Google Scholar]
  22. Guilak F, Jones WR, Ting-Beall HP, Lee G. The deformation behaviour and mechanical properties of chondrocytes in articular cartilage. Osteoarthr Cartilage. 1999;7:59–70. doi: 10.1053/joca.1998.0162. [DOI] [PubMed] [Google Scholar]
  23. Helenius J, Heisenberg CP, Gaub HE, Muller DJ. Single-cell force spectroscopy. J Cell Sci. 2008;121:1785–1791. doi: 10.1242/jcs.030999. [DOI] [PubMed] [Google Scholar]
  24. Hertz H. Ueber die Berührung fester elastischer Körper. Journal für die reine und angewandte Mathematik. 1881;92:156–171. [Google Scholar]
  25. Hirata H, Ohki K, Miyata H. Mobility of integrin α5β1 measured on the isolated ventral membranes of human skin fibroblasts. Biochim Biophys Acta. 2005;1723:100–105. doi: 10.1016/j.bbagen.2005.01.014. [DOI] [PubMed] [Google Scholar]
  26. Hutter JL, Bechhoefer J. Calibration of atomic-force microscope tips. Rev Sci Instrum. 1993;64:1868–1873. doi: 10.1063/1.1143970. [DOI] [Google Scholar]
  27. Hynes RO. Integrins: versatility, modulation, and signalling in cell adhesion. Cell. 1992;69:11–25. doi: 10.1016/0092-8674(92)90115-S. [DOI] [PubMed] [Google Scholar]
  28. International Organization for Standardization ISO (1992) Biological evaluation of medical devices—part 5. Tests for cytotoxicity: in vitro methods. ISO 10993-5
  29. International Organization for Standardization ISO (1997) Dentistry—preclinical evaluation of biocompatibility of medical devices used in dentistry—Test methods for dental materials. ISO 7405
  30. Kemmler R. Classical cadherins. Semin Cell Biol. 1992;3:149–155. doi: 10.1016/S1043-4682(10)80011-X. [DOI] [PubMed] [Google Scholar]
  31. Kothari S, Hatton PV, Douglas CWI. Protein adsorption to titania surfaces. J Mater Sci Mater Med. 1995;6:695–698. doi: 10.1007/BF00134303. [DOI] [Google Scholar]
  32. Kurrat R, Wälivaara B, Marti A, Textor M, Tengvall P, Ramsden JJ, Spencer ND. Plasma protein adsorption on titanium: comparative in situ studies using optical waveguide light mode spectroscopy and ellipsometry. Colloid Surface B. 1998;11:187–201. doi: 10.1016/S0927-7765(98)00039-3. [DOI] [Google Scholar]
  33. Lange R, Lüthen F, Nebe BJ, Rychly J, Beck U. Mathematical correlation between biomaterial and cellular parameters–critical reflection of statistics. Biomol Eng. 2007;24:526–530. doi: 10.1016/j.bioeng.2007.08.002. [DOI] [PubMed] [Google Scholar]
  34. Lange R, Elter P, Biala K, Matschegewski C, Stählke S, Löffler R, Fleischer M, Nebe BJ, Kern D, Beck U. Titanium surfaces structured with regular geometry–material investigations and cell morphology. Surf Interface Anal. 2010;42:497–501. doi: 10.1002/sia.3320. [DOI] [Google Scholar]
  35. Lin DC, Dimitriadis EK, Horkay F. Elasticity of rubber-like materials measured by AFM nanoindentation. Express Polym Lett. 2007;1:576–584. doi: 10.3144/expresspolymlett.2007.79. [DOI] [Google Scholar]
  36. Müller DJ, Helenius J, Alsteens D, Dufrêne YF. Force probing surfaces of living cells to molecual resolution. Nat Chem Biol. 2009;5:383–390. doi: 10.1038/nchembio.181. [DOI] [PubMed] [Google Scholar]
  37. N’Dri NA, Shyy W, Tran-Son-Tay R. Computational modelling of cell adhesion and movement using a continuum-kinetics approach. Biophys J. 2003;85:2273–2286. doi: 10.1016/S0006-3495(03)74652-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Puttock MJ, Thwaite G (1969) Elastic compression of spheres and cylinders at point and line contact. Nat. Stand. Lab. Techn. Paper No. 25, Commonwealth Scientific and Industrial Research Organization. Australia
  39. Roach P, Farrar D, Perry CC. Surface tailoring for controlled protein adsorption: effect of topography at the nanometer scale and chemistry. J Am Chem Soc. 2006;128:3939–3945. doi: 10.1021/ja056278e. [DOI] [PubMed] [Google Scholar]
  40. Rompen E, Domken O. The effect of material characteristics, of surface topography and of implant components and connections on soft tissue integration: a literature review. Clin Oral Imp Res. 2006;17:55–67. doi: 10.1111/j.1600-0501.2006.01367.x. [DOI] [PubMed] [Google Scholar]
  41. Rosenbluth MJ, Lam WA, Fletcher DA. Force microscopy of nonadherent cells: a comparison of leukemia cell deformability. Biophys J. 2006;90:2994–3003. doi: 10.1529/biophysj.105.067496. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Scheideler L, Geis-Gerstorfer J, Kern D, Pfeiffer F, Rupp F, Weber H, Wolburg H. Investigation of cell reactions to microstructured implant surfaces. Mater Sci Eng C. 2003;23:455–459. doi: 10.1016/S0928-4931(02)00321-1. [DOI] [Google Scholar]
  43. Schwartz MA, Ginsberg MH. Networks and crosstalk: integrin signalling spreads. Nat Cell Biol. 2002;4:E65–E68. doi: 10.1038/ncb0402-e65. [DOI] [PubMed] [Google Scholar]
  44. Singer SJ, Nicolson GL. The fluid mosaic model of the structure of cell membranes. Science. 1972;175:720–731. doi: 10.1126/science.175.4023.720. [DOI] [PubMed] [Google Scholar]
  45. Song W, Chen H. Protein adsorption on materials surface with nano-topography. Chin Sci Bull. 2007;52:3169–3173. doi: 10.1007/s11434-007-0504-6. [DOI] [Google Scholar]
  46. Swaisgood M, Schindler M. Lateral diffusion of lectin receptors in fibroblast membranes as a function of cell shape. Exp Cell Res. 1989;180:515–528. doi: 10.1016/0014-4827(89)90078-5. [DOI] [PubMed] [Google Scholar]
  47. Taubenberger A, Cisneros DA, Friedrichs J, Puech PH, Muller DJ, Franz CM. Revealing early steps of α2β1 integrin-mediated adhesion to collagen type i by using single-cell force spectroscopy. Mol Biol Cell. 2007;18:1634–1644. doi: 10.1091/mbc.E06-09-0777. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Weiss P. Cell Contact. Int Rev Cytol. 1958;7:391–423. doi: 10.1016/S0074-7696(08)62692-3. [DOI] [Google Scholar]
  49. Wu HW, Kuhn T, Moy VT. Mechanical properties of l929 cells measured by atomic force microscopy: effects of anticytoskeletal drugs and membrane crosslinking. Scanning. 1998;20:389–397. doi: 10.1002/sca.1998.4950200504. [DOI] [PubMed] [Google Scholar]
  50. Zagyansky Y, Edidin M. Lateral diffusion of concanavalin a receptors in the plasma membrane of mouse fibroblasts. Biochim Biophys Acta. 1976;433:209–214. doi: 10.1016/0005-2736(76)90188-7. [DOI] [PubMed] [Google Scholar]
  51. Zhang X, Wojcikiewicz E, Moy VT. Force spectroscopy of the leukocyte function-associated antigen-1/intercellular adhesion molecule-1 interaction. Biophys J. 2002;83:2270–2279. doi: 10.1016/S0006-3495(02)73987-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Zhu C. Kinetics and mechanics of cell adhesion. J Biomech. 2000;33:23–33. doi: 10.1016/S0021-9290(99)00163-3. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary material 1 (DOC 3668 kb) (3.6MB, doc)

Articles from European Biophysics Journal are provided here courtesy of Springer

RESOURCES