Population pharmacokinetic model and Bayesian estimator for two tacrolimus formulations – twice daily Prograf® and once daily Advagraf®

Abstract

AIM

To investigate the differences in the pharmacokinetics of Prograf® and the prolonged release formulation Advagraf® and to develop a Bayesian estimator to estimate tacrolimus inter-dose area under the curve (AUC) in renal transplant patients receiving either Prograf® or Advagraf®.

METHODS

Tacrolimus concentration–time profiles were collected, in adult renal transplant recipients, at weeks 1 and 2, and at months 1, 3 and 6 post-transplantation from 32 Prograf® treated patients, and one profile was collected from 41 Advagraf® patients more than 12 months post-transplantation. Population pharmacokinetic (popPK) parameters were estimated using nonmem®. In a second step, the popPK model was used to develop a single Bayesian estimator for the two tacrolimus formulations.

RESULTS

A two-compartment model with Erlang absorption (n= 3) and first-order elimination best described the data. In Advagraf® patients, a bimodal distribution was observed for the absorption rate constant (K_tr): one group with a K_tr similar to that of Prograf® treated patients and the other group with a slower absorption. A mixture model for K_tr was tested to describe this bimodal distribution. However, the data were best described by the nonmixture model including covariates (cytochrome P450 3A5, haematocrit and drug formulation). Using this model and tacrolimus concentrations measured at 0, 1 and 3 h post-dose, the Bayesian estimator could estimate tacrolimus AUC accurately (bias = 0.1%) and with good precision (8.6%).

CONCLUSIONS

The single Bayesian estimator developed yields good predictive performance for estimation of individual tacrolimus inter-dose AUC in Prograf® and Advagraf® treated patients and is suitable for clinical practice.

WHAT IS ALREADY KNOWN ABOUT THIS SUBJECT

• Tacrolimus is an immunosuppressant agent, largely used in kidney transplantation, with a narrow therapeutic range.

• Therapeutic drug monitoring of tacrolimus exposure improves the efficacy and toxicity of this drug.

• Separated Bayesian estimators have been developed to estimate tacrolimus exposure following administration of Prograf® and the prolonged release formulation Advagraf®.

WHAT THIS STUDY ADDS

• A population model was developed to compare the pharmacokinetics of 32 patients treated with Prograf® and 41 treated with Advagraf®.

• A mixture model and a model using formulation as covariates were developed to describe the bimodal distribution in the absorption rate following Advagraf® administration. Comparison of these two models showed that the nonmixture model was adequate.

• A single Bayesian estimator was developed to estimate the exposure for both formulations, which is more suitable for clinical practice.

Introduction

Prograf® and Advagraf® are two different formulations of tacrolimus, a potent immunosuppressant widely used in renal transplantation. Tacrolimus is characterized by a narrow therapeutic index and large inter- and intra-individual pharmacokinetic variability [1]. Advagraf®, a prolonged-release tacrolimus formulation is administered once daily, while Prograf®, the older immediate-release formulation, has to be given twice daily. Advagraf® was developed to increase compliance, which is important in the prevention of graft rejection and graft loss [2]. Because of a small therapeutic window and a better correlation between pre-dose level and effects than between dose and effect, therapeutic drug monitoring (TDM) based on trough whole blood tacrolimus concentrations is mandatory for both tacrolimus formulations. TDM helps to minimize the risk of acute rejection and the occurrence of adverse effects (mainly nephrotoxicity and, to a lesser extent, neurotoxicity) [3]. Results of Advagraf®de novo trials and conversion trials from Prograf® to Advagraf® showed that safety and efficacy are similar for both formulations and that the target trough concentration for TDM is the same [4, 5]. However, in clinical practice, physicians have observed that significantly different daily doses per kg were needed for tacrolimus administered twice (Prograf®) and once (Advagraf®) daily over the first 6 months post-transplantation to reach the same target concentrations (0.16 vs. 0.11, 0.14 vs. 0.08 and 0.12 vs. 0.08 mg kg⁻¹ at 1, 3 and 6 months, respectively) [6]. Although the relationship between tacrolimus exposure and patient outcome has not been well established, the last consensus report for Prograf® retained the area under the concentration−time curve from 0 to 12 h (AUC(0,12 h)) as the best marker of drug exposure [7] and provided target AUC values (150 to 200 ng ml⁻¹ h) in adult renal transplant patients.

The pharmacokinetics of tacrolimus are influenced by the single nucleotide polymorphisms within intron 3 of cytochrome P450 3A5 (CYP3A5). This leads to an alternative splice site in the pre-mRNA and results in a truncated enzyme [8]. Individuals that carry at least one CYP3A5*1 allele are considered to be CYP3A5 expressors (including CYP3A5*1/*3 and CYP3A5*1/*1). These patients (representing about 12% of the Caucasian population, Hapmap project: http://hapmap.ncbi.nlm.nih.gov/) require a 1.5 times higher starting dose compared with CYP3A5*3/*3 carriers to reach the predefined target exposure early after transplantation [9]. The same effect of this CYP3A5 polymorphism on tacrolimus apparent clearance was reported in several other studies [10–12]. Press et al. found, besides a higher apparent clearance in CYP3A5 expressors, a significant increased tacrolimus apparent clearance in patients treated with a prednisolone dose of more than 10 mg day⁻¹[10]. Furthermore, several studies found an association between increased haematocrit and decreased apparent clearance [13–15].

To perform TDM based on target AUC values, a reliable AUC estimation method is required, because measuring a full AUC based on numerous concentrations over the whole dose interval is impractical. A suitable alternative can be the development of estimators or equations based on a limited sampling strategy, i.e. a few blood samples collected during the early phase post-dose. Bayesian estimators were developed for both Prograf®[13, 15, 16] and Advagraf®[17], in renal as well as lung transplant patients. Up to now, no published Bayesian estimator can accommodate the two formulations of tacrolimus.

The aims of this study were (i) to build a population pharmacokinetic model for the two tacrolimus formulations to compare the pharmacokinetics and (ii) to develop a Bayesian estimator suited for both formulations of tacrolimus in renal transplant patients, intended for the AUC-based TDM of tacrolimus.

Methods

Patient population

Data were obtained from two pharmacokinetic trials complying with legal requirements and the declaration of Helsinki and approved by regional ethic committees [12, 15]. All the patients included gave their written informed consent. The first study consisted of 145 pharmacokinetic profiles, obtained from 32 de novo renal transplant patients. Patients were treated with Prograf® and received a standardized immunosuppressive regimen with tacrolimus (initial dose 0.1 mg kg⁻¹ day⁻¹, further adjusted on morning trough blood concentrations to reach a target between 10 and 15 ng ml⁻¹ for the first 6 weeks and 5 to 10 ng ml⁻¹ afterwards), mycophenolate mofetil (1 g twice daily) and oral prednisolone 1 mg kg⁻¹ day⁻¹ from day 1 to day 7, then 0.5 mg kg⁻¹ day⁻¹ from day 8 to day 14, tapered by 5 mg day⁻¹ each week down to 20 mg day⁻¹, decreased by 2.5 mg day⁻¹ each week down to 10 mg day⁻¹, with the dose maintained for 1 month and then decreased by 2.5 mg day⁻¹ each week until complete cessation, if clinically possible. Administration of interacting azole antifungals to the patients was prohibited. The second study included 41 pharmacokinetic profiles obtained from 41 adult stable renal transplant patients (more than 12 months post-transplantation) converted from cyclosporin A to Advagraf® for more than 6 months before the present study (initial dosage of tacrolimus 0.2 mg kg⁻¹ day⁻¹ and further adjusted as for the other study). The concomitant immunosuppressive regimen consisted of mycophenolate mofetil and oral prednisolone (mean dose 2.5 mg, ranging from 0 to 10 mg) (Table 1). No drugs interacting with CYP3A5 were allowed to be used in this study. In both studies, patients had to take their tacrolimus 0.5 h before a meal.

Table 1.

Demographics of the studied patients

Characteristics	Prograf® (n= 32)	Advagraf® (n= 41)	P value
Age (years)	55 (18–69)	53 (28–77)	0.8157
Sex (male/female)	19/13	19/22	0.3465
Weight (kg)	65 (46–97)	69 (45–116)	0.0217
Haematocrit (%)	32.3 (20.9–46.6)	38.5 (26.5–45.1)	<0.0001
Haemoglobin (g dl−1)	10.6 (6.5–15.7)	12.9 (10.5–15.1)	<0.0001
Creatinine (µmol l−1)	119 (63–928)	114 (82–907)	0.0866
Tacrolimus dose (mg day−1)	4 (0.5–9)	4 (2–10)	0.2725
Prednisolone dose (mg day−1)	20 (0–94)	2.5 (0–10)	<0.0001
CYP3A5*1/*3 genotype (n)			0.2211
*1/*1	0	1
*1/*3	1	4
*3/*3	31	36

Parameters are expressed as median and range; P value of Mann-Whitney test for continuous covariates and Fisher Exact test for categorical covariates.

Blood collection

In the Prograf® study, blood samples were collected in EDTA tubes at five periods post-transplantation: weeks 1 and 2, months 1, 3 and 6 (W1, W2, M1, M3 and M6, respectively). For all pharmacokinetic assessments, 10 samples were collected at pre-dose and 0.33, 0.66, 1, 1.5, 2, 3, 4, 6 and 9 h after tacrolimus dosing. Additionally, one sample at 12 h after tacrolimus intake was collected at W1 and W2 post-transplantation. In the Advagraf® study, one full PK profile of 12 blood samples was collected. Samples were taken at pre-dose and 0.33, 0.66, 1, 1.5, 2, 3, 4, 6, 9, 12, 24 h after Advagraf® dosing. Blood samples were stored at −20°C until analysis.

Tacrolimus assay

All blood samples were analyzed in the same laboratory. Tacrolimus was determined using a previously reported, validated turbulent flow chromatography-tandem mass spectrometry (TFC-MS/MS) method [15]. Briefly, online extraction was performed at a high flow rate (1.25 ml min⁻¹) on a Cyclone P®, 50-µm particle size (50 × 0.5 mm I.D.) column (Cohesive technologies, Milton Keynes, UK) in alkaline conditions. Chromatographic separation was performed in acidic conditions using a Propel C18 MS, 5 µm (50 × 3.0 mm I.D.) column (Cohesive technologies, Milton Keynes, UK) heated to 60°C, with a constant flow rate of 300 µl min⁻¹. Detection was performed using a TSQ Quantum Discovery MS/MS system (Thermo-Fisher, Les Ulis, France) equipped with an orthogonal electrospray ionization source and controlled by the Xcalibur computer program. MS/MS detection was performed in the positive ion, multiple reaction monitoring mode following two transitions for tacrolimus (m/z 821.5→768.6; m/z 821.5→786.4) and two for the internal standard ascomycin (m/z 809.3→756.4; m/z 809.3→564.4).

This method was fully validated for tacrolimus determination in whole blood. After testing different types of regression and weighing factors, we constructed the calibration curves using a 1/x weighted quadratic regression to obtain the best fit across the calibration range, based on the standard error of the fit and minimization of calibrator's bias. The lower limit of quantitation was 1 µg l⁻¹ and the calibration curves obtained from the lower limit of quantitation up to 100 µg l⁻¹ yielded r² > 0.998. The method was found to be accurate and precise with bias of −4.4 to 0.6% and a low coefficient of variation of −3.8 to 6.4% [15].

Genotype characterization

Patients' DNA was isolated from EDTA-treated blood as previously described in detail [18] and was characterized for the CYP3A5 A6986G SNP (rs776746) using a validated TaqMan allelic discrimination assay on an ABI PRISM 7000 Sequence Detection System (Applied Biosystems, Courtaboeuf, France). As a negative control, all runs included duplicates of a null sample. Deviation from the Hardy-Weinberg equilibrium was studied using Fisher's exact test in R software version 2.10.1 (R foundation for statistical computing, http://www.r-project.org).

Population pharmacokinetic analysis

The distribution of population parameters was studied with nonmem® version VI (GloboMax® LLC) using Wings for nonmem® version 614 (developed by N. Holford, available from http://wfn.sourceforge.net) [19]. Population pharmacokinetic analyses were performed using the first order conditional estimation (FOCE) method to improve the estimation of pharmacokinetic parameters and their variability.

One, two and three compartment structural models were tested. Two models were compared to describe the absorption process: (i) first order absorption with or without lag time and (ii) Erlang distribution (ADVAN5 SS5), which is a particular case of the gamma distribution [20] and was previously used for tacrolimus in renal transplant recipients [15]. Theoretically, as Advagraf® is a prolonged-release formulation of Prograf®, Advagraf® and Prograf® should be characterized by different typical absorption parameters. In certain situations, the population may be heterogeneous and the assumption of a unimodal distribution for random effects is no longer verified. In this case, using a mixture model can be a useful tool for investigating the presence of sub-populations in a given population [21]. A mixture model divides the population into several subpopulations with their own pharmacokinetic parameter estimates. The fraction of individuals belonging to each of the subpopulations is estimated, and each patient is allocated to one subpopulation.

Inter-patient variability (IPV) and inter-occasion variability (IOV) were described using exponential error models. The covariance of the parameters was studied during the modelling process. Additive, proportional and combined (i.e. additive and proportional) error models were tested to describe the residual variability.

Covariate analysis

The screening and selection of covariates was performed as part of population pharmacokinetic analysis following a classic stepwise approach [22]. In the first step, a covariate-free population pharmacokinetic model was computed. The potential covariates considered were demographic characteristics (gender, body weight (BW), age), post-transplantation period, prednisolone >10 mg day⁻¹, study factor (assumed to be similar to drug formulation), laboratory test results (haematocrit, haemoglobin and serum creatinine concentrations) and possession of at least one CYP3A5*1 allele. The influence of continuous covariates on pharmacokinetic parameters was tested systematically via a generalized modelling approach according to an allometric function. For example, the effect of body weight on apparent clearance (CL/F) was tested using the following equation:

where TV(CL) is the typical value of clearance for a patient with the median covariate value (medcov) and θBW is the estimated influential factor for body weight. The effect of categorical covariates, such as study factor, was tested using the equation:

in which Istudy is the indicator variable (0 = Advagraf®, 1 = Prograf®), θstudy the fraction of change in CL/F for patients treated with Prograf® and TV(CL) represents the CL/F for patients treated with Advagraf®. The effect of CYP3A5 genetic polymorphism was tested using the equation:

where TV(CL) represents the clearance of patients with cyp equal to 0 (i.e. non-expressers, or CYP3A5*3/*3 carriers) and TV(CL) × (θcyp) that of expressers (i.e. carriers of at least one CYP3A5*1 allele). Covariates were tested for all the pharmacokinetic parameters for which inter-patient variability was estimated. Statistical significance of the covariates was evaluated based on the objective function value (OFV) calculated with nonmem®, which is equal to minus twice the log likelihood. In the univariate analysis, a decrease of at least 3.84 (P < 0.05, 1 d.f.) was required for a covariate to be considered to be significantly linked with the pharmacokinetic variable. In a second step, all covariates showing a significant effect in univariate analysis were added simultaneously into an intermediate model and a stepwise backward elimination procedure was carried out, whereby each covariate was independently removed from the intermediate model to confirm its relevance. Covariates were kept in the final population pharmacokinetic model when the removal of the covariate resulted in an OFV increase of at least 10.83 (P < 0.001, 1 d.f.). The clinical relevance of the covariates was also appraised by evaluating the related change in IPV and IOV.

Evaluation of the model

The extent of shrinkage was evaluated in the final model for each parameter using R for nonmem®[23]. The final model selected was evaluated using a visual predictive check (VPC) to check its accuracy and robustness. A total of 1000 replicates of the original dataset were simulated using the final model to generate expected concentrations and the 90% prediction intervals. The observed data were overlaid on the prediction intervals and compared visually. Because the tacrolimus dose was different in each patient and the pharmacokinetics for tacrolimus were linear, the VPC was based on dose-normalized concentration. The total data set was split randomly into building data set (n= 49) and a validation data set (n= 24) using permutation tables. The popPK model was evaluated using the building data set. In this model, covariate analysis was performed using the same strategy as for the model including the whole population. Then the population parameters and variability estimates obtained with the whole data set and the building data set were compared. Furthermore, these data were used to develop a Bayesian estimator in an independent data set of patients.

Building of a Bayesian estimator

The best limited sampling strategy among the combinations of a maximum of three sampling times was selected in the building dataset based on the d-optimality criterion (implemented in Adapt II Pharmacokinetic/Pharmacodynamic Systems Analysis Software, Biomedical Simulations Resource, Los Angeles) computed on the population pharmacokinetic parameters. The study of optimal sampling design was also focused on CL/F. A total of 100 pharmacokinetic profiles consisting the three selected optimal sampling times was simulated using the building database (n= 49) and the mean CL/F obtained with these simulations was compared with the CL/F from the building data set with all concentration–time profiles (n= 49).

The predictive performance of the developed Bayesian estimator using the limited sampling strategy selected was evaluated in the validation data set. For this analysis, the Bayesian estimates of the inter-dose AUC (i.e. AUC(0,12 h) for Prograf® or AUC(0,24 h) for Advagraf®) were compared with the reference AUC values obtained using the linear trapezoidal method applied to the full profiles, as recommended by Sheiner & Beal [24], by calculating the bias (Equation 1) (mean prediction error, MPE) and precision (Equation 2) (root mean squared prediction error, RMSE).

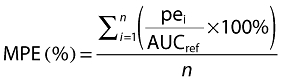(1)

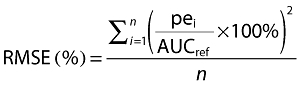(2)

n represents the number of pairs of estimated and measured AUC, AUC_ref is the calculated AUC using the trapezoidal rule and pe_i is the difference between the estimated and the reference AUC.

Of note, for 21 pharmacokinetic profiles (seven patients treated with Prograf®), the pre-dose value was taken as an estimate of the concentration at 12 h post-dose to compute the trapezoidal AUC(0,12 h), because this concentration value was missing.

Results

Patient characteristics

Thirty-two patients (145 PK profiles collected at W1, W2, M1, M3 and M6) were enrolled in the Prograf® study and 41 patients (41 PK profiles collected at >M12 post-transplantation) in the Advagraf® study. The characteristics of patients from both group are reported in Table 1. In two patients in the Advagraf® group, two missing covariate values were replaced by their respective median value (33.7% and 11.2 g dl⁻¹ for haematocrit and haemoglobin, respectively).

Genotyping results were consistent with the Hardy-Weinberg equilibrium.

Covariate free model

After testing the performance of different structural models, a two-compartment model with first-order elimination was found to best describe the data. The delayed and progressively increasing absorption process was characterized best by an Erlang absorption model with three transit compartments. Inclusion of IPV for absorption rate (K_tr), CL/F, apparent inter-compartmental clearance (Q/F), apparent central volume of distribution (V_c/F) and apparent peripheral volume of distribution (V_p/F) improved the fit of the model for each parameter and decreased significantly the OFV. IOV could be estimated for K_tr, V_c/F and CL/F and improved the model further (Table 2). Contrary to patients treated with Prograf®, patients with Advagraf® only had one pharmacokinetic profile collected, so that no inter-occasion variability could be calculated.

Table 2.

Characteristics of the covariate-free model

	Population mean		Inter-patient variability		Inter-occasion variability
Parameter	Estimate	SE	Estimate	95% CI	Estimate	95% CI
Ktr (h−1)	5.47	0.64	28%	0–41	30%	21–36
Q/F (l h−1)	57.6	3.1	57%	33–73
Vc/F (l)	238	5	47%	0–74	79%	62–89
Vp/F (l)	500 (Fixed)	–	–	–
CL/F (l h−1)	24.1	1.3	36%	21–46	35%	26–43

Objective function 6564 (proportional error = 9.74%; additive error = 1.36 ng ml⁻¹); CI is confidence interval, SE is standard error, K_tr is the absorption rate, F is oral bioavailability, CL is clearance, Q is inter-compartmental clearance, V_c is the central volume of distribution and V_p is the peripheral volume of distribution,

Figure 1 shows the probability density function of the absorption parameter Ktr estimated with the covariate-free model as a function of the tacrolimus formulation. It suggests a bimodal distribution of Ktr in the Advagraf® population. The Shapiro-Wilk test performed in R software version 2.10.1 (R foundation for statistical computing, http://www.r-project.org) confirmed a non-normal distribution of K_tr(W = 0.9362, P < 2.2E-16) in the Advagraf® group. One group of the patients treated with Advagraf® seemed to have an absorption rate similar to that of Prograf® patients and another group seemed to have a lower absorption rate. Consequently, a mixture model was tested to improve the fit of the model for K_tr. This mixture model resulted in a significant decrease of the OFV. The mixture model approach showed two mixed subpopulations for K_tr. One sub-population contained all the Prograf® patients plus 25 Advagraf® patients (K_tr= 5.74 h⁻¹), while the second consisted of 16 patients treated with Advagraf® (K_tr= 1.94 h⁻¹). To compare better the fit of this mixture model for K_tr with that of a nonmixture model, both these basic models were further refined using covariate analysis.

Figure 1.

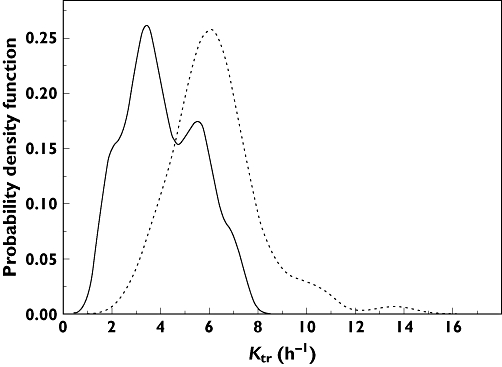
Probability density function of K_tr according to tacrolimus formulation, estimated using the covariate-free model. Advagraf (); Prograf ()

Covariate analysis for the mixture model

Univariate analysis showed significant associations for the following covariates: haematocrit, haemoglobin level, CYP3A5 status and corticosteroid co-treatment >10 mg day⁻¹ on CL/F; body weight, CYP3A5 status and study factor (i.e. study factor is assumed to be confused with formulation factor for Ktr) on V_c/F; body weight, haematocrit, haemoglobin level, study factor and corticosteroid co-treatement >10 mg day⁻¹ on K_tr. After the backward stepwise elimination process, covariates which remained significant in the final mixture model were the CYP3A5 status and haematocrit on CL/F and the study factor on V_c/F. Table 3 reports the parameter estimates for the fixed and random effects.

Table 3.

Tacrolimus pharmacokinetic parameters in renal transplant patients using the mixture model

	Final mixture model obtained in the whole dataset
	Population mean		IPV		IOV
Parameters	Estimate	SE	Estimate	95% CI	Estimate	95% CI
Ktr (h−1) subpopulation 1	5.74	0.58	16%	0–26	27%	18–33
Ktr (h−1) subpopulation 2	1.94	0.56	21%	0–50	27%	18–33
CL/F=θ1× ((HT/35)θ2) × (θ3CYP) θ1 (l h−1)	20.3	1.3	29%	13–39	32%	20–40
θ2	−1.05	0.37	–	–	–	–
θ3	2.39	0.67	–	–	–	–
Q/F (l h−1)	74	3.5	58%	0–95	–	–
Vc/F=θ4× (θ5study) θ4 (l)	552	11	33%	0–57	78%	57–95
θ5	0.23	0.25	–	–	–	–
Vp/F (l)	268	7	58%	14–80	–	–
% of patient in first Ktr group (subpopulation 1)	69	31	–	–	–	–

Objective function: 6156 (proportional error = 8.86%; additive error = 1.15 ng ml⁻¹), IPV is inter patient variability, IOV is inter-occasion variability, CI is confidence interval, SE is standard error, K_tr is the absorption rate, F is oral bioavailability, CL is clearance, Q is inter-compartmental clearance, V_c is the central volume of distribution and V_p is the peripheral volume of distribution, HT is haematocrit, CYP is CYP3A5 status = 0 for non-expressers and 1 for expressors, study is 0 for Advagraf® study (study 2) and 1 for Prograf® study(study 1).

Inclusion of these three covariates caused a decrease in OFV of 383 points compared with the covariate free model (P < 0.0001). The values obtained for IPV and IOV were similar in the model including covariates and the basic model: the IPV changed from 14% and 21% to 16% and 21% for K_tr1and K_tr2, respectively, from 33% to 29% for CL/F and from 31% to 33% for V_c/F. The final parameters estimated for the mixture model are presented in Table 3. The scatter plot of individual model-predicted (IPRED) and model-predicted (PRED) concentrations vs. observed concentrations showed no structural bias and the weighted residuals (WRES) were homogeneously distributed over the sampling time period (Figure 2). The estimates of shrinkage for K_tr subpopulation 1, K_tr subpopulation 2, V_c/F, CL/F, Q/F, and V_p/F were 30%, 45%, 24%, 22%, 37% and 34%, respectively. The overparameterization test gave a condition number = 962, which was close to the threshold (condition number < 1000).

Figure 2.

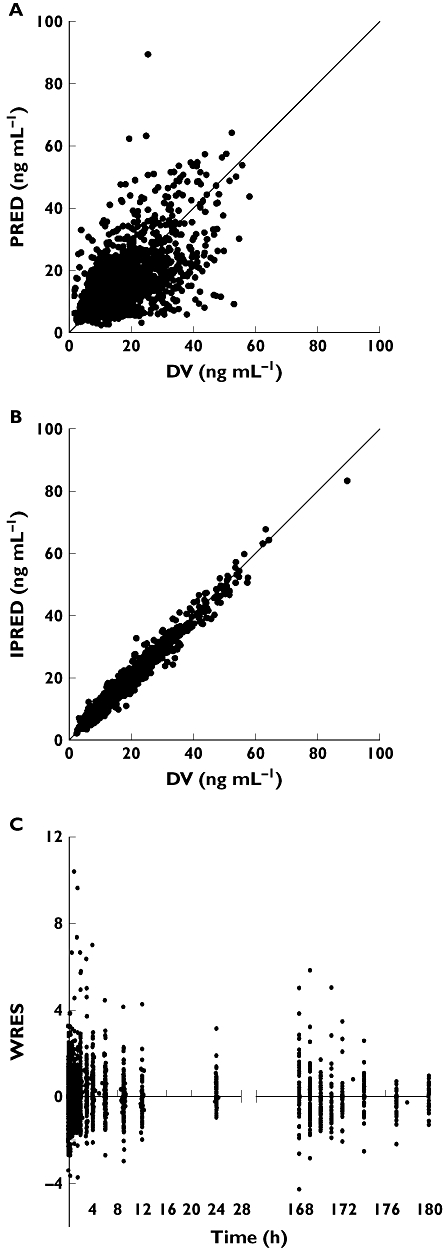
Scatter plots of (A) population model-predicted concentrations (PRED) and (B) individual model-predicted concentrations (IPRED) vs. observed concentrations (DV), and (C) weighted residuals (WRES) vs. time for the mixture model

Covariate analysis for the nonmixture model

The covariates significantly associated with pharmacokinetic parameters in the univariate analysis were haematocrit, haemoglobin level and CYP3A5 status on CL/F, post-transplantation period and study factor on V_c/F and study factor, body weight and post-transplantation period on K_tr (P < 0.05). These covariates were included in the intermediate model and, after the backward stepwise process, the covariates that remained significant in the final model were the haematocrit and CYP3A5 status on CL/F, the study factor on V_c/F and the study factor on K_tr. The results are presented in Table 4. Inclusion of these covariates caused a decrease in OFV of 465 points compared with the covariate-free model. The covariates could partly explain IPV, which decreased from 28% to 24% for Ktr, from 36% to 28% for CL/F and from 47% to 31% for V_c/F. The values obtained for IOV with the final model were close to those obtained with the covariate-free model. The final parameters estimated for the nonmixture model are presented in Table 4. The scatter plots of predicted (PRED) vs. observed concentration (DV) might show a small under-prediction of the highest concentrations. However, the individually predicted (IPRED) vs. observed concentrations showed no structural bias at all. WRES were homogeneously distributed over the sampling time period (Figure 3). The estimates of shrinkage for K_tr, V_c/F, CL/F and Q/F were 30%, 31%, 17% and 23%, respectively. The overparameterization test gave a condition number equal to 605 which implies that the model was not overparameterized (condition number < 1000).

Table 4.

Tacrolimus pharmacokinetic parameters in renal transplant patients using the final model

	Final model obtained in the whole dataset						Final model obtained in the model-building dataset
	Population mean		IPV		IOV		Population mean		IPV		IOV
Parameters	Estimate	SE	Estimate	95% CI	Estimate	95% CI	Estimate	SE	Estimate	95% CI	Estimate	95% CI
Ktr=θ1× (θ2study) θ1 (h−1)	3.34	0.51	24%	0–39	33%	19–43	3.39	0.67	23%	0–50	36%	0–59
θ2	1.53	0.40	–	–	–	–	1.50	0.58	–	–	–	–
CL/F=θ3× ((HT/35)θ4) × (θ5CYP) θ3 (l h−1)	21.2	1.3	28%	12–39	31%	25–37	21.6	1.5	27%	0–47	26%	14–35
θ4	−1.14	0.54	–	–	–	–	−1.32	0.52	–	–	–	–
θ5	2.00	0.73	–	–	–	–	2.09	1.08	–	–	–	–
Q/F (l h−1)	79	4	54%	0–77	–	–	82	5	54%	0–91	–	–
Vc/F=θ6× (θ7study) θ6 (l)	486	11	31%	0–61	75%	53–91	463	11	32%	0–69	68%	30–92
θ7	0.29	0.10	–	–	–	–	0.30	0.33	–	–	–	–
Vp/F (l)	271	7	60%	0–86	–	–	329	9	59%	0–88	–	–

Objective function: 6099 (proportional error = 11.3%; additive error = 0.71 ng ml⁻¹) for the model obtained in the whole dataset and proportional error = 12.08%; additive error = 0.51 ng ml⁻¹ for the model obtained in the model building dataset, IPV is inter patient variability, IOV is inter-occasion variability, CI is confidence interval, SE is standard error, K_tr is the absorption rate, F is oral bioavailability, CL is clearance, Q is inter-compartmental clearance, V_c is the central volume of distribution and V_p is the peripheral volume of distribution, HT is haematocrit, CYP is CYP3A5 status = 0 for non-expressers and 1 for expressors, study is 0 for Advagraf® study (study 2) and 1 for Prograf® study (study 1).

Figure 3.

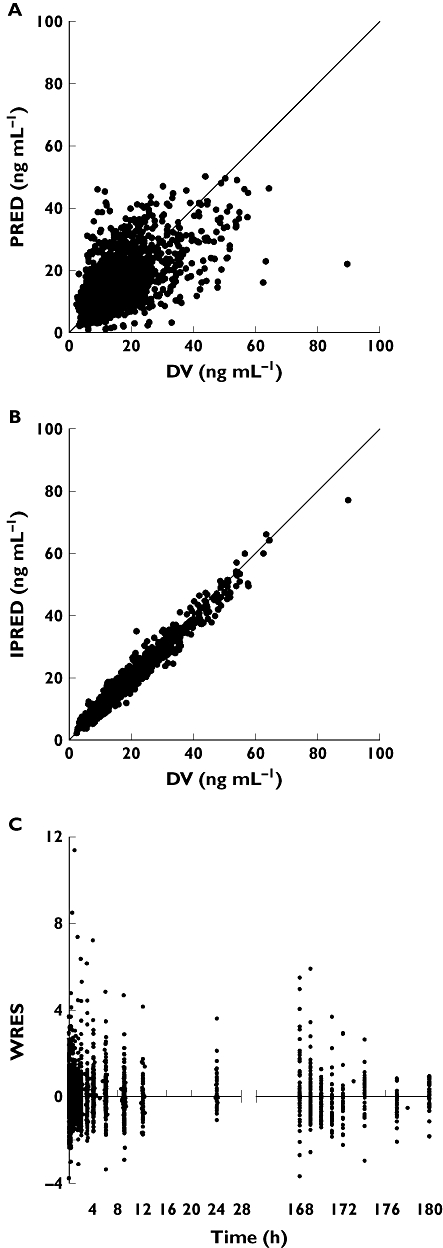
Scatter plots of (A) population model-predicted concentrations (PRED) and (B) individual model-predicted concentrations (IPRED) vs. observed concentrations (DV), and (C) weighted residuals (WRES) vs. time for the nonmixture model

Final model and validation

The mixture model was not found to be better than the nonmixture model, as higher OFV and shrinkage values, and similar IPV and IOV variabilities and residual error were obtained. The ‘study factor’ covariate seemed to explain adequately the variability of the absorption parameter. Finally, the nonmixture model with covariates was retained as the final model.

This final model was further evaluated using the VPC (Figure 4A), which shows that the average prediction of the simulated data matches the observed concentration–time profiles and that the variability is reasonably estimated when using the nonmixture model for all the patients. These graphs, representing a visual internal validation of the model, show that approximately 90% of the data fitted well within the 5th–95th percentiles (exact binomial test, 10.8% out of the observed range (95%CI 9.49% – 12.3%) and were symmetrically distributed around the median (Pearson's Chi-square test, P= 0.82). The VPC was stratified for CYP3A5 polymorphism (respective dose 4.13 mg for non-expressers and 6.88 mg for expressers), resulting in similarly good results in both non-expressors (Figure 4B) and expressors (Figure 4C).

Figure 4.

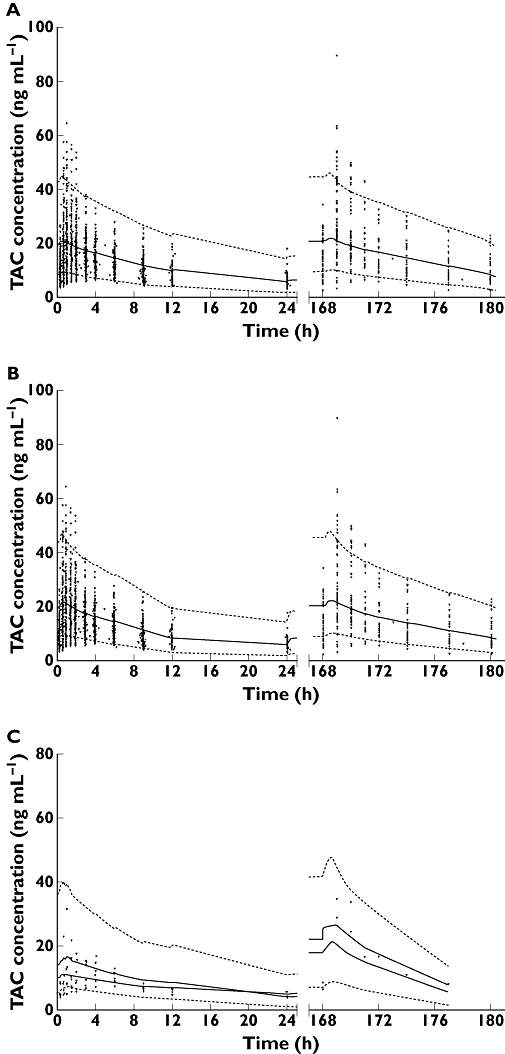
Evaluation of the final model using a visual predictive check. Shown are comparisons between the observed data (circles) for tacrolimus (TAC) concentrations and the 5th (bottom dashed line), 50th (solid line) and 95th (top dashed line) percentiles obtained from 1000 simulations for the global population standardized to a 4.25 mg dose (A), and as a function of CYP3A5 status, standardized to a 4.13 mg dose for non-expressers (B) and to a 6.88 mg dose for expressers (C)

After, the whole population was split into two groups (i.e. a data set of 49 patients used as building data set to obtain the population parameters and a validation set of 24 patients). The same significant covariates as previously in the whole dataset were identified in the building dataset, including 127 pharmacokinetic profiles. The population pharmacokinetic parameters obtained in this group were similar to the parameters obtained in the entire database (Table 4).

Bayesian estimator

The population pharmacokinetic parameters obtained from the building data set were used as priors for the development of the Bayesian estimator in the validation set of 24 patients. The optimal limited-sampling schedules obtained using ADAPT (d-optimality criterion) were 0, 1.2 and 3 h post-dose. The closest sampling times of these optimal times are 0, 1 and 3 h. On the other hand, several schemes containing three actual sampling times between 0 and 4 h post-dose were tested. On the basis of bias and precision, the best sampling schedule included concentrations obtained at 0, 1 and 3 h post-dose (Table 5). The Bayesian estimator based on this limited sampling strategy was characterized by accurate estimation of AUC(0,12 h) for Prograf® (mean bias = 1.3%, RMSE = 8.5%) as well as AUC(0,24 h) for Advagraf® (mean bias =−3.6%, RMSE = 8.2%) (Table 5). Only 1 out of the 58 estimated AUCs had a bias which was outside the ±20% interval.

Table 5.

Relative bias and precision for the 0, 1, 3 h sampling schedule as a function of formulation, period post-graft and CYP3A5 status

Group	Mean bias	Bias SE	Median bias	Range	RMSE	Number outside ±20%
Advagraf®	−3.6%	7.6%	−4.1%	−17.7–14.3%	8.2%	0/14
Prograf®	1.3%	8.5%	0.5%	−20.0–21.5%	8.5%	1/44
Early period (day 7 to day 14)	1.1%	10.6%	−0.2%	−20.0–21.5%	10.3%	1/18
Stable period (≥1 month)	−0.3%	7.5%	0.3%	−17.7–18.7%	7.4%	0/40
CYP expressors	1.8%	8.4%	2.3%	−9.1–11.6%	7.7%	0/5
CYP non-expressors	0.0%	8.7%	0.1%	−20–21.5%	8.6%	1/53

SE is standard error, RMSE is root mean squared prediction error, CYP is cytochrome P450 3A5.

Discussion

In this study, a single population pharmacokinetic model was developed to describe the pharmacokinetics of both tacrolimus formulations, Advagraf® and Prograf®, in renal transplant recipients. The final model was used to develop a Bayesian estimator able to estimate accurately tacrolimus inter-dose AUC following Advagraf® or Prograf® administration, using concentrations measured at 0, 1 and 3 h post-dose.

The tacrolimus concentration–time profiles were best described using a two-compartment model with first-order elimination. The absorption phase was described using three transit compartments. For the two formulations of tacrolimus, differences were seen in the absorption phase of the drug. On average, the absorption rate of Advagraf® was decreased as compared with Prograf®, due to the controlled release properties of this formulation. The absorption rate of Advagraf® showed high variability and a non-normal distribution (Figure 1). In some (31%) of the pharmacokinetic profiles, the absorption rate of Advagraf® was as fast as that of Prograf®. We hypothesized that these differences in the absorption rate could be best described using a mixture model for the absorption parameter K_tr, which divided the population into two groups with a fast and a slow absorption rate, respectively. In the mixture model, all patients treated with Prograf® and 31% of the Advagraf® treated patients had a fast absorption rate (K_tr= 5.74 h⁻¹), while the other 69% of patients treated with Advagraf® showed a slow absorption rate (K_tr= 1.94 h⁻¹). The mixture model was interesting because it could identify the sub-population to which a patient in the Advagraf® group belonged and in theory, the difference in the absorption rate could lead to different AUC profiles. However, this mixture model did not result in better fit. No covariate tested in the development step of the mixture model could explain the bimodal distribution observed for K_tr. Furthermore, the influence of ABCB1 exon12 (1236C > T) and exon 21 (2677G > T/A) were tested (i) on the absorption rate and (ii) on the mixture model subpopulation. However, no significant association was found with either one of these polymorphisms. Patients were advised to take their tacrolimus before their meal but it cannot be excluded that some took their tacrolimus during or after it, which could increase the variability in absorption rate and bioavailability [25]. Further investigations based on a much larger database have to be performed to explain this variability in absorption rate.

In the final population pharmacokinetic model, CYP3A5 polymorphism and haematocrit were significantly associated with tacrolimus apparent clearance. In the current analysis, tacrolimus apparent clearance was twice as high in patients with the CYP3A5*1/*3 or CYP3A5*1/*1 genotype (CL/F= 42 l h⁻¹) than in patients with the CYP3A5*3/*3 genotype (CL/F= 21 l h⁻¹). This relationship was previously reported in tacrolimus treated renal transplant recipients [11] and can be explained by the association between the *3 allele and the production of an inactive CYP3A5 protein. The haematocrit was inversely correlated with tacrolimus clearance. According to the model, a haematocrit increase from 30% to 40% caused a decrease in clearance from 25.3 to 18.2 l h⁻¹ in CYP3A5 non-expressors. Low haematocrit values probably result in a reduced fraction of tacrolimus accumulated in red blood cells [13]. This in turn resulted in an increased plasma free fraction available to be metabolized by the liver. Furthermore, a significant association between the study factor and V_c/F was observed. The apparent volume of distribution was 205 l in patients treated with Prograf® and 527 l in patients treated with Advagraf®. A possible explanation for this result might be the time post-transplantation: the Advagraf® population contained only patients in the stable period post-transplantation (median = 9 years post transplantation), whereas the Prograf® population contained only profiles obtained in the first 6 months post-transplantation. The apparent volume of distribution could change in the first years post-transplantation due to a reduction of corticosteroid dosage, increase of haematocrit and albumin concentration in the time post-transplantation [26]. Also body weight might contribute to the differences in V_c/F as body weight was a significant covariate in the univariate analysis, but it was not significant enough to be retained in the final model. However, the mean body weight was higher for patients treated with Advagraf® (P = 0.0217). These differences in apparent V_c were previously seen by Press et al. for Prograf® administered one or two times a day. These authors reported that V_c/F was almost 50% higher in patients treated with Prograf® once a day [10].

The final model was used to develop and validate a Bayesian estimator to estimate tacrolimus AUC on the basis of three sampling times. The best sampling strategy comprised concentrations measured at 0, 1, and 3 h after oral administration of Prograf® or Advagraf®. Bayesian estimates of the AUC yielded a mean bias of 0.1% and RMSE of 8.6%, which indicated that the estimator developed was accurate and precise, whatever was the post-transplantation period (early or stable), the drug formulation (Prograf® or Advagraf®) or the CYP3A5 phenotype (expressers or non-expressers). This predictive performance was comparable with that of previously reported Bayesian estimators dedicated to either Advagraf® or Prograf® (mean bias = 0.7% from −16% to 19%, RMSE = 9% for Advagraf®[12] and mean bias = 2% from −18% to 51%, RMSE = 11% for Prograf®[15]. There were more pharmacokinetic profiles of Prograf® available in the data set (n= 145) compared with Advagraf® (n= 41). However, this probably did not influence the analysis as there were no differences in the bias and RMSE between both formulations in the validation.

The major advantages of this study in which we developed a population pharmacokinetic model for both formulations in comparison with a model developed for a single formulation are that we could investigate the bimodal distribution of the absorption rate seen in the pharmacokinetic profiles of Advagraf® treated patients. Furthermore, combining all data increased the power of the analysis, without changing the precision of the results. Finally, the developed Bayesian estimator is more suitable for use in clinical practice because it can be used for all tacrolimus treated patients whatever formulation they are using.

This study has some limitations. The first one is the lack of early post-transplantation profiles in Advagraf® patients, which could be a possible explanation for the absence of performance improvement with the mixture model. Anyway, the Bayesian estimator developed cannot be used for Advagraf® patients in the early period post-graft. Secondly, concentrations at 12 h were missing in seven patients belonging to the validation group treated with Prograf®. In these patients, the pre-dose concentration was used as a surrogate of C_12h to calculate the trapezoidal AUC(0,12 h), which might have introduced a small bias in the reference AUC(0,12 h) values. In the Advagraf® study, no drugs which are known to inhibit or induced CYP3A5 were allowed. However, in the Prograf® study, only information about azole antifungal drugs was available. The other drugs known to interact with CYP3A5 can therefore influence tacrolimus clearance. These drugs might explain some of the unexplained variability seen in the Prograf® pharmacokinetics. However, we do not expect there to be major differences in co-medication on a population level between the two treatment groups.

In conclusion, a population pharmacokinetic model has been developed, which is accurate and precisely fits the pharmacokinetics of tacrolimus administered either as Prograf® or Advagraf®. As expected, differences between both formulations are mostly observed in the absorption phase. On average, absorption of Advagraf® is slower and more variable than that of Prograf®. The clearance of the drug is correlated with the patient's CYP3A5 phenotype and haematocrit. The final model was used to develop a Bayesian estimator, which can accurately estimate tacrolimus inter-dose AUC in renal transplant recipients based on concentrations measured at 0, 1 and 3 h after oral administration of Advagraf® or Prograf®.

Competing interests

There are no competing interests to declare.

This study was funded by the University Hospitals of Limoges and Toulouse, the University of Limoges, the French Agence Nationale de la Recherche and Astellas. We are also grateful to J. H. Comte for his excellent laboratory work and to Karen Poole for manuscript editing.