Assessing risk prediction models in case-control studies using semiparametric and nonparametric methods

Summary

The predictiveness curve is a graphical tool that characterizes the population distribution of Risk(Y) = P(D = 1|Y), where D denotes a binary outcome such as occurrence of an event within a specified time period and Y denotes predictors. A wider distribution of Risk(Y) indicates better performance of a risk model in the sense that making treatment recommendations is easier for more subjects. Decisions are more straightforward when a subject's risk is deemed to be high or low. Methods have been developed to estimate predictiveness curves from cohort studies. However early phase studies to evaluate novel risk prediction markers typically employ case-control designs. Here we present semiparametric and nonparametric methods for evaluating a continuous risk prediction marker that accommodate case-control data. Small sample properties are investigated through simulation studies. The semiparametric methods are substantially more efficient than their nonparametric counterparts under a correctly specified model. We generalize them to settings where multiple prediction markers are involved. Applications to prostate cancer risk prediction markers illustrate methods for comparing the risk prediction capacities of markers and for evaluating the increment in performance gained by adding a marker to a baseline risk model. We propose a modified Hosmer-Lemeshow test for case-control study data to assess calibration of the risk model that is a natural complement to this graphical tool.

1. Introduction

Criteria for evaluating a biomarker depend on the purpose for which it will be used. The key performance measure for a diagnostic marker is its classification accuracy, i.e. the ability to provide the correct diagnosis given a subject's true disease status. Classification accuracy of a continuous marker has been commonly assessed by the receiver operating characteristic (ROC) curve [1]. Classification, however, is not always the objective. Sometimes a marker is used mainly to predict risk of disease and to stratify the population into risk groups geared towards different treatment recommendations. Because of its popularity in the field of diagnostic testing, the ROC curve has been used frequently in this setting as well. However, as pointed out by Gail and Pfeiffer [2], Cook [3], and Pencina and others [4], criteria for evaluating a classification marker might be unnecessarily stringent for evaluating a risk prediction marker. In other words, the ROC curve may not be optimal when selecting a marker for risk prediction.

The predictiveness curve [5] was proposed by Pepe and others [6] and Huang and others [7] to evaluate a risk prediction marker or model. It characterizes the performance of a risk prediction model by displaying the population distribution of risk endowed by the model. Arguments for displaying the risk distribution have also appeared recently in the clinical literature [8]. A binary outcome D is considered here such as presence of disease or occurrence of an event within some specified time period. We write D = 1 for cases, subjects with a bad outcome and D = 0 for controls, subjects with a good outcome. Let Y be a vector of predictors of interest and let Risk(Y) = P(D = 1|Y) be the risk calculated based on Y. The predictiveness curve displays the risk distribution through the population quantiles, R(v) vs v for v ∈ (0, 1), where R(v) is the v^th quantile of Risk(Y). Equivalently, the inverse function, R⁻¹(p)= P{Risk(Y) ≤ p}, is the proportion of the population with risks less than or equal to p, the cumulative distribution function. If p_H corresponds to a high risk threshold, the capacity of the risk model to identify high risk subjects is 1 − R⁻¹(p_H). If p_L is a low risk threshold, R⁻¹(p_L) quantifies the capacity of the model to identify low risk subjects. Better risk markers put more subjects into high and low risk categories and fewer people into the intermediate range where treatment decisions are more difficult. In other words, a risk prediction model with larger variability in population quantiles, i.e. steeper predictiveness curve, has a better capacity to stratify risk.

For cohort studies, Huang and others [7] developed a semiparametric estimator of the predictiveness curve. However case-control studies, being smaller and more cost efficient than cohort studies, are the design of choice in early phases of biomarker development [9, 10]. Thus one objective of the current manuscript is to extend estimation to case-control designs. We describe two semiparametric methods. Large sample theory for these estimators was developed in Huang and Pepe [11] when Y is univariate. Here we consider the practical application of these methods. We examine methods for making inference in practical sample sizes and evaluate them using simulation studies. Importantly we extend the methods to accommodate multiple predictors as this often arises in real applications. In practice, robustness to modeling assumptions is always a concern. Another objective of the current paper is to develop a nonparametric estimator. We compare its performance with the semiparametric methods in simulations and in a real dataset. Moreover, we propose a measure accompanying the estimated predictiveness curve to formally test for calibration of the risk model.

We begin with models including only a single continuous marker or a pre-defined marker combination and later examine the extension to a general risk model. The problems caused by developing combinations and assessing them in the same dataset have been well recognized and the assessment of a predefined combination with independent test data is encouraged [12, 13]. In these circumstances our methods apply to evaluations with the test data. For example, Buyse and others [14] recently reported the performance of a gene expression signature combination previously developed by van't Veer and others [15] and van de Vijver and others [16]. Other examples of well known predefined combination scores are the Framingham score for cardiovascular events [17] and the Gail score for breast cancer risk [18].

Let ρ = P(D = 1) denote the prevalence of the bad outcome. We assume either that ρ is fixed at a specified value or that an estimate $\widehat{\rho }$ is available in addition to the case-control sample. For example, the prevalence is essentially known if obtained from a large population registry; alternatively, one can entertain various fixed values for ρ that might reflect prevalences in different populations, performing a “what if” exercise that allows one to surmise in which populations the biomarker would be useful and in which populations it might not. Settings where a prevalence estimate is available includes estimates from an independent cohort study reported in the literature, or estimates calculated from a parent cohort within which the case-control study is nested [10, 19]. When an estimate of ρ is obtained from an independent cohort or the parent cohort, variability in $\widehat{\rho }$ must be taken into account in computing variance of the predictiveness estimator.

We make the assumption that P(D = 1|Y) is monotone increasing in Y. If the risk is decreasing in Y, the marker can be negated to satisfy this assumption. Extensions discussed in section 6 accommodate non-monotone risk functions. Under the monotone increasing risk assumption, the v^th quantile of the marker corresponds to the v^th quantile of risk which implies that R(v) = Risk{F⁻¹(v)}. For estimation purposes we therefore need to estimate the risk function, Risk(Y) = P(D = 1|Y), as well as the marker distribution F(y) = P(Y ≤ y), and combine the two estimands to get the estimator for the risk quantile.

2. Estimation of the Risk Function

In this section, we consider estimation of the risk function as the first step in estimating the predictiveness curve. The risk can be estimated either using parametric or nonparametric methods. The former gives rise to semiparametric predictiveness curve estimates while the latter gives rise to fully nonparametric estimates.

2.1 Parametric Risk Functions: Logistic Regression

For case-control data, a logistic regression formulation of the risk model is convenient. We write it as

$$\text{logit}P(D=1\mid Y)=\text{logit}\left\{G(\theta ,Y)\right\}={\theta }_0+\eta ({\theta }_1,Y)$$ (2.1)

where η is monotone increasing in Y. For example, η(θ₁, Y) can take a linear form θ₁Y with θ₁ > 0. A more general and flexible model can involve the Box-Cox type transformation [20]. That is η(θ₁, Y) = θ₁₁Y^(θ₁₂) with θ₁₁ > 0, where Y^(θ₁₂) = (Y^θ₁₂ − 1)/θ₁₂ when θ₁₂ ≠ 0 and Y^(θ₁₂) = log Y when θ₁₂ = 0. In case-control studies, since the sampling rate of cases versus controls is fixed by design, the intercept term θ₀ in the risk model is not estimable. However, the odds ratio is still estimable, a fact that is routinely exploited in epidemiology [21]. The maximum likelihood estimator of the odds ratio from the retrospective likelihood can be obtained by maximizing the prospective likelihood of the case-control sample, pretending that the outcome is random and ignoring the outcome-dependent nature of the sampling [22, 23].

Let n_D and n_D̄ be the number of cases and controls respectively in the case-control sample. Applying the logistic regression model (2.1) to the data and then applying a shift $\text{log}\{\widehat{\rho }∕(1-\widehat{\rho })n_{\stackrel{‒}{D}}∕n_D\}$ to the intercept, we obtain $\widehat{\theta }=({\widehat{\theta }}_0,{\widehat{\theta }}_1)$, the maximum likelihood estimator of θ. This follows because the population odds is related to the sample odds as a result of the Bayes’ theorem:

$$\frac{P(D=1\mid Y)}{P(D=0\mid Y)}=\frac{P(D=1\mid Y,S)}{P(D=0\mid Y,S)}\frac{P(D=0\mid S)}{P(D=1\mid S)}\frac{P(D=1)}{P(D=0)},$$

where S is the indicator of being included in the case-control sample. Therefore to calculate the population risk from the model fit to case-control data, we add the term $\text{log}\{\widehat{\rho }∕(1-\widehat{\rho })n_{\stackrel{‒}{D}}∕n_D\}$ to the estimated intercept.

2.2 Nonparametric Risk Functions: Isotonic Regression

A more robust approach is to estimate the risk model nonparametrically. Again the risk is assumed to be monotone increasing in Y. We compute the nonparametric maximum likelihood estimator for the risk function subject to monotonicity using isotonic regression [24]. A heuristic explanation of the algorithm in this particular circumstance was given by Lloyd [25]. Specifically, marker data {y₁, . . . , y_n} are arranged in increasing order, followed by repetitive blocking and pooling of adjacent blocks until the sample proportion of cases within each block is non-decreasing. Finally, we calculate P̂(D = 1|Y = y_j, S), the proportion of diseased subjects within the block containing y_j. Case-control sampling again requires an adjustment to estimate the population risk function. Specifically we use the relationship

$$\frac{\widehat{P}(D=1\mid Y)}{\widehat{P}(D=0\mid Y)}=\frac{\widehat{P}(D=1\mid Y,S)}{\widehat{P}(D=0\mid Y,S)}\frac{n_{\stackrel{‒}{D}}}{n_D}\frac{\widehat{\rho }}{1-\widehat{\rho }}.$$

3. Estimation of the Marker Distribution and the Predictiveness Curve

In a case-control study, F cannot be estimated directly but can be estimated as a weighted average of the distributions of Y in the case and control subpopulations. Specifically, since F = ρF_D + (1 − ρ)F_D̄, we estimate ρ, F_D and F_D̄ and substitute the estimates to obtain the estimate of F. Two approaches to estimating F_D and F_D̄ are possible under the parametric and nonparametric risk modeling assumptions.

3.1 The Semiparametric Estimators of the Predictiveness Curve

3.1.1 The Semiparametric “Empirical” Estimator

A natural strategy to estimate F_D̄ and F_D is to use the corresponding empirical estimators which we denote by F̃_D̄ and F̃_D. Estimating F with $\tilde{F}=\widehat{\rho }{\tilde{F}}_D+(1-\widehat{\rho }){\tilde{F}}_{\stackrel{‒}{D}}$, the resulting semiparametric “empirical” estimators of R(v) and R⁻¹(p) are

$$\begin{array}{cc}\hfill \tilde{R}\left(v\right)& =G\left\{\widehat{\theta },{\tilde{F}}^{-1}\left(v\right)\right\}\text{for}v\in (0,1),\hfill \\ \hfill {\tilde{R}}^{-1}\left(p\right)& =\tilde{F}\left\{G^{-1}(\widehat{\theta },p)\right\}\text{for}p\in \{R\left(v\right):v\in (0,1)\},\hfill \end{array}$$

where G⁻¹(θ, p) = inf{y : G(θ, y) ≥ p}.

3.1.2 The Semiparametric “Maximum Likelihood” Estimator

Let f_D and f_D̄ denote density functions of the marker Y in the case and control populations respectively. Observe that the risk model (2.1) implies an exponential tilt relationship between marker densities among cases and controls

$$\mathcal{L}\mathrm{R}\left(Y\right)=f_D\left(Y\right)∕f_{\stackrel{‒}{D}}\left(Y\right)=\text{exp}\left\{{\theta }_0+\text{log}\left(\frac{1-\rho }{\rho }\right)+\eta ({\theta }_1,Y)\right\},$$ (3.1)

where $\mathcal{L}\mathrm{R}\left(Y\right)$ is called the likelihood ratio of Y. This relationship is not exploited when F_D and F_D̄ are estimated empirically [26, 11]. We have shown that by employing an empirical likelihood approach [27, 28, 29], the maximum likelihood estimators for F_D̄ and F_D are

$$\begin{array}{c}\hfill {\widehat{F}}_{\stackrel{‒}{D}}\left(y\right)=\frac{1}{n_{\stackrel{‒}{D}}}\sum _{i=1}^n\frac{I(Y_i\le y)}{1+\frac{n_D}{n_{\stackrel{‒}{D}}}\text{exp}\left\{{\widehat{\theta }}_0+\text{log}\left(\frac{1-\widehat{\rho }}{\widehat{\rho }}\right)+\eta ({\widehat{\theta }}_1,Y_i)\right\}}=\frac{1}{n}\sum _{i=1}^n\frac{I(Y_i\le y)}{\frac{n_{\stackrel{‒}{D}}}{n}+\frac{n_D}{n}\widehat{\mathcal{L}\mathrm{R}}\left(Y_i\right)},\hfill \\ \hfill {\widehat{F}}_D\left(y\right)=\frac{1}{n_{\stackrel{‒}{D}}}\sum _{i=1}^n\frac{\text{exp}\left\{{\widehat{\theta }}_0+\text{log}\left(\frac{1-\widehat{\rho }}{\widehat{\rho }}\right)+\eta ({\widehat{\theta }}_1,Y_i)\right\}I(Y_i\le y)}{1+\frac{n_D}{n_{\stackrel{‒}{D}}}\text{exp}\left\{{\widehat{\theta }}_0+\text{log}\left(\frac{1-\widehat{\rho }}{\widehat{\rho }}\right)+\eta ({\widehat{\theta }}_1,Y_i)\right\}}=\frac{1}{n}\sum _{i=1}^n\frac{\widehat{\mathcal{L}\mathrm{R}}\left(Y_i\right)I(Y_i\le y)}{\frac{n_{\stackrel{‒}{D}}}{n}+\frac{n_D}{n}\widehat{\mathcal{L}\mathrm{R}}\left(Y_i\right)},\hfill \end{array}$$

where ${\widehat{\theta }}_0$ is the logistic regression intercept adjusted by $\text{log}\{\widehat{\rho }∕(1-\widehat{\rho })n_{\stackrel{‒}{D}}∕n_D\}$, and $\widehat{\mathcal{L}\mathrm{R}}$ is the maximum likelihood estimator of $\mathcal{L}\mathrm{R}$ [11]. We use these estimators to compute $\widehat{F}=(1-\widehat{\rho }){\widehat{F}}_{\stackrel{‒}{D}}+\widehat{\rho }{\widehat{F}}_D$, and then plug $\widehat{\theta }$ and F̂ into G to get the semiparametric maximum likelihood estimators of R(v) and R⁻¹(p):

$$\begin{array}{cc}\hfill \widehat{R}\left(v\right)& =G\left\{\widehat{\theta },{\widehat{F}}^{-1}\left(v\right)\right\}\text{for}v\in (0,1),\hfill \\ \hfill {\widehat{R}}^{-1}\left(p\right)& =\widehat{F}\left\{G^{-1}(\widehat{\theta },p)\right\}\text{for}p\in \{R\left(v\right):v\in (0,1)\}.\hfill \end{array}$$

Note that the semiparametric estimators developed here for case-control studies generalizes the semiparametric estimator developed for cohort studies in Huang and others [7]. That is, when plugging in $\widehat{\rho }=n_D∕n$ from a cohort study, both the semiparametric maximum likelihood estimator and the semiparametric “empirical” estimator of the predictiveness curve equal to the cohort version proposed earlier [11].

Asymptotic distribution theory for the two estimators can be found in Huang and Pepe [11]. As an example, consider an ordinary logistic risk model: $\text{logit}\left\{G(\theta ,Y)\right\}={\theta }_0+{\theta }_1^{T}r\left(Y\right)$, where r(Y) is some monotone increasing function of Y. Suppose $\widehat{\rho }$ is estimated from a cohort independent of the case-control sample, or the parent cohort within which the case-control sample is nested, with the size of the cohort λ times the size of the case-control sample. Then we have

$$\begin{array}{cc}\hfill n\text{var}\left\{{\widehat{R}}^{-1}\left(p\right)\right\}& \simeq {\{F_D\left(p\right)-F_{\stackrel{‒}{D}}\left(p\right)\}}^2\rho (1-\rho )∕\lambda +V_{M1}\hfill \\ \hfill & +{\left\{\frac{\partial R^{-1}\left(p\right)}{\partial \theta }\right\}}^T\left\{\left(\begin{array}{cc}\hfill \frac{1}{\lambda \rho (1-\rho )}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)+V_{M2}\right\}\left\{\frac{\partial R^{-1}\left(p\right)}{\partial \theta }\right\}\hfill \\ \hfill & +2{\left\{\frac{\partial R^{-1}\left(p\right)}{\partial \theta }\right\}}^T\left\{\frac{F_D\left(t\right)-F_{\stackrel{‒}{D}}\left(t\right)}{\lambda }+V_{M3}\right\}.\hfill \end{array}$$ (3.2)

Analytic forms for V_M1, V_M2, V_M3 are provided in Appendix A. Similarly, we have

$$\begin{array}{cc}\hfill n\text{var}\left\{{\tilde{R}}^{-1}\left(p\right)\right\}& \simeq {\{F_D\left(p\right)-F_{\stackrel{‒}{D}}\left(p\right)\}}^2\rho (1-\rho )∕\lambda +V_{E1}\hfill \\ \hfill & +{\left\{\frac{\partial R^{-1}\left(p\right)}{\partial \theta }\right\}}^T\left\{\left(\begin{array}{cc}\hfill \frac{1}{\lambda \rho (1-\rho )}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)+V_{E2}\right\}\left\{\frac{\partial R^{-1}\left(p\right)}{\partial \theta }\right\}\hfill \\ \hfill & +2{\left\{\frac{\partial R^{-1}\left(p\right)}{\partial \theta }\right\}}^T\left\{\frac{F_D\left(t\right)-F_{\stackrel{‒}{D}}\left(t\right)}{\lambda }+V_{E3}\right\},\hfill \end{array}$$ (3.3)

where analytic forms for V_E1, V_E2, V_E3 are provided in Appendix A. Moreover, for v = R⁻¹(p), var {R̃(v)} ≃ {∂R(v)/∂v}² var {R̃⁻¹(p)} and var {R̂(v)} ≃ {∂R(v)/∂v}² var {R̂⁻¹(p)}. When ρ is fixed, essentially we have λ → ∞, thus terms involving 1/λ vanish in (3.2) and (3.3).

3.2 The Nonparametric Estimator

Similar to the semiparametric approach, we can estimate F_D and F_D̄ empirically with F̃_D̄ and F̃_D yielding $\tilde{F}=\widehat{\rho }{\tilde{F}}_D+(1-\widehat{\rho }){\tilde{F}}_{\stackrel{‒}{D}}$. Substituting the non-parametric risk estimator and F̃ we derive the nonparametric “empirical” estimators of R(v) and R⁻¹(p)as

$$\begin{array}{cc}\hfill \tilde{R}\left(v\right)& =\widehat{P}\left\{D=1\mid Y={\tilde{F}}^{-1}\left(v\right)\right\}v\in (0,1),\hfill \\ \hfill {\tilde{R}}^{-1}\left(p\right)& =\tilde{F}\left[\text{sup}\left\{y:\widehat{P}(D=1\mid Y=y)\le p\right\}\right]p\in \{R\left(v\right):v\in (0,1)\}.\hfill \end{array}$$

Alternatively, we can incorporate the estimated risk function into estimation of the marker distribution, as was done for the semiparametric procedure. Lloyd [25] showed that maximizing the joint likelihood of D and Y can be achieved by first obtaining P̂(D = 1|Y, S), and then estimating f_D̄ and f_D based on the relationship

$$\mathcal{L}\mathrm{R}\left(Y\right)=\frac{f_D\left(Y\right)}{f_{\stackrel{‒}{D}}\left(Y\right)}=\frac{P(D=1\mid Y,S)}{P(D=0\mid Y,S)}\frac{n_{\stackrel{‒}{D}}}{n_D}\propto \frac{P(D=1\mid Y,S)}{P(D=0\mid Y,S)}.$$

In particular, let ŵ(Y) = P̂(D = 1|Y, S)/P̂(D = 0|Y, S) and let κ denote {k : ŵ(Y_k) = ∞}. He demonstrated that by maximizing $\mathcal{L}(F_{\stackrel{‒}{D}},F_D)={\prod }_{i=1}^{n_D}{f}_{\stackrel{‒}{D}}\left(Y_{\stackrel{‒}{D}i}\right){\prod }_{j=1}^{n_D}{f}_D\left(Y_{Dj}\right)={\prod }_{i=1}^n{f}_{\stackrel{‒}{D}}\left(Y_i\right){\prod }_{j=1}^{n_D}\widehat{w}\left(Y_{Dj}\right)∕\mu$ with μ a normalizing factor, the estimators of f_D̄ and f_D are

$${\widehat{f}}_{\stackrel{‒}{D}}\left(Y_k\right)=\{\begin{array}{cc}\hfill \widehat{\mu }∕(n_D\widehat{w}\left(Y_k\right)+n_{\stackrel{‒}{D}}\widehat{\mu })\hfill & \hfill k\notin \kappa \hfill \\ \hfill 0\hfill & \hfill k\in \kappa \hfill \end{array}\phantom{\}},{\widehat{f}}_D\left(Y_k\right)=\{\begin{array}{cc}\hfill \widehat{w}\left(Y_k\right){\widehat{f}}_{\stackrel{‒}{D}}\left(Y_k\right)∕\widehat{\mu }\hfill & \hfill k\notin \kappa \hfill \\ \hfill 1∕n_D\hfill & \hfill k\in \kappa \hfill \end{array}\phantom{\}}$$ (3.4)

in the absence of ties. He also suggested that $\widehat{\mu }$ could be found by solving

$$\sum _{k\in \kappa }\frac{\mu }{n_D\widehat{w}\left(Y_k\right)+n_{\stackrel{‒}{D}}\mu }=1,$$ (3.5)

which is monotone increasing in μ.

The following new result, proved in Appendix B1, shows that when P(D = 1|Y, S) is estimated using isotonic regression, $\widehat{\mu }$ can be written down explicitly as a function of n_D̄ and n_D.

Theorem 1 When P(D = 1|Y, S) is estimated using isotonic regression, $\widehat{\mu }=n_D∕n_{\stackrel{‒}{D}}$.

Plugging $\widehat{\mu }$ into (3.4), we have

$${\widehat{f}}_{\stackrel{‒}{D}}\left(Y_k\right)=\{\begin{array}{cc}\hfill \frac{1}{n_{\stackrel{‒}{D}}\{\widehat{w}\left(Y_k\right)+1\}}\hfill & \hfill k\notin \kappa \hfill \\ \hfill 0\hfill & \hfill k\in \kappa \hfill \end{array}\phantom{\}},{\widehat{f}}_D\left(Y_k\right)=\{\begin{array}{cc}\hfill \frac{\widehat{w}\left(Y_k\right)}{n_D\{\widehat{w}\left(Y_k\right)+1\}}\hfill & \hfill k\notin \kappa \hfill \\ \hfill 1∕n_D\hfill & \hfill k\in \kappa \hfill \end{array}.\phantom{\}}$$

Estimating F with $\widehat{F}=\widehat{\rho }{\widehat{F}}_D+(1-\widehat{\rho }){\widehat{F}}_{\stackrel{‒}{D}}$, where F̂_D and F̂_D̄ denote the corresponding cumulative distribution functions, the nonparametric maximum likelihood estimators of R(v) and R⁻¹(p) are

$$\begin{array}{cc}\hfill \widehat{R}\left(v\right)& =\widehat{P}\left\{D=1\mid Y={\widehat{F}}^{-1}\left(v\right)\right\}\text{for}v\in (0,1),\hfill \\ \hfill {\widehat{R}}^{-1}\left(p\right)& =\widehat{F}\left[\text{sup}\left\{y:\widehat{P}(D=1\mid Y=y)\le p\right\}\right]\text{for}p\in \{R\left(v\right):v\in (0,1)\}.\hfill \end{array}$$

Interestingly, we have found that even if the nonparametric “empirical” and maximum likelihood procedures described above lead to different estimators of the marker distribution F, the corresponding predictiveness curve estimators are the same (Theorem 2). This fact is not true for the semiparametric estimators. A proof can be found in Appendix B2.

Theorem 2 When the risk model is estimated nonparametrically with isotonic regression, R̂(v) = R̃(v) and R̂⁻¹(p) = R̃⁻¹(p).

3.3 Area under the Predictiveness Curve

The area under the true predictiveness curve, ${\int }_0^{1}R\left(v\right)dv$, is equal to ρ [7]. This facilitates visual comparisons of predictiveness curves for two different risk models because, in a sense, it maintains them both on exactly the same scale. The steepness of curves can be compared more easily when both integrate to ρ. An analogous result holds for the nonparametric and semiparametric maximum likelihood estimators (Theorem 3) but not for the semiparametric “empirical” estimator.

Theorem 3 Let R̂(v) be the nonparametric or semiparametric maximum likelihood estimator of R(v) for v ∈ (0, 1) using the prevalence estimator $\widehat{\rho }$. Then ${\int }_0^1\widehat{R}\left(v\right)dv$, the area under the predictiveness curve estimate equals to $\widehat{\rho }$.

Proof of Theorem 3 is presented in Appendix B3. An implication of Theorem 3 is that for the nonparametric and semiparametric maximum likelihood estimators, the two areas sandwiched between the curve and the horizontal line are equal. To see this, let $v^{\ast }=\text{inf}\left\{v:\widehat{R}\left(v\right)\ge \widehat{\rho }\right\}$, then the area below the horizontal line at $\widehat{\rho }$ and above the estimated predictiveness curve is equal to ${\int }_0^{v^{\ast }}\left\{\widehat{\rho }-\widehat{R}\left(v\right)\right\}dv$, while the area above the horizontal line at $\widehat{\rho }$ and below the estimated predictiveness curve is equal to ${\int }_{v^{\ast }}^1\left\{\widehat{R}\left(v\right)-\widehat{\rho }\right\}dv$. According to Theorem 3,

$${\int }_0^1\widehat{R}\left(v\right)dv=\widehat{\rho }\Rightarrow {\int }_0^1\left\{\widehat{R}\left(v\right)-\widehat{\rho }\right\}dv=0\Rightarrow {\int }_0^{v^{\ast }}\left\{\widehat{R}\left(v\right)-\widehat{\rho }\right\}dv+{\int }_{v^{\ast }}^1\left\{\widehat{R}\left(v\right)-\widehat{\rho }\right\}dv=0\Rightarrow {\int }_0^{v^{\ast }}\left\{\widehat{\rho }-\widehat{R}\left(v\right)\right\}dv={\int }_{v^{\ast }}^1\left\{\widehat{R}\left(v\right)-\widehat{\rho }\right\}dv.$$

4. Simulation Studies

We conducted simulation studies in two settings to evaluate the performances of the proposed estimators. In each setting, data were generated to mimic a two-phase study. In the first phase, a random cohort sample is obtained and the disease status of every subject is determined. In the second phase, cases and controls were selected independently from the parent cohort and biomarker data was ascertained. The size of the cohort is chosen to be five times that of the nested case-control sample.

4.1 Simulation Setting 1

In the first simulation setting, a binary outcome status was generated with ρ = 0.2 from a cohort of size 5n and marker data were generated according to Y_D̄ ~ N(0, 1) and Y_D ~ N(μ_D, 1), for equal numbers of cases and controls, n_D = n_D̄ = n/2. The resulting risk function follows a linear logistic model. We explored sample sizes n ranging from 100 to 2,000. For each scenario, 5,000 Monte-Carlo simulations were conducted.

The semiparametric (based on the linear logistic model) and nonparametric estimators of the predictiveness curve were estimated using $\widehat{\rho }$ obtained from the cohort. Variance estimates for the semiparametric estimators were calculated using analytic formulae from the asymptotic theory which incorporates variability in $\widehat{\rho }$ (as provided in Appendix B1). Bootstrapping was also performed by separately resampling cases and controls for Y and resampling D from the parent cohort. Results pertaining to the choice μ_D = 1 are presented in Tables 1 - 4 for v = 0.1, 0.3, 0.5, 0.7, and 0.9 and for the corresponding values of p, p = R(v).

Table 1.

Bias of the semiparametric and nonparametric estimators for the linear logistic model. Also shown are biases of variance estimators based on asymptotic theory. Here n_D = n_D̄ = n/2. Size of the phase-one cohort for estimating $\widehat{\rho }$ is 5n. SPMLE denotes the semiparametric maximum likelihood estimator, SPE denotes the semiparametric “empirical” estimator, NPMLE denotes the nonparametric maximum likelihood estimator.

		v = 0.1	v = 0.3	v = 0.5	v = 0.7	v = 0.9
R(v)		0.045	0.094	0.15	0.24	0.43
% bias in R̂(v)
n = 100	SPMLE	4.47	–0.50	–1.39	–0.82	0.82
	SPE	5.13	–0.40	–1.18	–0.53	0.94
	NPMLE	–35.35	–9.42	–5.44	–3.27	2.86
n = 500	SPMLE	1.14	–0.06	–0.34	–0.13	0.16
	SPE	1.12	–0.06	–0.30	–0.07	0.15
	NPMLE	–13.15	–3.21	–1.86	–1.38	0.58
n = 2000	SPMLE	0.16	–0.13	–0.13	–0.07	0.11
	SPE	0.15	–0.13	–0.10	–0.06	0.10
	NPMLE	–4.72	–1.59	–0.83	–0.47	0.35
% bias in variance estimate of R̂(v)
n = 100	SPMLE	-4.44	7.91	7.28	1.54	-4.23
	SPE	-1.27	7.03	9.02	1.22	-4.35
n = 500	SPMLE	-1.99	1.47	3.63	2.11	-0.35
	SPE	–2.50	2.07	3.88	-1.92	2.48
n = 2000	SPMLE	–1.39	1.33	1.91	1.20	-0.49
	SPE	–1.13	1.65	2.31	1.65	-1.06
		p = 0.045	p = 0.094	p = 0.15	p = 0.24	p = 0.43
R–1(p)		0.1	0.3	0.5	0.7	0.9
% bias in R̂–1(p)
n = 100	SPMLE	12.68	0.39	–0.16	0.55	0.11
	SPE	12.90	0.38	–0.34	0.50	0.12
	NPMLE	80.50	15.00	5.86	2.06	–0.79
n = 500	SPMLE	2.43	0.02	0.002	0.11	0.03
	SPE	2.53	0.02	–0.04	0.06	0.04
	NPMLE	29.78	5.84	2.11	0.86	–0.23
n = 2000	SPMLE	0.94	0.15	0.05	0.04	–0.01
	SPE	0.94	0.14	0.03	0.04	–0.01
	NPMLE	12.84	2.47	0.98	0.34	–0.16
% bias in variance estimate of R̂–1(p)
n = 100	SPMLE	15.14	-6.80	-14.03	-11.01	9.52
	SPE	14.88	-5.62	-13.62	-9.67	8.81
n = 500	SPMLE	7.40	-6.14	-5.92	-5.86	5.54
	SPE	7.34	–6.12	-6.05	-5.87	3.58
n = 2000	SPMLE	2.75	-2.87	-3.08	-1.84	3.66
	SPE	2.70	-2.75	-2.36	-0.56	4.00

Table 4.

Efficiency (ratio of observed variances in simulation studies) of the semiparametric “empirical” estimator and nonparametric estimator relative to the semiparametric maximum likelihood estimator of the predictiveness curve in nested case-control studies for the linear logistic model. SPE denotes the semiparametric “empirical” estimator, NPMLE denotes the nonparametric maximum likelihood estimator. Here n = ∞ denotes the asymptotic variance.

		v = 0.1	v = 0.3	v = 0.5	v = 0.7	v = 0.9
R(v)		0.045	0.094	0.15	0.24	0.43
n = 100	SPE	1.02	0.97	0.97	0.90	0.91
	NPMLE	0.45	0.41	0.27	0.18	0.29
n = 500	SPE	0.98	0.98	0.96	0.90	0.89
	NPMLE	0.25	0.25	0.16	0.10	0.18
n = 2000	SPE	0.99	0.98	0.96	0.90	0.91
	NPMLE	0.17	0.16	0.10	0.06	0.11
n = ∞	SPE	0.99	0.97	0.97	0.90	0.91
		p = 0.045	p = 0.094	p = 0.15	p = 0.24	p = 0.43
R–1(p)		0.1	0.3	0.5	0.7	0.9
n = 100	SPE	0.99	0.99	0.96	0.91	0.91
	NPMLE	0.47	0.47	0.32	0.21	0.38
n = 500	SPE	0.99	0.98	0.95	0.90	0.90
	NPMLE	0.28	0.27	0.17	0.10	0.20
n = 2000	SPE	0.99	0.98	0.96	0.91	0.91
	NPMLE	0.18	0.16	0.10	0.06	0.12
n = ∞	SPE	0.99	0.97	0.97	0.90	0.91

First we consider the performance of the semiparametric estimators for R(v) and R⁻¹(p). We see that they have minimal bias for sample sizes as small as 100 (Table 1). Variance estimators that are based on analytic formulas from asymptotic theory agree well with the empirical variance from simulations when n_D + n_D̄ ≥ 500. This was also true for the bootstrap variance (results not shown). Coverage of the 95% Wald confidence intervals using asymptotic or bootstrap variance estimates are fairly close to the nominal level, except for a little undercoverage when n_D + n_D̄ ≤ 200 (Table 2). The intervals shown in Table 2 assumed that the logit transform of the estimator was normally distributed and had better coverage than symmetric intervals for the untransformed estimators.

Table 2.

Coverage of 95% Wald confidence intervals based on the semiparametric and nonparametric estimators in nested case-control studies for the linear logistic model, assuming the logit transform of the estimator is normally distributed. SPMLE denotes the semiparametric maximum likelihood estimator, SPE denotes the semiparametric “empirical” estimator, and NPMLE denotes the nonparametric maximum likelihood estimator.

		v = 0.1	v = 0.3	v = 0.5	v = 0.7	v = 0.9
R(v)		0.045	0.094	0.15	0.24	0.43
		Based on asymptotic variance estimate
n = 100	SPMLE	95.82	95.64	95.94	96.22	95.50
	SPE	95.78	95.58	96.38	96.04	95.44
n = 500	SPMLE	94.62	95.14	95.88	95.40	94.80
	SPE	94.64	95.30	95.78	95.42	94.52
n = 2000	SPMLE	95.00	95.38	95.32	95.06	94.96
	SPE	94.92	95.22	95.44	95.62	95.50
		Based on bootstrap variance estimate
n = 100	SPMLE	96.02	95.14	95.68	96.68	96.26
	SPE	96.04	95.02	96.02	96.86	96.04
	NPMLE	96.49	97.56	96.64	96.36	98.10
n = 500	SPMLE	95.06	94.94	95.30	95.28	95.18
	SPE	94.96	95.02	95.34	95.60	94.86
	NPMLE	96.57	94.76	95.16	95.30	96.04
n = 2000	SPMLE	95.20	95.18	94.78	95.22	94.94
	SPE	95.02	95.22	95.04	95.36	95.58
	NPMLE	94.58	94.08	94.84	94.62	94.90
		p = 0.045	p = 0.094	p = 0.15	p = 0.24	p = 0.43
R–1(p)		0.1	0.3	0.5	0.7	0.9
		Based on asymptotic variance estimate
n = 100	SPMLE	91.39	93.55	95.30	95.94	93.13
	SPE	91.22	93.97	95.50	96.26	93.63
n = 500	SPMLE	95.40	95.10	94.98	94.86	95.76
	SPE	95.32	94.86	94.94	94.82	95.76
n = 2000	95.40	94.82	94.80	94.94	95.28
	SPE	95.28	95.10	94.80	95.30	95.56
		Based on bootstrap variance estimate
n = 100	SPMLE	91.73	94.75	96.16	97.10	93.85
	SPE	91.62	94.99	96.28	96.98	94.06
	NPMLE	72.82	90.81	96.40	97.52	90.68
n = 500	SPMLE	95.16	95.32	95.48	95.32	94.78
	SPE	95.10	95.36	95.60	95.24	95.34
	NPMLE	83.21	93.08	96.26	96.66	93.20
n = 2000	SPMLE	94.86	94.92	95.04	95.10	94.84
	SPE	94.80	95.12	95.36	95.58	94.90
	NPMLE	89.08	94.14	95.22	95.68	94.58

Results are also shown in Table 3 for confidence intervals employing percentiles of the bootstrap distribution. We found that these confidence intervals performed best overall. Moreover, the corresponding lower and upper confidence limits are monotone increasing in v. This is a desirable property because, by definition, the predictiveness curve itself is monotone increasing. Having lower and upper pointwise confidence limit curves that are monotone increasing is consistent with monotonicity of the predictiveness curve. To see that the pointwise confidence limits are increasing in v, let R̂_b(v) be the estimate of R(v) based on the b^th bootstrap sample. We have R̂_b(v₁) ≤ R̂_b(v₂) for v₁ ≤ v₂ according to our estimation methods. As a result, the α^th percentile of R̂_b(v₁) is always smaller than or equal to the α^th percentile of R̂_b(v₂) among the same set of bootstrap samples. In our simulations, we chose α = 0.025 and α = 0.975.

Table 3.

Coverage of 95% percentile bootstrap confidence intervals based on the semiparametric and nonparametric estimators in nested case-control studies for the linear logistic model. SPMLE denotes the semiparametric maximum likelihood estimator, SPE denotes the semiparametric “empirical” estimator, and NPMLE denotes the nonparametric maximum likelihood estimator.

		v = 0.1	v = 0.3	v = 0.5	v = 0.7	v = 0.9
R(v)		0.045	0.094	0.15	0.24	0.43
n = 100	SPMLE	94.24	94.50	95.08	95.86	94.80
	SPE	94.58	94.64	95.28	96.36	94.98
	NPMLE	79.74	94.30	96.58	97.54	98.02
n = 500	SPMLE	94.18	94.18	94.42	95.88	94.22
	SPE	94.66	94.16	94.60	96.02	94.54
	NPMLE	93.04	95.92	97.18	97.40	98.20
n = 2000	SPMLE	94.38	94.52	94.66	94.72	94.22
	SPE	94.58	94.38	95.08	95.08	94.76
	NPMLE	94.80	96.66	97.44	97.80	97.96
		p = 0.045	p = 0.094	p = 0.15	p = 0.24	p = 0.43
R–1(p)		0.1	0.3	0.5	0.7	0.9
n = 100	SPMLE	94.24	94.54	95.04	95.90	94.80
	SPE	94.56	94.72	95.28	96.38	95.08
	NPMLE	79.74	94.36	96.62	97.60	98.06
n = 500	SPMLE	94.12	94.06	95.02	94.90	94.22
	SPE	94.22	94.46	95.40	95.18	94.62
	NPMLE	91.44	96.02	97.20	97.92	98.20
n = 2000	SPMLE	94.38	94.48	94.70	94.74	94.12
	SPE	94.58	94.42	95.12	95.10	94.74
	NPMLE	94.80	96.62	97.46	97.80	97.92

The nonparametric estimator of the predictiveness curve performed poorly relative to the semi-parametric estimators in this simulation setting. When sample sizes are smaller than 500, biases in estimates of R(v) and R⁻¹(p) are substantial, and confidence intervals suffer from undercoverage or overcoverage in many settings (Tables 2,3). Their efficiency is dramatically worse than the efficiencies of the semiparametric estimators (Table 4). This is especially true in large samples.

The two semiparametric estimators have similar performances in the simulations. Of note, the semiparametric “empirical” estimator is fairly efficient relative to the semiparametric maximum likelihood estimator (Table 4). Based on these limited simulations we recommend use of either of the semiparametric estimators in practice with confidence intervals constructed from percentiles of the bootstrap distribution when resampling is feasible, or from the logit transform with corresponding analytic variance formulas when bootstrapping is not feasible.

4.2 Simulation Setting 2

We investigated another simulation setting where marker Y follows a standard normal distribution, and the risk quantile follows a piece-wise linear form with cutpoint at the quintiles. Specifically, R(v) takes value 0, 0.1, 0.16, 0.2, 0.24, 0.3 at cutpoints v = 0, 0.2, 0.4, 0.6, 0.8, 1, and is linear in between. As before, we first simulate a cohort of size 5n, and then randomly sample n_D = n/2 cases and n_D̄ = n/2 controls from the cohort. The semiparametric estimators again are obtained assuming a linear logistic model. Tables 5 and 6 present bias, efficiency (in terms of mean squared error), and coverage of the 95% percentile bootstrap confidence intervals for the semiparametric and nonparametric estimators, for case-control sample sizes varying from 500 to 2,000. The semiparametric estimators that assume an incorrect working model, have poorer performance compared to that in the first simulation setting. For estimation of both R(v) and R⁻¹(p), they have nonignorable biases that do not dissapate as sample size increases. As a result, coverages of their confidence intervals are often seriously below the nominal level, especially in large sample size. The performance of the nonparametric estimator, nevertheless, is fairly consistent with that in the first simulation setting. Its bias is much smaller compared to that of the semiparametric estimators and decreases as sample size increases. Consequently, for certain quantiles, the mean squared error of the nonparametric estimator is smaller than that of the semiparametric estimators. In general, for a sample size greater than 500, the confidence interval constructed from the nonparametric estimators maintain coverage close to the nominal level.

Table 5.

Performances of the semiparametric and nonparametric estimators for R(v) when the predictiveness curve is piecewise linear. Here n_D = n_D̄ = n/2. Size of the phase-one cohort for estimating $\widehat{\rho }$ is 5n. SPMLE denotes the semiparametric maximum likelihood estimator, SPE denotes the semiparametric “empirical” estimator, NPMLE denotes the nonparametric maximum likelihood estimator.

		v = 0.1	v = 0.3	v = 0.5	v = 0.7	v = 0.9
R(v)		0.05	0.13	0.18	0.22	0.27
% bias in R̂(v)
n = 500	SPMLE	57.46	-9.06	-14.25	-9.24	4.72
	SPE	51.92	-10.74	-14.35	-8.02	7.70
	NPMLE	-13.25	-4.58	-2.55	-0.80	1.92
n = 1000	SPMLE	57.48	-8.87	-14.07	-9.13	4.57
	SPE	51.88	-10.53	-14.16	-7.94	7.54
	NPMLE	-8.42	-2.62	-1.38	-0.66	0.78
n = 2000	SPMLE	57.63	-8.74	-13.97	-9.11	4.46
	SPE	51.97	-10.38	-14.05	-7.90	7.36
	NPMLE	-4.54	-1.14	-0.71	-0.50	0.15
Efficiecya related to MLE
n = 500	SPE	1.19	0.81	0.98	1.22	0.66
	NPMLE	1.68	0.35	1.14	0.70	0.44
n = 1000	SPE	1.21	0.77	0.98	1.26	0.56
	NPMLE	2.57	0.43	1.65	0.97	0.48
n = 2000	SPE	1.22	0.75	0.99	1.29	0.50
	NPMLE	4.10	0.56	2.55	1.46	0.52
Coverage of 95% percentile boostrap CI
n = 500	SPMLE	30.16	79.22	16.70	46.18	90.06
	SPE	37.60	74.26	17.82	58.78	85.18
	NPMLE	92.44	96.18	96.64	96.78	97.56
n = 1000	SPMLE	5.92	65.32	1.64	18.60	87.36
	SPE	10.60	56.44	2.08	33.80	75.56
	NPMLE	94.52	96.54	96.84	96.94	97.62
n = 2000	SPMLE	0.06	43.04	0.00	2.16	79.06
	SPE	0.40	29.86	0.00	8.54	58.44
	NPMLE	95.60	96.90	97.20	97.32	97.46

^aefficiency in terms of mean squared error

Table 6.

Performances of the semiparametric and nonparametric estimators for R^–1(p) when the predictiveness curve is piecewise linear. Here n_D = n_D̄ = n/2. Size of the phase-one cohort for estimating $\widehat{\rho }$ is 5n. SPMLE denotes the semiparametric maximum likelihood estimator, SPE denotes the semiparametric “empirical” estimator, NPMLE denotes the nonparametric maximum likelihood estimator.

		p = 0.05	p = 0.13	p = 0.18	p = 0.22	p = 0.27
R–1(p)		0.1	0.3	0.5	0.7	0.9
% bias in R̂–1(p)
n = 500	SPMLE	-74.16	21.00	24.42	9.86	-2.01
	SPE	-71.15	23.93	23.28	8.27	-3.28
	NPMLE	19.68	7.85	5.52	1.53	-1.70
n = 1000	SPMLE	-76.78	21.13	24.07	9.65	-2.03
	SPE	-73.94	24.04	22.94	8.07	-3.32
	NPMLE	13.36	4.86	3.24	1.19	-0.99
n = 2000	SPMLE	-78.39	21.13	23.99	9.57	-2.04
	SPE	-75.62	24.02	22.83	7.97	-3.33
	NPMLE	8.28	2.99	1.59	1.05	-0.24
Efficiecya related to SPMLE
n = 500	SPE	1.05	1.20	1.17	1.21	1.17
	NPMLE	4.09	0.41	0.29	0.82	0.74
n = 1000	SPE	1.05	1.25	1.21	1.22	1.18
	NPMLE	6.68	0.32	0.29	1.05	0.73
n = 2000	SPE	1.06	1.29	1.23	1.23	1.19
	NPMLE	9.92	0.28	0.31	1.38	0.70
Coverage of 95% percentile boostrap CI
n = 500	SPMLE	30.28	79.30	16.74	46.14	90.04
	SPE	37.64	74.22	17.78	58.78	85.20
	NPMLE	92.40	96.14	96.64	96.78	97.58
n = 1000	SPMLE	5.94	65.32	1.64	18.56	87.40
	SPE	10.64	56.48	2.06	33.96	75.60
	NPMLE	94.44	96.54	96.78	96.96	97.64
n = 2000	SPMLE	0.06	42.94	0.00	2.16	79.06
	SPE	0.42	29.88	0.00	8.56	58.44
	NPMLE	95.62	96.96	97.24	97.30	97.46

^aefficiency in terms of mean squared error

Because of its robustness, the nonparametric estimator might be preferred in large studies where bias rather than precision is the major concern. On the other hand, in practice it is important to make the semiparametric model flexible to ensure a good fit, in light of its sensitivity to the risk model assumption. Comparing the nonparametric estimator with the semiparametric estimator provides an avenue for model checking. Later in this paper we propose a goodness-of-fit test to assess calibration formally.

5. Illustration

Levels of prostate specific antigen (PSA) and recent increases in levels of PSA (PSA velocity) are markers for prostate cancer. We evaluate them as predictors of the risk that a man will be diagnosed with prostate cancer if biopsied. These markers should only be used in decisions to take a biopsy if they are sufficiently informative of this risk. Data for evaluating these markers come from the Prostate Cancer Prevention Trial, a randomized prospective study with 7 years of follow-up [30]. Subjects were at least 55 years old, had serum PSA value less than 3.0 ng/ml at baseline and were scheduled for annual blood draws to measure serum PSA. Almost all subjects had a prostate biopsy taken at the end of study. We analyze data for the 5519 men on the placebo arm of the trial that had a prostate biopsy, a PSA measure during the year prior to biopsy and at least 2 PSA values from the 3 years prior to biopsy to calculate PSA velocity. The prevalence of prostate cancer in the cohort is $\widehat{\rho }=21.9\%$. We selected 250 cases and 250 controls at random from the cohort to simulate a nested case-control study. Thus the data for analysis consist of the prevalence estimate from the 5519 men in the parent cohort and PSA and PSA velocity for subjects in the case-control subset.

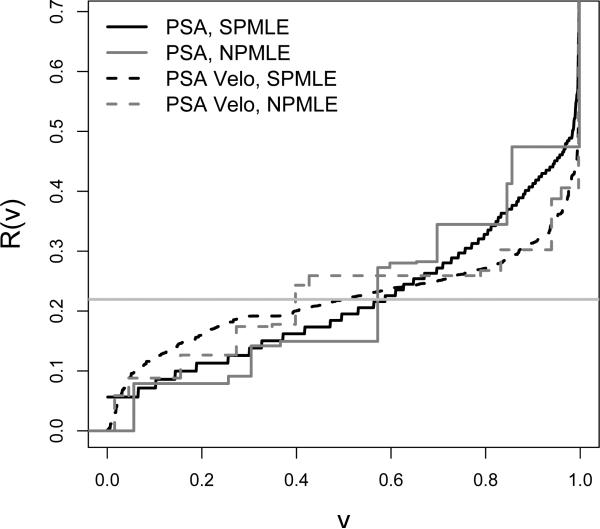
To implement the semiparametric methods for estimating predictiveness curves, for each marker a logistic regression risk model was employed using a Box-Cox transformation of the marker. The two semiparametric estimators of the predictiveness curves are very similar to each other for both PSA and PSA velocity and so only the semiparametric maximum likelihood estimators are displayed in Figure 1. Also displayed in Figure 1 are the nonparametric predictiveness curve estimates. Observe that the semiparametric curves are much smoother than the nonparametric ones, but agree with them, suggesting a good-fit for the semiparametric models. Overall, PSA has a steeper predictiveness curve, indicating that it is a better marker for predicting risk of prostate cancer than PSA velocity.

Figure 1.

The predictiveness curves for PSA and PSA velocity for predicting prostate cancer.

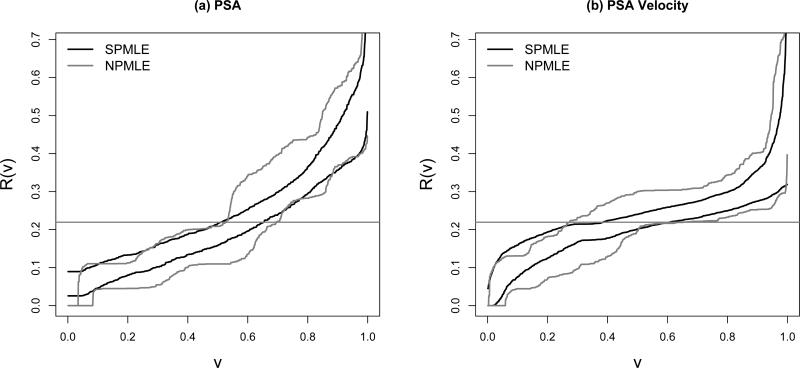
For the semiparametric estimators, the asymptotic and bootstrap variance estimates for R̂(v) and R̂⁻¹(p) are similar in magnitude (results not shown). Moreover, the Wald confidence intervals for R(v) and R⁻¹(p) are close to those based on percentiles of the bootstrap distributions. Here we present only the latter. The pointwise 95% percentile bootstrap confidence intervals for R(v) constructed from the semiparametric maximum likelihood estimators are displayed in Figure 2(a)(b). They are much narrower in comparison to those constructed from the nonparametric estimators.

Figure 2.

The 95% pointwise confidence intervals constructed from percentiles of the bootstrap distribution for the predictiveness curves of PSA and PSA velocity. SPMLE: semiparametric maximum likelihood estimator; NPMLE: nonparametric maximum likelihood estimator.

We next compare the predictive capacities of the two markers in terms of the 10^th and 90^th percentiles of their risk distributions and sizes of risk strata corresponding to a low risk threshold of 10% and a high risk threshold of 30% (Table 7 (a)). Results are presented for both the semiparametric maximum likelihood estimators and for the nonparametric estimators. P-values employ Wald tests based on differences in R(v) and R⁻¹(p) with variances estimated with the bootstrap. Using the semiparametric methods, PSA appears to have a better capacity to predict high risk of prostate cancer than does PSA velocity given that it has a larger value for R(0.9) as well as better capacity to predict low risk given that it has a smaller value for R(0.1). In addition, PSA categorizes more people into the low and high risk ranges as can be seen from semiparametric estimates of R⁻¹(0.1) and 1 − R⁻¹(0.3). In contrast, these comparisons are not significant based on the nonparametric methods due to their large sampling variabilities.

Table 7.

Comparisons between (a) PSA and PSA velocity and (b) between PSA and PSA plus other risk factors for predicting risk of prostate cancer. SPMLE denotes the semiparametric maximum likelihood estimator, NPMLE denotes the nonparametric maximum likelihood estimator.

Measure	Method		(a) PSA	PSA Velocity		pvalue
		Est	95% CI	Est	95% CI
R(0.1)	NPMLE	0.079	(0.043,0.110)	0.088	(0.044, 0.131)	0.730
	SPMLE	0.072	(0.046, 0.109)	0.122	(0.075, 0.159)	0.027
R(0.9)	NPMLE	0.474	(0.369, 0.577)	0.302	(0.253, 0.402)	0.005
	SPMLE	0.413	(0.356, 0.476)	0.313	(0.275, 0.356)	< 0.001
R–1(0.1)	NPMLE	0.304	(0.050, 0.39)	0.155	(0.019, 0.305)	0.178
	SPMLE	0.188	(0.073, 0.291)	0.06	(0.020, 0.142)	0.021
1 – R–1(0.3)	NPMLE	0.302	(0.140, 0.447)	0.168	(0.007, 0.501)	0.274
	SPMLE	0.244	(0.191, 0.296)	0.129	(0.030, 0.197)	0.009
R–1(0.3) – R–1(0.1)	NPMLE	0.393	(0.210, 0.664)	0.677	(0.301, 0.933)	0.100
	SPMLE	0.568	(0.443, 0.724)	0.811	(0.668, 0.935)	0.004

Measure	Method		(b) PSA	PSA + other factors		pvalue
		Est	95% CI	Est	95% CI
R(0.1)	SPMLE	0.072	(0.045, 0.109)	0.070	(0.039, 0.094)	0.798
R(0.9)	SPMLE	0.413	(0.356, 0.476)	0.429	(0.372, 0.502)	0.223
R–1(0.1)	SPMLE	0.188	(0.073, 0.291)	0.204	(0.109, 0.310)	0.595
1 – R–1(0.3)	SPMLE	0.244	(0.191, 0.296)	0.243	(0.203, 0.281)	0.952
R–1(0.3) – R–1(0.1)	SPMLE	0.568	(0.443, 0.724)	0.554	(0.436, 0.662)	0.667

6. Extending Semiparametric Estimation to Multiple Markers

The semiparametric estimators can be extended naturally to accommodate multiple predictors or to settings where the monotone increasing risk assumption is not true.

6.1 Inference

We present the generalized estimators here as well as their asymptotic distribution theory. In practice, since estimation of the asymptotic variance involves both numerical differentiation and nonparametric density estimation, we rely on resampling techniques rather than on asymptotic theory for inference.

Let Y be a vector of predictors that may include different functional forms of a single predictor (e.g. a set of spline basis functions) as well as interactions among predictors. Let F_R, F_DR, F_D̄R indicate the cumulative distribution functions for Risk(Y) in the general, case and control populations respectively. As before, we calculate $\widehat{Risk}\left(Y_i\right)$ as the predicted risk for subject i based on fitting a standard logistic regression model to case-control data with offset $\text{log}\{(1-\widehat{\rho })∕\widehat{\rho }{n}_D∕n_{\stackrel{‒}{D}})$. To estimate F_R we write F_R = ρF_DR + (1 − ρ)F_D̄R and substitute estimates for each component. The components F_DR and F_D̄R can be estimated “empirically” using ${\tilde{F}}_{DR}\left(p\right)={\sum }_{i=1}^{n_D}I\left\{\widehat{Risk}\left(Y_{Di}\right)\le p\right\}∕n_D$ and ${\tilde{F}}_{\stackrel{‒}{D}R}\left(p\right)={\sum }_{i=1}^{n_D}I\left\{\widehat{Risk}\left(Y_{\stackrel{‒}{D}i}\right)\le p\right\}∕n_{\stackrel{‒}{D}}$.

A more efficient approach is to use the semiparametric maximum likelihood estimates that are derived using arguments similar to those provided in Huang and Pepe [11] for the single marker setting:

$$\begin{array}{cc}\hfill {\widehat{F}}_{DR}\left(p\right)& =\frac{1}{n}\sum _{i=1}^n\frac{{\widehat{\mathcal{L}\mathrm{R}}}_R\left\{\widehat{Risk}\left(Y_i\right)\right\}I\left\{\widehat{Risk}\left(Y_i\right)\le p\right\}}{\frac{n_{\stackrel{‒}{D}}}{n}+\frac{n_D}{n}{\widehat{\mathcal{L}\mathrm{R}}}_R\left\{\widehat{Risk}\left(Y_i\right)\right\}},\hfill \\ \hfill {\widehat{F}}_{\stackrel{‒}{D}R}\left(p\right)& =\frac{1}{n}\sum _{i=1}^n\frac{I\left\{\widehat{Risk}\left(Y_i\right)\le p\right\}}{\frac{n_{\stackrel{‒}{D}}}{n}+\frac{n_D}{n}{\widehat{\mathcal{L}\mathrm{R}}}_R\left\{\widehat{Risk}\left(Y_i\right)\right\}},\hfill \end{array}$$

where ${\widehat{\mathcal{L}\mathrm{R}}}_R\left\{\widehat{Risk}\left(Y_i\right)\right\}=\widehat{Risk}\left(Y_i\right)∕\left\{1-\widehat{Risk}\left(Y_i\right)\right\}\times (1-\widehat{\rho })∕\widehat{\rho }$.

We write $\widehat{R}\left(v\right)={\widehat{F}}_R^{-1}\left(v\right)$ and R̂⁻¹(p) = F̂_R(p) for the semiparametric maximum likelihood estimators of the predictiveness curve and R̃(v) = F̃_R(p) and R̃⁻¹(p) = F̃_R(p) for the semiparametric “empirical” estimators. The following results are proved in Appendix B4. Here variability of $\widehat{\rho }$ is taken into account in calculating asymptotic variance of the predictiveness curve estimators, with details provided in Appendix B4.

Theorem 4 As n → ∞,

1. $\sqrt{n}\left\{{\widehat{R}}^{-1}\left(p\right)-R^{-1}\left(p\right)\right\}$ converges to a normal random variable with mean zero and variance

   $${\Sigma }_{2M.R}\left(p\right)=\text{var}\left[\sqrt{n}\{Q_M\left(p\right)-R^{-1}\left(p\right)\}\right]+{\left\{\frac{\partial R^{-1}\left(p\right)}{\partial \theta }\right\}}^T\text{var}\left\{\sqrt{n}(\widehat{\theta }-\theta )\right\}\left\{\frac{\partial R^{-1}\left(p\right)}{\partial \theta }\right\}+2{\left\{\frac{\partial R^{-1}\left(p\right)}{\partial \theta }\right\}}^T\text{cov}\left[\sqrt{n}\left(\widehat{\theta }-\theta \right),\sqrt{n}\{Q_M\left(p\right)-R^{-1}\left(p\right)\}\right],$$
2. $\sqrt{n}\left\{\widehat{R}\left(v\right)-R\left(v\right)\right\}$ converges to a normal random variable with mean zero and variance Σ_1M.R(v) = {∂R(v)/∂v}² Σ_2M.R{R(v)}, where

   $$Q_M\left(p\right)=\widehat{\rho }\frac{1}{n}\sum _{i=1}^n\frac{{\widehat{\mathcal{L}\mathrm{R}}}_R\left\{\widehat{Risk}\left(Y_i\right)\right\}I\{Risk\left(Y_i\right)\le p\}}{\frac{n_{\stackrel{‒}{D}}}{n}+\frac{n_D}{n}{\widehat{\mathcal{L}\mathrm{R}}}_R\left\{\widehat{Risk}\left(Y_i\right)\right\}}+(1-\widehat{\rho })\frac{1}{n}\sum _{i=1}^n\frac{I\{Risk\left(Y_i\right)\le p\}}{\frac{n_{\stackrel{‒}{D}}}{n}+\frac{n_D}{n}{\widehat{\mathcal{L}\mathrm{R}}}_R\left\{\widehat{Risk}\left(Y_i\right)\right\}}.$$
3. $\sqrt{n}\left\{{\tilde{R}}^{-1}\left(p\right)-R^{-1}\left(p\right)\right\}$ converges to a normal random variable with mean zero and variance

   $${\Sigma }_{2E.R}\left(p\right)=\text{var}\left[\sqrt{n}\{Q_E\left(p\right)-R^{-1}\left(p\right)\}\right]+{\left\{\frac{\partial R^{-1}\left(p\right)}{\partial \theta }\right\}}^T\text{var}\left\{\sqrt{n}(\widehat{\theta }-\theta )\right\}\left\{\frac{\partial R^{-1}\left(p\right)}{\partial \theta }\right\}+2{\left\{\frac{\partial R^{-1}\left(p\right)}{\partial \theta }\right\}}^T\text{cov}\left[\sqrt{n}\left(\widehat{\theta }-\theta \right),\sqrt{n}\{Q_E\left(p\right)-R^{-1}\left(p\right)\}\right],$$
4. $\sqrt{n}\left\{\tilde{R}\left(v\right)-R\left(v\right)\right\}$ converges to a normal random variable with mean zero and variance Σ_1E.R(v) = {∂R(v)/∂v}² Σ_2E.R{R(v)}, where

   $$Q_E\left(p\right)=\widehat{\rho }\frac{1}{n_D}\sum _{i=1}^{n_D}I\{Risk\left(Y_{Di}\right)\le p\}+(1-\widehat{\rho })\frac{1}{n_{\stackrel{‒}{D}}}\sum _{i=1}^{n_{\stackrel{‒}{D}}}I\{Risk\left(Y_{\stackrel{‒}{D}i}\right)\le p\}.$$

6.2 Illustration

We illustrate using the data described in Section 5. We compare the logistic risk model based on PSA alone with a more comprehensive risk model that combines PSA and other risk factors, namely family history of prostate cancer, digital rectal exam, and previous negative biopsies. All of these factors are highly statistically significant factors in determining risk [30].

A fundamental preliminary step in assessing the value of a risk model concerns calibration or model fit. The predictiveness curve can be helpful in this assessment [6]. We now illustrate how the assessment can be made with data from a nested case-control study by application to the model that includes other risk factors in addition to PSA. We let $\widehat{Risk}\left(Y\right)$ be risk estimates from the model employing PSA and other risk factors and partition the observations into deciles of the distribution for $\widehat{Risk}\left(Y\right)$. For k ∈ {1, . . . , K =10}, we estimate P̂(D = 1|k, S) as the observed proportion of cases within the k^th group. The population risk within the k^th group, P(D = 1|k) is then estimated according to

$$\frac{\widehat{P}(D=1\mid k)}{1-\widehat{P}(D=1\mid k)}=\frac{\widehat{P}(D=1\mid k,S)}{1-\widehat{P}(D=1\mid k,S)}\frac{n_{\stackrel{‒}{D}}}{n_D}\frac{1-\widehat{\rho }}{\widehat{\rho }}.$$

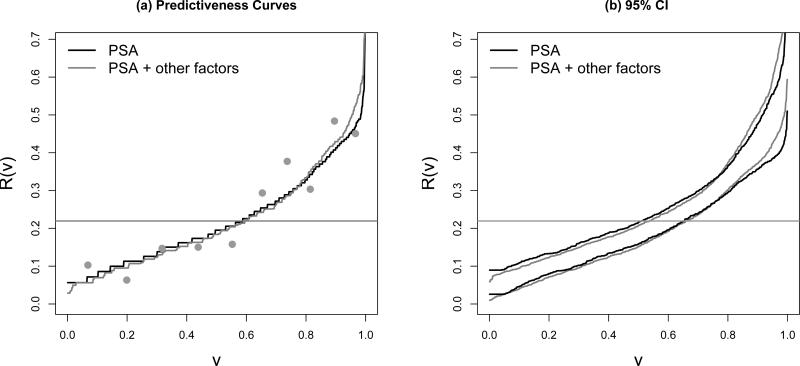
At the midpoints of the k^th group, a visual comparison can be made between these points and the predictiveness curve by superimposing the value of P̂(D = 1|k) on the predictiveness curve plot. This comparison of observed risk and average risk within deciles of modeled risk provides a graphical display of calibration as suggested previously [6] but now generalized to case-control data. According to Figure 3(a), there does not to appear be serious lack of fit of the risk model.

Figure 3.

(a) The semiparametric maximum likelihood estimates of predictiveness curves for PSA and PSA plus other factors for predicting risk prostate cancer,the dots are average risk within deciles of modeled risk based on the latter model; (b) their 95% pointwise confidence intervals using percentiles of the bootstrap distribution. The horizontal lines indicate disease prevalences.

Let ${\widehat{Risk}}^S$ be the risk estimate from the logistic regression applied to the case-control sample without correcting for the intercept term. We propose a Hosmer-Lemeshow measure of calibration to accompany the plot:

$$T=\sum _{k=1}^K\frac{{\left\{\widehat{P}(D=1\mid k)-{\widehat{R}}_k\right\}}^2}{{\widehat{R}}_k^2{(1-{\widehat{R}}_k)}^2∕\left\{n_k{\widehat{R}}_k^S(1-{\widehat{R}}_k^S)\right\}},$$ (6.1)

where ${\widehat{R}}_k^S$ is the average of ${\widehat{Risk}}^S$ within the k^th group, and R̂_k is a population version of it corrected for the biased sampling

$${\widehat{R}}_k=\left\{{\widehat{R}}_k^S\frac{n_{\stackrel{‒}{D}}}{n_D}\frac{\widehat{\rho }}{1-\widehat{\rho }}\right\}∕\left\{1+{\widehat{R}}_k^S\frac{n_{\stackrel{‒}{D}}}{n_D}\frac{\widehat{\rho }}{1-\widehat{\rho }}\right\}.$$

Within each discretized risk group, the term in the numerator of (6.1) is the squared difference between the ‘observed’ and ‘expected’ disease proportion in the population, while the term in the denominator is the estimated variance of this difference. Comparing this measure T with a ${\chi }_{K-2}^2$ distribution, we obtain a p-value for the test of calibration. The calculation of R̂_k and justification for this test are outlined in Appendix C. Our measure is a modification of the established Hosmer-Lemeshow test for case-control study [32], which compares observed and expected disease proportion in the case-control sample. The test without modification yields a valid test with case-control data. But the modified test is more tightly linked to the predictiveness curve and the measure of calibration upon which it is based does not vary with the case-control design. In our example, the modified test yields a p-value of 0.170 for the predictiveness curve employing PSA and other risk factors, suggesting a reasonable representation of the risk distribution in the population provided by the predictiveness curve.

Figure 3(a) displays the semiparametric maximum likelihood estimators of the predictiveness curves for PSA alone and for the model that includes other factors (the semiparametric “empirical” estimators are similar). The two risk models have very similar predictiveness curves. Confidence intervals for R(v) constructed with the semiparametric maximum likelihood estimators are presented in Figure 3(b). Sampling variability of estimates derived from the two risk models appears to be similar in magnitude.

Detailed results comparing the predictiveness curves of the two models are shown in Table 7(b). Briefly, the percentages of people classified into the low, high, or equivocal risk ranges are not significantly different between the two models, nor are the 10^th and 90^th percentiles of risk significantly different. Thus including other factors in the model in addition to PSA does not lead to a significant improvement in risk stratification even when these factors are all statistically significant in the multivariate logistic regression model. It reinforces our earlier argument that the risk model by itself is not enough to characterize the population performance of a risk prediction model.

An important issue pertaining to models with multiple predictors is over-fitting when the number of predictors gets large relative to the sample size. To account for potential over-fitting, we implemented 10-fold cross-validation to compare the predictiveness of the two models. Again, including other factors beside PSA in the risk model has trivial influence on risk stratification.

7. Discussion

It has been argued in both the applied [8] and biostatistical literature [2, 6] that displaying the population distribution of risk is useful for evaluating the potential impact of a risk model for risk stratifying the population. The key ideas of risk stratification tables, introduced by Cook and others [33] and Cook [34], are closely related. In particular, the margins of the two-way risk stratification table show the population distribution of risk achieved by the two models, albeit using discrete risk categories. Janes and others [35] show that the key information pertinent to comparing models is contained in the margins rather than in the cells of the table. Predictiveness curves provide more complete descriptions of the marginal risk distributions since they show risk distributions over a continuum of risk thresholds that could be used to define risk categories rather than only at a few pre-specified risk thresholds.

Methods for estimating predictiveness curves from cohort studies were developed previously. However, case-control designs are often preferred in biomarker development [9] and the goal of the current paper is to develop estimation procedures for use with case-control data. Here we discussed semiparametric methods that rely on a logistic regression form for the risk and a non-parametric method that relies on isotonic regression for estimating the risk. Another approach developed by Huang and Pepe [36] is based on the relationship between the predictiveness curve and the ROC curve. Here, we found that the nonparametric method is inefficient compared with the semiparametric methods and that valid inference requires large sample sizes. We recommend the semiparametric methods for use in practice because (i) simulations indicate that inferential procedures are adequate with realistic sample sizes, (ii) they accommodate risk models with multiple predictors, and (iii) they can be made flexible by employing flexible forms for the predictors in the logistic regression model. The last point is important to ensure good model fit by the semiparametric model. The nonparametric estimator has the advantage that it is completely robust but potentially very inefficient. Therefore it can be useful in large studies where precision is not an issue and minimum bias is desired. And it can be used for comparison with the semiparametric estimator in a single marker setting to further assess its goodness-of-fit. For a general logistic risk model allowing for multiple markers, we proposed a modified Hosmer-Lemeshow test assessing calibration of the risk model. It extends the established Hosmer-Lemeshow test for case-control data by mapping the difference between observed and established disease proportion at the case-control sample level to that at the population level. As a result, performance of the test under alternative hypothesis would potentially be less sensitive to factors such as case-control ratio. Based on limited simulation studies (results not shown), this modified test appears to have power comparable to that of the standard Hosmer-Lemeshow test and is more powerful in some settings when the proportion of cases in the case-control sample is high.

Pepe and others [6] proposed displaying the predictiveness curve and curves displaying true and false positive rates together for maximum information. Specifically, to evaluate a risk prediction marker, one will be interested in knowing not only 1 − R⁻¹(p), the proportion of the population with risk above p, but also the proportion of diseased subjects correctly classified (the true positive rate TPR(p) = P{Risk(Y) > p|D = 1}) and the proportion of non-diseased subjects incorrectly classified (the false positive rate FPR(p) = P{Risk(Y) > p|D = 0}), according to the classification rule ‘Risk(Y) > p’. Our semiparametric and nonparametric procedures developed in this manuscript yield estimators of F_DR, F_D̄R and F_R as by-products. These can be directly plugged into $\mathrm{TPR}\left(p\right)=F_{DR}\left\{F_R^{-1}\left(p\right)\right\}$ and $\mathrm{FPR}\left(p\right)=F_{\stackrel{‒}{D}R}\left\{F_R^{-1}\left(p\right)\right\}$ to estimate these quantities. Asymptotic theory for corresponding semiparametric estimators can be developed using techniques similar to those employed for estimators of the predictiveness curve.

Finally, for interested readers, fitting of the logistic regression and isotonic regression models can be performed using standard statistical software such as R. R programs for estimating the corresponding predictiveness curves and their asymptotic variances are available from the authors upon request.

Appendix A: Analytic Forms of the Asymptotic Variances for the Semiparametric Estimators of the Predictiveness Curve (for the Example in Section 3.1)

Let α = θ₀ − log{ρ/(1 − ρ)}, β = θ₁, and let η = n_D/n_D̄, we have

$$\begin{array}{cc}\hfill V_{M1}& ={(1-\rho )}^2(1+\eta )[F_{\stackrel{‒}{D}}\left\{G^{-1}(\theta ,p)\right\}-F_{\stackrel{‒}{D}}{\left\{G^{-1}(\theta ,p)\right\}}^2]+{\rho }^2\frac{1+\eta }{\eta }[F_D\left\{G^{-1}(\theta ,p)\right\}-F_D{\left\{G^{-1}(\theta ,p)\right\}}^2]-\left(\frac{1+\eta }{\eta }\right){\{\rho -(1-\rho )\eta \}}^2\left\{A_0\left\{G^{-1}(\theta ,p)\right\}-[A_0\left\{G^{-1}(\theta ,p)\right\},A_1{\left\{G^{-1}(\theta ,p)\right\}}^T]A^{-1}\left[\begin{array}{c}\hfill A_0\left\{G^{-1}(\theta ,p)\right\}\hfill \\ \hfill A_1\left\{G^{-1}(\theta ,p)\right\}\hfill \end{array}\right]\right\},\hfill \\ \hfill V_{E1}& ={(1-\rho )}^2(1+\eta )[F_{\stackrel{‒}{D}}\left\{G^{-1}(\theta ,p)\right\}-F_{\stackrel{‒}{D}}{\left\{G^{-1}(\theta ,p)\right\}}^2]+{\rho }^2\frac{1+\eta }{\eta }[F_D\left\{G^{-1}(\theta ,p)\right\}-F_D{\left\{G^{-1}(\theta ,p)\right\}}^2],\hfill \\ \hfill V_{M2}& =V_{E2}=\frac{1+\eta }{\eta }\left\{A^{-1}-\left(\begin{array}{cc}\hfill 1+\eta \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)\right\},\hfill \\ \hfill V_{M3}& =V_{E3}=\frac{1+\eta }{\eta }\left(\{\rho -\eta (1-\rho )\}{A}^{-1}\left[\begin{array}{c}\hfill A_0\left\{G^{-1}(\theta ,p)\right\}\hfill \\ \hfill A_1\left\{G^{-1}(\theta ,p)\right\}\hfill \end{array}\right]-\left[\begin{array}{c}\hfill \rho F_D\left\{G^{-1}(\theta ,p)\right\}-\eta (1-\rho )F_{\stackrel{‒}{D}}\left\{G^{-1}(\theta ,p)\right\}\hfill \\ \hfill 0\hfill \end{array}\right]\right),\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill A_0\left(t\right)& ={\int }_{-\infty }^t\frac{\text{exp}\{\alpha +{\beta }^{T}r\left(y\right)\}}{1+\eta \text{exp}\{\alpha +{\beta }^{T}r\left(y\right)\}}d{F}_{\stackrel{‒}{D}}\left(y\right),\hfill \\ \hfill A_1\left(t\right)& ={\int }_{-\infty }^t\frac{r\left(y\right)\text{exp}\{\alpha +{\beta }^{T}r\left(y\right)\}}{1+\eta \text{exp}\{\alpha +{\beta }^{T}r\left(y\right)\}}d{F}_{\stackrel{‒}{D}}\left(y\right),\hfill \\ \hfill A_2\left(t\right)& ={\int }_{-\infty }^t\frac{r\left(y\right)r{\left(y\right)}^T\text{exp}\{\alpha +{\beta }^{T}r\left(y\right)\}}{1+\eta \text{exp}\{\alpha +{\beta }^{T}r\left(y\right)\}}d{F}_{\stackrel{‒}{D}}\left(y\right),\hfill \\ \hfill & A=\left(\begin{array}{cc}\hfill A_0\hfill & \hfill A_1^T\hfill \\ \hfill A_1\hfill & \hfill A_2\hfill \end{array}\right),\hfill \end{array}$$

with A₀ = A₀(∞), A₁ = A₁(∞), A₂ = A₂(∞).

Appendix B: Proof of Theorems

B1: Proof of Theorem 1

Suppose there are m pooled groups after isotonic regression with ŵ(Y) < ∞. In the i^th group, there are m_i observations, among which m_Di are cases. Then for subject k (k ∉ κ) belonging to the i^th group, ŵ(Y_k) = m_Di/(m_i − m_Di).

Plugging $\widehat{\mu }=n_D∕n_{\stackrel{‒}{D}}$ into (3.5) results in

$$\sum _{k\notin \kappa }\frac{\widehat{\mu }}{n_D\widehat{w}\left(Y_k\right)+n_{\stackrel{‒}{D}}\widehat{\mu }}=\sum _{k\notin \kappa }\frac{\frac{n_D}{n_{\stackrel{‒}{D}}}}{n_D\widehat{w}\left(Y_k\right)+n_{\stackrel{‒}{D}}\frac{n_D}{n_{\stackrel{‒}{D}}}}=\sum _{i=1}^m\frac{\frac{n_D}{n_{\stackrel{‒}{D}}}{m}_i}{n_D\frac{m_{Di}}{m_i-m_{Di}}+n_{\stackrel{‒}{D}}\frac{n_D}{n_{\stackrel{‒}{D}}}}=\sum _{i=1}^m\frac{\frac{n_D}{n_{\stackrel{‒}{D}}}{m}_i(m_i-m_{Di})}{n_D{m}_{Di}+n_D(m_i-m_{Di})}=\sum _{i=1}^m\frac{m_i-m_{Di}}{n_{\stackrel{‒}{D}}}=\frac{n_{\stackrel{‒}{D}}}{n_{\stackrel{‒}{D}}}=1.$$

Since the term on the left-hand side of (3.5) is monotone increasing in μ, $\widehat{\mu }=n_D∕n_{\stackrel{‒}{D}}$ is the unique solution.

B2: Proof of Theorem 2

At the end of the isotonic regression, the estimated risks are constant within each block of marker values. Suppose there are m blocks with m_i subjects and m_Di cases in the i^th block. Let y₍₁₎, ..., y_(n) be the marker values in the case-control sample ordered increasingly, with y_(i1), ..., y_(imi) belonging to the i^th block, then P̂(D = 1|Y) is constant for Y ∈ {y_(i1), ..., y_(imi)}. Because the quantile function F⁻¹ is defined to be left continuous by convention, the nonparametric estimator R̂(v) or R̃(v) vs v is a step function where a jump is ready to be made (but not yet) at every v corresponding to the largest element in a block, i.e. v = F̂{y_(imi)} or v = F̃{Y_(imi)} for i = 1, ..., m.

Therefore, to show the equivalence between the two predictiveness curve estimators, all we need to show is that the sets of v′s where jumps are about to happen is the same between the two curves. In other words, we want to show that F̃ {y_(imi)} = F̂ {y_(imi)} for i = 1, ..., m.

Notice that

$$\begin{array}{cc}\hfill \tilde{F}\left\{y_{\left(i{m}_i\right)}\right\}& =\widehat{\rho }\frac{1}{n_D}\sum _{j=1}^{n_D}I\{Y_{Dj}\le y_{\left(i{m}_i\right)}\}+(1-\widehat{\rho })\frac{1}{n_{\stackrel{‒}{D}}}\sum _{j=1}^{n_{\stackrel{‒}{D}}}I\{Y_{\stackrel{‒}{D}j}\le y_{\left(i{m}_i\right)}\}\hfill \\ \hfill & =\widehat{\rho }\frac{1}{n_D}\sum _{l=1}^i{m}_{Dl}+(1-\widehat{\rho })\frac{1}{n_{\stackrel{‒}{D}}}\sum _{l=1}^i(m_l-m_{Dl})\hfill \end{array}$$

and that

$$\begin{array}{cc}\hfill \widehat{F}\left\{y_{\left(i{m}_i\right)}\right\}& =\widehat{\rho }\frac{1}{n}\sum _{j\notin \kappa ,j=1}^n\frac{\frac{m_{Dj}}{m_j-m_{Dj}}\frac{n_{\stackrel{‒}{D}}}{n_D}I\{Y_j\le y_{\left(i{m}_i\right)}\}}{\frac{n_{\stackrel{‒}{D}}}{n}+\frac{n_D}{n}\frac{m_{Dj}}{m_j-m_{Dj}}\frac{n_{\stackrel{‒}{D}}}{n_D}}+\widehat{\rho }\sum _{j\in \kappa ,j=1}^n\frac{I\{Y_j\le y_{\left(i{m}_i\right)}\}}{n_D}+(1-\widehat{\rho })\frac{1}{n}\sum _{j=1}^n\frac{I\{Y_j\le y_{\left(i{m}_i\right)}\}}{\frac{n_{\stackrel{‒}{D}}}{n}+\frac{n_D}{n}\frac{m_{Dj}}{m_j-m_{Dj}}\frac{n_{\stackrel{‒}{D}}}{n_D}}\hfill \\ \hfill & =\widehat{\rho }\frac{1}{n_D}\sum _{l\not\subset \kappa ,l=1}^i{m}_{Dl}+\widehat{\rho }\frac{1}{n_D}\sum _{l\subset \kappa ,l=1}^i{m}_l+(1-\widehat{\rho })\frac{1}{n_{\stackrel{‒}{D}}}\sum _{l=1}^i(m_l-m_{Dl})\hfill \\ \hfill & =\widehat{\rho }\frac{1}{n_D}\sum _{j\not\subset \kappa ,l=1}^i{m}_{Dl}+\widehat{\rho }\frac{1}{n_D}\sum _{l\subset \kappa ,l=1}^i{m}_{Dl}+(1-\widehat{\rho })\frac{1}{n_{\stackrel{‒}{D}}}\sum _{l=1}^i(m_l-m_{Dl})\hfill \\ \hfill & =\widehat{\rho }\frac{1}{n_D}\sum _{l=1}^i{m}_{Dl}+(1-\widehat{\rho })\frac{1}{n_{\stackrel{‒}{D}}}\sum _{l=1}^i(m_l-m_{Dl}).\hfill \end{array}$$

Consequently under the monotone increasing risk model assumption, the nonparametric “empirical” and model-based approaches lead to the same estimator of the predictiveness curve.

B3: Proof of Theorem 3

For a continuous marker Y, it has been shown that there is a one-to-one relationship between the predictiveness curve and the ROC curve [36]. That is, suppose P(D = 1|Y) is monotone increasing in Y, R(v) vs v can be represented as

$$\frac{\rho {\mathrm{ROC}}^{\prime }\left(t\right)}{\rho {\mathrm{ROC}}^{\prime }\left(t\right)+(1-\rho )}\text{vs}1-(1-\rho )t-\rho \mathrm{ROC}\left(t\right),t\in (0,1).$$

A similar result can be proved for the semiparametric maximum likelihood estimator. Suppose the unique marker value within the case-control sample is {y₁, ..., y_n} in increasing order. For a marker value y_i,

$$\begin{array}{cc}\hfill v_i& =\widehat{F}\left(y_i\right)=\widehat{\rho }{\widehat{F}}_D\left(y_i\right)+(1-\widehat{\rho }){\widehat{F}}_{\stackrel{‒}{D}}\left(y_i\right),\hfill \\ \hfill \widehat{R}\left(v_i\right)& =\widehat{P}(D=1\mid Y=y_i)=\frac{\widehat{P}(D=1,Y=y_i)}{\widehat{P}(D=1)}\hfill \\ \hfill & =\frac{\widehat{\rho }\widehat{P}(Y=y_i\mid D=1)}{\widehat{\rho }\widehat{P}(Y=y_i\mid D=1)+(1-\widehat{\rho })\widehat{P}(Y=y_i\mid D=0)}=\frac{\widehat{\rho }\widehat{\mathcal{L}\mathrm{R}}\left(y_i\right)}{\widehat{\rho }\widehat{\mathcal{L}\mathrm{R}}\left(y_i\right)+(1-\widehat{\rho })}.\hfill \end{array}$$

Next we generate the ROC curve, $\widehat{\mathrm{ROC}}\left(t\right)$, corresponding to the semiparametric maximum likelihood estimator of the predictiveness curve: (1) we order the support of the marker decreasingly; (2) we estimate the pair of TPF(c), FPF(c) where c = {y_n, ..., y₁, −∞} (here we define positive as Y > c instead of Y ≥ c to accommodate the convention that F̂ is right continuous); (3) we connect neighboring points by a straight line and define ${\widehat{\mathrm{ROC}}}^{\prime }\left(t\right)$ to be the right-hand derivative of $\widehat{\mathrm{ROC}}\left(t\right)$. Suppose F̂_D̄(y_i) = 1 − t_i, since $\widehat{\mathcal{L}\mathrm{R}}\left\{{\widehat{F}}^{-1}\left(v_i\right)\right\}=\widehat{\mathcal{L}\mathrm{R}}\left\{{\widehat{F}}_{\stackrel{‒}{D}}^{-1}(1-t_i)\right\}={\widehat{\mathrm{ROC}}}^{\prime }\left(t_i\right)$, we have that R̂(v) vs v can be represented as

$$\frac{\widehat{\rho }{\widehat{\mathrm{ROC}}}^{\prime }\left(t\right)}{\widehat{\rho }{\widehat{\mathrm{ROC}}}^{\prime }\left(t\right)+(1-\widehat{\rho })}\text{vs}1-(1-\widehat{\rho })t-\rho \widehat{\mathrm{ROC}}\left(t\right),t\in (0,1).$$

For the semiparametric maximum likelihood estimator, P̂(Y = y_i|D = 0) > 0, thus we have $\widehat{\mathcal{L}\mathrm{R}}\left(y_i\right)=\widehat{P}(Y=y_i\mid D=1)∕\widehat{P}(Y=y_i\mid D=0)<\infty$. That is, the derivative of the corresponding curve is always finite. Therefore, the semiparametric maximum likelihood estimator of the predictiveness curve corresponds to an ROC curve which is continuous and piecewise differentiable everywhere. Moreover the ROC curve is concave since P(D|Y) is monotone increasing in Y. We have

$$\begin{array}{cc}\hfill {\int }_0^1\widehat{R}\left(v\right)dv={\int }_{t=1}^{t=0}\frac{\widehat{\rho }{\widehat{\mathrm{ROC}}}^{\prime }\left(t\right)}{\widehat{\rho }\mathrm{R}\widehat{\mathrm{O}}{\mathrm{C}}^{\prime }\left(t\right)+(1-\widehat{\rho })}d\left\{1-(1-\widehat{\rho })t-\widehat{\rho }\widehat{\mathrm{ROC}}\left(t\right)\right\}& =-{\int }_{t=1}^{t=0}\frac{\widehat{\rho }{\widehat{\mathrm{ROC}}}^{\prime }\left(t\right)}{\widehat{\rho }{\widehat{\mathrm{ROC}}}^{\prime }\left(t\right)+(1-\widehat{\rho })}\left\{(1-\widehat{\rho })+\widehat{\rho }{\widehat{\mathrm{ROC}}}^{\prime }\left(t\right)\right\}dt\hfill \\ \hfill & =\widehat{\rho }{\int }_{t=0}^{t=1}{\widehat{\mathrm{ROC}}}^{\prime }\left(t\right)dt=\widehat{\rho }\left\{{\widehat{\mathrm{ROC}}}^{\prime }\left(1\right)-\widehat{\mathrm{ROC}}\left(0\right)\right\}=\widehat{\rho }\hfill \end{array}$$

For the nonparametric maximum likelihood estimator of the predictiveness curve, we can obtain the corresponding ROC curve similarly. This ROC curve is piecewise differentiable with finite derivative everywhere if P̂(D = 1|Y = y) < 1 for every y in the support of the marker. However, when we use isotonic regression to estimate the risk model, the estimated risk could be 1 if the largest marker measure comes from the case sample. This would lead to a vertical line from (0, 0) to (0, n_κ/n_D) in the corresponding ROC curve, where n_κ is the number of observations in κ. Nevertheless, the area under the estimated predictiveness curve is still equal to $\widehat{\rho }$ in this scenario because

$$\begin{array}{cc}\hfill {\int }_0^1\widehat{R}\left(v\right)dv=1\times \sum _{k\in \kappa }\widehat{f}\left(Y_k\right)+{\int }_{t=1}^{t=0^{+}}\frac{\widehat{\rho }{\widehat{\mathrm{ROC}}}^{\prime }\left(t\right)}{\widehat{\rho }{\widehat{\mathrm{ROC}}}^{\prime }\left(t\right)+(1-\widehat{\rho })}d\left\{1-(1-\widehat{\rho })t-\widehat{\rho }\widehat{\mathrm{ROC}}\left(t\right)\right\}& =\widehat{\rho }{n}_{\kappa }\frac{1}{n_D}+(1-\widehat{\rho })\times 0-{\int }_{t=1}^{t=0^{+}}\frac{\widehat{\rho }{\widehat{\mathrm{ROC}}}^{\prime }\left(t\right)}{\widehat{\rho }{\widehat{\mathrm{ROC}}}^{\prime }\left(t\right)+(1-\widehat{\rho })}\left\{(1-\widehat{\rho })+\widehat{\rho }{\widehat{\mathrm{ROC}}}^{\prime }\left(t\right)\right\}dt\hfill \\ \hfill & =\widehat{\rho }{n}_{\kappa }\frac{1}{n_D}+\widehat{\rho }{\int }_{t=0+}^{t=1}{\widehat{\mathrm{ROC}}}^{\prime }\left(t\right)dt=\rho n_{\kappa }\frac{1}{n_D}+\widehat{\rho }\left\{\widehat{\mathrm{ROC}}\left(1\right)-\widehat{\mathrm{ROC}}\left(0^{+}\right)\right\}\hfill \\ \hfill & =\widehat{\rho }{n}_{\kappa }\frac{1}{n_D}+\widehat{\rho }\left(1-\frac{n_{\kappa }}{n_D}\right)=\widehat{\rho }.\hfill \end{array}$$

B4: Proof of Theorem 4

For the semiparametric maximum likelihood estimator,

$$\sqrt{n}\left\{{\widehat{R}}^{-1}\left(p\right)-R^{-1}\left(p\right)\right\}=\sqrt{n}\left\{{\widehat{F}}_R\left(p\right)-F_R\left(p\right)\right\}=\sqrt{n}\left\{(1-\widehat{\rho }){\widehat{F}}_{\stackrel{‒}{D}R}\left(t\right)+\widehat{\rho }{\widehat{F}}_{DR}\left(t\right)-F_R\left(t\right)\right\}=A+B,$$

where

$$\begin{array}{cc}\hfill A=& \sqrt{n}\left[\widehat{\rho }\frac{1}{n}\sum _{i=1}^n\frac{{\widehat{\mathcal{L}\mathrm{R}}}_R\left\{\widehat{Risk}\left(Y_i\right)\right\}I\{Risk\left(Y_i\right)\le p\}}{\frac{n_{\stackrel{‒}{D}}}{n}+\frac{n_D}{n}{\widehat{\mathcal{L}\mathrm{R}}}_R\left\{\widehat{Risk}\left(Y_i\right)\right\}}+(1-\widehat{\rho })\frac{1}{n}\sum _{i=1}^n\frac{I\{Risk\left(Y_i\right)\le p\}}{\frac{n_{\stackrel{‒}{D}}}{n}+\frac{n_D}{n}{\widehat{\mathcal{L}\mathrm{R}}}_R\left\{\widehat{Risk}\left(Y_i\right)\right\}}-R^{-1}\left(p\right)\right]\hfill \\ \hfill =& \sqrt{n}\{Q_M\left(p\right)-R^{-1}\left(p\right)\},\hfill \\ \hfill B=& \sqrt{n}\left[\widehat{\rho }\frac{1}{n}\sum _{i=1}^n\frac{{\widehat{\mathcal{L}\mathrm{R}}}_R\left\{\widehat{Risk}\left(Y_i\right)\right\}I\{\widehat{Risk}\left(Y_i\right)\le p\}}{\frac{n_{\stackrel{‒}{D}}}{n}+\frac{n_D}{n}{\widehat{\mathcal{L}\mathrm{R}}}_R\left\{\widehat{Risk}\left(Y_i\right)\right\}}+(1-\widehat{\rho })\frac{1}{n}\sum _{i=1}^n\frac{I\left\{\widehat{Risk}\left(Y_i\right)\le p\right\}}{\frac{n_{\stackrel{‒}{D}}}{n}+\frac{n_D}{n}{\widehat{\mathcal{L}\mathrm{R}}}_R\left\{\widehat{Risk}\left(Y_i\right)\right\}}\right]\hfill \\ \hfill -& \sqrt{n}\left[\widehat{\rho }\frac{1}{n}\sum _{i=1}^n\frac{{\widehat{\mathcal{L}\mathrm{R}}}_R\left\{\widehat{Risk}\left(Y_i\right)\right\}I\{Risk\left(Y_i\right)\le p\}}{\frac{n_{\stackrel{‒}{D}}}{n}+\frac{n_D}{n}{\widehat{\mathcal{L}\mathrm{R}}}_R\left\{\widehat{Risk}\left(Y_i\right)\right\}}+(1-\widehat{\rho })\frac{1}{n}\sum _{i=1}^n\frac{I\left\{Risk\left(Y_i\right)\le p\right\}}{\frac{n_{\stackrel{‒}{D}}}{n}+\frac{n_D}{n}{\widehat{\mathcal{L}\mathrm{R}}}_R\left\{\widehat{Risk}\left(Y_i\right)\right\}}\right]\hfill \\ \hfill {=}^{\ast }& \sqrt{n}\left[\rho \frac{1}{n}\sum _{i=1}^n\frac{\mathcal{L}{\mathrm{R}}_R\left\{Risk\left(Y_i\right)\right\}I\{\widehat{Risk}\left(Y_i\right)\le p\}}{\frac{n_{\stackrel{‒}{D}}}{n}+\frac{n_D}{n}\mathcal{L}{\mathrm{R}}_R\left\{Risk\left(Y_i\right)\right\}}+(1-\rho )\frac{1}{n}\sum _{i=1}^n\frac{I\left\{\widehat{Risk}\left(Y_i\right)\le p\right\}}{\frac{n_{\stackrel{‒}{D}}}{n}+\frac{n_D}{n}\mathcal{L}{\mathrm{R}}_R\left\{Risk\left(Y_i\right)\right\}}\right]\hfill \\ \hfill -& \sqrt{n}\left[\rho \frac{1}{n}\sum _{i=1}^n\frac{{\widehat{\mathcal{L}\mathrm{R}}}_R\left\{\widehat{Risk}\left(Y_i\right)\right\}I\{Risk\left(Y_i\right)\le p\}}{\frac{n_{\stackrel{‒}{D}}}{n}+\frac{n_D}{n}{\widehat{\mathcal{L}\mathrm{R}}}_R\left\{\widehat{Risk}\left(Y_i\right)\right\}}+(1-\rho )\frac{1}{n}\sum _{i=1}^n\frac{I\{Risk\left(Y_i\right)\le p\}}{\frac{n_{\stackrel{‒}{D}}}{n}+\frac{n_D}{n}{\widehat{\mathcal{L}\mathrm{R}}}_R\left\{\widehat{Risk}\left(Y_i\right)\right\}}\right]\hfill \\ \hfill =& \sqrt{n}\{F_{\widehat{R}}\left(t\right)-F_R\left(t\right)\}+o_p\left(1\right)=\sqrt{n}\frac{\partial F_R\left(t\right)}{\partial \theta }\left(\widehat{\theta }-\theta \right)+o_p\left(1\right),\hfill \end{array}$$

where * holds under appropriate equicontinuity conditions [37].

Suppose $\widehat{\rho }$ is estimated from a cohort independent of the case-control sample, or the parent cohort where the case-control sampled is nested within. Assume the size of the cohort is λ times the size of the case-control sample. Let $Q_M^{\star },{\widehat{\theta }}^{\star }$ be the counterparts of Q_M, $\widehat{\theta }$ if we plug in true ρ where $\widehat{\rho }$ is originally used. Note that ${\widehat{\mathcal{L}\mathrm{R}}}_R\left\{\widehat{Risk}\right\}$ is independent of $\widehat{\rho }$ for a logistic regression risk model. Then, we have

$$\begin{array}{cc}\hfill & \text{var}\left[\sqrt{n}\{Q_M\left(p\right)-R^{-1}\left(p\right)\}\right]={\{F_{DR}\left(p\right)-F_{\stackrel{‒}{D}R}\left(p\right)\}}^2\rho (1-\rho )∕\lambda +\text{var}\left[\sqrt{n}\{Q_M^{\star }\left(p\right)-R^{-1}\left(p\right)\}\right],\hfill \\ \hfill & \text{var}\left\{\sqrt{n}\left(\widehat{\theta }-\theta \right)\right\}=\left(\begin{array}{cc}\hfill \frac{1}{\lambda \rho (1-\rho )}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)+\text{var}\left\{\sqrt{n}\left({\widehat{\theta }}^{\star }-\theta \right)\right\},\hfill \\ \hfill & \text{cov}\left[\sqrt{n}\left(\widehat{\theta }-\theta \right),\sqrt{n}\{Q_M\left(p\right)-R^{-1}\left(p\right)\}\right]=\frac{F_{DR}\left(p\right)-F_{\stackrel{‒}{D}R}\left(p\right)}{\lambda }+\text{cov}\left[\sqrt{n}\left({\widehat{\theta }}^{\star }-\theta \right),\sqrt{n}\{Q_M^{\star }\left(p\right)-R^{-1}\left(p\right)\}\right].\hfill \end{array}$$

To show this, use the first result as an example, note that

$$\text{var}\left[\sqrt{n}\{Q_M\left(p\right)-R^{-1}\left(p\right)\}\right]=\text{var}\left[\sqrt{n}\{Q_M\left(p\right)-Q_M^{\star }\left(p\right)\}\right]+\text{var}\left[\sqrt{n}\{Q_M^{\star }\left(p\right)-R^{-1}\left(p\right)\}\right]\simeq \sqrt{n}\{\widehat{\rho }{F}_{DR}\left(p\right)+(1-\widehat{\rho })F_{\stackrel{‒}{D}R}\left(p\right)-F_R\left(p\right)\}+\text{var}\left[\sqrt{n}\{Q_M^{\star }\left(p\right)-R^{-1}\left(p\right)\}\right](\ast ).$$

Since the two terms in (*) are asymptotically uncorrelated, we have

$$\text{var}\left[\sqrt{n}\{Q_M\left(p\right)-R^{-1}\left(p\right)\}\right]\simeq \text{var}\left[\sqrt{n}{\{F_{DR}\left(p\right)-F_{\stackrel{‒}{D}R}\left(p\right)\}}^2\text{var}\left(\widehat{\rho }\right)\right]+\text{var}\left[\sqrt{n}\{Q_M^{\star }\left(p\right)-R^{-1}\left(p\right)\}\right]={\{F_D\left(t\right)-F_{\stackrel{‒}{D}}\left(t\right)\}}^2\rho (1-\rho )∕\lambda +\text{var}\left[\sqrt{n}\{Q_M^{\star }\left(p\right)-R^{-1}\left(p\right)\}\right].$$

Finally, results for semiparametric “empirical” estimators can be derived following similar arguments.

Appendix C: The modified Hosmer-Lemeshow test for case-control data

Let observations in a case-control sample by divided into K groups according to distribution of ${\widehat{Risk}}^S$, the unmodified Hosmer-Lemeshow test for case-control study is defined as

$$HL=\sum _{k=1}^K\frac{{\left\{\widehat{P}(D=1\mid k,S)-{\widehat{R}}_k^S\right\}}^2}{{\widehat{R}}_k^S(1-{\widehat{R}}_k^S)∕n_k}.$$

Based on Bayes’ theorem, we have $\widehat{Risk}=g\left({\widehat{Risk}}^S\right)$ and ${\widehat{R}}_k=g\left({\widehat{R}}_k^S\right)$ for

$$g\left(x\right)=\frac{x}{1-x}\frac{n_D}{n_{\stackrel{‒}{D}}}\frac{\widehat{\rho }}{1-\widehat{\rho }}∕\left(1+\frac{x}{1-x}\frac{n_D}{n_{\stackrel{‒}{D}}}\frac{\widehat{\rho }}{1-\widehat{\rho }}\right).$$

Then for k = 1, . . . , K, we have $\widehat{P}(D=1\mid k)-{\widehat{R}}_k=g(\widehat{P}(D=1\mid k,S)-g\left({\widehat{R}}_k^S\right)$. Its variance under H₀ can be shown to be approximately equal to ${\widehat{R}}_k^2{(1-{\widehat{R}}_k)}^2∕\left\{n_k{R}_k^S(1-R_k^S)\right\}$ through Delta method. Therefore under $H_0,{\left\{\widehat{P}(D=1\mid k,S)-{\widehat{R}}_k^S\right\}}^2∕\left\{{\widehat{R}}_k^S(1-{\widehat{R}}_k^S)∕n_k\right\}$ and ${\left\{\widehat{P}(D=1\mid k)-{\widehat{R}}_k\right\}}^2∕\left[{\widehat{R}}_k^2{(1-{\widehat{R}}_k)}^2∕\left\{n_k{\widehat{R}}_k^S(1-{\widehat{R}}_k^S)\right\}\right]$ are asymptotically equivalent, which proves the asymptotic equivalence between T and HL.