Dendritic vulnerability in neurodegenerative disease: insights from analyses of cortical pyramidal neurons in transgenic mouse models

Abstract

In neurodegenerative disorders, such as Alzheimer’s disease, neuronal dendrites and dendritic spines undergo significant pathological changes. Because of the determinant role of these highly dynamic structures in signaling by individual neurons and ultimately in the functionality of neuronal networks that mediate cognitive functions, a detailed understanding of these changes is of paramount importance. Mutant murine models, such as the Tg2576 APP mutant mouse and the rTg4510 tau mutant mouse have been developed to provide insight into pathogenesis involving the abnormal production and aggregation of amyloid and tau proteins, because of the key role that these proteins play in neurodegenerative disease. This review showcases the multidimensional approach taken by our collaborative group to increase understanding of pathological mechanisms in neurodegenerative disease using these mouse models. This approach includes analyses of empirical 3D morphological and electrophysiological data acquired from frontal cortical pyramidal neurons using confocal laser scanning microscopy and whole-cell patch-clamp recording techniques, combined with computational modeling methodologies. These collaborative studies are designed to shed insight on the repercussions of dystrophic changes in neocortical neurons, define the cellular phenotype of differential neuronal vulnerability in relevant models of neurodegenerative disease, and provide a basis upon which to develop meaningful therapeutic strategies aimed at preventing, reversing, or compensating for neurodegenerative changes in dementia.

Introduction

Neocortical pyramidal neurons possess extensive apical and basilar dendritic trees, which integrate information from thousands of excitatory and inhibitory synaptic inputs. Dendrites respond to inputs with postsynaptic potentials, which are relayed to the soma where they are summed; if a threshold potential is exceeded, an action potential is generated. Voltage attenuation in space and time along dendrites is fundamental to summation and is influenced by a number of interacting morphological properties (such as diameter and length) and active properties (such as distribution of ion channels) of the dendritic shaft (Hausser et al. 2000; Kampa et al. 2007; Stuart and Spruston 2007; Henry et al. 2008). Further complexity arises from the presence of thousands of biophysically active dendritic spines, the principal receptive site for excitatory glutamatergic inputs to a neuron.

Dendrites and dendritic spines in particular are dynamic structures, which undergo significant changes across the life span. Under non-pathological conditions, the number of spines on pyramidal neuron dendrites increases substantially over the course of development, is reduced during maturation to adulthood, and remains relatively stable during adulthood (for review see Bhatt et al. 2009). Then, during normal aging, significant changes in spine number, distribution, and morphology occur (Duan et al. 2003). Spines also undergo significant structural modifications under conditions where synaptic strength is experimentally modified, usually with protocols designed to evoke longterm potentiation or long-term depression (for review see Alvarez and Sabatini 2007; Bhatt et al. 2009; Holtmaat and Svoboda 2009). In many neurodegenerative diseases, significant alterations in the dendritic arbor occur, together with substantial spine loss and alterations in spine morphology (reviewed in Halpain et al. 2005). Gaining an understanding of these sublethal changes to neurons, which detrimentally impact neuronal signaling, and ultimately cognitive function, is an important goal.

Transgenic mouse models have been useful for elucidating mechanisms of amyloid-and tau-induced pathology, although no single model fully recapitulates human disease (for review see Duff and Suleman 2004; Spires et al. 2005). Two of the most commonly employed mouse models of neurodegenerative disease are the Tg2576 amyloid precursor protein (APP) mutant mouse and the rTg4510 tau mutant mouse, which develop significant pathological aggregations of amyloid-beta (Aβ) and tau proteins, respectively. Tg2576 transgenic mice overexpress the Swedish double mutation of the human APP gene, which leads to progressive formation of soluble Aβ peptides and fibrillar Aβ deposits in the form of amyloid plaques. Increased Aβ levels in these mice are associated with progressive structural changes to neurons (although not with neuron death), and cognitive impairment (Hsiao et al. 1996). In the rTg4510 mouse model, expression of the P301L mutant human tau variant leads to progressive development of neurofibrillary tangles (NFTs), neuronal death, and memory impairment reminiscent of the pathology observed in human tauopathies (Santacruz et al. 2005).

In this review, we discuss changes in the structure and function of dendrites and spines of pyramidal neurons that are associated with pathological aggregation of Aβ and tau in these and other mouse models of neurodegenerative disease. We also discuss, as a point of comparison, the impact of normal brain aging on the morphofunctional properties of pyramidal neurons in aged macaque monkeys. This is not a comprehensive review of the literature on such changes in human neurodegenerative diseases or of the many studies of these changes in mouse models (for reviews see Duff and Suleman 2004; Spires and Hyman 2004; Lewis and Hutton 2005; Duyckaerts et al. 2008; Giannakopoulos et al. 2009). Rather, the focus here is specifically on our multidimensional collaborative efforts to understand the functional consequences of pathological changes in the structure of individual layer 3 frontal cortical pyramidal neurons in commonly employed mouse models of neurodegeneration. These studies focus on layer 3 pyramidal neurons in the neocortex because they are the principal neurons involved in corticocortical circuits that mediate many cognitive functions of the frontal cortex and may be selectively targeted in neurodegenerative disease (Morrison and Hof 1997, 2002; Hof and Morrison 2004). Following a brief overview of the normal structure and function of dendrites and spines, we describe technical details of our experimental approach and the analytical tools we have developed to reconstruct and quantify dendritic and spine structure in 3D in mouse and macaque monkey models (Rodriguez et al. 2003, 2006, 2008, 2009; Wearne et al. 2005; Rocher et al. 2008, 2009; Kabaso et al. 2009). Next, empirical structural and electrophysiological data obtained from frontal cortical pyramidal neurons in in vitro slices prepared from transgenic versus wild-type mice are discussed. Finally, we end with a description of the computational modeling approaches currently used by our group to provide insights on structure–function relationships in pyramidal neurons under pathological conditions mimicking those seen in human neurodegenerative diseases (Rothnie et al. 2006; Henry et al. 2008; Weaver and Wearne 2008; Kabaso et al. 2009).

Normal structure and function of dendrites and spines

Dendrites

The architecture of dendritic arbors varies extensively, from the relatively simple arbors of anterior horn neurons in the spinal cord, to the more complex cortical pyramidal neurons, to the extreme elaboration seen in cerebellar Purkinje neurons. Despite the large variability in the numbers of dendritic branches and their overall extent, most dendrites share certain fundamental characteristics, including that they are wide at the base and taper as they extend distally, and they branch at angles <90°. The organelles in dendrites are similar to those found in the soma; rough and smooth endoplasmic reticulum, free ribosomes, mitochondria, neurofilaments, and microtubules are all present, abundantly in the wide proximal bases, and decreasingly as dendrites move distally and decrease in diameter. As shown in Fig. 1a, layer 3 cortical pyramidal neurons have a skirt of basilar dendrites originating from the base and a main apical dendrite originating from the apex of their soma. The main apical dendrite gives rise to several oblique branches and, approximately at the intersection between layers 2 and 1, to an apical tuft that ascends to the pial surface. Importantly, the basilar and apical dendritic domains receive and integrate inputs from anatomically and functionally distinct presynaptic sources (for review see Spruston 2008). Basilar and proximal apical dendrites receive inputs from layer 4 neurons and from local-circuit neurons (Lubke et al. 2000; Feldmeyer et al. 2002). The apical tuft, which can comprise up to 50% of the dendritic arbor of a given neuron, is the principal recipient of monoaminergic modulatory inputs (Thierry et al. 1990), thalamic inputs (van Groen et al. 1999), and feedback intracortical connections (Rockland and Pandya 1979).

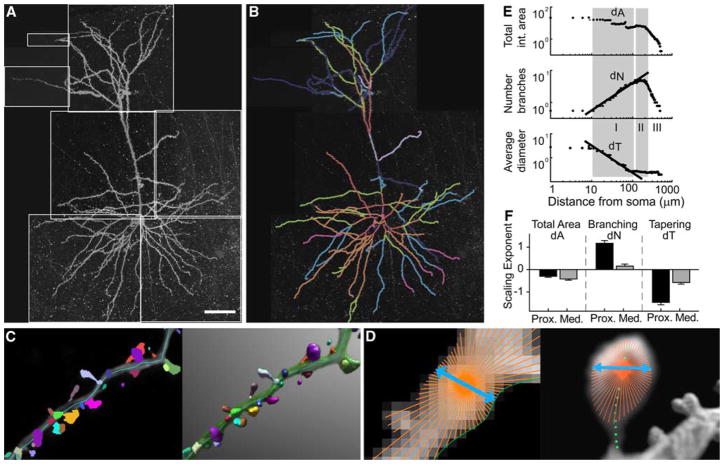
Fig. 1.

Structural properties of mouse neocortical pyramidal neurons. a 40 × CLSM image of a layer 3 pyramidal cell from the frontal cortex of a wild-type mouse. The neuron was filled with biocytin during patch-clamp recording and subsequently labeled with Alexastreptavidin 488. b 100 × CLSM image of the spiny dendrite shown within the red box in (a). c Electron micrograph showing the ultrastructure of a pyramidal neuron spine, with a prominent postsynaptic density and spine apparatus. Courtesy of Dr. Alan Peters. Scale bars a 40, b 5, c 0.5 μm

The structural properties of dendrites underlie their passive membrane (cable) properties, which are membrane capacitance C_m, specific membrane resistance R_m and axial resistivity R_a. These cable properties determine, at a fundamental level, the degree of summation of synaptic inputs and the spatial distribution of electrical signals. Because summation of synaptic inputs by dendrites is determined in large part by their structure, dendritic morphology plays a critical role in action potential generation (Mainen and Sejnowski 1996; Koch and Segev 2000; Euler and Denk 2001; Vetter et al. 2001; Krichmar et al. 2002; Ascoli 2003). Importantly, both branching topology and surface irregularities including dendritic varicosities (Surkis et al. 1998) contribute to the excitable properties of neurons. For example, recent simulation studies have demonstrated that marked differences in the efficacy of action potential back propagation in different neural types are attributable in large part to variations in dendritic morphology (for review see Stuart et al. 1997; Waters et al. 2005).

Integration of synaptic inputs by dendrites is mediated not only by basic passive cable properties, but also by active properties, which include the number and distribution of voltage, ligand, as well as second messenger-gated transmembrane ionic channels (reviewed in Migliore and Shepherd 2002; Magee and Johnston 2005; Johnston and Narayanan 2008; Nusser 2009). Dendrites possess a rich array of sodium, calcium, and potassium channels that are distributed either uniformly or non-uniformly across a given dendrite (for reviews, see Johnston et al. 1996; Migliore and Shepherd 2002; Magee and Johnston 2005; Johnston and Narayanan 2008; Nusser 2009). For example, layer 5 cortical pyramidal neuron dendrites possess a gradient of the hyperpolarization-activated mixed cationic HCN channels that increase in density from the soma to the apical tuft (Berger et al. 2001; Lorincz et al. 2002). The interaction of intrinsic ionic and synaptic conductances with passive properties determined by dendritic morphology can effectively alter the cable properties of the dendritic tree (Bernander et al. 1991; Segev and London 2000; Bekkers and Hausser 2007) adding a further layer of complexity to signaling by individual neurons. Computational modeling approaches have been extensively employed to shed light on dendritic structure–function relationships and into potential interactions between a multitude of dendritic active and passive properties. These approaches, as discussed at the end of this review, have been useful for gaining insight on dendrites that are too thin to be studied with electrophysiological approaches, and for providing empirical researchers with testable hypotheses relevant to the functional consequences of dendritic dystrophy in neurodegenerative diseases.

Dendritic spines

Dendrites of glutamatergic pyramidal neurons are studded by thousands of dendritic spines, which are the site of most of the glutamatergic synapses in the brain, that confer further functional complexity to these processes. Spine density, shape, and distribution are all important contributors to neuronal excitability that are superimposed on the electrophysiological properties of dendritic shafts (Wilson 1988; Stratford et al. 1989; Baer and Rinzel 1991; Tsay and Yuste 2002). Spines are small appendages that extend from approximately 0.5–3 lm from dendritic shafts and are usually <1 μm in diameter (Fig. 1b, c). Mouse layer 3 frontal cortical pyramidal neurons typically possess approximately 6,000 dendritic spines (Rocher et al. 2008). Spines can be broadly categorized as falling into one of several different morphological types, namely “thin”, “stubby”, “mushroom”, and “filopodia” which are normally seen in large numbers only during development (for review see Yuste and Bonhoeffer 2004; Bourne and Harris 2007). Although most spines do fall into one of these broad categories, serial electron microscopy reveals that there is also a continuum between the different morphological subtypes (Bourne and Harris 2007). Spine morphology determines the strength, stability and function of excitatory synaptic connections that subserve the neuronal networks underlying cognitive function. Smaller spines, such as the thin and filopodia types are less stable and more motile (Trachtenberg et al. 2002; Kasai et al. 2003; Holtmaat et al. 2005) and as a result, are more plastic than large spines such as the mushroom and stubby types (Grutzendler et al. 2002). The size and morphology of the spine head is correlated with the number of docked presynaptic vesicles (Schikorski and Stevens 1999) and the number of postsynaptic receptors (Nusser et al. 1998), and hence with the size of synaptic currents and synapse strength. In addition, a small head size permits fast diffusion of calcium within the spine, while the neck length shapes the time constant for calcium compartmentalization (for review see Yuste and Bonhoeffer 2001; Nimchinsky et al. 2002), modulating postsynaptic mechanisms that play an important role in synaptic plasticity linked to functions, such as learning and memory (Holthoff et al. 2002; Alvarez and Sabatini 2007; Bloodgood and Sabatini 2007). Spine neck length and diameter also affect diffusional coupling between dendrite and spine (Svoboda et al. 1996; Yuste et al. 2000; Bloodgood and Sabatini 2005), and spine density and shape regulate the degree of anomalous diffusion of chemical signals within the dendrite (Santamaria et al. 2006). Spine morphology also varies dynamically in response to synaptic activity (Lendvai et al. 2000; Hering and Sheng 2001; Zuo et al. 2005).

Over the past few decades, it has become increasingly evident that local dendritic spine structure and distribution (Matus and Shepherd 2000) play a key role in the electrical and biochemical signaling of dendrites (Nimchinsky et al. 2002; Matus 2005; Bourne and Harris 2007). However, spines present challenges to the standard cable model of dendrites. The common way to model the effects of spines in a passive cable equation model is to reduce the membrane resistance and increase the membrane capacitance by a factor proportional to the increased membrane surface area due to spines (Jaslove 1992). This modification predicts that voltage should attenuate more drastically in space along spiny dendrites, relative to their smooth counterparts. Because of their capacity for plasticity and because they are the location of most excitatory synapses in the cerebral cortex, accurately characterizing the structure of dendritic spines is essential for understanding their contributions to neuronal, and ultimately to cognitive function.

Current methods used to study the structure of dendrites and spines

Experimental approaches

The most widely employed method used to study the dendritic structure of neurons has historically been the Golgi impregnation method, in which neurons are impregnated by silver chromate following incubation in potassium dichromate and silver nitrate. This method was developed by Camillo Golgi and used by Ramón y Cajal in his seminal descriptions of neurons at the turn of the twentieth century (Ramón y Cajal 1911; Garcia-Lopez et al. 2007). The Golgi method has been used in innumerable studies designed to examine the normal structure of neurons, as well as changes in neuronal structure across the lifespan or under pathological conditions. This approach has been used in a number of studies designed to examine the effects of Alzheimer’s disease (AD) on neuronal structure (Paula-Barbosa et al. 1980; Probst et al. 1983; Ferrer et al. 1990; Flood 1991; Gertz et al. 1991; Scott 1993; Garcia-Marin et al. 2007). However, the Golgi technique has a number of significant drawbacks that make it suboptimal for high-resolution analyses of neuronal structure. First, it is capricious; neurons are stained in a random and unpredictable manner. Second, axons and distal dendritic processes are often incompletely impregnated, and given that dendritic retraction and extension is a common feature of pathological states, this is a significant methodological drawback. Third, as neurons are not fluorescently labeled, they cannot be analyzed at very high resolution in 3D with confocal laser scanning microscopy (CLSM) or with multiphoton laser scanning microscopy (MPLSM).

Improved techniques using fluorescence labeling to assess the details of dendrite and dendritic spine structure are now available. These techniques are ideally suited for imaging neurons at a very high resolution with CLSM/MPLSM for subsequent 3D reconstruction. In lightly fixed tissue, neurons can be well filled by intracellular injection of fluorescent dyes, such as Lucifer Yellow (Rho and Sidman 1986; Buhl and Lübke 1989). In living tissue, DiOlistic labeling using the ballistic delivery of lipophilic dye-coated particles (Moolman et al. 2004; Tsai et al. 2004) and GFP labeling with the gene transfer technique by viral vectors (Spires et al. 2005) have been used in the examination of changes in the structural properties of neurons in transgenic mouse models of AD. In these studies, transcranial two-photon laser scanning microscopy of fluorescently labeled neurons was used to great advantage in the study of dendritic and spine changes in vivo, as a consequence of proximity to amyloid plaques in cortical pyramidal neurons in Tg2576 APP mutant mice (e.g., Tsai et al. 2004; Spires et al. 2005). Injection of biocytin during electrophysiological recordings and subsequent incubation of the tissue with fluorescent avidin compounds is a useful means by which both the function and structure of individual neurons can be characterized. We have used this approach to examine structure–function relationships in neurons from mouse models of neurodegenerative disease (Rocher et al. 2008, 2009) and from normally aging macaque monkeys. Biocytin filling during recordings yields exquisitely labeled dendrites, spines and axons (Figs. 1, 2, 3, 4, 5), and allows for the correlation of high-resolution morphometric data with detailed electrophysiological data, providing important information on structure–function relationships.

Fig. 2.

Analytical methods to quantify morphological structure. a xy projection of the montage of CLSM tiled image stacks from a wildtype mouse layer 3 frontal cortical pyramidal neuron. Scale bar 40 μm. b Tree structure from the data shown in (a), extracted using NeuronStudio. c Automatic spine detection and visualization in NeuronStudio. Left automatically detected spines overlaid on a maximum projection of a typical dataset; right the same data and spines volume-rendered in 3D. d Left 2D Rayburst sample used for diameter estimation. Rays cast using the sampling core is shown in orange with the one chosen as the diameter shown in blue. The green line indicates the surface detected by the Rayburst samples. Right spine diameter estimation using a 2D Rayburst run at the center of mass (small green squares) of a single layer. The blue line indicates the resulting width of the structure as calculated by Rayburst, and provides an approximate length of 0.7 μm. e Optimized fits of scaling exponents (black fitted lines) and optimal scaling regions (gray shaded bands) for the apical dendrites of a typical layer 3 pyramidal cell projecting from superior temporal cortex to area 46 (see Kabaso et al. (2009) for details). f Contributions of branching and tapering exponents to global mass scaling (measured by total area exponent dA) in spine-corrected apical dendrites of long projection neurons of young rhesus monkeys, in the proximal and medial scaling regions (I, II in e). The total branching and tapering vary across the two scaling regions, yet the total area in each region is conserved [modified from Wearne et al. (2005) and Kabaso et al. (2009)]

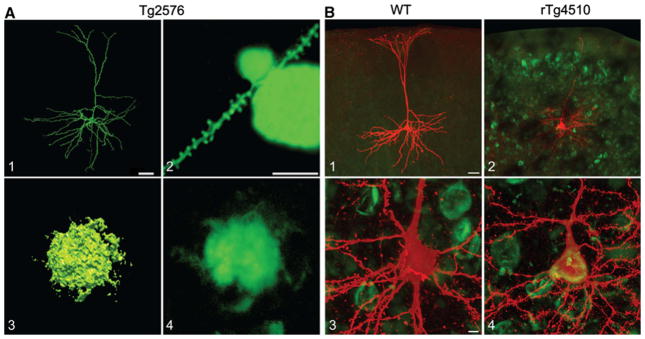
Fig. 3.

Pathological features and filled pyramidal neurons from Tg2576 and rTg4510 mice. a CLSM images of a Tg2576 pyramidal neuron (1) and a dendritic spine traversing an Aβ plaque (2), 3 and 4 show CLSM images of Aβ plaques. b CLSM images of a typical wild-type neuron (1) and a rTg4510 neuron pyramidal neuron containing an NFT (2), 3 and 4 show higher magnification views of the neuronal somata seen in 1 and 2; b modified from Rocher et al. (2009). Scale bars A1 40 μm, A2–4 10 μm, B1, 2 40 μm, B3, 4 5 μm

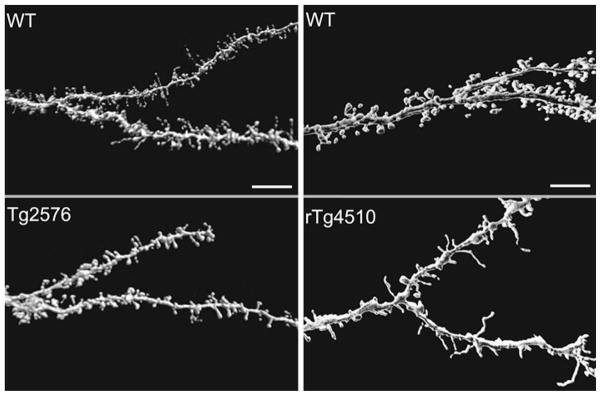
Fig. 4.

Dendritic spine loss in pyramidal neurons from Tg2576 and rTg4510 mice. CLSM images of dendritic segments with spines of neurons from wild-type (top) and transgenic (bottom) mice. Scale bars 10 μm [modified from Rocher et al. (2008, 2009)]

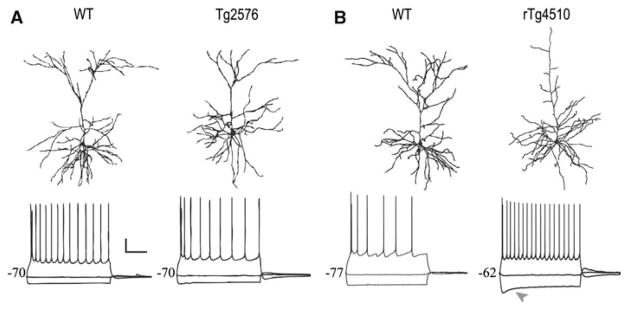
Fig. 5.

Action potential firing properties of pyramidal neurons from Tg2576 and rTg4510 mice. a Top × 40 CLSM images showing representative dendritic morphology for wild-type and Tg2576 neurons, bottom action potential firing properties of typical neurons. b Top 40 × CLSM images showing representative dendritic morphology for wildtype and rTg4510 neurons, bottom action potential firing properties of typical neurons. Grey arrowhead indicates depolarizing sag. Scale bar 20 mV, 500 ms [modified from Rocher et al. (2008, 2009)]

3D reconstruction and analytical approaches

Early methods for digitizing 3D neuronal structures relied on interactive manual tracing from a computer screen (Capowski 1985). These methods were time-consuming, subjective, and lacked precision. In recent years, automated methods have been developed that use image analysis algorithms to extract neuronal morphology directly from 3D microscopy and overcome the limitations of manual techniques (Koh et al. 2002; He et al. 2003; Wearne et al. 2005). Newer methods use pattern recognition routines to track or detect a structure locally without the need for global image operations (Al-Kofahi et al. 2002; Streekstra and van Pelt 2002; Schmitt et al. 2004; Myatt et al. 2006; Santamaria-Pang et al. 2007). Most are designed to work on a broad range of signal-to-noise ratios and even on multiple imaging modalities. This results in increased computational complexity, which makes the use of these methods as interactive reconstruction tools for high-resolution data less than optimal.

In our studies of neuronal structure, morphological reconstruction is performed using NeuronStudio, a neuron morphology reconstruction software tool (http://www.mssm.edu/cnic/tools.html), developed by Wearne et al. (2005) and Rodriguez et al. (2006, 2008, 2009). Neuron- Studio has been designed for low computational complexity to allow interactive semi-automated extraction of neuronal morphology from medium to high-quality de-convolved 3D CLSM and MPLSM image stacks of fluorescently labeled neurons. It features automated extraction of dendrites and dendritic spines as well as a rich set of manual editing and visualization modalities. Figure 2a shows an xy projection of CLSM data from a wild-type mouse layer 3 cortical pyramidal neuron and Fig. 2b shows the automated reconstruction of the neuron’s dendritic arbor obtained using NeuronStudio. Because fluorescence intensity can vary with adequacy of filling, imaging depth and xy spatial extent in CLSM and MPLSM image stacks, data segmentation within NeuronStudio adapts the iterative self-organizing data analysis (ISODATA) method (Ridler and Calvard 1978) to compute local thresholds dynamically. This method is appropriate for datasets exhibiting a bimodal distribution of intensity values, such as the grayscale images characteristic of de-convolved LSM image stacks.

Automated 3D reconstruction of dendritic arbors

To reconstruct the dendritic arbors automatically from an image, we first look to extract the ‘centerline’ of each dendritic segment: the line that identifies the center of the dendrite as it traverses through space (blue line in Fig. 2c). In NeuronStudio, dendritic centerline extraction is performed using the voxel scooping method (Rodriguez et al. 2009). Voxel scooping is an efficient algorithm for centerline extraction from volumetric datasets of fluorescently labeled neurons obtained by CLSM imaging. Starting from a seed location inside the structure, the method iteratively carves thin cross sectional layers of object voxels (‘scoops’) that are clustered based on the connectivity. Each cluster contributes a node along the centerline, which is created by connecting successive nodes until all object voxels are exhausted. The actual position where each node is created depends on a number of cluster parameters to ensure proper centering along the dendrite. The addition of voxels to each cluster is also done in a way that allows the algorithm to advance into the structure while adjusting for directional changes. The scooping method provides an optimal balance between computational efficiency and tracing accuracy that is suitable for interactive neuron tracing applications. The resulting model is amenable to manual editing and is compatible with compartment modeling packages such as NEURON (Carnevale and Hines 2006) and GENESIS (Bower and Beeman 1998), and with morphometry analysis software such as L-Measure (Scorcioni and Ascoli 2001).

Diameter estimation in NeuronStudio is performed using the Rayburst sampling algorithm (Rodriguez et al. 2006) to determine the minimum wall-to-wall span at each node location inside the dendrite or spine (Fig. 2d). For data acquired by LSM, the point-spread function of the microscope can distort the apparent thickness of branches significantly along the direction of the optic axis (usually the z axis of the data). Although this is largely reduced by deconvolution, residual smear along the optic axis is not uncommon. The 2D variant of the Rayburst algorithm is insensitive to residual smear along the optic axis, and can produce a reliable estimate of branch diameter regardless of the orientation of the branch within the image stack when run centrally within a branch of approximately circular cross section.

Automated 3D reconstruction of dendritic spines

The assessment of spine numbers and distribution and their classification into subtypes has historically been a labor intensive and relatively inaccurate process. Spine numbers could only be estimated because spines extending primarily in the z plane relative to the dendritic shaft could not be counted. With the advent of CLSM, accurate 3D spine assessment came a step closer, but was still a highly timeconsuming and labor-intensive undertaking. Improving upon previous spine detection algorithms (Koh et al. 2002; Cheng et al. 2007), Rodriguez et al. (2008) devised an efficient and robust method for automated spine detection, available in NeuronStudio. To detect spines, NeuronStudio begins by building concentric layers of voxels around a previously computed model of the dendritic structure. Voxels are segmented by interpolating ISODATA thresholds computed at each node along the dendritic model. The algorithm only processes object voxels within a maximum user-specified distance from the model and makes use of space partitioning to achieve faster processing. Individual spines are detected by clustering voxels in layers starting from the most distal voxels. For each processed object voxel, the algorithm computes the distance to the model’s surface (DTS). Any voxel having no neighbor with a greater DTS is considered a local maximum or tip and is evaluated as a possible spine. Using this maximum as a first layer, each iteration of the algorithm builds a new layer by first adding unvisited voxels directly connected to the previous layer and then expanding the new layer with any connected voxels having a DTS value equal or greater than the lowest DTS in the layer. This results in the formation of thin concentric layers that are used to measure the shape of a protrusion and to determine if a spine has been found. The algorithm also measures the Rayburst diameter at the center of each layer to build a measurement profile that is used to further characterize the spine shape into thin, stubby, or mushroom morphologic types. An example of spines characterized by NeuronStudio’s spine detection algorithms is shown in Fig. 2d.

3D measures of spatial complexity

Traditionally, Sholl analysis (1953) has been used in two dimensions to quantify the spatial complexity of dendritic branching patterns with increasing distance from the soma. Fractal analyses have also been used (Smith et al. 1989; Caserta et al. 1995; Jelinek and Elston 2001; Henry et al. 2002) to quantify spatial complexity as a power law scaling exponent, describing the rate of change of the number of branches over a large portion of the dendrites, and best visualized as the slope of a log–log plot of these two quantities. We have recently extended this work (Rothnie et al. 2006; Kabaso et al. 2009) to include three power law exponents describing global spatial complexity: rates of change of dendritic mass, branching, and taper.

We analyzed these power law exponents (log–log slopes) in two types of layer 3 pyramidal neurons of rhesus monkeys: those located in the superior temporal cortex with ‘long’ corticocortical projections to area 46, and those with ‘local’ projections within area 46. We studied apical and basal dendrites separately, and compared results in young and old rhesus monkeys (Duan et al. 2003; Kabaso et al. 2009). Consistently in each of these neurons, we found that the rate of change of dendritic mass was constant in two distinct regions of the dendrites (Rothnie et al. 2006; Kabaso et al. 2009). These regions (region I: ‘proximal’ and region II: ‘medial’) and associated scaling exponents are shown in Fig. 2e for the apical dendrites of a typical long projection neuron from a young monkey. The mean and standard errors of scaling exponents for all young long projection neurons are shown in Fig. 2f.

Rothnie et al. (2006) revealed a form of global mass homeostasis in these neurons: the rates of branching and tapering in each of the two regions were inversely related, so that the spatial gradient of dendritic mass with distance from the soma was constant. Significantly, we found that the compensation of branching and tapering was maintained across the different projection types, and even with aging, so that the spatial gradient of dendritic mass in the proximal and medial regions was constant (Kabaso et al. 2009). This global mass homeostasis might be due to some kind of control mechanism intrinsic to the neuron (Samsonovich and Ascoli 2006) that is conserved in aging. It will be instructive to evaluate whether such global mass homeostasis is maintained during neurodegeneration.

In conclusion, these analytical tools provide rapid, objective analyses of the high-resolution data that we collect from wild-type and transgenic mouse neurons. With NeuronStudio, we are able to perform analyses of differences in dendrite diameter and spine shapes that were not available previously, and these kinds of studies are currently ongoing in our laboratories. Moving forward, we will evaluate whether the global patterns in spatial complexity observed in rhesus monkey pyramidal neurons are similarly present in mouse neurons. We will also compare the spatial complexity of wild-type and transgenic neurons to determine whether global mass homeostasis is conserved in neurodegeneration as it seems to be in aging.

Alterations in the structure of dendrites and spines of cortical pyramidal neurons in Tg2576 and rTg4510 mutant mice

Dendritic changes in neurodegenerative disease

Numerous studies have demonstrated pervasive and significant changes in neuronal morphology in AD and other neurodegenerative diseases (Anderton et al. 1998; Falke et al. 2003; Knobloch and Mansuy 2008; Giannakopoulos et al. 2009; Tackenberg et al. 2009). Proximity to fibrillar Aβ plaques, both in AD and in mouse models which overexpress APP, has been positively associated with dystrophic dendrites and axons, aberrant sprouting and curvature of dendritic processes and loss of dendritic spines with accompanying synapse loss in hippocampal and neocortical pyramidal cells (Knowles et al. 1999; Le et al. 2001; Urbanc et al. 2002; Tsai et al. 2004; Spires et al. 2005; for review Spires and Hyman 2004). For example, Tsai et al. (2004) showed prevalent axonal varicosities and reduced diameter of dendrites directly traversing or closely apposed to fibrillar Aβ plaques in PSAPP transgenic mice and Spires et al. (2005) reported significantly altered trajectories of dendrites from neocortical pyramidal neurons near Aβ plaques in Tg2576 mice.

The effects of soluble Aβ on dendritic structure are less well characterized. Using the dendritic and spine reconstruction and analysis methods provided in NeuronStudio, we examined the morphological and electrophysiological properties of layer 3 frontal cortical pyramidal neurons in brain slices from 12-month-old Tg2576 mice (an age at which soluble Aβ levels are high but there are few Aβ plaques). Whole-cell patch-clamp recording with simultaneous biocytin filling of neurons was used for a detailed and comprehensive assessment of the dendritic morphology of entire neurons (Fig. 3a). Dendritic properties of pyramidal neurons from 12-month-old Tg2576 mice were notably altered from those from wild-type mice, exhibiting significantly increased spatial extents, lengths, and volumes across the full expanse of both apical and basal dendritic arbors (Rocher et al. 2008).

In another study, we examined morphological changes in the Tg2576 mouse frontal pyramidal neurons at 9 and 24 months of age, using cell filling with Lucifer Yellow in lightly fixed tissue (Dickstein et al. unpublished data). There was no difference in dendritic structure between the Tg2576 and wild-type neurons at 9 months of age, prior to substantial deposition of plaques. However at 24 months of age, when amyloid plaques are abundant, we observed a significant reduction in apical dendritic length when compared with wild type in layer 3 pyramidal neurons ( ~ 22% decrease). Taken together, data from these studies indicate that dendritic structure is modified with time in Tg2576 cortical pyramidal neurons, with an initial elongation at 12 months followed by regression at 24 months.

In contrast to studies on the effects of Aβ on dendritic morphology, very little is known about the effects of mutated tau on neuronal structure. Under normal conditions, the microtubule-associated protein tau plays a key role in stabilization and assembly of microtubules, which are critical for the maintenance of normal cellular morphology and cellular trafficking (Conde and Caceres 2009). In neurodegenerative diseases, such as AD and animal models of tauopathy, mutated and/or overexpressed tau becomes hyperphosphorylated, disengaged from microtubules and relocalized from the axon to the somata and dendrites where it aggregates in the form of NFTs and neuropil threads, respectively (Spires-Jones et al. 2009). The overexpression of tau, like that which occurs in rTg4510 mice, has been shown to result in destabilization of the dendritic cytoskeleton and compromised intracellular trafficking (Hall et al. 2000, 2001). Although there is a strong positive relationship between the number of NFTs and the severity of neurodegeneration and dementia in AD, recent studies question whether NFTs are themselves toxic to neurons. There is an apparent dissociation between the presence of an NFT and neuron death as demonstrated by Andorfer et al. (2005) who found that in htau mice (which overexpress wild-type human tau), substantial neuronal death precedes NFT formation, and dying neurons lack evidence of fibrillar tau aggregates. In a recent study, we assessed the effect of overexpression of mutant tau on neuronal structure and function in rTg4510 mice at 8.5 months of age (Rocher et al. 2009). Forty-two percent of the rTg4510 neurons assessed in this study contained a thioflavin S-positive NFT in the somata, and the remaining 58% did not stain with thioflavin S (Fig. 3b). The majority of rTg4510 neurons (65%) exhibited marked atrophy or complete loss of the apical dendritic tuft. This morphological remodeling occurred regardless of the presence or the absence of NFTs. Further, both apical and basal dendrites of rTg4510 neurons demonstrated significantly diminished length and complexity. Recently, Dickstein et al. (this issue) compared the dendritic structure of cortical pyramidal neurons from htau mice at 3 months of age, when hyperphosphorylated tau is present, but NFTs are not, to neurons at 12 months of age when NFTs are evident. There were no significant differences in apical or basal dendritic length between neurons from the two age groups; however, neurons from 12-month-old mice had significantly more complex proximal apical dendrite branching patterns as compared to neurons from younger mice ( ~ 15% increase in density in the segments 30–120 lm from the soma). Future studies will compare neurons from htau mice versus those from wild-type controls and also examine alterations to dendritic structure in htau mice at older ages when tauopathy is more established.

Spine changes in neurodegenerative disease

Many studies have shown that dendritic spines are particularly vulnerable in AD and in mouse models of AD (for review see Knobloch and Mansuy 2008; Giannakopoulos et al. 2009). Loss of approximately half of dendritic spines has been reported for cortical pyramidal neuron dendrites directly traversing or closely apposed to Ab plaques in aged PSAPP (46%; Tsai et al. 2004) and Tg2576 mice (50%; Spires et al. 2005). Although the majority of studies have concentrated principally on morphological alterations of neurons associated with fibrillar plaques, comparable changes have been observed in areas devoid of Aβ deposits. In neurons from PSAPP mice, spine loss has been reported in regions with minimal or no fibrillar Aβ (Tsai et al. 2004), and in Tg2576 mice there is a substantial ~ 25% loss of spines on dendrites not in close proximity to Aβ plaques (Spires et al. 2005).

To determine the effect of endogenous soluble Aβ species on neuronal morphology in young Tg2576 mice prior to substantial plaque deposition, we assessed the number, density, and distribution of spines across the entire apical and basal dendritic arbors of layer 3 frontal cortical pyramidal neurons from Tg2576 versus wild-type mice at 12 months of age (Rocher et al. 2008). Spines were evaluated in 3D using high-resolution confocal imaging followed by automated spine detection with NeuronStudio. Although the distribution and mean total number of dendritic spines did not differ between the two groups, neurons from Tg2576 mice exhibited a significantly decreased mean density of spines per unit dendritic volume in both the apical and basal trees (Fig. 4). Comparable to reductions reported by others for individual dendritic segments (Tsai et al. 2004; Spires et al. 2005), spine density was significantly decreased (−26%) across the entire dendritic arbor in Tg2576 neurons. There was a strong relationship between spine number and total neuron volume in individual neurons, indicating that the total number of spines is preserved in Tg2576 neurons as a result of concomitant dendritic lengthening. During the early stage of disease progression prior to substantial plaque formation, but at which time, soluble Aβ species are abundant, it is plausible that the total number of dendritic spines ismaintained through compensatory dendritic elongation. At later stages, the formation of plaques is accompanied by abnormal neurite curvature and continued spine loss. It is at this time,when the Aβ load is much higher, that progressive alterations in neuronal morphology will likely lead to significant functional consequences such as altered synaptic integration as observed in vivo in mice with fibrillar Aβ plaques (Stern et al. 2004).

In a recent study on pyramidal neurons from 9-monthold versus 24-month-old Tg2576 mice (Dickstein et al. unpublished data), there was a shift in the proportion of morphological subtypes of spines, with a significant reduction in number of mushroom and stubby spines and an increase in the number of thin spines. This shift in spine type was accompanied by a change in specific spine volumes with thin spines of neurons from 24-month-old mice having significantly larger volumes than those from 9-month-old mice. Larger thin spines may represent a regression of mushroom spines suggesting a loss of stable, mature spines in neurons from 24-month-old Tg2576 mice.

There is not much information available about the effects of tauopathy on dendritic spines of cortical pyramidal neurons. Evidence that spine numbers are reduced comes from studies showing a ~ 40% decrease in the density of synaptophysin labeling in the prefrontal cortex (PFC) of patients with frontotemporal dementia (Liu et al. 1996) and studies of synaptic markers in transgenic mouse models of tauopathy. There is a reduction in spinophilin and synaptophysin labeling and spine–synapse density in the hippocampus of the ΔK280 proaggregation model of tauopathy (Mocanu et al. 2008), and a similar reduction in synaptotagmin and synaptophysin immunoreactivity in the hippocampus of the THY-Tau22 mouse model (Schindowski et al. 2006). We recently demonstrated that, in addition to dramatically altering the dendritic shafts of cortical pyramidal neurons, mutated tau expression leads to a significant ~ 30% reduction in dendritic spine density on pyramidal neurons from rTg4510 mice (Fig. 4; Rocher et al. 2009). Further, in neurons from htau mice, there were significant differences in apical spine density in cells from mice at 3 versus 12 months of age with no differences in basal dendrites (Dickstein et al. this issue). The changes in spine number were accompanied by a significant decrease ( ~ 44%) in overall spine volume in dendrites of neurons from 6 and 12-month-old htau mice. Interestingly, as with spines in the aged Tg2576 mice, there was a shift from stable mushroom spines to thin spines with an increase ( ~ 17%) in the volume of thin spines, indicating that comparable mechanisms of spine destabilization may occur in these two mouse models.

In summary, significant structural changes are induced in dendrites and spines by aberrant tau and amyloid, which could be expected to have significant functional consequences. Importantly, there is growing evidence that these morphological changes are reversible, at least in mouse models of neurodegenerative disease. For example, recent studies have demonstrated reversal of dendritic pathology in APP/PS1 mutant mice upon treatment with both rolipram and TAT-HA-Uch-L1 (Smith et al. 2009) or with Aβ immunotherapy in Tg2576 and APP/PS1 mice (Lombardo et al. 2003; Biscaro et al. 2009; Rozkalne et al. 2009).

Functional consequences of neurodegenerative morphological changes

Insights from electrophysiological studies

As summarized above, the structural characteristics of individual neurons fundamentally determine their functionality with respect to both synaptic integration and firing properties. Therefore, it is likely that the altered morphology of Tg2576 and rTg4510 pyramidal neurons result in modifications of functional electrophysiological properties of individual neurons and downstream neuronal network properties. However, there is a dearth of information on the functional consequences of significant morphological changes in APP and tau transgenic mice. Some insight has been provided by studies in which soluble Aβ protofibrils exogenously applied to isolated embryonic rat neocortical neurons elicited a marked increase in neuronal excitability (Hartley et al. 1999) and inhibition of A and D type outward potassium currents (Ye et al. 2003). Several studies have demonstrated that basal glutamatergic synaptic transmission (assessed with extracellular field potential recordings) is significantly reduced in populations of cells in the hippocampus and neocortex of APP transgenic mice as compared to control mice (Larson et al. 1999; Hsia et al. 1999; Giacchino et al. 2000; Fitzjohn et al. 2001; Roder et al. 2003; Brown et al. 2005). In addition, a significant reduction in LTP in the hippocampus of Tg2576 mice has been reported (Chapman et al. 1999; Kamenetz et al. 2003; Wang et al. 2004) and intracerebroventricular injection of soluble Aβ protein inhibits hippocampal LTP in vivo, providing evidence for a role for soluble Aβ in this effect (Walsh et al. 2002; Klyubin et al. 2004). Finally, a recent in vivo study using a genetically encoded calcium indicator to assess neuronal calcium levels in spines and dendrites showed disrupted calcium homeostasis and dystrophic neurites in close proximity to amyloid plaques in APP/PS1 mutant mice (Kuchibhotla et al. 2008).

In our electrophysiological studies of layer 3 frontal cortical pyramidal neurons, we found no significant difference in passive membrane or action potential firing properties between Tg2576 neurons and wild-type neurons (Rocher et al. 2008; Fig. 5a). Importantly, despite a significant reduction in dendritic spine density, the frequency, amplitude, and kinetics of spontaneous excitatory synaptic currents in the same neurons also remained unchanged. This preservation of glutamatergic signaling was likely due to the maintenance of spine numbers, despite reductions in spine density due to elongation of dendritic processes. It remains to be seen whether there are more marked functional consequences of the more dramatic structural alterations seen in pyramidal neurons from older Tg2576 mice.

In a recent study on layer 3 cortical pyramidal neurons from 8.5-month-old rTg4510 mice (Rocher et al. 2009), we observed major alterations in dendritic architecture (loss of the apical tuft), and spine density changes that could lead to substantial modification of functional electrophysiological properties, particularly with regard to integration of synaptic inputs. Direct measurement of electrophysiological properties in these cells with whole-cell patch-clamp recordings revealed that input resistance and membrane time constant were comparable between rTg4510 and wildtype neurons. These findings are expected as both properties are related to soma and total neuron surface area, which were similar between both groups. Importantly, resting membrane potential was significantly depolarized in rTg4510 neurons. This is possibly due to the significantly increased depolarizing “sag” potential also observed in rTg4510 neurons, disturbances in ATPase pump function linked to mitochondrial dysfunction, and/or decreased inhibitory synaptic inputs. In addition, rTg4510 neurons exhibited increased action potential firing frequency, reflecting the reduction in depolarization required to elicit action potentials (Fig. 5b). The implications of this excitability increase for the activity of individual neurons and networks of neurons are significant, and could be viewed as both potentially detrimental and beneficial. Increased excitability could be detrimental in that the dynamic range for the modulation of the rTg4510 neurons would necessarily be reduced due to a “ceiling effect” in which they are closer tomaximal firing rates than are wild-type neurons when depolarized from rest. On the other hand, increased excitability may favor maintenance of more normal network behavior in the face of significantly reduced glutamatergic synaptic transmission within a network.

Clearly, there is a need for many more studies on the functional electrophysiological consequences to individual neurons of the significant structural changes in neurodegenerative disease. Given the lack of such studies, and also technical considerations such as space clamp limitations and the impossibility of recording from distal dendrites or spines, the use of modeling methods to understand potential functional consequences of structural changes is very important.

Insights from modeling

For nearly 60 years, mathematical models have been used to investigate neuronal function. Hodgkin and Huxley’s (1952) mathematical model of action potential generation predicted the existence of ion channels, decades before ion channels were observed experimentally (Neher and Sakmann 1976). Other models were groundbreaking in describing how dendrites filter signals as passive electrical cables (Rall 1959; Goldstein and Rall 1974), but were limited in their ability to apply directly to realistic morphologic data. Since then, applications of mathematical techniques (Fitzhugh 1961; Nagumo et al. 1962; Rinzel and Ermentrout 1989), advances in computational software (Bower and Beeman 1998; Carnevale and Hines 2006), model reduction (Clements and Redman 1989; Pinsky and Rinzel 1994), and computing power have resulted in models that have great potential for yielding insights into neuronal function. In particular, models have shown that morphology is a critical determinant of neuronal firing properties (Zador et al. 1995; Mainen and Sejnowski 1996; Vetter et al. 2001; Schaefer et al. 2003; Stiefel and Sejnowski 2007). The effects of morphology are further amplified by the actions of ion channels distributed throughout the dendrites (for review see Johnston and Narayanan 2008), both of which shape patterns of synaptic input. Our ability to understand neuronal function depends largely on analysis of the nonlinear interactions between morphology, electrical membrane properties, and synaptic input.

Electrotonic analysis

Electrotonic analysis (Rall 1969; Brown et al. 1992; Tsai et al. 1994; Carnevale et al. 1997) predicts how neuronal morphology interacts with passive membrane parameters (membrane capacitance C_m, specific membrane resistance R_m and axial resistivity R_a) to affect the propagation of electrical signals. For each point in the dendritic tree, the log attenuation L_ij is defined as the natural log of voltage attenuation from point i to point j. By computing L_ij everywhere throughout the dendrites, a neuron’s anatomical structure can be transformed into an intuitive visual representation (“morphoelectrotonic transform”; Zador et al. 1995) of how that structure affects electrical signal transfer.

In a recent publication (Kabaso et al. 2009), we analyzed the electrotonic effects of age-related morphological changes in pyramidal neurons of the rhesus monkey PFC. Figure 6a shows the log attenuation of voltage flowing outward from the soma to the dendrites, for a layer 3 PFC pyramidal neuron from a young rhesus monkey (Kabaso et al. 2009). The log attenuation of voltage flowing inward from the dendrites toward the soma is defined similarly (Kabaso et al. 2009). Outward voltage attenuation in the apical dendrites was significantly reduced with age, both in “long” projection neurons from the superior temporal cortex to the PFC, and in “local” projection neurons within the PFC. In long projection neurons, inward voltage attenuation of apical dendrites was significantly reduced with age as well. Thus, if the age-related morphologic changes are not compensated by altered ion channel densities or kinetics, synaptic potentials would remain larger, and propagate more quickly, through the apical dendrites of old long projection neurons. Likewise, action potentials backpropagating through the apical dendrites of both long and local projection neurons would be larger and faster in old neurons. The reduction in spine densities with aging contributed strongly to our findings: voltage attenuation in the dendrites is not significantly different among the age groups when spine surface areas were not included (Kabaso et al. 2009).

Fig. 6.

Morphological degeneration significantly affects dendritic signal propagation. a Anatomical reconstruction (left) and outward morphoelectrotonic transform (right) of a typical young rhesus layer 3 pyramidal cell projecting from superior temporal cortex to the PFC. Transformed apical dendrites are shown in red. b Similar to a, for an analogous neuron from an old rhesus monkey. c Effects of age-related degeneration on mean outward and outward attenuation transforms. Histograms shows mean ± SEM for the young (n = 24) and old (n = 19) neuron groups (*P<0.05, **P<0.01) [modified from Kabaso et al. (2009)]

Anomalous diffusion in dendrites and spines

At the fundamental microscopic level, cortical functioning is dependent on the diffusion of ions and other molecules that subserve electrical and chemical signaling in the brain. Important recent discoveries have revealed that the characteristics of this diffusion are altered by the morphology and distribution of dendritic spines (Santamaria et al. 2006), and by the size and distribution of Aβ plaques (Mueggler et al. 2004; Banks and Fradin 2005). Both effects, trapping by dendritic spines and molecular crowding by amyloid plaques, result in anomalous subdiffusion in which the spatial variance grows as a sublinear power law in time (Metzler and Klafter 2000). In recent work, we introduced a new cable model for a cylindrical dendrite segment (Henry et al. 2008; Langlands et al. 2008, 2009) in which diffusion constants are replaced by timedependent operators with fractional-order exponents. We extended our derivation beyond the single dendrite level, demonstrating that anomalous subdiffusion of ions changes the electrotonic properties and firing rates of neurons (Langlands et al. 2009). Our studies are part of a larger effort to understand how spine morphologies and intracellular calcium dynamics affect signaling between dendrites and spines (Svoboda et al. 1996; Araya et al. 2006; Schmidt et al. 2007; Fedotov and Méndez 2008; Saftenku 2009; Schmidt and Eilers 2009). As reliable data on spine morphologies, intracellular calcium dynamics and ionic diffusion become increasingly available, equations describing anomalous subdiffusion will become more commonplace in computational modeling. These advances will lead to computational analyses of the effects of neurodegenerative changes to neurons on intracellular electrodiffusion.

Comparing active and morphological parameters

Computational studies often identify “active” parameters (those that control ionic membrane channels and intracellular calcium dynamics), which drive neuronal firing patterns, but discount the role of morphology (Goldman et al. 2001; Prinz et al. 2003, 2004; Olypher and Calabrese 2007; Taylor et al. 2009). We have used mathematical sensitivity analysis (Saltelli et al. 2000) to quantify how dendritic morphology affects neuronal firing patterns, and to compare these effects directly against those of active parameters (Weaver and Wearne 2008). Briefly, we perturb one parameter while keeping the rest constant, and define the sensitivity of an output to that parameter as the percentage change in output normalized by the percentage change in the parameter.

Figure 7a, b shows the sensitivity of spontaneous firing rate to parameter perturbations, for a model comprising a soma and unbranched cylindrical dendrite. For one combination of parameters called ‘Model 1’, the model fires action potentials spontaneously as shown by the solid black line of Fig. 7a. When the maximal conductance of the persistent sodium current g¯_NaP was increased by 20% (Fig. 7a, thin red line), the firing rate increased by 50%; therefore the sensitivity of firing rate to ḡ_NaP was 50%/20% = +2.5. In contrast, reducing dendritic diameter by 20% increased firing rate by 67%, so that the sensitivity of firing rate to dendrite diameter was 67%/−20% = −3.35: a larger effect than that of ḡ_NaP which acts in the opposite direction. Importantly, these sensitivities depend greatly on the combination of active parameters used in the model, even among models with similar output (compare Fig. 7a, b). Both experimental (Chiba et al. 1992; Bucher et al. 2005; Swensen and Bean 2005; Schulz et al. 2006) and computational studies (Goldman et al. 2001; Prinz et al. 2003, 2004; Achard and De Schutter 2006; Weaver and Wearne 2008; Taylor et al. 2009) have shown that neurons can have similar outputs. Therefore, any sensitivity analysis must be carried out over a wide range of models consistent with experimental data. In doing this, we found some models for which dendrite diameter affected neuronal firing rate even more than the active parameters (Weaver and Wearne 2008). Extrapolating these results to the transgenic studies reviewed here suggests that the morphology of cortical neurons can contribute significantly to the observed physiology. It will be important to evaluate how the sensitivity of neuronal function to morphology and active parameters are affected by neurodegeneration. To do so, it is particularly important to have morphological and physiological data from the very same neurons. This work is ongoing within our research group (Yadav et al. 2008a, b, 2009). Application to the transgenic models described in this review will reveal more insight into the future.

Fig. 7.

Using sensitivity analysis to predict parameter compensations that counteract the effect of morphological perturbation. a Comparison of morphological (Diam.) and conductance parameter ḡ_NaP perturbations of two model neurons with different combinations of membrane conductances, but similar output firing patterns. Thick black line shows the somatic voltage trace of the unperturbed model. Dashed green line shows the response to a 20% decrease in Diam.; thin red line shows the response to a 20% increase in ḡ_NaP. Inset bar plot shows the normalized sensitivity coefficients of firing rate to Diam. and ḡ_NaP: positive to ḡ_NaP negative and of greater magnitude to Diam. b Perturbations of the second model: analogous to those in a, except that the thin red line shows the response to a 10% increase in ḡ_NaP Sensitivity to Diam. is small and negative, while sensitivity to ḡ_NaP is large and positive. c In a model of goldfish precerebellar neurons (morphology shown inset), a 15% reduction in Diam. increased firing rate by 20.3% relative to the unperturbed value. d The compensatory perturbations of two different conductance parameters (ḡ_NaP in red, shifted vertically up; ḡ_A in blue, shifted down) were predicted from their firing rate sensitivities (inset bar plots). The blue and red compensated traces overlie the unperturbed (black) trace very closely, demonstrating excellent compensation [modified from Weaver and Wearne (2008)]

Predicting compensations for morphological neurodegeneration

Perhaps, the most important application of sensitivity analysis to predict how parameters should compensate for one another to maintain a desired output (Olypher and Calabrese 2007; Weaver and Wearne 2008). Specifically, we have shown that perturbations of active parameters could counteract the effects of morphological changes (Weaver and Wearne 2008) like those that occur with neurodegeneration. As an example, Fig. 7c shows the effect of a 15% reduction in dendrite diameter on the firing rate of a morphologically faithful model of a precerebellar hindbrain neuron from goldfish (shown inset). Using the sensitivities of firing rate computed as described above, we predicted the precise perturbations needed of either ḡ_NaP (−11.3%) or of the A type potassium conductance ḡ_A (+25.4%) to compensate for the effect of the reduced diameter (Fig. 7d) (Weaver and Wearne 2008). We chose these parameters for compensations because neuronal firing rate was highly sensitive to them. Future compensatory predictions could be based on the experimental identification of active parameters that are most changed with neurodegeneration.

Application to transgenic mouse models

Our modeling results make several predictions that may apply to transgenic mouse models of neurodegeneration. First, changes in dendrite length, diameter, and spine densities/numbers in transgenic neurons compared to wildtype neurons may significantly impact the attenuation of signals to and from the soma. This may happen over an entire neuron, or in limited regions, such as dendrites passing through or near fibrillar amyloid deposits, or in apical tufts that undergo atrophy. Long projection neurons are particularly vulnerable in AD (Hof et al. 1990; Bussiére et al. 2003; Hof and Morrison 2004), giving greater weight to the significant differences in voltage attenuation observed in long projection neurons (Kabaso et al. 2009). Second, changes in spine density may affect the diffusion rate of intracellular messengers and ions. Elongated dendrites may result in less trapping of electrical and chemical signals within spines; this phenomenon may be functionally significant. We must also consider how spine loss might impact the amount of excitatory input that a neuron receives. Finally, it is likely that interactions between morphology and active parameters vary between wild-type and transgenic neurons. To study this more fully we must measure both detailed morphological properties and ionic currents in wild-type and transgenic neurons. To evaluate the degree to which these predictions truly apply to the transgenic mouse models, we will apply the mathematical methods described here directly to the transgenic data that we have collected. These computational studies will likely lead to explicit predictions of which parameters to change, and by how much, to counteract morphological changes that affect physiological function in neurodegenerative disease.