Abstract
Many natural sounds such as speech contain concurrent amplitude and frequency modulation (AM and FM), with the FM components often in the form of directional frequency sweeps or glides. Most studies of modulation coding, however, have employed one modulation type in stationary carriers, and in cases where mixed-modulation sounds have been used, the FM component has typically been confined to an extremely narrow range within a critical band. The current study examined the ability to detect AM signals carried by broad logarithmic frequency sweeps using a 2-alternative forced-choice adaptive psychophysical design. AM detection thresholds were measured as a function of signal modulation rate and carrier sweep frequency region. Thresholds for detection of AM in a sweep carrier ranged from -8 dB for an AM rate of 8 Hz to -30 dB at 128 Hz. Compared to thresholds obtained for stationary carriers (pure tones and filtered Gaussian noise), detection of AM carried by frequency sweeps substantially declined at low (12 dB at 8 Hz) but not high modulation rates. Several trends in the data, including sweep- versus stationary-carrier threshold patterns and effects of frequency region were predicted from a modulation filterbank model with an envelope-correlation decision statistic.
Keywords: psychoacoustics, frequency sweep, FM, modulation, psychophysics
Introduction
Many naturally occurring sounds are modulated in both amplitude and frequency; important examples include speech and other conspecific communication signals in mammals, marine species, birds, and even insects (Coscia et al., 1991; Dankiewicz et al., 2002; Dear & Simmons, 1993; Fant, 1970; Huber & Thorson, 1985; Klump & Langemann, 1992; Ryan & Wilczynskin, 1988; Sabourin et al., 2008). Because amplitude- and frequency-modulated (AM and FM) sounds are the building blocks of complex sounds, understanding how the auditory system processes these important signals has both practical and theoretical implications (Kay, 1982; Moore & Sek, 1992; Saberi, 1995, 1998; Luo et al., 2007). Most prior studies of modulation processing, however, have been one dimensional in that either temporal envelope modulation is varied while spectral modulation is kept constant or vice versa, and while these studies have provided valuable insights into modulation detection and discrimination, less is known about how the auditory system processes mixed-modulated sounds (combined FM and AM). In studies that have examined processing of mixed-modulated sounds, the FM component has typically been sinusoidal with an extremely restricted narrow spectral range of a few hertz to at most about 100 hertz, with peak frequency deviations often confined to well within a critical band. No prior study has examined AM detection in an FM carrier that sweeps through broader regions of the spectrum comprising multiple critical bands.
In recent years the study of broad directional sweeps as a common component of communication signals has substantially increased. Speech sounds contain significant FM information in the form of frequency glides and formant transitions which provide cues to phonemic identification (Fant, 1970; Gordon & O'Neill, 1998; Liberman et al., 1956; Pickett, 1980). FM sweeps also play an important role in processing of tonal languages (e.g., Mandarin or Thai) where pitch contour variations affect lexical distinction (Howie, 1976; Luo et al., 2007; Stagray et al., 1992). The study of FM sweeps in speech has also had practical applicability to language processing in children afflicted with language-based learning impairment. Tallal et al. (1996) for example have shown that reducing the FM rate of formant transitions and amplifying their levels relative to steady state (non FM) parts of a phoneme significantly improve the ability of these children to identify speech sounds. Directional FM sweeps have also become important signals in many other areas of hearing research, including auditory scene analysis (Bregman, 1994; Crum & Hafter, 2008) where consistency of multiple FM glides in different frequency regions provide powerful cues to auditory object formation and stream segregation, as well as in the study of infant hearing development (Colombo & Horowitz, 1986) and even music perception (d'Alessandro et al., 1998).
The current study was both broadly motivated to contribute further to this growing body of empirical research, and more specifically motivated by three theoretical questions: First, how is temporal-modulation detection affected by imposing the modulation envelope onto a spectrally broad non-stationary carrier requiring integration of AM cues at different instances of time across different auditory filters. It is a priori unknown whether substantially different threshold patterns might emerge from use of dynamic frequency sweep carriers, particularly since an entirely different population of direction-sensitive FM-selective neurons may be involved in coding information carried in sweeps (Poeppel et al., 2004; Woolley et al., 2005; Andoni et al., 2007; Gittelman et al., 2009). Second, it is well-established that an FM sound is transduced into an AM signal as its instantaneous frequency sweeps through the passband of a filter (Blauert, 1981; Moore & Sek, 1992; Saberi and Hafter, 1995; Hsieh and Saberi, 2009). Does the AM induced by the unidirectional FM sweep at the outputs of auditory filters mask the signal AM modulation, and if so to what extent and under what circumstances? Third, can recently developed modulation filterbank (MFB) models (Dau et al., 1996, 1997) predict the patterns of modulation masking observed for a frequency sweep carrier, and what insights might be gained form this analysis concerning factors that limit modulation detection in these putative filters (e.g., internal limiting noise at different frequency regions)?
Specifically, in the current study, we examined the ability to detect monaural sinusoidal AM in directional FM carriers for AM rates from 8 to 128 Hz. Rates in this range have been shown to produce large differences in detection or discrimination thresholds and have been extensively used in studies of AM and FM sounds (Riesz, 1928; Zwicker, 1952; Lee, 1994; Yost and Sheft, 1997; Chi et al., 1999; Strickland, 2000; Eddins, 2001). In addition, we examined AM detection in FM carriers that swept across wide ranges of frequency at different frequency regions (e.g., 1-5, 5-9 kHz) to determine if detection of modulation in sweeps is a function of frequency region, whether these threshold patterns are distinct from those reported for stationary carriers at different regions (Eddins, 1993, 1999) and what this may imply about factors that limit AM detection in broadband sweeps. For comparison, we also examined AM detection for stationary carriers (tones and noisebands) at different modulation rates and frequency regions, and compared thresholds obtained from dynamic and stationary carriers at low and high modulation rates with those predicted from a modulation filterbank model.
Methods
Stimuli & Apparatus
Stimuli were generated using Matlab software (Mathworks) on a Dell PC (Dimension 8400) and presented at a rate of 44.1 kHz through 16-bit digital-to-analog converters (Creative Sound Blaster Audigy 2ZS) and through Sennheiser headphones (HD 470) in a double-walled steel acoustically isolated chamber (Industrial Acoustics Company). The amplitude-modulated logarithmic FM sweeps were generated from Eq. 1:
| [1] |
where fs and fe represent the starting and ending sweep frequencies in hertz, Ts is stimulus duration, m is the amplitude modulation depth, fAM is the amplitude-modulation rate, and ϕ is the AM envelope phase which was randomly selected on each presentation from a uniform(0,2π) distribution (Fig. 1).
Figure 1.
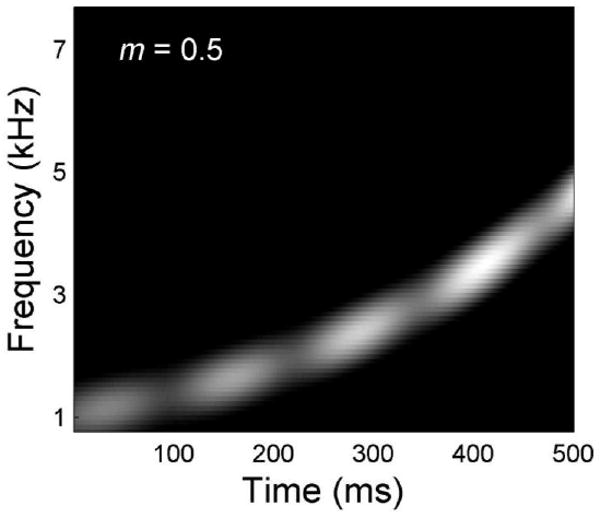
Spectrogram of a logarithmic FM carrier that sweeps from 1 to 5 kHz. An AM signal with a modulation depth of 50% (m=0.5; -6 dB) is imposed on the carrier.
The stimulus duration was 500 ms. There were ten experimental conditions for FM-sweep stimuli which included five AM rates (8, 16, 32, 68, and 128 Hz) by two regions of the spectrum through which the FM swept (1 to 5 kHz or 5 to 9 kHz). These frequency regions were selected to cover two distinct but broad regions at low and high frequencies, within the general range of frequencies used in prior studies of AM detection (e.g., Eddins, 1999). In addition, there were ten control conditions which included 3 pure-tone carriers (1, 5, and 9 kHz) and two bandpass Gaussian noise carriers (1-5 or 5-9 kHz) by two modulation rates (8 and 32 Hz; random phase). We selected these two rates as examples of relatively slow and more moderate modulation rates, which our pilot runs and model analysis suggested would generate markedly different threshold patterns. Furthermore, these two rates may have at least some relevance to speech processing (Pickett, 1980; Fant, 1970; Saberi and Perrott, 1999). An 8-Hz AM falls within the range of syllable rates (3 to 8 Hz), and a 32-Hz AM has a period that falls within the general range of phonemic durations (30 to 50 ms).
In addition, in a post-hoc control experiment, we included a condition that equated sweeps on an octave scale. Note that the two frequency regions from 1-5 and 5-9 kHz, while producing equal sweep rates on a linear scale, will produce two different sweep rates on an octave scale, with the 1-5 kHz FM sweeping at a rate of 4.6 octaves/s and the 5-9 kHz FM sweeping at a rate of 1.7 octaves/s. In order to additionally investigate AM detection performance based on constant octave velocity at two frequency regions, we also measured thresholds for a 1-1.8 kHz FM sweep (1.7 octaves/s). As will be described in the Discussion section, both these comparisons were useful to our analyses.
Before imposing the AM signal on sweep carriers, the sweep was filtered with the inverse of the headphone transfer function to reduce amplitude envelope modulation cues induced by variations in the headphone's frequency response as the carrier swept through different frequency regions. The transfer function was measured by presenting the 500 ms sweep through the headphones and measuring the headphone's output at a sampling rate of 44.1 kHz using a 6cc coupler, 0.5-inch microphone (Brüel & Kjær Model 4189), amplifier (Nexus, Brüel & Kjær), and a 16-bit A-to-D converter (Creative Sound Blaster Audigy 2ZS). The temporal envelope of the recorded output was then extracted using the Hilbert transform and all sweep stimuli were multiplied with the inverse of this envelope prior to presentation through headphones. Analysis of the corrected waveforms showed that the amplitude envelopes were flattened to within 0.5 dB of mean level across the entire range of frequency sweeps tested.1 The stimulus level was set to 60 dB SPL and this level was roved by plus and minus 10 dB on each presentation to eliminate any concerns over potential subtle loudness cues or discrimination of estimates of instantaneous intensity in modulation troughs (Forrest and Green, 1987; Stellmack et al., 2006). All stimuli had linear rise/decay times of 20 ms and were presented monaurally to the subject's right ear.
Procedures
Three normal-hearing adults served as subjects. All subjects were highly practiced in psychoacoustic experiments and were additionally practiced on the various conditions of the experiment for two hours prior to data collection. The experiment was run in a block design in which the AM rate and sweep frequency region were held constant within a run. Each subject completed 4 runs per each experimental condition in a random-block design. Each run consisted of 50-trials in a 2-interval forced-choice (2IFC), 2-down 1-up adaptive design which tracks the subject's 70.7% correct-response threshold (Wetherill and Levitt, 1965; Levitt, 1971).
On each trial of a run, two 500ms FM sweeps were presented, separated by an interstimulus interval of 300ms. One of two intervals was randomly selected on that trial to contain the AM signal, and the subject's task was to identify which of the two intervals contained the signal. The subject then pressed a number key 1 or 2 to record their response. The initial depth of the AM signal was set to 100% (i.e., m =1 in Eq. 1). Two successive correct responses led to a reduction in modulation depth by a stepsize of 4 dB up to the fourth reversal and 2 dB thereafter. An incorrect response led to an increase in m by the same stepsize. The first 3 or 4 track-reversals from each run were discarded and threshold was estimated as the average of the stimulus values on the remaining even-number of reversal. Usually, six to eight reversals went into the calculation of each threshold. Visual feedback was provided after each trial in two forms: first, a plot of the staircase response (dB as a function of trial number) was shown on the monitor with trial-by-trial update. Second, the interval that contained the signal on that trial was identified by text on the monitor. All procedures were approved by the University of California, Irvine's Institutional Review Board.
Results
Figure 2 shows results for three subjects with their averaged performance shown in the bottom-right panel. The abscissa shows AM rate and the ordinate shows modulation depth. Each point for each subject's data is based on 4 threshold estimates and error bars represent +/- 1 standard deviation. The filled symbols show data for the 1 to 5 kHz sweep and the open symbols for the 5 to 9 kHz sweep. Several trends are clear in these data. First, thresholds improve by approximately 20 dB as the AM rate is increased from 8 to 128 Hz. Second, there is an interaction effect between modulation rate and the sweep frequency region. At the lowest modulation rate of 8 Hz, an FM that sweeps from 1-5 kHz produces higher thresholds than one that sweeps from 5-9 kHz (t(11)=3.25, p<0.01), whereas this trend reverses for the highest modulation rates (significant at 128 Hz; t(11)=4.51, p<0.005). A two-way (5×2) repeated-measures ANOVA showed a significant effect of AM rate (F4,44= 210.42, p<0.001), a significant effect of the sweep frequency region (F1,11= 13.54, p<0.005), and a significant interaction effect between rate and frequency region (F4,44= 13.80, p<0.001).
Figure 2.

Thresholds for detection of AM in a frequency-sweep carrier as a function of AM rate and sweep frequency region. Data are shown for three individual subjects (S1-S3) and their average (bottom-right panel). Error bars are ±1 standard deviation.
Figure 3 shows AM-detection thresholds for 3 pure-tone carriers of 1, 5, and 9 kHz modulated at 8 Hz (top panel) or 32 Hz (bottom panel). Thresholds for the 1-5 and 5-9 kHz FM sweeps from Fig. 2 are also shown for comparison. Each bar shows averaged data from three subjects. Thresholds are significantly poorer when subjects try to detect an AM signal in an FM sweep compared to a stationary pure-tone carrier, particularly for the lower modulation rate of 8 Hz. For an AM rate of 32 Hz, thresholds are still higher for the FM sweep relative to those for pure-tone carriers, but this difference is not as large. We did not observe a significant difference in thresholds across the three pure-tone conditions. A one-way ANOVA on the data of the top panel of Fig. 3 (8-Hz AM) showed a significant effect of carrier type, i.e., sweep vs. pure-tone (F4,44= 96.58, p<0.001). A similar but smaller effect was also observed for the 32-Hz condition shown in the bottom panel of Fig. 3 (F4,44= 9.55, p<0.001).
Figure 3.

AM-detection thresholds for three pure-tone carriers of 1, 5, and 9 kHz and two FM carriers sweeping from 1 to 5 and from 5 to 9 kHz. Top panel shows data for detection of an 8-Hz AM signal and bottom panel for a 32-Hz AM. Data are averaged from 3 subjects. Error bars are one standard deviation.
Figure 4 shows averaged thresholds for detection of AM in bandpass noise carriers.2 For comparison, thresholds for FM sweeps are also shown (black bars). Top and bottom panels show data for the 8 and 32 Hz AM rates respectively. The left set of bars in each panel show data for the 1 to 5 kHz region, i.e., an FM that sweeps from 1 to 5 kHz or a noiseburst bandpass filtered between 1 to 5 kHz. Right set of bars show data for the 5 to 9 kHz region. As with pure-tone carriers, detection of an 8-Hz AM in noise carriers is significantly easier than AM detection in an FM sweep. A two-way ANOVA on the data of the top panel showed a significant effect of carrier type (F1,11=95.12, p<0.001), but no significant effect of frequency region (F1,11=1.96, n.s.) and no interaction effect (F1,11=3.66, n.s.). For the 32-Hz AM signal (bottom panel) we found no significant effect of carrier type (F1,11=0.83, n.s.), frequency region (F1,11=1.88, n.s.), or interaction (F1,11=0.43, n.s.).
Figure 4.
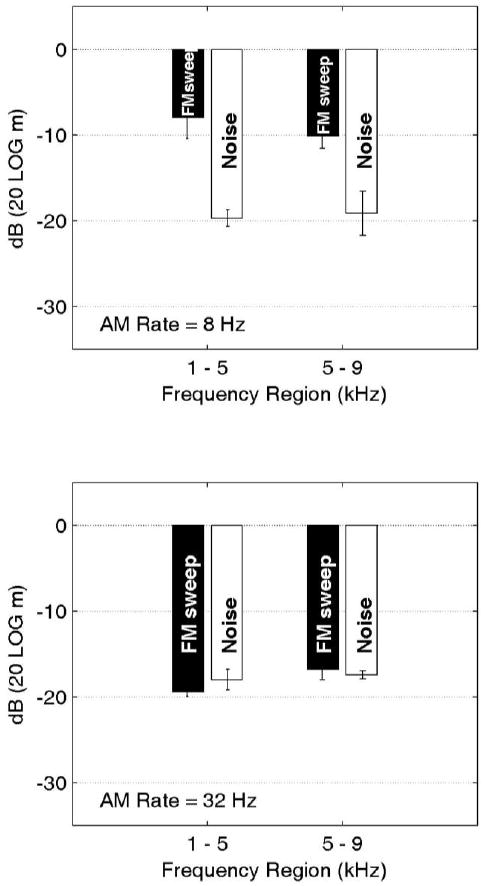
AM-detection thresholds for bandpass noise carriers filtered either between 1 to 5 or 5 to 9 kHz. Top and bottom panels show data for 8 and 32 Hz AM rates respectively. For comparison, thresholds for sweep carriers are also shown. Error bars are one standard deviation.
Figure 5 shows results of the post-hoc experiment in which the two frequency ranges of interest were equal on an octave scale (1-1.8 and 5-9 kHz).2 Two trends are evident: first, the interaction effect between modulation rate and frequency region has been eliminated, and second, performance for the lower frequency region is now superior to that for the higher frequency range. This is a reversal of the trend observed in Fig. 2 at the lowest modulation rates.
Figure 5.

Thresholds for detection of AM in a frequency-sweep carrier as a function of AM rate and sweep frequency region. The two regions are equal-octave intervals. Data are shown for three individual subjects and their average (bottom-right panel). Error bars are ±1 standard deviation.
Discussion
Our results show that detection of AM is significantly more difficult when the modulation signal is imposed on a dynamic carrier that sweeps across wide frequency regions. This is particularly true for lower AM rates. Given a fixed rate of frequency sweep, the lower AM rate of 8 Hz results in less pronounced amplitude envelope fluctuations within a given auditory filter, and hence a less detectable signal relative to the higher modulation rate of 32 Hz. As the instantaneous frequency of a dynamic carrier sweeps through the passband of auditory filters, the outputs of these filters increase and then decrease in their amplitude envelopes. A slow AM signal imposed on such filter output activity may be difficult to distinguish from the within-channel amplitude envelope changes associated with the FM sweep.
Figure 6 shows outputs of a GammaTone auditory filter centered on 3.1 kHz followed by a Meddis haircell model in response to different FM sweeps (Holdsworth et al., 1988; Meddis et al., 1990; Slaney, 1998). Top-left panel shows this filter's output in response to an unmodulated (no AM) sweep from 1 to 5 kHz. Note the FM-to-AM conversion as the sweep enters and exits the filter's passband. The middle-left panel shows the output of the same filter when an 8-Hz sinusoidal AM (at 25% depth) is imposed on the sweep. Note that the two filter outputs (top and middle left) are nearly identical suggesting that detection of this low-rate AM would be difficult in a sweep carrier. Bottom-left panel shows the filter's output in response to a 32-Hz AM (25% depth) imposed on the FM-sweep carrier. Clearly, there is more fluctuation of the filter's output in response to this higher-rate AM. Middle- and bottom-right panels show the same filter's output in response to a 50% depth AM with rates of 8 and 32 Hz respectively carried by the same frequency sweep. We additionally calculated the correlation coefficient between the envelopes of the filter's outputs (shown in red) for the no-AM sweep (top-left panel) compared to amplitude-modulated frequency sweeps with various rates and depths of sinusoidal AM. Because correlation coefficients are compressive at high values (ceiling of 1) we normalized the coefficients using Fisher's r-to-z transform (z=[ln(1+r)-ln(1-r)]/2; McNemar, 1969; Richards, 1987) and plotted the results in the top-right panel of Fig. 6. The results are a family of curves that show a decline in envelope correlation with increased AM rate and depth, consistent with our data that shows smaller threshold differences between sinusoidal and sweep carriers as the AM rate is increased from 8 to 32 Hz (Fig. 3).
Figure 6.

Response of an auditory filter model with a resonant frequency of 3.1 kHz to a 1-5 kHz FM sweep. Top-left panel shows the filter's response to a sweep without an AM signal. Middle- and bottom-left panels show the filter's response to the same sweep-carrier amplitude modulated at 8 or 32 Hz (25% modulation depth). Middle- and bottom-right panels show this filter's response to 8 and 32-Hz AM signals modulated at 50% depth. Red curves show envelopes of the filter's response. Top-right panel shows the correlation between filter-output envelopes of a no-AM sweep (from the top-left panel) and sweeps with various AM rates and depths. The correlation coefficients have been transformed to z values (see text).
This analysis suggests that envelope correlation may provide a potent cue to AM signal detection in FM sweeps. To quantitatively analyze the patterns of change in AM detection thresholds as a function of AM rate, frequency region, and carrier type (sweep vs. noise), we extended the previous single-channel correlation analysis to predictions of a Modulation Filterbank Model (Dau et al., 1996; Dau et al., 1997; Ewert and Dau, 2000). The model used here consisted of a GammaTone filterbank with 30 logarithmically spaced filters from 500 to 12000 Hz, each of which was followed by haircell-model processing. Temporal envelopes from each of 30 outputs was extracted and filtered with a modulation filterbank consisting of 5 filters with a Q of 1 and resonant frequencies of 4, 8, 16, 32, and 64 Hz.3 The single free parameter of the model was the variance of internal noise. The noise was independently added to each of the 30×5 outputs (30 peripheral filters × 5 modulation filters).
A decision statistic was computed for a 2IFC design in which the correlation between a template and the stimulus in each of the two intervals was determined at the output of each modulation filter at each peripheral filter. Following Dau et al. (1997), the template waveform was the same as the signal (processed through the same filterbank) but at a high signal-to-noise ratio (m=1; plus internal noise), i.e., a memory representation of the expected signal. A multi-dimensional correlation space was calculated separately for the signal and non-signal intervals. The decision statistic was based on the integral of the correlation space across peripheral auditory filters at the output of the modulation filter centered on the signal modulation rate. For example, if the signal was a 32-Hz AM, the correlation space at the 32-Hz modulation filter was integrated across all peripheral filters, with the assumptions that subjects would optimally monitor activity within the on-frequency modulation channel in a signal-known decision model and select, as the signal interval, that which had a larger correlation integral. While other decision statistics may also be computed4, we selected cross-correlation analysis as the optimal decision statistic (Dau et al. 1997; Green and Swets, 1966) and because it provided reasonable predictions of the observed patterns of data.
Figure 7 shows the correlation space, with a zero cross-correlation lag, calculated for an FM carrier that sweeps from 1 to 5 kHz with an AM signal of 8 Hz (top panels) and 32 Hz (bottom panels). Left panels show the no-signal-interval condition, the middle panels show the signal-interval conditions, and the right panels show the difference between the signal and no-signal intervals. Note that when the signal is 8 Hz, little difference is observed between the signal and no-signal correlation patterns. There is substantial envelope correlation at the outputs of low-frequency modulation filters even in the no-signal intervals because, as described earlier, when an FM stimulus sweeps through the passband of an auditory filter, it generates a slow temporal modulation envelope, whether or not the sweep carries an AM signal. The 8-Hz ripple observed in the non-signal interval of Fig. 7 results from the 8-Hz modulation in the template. The small peak at 1-kHz extending across all modulation filters is caused by the stimulus onset.5 Bottom panels of Fig. 7 show the same type of correlation space, but for an AM signal of 32 Hz. Note that in this case, monitoring the output of the modulation filter centered on the signal modulation rate will result in distinct correlation patterns across the signal and non-signal intervals, and thus substantially lower AM thresholds relative to the 8-Hz condition.
Figure 7.
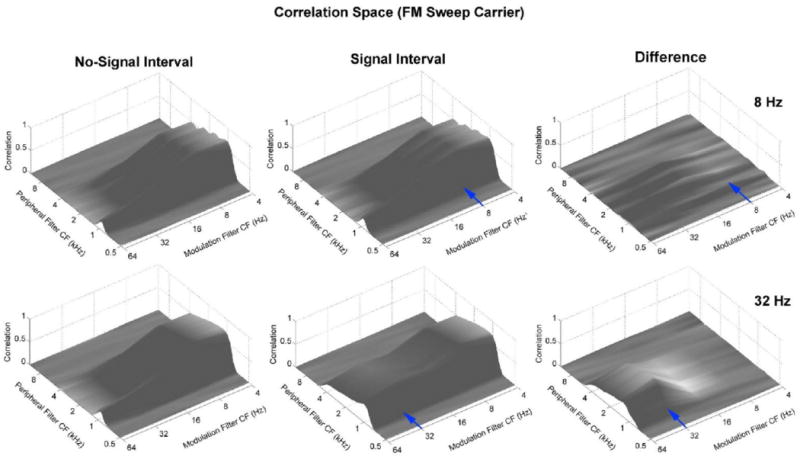
Correlation space from a modulation filterbank model, shown for no-signal intervals (left panels), signal intervals (middle panels), and their difference (right panels). Top row shows results for an 8-Hz AM signal, and bottom row for a 32-Hz AM signal, both carried by a 1-5 kHz sweep.
Figure 8 shows the correlation space calculated for a noise carrier bandpass filtered between 1 and 5 kHz. Markedly different correlation patterns are observed for a noise carrier relative to the sweep carrier, particularly when the AM signal is 8-Hz. Clearly, the pattern in the no-signal interval can be more easily distinguished from the 8-Hz signal-interval pattern when the carrier is a noise band. Not surprisingly, the correlation patterns associated with a 32-Hz signal interval also are significantly different than those of the corresponding no-signal interval when the carrier is a noise band. Thus, the patterns shown in Figs. 7 and 8 are consistent with the observed pattern of data, that an 8-Hz AM signal is significantly more detectable in a noiseband carrier, and that a 32-Hz AM signal is more easily detectable than an 8 Hz signal when carried by an FM sweep.
Figure 8.
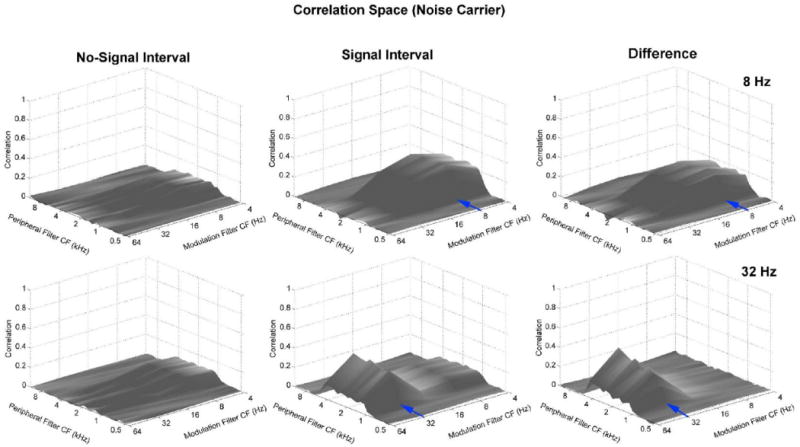
Same as Fig. 6 but for Gaussian noiseband carrier bandpass filtered between 1 to 5 kHz.
Left panels of Fig. 9 show quantitative predictions from this model for the data shown in Fig. 4 which are replotted here to facilitate comparison. We first describe the model's predictions for the 1-5 kHz frequency region (left set of bars in the top and bottom panels). The variance of internal noise, which was the single free parameter of the model, was adjusted such that threshold for the FM sweep with an 8-Hz AM signal (top panel, left black bar) equaled that observed in the data (approximately -8dB at 71% correct detection level). Each bar shows the model's prediction from a 5000-trial Monte Carlo simulation. The general trends in the data are well predicted by the MFB model. Significant improvement in performance is observed at 8 Hz when the carrier is switched from a sweep to a noiseband. In addition, substantially lower thresholds are obtained for a 32-Hz AM signal, and slightly poorer thresholds are observed for the 32-Hz AM noiseband compared to the 32-Hz AM carried by the FM sweep (bottom-left bars) similar to that observed in the data of Fig. 4. While the model does predict significant improvements for an 8-Hz AM noiseband, it does underestimate the amount of improvement by a few dB. Nonetheless, with a single free parameter, the patterns of change in threshold are well captured by the model.
Figure 9.

Left panels: Predictions from an MFB model for sweep and noiseband carriers at two AM rates, and two frequency regions. The predicted patterns are similar to those shown in Fig. 4, which are replotted here to facilitate visual comparison.
The right bars in the left panels of Fig. 9 show model predictions for the 5-9 kHz region. An interesting finding was that the internal noise parameter for this frequency region had to be adjusted to a different value than that for the 1-5 kHz region. The parameter was adjusted to anchor the 8-Hz sweep (top left panel, right black bar) to the empirically measured threshold of -10 dB. With this one adjustment, similar patterns of performance were observed in the 5 to 9 kHz region across stimulus conditions as those observed for the 1-5 kHz regions and consistent with the trends seen in the data. The ratio of low- to high-frequency internal noise magnitude estimated from the model was σL/σH=1.85. That the variance of internal noise had to be adjusted separately for the two frequency regions suggests that either the noise that limits modulation information received by the putative modulation filterbank from the higher-frequency peripheral filters has a lower variance than the noise in the lower peripheral channels, or that the slower sweep rate on log frequency at the higher frequency region allows for better detection of the modulation signal. Eddins (1999) has quite convincingly shown that temporal resolution, measured using AM detection, is independent of the frequency regions across a wide region of the spectrum from 0.5 to 12.8 kHz, suggesting that the limiting internal noise has a uniform magnitude across various regions of the spectrum. This can easily be tested in the model by comparing predictions for the 1-1.8 kHz sweep to that for the 5-9 kHz sweep which cover an equal interval on an octave scale and thus matched logarithmic sweep velocities. The ratio of the low- to high-frequency region's internal-noise magnitudes resulting in 71% correct detection in this latter case was remarkably close to 1, σL/σH=0.99, consistent with what would be predicted from findings of Eddins (1999).
In summary, our findings show that the ability to detect AM in a frequency-sweep carrier is poorer at low modulation rates by as much as 20 dB relative to high rates (8 vs. 128 Hz). Furthermore, at the low modulation rate of 8 Hz, thresholds for stationary carriers (e.g., noiseband) are substantially lower than that for sweep carriers. This difference in AM detection ability across stationary and dynamic carriers is eliminated as modulation rate is increased to 32 Hz. This trend was predicted from a MFB model which suggested that an FM sweep generates a slowly modulating envelope at the outputs of peripheral auditory filters that causes modulation masking at the outputs of low-frequency modulation filters. Interestingly, prior studies using sinusoidal MM waveforms that have examined the constructive summation of FM and AM cues have shown that only for low-rate sinusoidal modulation (e.g., 4 Hz), AM and FM cues that are separately subthreshold can be detected in mixed modulation (Ozimek and Sek, 1987; Moore and Sek, 1992). This demonstrates summation of information at low but not high modulation rates. An analysis of psychometric functions measured for these waveforms has also suggested that the AM and FM cues in slowly modulating MM sounds are not processed independently (Moore and Sek, 1992). In a related study, Chi et al. (1999) used a broadband complex that comprised 92 fixed-frequency tones whose amplitudes were sinusoidally modulated to study MM processing. While their stimuli did not contain continuous FM sweeps, they did simulate a ripple along time and discretized frequency space. Their results also suggested stronger influence of modulation information on detection thresholds at low modulation rates (i.e., a lowpass effect). All these prior findings are, in general, consistent with our results and the idea that slowly modulating amplitude envelopes, whether induced by an FM that sweeps through a filter's passband or is imposed on a stationary carrier, is extremely effective in masking a modulation signal. This finding also has broader implications for processing complex natural sounds. Speech intelligibility, for example, is significantly affected by information carried in low-rate (syllabic) temporal envelope structures (Shannon et al., 1995, Drullman et al., 1994; Saberi and Perrott, 1999), and low-rate AM cues are masked more significantly by the temporal envelope modulation induced by FM glides within auditory filters. Other trends in our data were also predicted by the MFB model, including that of equal internal-noise variances that limit AM detection at high and low frequency regions. This latter finding is consistent both with results of Eddins (1999) who has shown that AM detection is not dependent on carrier frequency, as well as with results of Moore and Sek (1994) who have shown that MM cues are processed similarly at different carrier frequencies (1 kHz or 6 kHz). These findings, in general, provide insight into how modulation cues are processed in an important class of acoustic signals, i.e., broadband directional sweeps, and further validate existence of a putative second-order modulation filterbank in the central auditory system.
Acknowledgments
We thank Bruce G. Berg, Virginia Richards, Brian C. J. Moore, and two anonymous reviewers for helpful comments. Work supported by grants from the National Science Council, Taiwan NSC 98-2410-H-008-081, NSF BCS0477984, and NIH R01DC009659.
List of abbreviations
- FM
frequency modulation
- AM
amplitude modulation
- MM
mixed modulation
- MFB
modulation filterbank
Footnotes
This procedure corrects the transfer function at the output of the headphones, but clearly not at the middle or inner ears which have their own unique transfer functions. This correction, nonetheless, is an improvement over prior studies that have used broad FM sweeps. Our goal here was simply to ensure that the acoustic signal at the entrance of the ear canal was free from AM cues introduced by the apparatus, and consider any subsequent AM cue introduced by the auditory system itself, including those by the peripheral structures, to be a natural feature of processing frequency sweeps.
Two of the subjects were the same as those who participated in the earlier part of the study, and the third was a new participant who had extensive experience as a subject in auditory experiments. This subject also ran in a subset of the original sweep conditions to ensure proper comparison across conditions.
We originally started with 8 filters with center frequencies from 2 to 256 Hz, but because our analysis was confined to AM rates of 8 and 32 Hz, and because our initial analysis showed that the additional range of filter CFs has no effect on predictions, we reduced the range of filter CFs to 4-64 Hz to reduce computational load.
Other decision statistics have been based on the ratio of max to min amplitude, crest factor (envelope maximum scaled by the rms power), fourth moment (a measure of fluctuation in envelope power), average slope, or other cues (Strickland, 2000; Eddins, 2001). A comparison of these decision statistics with the correlation measure used here is beyond the scope of the present paper.
Reversing the sweep direction, i.e. from 5 to 1 kHz, shifted this peak to the 5 kHz region.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
I-Hui Hsieh, Institute of Cognitive Neuroscience, National Central University, Jhongli City Taiwan.
Kourosh Saberi, Department of Cognitive Sciences and Center for Cognitive Neuroscience, University of California, Irvine, CA 92697.
References
- Andoni S, Li N, Pollak GD. Spectrotemporal receptive fields in the inferior colliculus revealing selectivity for spectral motion in conspecific vocalizations. J Neurosci. 2007;27:4882–4893. doi: 10.1523/JNEUROSCI.4342-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blauert J. Lateralization of jittered tones. J Acoust Soc Am. 1981;70:694–698. doi: 10.1121/1.386932. [DOI] [PubMed] [Google Scholar]
- Bregman AS. Auditory Scene Analysis: The Perceptual Organization of Sound. MIT Press; Cambridge, MA: 1994. [Google Scholar]
- Chi T, Gao Y, Guyton MC, Ru P, Shamma S. Spectro-temporal modulation transfer functions and speech Intelligibility. J Acoust Soc Am. 1999;106:2719–2732. doi: 10.1121/1.428100. [DOI] [PubMed] [Google Scholar]
- Colombo J, Horowitz FD. Infants attentional responses to frequency modulated sweeps. Child Development. 1986;57:287–291. doi: 10.1111/j.1467-8624.1986.tb00027.x. [DOI] [PubMed] [Google Scholar]
- Coscia EM, Phillips DP, Fentress JC. Spectral analysis of neonatal wolf vocalizations. Bioacoustics. 1991;3:275–293. [Google Scholar]
- Crum PA, Hafter ER. Predicting the path of a changing sound: velocity tracking and auditory continuity. J Acoust Soc Am. 2008;124:1116–1129. doi: 10.1121/1.2945117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- d'Alessandro C, Rosset S, Rossi JP. The pitch of short-duration fundamental frequency glissandos. J Acoust Soc Am. 1998;104:2339–2348. doi: 10.1121/1.423745. [DOI] [PubMed] [Google Scholar]
- Dankiewicz LA, Helweg DA, Moore PW, Zafran JM. Discrimination of amplitude-modulated synthetic echo trains by an echolocating bottlenose dolphin. J Acoust Soc Am. 2002;112:1702–1708. doi: 10.1121/1.1504856. [DOI] [PubMed] [Google Scholar]
- Dear SP, Simmons JA, Fritz J. A possible neuronal basis for representation of acoustic scenes in auditory cortex of the big brown bat. Nature. 1993;364:620–623. doi: 10.1038/364620a0. [DOI] [PubMed] [Google Scholar]
- Dau T, Kollmeier B, Kohlrausch A. Modeling auditory processing of amplitude modulation .2. Spectral and temporal integration. J Acoust Soc Am. 1997;102:2906–2919. doi: 10.1121/1.420345. [DOI] [PubMed] [Google Scholar]
- Dau T, Püschel D, Kohlrausch A. A quantitative model of the “effective” signal processing in the auditory system: I. Model structure. J Acoust Soc Am. 1996;99:3615–3622. doi: 10.1121/1.414959. [DOI] [PubMed] [Google Scholar]
- Drullman R, Festen JM, Plomp R. Effect of reducing slow temporal modulations on speech reception. J Acoust Soc Am. 1994;95:2670–2680. doi: 10.1121/1.409836. [DOI] [PubMed] [Google Scholar]
- Eddins DA. Amplitude-modulation detection of narrow-band noise – Effects of absolute bandwidth and frequency region. J Acoust Soc Am. 1993;93:470–479. [Google Scholar]
- Eddins DA. Amplitude-modulation detection at low- and high audio frequencies. J Acoust Soc Am. 1999;105:829–837. doi: 10.1121/1.426272. [DOI] [PubMed] [Google Scholar]
- Eddins DA. Measurement of auditory temporal processing using modified masking period patterns. J Acoust Soc Am. 2001;109:1550–1558. doi: 10.1121/1.1356024. [DOI] [PubMed] [Google Scholar]
- Ewert SD, Dau T. Characterizing frequency selectivity for envelope fluctuations. J Acoust Soc Am. 2000;108:1181–1196. doi: 10.1121/1.1288665. [DOI] [PubMed] [Google Scholar]
- Fant GCM. Acoustic Theory of Speech Production. Mouton; The Hague, Netherlands: 1970. [Google Scholar]
- Forrest TG, Green DM. Detection of partially filled gaps in noise and the temporal modulation transfer function. J Acoust Soc Am. 1987;82:1933–1943. doi: 10.1121/1.395689. [DOI] [PubMed] [Google Scholar]
- Gittelman JX, Li N, Pollak GD. Mechanisms Underlying Directional Selectivity for Frequency-Modulated Sweeps in the Inferior Colliculus Revealed by In Vivo Whole-Cell Recordings. J Neurosci. 2009;29:13030–13041. doi: 10.1523/JNEUROSCI.2477-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon M, O'Neill WE. Temporal processing across frequency channels by FM selective auditory neurons can account for FM rate selectivity. Hearing Res. 1998;122:97–108. doi: 10.1016/s0378-5955(98)00087-2. [DOI] [PubMed] [Google Scholar]
- Green DM, Swets JA. Signal Detection Theory and Psychophysics. Wiley; New York: 1966. [Google Scholar]
- Hsieh I, Saberi K. Detection of spatial cues in linear and logarithmic frequency-modulated sweeps. Attention, Perception, & Psychophysics. 2009 doi: 10.3758/APP.71.8.1876. in press. [DOI] [PubMed] [Google Scholar]
- Holdsworth J, Nimmo-Smith I, Patterson R, Rice P. Annex C of the SVOS final report (Part A: The auditory filter bank), APU (Applied Psychology Unit) Report 2341. Cambridge, UK: 1988. Implementing a Gammatone filter bank. [Google Scholar]
- Howie JM. Acoustical Studies of Mandarin Vowels and Tones. Cambridge University Press; Cambridge, Englans: 1976. [Google Scholar]
- Huber F, Thorson J. Cricket auditory communication. Scientific American. 1985;253:60–68. [Google Scholar]
- Kay RH. Hearing modulation in sounds. Physiological Review. 1982;62:894–975. doi: 10.1152/physrev.1982.62.3.894. [DOI] [PubMed] [Google Scholar]
- Klump GM, Langemann U. The detection of frequency and amplitude modulation in the European starling Sturnus-vulgaris psychoacoustics and neurophysiology. Advances in the Biosciences. 1992;83:353–359. [Google Scholar]
- Lee JM. Amplitude-modulation rate discrimination with sinusoidal carriers. J Acoust Soc Am. 1994;96:2140–2147. doi: 10.1121/1.410156. [DOI] [PubMed] [Google Scholar]
- Levitt HL. Transformed up-down methods in psychophysics. J Acoust Soc Am. 1971;49:467–477. [PubMed] [Google Scholar]
- Liberman AM, Delattre PC, Gerstman LJ, Cooper FS. Tempo of frequency change as cue for distinguishing classes of speech sounds. J Experimental Psych. 1956;52:127–137. doi: 10.1037/h0041240. [DOI] [PubMed] [Google Scholar]
- Luo H, Boemio A, Gordon M, Poeppel D. The perception of FM sweeps by Chinese and English listeners. Hearing Research. 2007;224:75–83. doi: 10.1016/j.heares.2006.11.007. [DOI] [PubMed] [Google Scholar]
- Luo H, Wang Y, Poeppel D, Simon JZ. Concurrent encoding of frequency and amplitude modulation in human auditory cortex: Encoding transition. J Neurophysol. 2007;98:3473–3485. doi: 10.1152/jn.00342.2007. [DOI] [PubMed] [Google Scholar]
- McNemar Q. Psychological Statistics. John Wiley & Sons; New York: 1969. [Google Scholar]
- Meddis R, Hewitt MJ, Shackleton TM. Implementation details of a computation model of the inner hair-cell/auditory-nerve synapse. J Acoust Soc Am. 1990;87:1813–1816. [Google Scholar]
- Moore BCJ, Sek A. Detection of combined frequency and amplitude-modulation. J Acoust Soc Am. 1992;92:3119–3131. doi: 10.1121/1.404208. [DOI] [PubMed] [Google Scholar]
- Moore BCJ, Sek A. Effects of carrier frequency and background-noise on the detection of mixed modulation. J Acoust Soc Am. 1994;96:741–751. doi: 10.1121/1.410312. [DOI] [PubMed] [Google Scholar]
- Ozimek E, Sek A. Perception of amplitude and frequency modulated signals (mixed modulation) J Acoust Soc Am. 1987;82:1598–1603. doi: 10.1121/1.395149. [DOI] [PubMed] [Google Scholar]
- Pickett JM. The Sounds of Speech Communication. University Park Press; Baltimore, MD: 1980. [Google Scholar]
- Poeppel D, Guillemin A, Thompson J, Fritz J, Bavelier D, Braun AR. Auditory lexical decision, categorical perception, and FM direction discrimination differentially engage left and right auditory cortex. Neuropsychologia. 2004;42:183–200. doi: 10.1016/j.neuropsychologia.2003.07.010. [DOI] [PubMed] [Google Scholar]
- Richards VM. Monaural envelope correlation perception. J Acoust Soc Am. 1987;82:1621–1630. doi: 10.1121/1.395153. [DOI] [PubMed] [Google Scholar]
- Riesz RR. DifferentiaI lntensity Sensitivity of the Ear for Pure Tones. Phys Rev. 1928;31:867–875. [Google Scholar]
- Ryan MJ, Wilczynskin W. Convolution of sender and receiver: effect on local mate preference in cricket frogs. Science. 1988;240:1786–1788. doi: 10.1126/science.240.4860.1786. [DOI] [PubMed] [Google Scholar]
- Saberi K. Lateralization of comodulated complex waveforms. J Acoust Soc Am. 1995;98:3146–3156. doi: 10.1121/1.413804. [DOI] [PubMed] [Google Scholar]
- Saberi K. Modeling interaural delay sensitivity to frequency modulation at high frequencies. J Acoust Soc Am. 1998;103:2551–2564. doi: 10.1121/1.422776. [DOI] [PubMed] [Google Scholar]
- Saberi K, Hafter ER. A common neural code for frequency and amplitude-modulated sounds. Nature. 1995;374:537–539. doi: 10.1038/374537a0. [DOI] [PubMed] [Google Scholar]
- Saberi K, Perrott DR. Cognitive restoration of reversed speech. Nature. 1999;398:760. doi: 10.1038/19652. [DOI] [PubMed] [Google Scholar]
- Sabourin P, Gottlieb H, Pollack GS. Carrier-dependent temporal processing in an auditory interneuron. J Acoust Soc Am. 2008;123:2910–2917. doi: 10.1121/1.2897025. [DOI] [PubMed] [Google Scholar]
- Shannon RV, Zeng FG, Kamath V, Wygonski J, Ekelid M. Speech recognition with primarily temporal cues. Science. 1995;270:303–304. doi: 10.1126/science.270.5234.303. [DOI] [PubMed] [Google Scholar]
- Slaney M. Technical Report #1998-010. Interval Research Corporation; Palo Alto, California: 1998. Auditory toolbox: A Matlab toolbox for auditory modeling work. [Google Scholar]
- Stagray JR, Downs D, Sommers RK. Contributions of the fundamental, resolved harmonics, and unresolved harmonics in tone-phoneme identification. J Speech Hearing Res. 1992;35:1406–1409. doi: 10.1044/jshr.3506.1406. [DOI] [PubMed] [Google Scholar]
- Strickland EA. The effects of frequency region and level on the temporal modulation transfer function. J Acoust Soc Am. 2000;107:942–952. doi: 10.1121/1.428275. [DOI] [PubMed] [Google Scholar]
- Tallal P, Miller SL, Bedi G, Byma G, Wang XQ, Nagarajan SS, Schreiner C, Jenkins WM, Merzenich MM. Language comprehension in language-learning impaired children improved with acoustically modified speech. Science. 1996;271:81–84. doi: 10.1126/science.271.5245.81. [DOI] [PubMed] [Google Scholar]
- Wetherill GB, Levitt H. Sequential estimation of points on a psychometric function. Brit J Math Stat Psychol. 1965;18:1–10. doi: 10.1111/j.2044-8317.1965.tb00689.x. [DOI] [PubMed] [Google Scholar]
- Woolley SMN, Casseday JH. Processing of modulated sounds in the zebra finch auditory midbrain: Responses to noise, frequency sweeps, and sinusoidal amplitude modulations. J Neurophysiol. 2005;94:1143–1157. doi: 10.1152/jn.01064.2004. [DOI] [PubMed] [Google Scholar]
- Yost WA, Sheft S. Temporal modulation transfer functions for tonal stimuli: Gated versus continuous conditions. Auditory Neurosci. 1997;3:401–414. [Google Scholar]
- Zwicker E. Die Grenzen der Hörbarkeit der Amplitudenmodulation und der Frequenzmodulation eines Tones (Limits to the audibility of amplitude modulation and frequency modulation of tones) Acustica. 1952;2:125–133. [Google Scholar]


