PHOENIX: A Scoring Function for Affinity Prediction Derived Using High-Resolution Crystal Structures and Calorimetry Measurements

Abstract

Binding affinity prediction is one of the most critical components to computer-aided structure-based drug design. Despite advances in first-principle methods for predicting binding affinity, empirical scoring functions that are fast and only relatively accurate are still widely used in structure-based drug design. With the increasing availability of X-ray crystallographic structures in the Protein Data Bank and continuing application of biophysical methods such as isothermal titration calorimetry to measure thermodynamic parameters contributing to binding free energy, sufficient experimental data exists that scoring functions can now be derived by separating enthalpic (ΔH) and entropic (TΔS) contributions to binding free energy (ΔG). PHOENIX, a scoring function to predict binding affinities of protein-ligand complexes, utilizes the increasing availability of experimental data to improve binding affinity predictions by the following: model training and testing using high-resolution crystallographic data to minimize structural noise, independent models of enthalpic and entropic contributions fitted to thermodynamic parameters assumed to be thermodynamically biased to calculate binding free energy, use of shape and volume descriptors to better capture entropic contributions. A set of 42 descriptors and 112 protein-ligand complexes were used to derive functions using partial least squares for change of enthalpy (ΔH) and change of entropy (TΔS) to calculate change of binding free energy (ΔG), resulting in a predictive r² (r²_pred) of 0.55 and a standard error (SE) of 1.34 kcal/mol. External validation using the 2009 version of the PDBbind “refined set” (n = 1612) resulted in a Pearson correlation coefficient (R_p) of 0.575 and a mean error (ME) of 1.41 pK_d. Enthalpy and entropy predictions were of limited accuracy individually. However, their difference resulted in a relatively accurate binding free energy. While the development of an accurate and applicable scoring function was an objective of this study, the main focus was evaluation of the use of high-resolution X-ray crystal structures with high-quality thermodynamic parameters from isothermal titration calorimetry for scoring function development. With the increasing application of structure-based methods in molecular design, this study suggests that using high-resolution crystal structures, separating enthalpy and entropy contributions to binding free energy, and including descriptors to better capture entropic contributions may prove to be effective strategies towards rapid and accurate calculation of binding affinity.

INTRODUCTION

Predicting binding affinity is one of the most critical and challenging components to computer-aided structure-based drug design.^1,2 Methods for predicting binding affinity are instrumental in a variety of applications, including molecular docking to identify a native binding mode, virtual screening of compound libraries to identify lead compounds, and lead optimization for enhancing binding affinity and target specificity.^3-5 Despite significant advances in first-principle methods for predicting binding affinity^6-10, empirical scoring functions that are fast and relatively accurate are still widely used in drug discovery.¹¹ For virtual screening studies where libraries up to millions of compounds are screened against a target of interest, a scoring function is needed to rapidly assess multiple binding modes of each multiple conformers generated for each compound. This is also the case for in silico lead optimization where a large number of analogs are computationally constructed and assessed. In addition to speed of evaluation for virtual screening, other scoring functions can be accurate at an atomic level for structure-based drug design in characterizing the dominant physical forces in molecular recognition during ligand binding. Moreover, empirical scoring functions should be transferable and not require careful individual validation for each system under study, making them more suitable for use in new problems with limited experimental data.

Empirical scoring functions aim to represent the atomic interactions of protein-ligand complexes by the use of relatively simple quantitative descriptors to capture the physicochemical forces governing protein-ligand complex formation. The underlying assumption in scoring functions is that the physical and chemical interactions of protein-ligand interactions can be quantitatively captured using a set of descriptors, and the sum of these descriptors will accurately predict binding affinities. In practice, each descriptor is weighted by a coefficient, derived by a linear regression method through training on experimental data from binding assays, resulting in an equation for calculating binding affinities. Over the last 20 years, a number of scoring functions have been developed, with some notable ones being SCORE1¹², SCORE2¹³, ChemScore¹⁴, X-Score¹⁵, Lig-Score¹⁶, DrugScore¹⁷, CScore¹⁸, GOLD^19,20, PLP²¹, and SFCscore²². These scoring functions differ by their choice and implementation of descriptors to capture the physicochemical interactions, the size and diversity of the training set, and the regression method used to derive the predictive equations. A number of reviews on scoring functions and assessments of their performance and applicability have been published.^23-29

Empirical scoring functions generally predict either the free energy of binding (ΔG) or the dissociation constant (K_d), each of which can be derived from the other. Recent calorimetric studies have elucidated the compensating enthalpic and entropic changes associated with binding free energy.^30-33 In a review from Ladbury, Klebe, and Freire, the binding free energies of first-in-class HIV-1 protease and HMG-CoA reductase inhibitors were shown to be due largely from optimizing entropy (ΔS), while improving binding affinity of subsequent analogs was predominantly the result of improving enthalpy (ΔH).³⁴ Marlow et al. has experimentally demonstrated that changes in protein conformational dynamics can serve as an indication of the changes in protein conformation entropy, which may also play an important role in high-affinity protein-ligand complexes.³⁵ Roy and Laughton have demonstrated using molecular dynamics simulations the importance of phenomena such as entropy-entropy compensation, dewetting of the protein binding site, and ligand configuration entropy in the form of rotational freedom in contributing to changes in entropy.³⁶ Because the binding free energy is composed of these compensating thermodynamics forces, the ability to accurately predict enthalpy (ΔH) and entropy (TΔS) independently should provide additional insight during structure-based drug design studies. Results from these experimental and theoretical studies illustrate the importance of considering both enthalpy and entropy contributions separately and in a greater detail for structure-based drug design studies.

Current empirical scoring functions contain descriptors that mainly take into account the changes of enthalpy (ΔH) in binding, and have used rudimentary methods such as the number of rotamers on a ligand, calculated partition coefficient (XlogP), and complementary hydrophobic surface area estimation to describe changes in entropic forces (TΔS). The lack of an accurate entropic description of protein-ligand interactions is surely the major reason why scoring function accuracy has been limited; they can predict enthalpic contributions accurately, but fail to predict entropic contributions, resulting in limited accuracy in predicting binding free energy. In the development of PHOENIX, addition terms to describe the shape and volume of both the ligand and protein binding site were included to implicitly capture the desolvation and ligand expulsion of solvent from the binding site contributing to entropic changes. Volume-based descriptors may also heuristically capture the rotational and translation entropy contributing to the configurational entropy of the system. Developing entropy models using shape and volume-based descriptors should lead to more accurate binding affinity predictions.

Development of PHOENIX aimed to take advantage of the increasing application of isothermal titration calorimetry (ITC) in medicinal chemistry and the recent availability of databases (PDBcal³⁷ and SCORPIO³⁸) containing both X-ray crystallographic structures of protein-ligand complexes and ITC experimental determination of both enthalpic and entropic contributions to binding free energy. PHOENIX, derived from the VALIDATE³⁹ scoring function, includes additional shape and volume-based descriptors to better capture entropic contributions typically not accounted for in scoring functions. A diverse set of 112 protein-ligand complexes with resolution ≤ 2.0 Å and thermodynamics parameters measured from ITC was used for training. A set of 42 descriptors, including 7 shape and volume descriptors calculated using FPOCKET⁴⁰, were used as a heutistic method to capture the physicochemical forces underlying protein-ligand interactions. Partial least squares of latent variables (PLS) was used to assign coefficients for each descriptor, and to independently derive regression equations to calculate ΔH and TΔS.

METHODS

Training Set

Information on protein-ligand complexes with crystallographic structures and thermodynamic parameters from isothermal titration calorimetry were obtained from PDBcal³⁷ and SCORPIO³⁸ databases. Experimental values of ΔG, ΔH, and TΔS were obtained from the database websites (http://www.pdbcal.org and http://scorpio.biophysics.ismb.lon.ac.uk/scorpio.html), while X-ray crystallographic structures were downloaded from the Protein Data Bank (PDB). Only structures of complexes with a crystallographic resolution ≤2.5 Å were used in the intial compilation of the training set. Additional metrics such as free R value (R_free)⁴¹ and diffraction-component precision index (DPI)⁴² were used to assess structural quality. R_free is a measure of the degree to which an atomic model predicts a subset of the observed diffraction data that has been omitted from the refinement process (see Supporting Information for equation). DPI is a measure of the quality of the structural model derived from the diffraction data (see Supporting Information for equation). However, due the to scarcity of complexes with a resolution of ≤2.5 Å, ITC parameters, and R_free values, the resolution (≤2.0 Å) was used as the final criteria to obtain the PHOENIX training set of 112 complexes. Nine different subsets of the 162 complexes were evaluated for predictive ability: Set 68, includes structures with resolutions ≤2.0 Å, R_free ≤0.3, DPI ≤0.3, ligand molecular weight <1000 daltons, ΔH, TΔS; Set 82, includes structures with resolutions ≤2.0 Å, R_free ≤0.3, DPI ≤0.3, ligand molecular weight <1000 daltons; Set 91, includes structures with resolutions ≤2.0 Å, R_free ≤0.3, DPI ≤0.3; Set 105, includes structures with resolutions ≤2.0 Å, ligand molecular weight <1000 daltons; Set 112, includes structures with resolutions ≤2.0 Å; Set 127, includes structures with resolutions ≤2.0 Å, 15 complexes with resolution between 2.0 and 2.5 Å also present in PDBbind test set; Set 140, includes structures with resolutions ≤2.25 Å; Set 153, includes structures with resolutions ≤2.5 Å, ligand molecular weight <1000 daltons; Set 162, includes structures with resolutions ≤2.5 Å. These subsets were selected to evaluate whether the quality of the crystal structures and diversity of the training set impacted the performance of the scoring function. Of the 9 subsets tested, Set 112 (Table 3) (resolutions ≤2.0 Å) resulted in the best performing binding free energy (ΔG) model.

Table 3.

Partial least squares (PLS) regression statistics of the change in enthalpy (ΔH) (A), change in entropy (TΔS) (B), and change in binding free energy (ΔG) (C) predictions from various derivations of the PHOENIX scoring function. Values presented include the number of complexes used in the training set (Number of Complexes), the number of components used to derive the PLS model (Number of Components), the correlation coefficient (r²), the standard error (s), and F-value (F). The number at the end of the scoring function name indicates the number of complexes used in the training set (e.g., PHOENIX_DH_68, training set of 68 complexes). The final PHOENIX scoring functions (n = 112) used for energetics predictions are indicated in bold lettering.

A.
Scoring Function	Number of Complexes	Number of Components	Correlation Coefficient (r2)	Standard Error (s) (kcal/mol)	F-value (F)
PHOENIX_DH_68	68	3	0.645	4.03	38.69
PHOENIX_DH_82	82	4	0.566	6.1	25.09
PHOENIX_DH_105	105	2	0.442	6.79	40.44
PHOENIX_DH_112	112	3	0.497	6.44	35.6
PHOENIX_DH_127	127	3	0.503	6.24	41.44
PHOENIX_DH_140	140	3	0.447	6.37	36.64
PHOENIX_DH_153	153	4	0.48	6.22	34.15
PHOENIX_DH_162	162	4	0.466	6.26	34.3

B.
Scoring Function	Number of Complexes	Number of Components	Correlation Coefficient (r2)	Standard Error (s) (kcal/mol)	F-value (F)
PHOENIX_TDS_68	68	3	0.735	3.81	59.2
PHOENIX_TDS_82	82	5	0.722	4.92	39.45
PHOENIX_TDS_105	105	2	0.55	6.06	62.26
PHOENIX_TDS_112	112	3	0.605	5.69	55.17
PHOENIX_TDS_127	127	3	0.606	5.63	63.01
PHOENIX_TDS_140	140	2	0.478	6.29	62.7
PHOENIX_TDS_153	153	3	0.512	6.2	52.1
PHOENIX_TDS_162	162	3	0.534	6.03	60.29

C.
Scoring Function	Number of Complexes	Predictive r2 (r2pred)	Standard Error (s) (kcal/mol)
PHOENIX_DG_68	68	0.61	1.19
PHOENIX_DG_82	82	−7.00	5.54
PHOENIX_DG_105	105	0.43	1.55
PHOENIX_DG_112	112	0.55	1.34
PHOENIX_DG_127	127	0.44	1.44
PHOENIX_DG_140	140	−0.89	2.62
PHOENIX_DG_153	153	−0.13	2.01
PHOENIX_DG_162	162	0.30	1.56

Structure Preparation

Protein-ligand complexes downloaded from the PDB were prepared as follows. Protein structure was extracted from the complex using SYBYL 7.3. Water molecules present in the complex were kept as part of the protein structure for an explicit solvent representation. In cases where multiple chains or subunits were present, the chain or subunit that was most complete was selected, which was chain A in most cases. Missing side chains and neutral terminal groups were added by the Biopolymer Structure Preparation function. Hydrogens were added to both the protein and water using the Biopolymer dictionary. The ligand was extracted from the complex and atom types were assessed and reassigned, if necessary. Hydrogens were added to all atoms. The resulting protein and ligand structures were saved in mol2 format.

External Test Sets

External validation sets include three versions of the PDBbind “refined set” (2002, 2004, and 2009)^43,44 and the 2007 PDBbind “core set” downloaded from the PDBbind site (http://www.pdbbind.org.cn/). Previous scoring function development studies by Wang, Lu, Fang, and Wang.²⁶ and Sotriffer, Sanschagrin, Matter, and Klebe.²² used both the 2002 and 2004 versions as benchmark sets, thus were assessed in this study for comparison purposes. The 2002 version contains 800 complexes, the 2004 version contains 1091 complexes, and the 2009 version contains 1741 protein-ligand complexes with resolution ≤2.5 Å. The 2007 “core set”, which consists of 195 complexes with non-redundant protein families and diversity of ligand structures and binding affinities, was also used to assess the general applicability of PHOENIX. A number of docking and scoring assessments have used this “core set” as a diverse set benchmark.²⁹ The protein and ligand structures were downloaded from the PDBbind database. Structures of the proteins were prepared using the same procedure as the training set. The ligands did not require any preparation and were used as is. For the 2004 and 2009 sets, 1071 out of 1091 were used in the 2004 set, while 1612 of 1741 were used in the 2009 set.

Descriptor Set

A set of 42 descriptors were used to derive the PHOENIX scoring function, as listed in Table 1. Of that set, the first 34 of the descriptors listed were calculated using the VALIDATE scoring function³⁹. The calculated partition coefficient, XlogP, was computed based on the Wang, Fu, and Lai⁴⁵ study using FILTER⁴⁶. FPOCKET⁴⁰, a cavity detection program based on Voronoi tessellation and alpha spheres, was used to obtain 7 volume-based descriptors to describe the ligand and protein binding site.

Table 1.

Coefficients and intercepts derived from partial least squares regression for the descriptor set (n = 42) used in the final PHOENIX scoring function for change in enthalpy (ΔH) and change in entropy (TΔS) equations.

Descriptor	ΔH	TΔS	ΔG
INTERCEPT	−7.064	−1.619	−5.445
Electrostatic Interaction Energy	−0.006	−0.005	−0.001
Steric Interaction Energy	0.008	0.004	0.004
Steric Fit	−0.064	−0.085	0.021
Rotatable Bonds	0.002	0.001	0.001
Ligand Strain Energy	0.023	0.008	0.015
Hydrophobic/Hydrophobic Contact Surface Area 1	0.004	0.007	−0.003
Hydrophilic/Hydrophilic Contact Surface Area 1 (Opposite Charge)	0.009	0.011	−0.002
Hydrophobic/Hydrophilic Contact Surface Area 1	0.009	0.012	−0.003
Hydrophilic/Hydrophilic Contact Surface Area 1 (Same Charge)	0.006	0.011	−0.005
Hydrophobic/Hydrophobic Contact Surface Area 2	0.001	0.001	0
Hydrophilic/Hydrophilic Contact Surface Area 2 (Opposite Charge)	0.006	0.006	0
Hydrophobic/Hydrophilic Contact Surface Area 2	0.003	0.004	−0.001
Hydrophilic/Hydrophilic Contact Surface Area 2 (Same Charge)	−0.002	0	−0.002
Ligand Total Hydrophobic Surface Area	0	0.001	−0.001
Ligand Total Hydrophilic Surface Area	−0.003	−0.004	0.001
Flexibility Index(Rot Bonds/ Non Term Bonds)	3.549	3.424	0.125
Ligand Buried Hydrophobic Surface Area	0	0.001	−0.001
Ligand Buried Hydrophilic Surface Area	−0.006	−0.006	0
Ligand Exposed Hydrophobic Surface Area	−0.001	−0.001	0
Ligand Exposed Hydrophilic Surface Area	−0.003	−0.004	0.001
Receptor Buried Hydrophobic Surface Area	−0.001	0.001	−0.002
Receptor Buried Hydrophilic Surface Area	−0.002	0.002	−0.004
Receptor Exposed Hydrophobic Surface Area	0	0	0
Receptor Exposed Hydrophilic Surface Area	0	0	0
Normalized Ligand Buried Hydrophobic Surface Area	3.487	3.695	−0.208
Normalized Ligand Buried Hydrophilic Surface Area	−2.814	−2.906	0.092
Normalized Ligand Exposed Hydrophobic Surface Area	−4.324	−3.101	−1.223
Normalized Ligand Exposed Hydrophilic Surface Area	−2.993	−5.661	2.668
Total Ligand/Receptor Hydrogen Bonds	0.044	0.032	0.012
Ligand Total Donor/Acceptor Count	−0.059	−0.072	0.013
Ligand Total Hydrogen Bond Atoms	0.007	−0.008	0.015
Ligand Total Buried Donor/Acceptor Count	−0.114	−0.129	0.015
Receptor Total Donor/Acceptor Count	0.053	0.045	0.008
Receptor Total Buried Donor/Acceptor Count	0.079	0.082	−0.003
Partition Coefficient	0.024	0.115	−0.091
Ligand Volume	−0.001	−0.001	0
Pocket Volume	−0.001	−0.001	0
Number of Alpha Spheres	0.004	0.009	−0.005
Proportion of Apolar Alpha Spheres	−4.253	−4.039	−0.214
Mean Local Hydrophobic Density	−0.159	−0.137	−0.022
Polarity Score	0.124	0.114	0.01
Alpha Sphere Density	0.012	−0.019	0.031

VALIDATE parameters were determined by using both molecular mechanics a heuristics approach in combination with parameters derived from molecular mechanics. Parameters derived from molecular mechanics include electrostatic interaction energy (EIE), steric interaction energy (SIE), and ligand strain energy (LSE). EIE accounts for the electrostatic interactions that contribute to the specificity of protein-ligand interactions, and was calculated using the MacroModel program. Charges for the protein and ligand were derived from the OPLS-AA force field. Nonbonded electrostatic interaction energy was calculated using the explicit sum of the Coulombic potentials. SIE was computed from the explicit sum of the Lennard-Jones potentials, where the required parameters were derived from the OPLS-AA force field. LSE was calculated based on the difference between the energy of the ligand in the binding site and the energy of the ligand by itself.

Descriptors derived from heuristics for both the ligand and protein include steric fit, number of rotatable bonds, total number of ligand/protein hydrogen bonds, total donor/acceptor count, total hydrogen-bond atoms, and number of buried hydrogen-bond atoms. Steric fit (SF) was used to describe the close packing interactions between the protein and ligand. In order to quantitate surface complementarity between protein and ligand, descriptors were used to capture lipophilic complementarity (nonpolar/nonpolar), hydrophilic complementarity (polar/polar, opposite charge), lipophilic/hydrophilic complementarity (polar/nonpolar), and hydrophilic noncomplementarity (polar/polar, like charge). Two separate methods were used. The first method used an absolute surface area between the protein and ligand similar to the method used by Bohm¹². The second method was based on a pairwise sum estimate, similar to the approach by Kellogg et al⁴⁷. For a detailed description of the implementation and underlying theory of the 34 VALIDATE descriptors, refer to the original study by Head et al.³⁹

As a heuristic method to capture entropic contributions, volume descriptors were used to represent the amount of water molecules displaced from the protein binding site, as well as the desolvation process of ligand going from unbound to bound state. FPOCKET⁴⁰, a cavity detection program based on Voronoi tessellation and alpha spheres, was used to obtain 7 volume-based descriptors to describe the ligand and protein binding site (ligand volume, pocket volume, number of alpha spheres, proportion of apolar alpha spheres, mean local hydrophobic density, polarity score, alpha sphere density).

Feature selection strategies such as excluding descriptors with a correlation coefficient ≥0.95 of another descriptor, or excluding descriptors that displayed minimal correlation to the thermodynamics parameters (≤0.01, ≤0.05) were assessed to identify a set of descriptors leading to the best performance. In addition, attempts were made to separate ΔH and TΔS descriptors by deriving simpler models using subsets (n = 20-30) of the final descriptors set (n = 42) which contribute qualitatively to each thermodynamic force, to test if more accurate predictions could be achieved. After excluding the descriptors with high correlation and descriptors with low correlation to ΔH and TΔS as well as separating descriptors for each thermodynamic force, the models resulted in less accurate predictions when assessing the 2002 version of PDBbind; therefore all 42 descriptors were used in as the PHOENIX scoring function.

Function Parameterization

The weight coefficients for each descriptor and equation for predicting ΔH and TΔS were derived by using PLS in SYBYL 7.3. All 42 descriptors were used as input parameters. To derive the regression equations, leave-one-out cross validation was initially performed to identify the optimal number of components to use for the PLS model. The PLS model was subsequently constructed using the number of components with the highest q² and least error to calculate the constant and coefficients for each descriptor. Regression statistics such as r², standard error, and F-value were used to assess the predictive ability of the models. The fraction of relative contribution of each descriptor to change in enthalpy (ΔH), change in entropy (TΔS), and change in binding free energy (ΔG) is listed in Table 2, and the coefficients and intercepts derived from partial least squares regression for the final PHOENIX scoring function (n = 112) are listed in Table 3.

Table 2.

Descriptor set (n = 42) used in the final PHOENIX scoring function and its relative contribution to change in enthalpy (ΔH), change in entropy (TΔS), and change in binding free energy (ΔG) calculations. Descriptors are sorted by relative fraction to change in binding free energy (ΔG) in descending order.

Descriptor	ΔH	TΔS	ΔG
Mean Local Hydrophobic Density	0.08	0.063	0.072
Flexibility Index (Rot Bonds/ Non Term Bonds)	0.066	0.059	0.063
Receptor Total Buried Donor/Acceptor Count	0.063	0.061	0.062
Pocket Volume	0.052	0.051	0.052
Electrostatic Interaction Energy	0.054	0.043	0.049
Hydrophobic/Hydrophilic Contact Surface Area 2	0.043	0.049	0.046
Proportion of Apolar Alpha Spheres	0.049	0.043	0.046
Hydrophobic/Hydrophilic Contact Surface Area 1	0.04	0.049	0.045
Polarity Score	0.048	0.04	0.044
Normalized Ligand Buried Hydrophobic Surface Area	0.035	0.034	0.035
Ligand Total Donor/Acceptor Count	0.031	0.035	0.033
Ligand Buried Hydrophilic Surface Area	0.034	0.03	0.032
Ligand Total Buried Donor/Acceptor Count	0.031	0.032	0.032
Ligand Total Hydrophilic Surface Area	0.029	0.028	0.029
Ligand Strain Energy	0.04	0.014	0.027
Steric Interaction Energy	0.035	0.016	0.026
Normalized Ligand Buried Hydrophilic Surface Area	0.026	0.025	0.026
Hydrophilic/Hydrophilic Contact Surface Area 2 (Opposite Charge)	0.024	0.023	0.024
Hydrophilic/Hydrophilic Contact Surface Area 1 (Opposite Charge)	0.02	0.024	0.022
Hydrophobic/Hydrophobic Contact Surface Area 1	0.015	0.025	0.02
Hydrophilic/Hydrophilic Contact Surface Area 1 (Same Charge)	0.014	0.024	0.019
Ligand Volume	0.021	0.015	0.018
Receptor Exposed Hydrophobic Surface Area	0.013	0.02	0.017
Normalized Ligand Exposed Hydrophilic Surface Area	0.012	0.021	0.017
Normalized Ligand Exposed Hydrophobic Surface Area	0.019	0.013	0.016
Receptor Exposed Hydrophilic Surface Area	0.009	0.02	0.015
Ligand Exposed Hydrophilic Surface Area	0.011	0.015	0.013
Receptor Total Donor/Acceptor Count	0.015	0.011	0.013
Partition Coefficient	0.005	0.021	0.013
Hydrophobic/Hydrophobic Contact Surface Area 2	0.007	0.016	0.012
Total Ligand/Receptor Hydrogen Bonds	0.013	0.009	0.011
Receptor Buried Hydrophilic Surface Area	0.008	0.011	0.01
Ligand Buried Hydrophobic Surface Area	0.004	0.013	0.009
Number of Alpha Spheres	0.005	0.012	0.009
Receptor Buried Hydrophobic Surface Area	0.006	0.009	0.008
Steric Fit	0.006	0.007	0.007
Ligand Exposed Hydrophobic Surface Area	0.008	0.004	0.006
Ligand Total Hydrophobic Surface Area	0.001	0.008	0.005
Hydrophilic/Hydrophilic Contact Surface Area 2 (Same Charge)	0.007	0.001	0.004
Ligand Total Hydrogen Bond Atoms	0.002	0.002	0.002
Alpha Sphere Density	0.001	0.002	0.002
Rotatable Bonds	0.001	0.001	0.001

RESULTS

Regression Analysis

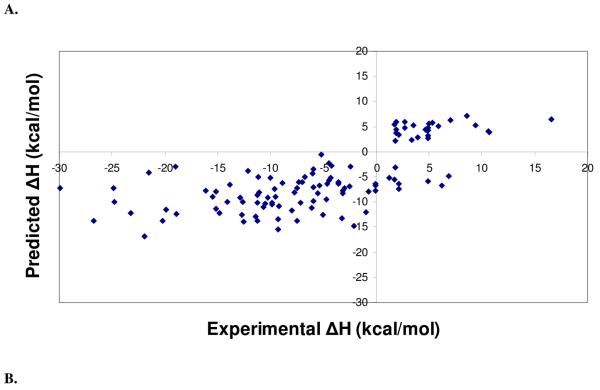
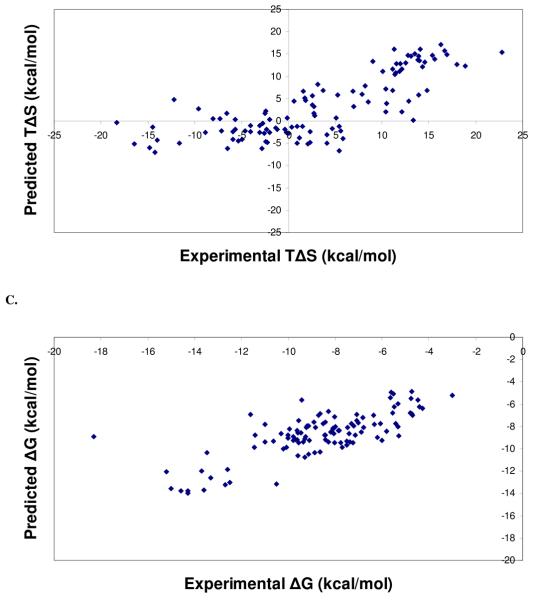
Regression and leave-one-out cross validation statistics of the different training sets used for PHOENIX are listed in Table 3, along with statistics for change of enthalpy (Table 3A), change in entropy (Table 3B), and change in binding free energy (Table 3C). Although the training set of 68 complexes resulted in the best regression statistics and standard errors, equations derived using the training set of 112 complexes were used since its performance on the external test sets were better than ones using the other test sets. Selecting the training set with the best regression or cross-validations statistics to use for external predictions can lead to using a model that may simply be overfitted to the training set. Regression analysis on the different training sets demonstrated that good fits were obtained using partial least squares on the set of 42 descriptors. Figure 2 shows the experimental versus predicted values of change of enthalpy (ΔH) (Figure 2A), change of entropy (TΔS) (Figure 2B), and change of binding free energy (ΔG) (Figure 2C).

Figure 2.

Scatter plots from regression analyses of the final PHOENIX training set (n = 112). Calculated versus experimental values for change in enthalpy (ΔH) (A), change in entropy (TΔS) (B), and change in binding free energy (ΔG) (C) for complexes in the final PHOENIX training set. Regression and leave-one-out cross validation statistics are as follows: change in enthalpy (ΔH), r² = 0.50, s = 6.44 kcal/mol, q² = 0.37, S_PRESS = 7.24 kcal/mol; change in entropy (TΔS), r² = 0.61, s = 5.69 kcal/mol, q² = 0.48, S_PRESS = 6.50 kcal/mol; change in binding free energy (ΔG), r² = 0.55, s = 1.34 kcal/mol.

The training set with 112 complexes resulted in models that did not lead to good regression statistics compared with results using the training set of 68 complexes. One possible reason for this is the larger training set contained a wider variety of protein-ligand complexes, especially ones that were difficult to predict, such as streptavidin and biotin complexes. Change in enthalpy and change in entropy values did not vary as much in the set of 68 complexes as the larger training sets, resulting in smaller errors and a better linear fit. However, when validating the model on external test sets such as PDBbind, enthalpy, and entropy, and binding free energy regression equations derived using the set of 112 complexes resulted in better regression statistics, which indicates that diversity in both structural data and thermodynamics data may be necessary to achieve robust predictive ability. When tested using the larger training sets (n = 127, 140, 153, 162) which included structures between 2 and 2.5 Å resolution, the performance on the external test sets did not improve. While increasing the size of the training set generally leads to more predictive models, in this case, results from this study suggest that inclusion of lower-resolution structures may actually introduce noise, leading to less predictive binding affinity calculations.

Internal cross-validation

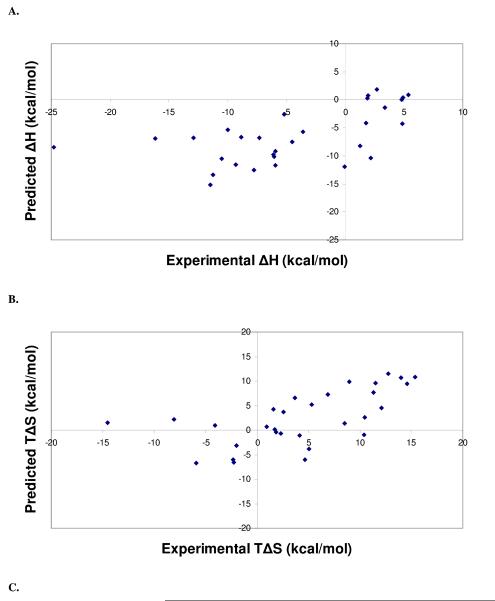
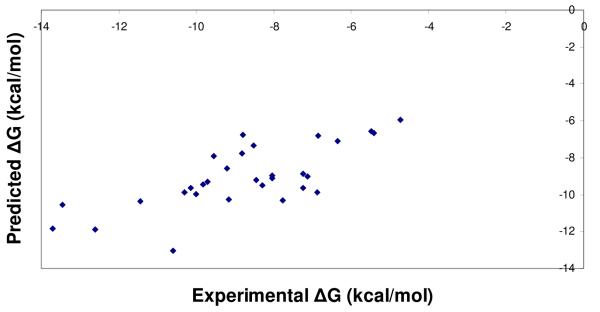
Cross-validation studies were performed on the PHOENIX scoring function trained with 112 complexes. The set of 112 complexes was divided into a set of 82 complexes for training, and a set of 30 complexes for testing. PLS was used to derive regression equations, which resulted in the following regression and leave-one-out cross validation statistics: r² = 0.43, s = 7.27 kcal/mol (2 components), q² = 0.34, SPRESS = 7.83 kcal/mol for change of enthalpy (ΔH); r² = 0.56, s = 6.37 kcal/mol (2 components), q² = 0.48, SPRESS = 6.89 kcal/mol for change of entropy (TΔS). These equations were used to calculate the thermodynamics contributions in the test set. Figure 3 displays the experimental versus predicted values for ΔH, TΔS, and ΔG. Predicted statistics for the test set of 30 complexes were as follows: ΔH, r² = 0.25, s = 6.32 kcal/mol; TΔS, r² = 0.31, s = 6.01 kcal/mol; ΔG, r² = 0.52, s = 1.53 kcal/mol. While the ΔH and TΔS calculations resulted in sizable errors, calculating their difference to obtain binding free energy led to a standard error within a reasonable accuracy range.

Figure 3.

Scatter plots from leave-one-out cross validation analyses of the final PHOENIX training set (n = 112), separated into a training set of 82 complexes and a test set of 30 complexes. Calculated versus experimental values for change in enthalpy (ΔH) (A), change in entropy (TΔS) (B), and change in binding free energy (ΔG) (C) from the internal cross-validation analyses are presented. Regression statistics are as follows: change in enthalpy (ΔH), r² = 0.25, s = 6.32 kcal/mol; change in entropy (TΔS), r² = 0.31, s = 6.01 kcal/mol; change in binding free energy (TΔS), r² = 0.52, s = 1.53 kcal/mol.

Testing on external data sets

To better assess the performance of PHOENIX on accuracy and applicability of affinity predictions, the scoring function trained with 112 complexes was tested on 4 different versions (2002, 2004, and 2009 refined sets; 2007 core set) of the PDBbind. For the sake of comparison, the assessment was performed in a similar fashion to the scoring function studies of Wang, Lu, Fang, and Wang,²⁶ Sotriffer, Sanschagrin, Matter, and Klebe,²² and Cheng, Li, Li, Liu, and Wang²⁹. Note the use of a different set of statistical metrics (e.g., Pearson correlation coefficient, Spearman correlation coefficient, etc.) to assess the performance on the external data set for comparison purposes with previous scoring function studies. To assess the performance of PHOENIX in a greater detail, correlation evaluation was performed on protein-ligand complexes categorized based on resolutions, protein families, and binding affinities in the 2002 version. The 2004 and 2009 refined sets were used to assess the performance of PHOENIX on larger and more diverse data sets. The 2007 core set, consisting of 195 complexes with 65 protein families with 3 ligands of different affinities (low-, medium-, and high-affinity), was used to assess performance on a non-redundant and diverse set of complexes.

Correlation evaluation results for the 2002 version of PDBbind compared to scoring functions in the Wang, Lu, Fang, and Wang study and SFCscore are summarized in Table 4. Based on the correlation evaluation of PDBbind 2002, the performance of PHOENIX is comparable to the top-performing scoring functions (e.g., SFCscore and X-Score::HMScore).

Table 4.

Correlation evaluation of the PHOENIX scoring function using different training sets on the PDBbind v2002 (n = 796) database. Correlation statistics include Pearson correlation coefficient (R_p), Spearman correlation coefficient (R_s), standard deviation (SD), mean error (ME), slope (a) in the linear regression (y = ax + b), and intercept (b). The number after the scoring function indicates the total number of complexes used for training (e.g., PHOENIX_68, training set of 68 complexes). The final PHOENIX scoring function (PHOENIX_112) is indicated in bold lettering.

Scoring Function	Rp	Rs	SD	ME	a	b
PHOENIX_68	0.499	0.518	2.04	1.62	0.33	4.09
PHOENIX_82	0.41	0.449	6.27	5.94	0.38	8.34
PHOENIX_105	0.473	0.502	2.06	1.6	0.43	3.25
PHOENIX_112	0.524	0.559	1.98	1.56	0.37	4.27
PHOENIX_127	0.517	0.534	2.07	1.65	0.33	4.77
PHOENIX_140	0.424	0.445	2.91	2.41	0.41	2.32
PHOENIX_153	0.333	0.339	2.24	1.81	0.21	4.54
PHOENIX_162	0.492	0.513	2.17	1.72	0.34	3.62

Resolutions

To assess the performance of PHOENIX on affinity predictions for low- and high-resolution complexes, the 2002 version of PDBbind was categorized into 2 sets: a high-resolution (≤2Å) set of 494 complexes, and a low-resolution (2 ≤ 2.5 Å) set of 302 complexes. Correlation evaluation results are listed in Table 6. PHOENIX affinity predictions on the high-resolution set were comparable to ones obtained from the X-Score functions (HPScore, HMScore, HSScore). PHOENIX affinity predictions on the low-resolution set were inferior to ones obtained from the 3 X-Score functions. PHOENIX, as well as the X-Score functions, provided better correlation statistics for the high-resolution set than the low-resolution set. One point to note is that the high-resolution set has 192 more complexes compared to the low-resolution set, yet still achieved better correlation statistics. These results may suggest that scoring functions in general can achieve more accurate predictions using higher-resolution and perhaps higher-quality X-ray crystal structures compared to using low-resolution and low-quality structures.

Table 6.

Correlation evaluation of the PHOENIX scoring function compared to X-Score scoring functions on high- (0 ≤ 2 Å) and low-resolution (2 ≤ 2.5 Å) complexes of the PDBbind 2002 set. Correlation statistics presented are the number of complexes tested (N), Pearson correlation coefficient (R_p), standard deviation (SD), mean error (ME), Spearman correlation coefficient (R_s).

	High (0 ≤ 2 Å)					Low (2 ≤ 2.5 Å)
Scoring Function	N	Rp	SD	ME	Rs	N	Rp	SD	ME	Rs
PHOENIX	494	0.558	1.92	1.52	0.586	302	0.468	2.06	1.60	0.511
X-Score::HPScore	494	0.597	1.95	1.55	0.615	302	0.492	2.13	1.68	0.525
X-Score::HMScore	494	0.575	2.03	1.62	0.589	302	0.480	2.19	1.73	0.525
X-Score::HSScore	494	0.614	1.89	1.49	0.640	302	0.493	2.07	1.62	0.536

Protein Families

Three protein families were selected from the 2002 version of PDBbind set to test the performance of PHOENIX on these special cases: HIV-1 protease, trypsin, carbonic anhydrase II. Table 7 lists the correlation evaluation statistics. The correlation statistics from PHOENIX on the HIV-1 protease set (R_p = 0.563, SD = 1.65, ME = 1.35, R_s = 0.434) is better than most of the scoring functions in the Wang, Lu, Fang, and Wang study in terms of R_p, and comparable to the top-performing scoring functions (Cerius2::LigScore, R_p = 0.528; GOLD::GoldScore_opt, R_p = 0.555). This may be due to the inclusion of explicit waters in PHOENIX; water molecules play a critical role in the binding of HIV-1 protease inhibitors. For the trypsin complexes, the correlation statistics from PHOENIX were inferior compared to the other scoring functions tested. Perhaps, the descriptors used in PHOENIX cannot adequately capture the electrostatics involved in the binding of trypsin inhibitors due to the use of monopole electrostatics, which led to larger errors in the affinity calculations. Another potential reason for the poorer performance is that only 2 trypsin complexes were included in the PHOENIX training set, while other scoring functions included a larger set of trypsin complexes in their training sets. As the availability of crystal structure of complexes with ITC data increases, more trypsin complexes can be included in the training set to improve affinity calculations. For the set of carbonic anhydrase II complexes, the correlation statistics from PHOENIX were comparable to the other scoring functions. SFCscore performed the best, which may primarily be due to the descriptors used to capture interactions with metal atoms present in the binding pocket; metals are involved in critical interactions with the ligand for this class of metalloenzymes. Inferior performance in affinity predictions for the carbonic anydrase set may be due to the fact that PHOENIX does not contain any descriptors to capture ligand interactions with metal atoms. Again, the use of more sophisticated representation of electrostatic interactions should improve predictability.

Table 7.

Correlation evaluation of the PHOENIX scoring function compared to other commonly used scoring functions on three subsets (HIV-1 Protease, Trypsin, Carbonic Anhydrase II) of the PDBbind 2002 set. Correlation statistics presented are the number of complexes tested (N), Pearson correlation coefficient (R_p), standard deviation (SD), mean error (ME), Spearmen correlation coefficient (R_s). Results from the commonly used scoring functions taken from the Wang et al. study²⁶ are presented for comparison purposes.

	HIV-1 Protease					Trypsin					Carbonic Anhydrase II
Scoring Function	N	Rp	SD	ME	Rs	N	Rp	SD	ME	Rs	N	Rp	SD	ME	Rs
	8		1.6	1.3		4		1.9	1.3		3		3.2	2.9
PHOENIX	2	0.563	5	5	0.434	0	0.476	0	8	0.574	9	0.539	6	7	0.444
	7					4					3
SFSscore::met	4	0.361	na	na	0.312	0	0.853	na	na	0.848	7	0.717	na	na	0.485
	8		1.2	1.0		4		1.1	0.8		3		1.1	0.8
X-Score::HPScore	2	0.429	5	1	0.436	5	0.754	5	8	0.725	9	0.544	8	5	0.547
	8		1.2	1.0		4		0.9	0.7		3		1.2	0.9
X-Score::HMScore	2	0.379	8	4	0.334	5	0.823	9	5	0.824	9	0.495	3	5	0.341
	8		1.2	1.0		4		1.1	0.9		3		1.2	0.9
X-Score::HSScore	2	0.400	7	5	0.322	5	0.753	5	1	0.766	9	0.417	8	1	0.448
	8		1.2	1.0		4		1.0	0.8		3		1.1	0.8
DrugScore::Pair	2	0.377	8	4	0.315	5	0.780	9	2	0.818	9	0.622	0	3	0.501
	8		1.2	1.0		4		1.2	0.9		3		1.2	0.9
DrugScore::Surf	2	0.401	7	2	0.317	5	0.674	9	9	0.753	9	0.512	1	7	0.269
	8		1.2	1.0		4		1.0	0.8		3		1.1	0.8
DrugScore::Pair/Surf	2	0.384	8	4	0.322	5	0.780	9	2	0.807	9	0.623	0	3	0.495
	8		1.3	1.0		4		1.3	0.9		3		1.1	0.8
Sybyl::D-Score	2	0.342	0	3	0.305	5	0.617	7	8	0.736	9	0.584	4	6	0.441
	8		1.3	1.0		3		1.0	0.8		3		1.0	0.8
Sybyl::PMF-Score	2	0.246	4	9	0.226	7	0.513	2	6	0.523	9	0.655	7	0	0.652
	8		1.3	1.0		4		1.4	1.0		3		1.0	0.7
Sybyl::G-Score	2	0.350	0	5	0.335	5	0.580	2	6	0.728	9	0.643	8	9	0.649
	8		1.2	1.0		4		1.1	0.9		3		1.1	0.7
Sybyl::ChemScore	2	0.376	8	5	0.350	5	0.761	3	1	0.749	9	0.609	2	6	0.663
	8		1.3	1.0		4		1.3	1.0		3		1.1	0.8
Sybyl::F-Score	0	0.361	1	8	0.375	5	0.663	1	5	0.610	5	0.371	5	7	0.145
	8		1.1	0.9		4		1.5	1.2		1		1.7	1.3
Cerius2::LigScore	1	0.528	8	9	0.496	0	0.392	9	7	0.467	8	0.154	8	4	−0.323
	8		1.2	1.0		4		1.1	0.8		3		0.9	0.7
Cerius2::PLP1	2	0.458	3	2	0.395	5	0.729	9	8	0.785	9	0.718	8	6	0.606
	8		1.2	1.0		4		1.1	0.8		3		0.9	0.6
Cerius2::PLP2	2	0.438	5	3	0.414	5	0.754	5	4	0.802	9	0.735	6	7	0.781
	8		1.2	1.0		4		1.0	0.8		3		1.1	0.8
Cerius2::PMF	2	0.411	6	3	0.342	3	0.775	6	5	0.740	9	0.604	2	7	0.603
	8		1.3	1.1		4		1.2	1.0		3		1.2	0.8
Cerius2::LUDI1	2	0.208	5	1	0.123	5	0.670	9	1	0.698	8	0.065	1	6	0.335
	8		1.3	1.1		4		1.2	0.9		3		1.2	0.8
Cerius2::LUDI2	2	0.274	3	1	0.181	5	0.696	5	5	0.725	9	0.470	5	9	0.519
	8		1.3	1.1		4		1.2	1.0		3		1.2	0.9
Cerius2::LUDI3	2	0.248	4	0	0.174	5	0.679	8	0	0.690	9	0.433	7	1	0.554
	6		1.2	1.0		3		1.6	1.3		3		1.2	0.9
GOLD::GoldScore	9	0.386	5	0	0.391	6	0.029	5	2	−0.012	4	0.539	5	0	0.420
	7		11	0.9		4		1.4	1.1		3		1.1	0.8
GOLD::GoldScore_opt	8	0.555	3	2	0.579	2	0.590	1	4	0.673	7	0.585	7	6	0.532
	7		1.1	0.9		4		1.6	1.3		3		1.2	0.8
GOLD::ChemScore	8	0.404	9	8	0.386	4	0.388	1	3	0.348	9	0.498	2	9	0.307
	8		1.2	1.0		4		1.4	1.2		3		1.0	0.8
GOLD::ChemScore_opt	0	0.429	4	2	0.393	4	0.520	9	1	0.565	9	0.639	8	0	0.454
	8		1.3	1.0		4		1.7	1.3		3		1.1	0.7
HINT	2	0.313	2	4	0.264	5	0.135	3	7	0.251	9	0.599	3	8	0.689

Affinities

The 2002 version of PDBbind was categorized into 3 groups: low-affinity (pK_d < 5), medium-affinity (5 ≤ pK_d ≤ 8), and high-affinity (pK_d > 8). PHOENIX was assessed on its ability to calculate a binding affinity that results in the same group as the experimental binding affinity. Results from this study are listed in Table 8. PHOENIX correctly categorized 27% of the low-affinity complexes, 100% of the medium-affinity complexes, and 61% of the high-affinity complexes. PHOENIX performed the best on the medium- and high-affinity complexes compared to the scoring functions from previous studies. The performance on the low-affinity group was the second best (best was SFCscore). This assessment demonstrated that PHOENIX can estimate affinities within a reasonable accuracy range to readily distinguish between a tight-binding ligand from a low-affinity ligand. As minimizing false-positive rates is a significant challenge in computer-aided molecular design, PHOENIX may prove to be advantageous for affinity estimations and relative rankings as well as binding pose prediction, especially when applied to high-resolution structures with high-quality experimental data.

Table 8.

Assessment of the ability of the PHOENIX scoring function to classify complexes into three binding affinity groups: low-affinity (pK_d < 5.0), medium-affinity (5.0 ≤ pK_d ≤ 8.0), and high-affinity (pK_d > 8.0). The number of correctly categorized complexes and total number of complexes in each category, as well as the percentage of the correctly categorized complexes are presented for PHOENIX and the commonly used scoring functions take from the Wang et al. study²⁶ for comparison purposes.

Scoring Function	Low	Medium	High
PHOENIX	52/205=27%	417/417=100%	112/193=61%
SFSscore::met	88/191=46%	309/417=74%	86/192=45%
X-Score::HPScore	33/205=16%	358/402=89%	48/193=25%
X-Score::HMScore	41/205=20%	348/402=87%	65/193=34%
X-Score::HSScore	29/205=14%	350/402=87%	53/193=27%
DrugScore::Pair	24/205=12%	359/402=89%	45/193=23%
DrugScore::Surf	11/205=5%	362/402=90%	45/193=23%
DrugScore::Pair/Surf	24/205=12%	358/402=89%	47/193=24%
Sybyl::D-Score	0/205=0%	384/402=96%	2/193=1%
Sybyl::PMF-Score	0/196=0%	395/396=99%	0/193=0%
Sybyl::G-Score	12/205=6%	359/402=89%	30/193=16%
Sybyl::ChemScore	38/204=19%	349/400=87%	40/193=21%
Sybyl::F-Score	0/182=0%	362/362=100%	0/188=0%
Cerius2::LigScore	11/186=6%	340/366=93%	16/165=10%
Cerius2::PLP1	24/205=12%	364/401=91%	35/193=18%
Cerius2::PLP2	30/205=15%	363/402=90%	32/193=17%
Cerius2::PMF	0/202=0%	390/400=97%	3/193=2%
Cerius2::LUDI1	1/203=0%	379/394=96%	9/193=5%
Cerius2::LUDI2	6/205=3%	378/401=94%	15/193=8%
Cerius2::LUDI3	1/205=0%	387/402=96%	9/193=5%
GOLD::GoldScore	0/178=0%	331/339=98%	4/177=2%
GOLD::GoldScore_opt	3/200=1%	366/385=95%	11/187=6%
GOLD::ChemScore	8/177=5%	345/376=92%	37/188=20%
GOLD::ChemScore_opt	20/187=11%	346/386=90%	38/189=20%
HINT	2/205=1%	388/402=97%	11/193=6%

Recent versions of PDBbind

Recent versions of the PDBbind dataset (2004 and 2009) were used as external test sets for scoring function validation. The correlation statistics for the 2004 version (n = 1073), also used as a test set in the development of SFCscore, are listed in Table 8, and the ones for the 2009 version (n = 1612) are listed in Table 9. Based on the results from the 2004 and 2009 “refined sets”, PHOENIX demonstrated comparable performance compared with the X-Score functions and SFCscore (the better performing scoring functions). Also, results from the larger and more diverse 2004 and 2009 PDBbind refined sets demonstrated the robustness of PHOENIX in predicting affinities for various types of protein-ligand interactions.

Table 9.

Correlation evaluation of the PHOENIX scoring function on the PDBbind 2004 (n = 1073) refined set. Correlation statistics include number of complexes tested (N), Pearson correlation coefficient (R_p), standard deviation (SD), mean error (ME), slope (a) in the linear regression (y = ax + b), and intercept (b). Results from the X-Score scoring functions are presented for comparison purposes.

Scoring Function	Rp	Rs	SD	ME	a	b
PHOENIX	0.515	0.554	2.00	1.57	0.35	4.46
X-Score::HPScore	0.557	0.589	2.00	1.57	0.32	4.24
X-Score::HMScore	0.540	0.572	2.06	1.63	0.29	4.23
X-Score::HSScore	0.561	0.593	1.95	1.53	0.36	4.27

Diverse and non-redundant test set

To further assess the performance of PHOENIX compared with other scoring functions, the PDBbind 2007 core set was used to represent a diverse, yet non-redundant, set of protein-ligand complexes. The 2007 core set includes 65 unique protein family members, each with a low-, medium-, and high-affinity ligand. Binding affinities ranged from 1.40 to 13.96 pK_d, molecular weight from 103 to 974, and number of ligand rotatable bonds from 0 to 32. Performance in the “scoring power” test similar to the Cheng et al. study was used to assess PHOENIX. The statistics from correlation evaluation on affinity predictions are listed in Table 10. To test whether scoring functions provided value over the use of a simple descriptor, the number of heavy atoms was assessed as a scoring method. PHOENIX resulted in the second highest Pearson correlation coefficient, however, the mean error was more than twice as large as the second largest (1.70 compared to 0.71), suggesting that there is still significant room for improvement in the accuracy of affinity predictions.

Table 10.

Correlation evaluation of the PHOENIX scoring function on the PDBbind 2009 (n = 1612) refined set. Correlation statistics include number of complexes tested (N), Pearson correlation coefficient (R_p), standard deviation (SD), mean error (ME), slope (a) in the linear regression (y = ax + b), and intercept (b). Results from the X-Score scoring functions are presented for comparison purposes.

Scoring Function	Rp	Rs	SD	ME	a	b
PHOENIX	0.575	0.591	1.76	1.41	0.44	3.98
X-Score::HPScore	0.571	0.589	1.78	1.43	0.36	4.05
X-Score::HMScore	0.563	0.581	1.84	1.48	0.34	4.03
X-Score::HSScore	0.565	0.584	1.75	1.42	0.40	4.10

To assess the “ranking power” of PHOENIX as performed in the Cheng et al. study, each of the 65 families were assessed to check if the low-, medium-, and high-affinity ligand were ranked in the correct order. Families that were ranked correctly for all 3 complexes were given a score of 1, while a score of 0 is given if there is any deviation from the correct ranking (e.g, low, high, medium; medium, high, low). The success rate in the “ranking power” study of the 2007 core set is listed in Table 11. PHOENIX achieved a success rate of 46.2%, which ranks amongst the best-performing functions, with only 4 other scoring functions with a higher success rate (X-Score::HSscore, 58.5%; DS::PLP2, 53.8%; DrugScoreCSD, 52.3%; SYBYL::ChemScore, 47.7%). The performance of PHOENIX in this study demonstated its utility in structure-based design to correctly rank relative affinities for various types of protein-ligand complexes.

Table 11.

Correlation evaluation of the PHOENIX scoring function on the PDBbind 2007 core set. Correlation statistics include number of complexes tested (N), Pearson correlation coefficient (R_p), standard deviation (SD), and mean error (ME). The “Number of Heavy Atoms” was used as a benchmark to assess scoring function enrichment. Results from the commonly used scoring functions taken from the Wang et al. study²⁶ are presented for comparison purposes.

Scoring Function	N	Rp	SD	ME
PHOENIX	194	0.616	2.16	0.644
X-Score::HMScore	195	0.644	1.83	0.705
DrugScoreCSD	195	0.569	1.96	0.627
SYBYL::ChemScore	195	0.555	1.98	0.585
DS::PLP1	195	0.545	2.00	0.588
GOLD::ASP	193	0.534	2.02	0.577
SYBYL::G-Score	195	0.492	2.08	0.536
DS::LUDI3	195	0.487	2.09	0.478
DS::LigScore2	193	0.464	2.12	0.507
GlideScore-XP	178	0.457	2.14	0.435
DS::PMF	193	0.445	2.14	0.448
GOLD::ChemScore	178	0.441	2.15	0.452
Number of Heavy Atoms	195	0.431	2.15	0.517
SYBYL::D-Score	195	0.392	2.19	0.447
DS::Jain	189	0.316	2.24	0.346
GOLD::GoldScore	169	0.295	2.29	0.322
SYBYL::PMF-Score	190	0.268	2.29	0.273
SYBYL::F-Score	185	0.216	2.35	0.243

PHOENIX scoring function

The final PHOENIX scoring functions (used to predict ΔH, TΔS, and ΔG (ΔH-TΔS)) that resulted in the best performance across multiple versions (2002, 2004, 2009 refined sets; 2007 core set) and subsets (resolutions, protein families, affinities from v2002) of the PDBbind database used a training set of 112 structurally and energetically diverse complexes. A set of 42 descriptors were included in the ΔH, TΔS, and ΔG (ΔH-TΔS) models: 34 derived from molecular mechanics calculations, various surface area terms, hydrogen-bond donors and acceptor count from VALIDATE; 1 to estimate the ligand partition coefficient (XlogP); 7 shape- and volume-based descriptors from FPOCKET to better capture entropic contributions. Partial least squares was used to assign coefficients to each of the terms to derive the “master equation” to calculate ΔH, TΔS, and ΔG. While change in enthalpy (ΔH) and change in entropy (TΔS) predictions were of limited accuracy (standard errors of ~6 kcal/mol) individually, the difference between their individual predictions resulted in a relatively accurate change in binding free energy (ΔG) (standard errors of 1.5 kcal/mol). External validation using the 2009 version of the PDBbind “refined set” (n = 1612) (most comprehensive high-quality data set for assessing scoring functions) resulted in a Pearson correlation coefficient (R_p) of 0.575 and a mean error (ME) of 1.41 pK_d, which demonstrated its relative accuracy and robustness in predicting binding affinities.

DISCUSSION

Predicting binding affinity of protein-ligand interactions remains one of the most critical and challenging problems in computer-aided drug design. The PHOENIX scoring function, derived using a training set of high-resolution structures (n = 112) and calorimetry measurements for change of enthalpy (ΔH) and change of entropy (TΔS) from ITC, has demonstrated an ability to achieve accurate binding affinity predictions across 4 large and diverse sets of protein-ligand complexes (PDBbind 2002, 2004, 2009 refined sets; 2007 core set) using a modest number of descriptors (n = 42) to capture key physicochemical interactions. Nine descriptors contributing the most (>4%) to binding free energy (mean local hydrophobic density, flexibility index, receptor total buried donor/acceptor count, pocket volume, electrostatic interaction energy, hydrophobic/hydrophilic contact surface area 2, proportion of apolar alpha spheres, hydrophobic hydrophilic contact surface area 1, polarity score) aimed to capture the key physical forces underlying protein-ligand interactions: enthalpic contributions via van der Waals interactions, hydrogen bonding at the binding site, electrostatics for specificity; entropic contributions via volume and polarity features of binding site and ligand conformational entropy. Overall, the relative contributions from each of the descriptors were fairly distributed (ranging from 0.001 to 0.072), which suggested that each descriptor contains some degree of information for capturing the physics of protein-ligand interactions. Perhaps the use of a larger and more physically-accurate set of descriptors in future studies may help in further capturing the atomic-level details underlying molecular recognition in protein-ligand interactions.

Despite the promising performance in predicting binding affinities, some limitations of PHOENIX have been revealed. The enthalpy (ΔH) and entropy (TΔS) regression and internal cross-validation results suggest that there is significant room for improvement in deriving these equations. The individual thermodynamics parameters (ΔH and TΔS) displayed only modest predictive ability with relatively large errors (6-7 kcal/mol). There are several possible reasons for this. Scoring function would benefit from training on a larger and more structurally and thermodynamically diverse set of complexes. More physically-accurate descriptors are needed to more accurately capture and separate enthalpic and entropic contributions due to entropy/enthalpy compensation. Descriptors that can better separate enthalpic (ΔH) and entropic (TΔS) contributions are needed to derive more accurate independent thermodynamic models. However, developing descriptors to capture primarily enthalpy or entropy is a challenging feat in itself, since any physicochemical interactions that can be experimentally quantitated are correlated and will contain, to some degree, both thermodynamic forces (e.g, flexibility index and total ligand surface area). Inclusion of descriptors to explicitly capture hydrogen bonding interactions may lead to more accurate ΔH predictions. Descriptors to better capture electrostatics interactions such as pi-cation interactions may also help with predicting enthalpy changes. To better quantitate entropic contributions, descriptors to take into account conformational changes of the binding site, such as quantitating the rotatmers of the side chains involved in the complex, may provide a measure of entropy changes from the protein upon ligand binding (entropy-entropy compensation).⁴⁸ Classifying water molecules in the binding site according to their energetic preferences as a means to model dewetting will be useful for capturing the entropy change upon ligand binding and displacement of binding-site water molecules.^49-52 Inclusion of multiple binding modes to better represent conformational and configurational entropy may help to derive more accurate change in entropy (TΔS) models as been demonstrated in theoretical studies.^53-57 Moreover, larger sets of high-quality and structurally and thermodynamically diverse protein-ligand complexes will certainly be necessary to achieve more representative statistics for the different protein families and ligand structures.

As presented earlier, the change in enthalpy (ΔH) and change in entropy (TΔS) calculations were of limited relative accuracy. However, the change in binding free energy (ΔG) calculations was within relative accuracy compared with other commonly used scoring functions. The relative accuracy predicted by the ΔG model (difference of ΔH and TΔS model predictions) may have resulted from the cancellation of the overestimated values from independent ΔH and TΔS calculations, since the regression coefficient signs are in the same direction for both forces. Overestimates of ΔH and TΔS may have been due to the high correlation between the physicochemical descriptors used (e.g., “flexibility index” to capture conformational entropy is correlated to terms estimating total ligand surface area to capture van der Waals interactions to enthalpy), which were originally intended to be used to estimate ΔG. In other words, a descriptor used to estimate TΔS contributions (e.g., flexibility index) may also capture, to some degree, the physical forces underlying ΔH contributions (e.g., ligand total surface area). As an attempt to separate ΔH and TΔS descriptors, simpler models using subsets (n = 20-30) of the final descriptors set (n = 42) that are intuitive to contribute qualitatively to each thermodynamic force were used to test if more accurate predictions can be achieved. However, resulting predictions by these “feature selection” models were not as accurate as the predictions calculated using models with the full descriptors set. As mentioned before, descriptors that can better distinguish between ΔH and TΔS contributions should be developed and included in future development of accurate thermodynamically-based scoring functions.

In developing scoring functions, the inherent inaccuracy of the experimental data, which has been highlighted by a number of scoring function and structure-based design studies, remains the culprit to the limited accuracy in binding affinity predictions. In X-ray crystallography, conditions used to induce crystalization are often in dramatic contrast to physiological conditions under which protein-ligand interactions occur. Another potential source of error is from the thermodynamics measurements by ITC. Experiments conducted with ITC have often been performed under varying temperature and buffer conditions (e.g., salt concentration, pH), that may lead to marked variations in the thermodynamics measurements, as recently pointed out by Myszka et al⁵⁸. Chodera and Dill have also observed large discrepancies in ΔH measurements from ITC (unpublished). Inclusion of such ITC data in the training sets may not necessarily represent the magnitude of thermodynamics forces under physiological conditions. As the use of ITC increases to measure thermodynamics forces in protein-ligand interactions, diverse structural and thermodynamics data performed under homogenous conditions should become available to help alleviate these limitations.

CONCLUSIONS

Towards development of an empirical scoring function to achieve more accurate binding affinity predictions, high-resolutions X-ray crystal structures of protein-ligand complexes and thermodynamic parameters measured by ITC was used to derive models to calculate enthalpic and entropic contributions to binding free energies. Shape and volume-based descriptors were used as a heuristic method to implicitly capture changes in desolvation entropy and ligand configurational entropy. PHOENIX demonstrated accurate binding affinity predictions comparable to the top-performing scoring functions based on an extensive series of tests on the 4 versions of the PDBbind database. To our knowledge, this is the first empirical scoring function developed using thermodynamics parameters from ITC as a strategy to derive regression equations to calculate binding affinity.

Predicting binding affinities is the most critical and also challenging component of structure-based drug design. Often times, a docking program may identify a compound in the native low-energy conformation, but without an accurate scoring function, will be categorized as a non-binder, rendering the docking program of minimal value. Because of the high false-positive and false-negative rates associated with computer-aided drug design methodologies, development of an accurate and reliable scoring function is absolutely necessary for enhancing the performance of these in silico design tools. Development of the PHOENIX scoring function demonstrated the use of high-resolution structural complexes and thermodynamics parameters for model training can be the key advances towards achieving more accurate binding affinity predictions.

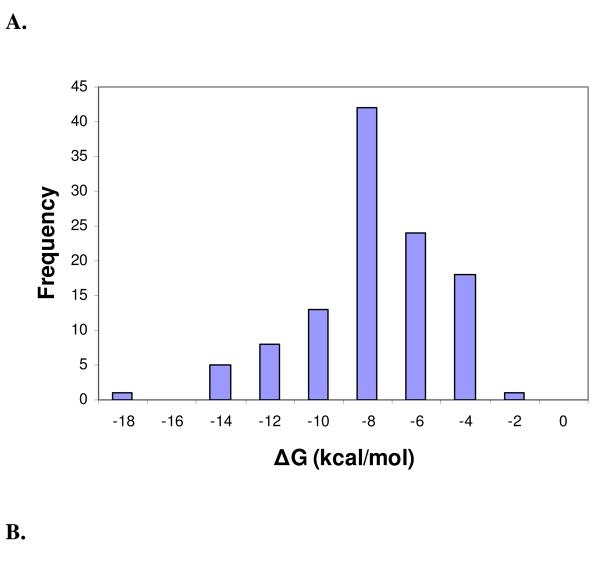
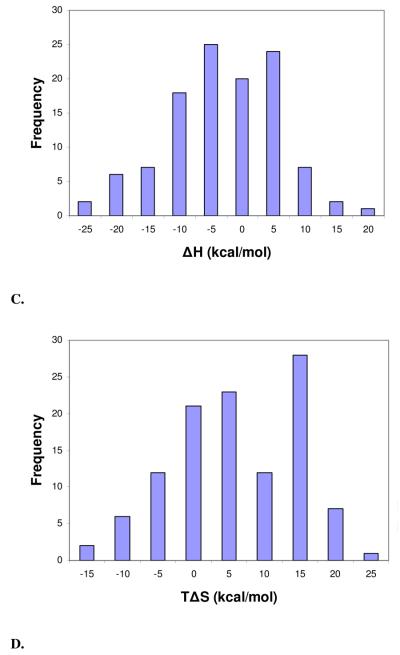
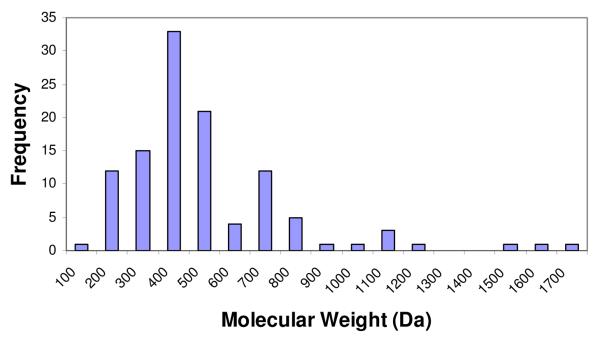
Figure 1.

Distribution histograms of the change in binding free energy (ΔG) (mean = −8.73 kcal/mol, std. dev. = 2.73 kcal/mol) (A), change in enthalpy (ΔH) (mean = −5.40 kcal/mol, std. dev. = 8.96 kcal/mol) (B), change in entropy (TΔS) (mean = 3.31 kcal/mol, std. dev. = 8.92 kcal/mol) (C), and molecular weight (mean = 455.25 Da, std. dev. = 273.11 Da.) (D) of complexes in the final PHOENIX training set (n = 112).

Table 5.

Correlation evaluation of the PHOENIX scoring function compared to other commonly used scoring functions on the PDBbind v2002 set. Correlation statistics presented are the number of complexes tested (N), Pearson correlation coefficient (R_p), standard deviation (SD), mean error (ME), slope (a) in the linear regression (y = ax + b), and intercept (b). Results from the commonly used scoring functions taken from the Wang et al. study²⁶ are presented for comparison purposes.

Scoring Function	N	Rp	SD	ME	a	b
PHOENIX	796	0.524	1.98	1.56	0.37	4.27
SFCscore::met	800	0.585	1.8	1.37	0.82	1.23
X-Score::HPScore	800	0.514	1.89	1.47	0.71	2.03
X-Score::HMScore	800	0.566	1.82	1.42	0.92	1.18
X-Score::HSScore	800	0.506	1.9	1.48	0.93	1.24
DrugScore::Pair	800	0.473	1.94	1.51	4.90E-06	4.1
DrugScore::Surf	800	0.463	1.95	1.53	7.20E-05	4.48
DrugScore::Pair/Surf	800	0.476	1.94	1.5	4.70E-06	4.09
Sybyl::D-Score	800	0.322	2.09	1.67	9.70E-03	5
Sybyl::PMF-Score	785	0.147	2.16	1.74	6.43E-03	5.92
Sybyl::G-Score	800	0.443	1.98	1.56	9.13E-03	4.34
Sybyl::ChemScore	797	0.499	1.91	1.5	9.10E-02	3.9
Sybyl::F-Score	732	0.141	2.19	1.77	2.10E-02	6.06
Cerius2::LigScore	717	0.406	2	1.57	0.79	4.63
Cerius2::PLP1	800	0.458	1.96	1.52	2.30E-02	4.09
Cerius2::PLP2	800	0.455	1.96	1.53	2.60E-02	3.93
Cerius2::PMF	795	0.253	2.13	1.71	1.10E-02	5.37
Cerius2::LUDI1	790	0.334	2.08	1.66	2.60E-03	4.88
Cerius2::LUDI2	799	0.379	2.04	1.62	4.20E-03	4.28
Cerius2::LUDI3	800	0.331	2.08	1.67	3.20E-03	4.68
GOLD::GoldScore	694	0.285	2.16	1.72	2.40E-02	5.33
GOLD::GoldScore_opt	772	0.365	2.06	1.63	3.00E-02	4.7
GOLD::ChemScore	741	0.423	2	1.56	8.50E-02	4.65
GOLD::ChemScore_opt	762	0.449	1.96	1.52	8.60E-02	4.41
HINT	800	0.33	2.08	1.65	0.2	6.36

Table 12.

Success rates for correctly ranking the low-, medium-, and high-affinity ligands in the PDBbind 2007 core set for the PHOENIX scoring function and 16 other commonly used scoring functions taken from the Cheng et al. study²⁹.

Scoring function	Success rate (%)
PHOENIX	46.2
X-Score::HSScore	58.5
DS::PLP2	53.8
DrugScoreCSD	52.3
SYBYL::ChemScore	47.7
SYBYL::D-Score	46.2
SYBYL::G-Score	46.2
GOLD::ASP	43.1
DS::LUDI3	43.1
DS::Jain	41.5
DS::PMF	41.5
SYBYL::PMF-Score	38.5
GOLD::ChemScore	36.9
DS::LigScore2	35.4
GlideScore-XP	33.8
Number of Heavy Atoms	32.3
SYBYL::F-Score	29.2
GOLD::GoldScore	23.1