Quality Degradation in Lossy Wavelet Image Compression

Abstract

The objective of this study was to develop a method for measuring quality degradation in lossy wavelet image compression. Quality degradation is due to denoising and edge blurring effects that cause smoothness in the compressed image. The peak Moran z histogram ratio between the reconstructed and original images is used as an index for degradation after image compression. The Moran test is applied to images randomly selected from each medical modality, computerized tomography, magnetic resonance imaging, and computed radiography and compressed using the wavelet compression at various levels. The relationship between the quality degradation and compression ratio for each image modality agrees with previous reports that showed a preference for mildly compressed images. Preliminary results show that the peak Moran z histogram ratio can be used to quantify the quality degradation in lossy image compression. The potential for this method is applications for determining the optimal compression ratio (the maximized compression without seriously degrading image quality) of an image for teleradiology.

THE PICTURE ARCHIVING AND COMMUNICATION SYSTEM¹ (PACS) utilizes digital technologies for the acquisition, storage, and transmission of radiological images. One of the major difficulties in operating a digital radiology facility is the sheer volume of image data that must be handled. Although recent advances in computer technology have increased the data storage capacity and communication speeds, they alone are not sufficient to overcome this problem. Image compression techniques can be employed to reduce the data volume into a more manageable size without significantly compromising image quality. Digital image compression² is divided into two categories defined as lossless and lossy. Lossless techniques³ include run length encoding, Huffman coding, differential pulse code modulation, and Lempel-Ziv , which enable the complete image to be reconstructed from the compressed data set as a perfect reproduction of the original. Lossless compression can reduce the image size only by a factor of 2 to 3. Much higher compression ratios are desirable to produce a more substantial compression impact. Lossy techniques enable significantly higher compression levels with slight quality degradation.

Quality evaluation can be performed subjectively or objectively. The receiver operating characteristic (ROC) analysis is the dominant technique for subjectively evaluating image quality. In an ROC study,⁴ radiologists are asked to review compressed images with or without an abnormality and to provide a binary decision along with their degree of certainty. The diagnostic accuracies of these images were then compared with the original images. The ROC analyses are expensive and time-consuming. A typical ROC study would require evaluation of more than 300 images to obtain a statistically significant result.²

Objective image quality evaluations are attractive because they are easy to perform and independent of viewing conditions and individual observers. Recent researches used a human visual system (HVS) that incorporated a simple model into the objective measures leading to a better correlation with the human observer response.⁵ However, the HVS is too complex to fully understand using present psychophysical means. The normalized mean squared error (NMSE) is the most commonly used method to measure the quality changes in compressed images.^{6,7,8,9,10,11} The NMSE is a measure of the image difference that is formed by taking the mean of the squared differences between all corresponding pixels in the original and the compressed images. The guidance document for PACS requires that manufacturers report to PDA the NMSE of their lossy compression technique.¹² The NMSE is sensitive to degradation, with alterations in its value depending on the image content and degree of degradation. However, NMSE does not provide any information regarding the type of loss that causes the quality deterioration, and it does not correlate well with subjective quality measurements.

The purpose of this study was to establish a quality degradation model in lossy compression and present a method for measuring the image quality. Based on this model, the optimal compression can be determined for each image before compression is performed. In the following paragraphs we briefly describe the irreversible compression method. The method for using the Moran I test to measure the quality change is then introduced. The measurement results from various medical images are then be presented.

IRREVERSIBLE IMAGE COMPRESSION

Irreversible image compression² involves three processes: (i) image transformation, (ii) quantization, and (iii) entropy encoding. Image transformation, also referred to as decorrelation, performs transformation (mostly cosine or wavelet transform) on the image to eliminate redundant information and provide a suitable coefficient for entropy coding.^13,14 Quantization is then applied to the transformation coefficients according to a predefined quantization table. The effect of quantization is to drive small coefficients (predominantly at high frequencies) to zero. It achieves compression by representing these coefficients with a precision not greater than that necessary to achieve the desired image quality. An entropy encoding method (Huffman or arithmetic coding) is then employed to further reduce the data volume.

Quantization is irreversible, and it is the cause of quality loss in compressed images. As the compression ratio increases, a greater number of high-frequency components are removed and the image becomes smoother. The major contributing factors to the high-frequency parts are statistical noise and structural edges. The quality loss is caused by the effects of denoising and edge blurring, and it can be quantified by measuring the smoothness of the compressed image.

MORAN I TEST

The Moran I test^15,16 has been employed to evaluate the spatial autocorrelation of mapped data. In this study, it was used to measure the smoothness in an image. The Moran coefficient I for a pixel is calculated as:

where f_i is the gray level of pixel i,

is the mean gray level inside a r × c window centered on that pixel, δ_ij = 1 if pixels i and j are adjacent, and 0 otherwise. Further, S₀ = 4rc − 2r − 2c, is the number of contiguous pairs inside the window, and N (= r × c) is the total number of pixels. If the pixels inside the window are randomly distributed, the variable I can be approximated using a normal distribution (when N is large enough) with mean and variance given by

and

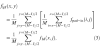where

, S₁ = 2S₀, and S₂ = 8(8rc – 7r – 7c + 4). For a smooth region, the gray levels of adjacent pixels are more or less the same and the calculated I is larger. Note that I = 1 when all pixels have the same gray levels. The standardized normal statistic

is the smoothness measurement around a pixel. Thus, the Moran I test can be used to detect the quality change in a compressed image caused by the smoothing effects.

z-HISTOGRAM AND PEAK RATIO

The variation around a pixel is measured by calculating the Moran z value for a 9 × 9 window centered on that pixel. The window size is selected such that the result is statistically meaningful, and yet it is small enough to reflect local variation. The histogram of the z values for all pixels in the image can be used to represent the quality of the image. Figure 1 shows the z-histogram of a typical magnetic resonance imaging (MRI) head image. There are two peaks in the histogram. The lower z peak corresponds to the areas outside the skull that are predominantly noise. The high z peaks at about z = 9 (equivalent to I = 0.8) representing most pixels of the image are uniformly distributed structures. In general, the quality evaluation of an image is performed on regions of interest and, in this case, inside the skull. Thus, we use only pixels inside the skull for head image studies. Figure 2 shows the z-histogram of the same MRI image for various degrees of compression. As the compression ratio increases, the image becomes smoother and the histogram curve shifts toward higher z regions and its peak value increases correspondingly. The peak ratio is defined as the ratio of peak values of the z-histogram between the compressed and original images. The peak ratio increases with compression ratio and can serve as an indication of image degradation in lossy compression. The peak ratio is selected over other parameters like histogram mean (

) for its higher sensitivity to the change of compression ratio.

Figure 1.

The z-histogram of a typical MRI head image.

Figure 2.

The z-histogram of the same MRI image shown in Figure 1 (for pixels inside the skull only) at various degrees of compression. The peak ratio is defined as the ratio of peak height between the compressed and original images.

IMAGE DATA

Numerous images for each digital modality (body CT, head MRI T1 weighted (T1W), head MRI T2W, and chest CR) were randomly selected from different patients for this study. All images were compressed using wavelet compression software “Apollo” (Pegasus Imaging Corporation, Tampa, FL). The Pegasus wavelet encoding is similar to that used in the JPEG 2000 standard. All measurements were performed for images with compression ratios of 59, 49, 35, 30, 25, 23, 20, 18, 16, 14, 12, 10, 8, 7, and 5.

RESULTS

A CT image was used first to test the edge blurring and denoising effect on the peak ratio. The image was filtered using an average filter to simulate the edge blurring effects. The filter window sizes can be adjusted to produce images with various degrees of edge blurring. The peak ratios of the z histogram and NMSE between each filtered images and original image were calculated. Figure 3 plots the peak ratio and NMSE as a function of the window size. The peak ratio was demonstrated to increase with the increasing degree of edge blurring. This is highly consistent with NMSE.

Figure 3.

The peak ratio (○) and NMSE (×) versus window size of the average filter to simulate the effect of edge blurring.

Because noise occupies the least significant bit planes, we can simulate the denoising effect by nullifying those bits. When a greater number of least significant bit planes is zeroed, more noise is smoothed out. We gradually increase the number of bit planes to be nullified and perform the Moran test on these denoised images. Figure 4 shows the peak ratios as a function of number of bit planes nullified. The peak ratio decreases as the number of bits increases; ie, the peak ratio decreases with the degree of denoising. Note that the change in peak ratio in denoising the bit planes is much smaller than the blurring effects from the averaging filter. The NMSEs of the denoising images are also plotted in Figure 4. The NMSE increases with the number of bit planes nullified. The NMSE only calculates the sum of errors between corresponding pixels. It does not provide any information regarding the type of loss that causes the quality deterioration. The Moran peak ratio shows different trends for the effects of smoothing or denoising.

Figure 4.

The peak ratio (○) and NMSE (×) versus number of bits removed to simulate the effect of denoising.

Figures 5, 6, 7, 8 show the peak ratio for the CT, MRT1, MRT2, and CR images, respectively, as a function of the compression ratio. Note that at a low compression ratio, all of the peak ratio curves are nearly constant and they actually appear hollow for all images except CT. It has been reported^17,18 that radiologists prefer images processed with low levels of compression. This preference can be attributed to the “denoising” effect of the compression algorithm at low levels. At high compression ratios, the image qualities deteriorate mainly because of the blurring and the curves ascend linearly with the compression ratio.

Figure 5.

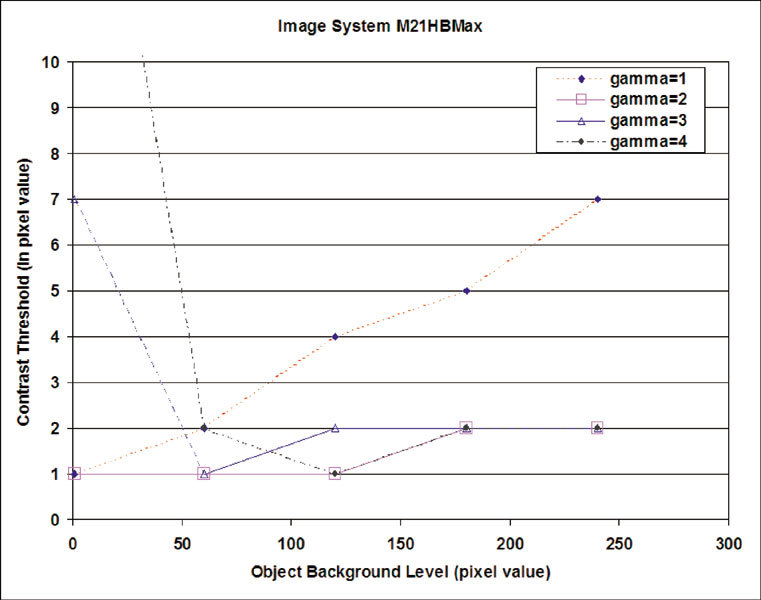
The peak ratio of the body CT images as a function of compression ratio.

Figure 6.

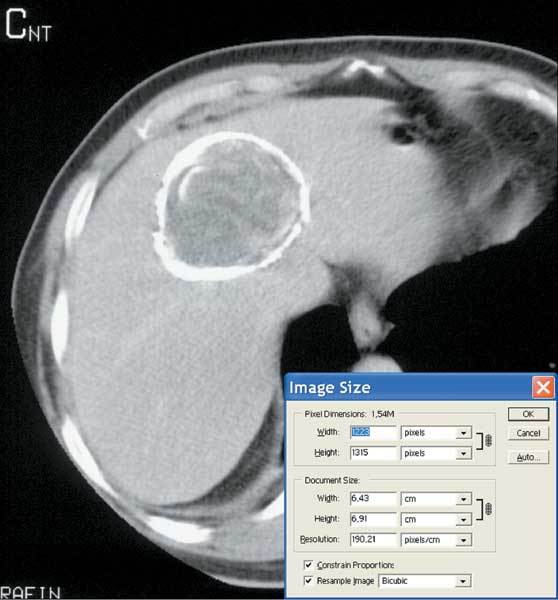
The peak ratio of the head MRI T1W images (for pixels inside the skull only) as a function of compression ratio.

Figure 7.

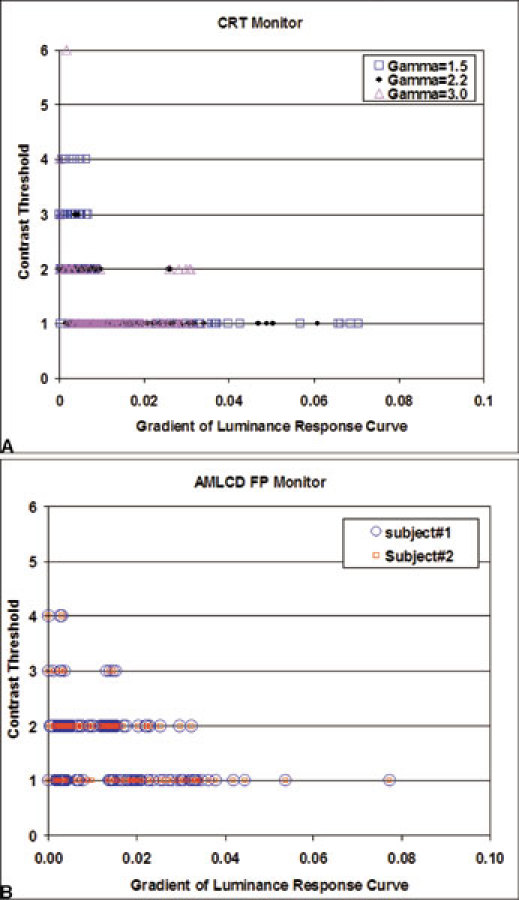
The peak ratio of the head MRI T2W images (for pixels inside the skull only) as a function of compression ratio.

Figure 8.

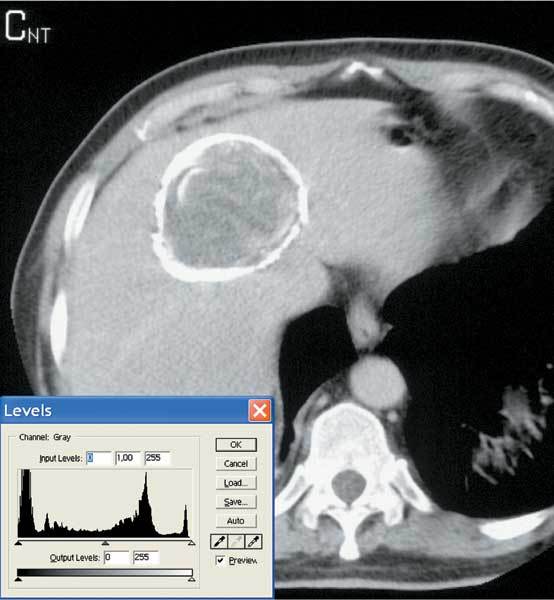
The peak ratio of the chest CR images as a function of compression ratio.

DISCUSSION AND CONCLUSIONS

For lossy compression in medical imaging, it is natural to question whether any clinically important information has been compromised. To solve this, a reliable way to quantify the quality degradation in compression is necessary. The image compression affects image quality through edge blurring and denoising. Both effects cause changes in the image smoothness. The Moran test is a measurement of the spatial correlation and is a good indication of quality smoothness. We used the peak Moran test ratio to measure the quality changes resulting from compression. The results were in good agreement with the ROC study. It is concluded that the Moran I test is a powerful tool for measuring quality degradation in image compression.

Note that the shapes of the peak ratio curves from different modalities are similar. This means that the compression effects on images are the same for all modalities. However, the degree of blurring caused by compression is dependent on the contrast of the original image; the blurring effects are less obvious for images with higher contrast. The CR images are formed using x-ray projection. X-ray contrasts are smaller than tomographic images. The CT body contrast is not as good as that for head MRI. As a result, the CR images have the highest slopes, followed by CT and MRI.

For CR chest images, an increasing number of reports have suggested that compression levels as high as 20 can be used before significantly compromising the diagnostic efficacy of the image.² The question is, what level of compression is acceptable^{19,20,21,22,23} or, what is the optimal compression ratio for an image? The optimal compression is useful for teleradiology or PACS (picture archiving and communication systems) applications. The optimal compression achieves the maximum compression ratio without downgrading the image quality; ie, the quality degradation caused by compression is less than or equal to the inherent noise in the original image. From Figures 5, 6, 7, 8, each modality is so coherent that the peak ratio curves go downward and then upward in response to the compression ratio, indicating the existence of optimal compression. The beginning point of the peak ratio curve is a good approximation of the inherent noise for each image modality. By drawing a horizontal line from that point, the optimal compression ratio can be estimated from the intersection of the curve with the line. From this, we can reason that the optimal compression ratios are around 15 for most modalities. This result is close to the previous results of a study.²