Alternate states of proteins revealed by detailed energy landscape mapping

Abstract

What conformations do protein molecules populate in solution? Crystallography provides a high-resolution description of protein structure in the crystal environment, while NMR describes structure in solution but using less data. NMR structures display more variability, but is this because crystal contacts are absent or because of fewer data constraints? Here we report unexpected insight into this issue obtained through analysis of detailed protein energy landscapes generated by large-scale, native-enhanced sampling of conformational space with Rosetta@HOME for 111 protein domains. In the absence of tightly associating binding partners or ligands, the lowest-energy Rosetta models were nearly all <2.5Å C_αRMSD from the experimental structure; this result demonstrates that structure prediction accuracy for globular proteins is limited mainly by the ability to sample close to the native structure. While the lowest-energy models are similar to deposited structures, they are not identical; the largest deviations are most often in regions involved in ligand, quaternary, or crystal contacts. For ligand binding proteins, the low energy models may resemble the apo structures, and for oligomeric proteins, the monomeric assembly intermediates. The deviations between the low energy models and crystal structures largely disappear when landscapes are computed in the context of the crystal lattice or multimer. The computed low-energy ensembles, with tight crystal-structure-like packing in the core, but more NMR-structure-like variability in loops, may in some cases resemble the native state ensembles of proteins better than individual crystal or NMR structures, and can suggest experimentally testable hypotheses relating alternative states and structural heterogeneity to function.

Introduction

The Rosetta molecular modelling methodology has been used to predict the structures of small globular proteins (1–3) and design new proteins (4–6). For both structure prediction and design Rosetta carries out large scale stochastic sampling guided by a physically realistic all-atom energy function. In structure prediction Rosetta seeks the lowest energy conformation for a given sequence, in design, the lowest energy sequence for a given conformation. While in many cases successful, often Rosetta structure predictions are not correct and Rosetta designs do not have the desired structure or function. It is unclear whether such failures are due to inaccuracies in the energy function or lack of sufficient sampling.

With the original goal of large-scale testing of the Rosetta all atom energy function, we used native-enhanced sampling to generate detailed maps of the energy landscapes of 111 protein domains. Hundreds of thousands of independent Monte Carlo trajectories were carried out for each protein using the Rosetta@HOME distributed computing project (7). Each trajectory consists of an initial low-resolution search followed by detailed all-atom refinement (1). To enhance sampling near the native structure, which is generally sampled quite rarely, in a subset of the trajectories bias towards the native structure was included in the move set used in the initial search and in the selection of coarse-grained models for all-atom refinement (see Methods for a detailed description of the sampling approach). Each trajectory ends up in a local energy minimum, and the hundreds of thousands of local minima together provide a detailed map of the energy landscape.

Most of the energy landscapes had steep "funnels" down to low-energy minima close to the experimentally determined structure (see below), but in some cases the lowest energy structures had significant local deviations from the experimental structure. There is no well-established protocol for determining whether low-energy computed models may have features more representative of proteins in solution than deposited experimentally determined structures since the gold standard for structure prediction is, correctly, the structures in the PDB. However, several of us have extensive experience both with structure comparison and with analysis and correction of errors in experimentally determined protein structures, on the basis of which we can attempt to assess whether differences between model and target structures are due to shortcomings in the former or the latter. Guided by this experience, the lowest-energy models were compared to the deposited coordinates for each protein and to other experimental structures of the same protein, to assess if the differences represented shortcomings of the energy function or unmodelled aspects such as ligands, or whether they could represent valid alternative structures.

Results

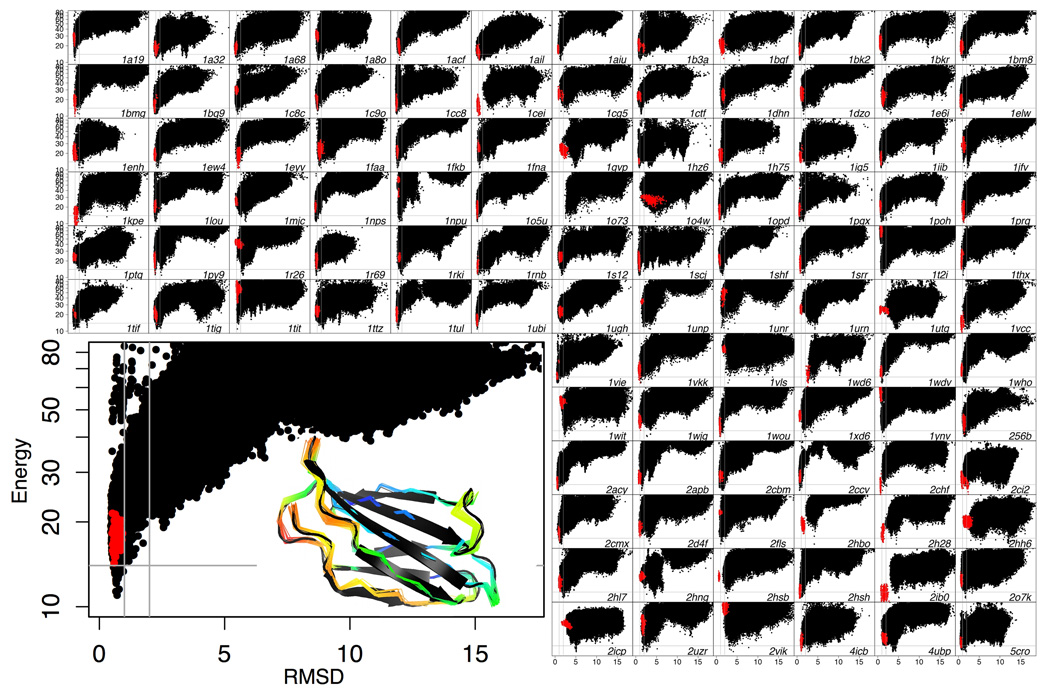
Projections of the energy landscape produced in the large-scale Rosetta@HOME calculations onto the Rosetta-energy vs. C_αRMSD (C_αroot mean square deviation) axes are shown in Figure 1 for each of the 111 proteins and, in more detail, S1. A striking feature of these maps is that the native structure almost always lies in a deep energy minimum: protein conformations with C_αRMSD to the deposited structure of greater than 4Å almost always have higher energies. For 41% of the proteins examined the lowest-energy model is within 1.2Å C_αRMSD from the deposited structure and for 72% it is within 2.5Å C_αRMSD. Of all the residues simulated, 50% show C_α–C_αdeviations of less than 0.3Å and 90% show deviations of less than 0.8Å from the corresponding native residue after global superposition of the lowest-energy model onto the target structure (28% of the low energy models can still be above 2.5Å C_αRMSD because a small number of significant local C_α-C_αdeviations can have a large effect on global C_αRMSD).

Fig. 1.

Computed energy landscapes. Each panel represents a different protein. The y-axis is the Rosetta all-atom energy and the x-axis the C_αRMSD from the crystal structure; red dots are models relaxed from the crystal structure. The inset shows the energy landscape for 1TEN (a fibronectin type III domain) in more detail and a superposition of the models within 4 energy units of the lowest-energy model (indicated by the horizontal gray line in the plot) on the crystal structure (black). Colors indicate amount of variation in the Rosetta ensemble (blue, low; red, high); variation is concentrated towards the loops. The vertical gray bars indicate the 1Å and 2Å points. Note that the y-axis has been compressed at higher values to fit in the high-energy states without losing detail at the lower (more interesting) energies. For 41% of the proteins examined the lowest-energy structure is within 1.2Å C_αRMSD from the deposited crystal structure (as for 1TEN), and for 70% it is within 2.5Å C_αRMSD (see also Fig. 2b).

This is a non-trivial observation given that there has been considerable discussion of whether the energy functions developed for macromolecular modelling, which involve numerous simplifications and approximations, are accurate enough for consistent high-resolution protein structure prediction. The energy landscapes in Figure 1 taken collectively imply that current macromolecular energy functions are sufficiently accurate for good structure prediction, but the available computing power and sampling algorithms are still insufficient to sample reliably within 1–2Å C_αRMSD of the native structure, as needed for a model to be recognized as native-like based on its very low energy. This is confirmed by the fact that, when native and homologous information is left out of the sampling procedure, the lowest energy structures are only within 2.5Å C_αRMSD for 7% of cases. Further, the average energy of the lowest energy structure found when sampling without native or homologous fragments is 12.5 energy units higher than when including native information to enhance native sampling.

Closer inspection of the 111 energy landscapes revealed that while the computed global minimum is almost always close to the native structure, it is rarely identical. The investigation of these quite unanticipated differences is the main focus of this paper. Superpositions of the lowest-energy models found in the landscape explorations onto the experimentally determined structure are shown in Figure S1. The low-energy models are often very close to the experimentally determined structures in the core (defined as <10Ų solvent accessible surface area (SASA) per residue from DSSP (8)), where the average C_α-C_αdeviation is <0.9Å. However, exposed loop regions (>120 Ų SASA) generally vary more, with an average C_α-C_αdeviation of >2.3Å, and in some cases the low-energy models converge on loop structures quite distinct from the experimental structure. In a small number of cases the deviations also involve significant movement of peripheral secondary structure elements. These discrepancies could reflect inaccuracies in the Rosetta energy function, which cause the computed energy minimum to not be coincident with the actual free energy minimum. Such cases (see Supplement) provide invaluable information for future force field development. As described in the following paragraphs, however, a significant subset of the discrepancies do not appear to be due to energy function errors.

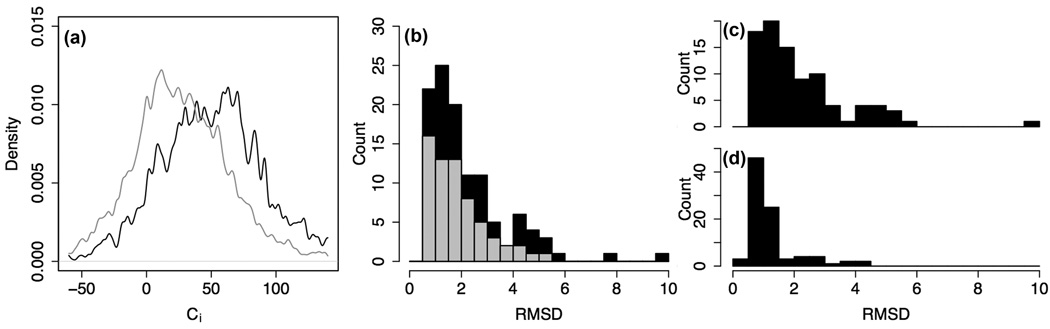
Reconstruction of the crystal lattice showed that for many proteins the largest discrepancies were at or near crystal contact sites, or in quaternary contacts in the case of oligomeric proteins. To quantify this effect, we used as a measure of the influence of intermolecular or crystal interactions on the conformation of a residue the difference C_i = N_M - N_L, where N_M is the number of contacts made by the residue within the folded monomer and N_L is the number of contacts made with other monomers through lattice or oligomeric interactions. The structural deviations are more often found at sites where intermolecular interactions contribute a dominant share of the contacts (Figure 2a).

Fig. 2.

Origins of structural deviations. a) Histogram of contact number C_i for residues with C_a-C_a displacement from the crystal structure of more than 0.75Å (gray) and less than 0.75Å (black). The contact number is the number of intra-molecular interactions made by a residue minus the number of intermolecular contacts made by that residue in the crystal. A negative C_i indicates that the residue is stabilized primarily by crystal contacts or interactions with a ligand. Deviations in the calculated global minima are generally larger when the number of contacts across the crystal or oligomer interface exceeds the number of intramolecular contacts of a residue. However, note that in many cases the effects of missing crystal or quaternary contacts propagate quite far away from the actual site of contact, making it difficult to quantify this effect accurately. b) Histogram of the C_aRMSD from the native structure of the lowest-energy structure for each protein simulated. Black bars: proteins with strongly interacting binding partners; gray: all others. 12 out of 16 proteins with deviations above 4Å C_aRMSD are oligomeric in solution. c) and d) C_aRMSD distributions for 90 proteins simulated in isolation and (c) in the crystal and/or oligomeric environment (d), where most large deviations disappear.

The correlation between structural deviations and lattice interactions suggests the hypothesis that the deviations between Rosetta minima and crystal structure are in many cases not due to Rosetta energy function artifacts, but rather to crystal or multimer packing interactions. To test this hypothesis, we repeated the energy landscape mapping using the same large-scale sampling approach as earlier, but in the context of the native crystal lattice and oligomeric interactions. To do so, we superimposed the independently folded, low-resolution models generated by Rosetta onto the target crystal structure. We then used the crystallographic rigid-body transforms to build a repeating lattice out of the model and carried out all-atom refinement. The relationship of the model to the lattice was allowed to shift slightly during refinement (details in Methods). If the deviations were due to intermolecular interactions not modelled in the original calculations on isolated monomers, then inclusion of these interactions should considerably reduce the discrepancies. Indeed, as shown statistically in Figure 2c,d and for four examples in Figure 3, in many cases the calculations carried out in the presence of crystal contacts converge on minima considerably closer to the experimentally determined structures than the original isolated monomer calculations.

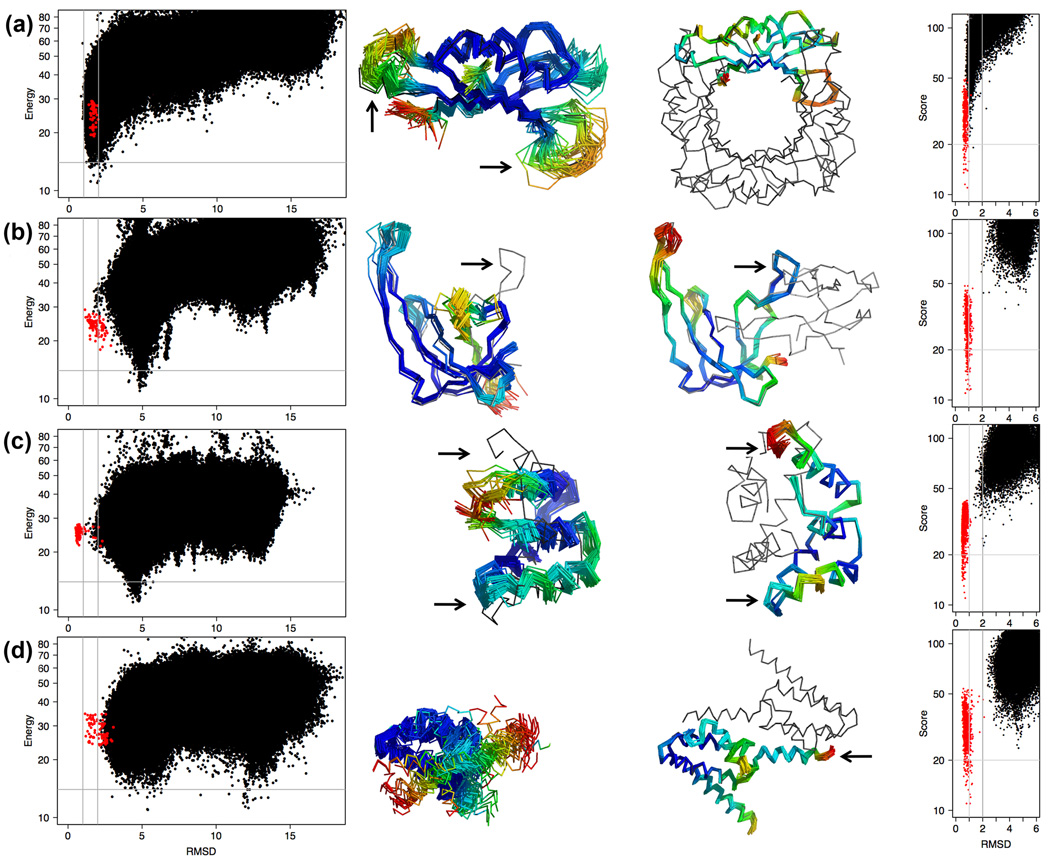
Fig. 3.

Energy landscapes of monomeric vs. oligomeric states of proteins. The left-hand side shows a landscape plot and lowest-energy ensemble for each isolated protein. The right-hand side shows the same proteins simulated in the crystal environment, including their oligomeric binding partners. Colors indicate amount of variation in the Rosetta ensemble (blue, low; red, high), highest at loops and ends. In all but the first case, the lowest-energy models deviate significantly from the deposited coordinates locally, near the oligomeric binding sites. a) 1DHN, dihydroneopterin aldolase. Two long loops (see arrows) show similar conformations but much more variability when the rest of the tetrameric ring is not simulated. b) 1GVP, gene V protein from Ff phage. In isolated simulations the hairpin at top right (see arrow) collapses onto the body of the protein, while in the dimer it makes extensive contacts across the interface. Note that another long, protruding hairpin does not collapse. c) 1UTG, uteroglobin. Pairs of interface helices (see arrows) spread apart to form the dimer, rather than the commoner movement of a single chain-terminal helix (as in part d). d) 2HH6, BH3980 from Bacillus halodurans. The C-terminal helix (see arrow) populates two separate and variable positions (the two red ends) in the monomer, one of which matches the experimentally observed position across the dimer interface.

In many cases the missing crystal contacts represent the biologically relevant quaternary interactions of proteins with tightly associated binding partners and ligands (Figure 2b–d, 3, and 4) and thus the minima identified in the isolated monomer simulations are likely to be more representative of apo structures or oligomer assembly intermediates, prior to complex formation. This is clearly the case for the RNA-binding protein in Figure 4. Calculations such as presented in Figure 3 provide potential insight into monomeric forms of oligomeric proteins (the presumed state before oligomerization), which is difficult to obtain experimentally. Our results suggest that at least for a fraction of proteins the binding interface is not fully pre-formed and the conformation of the protein depends considerably on the presence of the binding partner. This implies that accurate prediction of the biologically relevant structures of even relatively simple oligomeric or strongly ligand-dependent proteins will require simultaneous modelling of the interacting partners(9) which poses a significant challenge for current protein structure prediction or modelling methods(10).

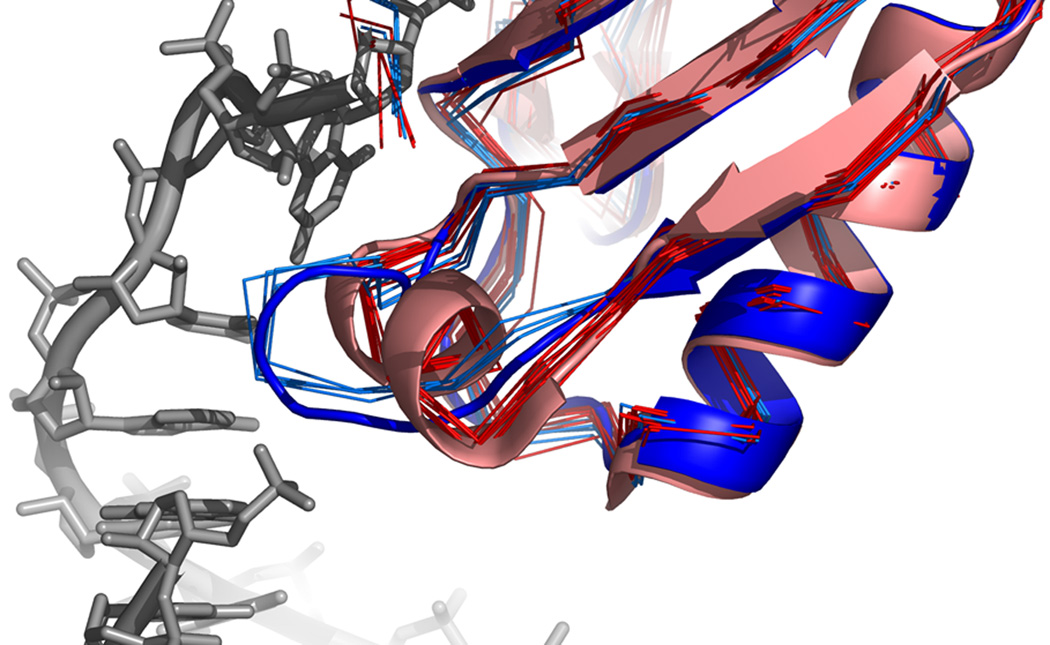
Fig 4.

Influence of binding partner. The simulation of 1URN identifies two pronounced minima in the main RNA binding loop 46–52. One (thin blue backbones) matches the conformation found in 1URN (thick blue backbone) contacting the RNA, while the other (thin red backbones) forms a short helix matching the unbound conformation found in 1NU4 chain A (thick red backbone), a crystal structure of the apo form of this protein. Rosetta ranks these two minima (in the absence of RNA) equal in energy, suggesting that both the bound and apo conformations could be sampled in solution. This is further supported by the fact that chain B in 1NU4 is in a conformation close to that of 1URN.

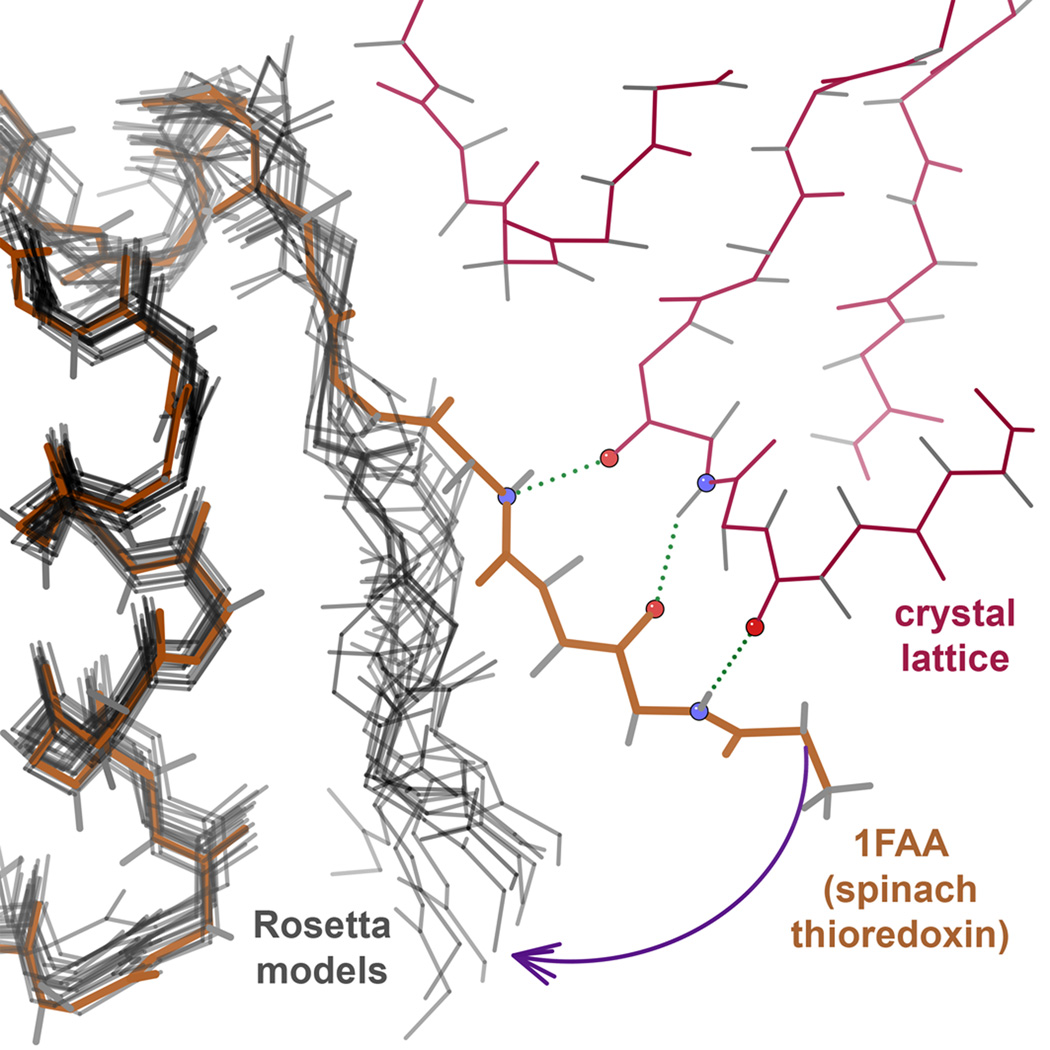
In other cases, however, the crystal contacts are probably not biologically relevant. One example is the N-terminus of 1FAA (Figure 5), which reaches across to form a β-sheet interaction with a neighboring molecule (not a biological multimer); in the Rosetta ensemble the N-terminus is quite variable but hugs the surface of its own molecule. Thus, we considered the possibility that the minima found in the original landscape explorations may in some cases represent states actually accessible to the real protein in solution, which were not populated in the crystallized form. The differences between the computed minima and the crystal structures fall mainly into two categories.

Fig. 5.

Effect of crystal packing interactions. In a crystal structure of a monomeric spinach thioredoxin (1FAA) (brown), the N-terminus engages in significant β-sheet-like contacts to the crystal lattice neighbor (pink). In the isolated monomer simulation, the “pull” from the crystal contact is absent, and Rosetta’s low energy models (gray) adopt a wide range of conformations that all collapse toward the body of the protein.

In the first category are cases where the computed models exhibit considerably more variation than indicated by the crystal structure. Often the computed ensemble includes the crystal conformation (Figure 6a–c and S2), but this is not always the case (Figure 5). Here the crystal environment may be favoring a particular conformation over others, while in solution more conformations are isoenergetic and accessible.

Fig. 6.

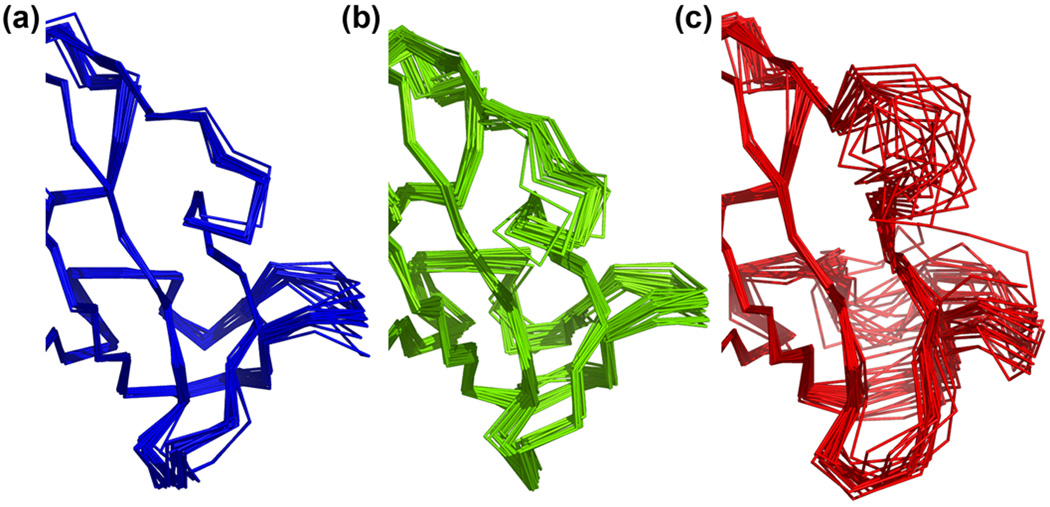
Comparison of X-ray, computed, and NMR ensembles (a–c) Simulation of immunophilin FK506 binding protein (1FKB) yields a funnel-like landscape with a well-converged minimum at ~1Å from the deposited coordinates. Examination of the lowest-energy models revealed a core perfectly superimposable (including the sidechains) but with subtle differences in the loops. a) Superposition of 21 different crystal structures (13). b) Rosetta ensemble of lowest-energy models. c) NMR ensemble from 1FKR. The structural flexibility of the Rosetta ensemble (green), particularly in the loops, exceeds that implied by the B-factors of any given crystal structure, and better matches the ensemble of multiple crystal structures (blue). The NMR ensemble (red) displays even more variability, with complete disorder around a somewhat different conformation in the upper loop.

In the second category the computed models converge on a conformation clearly different from the crystal structure, with the native conformation higher in Rosetta energy. In a number of cases, structures solved in a different crystal lattice (e.g., Figure 7) or by NMR (Figure S2) were found to match or support the conformations preferred by Rosetta. In this case the crystal environment presumably stabilizes an energy minimum less favorable in solution (such as shown for the loop in Figure 7).

Fig. 7.

Illustration of the influence of crystal packing interactions on energy landscapes for an external loop. a) The isolated monomer simulation of human beta2-microglobulin (2D4F) identifies a considerably deeper minimum at ~3–4Å C_aRMSD from the deposited structure. (Note that the core 92 of 109 residues still superimpose to 1.3Å C_aRMSD.) The inset shows the lowest-energy models (green) superimposed on 2D4F (red) and an alternative crystal structure in a different crystal environment (1A9B, blue). Note the loop (residues 12–21), which differs greatly from 2D4F but makes extensive interactions with the main body of the protein in the Rosetta models, in 1A9B, and in NMR structure 1JNJ (not shown). b) Simulation in the crystal environment (using the 2D4F lattice parameters) shifts the deep energy minimum such that the conformation in the deposited crystal structure is now the most favorable, with loop 12–21 making extensive crystal contacts with neighboring unit cells (gray).

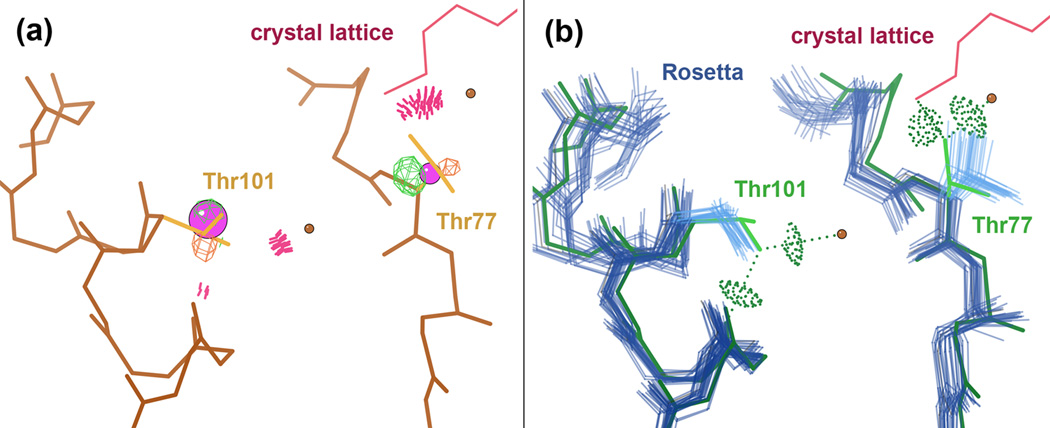
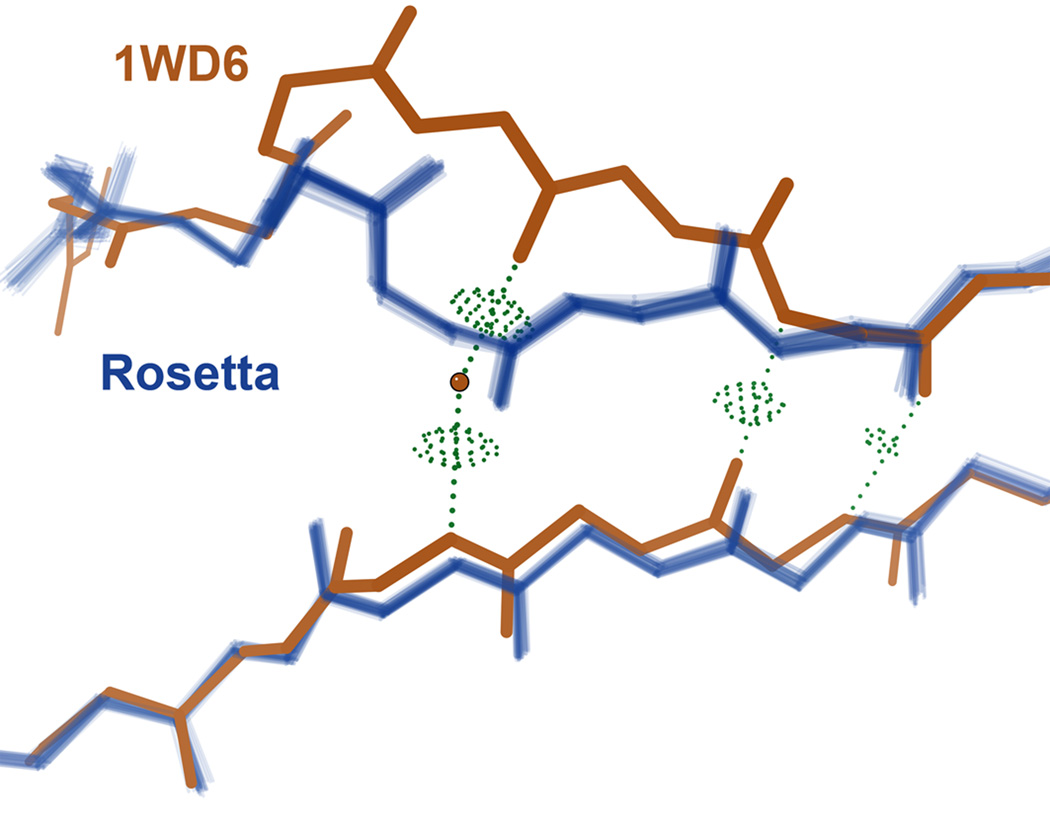
We also examined how well the low-energy models recapitulate sidechain rotamers (see Methods). The overall accuracy is 56%, but this ranges from 29% for highly exposed to 76% for highly buried residues (<10 to >120 Ų SASA). Over a third (34%) of the over 100 individual sidechain deviations we examined in detail seem related to crystal contacts, and in nearly half (48%) of the cases, the Rosetta version is supported by independently solved structures, electron density, and/or correction of fitting errors in the deposited structure (see Methods). For example, two Thr sidechains in 1BKR were deposited as rotamer outliers with resulting steric clashes, but Rosetta’s alternatives adopt the correct 180° flipped alternatives, which are corroborated by an independently re-refined version of the structure (Figure 8). Many of the remaining deviations provide insight into deficiencies of the current Rosetta force field, e.g. the lack of an explicit solvent model, which precludes correct placement of one end of a βstrand in 1WD6 (Figure 9) and of a Gln side chain in 1VKK (as illustrated in the interactive Supplement).

Fig. 8.

Correction of local errors in a deposited crystal structure. a) MolProbity detects errors by several criteria for Thr77 and Thr101 in a crystal structure of calponin homology domain (1BKR): rotamer outliers, Cβ deviations (pink balls), and steric clashes (pink spikes) to surrounding waters (brown balls) and protein atoms (to a Lys sidechain of another molecule in the crystal in the case of Thr77). Furthermore, the Cβ atoms for both Thr sidechains fall nearer to negative 5σ Fo–Fc difference density peaks (orange mesh) than to positive peaks (green mesh), indicating a mismatch to the experimental data. b) The majority of Rosetta’s low energy models (blue) flip both sidechains by 180° (30) to eliminate clashes, establish hydrogen bonds with surrounding atoms, and fortuitously better fit the difference density. A structure independently re-refined against the original diffraction data by the Richardson Lab (green) corroborates this flip. Note that Rosetta’s backbone is somewhat mobile, especially for Thr77, perhaps because stabilizing effects from the explicit water molecules and the crystal contact are not modeled. Nevertheless, in this case at least, Rosetta’s energy function is sufficient to detect the proper sidechain conformations.

Fig. 9.

Example of an erroneous computed alternate conformation. For the protein JW1657 from E. coli (1WD6, brown), an explicit water molecule (brown ball) peels apart the two strands of a parallel β sheet while maintaining excellent hydrogen bonds (green dots) to maintain the protein’s structural integrity. Rosetta cannot consider the possibility of an explicit water molecule because it employs an implicit solvent model; therefore the computed low energy models revert to overly idealized (and in this case incorrect) β structure. The low B-factor (13.8) of the water suggests it is well ordered and precisely placed, and chain B of 1WD6 as well as other homologs confirm its position.

Discussion

Often the lowest energy structures described in this paper are in near-perfect agreement with the deposited structures (e.g., 1TEN in Figure 1), and nearly all cases show only localized differences. This result, over a broad set of 111 different protein domains, suggests that the performance of Rosetta in structure prediction is currently more limited by conformational sampling than by the accuracy of the energy function. (We cannot exclude the possibility that more thorough sampling could reveal lower energy minima further from the native structure.)

The view of protein structures provided by these low-energy minima or ensembles is intermediate between those provided by X-ray crystallography and NMR spectroscopy. The cores are very well defined with closely packed and well relaxed backbone and side-chain conformations as in high-resolution crystal structures, while the loops can exhibit considerable variability. NMR and X-ray crystallography both show some local regions to be mobile, but crystal contacts often artificially limit some such regions to a single conformation (11–13). The set of mobile regions evident in the low-energy Rosetta ensembles in many cases matches the mobile regions in NMR ensembles (see Figure 4a–c, and many examples in the Supplement).

There are a number of cases in which the lowest energy structures sampled by Rosetta are more than 2Å RMSD from the native structure and clearly lower in energy than more native-like structures. In some cases the discrepancy is probably due to defects in the energy function, such as lack of explicit solvent. Interestingly, however, detailed comparative analysis in many cases found evidence that the differing Rosetta structures represent valid alternatives such as apo or monomeric forms of the protein, correction of minor local errors, conformations represented in structures with different crystal contacts, or even a different step in a catalytic cycle (Figure 10).

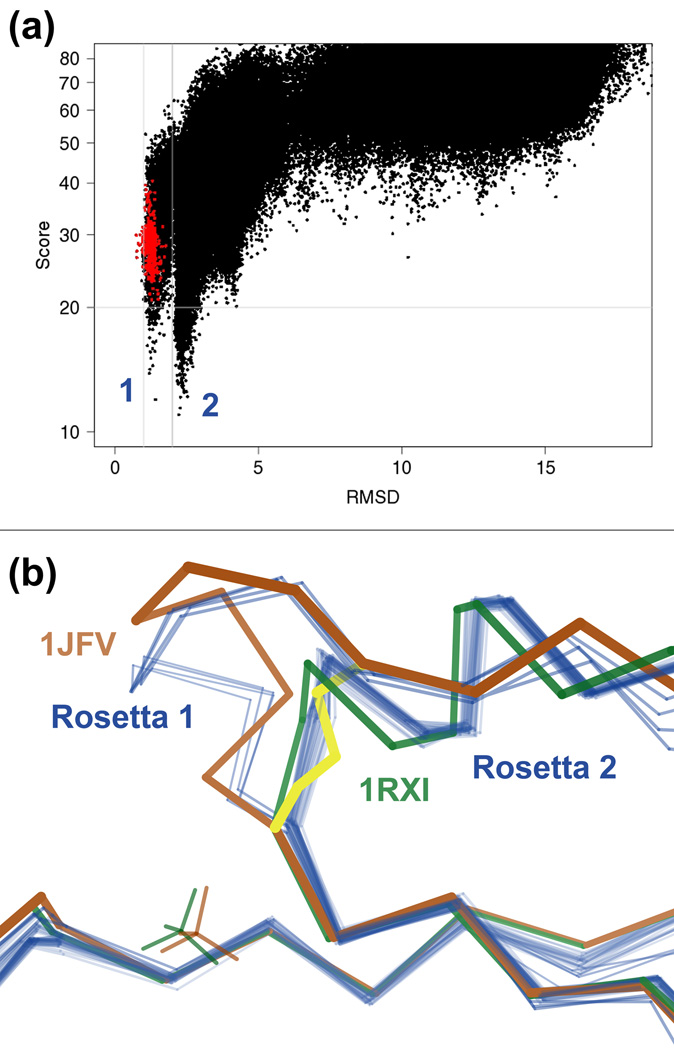
Fig. 10.

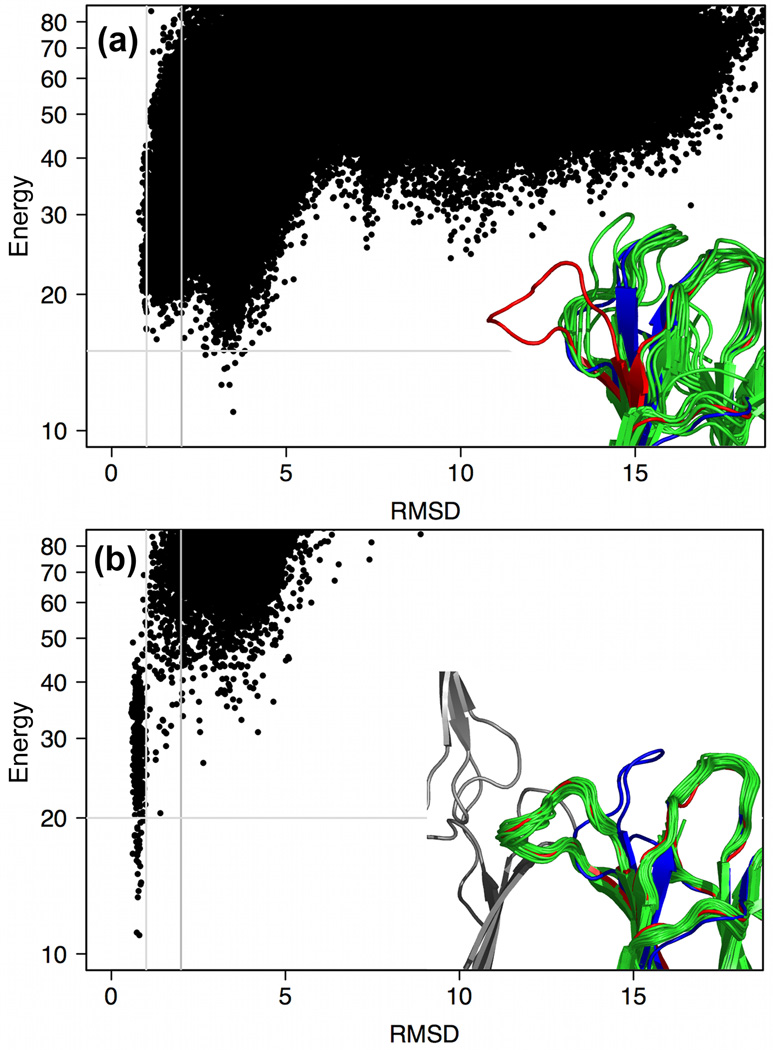
Discovery of a functionally relevant state in an active site. a) Score vs. C_αRMSD plot for isolated monomer simulation of arsenate reductase (1JFV). The y-axis is the Rosetta all-atom energy and the x-axis the C_αRMSD from the crystal structure; red dots are models relaxed from the crystal structure. Rosetta identifies two distinct low-energy funnels, suggesting the presence of two nearly isoenergetic yet distinct states in the real protein. b) Arsenate reductase undergoes a Cys10-Cys82-Cys89 disulfide cascade as part of its reaction cycle. The oxidized crystal structure 1JFV (brown) has a C10S mutation to capture the end point of this cascade, SS 82–89 (yellow). Some of the low energy models from the isolated monomer simulation (blue) match the disulfide-flanked loop in the oxidized crystal structure (left funnel in part a), but most adopt a disulfide-free miniature helix instead (right funnel in part a). A reduced form of the protein (1JF8, not shown) and a double C10S/C82S mutant (1RXI, green) corroborate the computed alternate conformation as a valid stage in the reaction cycle. Perchlorate ions appear in both 1JFV and 1RXI (brown and green tetrahedra) and thus appear not to strongly bias the loop conformation. The fact that the alternate energy minimum persists in the crystal lattice simulation argues against the possibility that crystal contacts to the loop in 1JFV significantly influence its energy relative to that of the alternate helix.

These cases of confirmed alternatives, along with the generally high quality of target recapitulation, suggest two new roles for Rosetta, each with native-enhanced sampling of a different sort. The first is to aid in the process of structure determination by providing high-quality ensembles for local regions of NMR or crystal structures where there is essentially no experimental data (few or no NMR restraints, or no electron density above noise level) or where other measures (NMR relaxation rates, peak widths, etc., or large crystallographic B-factors or targeted alternate searches (14)) show there should be more than one conformation. Rosetta has already been used to determine (15) or to improve (16) entire NMR structures, but the further use suggested here would concentrate on individual mobile loops. NMR inadequately samples these loops, whereas new ensemble methods in crystallography (17–18) result in limited variability because they refine each model separately against the data rather than refining the ensemble collectively.

The second new role is that starting from a single experimental structure of a relatively small protein, well-converged non-native minima obtained by the process used here could provide very plausible hypotheses for alternative conformations or local variability accessible under other conditions difficult to achieve, or not yet achieved, experimentally - such as monomeric, outside a crystal lattice, and with or without ligands or other binding partners. Such a methodology would complement other computational approaches. Elastic-network and similar calculations have the advantage that they can deal with large movements and with large structures (19), but the resulting alternative models are only approximate. Molecular dynamics (MD) simulations have often been used to predict such alternatives and are especially effective when combined with certain types of NMR data (20–25), but the difficulty of extensive sampling in MD (due to the femtosecond step size required for numerical stability) has precluded the generation of dense landscapes for a large set of medium-sized protein domains to validate commonly used molecular mechanics energy models (26).

The results described here, as well as recent NMR studies (21–23), further support a plastic view of protein structure in which certain regions are able to access a multitude of nearly isoenergetic minima and thus are very sensitive to environmental effects both in vitro such as crystallization and in vivo such as ligand binding. After further validation by comparison to experiments, both the global minima and the nearby excited states identified in native-enhanced Rosetta calculations should provide a wealth of information on structures in solution, fluctuations and allosteric states, and protein function more generally.

Methods

We examined a set of 111 small, globular proteins chosen to include a variety of structural features. Of the structures examined, 17 specifically bind a ligand, 60 are oligomeric, 37 contain at least one disulfide bond, and 3 are minimized average NMR structures. The proteins range in size from 50 to 150 residues. For each protein we ran 3 sampling runs using the normal Rosetta fragment insertion approach (27). In the first set we excluded fragments from homologous structures in the PDB, in the second set we used all the fragments available (a library of 400 fragments for each residue position) but not including fragments from identical sequences, and in the third set we added a single native fragment to the library for each residue position. Thus the three sets were slightly biased to explore the non-native region, the near native region, and the very near native region respectively. From set 1 and 2 we chose 4000 low-energy models preserving the sampling density found at each C_αRMSD value, thus representing largely non-native states due to the vastness of conformation space. From sets 2 and 3 we chose 4000 further low-energy models, this time spread evenly across the C_αRMSD coordinate, thus increasing the relative numbers of near native conformations. Native fragments were included in set 3 in order to explore the near-native space only, and thus models were only chosen below 6Å C_αRMSD. As a result, in most cases this initial step generated low-resolution decoys spanning a broad range of C_αRMSD (~0–20Å).

For each of these initial low-resolution structures we initiated about 50 all-atom sampling (relax) runs, each of which explored the local conformational space around the initial low-resolution model ending in a deep local minimum. We used a new and more powerful local all-atom search algorithm (FastRelax) than previously used with Rosetta. It consists of several rounds of extensive all-atom repacking and energy minimization while slowly ramping up the weight of the repulsive part of the Van der Waals energy function component from 2% to 100% of its final value. This allows the sidechains to slowly adopt their packed conformations and resolve clashes without the protein unfolding due to overly large repulsive forces. The ramping is repeated 18 times and the lowest-energy structure encountered during the trajectory is kept as the final relaxed structure. The repacking step (28) consists of a non-deterministic Monte Carlo Simulated Annealing run which stochastically searches combinations of side-chain conformations chosen from a library of possible rotamers (29).

We found this algorithm a highly effective way to locally minimize the energy of a structure and it appears to be more efficient than Monte Carlo with Minimization with small perturbations. Because the structure changes up to 3Å C_αRMSD from its starting point during this process and the result is stochastically dependent on the choice of sidechain rotamers inserted, we applied this algorithm ~50 times to each starting structure, resulting in ~50 distinct structures. These structures essentially explore the local conformational space around the starting structure with a radius of 2–3Å C_aRMSD.

In total, for each protein we generated about ~600,000 relaxed all-atom structures; a grand total of 80 million different minima were processed. In addition we also subjected the original crystal coordinates to the same all-atom relaxation protocol, to ensure the energy minimum of the deposited PDB structure was included in the landscape. In most of the proteins studied, however, a fraction of the structures that were refolded from fragments appear to have converged on the same energy minimum as the relaxed natives, suggesting that our sampling strategy is indeed efficient, at least in the general vicinity of the native state.

In order to ensure that the recapitulation of the native state during refolding was not simply an artifact of including native-like fragments, we also carried out a control run in which random backbone perturbations (“jitters”) were applied to the structures before the all-atom relaxation procedure. The average phi/psi deviations were ±5 degrees, with average C_αRMSD changes of 1–2Å. This procedure produced landscapes very similar to the sampling runs without jittering, with the near-native state sampling largely unaffected (data not shown). This confirmed that the Rosetta energy function indeed guides the models into the minima found, rather than the computed minima being exactly predefined by the fragment sets used.

Simulations in the crystal were performed by extracting the unit cell parameters and space group from the original PDB file and reconstructing the lattice. All subunits in contact with the central molecule were explicitly modeled during the simulation. Due to technical limitations this was only possible for lattices with a single monomer per asymmetric unit (89/108 crystal structures). The models from the low-resolution simulations were placed onto all the molecules in the native lattice by superimposition and then relaxed multiple times. This Rosetta all-atom relax procedure was carried out as described above. Although only the torsional degrees of freedom of one subunit were explicitly modeled, all conformational changes to the central subunit were propagated to all symmetric copies. The unit cell size was not permitted to change during this process, but the rigid body position of the molecule within the asymmetric unit was varied along the degrees of freedom (DOFs) that changed the system: three rotational DOFs and up to three translational DOFs depending on the space group. Some initial lattice placements resulted in severe steric clashes, but as with ordinary FastRelax, the initial reduction of repulsive weight reduced the likelihood of initial steric clashes blowing up a given simulation.

To address the basis of deviations from the target crystal structures, we used MolProbity quality criteria (30) and electron density maps, followed by trial rebuilding (31, 32), to identify cases where Rosetta has repaired an error in the deposited crystal structure. We also examined any available crystal or NMR structures with 60–100% sequence identity – obtained via BLAST search using PDB sequences – as an independent source of validation for differences between the low-energy models and the target structures. Although it was not possible in every case to reach a strong conclusion, all significant deviations in the entire set of 111 proteins were examined in this manner; see Supporting Information for much more detailed analysis.

To assess recapitulation of sidechain rotamers, each sidechain in the low-energy models and deposited crystal structures was first assigned to a named rotamer (33) using the smoothed, multidimensional χ-angle distributions (B-factor and resolution filtered) in MolProbity (30). Accuracy for each low-energy model was then defined as the percentage of valid deposited rotamers matched by the corresponding computed rotamer. This score was recently employed for homology model assessment and is described in more detail elsewhere (34).