A Three-Dimensional Multiscale Model for Gas Exchange in Fruit^,,,

Abstract

Respiration of bulky plant organs such as roots, tubers, stems, seeds, and fruit depends very much on oxygen (O₂) availability and often follows a Michaelis-Menten-like response. A multiscale model is presented to calculate gas exchange in plants using the microscale geometry of the tissue, or vice versa, local concentrations in the cells from macroscopic gas concentration profiles. This approach provides a computationally feasible and accurate analysis of cell metabolism in any plant organ during hypoxia and anoxia. The predicted O₂ and carbon dioxide (CO₂) partial pressure profiles compared very well with experimental data, thereby validating the multiscale model. The important microscale geometrical features are the shape, size, and three-dimensional connectivity of cells and air spaces. It was demonstrated that the gas-exchange properties of the cell wall and cell membrane have little effect on the cellular gas exchange of apple (Malus × domestica) parenchyma tissue. The analysis clearly confirmed that cells are an additional route for CO₂ transport, while for O₂ the intercellular spaces are the main diffusion route. The simulation results also showed that the local gas concentration gradients were steeper in the cells than in the surrounding air spaces. Therefore, to analyze the cellular metabolism under hypoxic and anoxic conditions, the microscale model is required to calculate the correct intracellular concentrations. Understanding the O₂ response of plants and plant organs thus not only requires knowledge of external conditions, dimensions, gas-exchange properties of the tissues, and cellular respiration kinetics but also of microstructure.

Respiration of bulky plant organs such as roots, tubers, stems, seeds, and fruit depends very much on oxygen (O₂) availability and often follows a Michaelis-Menten-like response (Hertog et al., 1998; Lammertyn et al., 2001; Génard and Gouble, 2005; Armstrong et al., 2009; Borisjuk and Rolletschek, 2009). Interestingly, the respiration rate has been observed to decrease with O₂ concentration even at a value well above the K_m value of cytochrome c oxidase (Geigenberger, 2003; Armstrong et al., 2009). Two hypotheses have been proposed to explain these observations. Some authors have shown using in situ O₂ measurements or gas-diffusion models that in bulky plant organs the diffusional resistance of the tissue causes an O₂ gradient decreasing toward the center of the plant organ, thereby possibly limiting O₂ availability as a substrate for respiration (Bidel et al., 2000; Rolletschek et al., 2004; Ho et al., 2008; Borisjuk and Rolletschek, 2009). Other authors have assumed the occurrence of metabolic regulation of the respiration rate based on a signal produced by a yet unknown O₂ sensor (Geigenberger et al., 2000). While these theories are not mutually exclusive, the diffusion hypothesis has been questioned by authors such as Geigenberger (2003) and Gupta et al. (2009). Indeed, even in the center of bulky plant organs, the measured or simulated local O₂ concentration is often above the K_m value of cytochrome c oxidase (van Dongen et al., 2003; Ho et al., 2010), indicating that O₂ would not be a rate-limiting substrate. Yet, the K_m value of respiration of plant organs where the diffusion path is short is generally smaller than when it is long; this suggests that diffusion does play a role, as the diffusion rate is known to be inversely proportional to the diffusion path length (Nobel, 1991). To better understand this paradox, we have investigated O₂ diffusion in bulky fruit in greater detail. As there are no noninvasive experimental measurement techniques available for measuring in vivo O₂ concentrations in fruit, we decided to use a gas-exchange model for carrying out in silico experiments.

Continuum gas-exchange models have been developed to describe the gas exchange of fruit (Mannapperuma et al., 1991; Lammertyn et al., 2003; Ho et al., 2008, 2010). These models operate at the fruit scale (macroscale) and are based on Fick’s law, which assumes that the gas concentration gradient is the driving force for diffusion. Microstructural features such as pores, cell walls, membranes, and the cytoplasm are incorporated into a few apparent model parameters such as O₂ and carbon dioxide (CO₂) diffusivities that need to be determined experimentally (Lammertyn et al., 2003, Ho et al., 2008). However, the microscale architecture of plant tissue defined by the cells and the intercellular space contributes to a large extent to gas transport in the tissue (Parkhurst and Mott, 1990; Parkhurst, 1994; Aalto and Juurola, 2002; Mendoza et al., 2007; Verboven et al., 2008), and to date, little attention has been paid to this. Microscale gas exchange in plant organs was first investigated using theoretical models applied to leaves (Parkhurst et al., 1988; Parkhurst and Mott, 1990; Vesala et al., 1996; Aalto and Juurola, 2002). These models were constructed using basic geometrical elements such as spheres and cylinders. However, the models were relatively crude compared with the actual irregular microstructure of the tissue. Also, extension to bulky plant organs is not straightforward, because the level of microstructure details that these models provide in relation to the size of such organs would require excessive computer resources.

Recently, we presented a two-dimensional (2-D) microscale gas-exchange model (Ho et al., 2009) that featured a virtual tissue model based on light microscopic images of fruit (Mebatsion et al., 2006) and took into account the membrane resistance for O₂ and CO₂. Simulations showed that O₂ transport mainly occurred through the intercellular space and less through the cytoplasm, while CO₂ was transported at equal rates through both phases. The model, however, predicted that considerable gas flow would occur through the cell walls, which is unlikely as their polysaccharide constituents would be completely hydrated in vivo and form a composite material with an even lower gas permeability than that of the cytosol. This might be caused by the lack of connectivity of air spaces in the tissues when observed in two dimensions. Indeed, in three dimensions, a strongly connected network of intercellular spaces has been observed in plant organs (Kuroki et al., 2004; Mendoza et al., 2007; Verboven et al., 2008), with pores of various sizes and shapes interconnected in different arrangements. Our understanding of gas exchange related to metabolic process and, hence, would greatly benefit from a quantitative three-dimensional (3-D) analysis.

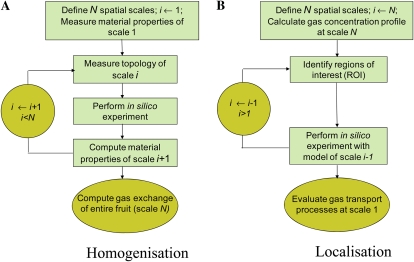
Although it would provide detailed predictions of the local gas concentrations, a microscale model that covers entire bulky plant organs is currently not feasible because of the excessive computer resources required to solve such a model. A multiscale modeling paradigm provides an alternative approach for combining the relative simplicity of continuum-type models defined at the macroscale level with the level of detail provided by models incorporating the microscale features in the regions of interest. A multiscale gas-exchange model is basically a hierarchy of models that describe the gas-exchange phenomena at different spatial scales. These models are coupled via multiscale analysis in which the model results relevant to the macroscale are linked to simulations at the microscale by means of homogenization and localization procedures (Fig. 1).

Figure 1.

Schematic of the multiscale paradigm. A, Homogenization involves calculating apparent material properties of the model at some scale i from simulations with the model that operates at the lower scale i 2 1. B, In localization, special regions of interest (ROI) are identified at some scale of interest i; more detailed simulations are then carried out in these regions of interest using the model that operates at scale i 2 1 [See online article for color version of this figure.]

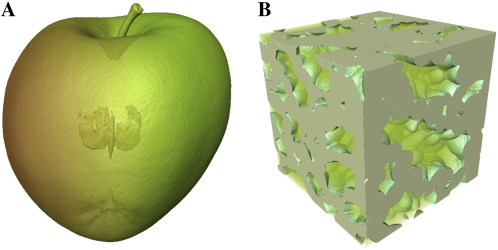
In this article, exchange of O₂ and CO₂ in apple (Malus × domestica) fruit is investigated via a multiscale model. The model incorporates the actual 3-D microstructure of the tissue as obtained by means of synchrotron radiation tomography (Fig. 2). We will use the model to investigate the following hypotheses.

Figure 2.

X-ray computed tomography images of an intact apple (A) and a cubical apple cortex tissue sample (B).

Unlike in the previously published 2-D model of Ho et al. (2009), the cell wall and plasma membrane diffusion resistances affect microscale gas flow only marginally.

While gas transport in apple fruit proceeds mainly through the intercellular channels, the symplast provides an additional transport route for CO₂ because of the larger solubility of CO₂ in water compared with that of O₂.

Because of differences in microscale interconnectivity of the tissue, local cellular gas concentrations may be even smaller than those predicted by a continuum model or measured with invasive O₂ sensors and, incidentally, even smaller than the K_m of cytochrome c oxidase.

Differences in microstructure may explain differences in gas diffusion and, consequently, intracellular concentrations in fruit as well as other plant organs under hypoxia or anoxia.

RESULTS

Comparison of Computed Microscale Gas Exchanges with Measurements

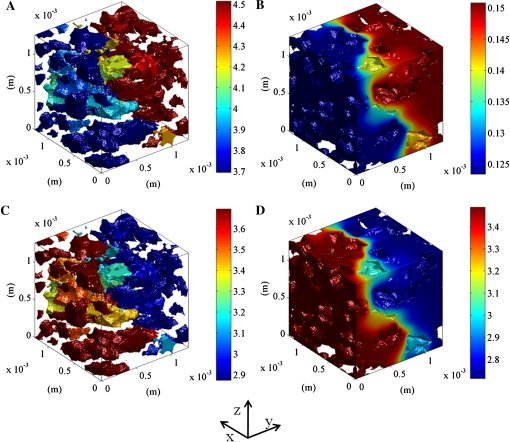
Direct validation of the microscale model would involve comparing local O₂ and CO₂ measurements with model predictions. While microscale sensors are available for O₂ (Rolletschek et al., 2004; Ho et al., 2010), for various practical reasons it was not feasible to carry out local O₂ measurements at well-specified positions in the same samples that were used for 3-D synchrotron imaging. Also, such invasive measurements would most likely have an effect on the local gas transport itself. Therefore, we decided to adopt an indirect validation method that consisted of calculating the apparent diffusivity of the microscopic samples of cortex tissue from a computer experiment in which we applied (arbitrary) gas partial pressure differences of 2 kPa (Fig. 3). These calculated diffusivities were then compared with experimental values obtained from diffusion measurements on disc-shaped samples of cortex tissue.

Figure 3.

Simulated O₂ and CO₂ concentrations in a typical sample of cortex tissue of apple Jonagold. At the left of the computational domain, the O₂ and CO₂ partial pressures were set to 9 kPa; at the right side, the O₂ and CO₂ partial pressures were set to 11 and 7 kPa, respectively, to ensure a partial pressure difference of 2 kPa for both gases. The lateral sides of the sample were assumed to be impermeable. A and C, O₂ and CO₂ concentrations in the intercellular space. B and D, O₂ and CO₂ concentrations in the cell. The color bar indicates the gas concentration (mol m⁻³).

The results are given in Table I. Increasing the sample size reduced the variation of the calculated apparent O₂ and CO₂ diffusivity to values of the same order of magnitude as that of the measured values. It was further shown that the mean O₂ and CO₂ diffusivity of tissue converged to 1.26 × 10⁻⁸ m² s⁻¹ and 3.19 × 10⁻⁸ m² s⁻¹, respectively (for details, see Supplemental Text S3 and S4 and Supplemental Figs. S3–S5). These values were close to the actual measured ones. Therefore, we concluded that the model allows estimating apparent diffusivities based on simulation of gas transport in the 3-D microstructure, taking into account the microstructure topology and its stochastic properties.

Table I. Apparent diffusivities of O₂ and CO₂ in parenchyma tissue of Jonagold apple.

Values shown are ±sd. Asterisks indicate apparent diffusivity of stochastic simulations for a larger sample containing random effective diffusivities computed from simulated 3-D microscale (*) and measurement along the radial direction at a relative position (x/R) of 0.35 to 0.65 (**).

Type	No. of Samples	Sample	O2 Diffusivity	CO2 Diffusivity
		mm	m2 s−1
Measurement	8	22 × 22 × 2.5	(1.01 ± 0.62) × 10–8 **	(3.51 ± 1.23) × 10–8 **
Microscale model	16	1.28 × 1.28 × 1.28	(4.60 ± 10.02) × 10−8	(5.85 ± 10.04) × 10–8
	8	2.0 × 2.0 × 2.0	(2.43 ± 2.13) × 10−8	(4.07 ± 2.50) × 10−8
Stochastic simulation	500	3.84 × 3.84 × 2.56	(2.06 ± 1.15) × 10–8*	(3.75 ± 1.10) × 10–8*
Stochastic simulation	500	5.12 × 5.12 × 5.12	(1.37 ± 0.39) × 10–8*	(3.30 ± 0.29) × 10–8*
Stochastic simulation	500	7.68 × 7.68 × 7.68	(1.41 ± 0.24) × 10–8*	(3.34 ± 0.2) × 10–8*

Validity of the Multiscale Model of Gas Exchange

In a next step, we investigated the validity of the multiscale model for gas exchange. As we earlier validated the macroscale model (Ho et al., 2010), we only needed to investigate whether the homogenization procedure would yield reliable results. We decided to follow a similar procedure as in the validation of the microscale model: rather than comparing local O₂ and CO₂ concentrations, we used the multiscale model to predict gas exchange of an entire fruit in a contained environment and compared this with actual measured values. The homogenization procedure consisted of incorporating the apparent O₂ and CO₂ diffusivity of cortex and skin tissue calculated from the microscale model into the macroscale gas-exchange model.

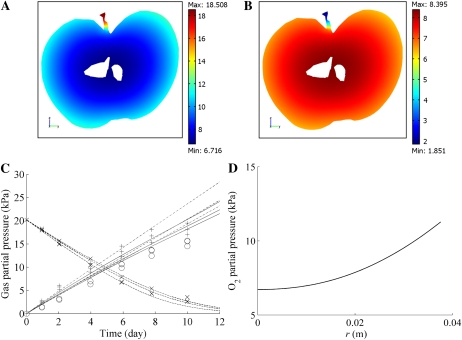
Typical macroscopic O₂ and CO₂ concentration profiles in the fruit are shown in Figure 4, A and B, and Supplemental Figure S2 in kPa. The diffusion barriers and tissue respiration caused a decrease of the O₂ partial pressure and an increase of the CO₂ partial pressure inside the fruit relative to the external O₂ and CO₂ gas partial pressures. Large O₂ and CO₂ concentration gradients can be observed over the skin (in the epidermis and the subepidermal cell layers). This resulted from the low diffusion properties of the skin compared with the cortex.

Figure 4.

A and B, O₂ and CO₂ partial pressure distribution in a vertical slice along the vertical axis of the fruit stored at 20 kPa O₂, 0 kPa CO₂, and 20°C. The macroscale model was used for the computation. Color bars indicate the gas partial pressure (kPa). C, O₂ and CO₂ concentrations as a function of time in a closed jar containing a Jonagold apple. The dashed lines and solid line indicate the computed O₂ and CO₂ partial pressures in the jar, respectively; crosses and circles indicate the measured O₂ and CO₂ gas partial pressures for initial conditions equal to 20 kPa O₂, 0 kPa CO₂, and 10°C. The dashed-dotted lines and plus symbols indicate the simulated and measured CO₂ gas partial pressures in the jar, respectively, for initial conditions equal to 0 kPa O₂, 0 kPa CO₂, and10°C. For both sets of initial conditions, three experiments with different fruit were carried out and simulated. D, Radial O₂ partial pressure profile in cortex tissue from the center to the boundary of the fruit (r = 38.6 mm). The O₂ and CO₂ concentrations of the external atmosphere were equal to 20 and 0 kPa CO₂, respectively, and the temperature was 20°C.

In Figure 4C the model predictions of the change with time of O₂ and CO₂ concentrations in the head space of several closed jars containing a cv Jonagold apple are compared with experimental measurements. The O₂ partial pressure decreased during the measurement due to O₂ consumption of the fruit by respiration, while the corresponding CO₂ production caused the CO₂ partial pressure to increase. At 0 kPa O₂, CO₂ was produced by fermentation, and this further increased the CO₂ partial pressure. The predicted O₂ and CO₂ partial pressure profiles compared very well with the experimental data, thereby validating the multiscale model.

Effects of Cell Wall and Cell Membrane on Microscale Gas Exchange

Gas exchange between the intercellular space and the cytoplasm must overcome a series of resistances through the cell wall and the cell membrane. Little is known about cell wall and membrane permeability for respiratory gases, so we investigated how sensitive the calculated gas exchange was to these parameters. The cellular conductance is here defined as the gas flux between air spaces and cells divided by the mean local gas concentration difference between the intercellular space and the cells (for details, see Supplemental Text S5).

A sensitivity analysis on parenchyma tissue revealed that the intracellular gas diffusivity and solubility (as expressed by the Henry constant) were the most important parameters that determine the overall cellular conductance, while the permeability of cell membrane and cell wall did not play a major role (Supplemental Text S7; Supplemental Table S4).

To analyze the effect of the cell wall and cell membrane permeability on the gas exchange inside a cluster of cells, the equivalent diffusivity of the cluster was calculated by assuming a series model for the resistance with respect to gas exchange using data given in Supplemental Table S1. The resulting overall cluster diffusivity values for O₂ and CO₂ were equal to 97% and 96% of those of the cytoplasm, respectively. Reducing the diffusivity of the cell wall by 50% resulted in a decrease of cluster diffusivity for both O₂ and CO₂ by only 3% (Supplemental Table S3).

Including the cell wall in the model for all cells in the 3-D synchrotron images and comparing the results with the above simplified approach resulted in a decrease of the cellular conductance of only 6.6%. The above considerations indicate that this simplification will hardly affect the computation of gas concentration profiles. The transport properties of the cell wall and membrane thus have little effect on the cellular gas exchange and hence do not need to be known accurately for the purposes of this paper. These findings are very different from those resulting from the 2-D model of Ho et al. (2009) and clearly show the value of a full 3-D gas-exchange model.

Transport Routes for O₂ and CO₂

CO₂ transport in the cells is more complex than O₂ transport because, depending on the pH, CO₂ is in equilibrium with HCO₃⁻ in water (Supplemental Text S8). For both molecules, the diffusivity values are about 4 orders of magnitude larger in air than in water. This would imply that both O₂ and CO₂ would be transported mostly through the intercellular space rather than through the cells and that the apparent diffusivity of CO₂ in tissue would also be smaller than that of O₂. Yet, in previous research, we found the opposite (Ho et al., 2010). A possible explanation of this paradox would be that the larger solubility of CO₂ in water would mean that the cells would provide an additional transport route for CO₂.

First, we investigated the concentration profiles of O₂ and CO₂ in a typical apple cortex tissue sample (Fig. 3, A and B). The resulting 3-D gas concentration profiles show that, on a molar basis, the O₂ concentration inside the cells is 1 order of magnitude smaller than that in the intercellular spaces (Fig. 3, A and B), because O₂ has a low solubility in the cell (Henry’s constant for O₂ at 20°C is 1.37 × 10⁻² mol m⁻³ kPa⁻¹). The CO₂ concentration profiles are shown in Figure 3, C and D. The high CO₂ concentration in the cytoplasm is due to the high solubility of CO₂ in the cytoplasm (Henry’s constant for CO₂ at 20°C is 3.876 × 10⁻¹ mol m⁻³ kPa⁻¹). As a result, the CO₂ concentration in the intercellular space and in the cells has the same order of magnitude.

Next, we considered differences in O₂ and CO₂ fluxes through the cells. The calculated cellular O₂ and CO₂ conductance was 3.45 × 10⁻⁶ and 7.84 × 10⁻⁵ m s⁻¹ (corresponding to 1.42 × 10⁻⁶ and 3.2 × 10⁻⁵ mol m⁻² s⁻¹ kPa⁻¹), respectively. The cellular conductance of CO₂ is thus more than 20 times higher than that of O₂. This confirms that the cells do provide an additional route for CO₂ transport through the tissue but not for O₂.

K_m,O2 of Intact Plant Organs

Respiration plays a central role in the overall metabolism of a plant and, therefore, is often used as a general measure of the metabolic activity of the plant. Michaelis-Menten kinetics and variants have been applied often to describe the effect of the gas concentration on the O₂ uptake rate (Hertog et al., 1998; Lammertyn et al., 2001). The Michaelis-Menten constant K_m,O2 for respiration of intact plant organs is actually an apparent value, since it also depends on the gas diffusion properties of the tissue.

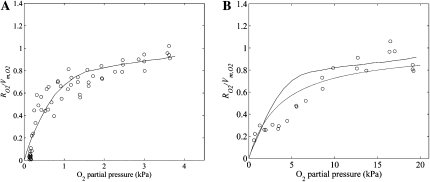
A multiscale gas-exchange experiment was carried out in silico to validate the dependence of K_m,O2 of intact fruit on temperature. The K_m,O2 (mol m⁻³) value of the cell was set equal to 3 μm (3 × 10⁻³ mol m⁻³; Lammertyn et al., 2001). The normalized O₂ consumption rates are shown in Figure 5 as a function of the external O₂ partial pressure. At 1°C, there is good agreement between model predictions and measurements (Fig. 5A). The calculated K_m,O2 of intact fruit at 1°C was 0.6 kPa. However, at 10°C, the calculated K_m,O2 was as large as 2.9 kPa, so at this temperature, the agreement between predictions and measurements was worse (Fig. 5B). Moreover, there clearly is a large effect of fruit size on the Michaelis-Menten constant K_m,O2 for respiration of intact fruits (Supplemental Fig. S7).

Figure 5.

Normalized O₂ consumption (R_O2/V_m,O2) of intact apple fruit as a function of the ambient O₂ partial pressure at 1°C (A) and 10°C (B). Solid lines represent computed results from the multiscale model, while circles indicate the measurements. The dashed line in B represents the modeled Michaelis-Menten kinetics of O₂ consumption of the intact apple at 10°C with K_m,O2 = 3.76 kPa (Hertog et al., 1998).

Gas Concentrations and Gradients in the Cells and Air Spaces

We used the multiscale localization approach to investigate the heterogeneity of the O₂ and CO₂ concentrations and gradients in and between cells. Therefore, we carried out in silico experiments simulating a sample of cortex tissue (1.28 mm × 1.28 mm × 1.28 mm) at the position in the center of the fruit where the O₂ and CO₂ partial pressures were lowest and highest, respectively. Fruit was assumed to be stored in ambient air (20 kPa O₂ and 0 kPa CO₂ at 20°C), and the macroscale model was numerically solved for these boundary conditions. To one side of the computational domain representing the sample of cortex tissue, we applied the O₂ and CO₂ partial pressures (6.72 kPa O₂ and 8.39 kPa CO₂) that were calculated from the macroscale model at that particular position; the opposite side was assumed to be impermeable, as it was located in the center of the fruit. Also, the other sides were assumed to be impermeable for reasons of simplicity.

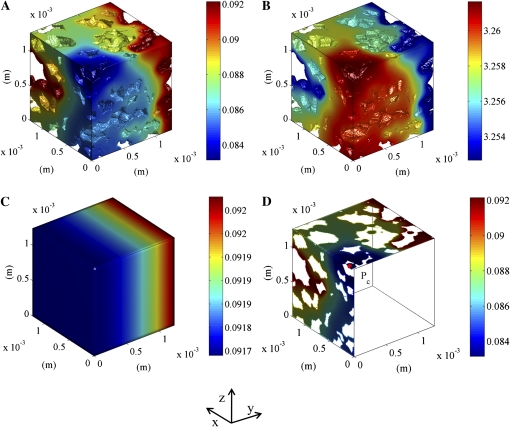
Figure 6, A and B, shows the distribution of the O₂ and CO₂ concentrations in the cells of one particular sample. The calculated gas concentrations in this small sample are very heterogeneous. The large local concentration gradients result from tissue respiration and diffusion limitations. There is a clear concentration gradient inside the cells. Figure 6C shows the corresponding gas concentrations calculated from the macroscale, which does not distinguish individual cells. In this case, the intracellular gradients and the gradients across cell clusters are not resolved, and only a profile in the direction of macroscopic diffusion (y direction) is obtained (Fig. 6C). Figure 6D shows the O₂ concentration in the cells in xz and xy planes through a critical point in the microscale model (defined as the position with minimal O₂ and maximal CO₂ concentrations).

Figure 6.

Simulated intracellular O₂ and CO₂ concentration distributions in cortex tissue of a Jonagold apple near the core. The left side of the sample was assumed to be at the center of the apple and impermeable. At the right side, the partial pressure computed using the macroscale model at the corresponding position was applied (6.7219 kPa O₂ and 8.392 kPa CO₂). The other sides of the sample were assumed to be impermeable. The color bars indicate the gas concentrations (mol m⁻³). A and B, O₂ and CO₂ concentrations inside the cells, respectively. C, Simulated macroscopic O₂ concentration. D, Cross section showing the O₂ concentration inside the cell with an indication of the critical point P_c (minimal O₂ and maximal CO₂ in the tissue).

Simulations based on eight different microscale geometries confirmed that the local microscale concentrations and concentration gradients were different from those of the macroscale model (Table II). The minimum intracellular O₂ concentration in the microscale model was 0.69 ± 0.19 kPa lower than that in the macroscale model, while the maximum microscale CO₂ concentration was 0.021 ± 0.007 kPa larger than that in the macroscale model. The local intracellular concentration gradients computed from the microscale model (0.97 kPa mm⁻¹ for O₂ and 0.037 kPa mm⁻¹ for CO₂) were significantly higher than those expected from the macroscale model (1.93 × 10⁻² kPa mm⁻¹ for O₂ and 5.6 × 10⁻³ kPa mm⁻¹ for CO₂). The simulation results also showed that the gas concentration gradients were less steep in the air space (5.08 × 10⁻⁵ and 4.48 × 10⁻⁵ kPa mm⁻¹ for O₂ and CO_2, respectively) compared with those in the cells.

Table II. Calculated gas-exchange characteristics at the microscale.

The critical gas concentrations are the minimal and maximal intracellular O₂ and CO₂ concentrations, respectively. Values are expressed in terms of partial pressure by using Henry’s law. The macroscale model was computed with the measured apparent diffusivities from Table I. CO₂ (a) and CO₂ (b) represent microscale simulations of CO₂ diffusion without and with HCO₃⁻ transport in the cytoplasm, respectively (Supplemental Text S8). The values reported for the microscale model are the average simulated values for eight different tissue geometries ± sd.

Scale	Variable	O2	CO2 (a)	CO2 (b)
Microscale (1.28 × 1.28 × 1.28 mm3)	Critical concentration (kPa)	6.0 ± 0.19	8.421 ± 0.008	8.419 ± 0.007
	Local concentration gradient (kPa mm−1)
	Cell	0.97 ± 0.19	0.039 ± 0.009	0.0368 ± 0.008
	Intercellular space	5.08 × 10−5	4.72 × 10−5	4.48 × 10−5
	Maximal local concentration gradient (kPa mm−1)	19.9 ± 7.3	0.78 ± 0.29	0.73 ± 0.26
	Cellular conductance (m s−1)	(3.45 ± 1.13) × 10−6	(7.98 ± 2.53) × 10−5	(7.84 ± 2.37) × 10−5
Macroscale	Critical concentration (kPa)	6.696	8.399
	Local concentration gradient (kPa mm−1)	1.93 × 10−2	5.6 × 10−3

Multiscale Analysis of Gas Exchange in Hypoxic Conditions

Apples are often stored under controlled atmosphere conditions to extend their commercial storage life up to 1 year. When the O₂ concentration is too low, fermentation has been observed experimentally, indicating anoxia (Ke et al., 1991). A multiscale gas-exchange analysis was carried out to help explain these observations.

In a first step, we used the macroscale model to calculate the macroscopic gas concentration profile in a Jonagold apple. We assumed that apples were stored at typical commercial storage conditions of 1% O₂, 2.5% CO₂, and 1°C. Then, in a second step, we carried out microscale simulations at the position near the core of the fruit where the O₂ concentration was found to be the lowest (Supplemental Fig. S6). This region was considered to be most susceptible to anoxia. The corresponding local intracellular O₂ concentration near the core was 1.45 ± 0.12 μm, well above the threshold of the Michaelis-Menten constant K_m,O2 of cytochrome c oxidase, the rate-limiting enzyme in the oxidative phosphorylation, which is 0.14 μm (Millar et al., 1994). In such conditions, fermentation would be unlikely.

The multiscale analysis was repeated for an O₂ concentration of 0.2% O₂, which is known to cause fermentation symptoms inside the fruit. The macroscale model predicted that the lowest O₂ concentration was 0.15 μm, still higher than the K_m of cytochrome c oxidase. However, the local O₂ concentration calculated at the microscale at this position decreased to as low as 0.088 μm, well below the K_m of cytochrome c oxidase. We thus concluded that, unlike the macroscale model, the microscale model predicted an O₂ concentration at which respiration virtually stalls and fermentation may become likely to occur. The analysis clearly demonstrated that the onset of fermentation depends on the respiratory activity as well as on the microscopic structure of the tissue.

DISCUSSION

The microstructure of biological materials has apparently evolved to facilitate the transport of respiratory gases for physiological processes such as respiration and photosynthesis. New insights into these physiological processes can be obtained by incorporating this structural information into computer models for gas exchange, as illustrated in this article for fruit as a model system for bulky plant organs.

The multiscale approach presented calculates the tissue gas-exchange properties of the macroscale using the microscale, or vice versa, the local concentrations in the microscale from macroscopic gas concentration gradients. This approach provides a computationally feasible and accurate analysis of the cell metabolism in any plant organ. While we validated the macroscale submodel previously (Ho et al., 2010), in this paper we also validated the microscale submodel and the overall multiscale model successfully. The size of the computational domain for the microscale submodel is important: the variability of the calculated diffusivities increases with decreasing size. Using in silico microscale gas-exchange experiments, we discovered large local concentration gradients in the tissue that were not revealed by simulations at the macroscale. Also, the simulations indicated that the microscale topology of plant tissue determines gas exchange to a large extent. As several authors (Schotsmans et al., 2004; Pham et al., 2008) have shown that gas diffusivity values of pome fruit varies among species and even genotypes, these differences in tissue diffusivity could indeed be due to differences in microstructural features of their tissues. Our approach provides perspectives to study this relationship in a more structured way by changing microstructural features artificially and directly evaluating the effect on gas diffusivity by computer modeling. We are currently exploring this path.

The microscale model does not account for effects due to the compartmentalization of the cell. Because of limitations of computational resources, it was not possible to explicitly model the vacuole and the mitochondria. Preliminary simulations using a previously developed 2-D model indicated that the effect of compartmentalization on the intracellular O₂ distribution was negligible; however, a large effect on the intracellular CO₂ distribution was observed, depending on the permeability of the tonoplast for HCO₃⁻. There was no effect of the compartmentalization on the overall microscale gas flux of either O₂ or CO₂, though. Future research should address the effects of cellular compartmentation on the intracellular CO₂ concentration; a 3-D cellular gas transport model would be useful for this purpose.

Our computations showed that because of the high solubility of CO₂ compared with that of O₂, the conductance of CO₂ is 20 times larger than that of O₂. This implies that the cell provides an additional transport route for CO₂ but not for O₂. This is in line with previous calculations using a 2-D model (Ho et al., 2009) and explains the paradox that the apparent diffusivity of CO₂ in tissue is larger than that of O₂, although the size of the molecule would predict the opposite. The simulated cellular conductance of CO₂ of Jonagold apple parenchyma cells was smaller than that of the mesophyll conductance in leaves found in the literature. Warren (2008) found values of CO₂ mesophyll conductance for plant leaves of Solanum lycopersicum, Phaseolus vulgaris, and Eucalyptus regnans of 0.35, 0.34, and 0.14 mol m⁻² s⁻¹, respectively (corresponding to 0.35, 0.34, and 0.14 mol m⁻² s⁻¹ bar⁻¹). Yin and Struik (2009) reported values from 0.033 to 0.138 mol m⁻² s⁻¹ bar⁻¹ for CO₂ mesophyll conductance of wheat (Triticum aestivum) leaves with different methods. The conductance value is quite dependent on the size of the cells and the degree of cell compactness in the tissue. Decreasing the cell diameter by one-half increases the cellular conductance of a single cell by 50%. Also, apple cortex cells cluster into larger cell zones; this decreases the surface for gas-liquid exchange and reduces the overall gas conductance due to the low gas diffusivity in water. The average ratio of cellular gas-exchange surface to the cell volume for the eight different samples we used here was 6.81 mm⁻¹. Considering a mean cell diameter of apple parenchyma cells equal to 107 μm (Mebatsion et al., 2009), the exchange surface of the cell is only about 12.2% of the total cell surface. Compact cell assemblies reduce the gas-liquid exchange surface and could increase the barrier to gas diffusion. The simulation results indicate that a single cell of 107 μm diameter having 100% air-contact surface has a larger cellular conductance (1.6 times for O₂ and CO₂) than the mean values of the tissues studied here.

An intriguing result from our previous 2-D microscale gas transport model was the unrealistically high O₂ and CO₂ diffusivities of the cell wall, which would indicate its importance as a pathway for gas diffusion where there are no air spaces between cells. The 3-D model clearly showed that this result was wrong: the high value was due to the underestimation of the connectivity of the intercellular space by the 2-D model. In fact, we found that the cell wall and membrane only marginally affect gas transport at the microscale of the apple tissue.

Based on our simulations, we showed that the K_m,O2 value of respiration of intact apples, which describes the response of respiration to O₂ availability, is an apparent parameter that depends on gas transport inside the fruit but also on the external conditions that are applied. Furthermore, the multiscale model clearly showed that the local O₂ concentration in the cells may be much smaller than that estimated from simpler macroscale models. This helps explain the susceptibility of fruit tissue to anoxia- related physiological disorders that have been observed during storage under controlled atmosphere conditions. A simulation with the multiscale model showed that the local intracellular O₂ concentration near the core was well above the known estimated Michaelis-Menten constant of cytochrome c oxidase, which is considered to be the rate-limiting enzyme in respiration. ATP availability is thus supplied by the normal respiration pathway.

This may explain why Jonagold apple fruit can be stored for up to 10 months without risk of developing storage disorders due to fermentation (Saquet et al., 2000). Only when the O₂ concentration of the storage atmosphere was reduced to 0.2% did the local O₂ concentration decrease below the K_m of cytochrome c oxidase. Interestingly, the O₂ concentration computed with the macroscale model was well above this threshold value and would not explain the occurrence of fermentation. In this context, Colmer and Voesenek (2009) suggested that in conditions of hypoxia, as observed during flooding of some plant species, gas diffusion limitations would provide an alternative physical explanation for an active down-regulation of the rate of respiration, as was suggested by Geigenberger (2003). In this paper, we provide further evidence of the Colmer and Voesenek (2009) hypothesis showing that the local O₂ concentration may be even smaller than predicted from a simple diffusion model. Further research is required to clarify the regulation of respiration in bulky plant organs.

MATERIALS AND METHODS

Materials

Apples (Malus × domestica ‘Jonagold’) were picked at the preclimacteric stage on September 25, 2006, at the experimental orchard of the Research Station of Fruit Growing (Velm, Belgium). Fruits were cooled and stored under controlled atmosphere conditions (1 kPa O₂, 2 kPa CO₂, 0.8°C) up to the time of the experiment in November 2006. Picking data and cooling procedures were according to optimal commercial practices to preserve fruit quality during long-term storage.

Diffusivity Measurements

Samples of cortex tissue were first cut with a professional slice cutter (EH 158-L; Graef), from which cylinders with a diameter of 2.5 cm were cut with a cork borer. The thickness of samples ranged from 2 to 3 mm, measured with a digital caliper (accuracy of ±0.01 mm; Mitutoyo). Radial cortex tissue samples were then taken at the equatorial region of the apple. Skin samples were taken as outlined above but included only cuticle to outer cortex cell layers. Cylindrical samples with a thickness on the order of 0.6 mm were obtained by means of a razor blade.

The apparent diffusivity of the sample was measured with the setup and procedures developed by Ho et al. (2006a). Once the sample was mounted between the measurement and the flushing chamber of the diffusion cell, the former was flushed with a gas mixture composed of 69 kPa N₂, 30 kPa O₂, and 1 kPa CO₂; for the flushing chamber, the gas composition was 85 kPa N₂, 5 kPa O₂, and 10 kPa CO₂. In this way, O₂ and CO₂ concentration differences were established between the two chambers. The gases were humidified and passed through a heat exchanger to prevent the sample from drying and cooling down while flushing the two chambers. The flow rate was set to 10 L h^–1. After 30 min, the inlet and outlet valves of the measurement chamber were closed, and both gases started to diffuse through the tissue sample driven by their concentration differences. The decrease in O₂ partial pressure, the increase in CO₂ partial pressure, and total pressure of the measurement chamber were monitored each 20 s for 6 h. The O₂ and CO₂ concentrations were measured in the measurement chamber with fluorescent optical probes (Foxy-Resp and FCO2-R; Ocean Optics). The difference in total pressure between the two chambers was logged (PMP 4070; GE Druck) and was kept smaller than 1.5 kPa to minimize permeation.

O₂ and CO₂ diffusivities of tissue were estimated by fitting the solution of the macroscopic diffusion transport equation for O₂ and CO₂ to the measured concentration profiles in the measurement chamber. The N₂ diffusivity was determined indirectly from the total pressure and the O₂ partial gas pressure of the binary O₂-N₂ gas mixture (Ho et al., 2006b).

Permeation properties of apple tissue were determined by measuring the total pressure difference between two chambers separated by a tissue sample (Ho et al., 2006b). Both chambers were flushed with humidified N₂ gas at 10 L h^–1. The pressure was adjusted to provide a 6-kPa pressure difference between the measurement and flushing chamber. The inlet and outlet valves of one chamber were closed, and the decrease in pressure of this chamber was monitored for at least 4 h. The permeability was then estimated from this pressure drop using the procedure described by Ho et al. (2006b).

Microscale Gas-Exchange Model

Model Features

The microscale gas-exchange model included equations for the transport of respiratory gases in the intercellular space and through the cell wall and plasmalemma into the cytoplasm and incorporated the actual tissue microstructure as obtained from synchrotron radiation tomography images. Cellular respiration was modeled as well. From earlier simulations with a 2-D microscale model including the vacuole (Ho et al., 2009) and additional simulations with a 2-D microscale model that also included mitochondria (Supplemental Text S9; Supplemental Figs. S8 and S9), we found that modeling the vacuole and mitochondria explicitly had a small effect on the O₂ distribution inside the cells; the intracellular CO₂ distribution was affected considerably (Ho et al., 2009). Including the compartmentalization hardly affected the overall gas transport through the tissue, though. Therefore, it seemed reasonable to assume for the purpose of this article that the cytoplasm can be considered as a lumped homogeneous liquid, but the calculated intracellular CO₂ distribution should be interpreted with care. Future research should address the effects of intracellular compartmentation on 3-D CO₂ exchange in more detail.

O₂, CO₂, and HCO₃⁻ transport in the intercellular spaces and in the (lumped) cytoplasm was modeled with diffusion equations and transport between these compartments by means of a permeation equation. In the cytoplasm for both the O₂ and CO₂, the transport equation incorporated Michaelis-Menten kinetics for respiration and fermentation. For simplicity, we assumed that the respiratory activity did not change during the storage period; apple fruit are actually picked just before the climacteric rise to keep respiration as small as possible. We also did not distinguish between the normal and alternative respiration pathways. The model can easily be expanded to include, for example, an additional production term representing the alternative respiration pathway.

3-D Microstructure and Numerical Solution

The 3-D microstructure of Jonagold cortex tissue was recorded from synchrotron radiation tomography images as described by Verboven et al. (2008). Synchrotron x-ray computed tomography was performed at beamline ID19 of the European Synchrotron Radiation Facility in Grenoble, France. As a result, a series of slices that give detailed structural information about the 3-D nature of the material was obtained. The absorption images were segmented into intercellular space and cells based on a grayscale threshold with the Avizo image-processing software (Visualization Group Sciences; Verboven et al., 2008).

The microscale gas-exchange model was solved over the 3-D microstructure geometry using the finite volume method (Versteeg and Malalasekera, 1995). 3-D tomographic images of fruit tissue samples with edge dimensions of 1.28 mm were discretized into 2,097,152 cubical control volumes with an edge of 10 μm. The model equations (Supplemental Text S1) were discretized over the finite volume grid to yield a linear system of algebraic equations on the unknown concentrations at the nodes. The linear equation system was solved by the Generalized Minimal Residual Method procedure available in Matlab (The Mathworks). The program was run on a 16-GB RAM node (Opteron 250; Xenon 5420 and Xenon 5560) of the High-Performance Computer at the Katholieke Universiteit Leuven.

Macroscale Gas-Exchange Model

Model Features

In the macroscopic approach, the tissue was considered as a homogenous continuum and the modeling was carried out on the lumped properties of pores, cell wall, cell membrane, and intracellular liquid phase; microstructural features were neglected. We used a permeation-diffusion-reaction model we had developed earlier (Ho et al., 2008, 2010) to study gas exchange due to respiration of intact fruit with the external gas atmosphere at the macroscale. Gas concentration gradients were the driving force for gas exchange. Differences in diffusion rates of the different gases led to total pressure gradients that caused convective exchange as described by Darcy’s law.

We used the noncompetitive inhibition Michaelis-Menten model to describe O₂ consumption and CO₂ production of fruit tissue (Ho et al., 2008, 2010).

The gas transport properties of the fruit tissue were measured using the fluorescent optical probes described above. The methodology for measuring the parameters of the respiration kinetics and the corresponding results are described in Supplemental Text S2, Supplemental Table S2, and Supplemental Figure S1.

Geometry Reconstruction and Numerical Solution

Intact fruit were scanned by computed tomography using a Microfocus Computer Tomography AEA Tomohawk system, available at the Department of Metallurgy and Materials at Katholieke Universiteit Leuven. The voltage and current of the x-ray source (Philips HOMX 161) were set to 85 keV and 0.41 mA, respectively. Frame averaging of 16 images and an angular increment of 0.5° were used in a scan over 187°. A 2-mm aluminum filter was placed before the detector to increase the signal-to-noise ratio. Projection images with a pixel size of 82.6 μm were obtained. NRecon software (Skyscan) was used to reconstruct cross-sectional images. These were subsequently loaded into the Avizo software (VSG SAS) and segmented into apple tissue and air by setting a grayscale threshold using the label-field module. A tetrahedral surface was generated to describe the geometric information of the fruit.

The macroscale gas-exchange model was numerically solved using the finite element method (Comsol 3.5; Comsol).

Multiscale Model

A multiscale model was constructed by coupling the microscale and macroscale models by computer simulations (Fig. 1). Two spatial scales were considered for this article. In a first homogenization (upscaling) procedure, O₂ and CO₂ concentration differences of 2 kPa were applied over the microscale geometry and the corresponding fluxes were calculated by means of the microscale model. From these fluxes and the length of the sample, the apparent diffusion coefficients of the microscale sample were calculated. These diffusion coefficients were incorporated into the macroscale model, which was then used to calculate macroscopic gas concentration profiles.

To investigate the gas exchange at the cellular level, a localization (downscaling) procedure was applied by analyzing the microscale from the computed results at the macroscale. First, the gas distribution inside the fruit was calculated at the macroscale using the apparent transport properties as described earlier. The critical zone was then identified as the zone with extreme gas concentrations. In the subsequent localization procedure, the microscale model was used to analyze the transport processes in the critical zones at the cellular level. The finite element discretization procedure that was used to numerically solve the transport equations assumes that the solution is continuous over the computational domain and explicitly defines an interpolating polynomial in every finite element. The boundary conditions of a microscale computational domain, therefore, can be extracted directly from the macroscale simulation through simple interpolation. Here, we assumed continuity of the gas concentrations between the macroscale and microscale models rather than flux continuity. At microscale boundary surfaces located in the cytoplasm, the interpolated macroscale gas concentrations were converted to equivalent liquid concentrations using Henry’s law.

Supplemental Data

The following materials are available in the online version of this article.

• Supplemental Figure S1. Gas-diffusion and respiration measurement on apple tissue samples.

• Supplemental Figure S2. O₂ and CO₂ partial pressure distribution of the intact fruit at 20 kPa O₂ and 0 kPa CO₂ at 208C.

• Supplemental Figure S3. Computational domain for Monte Carlo analyses.

• Supplemental Figure S4. Probability density distribution of the overall apparent diffusivity of O₂ and CO₂ based on Monte Carlo simulations for different computational domains.

• Supplemental Figure S5. Effect of size of the computational domain on apparent O₂ and CO₂ diffusivities calculated by means of Monte Carlo simulation.

• Supplemental Figure S6. O₂ distribution of the intact fruit and microscopic tissue at typical commercial storage conditions.

• Supplemental Figure S7. Normalized oxygen consumption (R_O2/V_m,O2) of intact apple fruit as a function of the ambient O₂ partial pressure at 108C with three different apple radii.

• Supplemental Figure S8. Simulated intracellular O₂ concentration in cortex tissue of Jonagold apple near the core for the model without and with compartments of mitochondria and vacuoles.

• Supplemental Figure S9. Simulated intracellular CO₂ concentration in cortex tissue of Jonagold apple near the core for the model without and with compartments of mitochondria and vacuoles.

• Supplemental Table S1. Physical parameters of the microscale gas transport model.

• Supplemental Table S2. Gas transport properties and respiration kinetics parameters of macroscale model.

• Supplemental Table S3. Effect of cell wall diffusivity (D_w) on equivalent diffusivity of a cell cluster (D_cluster).

• Supplemental Table S4. Relative sensitivity of cellular conductance of O₂ and CO₂ with respect to the microscale model parameters.

• Supplemental Text S1. Microscale gas-exchange model.

• Supplemental Text S2. Macroscale gas-exchange model.

• Supplemental Text S3. Monte Carlo simulations.

• Supplemental Text S4. Richardson extrapolation.

• Supplemental Text S5. Cellular conductance.

• Supplemental Text S6. Local gas concentration gradient.

• Supplemental Text S7. Sensitivity analysis.

• Supplemental Text S8. Effect of cell pH on CO₂ exchange.

• Supplemental Text S9. Effect of compartmentalization on intracellular gas transport.