Abstract
Detection of the optic nerve head (ONH) is a key preprocessing component in algorithms for the automatic extraction of the anatomical structures of the retina. We propose a method to automatically locate the ONH in fundus images of the retina. The method includes edge detection using the Sobel operators and detection of circles using the Hough transform. The Hough transform assists in the detection of the center and radius of a circle that approximates the margin of the ONH. Forty images of the retina from the Digital Retinal Images for Vessel Extraction (DRIVE) dataset were used to test the performance of the proposed method. The center and boundary of the ONH were independently marked by an ophthalmologist for evaluation. Free-response receiver operating characteristics (FROC) analysis as well as measures of distance and overlap were used to evaluate the performance of the proposed method. The centers of the ONH were detected with an average distance of 0.36 mm to the corresponding centers marked by the ophthalmologist; the detected circles had an average overlap of 0.73 with the boundaries of the ONH drawn by the ophthalmologist. FROC analysis indicated a sensitivity of detection of 92.5% at 8.9 false-positives per image. With an intensity-based criterion for the selection of the circle and a limit of 40 pixels (0.8 mm) on the distance between the center of the detected circle and the manually identified center of the ONH, a successful detection rate of 90% was obtained with the DRIVE dataset.
Key words: Retinal images, fundus images, optic nerve head (ONH), Hough transform, Sobel operators, Canny method, FROC analysis
Introduction
Screening programs for retinopathy are in effect at many health care centers around the world. Such programs require large numbers of fundus images of the retina to be analyzed for the presence of pathology. Automation of retinal image analysis could provide a number of benefits. An important prerequisite for automated or computer-aided analysis of images of the retina is the accurate localization of the main anatomical features in the image, notably the optic nerve head (ONH), also known as the optic disc.1,2 The ONH appears toward the left-hand or right-hand side of a fundus image as an approximately circular area, roughly one-sixth the width of the image in diameter, brighter than the surrounding area, and as the convergent area of the network of blood vessels.3 In an image of a normal retina, all of the properties mentioned above (shape, color, size, and convergence) contribute to the identification of the ONH.
Digital analysis of retinal images has the potential to enhance quantitative and standardized analysis of retinal pathological lesions and vessel abnormalities. Different types of retinopathy, including retinopathy of prematurity,4 diabetic retinopathy,5 and age-related macular degeneration,6 may be detected and analyzed using digital image processing and pattern analysis techniques. Standardized identification and localization of retinal lesions could contribute to improved diagnosis, treatment, and management of retinopathy. In the process of analysis of retinal pathology, normal structures need to be located and identified. The locations and characteristics of normal anatomical landmarks may be subsequently used in the detection and analysis of abnormal features. Towards this end, we propose a method for the detection of the ONH.
Review of Methods for the Detection of the Optic Nerve Head
We present here a selective review of recently proposed methods and algorithms to locate the ONH in images of the retina.
Property-Based Methods
Based on the brightness and roundness of the ONH, Park et al.2 presented a method using algorithms which include thresholding, detection of object roundness, and circle detection. The successful detection rate obtained was 90.25% with the 40 images in the Digital Retinal Images for Vessel Extraction (DRIVE) dataset.7,8 Similar methods have been described by Barrett et al.9 ter Haar10 and Chrástek et al.11,12 Sinthanayothin et al.13 located the ONH by identifying the area with the highest variation in intensity using a window size equal to that of the ONH. The images were preprocessed using an adaptive local contrast enhancement method applied to the intensity component. The method was tested with 112 images obtained from a diabetic screening service; a sensitivity of 99.1% was achieved.
Matched Filter
In the work of Osareh et al.,14 a template image was created by averaging the ONH region of 25 color-normalized images. After locating the center of the ONH by using the template, gray-scale morphological filtering and active-contour modeling were used to locate the ONH region. An average accuracy of 90.32% in locating the boundary of the ONH was reported, with 75 images of the retina.
The algorithm proposed by Youssif et al.15 is based on matching the expected directional pattern of the retinal blood vessels in the vicinity of the ONH. A direction map of the segmented retinal vessels was obtained by a two-dimensional (2D) Gaussian matched filter. The minimum difference between the matched filter and the vessels’ directions in the surrounding area of each ONH center candidate was found. The ONH center was detected correctly in 80 out of 81 images (98.77%) from a subset of the Structured Analysis of the Retina (STARE) dataset16,17 and all of the 40 images (100%) of the DRIVE dataset. A similar method has been implemented by ter Haar.10
A template-matching approach was implemented by Lalonde et al.18 The design relies on a Hausdorff-based template-matching technique using edge maps, guided by pyramidal decomposition for large-scale object tracking. The proposed methods were tested with a dataset of 40 fundus images of variable visual quality and retinal pigmentation, as well as of normal and small pupils. An average error of 7% in positioning the center of the ONH was reported.
Geometrical Model
The method proposed by Foracchia et al.19 is based on a preliminary detection of the major retinal vessels. A geometrical parametric model, where two of the model parameters are the coordinates of the ONH center, was proposed to describe the general direction of retinal vessels at any given position. Model parameters were identified by means of a simulated annealing optimization technique. The estimated values provided the coordinates of the center of the ONH. An evaluation of the proposed procedure was performed using a set of 81 images from the STARE dataset, containing both normal and pathological images. The position of the ONH was correctly identified in 79 out of the 81 images (97.53%).
Fractal-Based Method
Ying et al.20 proposed an algorithm to differentiate the ONH from other bright regions, such as hard exudates and artifacts, based on the fractal dimension related to the converging pattern of the blood vessels. The ONH was segmented by local histogram analysis. The scheme was tested with the DRIVE dataset and identified the ONH in 39 out of 40 images.
Warping and Random Sample Consensus
A method was proposed by Kim et al.21 to analyze images obtained by retinal nerve fiber layer photography. In their proposed method, the center of the ONH was selected as the brightest point and an imaginary circle was defined. Applying the random sample consensus technique, the imaginary circle was first warped into a rectangle and then inversely warped into a circle to find the boundary of the ONH. The images used to test the method included 43 normal images and 30 images with glaucomatous changes. The reported performance of the algorithm was 91% sensitivity and 78% positive predictability.
Convergence of Blood Vessels
Hoover and Goldbaum16 used fuzzy convergence to detect the origin of the blood vessel network which can be considered as the center of the ONH in a fundus image. Their method was tested using 30 images of normal retinas and 51 images of retinas with pathology from the STARE dataset, containing such diverse symptoms as tortuous vessels, choroidal neovascularization, and hemorrhages that obscure the ONH. The rate of successful detection achieved was 89%. Fleming et al.1 used the elliptical form of the major retinal blood vessels to obtain an approximate region of the ONH, which was then refined based on the circular edge of the ONH. The methods were tested on 1,056 sequential images from a retinal screening program. In 98.4% of the cases tested, the error in the ONH location was less than 50% of the diameter of the ONH.
Tensor Voting and Adaptive Mean-Shift
The method proposed by Park et al.22 was based on tensor voting to analyze vessel structures; the position of the ONH was identified by mean-shift-based mode detection. Park et al. used three preprocessing stages through illumination equalization to enhance local contrast and extract vessel patterns by tensor voting in the equalized images. The position of the ONH was identified by mode detection based on the mean-shift procedure. Their method was evaluated with 90 images from the STARE dataset and achieved 100% success rate on 40 images of normal retinas and 84% on 50 images of retinas with pathology.
Genetic Algorithms
Carmona et al.23 proposed a method to obtain an ellipse approximating the ONH using a genetic algorithm. The parameters characterizing the shape of the ellipse obtained were also provided by the algorithm. Initially, a set of hypothesis points were obtained that exhibited geometric properties and intensity levels similar to the ONH contour pixels. Next, a genetic algorithm was used to find an ellipse containing the maximum number of hypothesis points in an offset of its perimeter, considering some constraints. The method is designed to locate and segment the ONH in the images of the retina without any intervention by the user. The method was tested with 110 images of the retina. The results were compared with a gold standard, generated from averaging different contours traced by experts; the results for 96% of the images had less than 5 pixels of discrepancy. Hussain24 proposed a method combining a genetic algorithm and active-contour models; no quantitative results were reported.
We have developed a method for the detection of the ONH including steps for the preprocessing of the images using morphological filters, detecting edges using the Sobel or Canny method, detecting circles using the Hough transform, and selecting the best-fitting circle.25 The procedures in this method and the results obtained are described in detail in the following sections.
Methods
Datasets and Annotation of Images of the Retina
Fundus images of the retina from the DRIVE dataset,7,8 which contains 40 images, are used in the present work. The images in the DRIVE dataset are of size 584 × 565 pixels each, with a field of view of 45° and an approximate spatial resolution of 20 μm/pixel.11 Out of the 40 images in the DRIVE dataset, 33 are normal and seven contain signs of diabetic retinopathy.7,8
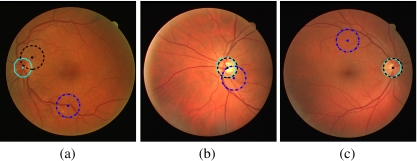
The performance of the proposed method was evaluated by comparing the detected center and boundary of the ONH to the same as independently marked by an ophthalmologist and retina specialist (A.L.E.). The center and the contour of the ONH were drawn on each image, by magnifying the original image by 300% using the software ImageJ.26 When drawing the contour of the ONH, attention was paid so as to avoid the rim of the sclera (scleral crescent or peripapillary atrophy) and the rim of the optic cup, which, in some images, may be difficult to differentiate from the ONH. When labeling the center of the ONH, care was taken not to mark the center of the optic cup or the focal point of convergence of the central retinal vein and artery. Figure 1 illustrates the features mentioned above on two examples.
Fig. 1.
a Image 07 from the DRIVE dataset. b Image 07 with the ONH and scleral crescent marked. The triangle is the center of the ONH marked by the ophthalmologist. The circle corresponds to the focal point of convergence of the blood vessels. c Image 18. d Image 18 with the ONH and optic cup marked.
Preprocessing of Images
After normalizing each component of the original color image (dividing by 255), the result was converted to the luminance component Y, computed as Y = 0.299R + 0.587G + 0.114B, where R, G, and B are the red, green, and blue components, respectively, of the color image. The effective region of the image was thresholded using the normalized threshold of 0.1; the threshold was determined experimentally. The artifacts present in the images at the edges were removed by applying morphological erosion27 with a disc-shaped structuring element of diameter 10 pixels. A mask was generated with the obtained effective region.
In order to avoid the detection of edges at the border of the effective region, each image was extended beyond the limits of its effective region.28,29 First, a 4-pixel neighborhood was used to identify the pixels at the outer edge of the effective region. For each of the pixels identified, the mean gray level was computed over all pixels in a 21 × 21 neighborhood that were also within the effective region and assigned to the corresponding pixel location. The effective region was merged with the outer edge pixels, forming an extended effective region. The procedure was repeated 50 times, extending the image by a ribbon of width 50 pixels. The original version of the testing image 05 in the DRIVE dataset is shown in Figure 2a; the corresponding preprocessed image is shown in Figure 2b.
Fig. 2.
a DRIVE testing image 05. b Preprocessed luminance image. c Binary edge image obtained using the Sobel operators. The threshold was set to be 0.02 of the normalized intensity. d Hough space with c = 31 pixels. e Hough space with c = 41 pixels. f Hough space with c = 50 pixels. g Successfully detected ONH, with distance = 0.1 mm and overlap = 0.79.
After preprocessing, a 5 × 5 median filter was applied to the luminance (gray-scale) image to remove outliers in the image. Then, the maximum intensity in each image was calculated to serve as a reference intensity for the selection of the best-fitting circular approximation of the ONH.
Detection of Edges
The Sobel operators27,30 for the horizontal and vertical gradients are defined as follows:
 |
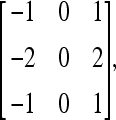1 |
 |
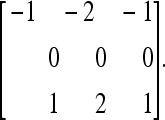2 |
The horizontal and vertical components of the gradient, Gx(x,y) and Gy(x,y), respectively, were obtained by convolving the preprocessed gray-scale image with the corresponding Sobel operators. The combined gradient magnitude was obtained as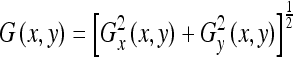 
. A threshold was applied to the gradient magnitude image to obtain a binary edge map. The MATLAB31 version of the Sobel operators was used, and the threshold for each image in the DRIVE dataset was set to be 0.02 of the normalized intensity; the threshold was determined experimentally. The resulting binarized edge image is shown in Figure 2c for the test image shown in Figure 2a.
In a related preliminary work,25 we compared the performance of edge maps obtained using the Sobel operators and the Canny method.32 The sparse edge maps provided by the Sobel operators led to a higher accuracy in the detection of the ONH than the edge maps with connected lines provided by the Canny method. Based on this result, in the present work, only the Sobel operators were used.
The Hough Transform for the Detection of Circles
Hough33 proposed a method to detect straight lines in images. The Hough transform has been extended to identify circles and other parameterized geometrical shapes.34,30,27 The points lying on the circle:
 |
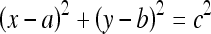3 |
are represented by a single point in the three-dimensional (3D) parameter space (a,b,c) with an accumulator of the form A(a,b,c), which is also known as the Hough space. Here, (a,b) is the center and c is the radius of the circle. The procedure to detect circles involves the following steps:
Obtain a binary edge map of the image.
Set values for a and b.
Solve for the value of c that satisfies Eq. 3.
Increment the accumulator that corresponds to (a,b,c).
Update values for a and b within the range of interest and go back to step 3.
Planes of the Hough space for the testing image 05 in the DRIVE dataset with c = 31, 41, and 50 pixels are shown in Figure 2d–f, respectively. Each local maximum in each plane of the Hough space corresponds to a possible circle with the corresponding radius and center in the original image. By analyzing the various local maxima in the Hough space, we can find the best-fitting circular approximation of the ONH with the corresponding center and radius, as described in the following section.
Procedure for the Detection of the ONH
Because the ONH usually appears as a circular region, an algorithm for the detection of circles may be expected to solve the problem.25 The Hough accumulator is a 3D array, each cell of which is incremented for each nonzero pixel of the edge map that meets the stated condition. For example, the value for the cell (a,b,c) in the Hough accumulator is equal to the number of edge map pixels of a potential circle in the image with the center at (a,b) and radius c. In the case of the images in the DRIVE dataset, the size of each image is 584 × 565 pixels; the spatial resolution of the images is about 20 μm/pixel. The physical diameter of the ONH is about 1.5 mm, on average.18 Assuming the range of the radius of a circular approximation to the ONH to be 600–1,000 μm, the range for the radius c was determined to be 31–50 pixels. Hence, the size of the Hough accumulator was set to be 584 × 565 × 20. The potential circles indicated by the Hough accumulator were ranked, and the top 30 were selected for further analysis.
Because we expect the ONH to be one of the bright areas in the image, a threshold equal to 0.9 times the reference intensity (determined for each image as described in the “Preprocessing of Images” section) was used to check the maximum intensity within a circular area with half of the radius of the potential circle. If the test failed, the circle was rejected, and the next circle was tested.
Evaluation Using Overlap and Distance
The results of detection of the ONH consist of the center point and the radius of a circle. In order to evaluate the accuracy of the results, for each image, the Euclidean distance between the detected center and the corresponding center marked by the ophthalmologist was computed in pixels and converted to millimeters. In addition, the overlap between the circular approximation and the contour of the ONH drawn by the ophthalmologist was computed as:
 |
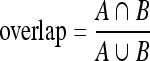4 |
where A is the region marked by the ophthalmologist and B is the region detected by the proposed method. The value of overlap is limited to the range [0, 1].
Analysis using Free-Response Receiver Operating Characteristics
Free-response receiver operating characteristics (FROC) are displayed on a plot with the sensitivity of detection on the ordinate and the mean number of false-positive responses per image on the abscissa.35 FROC analysis is applicable when there is no specific number of true negatives, which is the case in the present study.
For FROC analysis, the top ten potential circles in the Hough space were selected in order to test for the detection of the ONH. For the images in the DRIVE dataset, a result was considered to be successful if the detected ONH center is positioned within the average radius of 0.8 mm (40 pixels) of the manually identified center; otherwise, it was labeled as a false-positive.
Results
The proposed method was tested with the 40 images from the DRIVE dataset.7,8 The edge images obtained using the Sobel operators were binarized using a fixed threshold of 0.02. If the threshold is set too low, there will be more nonzero pixels in the edge map, leading to more computation with the Hough transform. If the threshold is too high, there could be very few nonzero pixels to define an approximate circle around the ONH, which could cause the detection method to fail. An optimal threshold may need to be determined for each dataset. Figure 2g shows the result of detection for the test image in Figure 2a. This is an example of successful detection, with distance = 0.1 mm and overlap = 0.79 with reference to the center and contour of the ONH drawn by the ophthalmologist (not shown in the figure).
Figure 3 shows three further examples from the DRIVE dataset. In each case, the dash–dot circle corresponds to the global maximum in the Hough parameter space; the dashed circle corresponds to the highest local maximum in the Hough space that also meets the condition based on 90% of the reference intensity; the contour in solid line is the contour of the ONH marked by the ophthalmologist.
Fig. 3.
a Test image 03 of the DRIVE dataset. Distance = 1.15 mm, overlap = 0.12 with the intensity condition. The dash–dot circle corresponds to the global maximum in the Hough parameter space. The dashed circle corresponds to the highest local maximum in the Hough space that also meets the condition based on 90% of the reference intensity. The contour in solid line is the contour of the ONH marked by the ophthalmologist. b Test image 04 of the DRIVE dataset. Distance = 0.06 mm, overlap = 0.88 with the intensity condition. c Test image 10 of the DRIVE dataset. Distance = 0.04 mm, overlap = 0.90 with the intensity condition.
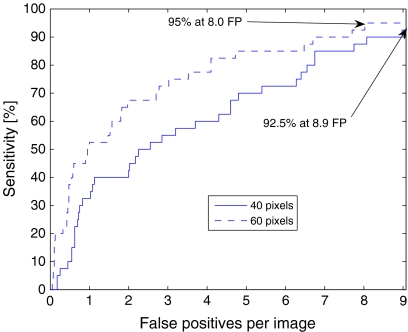
The results of the evaluation of detection of the ONH for the DRIVE dataset are shown in Table 1. The mean distance of the detected center of the ONH with the intensity-based condition is 0.36 mm (18 pixels); the average overlap is 0.73. With the condition for successful detection defined as a distance of less than 40 pixels between the detected and the manually marked centers, the rate of successful detection is 90%. The FROC curve for the DRIVE dataset is shown in Figure 4, which indicates a sensitivity of 92.5% at 8.9 false-positives per image; note that the intensity-based condition for the selection of circles is not applicable in FROC analysis.
Table 1.
Statistics of the Distance and Overlap between the Manually Marked and the Detected ONH for the 40 Images in the DRIVE Dataset
| Method | Distance, mm (pixels) | Overlap | ||||||
|---|---|---|---|---|---|---|---|---|
| Mean | Min | Max | SD | Mean | Min | Max | SD | |
| First peak in Hough space | 1.05 (52.5) | 0.03 (1.5) | 7.53 (376.5) | 1.87 (93.5) | 0.58 | 0 | 0.95 | 0.36 |
| Peak selected using intensity condition | 0.36 (18) | 0.02 (1.0) | 6.17 (308.5) | 1.00 (50) | 0.73 | 0 | 0.95 | 0.25 |
Min minimum, Max maximum, SD standard deviation
Fig. 4.
FROC curve for the DRIVE dataset (40 images). The threshold for successful detection is 40 pixels from the manually marked center for the solid line and 60 pixels for the dashed line. FP false-positive.
If the condition for successful detection is defined as a distance of less than 60 pixels between the detected and the manually marked centers, as used by Youssif et al.,15 the overall accuracy increases to 95%. FROC analysis leads to a sensitivity of 95% at 8.0 false-positives per image.
Discussion
In Table 2, we have listed the success rates of locating the ONH reported by several methods published in the literature and reviewed in the “Review of Methods for Detection of the Optic Nerve Head” section. However, there is no established standard for successful detection. In Table 3, we have listed the various methods used to evaluate the detection of the ONH with the DRIVE dataset. Many of the published reports are not clear about how a successful detection is defined. Some researchers used their own datasets instead of the publicly available datasets, which makes comparative analysis difficult. Furthermore, in our work, an ophthalmologist marked the center and contour of the ONH for use as the ground truth; in the other works reported in the literature, it is not clear if an ophthalmologist marked the ONH for evaluation of the results. Although our success rate with the DRIVE dataset is not the highest among the works listed in Table 2, our proposed method has the advantage that it does not require preliminary detection of blood vessels, and hence, has lower complexity than the other methods reported. The difference of 1 pixel between the average distance of the results of Youssif et al.15 and our results is negligible. Similar methods used by Barrett et al.,9 ter Haar,10 and Chrástek et al.11,12 were not tested with the publicly available DRIVE dataset to facilitate comparative analysis. Another advantage of the proposed method is that it can locate the center of the ONH and provide a circular approximation to its boundary. The circular approximation may be further processed using active contours or other methods to obtain improved estimates of the boundary of the ONH. However, our method might fail when the ONH is dim or blurred because we use the expected property that the ONH is one of the bright areas in the image.
Table 2.
Comparison of the Efficiency of Locating the ONH in Images of the Retina obtained by Different Methods
| Method of detection | DRIVE (%) | STARE (%) | Other dataset (%) |
|---|---|---|---|
| Park et al.2 | 90.3 | – | – |
| Sinthanayothin et al.13 | – | – | 99.1 |
| Osareh et al.14 | – | – | 90.3 |
| Youssif et al.15 | 100 | 98.8 | – |
| Lalonde et al.18 | – | – | 93 |
| ter Haar10 | – | 93.8 | – |
| Foracchia et al.19 | – | 97.5 | – |
| Ying et al.20 | 97.5 | – | – |
| Kim et al.21 | – | – | 91 |
| Hoover and Goldbaum16 | – | 89 | – |
| Fleming et al.1 | – | – | 98.4 |
| Park et al.22 | – | 91.1 | – |
| Our proposed method | 90 or 95 | – | – |
In our method, for the images of the DRIVE dataset, a result was considered to be successful if the detected ONH center is positioned within 40 pixels of the manually identified center. The efficiency increases to 95% if the distance limit is changed to 60 pixels, as used by Youssif et al.15
Table 3.
Comparison of Different Methods Tested with the DRIVE Dataset, in terms of the Distance between the Manually Marked and the Detected Center
| Authors | Method | Manual marking | Average distance (pixels) | Definition of success (pixels) |
|---|---|---|---|---|
| Park et al.2 | Brightness and Hough transform | Yes | Not provided | Not specified |
| Youssif et al.15 | Direction matched filter | Yes | 17 | 60 |
| Ying et al.20 | Brightness and local fractal analysis | No | Not provided | Not specified |
| Our proposed method | Brightness and Hough transform | Yes | 18 | 40 |
The definition of success is specified as the maximum allowed distance between the manually marked and the detected center for a successful detection
We have performed analysis of the results in two different ways. One approach involves the assessment of the overlap and distance between the manually marked and detected ONHs. The second approach is based on FROC analysis, which has not been reported in any of the published works on the detection of the ONH.
From Table 1, we can find that, with the inclusion of selection based on the reference intensity, the average distance has been reduced and the average overlap has been increased, leading to better performance of the proposed method with the DRIVE dataset.
Misleading features that affected the performance of the method were grouped by the ophthalmologist (A.L.E.) into white lesions (two images) and vessel curvature (one image). A preliminary study25 on the application of the proposed method to the STARE dataset indicated poor performance in the detection of the ONH due to misleading pathological features.
Further work and other approaches are required to develop methods that can provide high rates of successful detection of the ONH with images including several types of pathology. We are exploring the potential application of Gabor filters29,36 and phase portrait analysis37 for the detection of the ONH as the location of convergence of the retinal blood vessels.38
Conclusion
We have proposed a method for the automatic detection of the ONH in fundus images of the retina. The proposed methods performed very well with the 40 images in the DRIVE dataset, with an average distance of 0.36 mm and overlap of 0.73 with reference to the centers and contours of the ONH marked by an ophthalmologist.
Further studies are required to incorporate additional characteristics of the ONH to improve the efficiency of detection, especially in the case of images of retina affected by pathology.
Acknowledgments
This work was supported by the Natural Sciences and Engineering Research Council of Canada.
References
- 1.Fleming AD, Goatman KA, Philip S, Olson JA, Sharp PF. Automatic detection of retinal anatomy to assist diabetic retinopathy screening. Phys Med Biol. 2007;52:331–345. doi: 10.1088/0031-9155/52/2/002. [DOI] [PubMed] [Google Scholar]
- 2.Park M, Jin JS, Luo S: Locating the optic disc in retinal images. In Proceedings of the International Conference on Computer Graphics, Imaging and Visualisation, IEEE, Sydney, QLD, Australia, July, 2006, p 5
- 3.Michaelson IC, Benezra D. Textbook of the Fundus of the Eye. 3. Edinburgh, UK: Churchill Livingstone; 1980. [Google Scholar]
- 4.Ells A, Holmes JM, Astle WF, Williams G, Leske DA, Fielden M, Uphill B, Jennett P, Hebert M. Telemedicine approach to screening for severe retinopathy of prematurity: a pilot study. Ophthalmology. 2003;110(11):2113–2117. doi: 10.1016/S0161-6420(03)00831-5. [DOI] [PubMed] [Google Scholar]
- 5.Patton N, Aslam TM, MacGillivray T, Deary IJ, Dhillon B, Eikelboom RH, Yogesan K, Constable IJ. Retinal image analysis: concepts, applications and potential. Progr Retin Eye Res. 2006;25(1):99–127. doi: 10.1016/j.preteyeres.2005.07.001. [DOI] [PubMed] [Google Scholar]
- 6.Acharya R, Tan W, Yun WL, Ng EYK, Min LC, Chee C, Gupta M, Nayak J, Suri JS. The human eye. In: Acharya R, Ng EYK, Suri JS, editors. Image Modeling of the Human Eye. Norwood, MA: Artech House; 2008. pp. 1–35. [Google Scholar]
- 7.Staal J, Abràmoff MD, Niemeijer M, Viergever MA, Ginneken B. Ridge-based vessel segmentation in color images of the retina. IEEE Trans Med Imag. 2004;23(4):501–509. doi: 10.1109/TMI.2004.825627. [DOI] [PubMed] [Google Scholar]
- 8.DRIVE: Digital Retinal Images for Vessel Extraction, http://www.isi.uu.nl/Research/Databases/DRIVE/, accessed on March 24, 2008
- 9.Barrett SF, Naess E, Molvik T. Employing the Hough transform to locate the optic disk. Biomed Sci Instrum. 2001;37:81–86. [PubMed] [Google Scholar]
- 10.ter Haar F: Automatic localization of the optic disc in digital colour images of the human retina. Master’s thesis, Utrecht University, Utrecht, The Netherlands, 2005
- 11.Chrástek R, Skokan M, Kubecka L, Wolf M, Donath K, Jan J, Michelson G, Niemann H: Multimodal retinal image registration for optic disk segmentation. In Methods of Information in Medicine, German BVM-Workshop on Medical Image Processing, Schattauer GmbH, Germany, volume 43, 2004, pp 336–342 [PubMed]
- 12.Chrástek R, Wolf M, Donath K, Niemann H, Paulus D, Hothorn T, Lausen B, Lämmer R, Mardin CY, Michelson G. Automated segmentation of the optic nerve head for diagnosis of glaucoma. Med Image Anal. 2005;9(4):297–314. doi: 10.1016/j.media.2004.12.004. [DOI] [PubMed] [Google Scholar]
- 13.Sinthanayothin C, Boyce JF, Cook HL, Williamson TH. Automated localisation of the optic disc, fovea, and retinal blood vessels from digital colour fundus images. Br J Ophthalmol. 1999;83(4):902–910. doi: 10.1136/bjo.83.8.902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Osareh A, Mirmehd M, Thomas B, Markham R. Comparison of colour spaces for optic disc localisation in retinal images. In Proceedings 16th International Conference on Pattern Recognition, Quebec City, Quebec, Canada, 2002, pp 743–746
- 15.Youssif AAHAR, Ghalwash AZ, Ghoneim AASAR. Optic disc detection from normalized digital fundus images by means of a vessels’ direction matched filter. IEEE Trans Med Imag. 2008;27(1):11–18. doi: 10.1109/TMI.2007.900326. [DOI] [PubMed] [Google Scholar]
- 16.Hoover A, Goldbaum M. Locating the optic nerve in a retinal image using the fuzzy convergence of the blood vessels. IEEE Trans Med Imag. 2003;22(8):951–958. doi: 10.1109/TMI.2003.815900. [DOI] [PubMed] [Google Scholar]
- 17.Structured Analysis of the Retina, http://www.ces.clemson.edu/˜ahoover/stare/, accessed on March 24, 2008
- 18.Lalonde M, Beaulieu M, Gagnon L. Fast and robust optic disc detection using pyramidal decomposition and Hausdorff-based template matching. IEEE Trans Med Imag. 2001;20(11):1193–1200. doi: 10.1109/42.963823. [DOI] [PubMed] [Google Scholar]
- 19.Foracchia M, Grisan E, Ruggeri A. Detection of optic disc in retinal images by means of a geometrical model of vessel structure. IEEE Trans Med Imag. 2004;23(10):1189–1195. doi: 10.1109/TMI.2004.829331. [DOI] [PubMed] [Google Scholar]
- 20.Ying H, Zhang M, Liu JC: Fractal-based automatic localization and segmentation of optic disc in retinal images. In Proceedings of the 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, IEEE, Lyon, France, August 23–26, 2007, pp 4139–4141 [DOI] [PubMed]
- 21.Kim SK, Kong HJ, Seo JM, Cho BJ, Park KH, Hwang JM, Kim DM, Chung H, Kim HC: Segmentation of optic nerve head using warping and RANSAC. In Proceedings of the 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, IEEE, Lyon, France, August 23–26, 2007, pp 900–903 [DOI] [PubMed]
- 22.Park J, Kien NT, Lee G: Optic disc detection in retinal images using tensor voting and adaptive mean-shift. In IEEE 3rd International Conference on Intelligent Computer Communication and Processing, ICCP, Cluj-Napoca, Romania, 2007, pp 237–241
- 23.Carmona EJ, Rincon M, García-Feijoó J, Martínez de-la Casa JM. Identification of the optic nerve head with genetic algorithms. Artif Intell Med. 2008;43(3):243–259. doi: 10.1016/j.artmed.2008.04.005. [DOI] [PubMed] [Google Scholar]
- 24.Hussain AR: Optic nerve head segmentation using genetic active contours. In Proceeding International Conference on Computer and Communication Engineering, IEEE, Kuala Lumpur, Malaysia, May 13–15, 2008, pp 783–787
- 25.Zhu X, Rangayyan RM: Detection of the optic disc in images of the retina using the Hough transform. In Proceedings of the 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, IEEE, Vancouver, BC, Canada, August 20–24, 2008, pp 3546–3549 [DOI] [PubMed]
- 26.Image Processing and Analysis in Java, http://rsbweb.nih.gov/ij/, accessed on September 3, 2008
- 27.Gonzalez RC, Woods RE. Digital Image Processing. 2. Upper Saddle River, NJ: Prentice Hall; 2002. [Google Scholar]
- 28.Soares JVB, Leandro JJG, Cesar RM, Jr., Jelinek HF, Cree MJ. Retinal vessel segmentation using the 2-D Gabor wavelet and supervised classification. IEEE Trans Med Imag. 2006;25(9):1214–1222. doi: 10.1109/TMI.2006.879967. [DOI] [PubMed] [Google Scholar]
- 29.Rangayyan RM, Ayres FJ, Oloumi F, Oloumi F, Eshghzadeh-Zanjani P. Detection of blood vessels in the retina with multiscale Gabor filters. J Electron Imaging. 2008;17(2):023018. doi: 10.1117/1.2907209. [DOI] [Google Scholar]
- 30.Rangayyan RM. Biomedical Image Analysis. Boca Raton, FL: CRC; 2005. [Google Scholar]
- 31.The MathWorks, http://www.mathworks.com/, accessed on March 24, 2008
- 32.Canny J. A computational approach to edge detection. IEEE Trans Pattern Anal Mach Intell. 1986;PAMI-8(6):670–698. doi: 10.1109/TPAMI.1986.4767851. [DOI] [PubMed] [Google Scholar]
- 33.Hough PVC: Method and means for recognizing complex patterns. US Patent 3,069,654, December 18, 1962
- 34.Duda RO, Hart PE. Use of the Hough transformation to detect lines and curves in pictures. Commun ACM. 1972;15(1):11–15. doi: 10.1145/361237.361242. [DOI] [Google Scholar]
- 35.Egan JP, Greenberg GZ, Schulman AI. Operating characteristics, signal detectability, and the method of free response. J Acoust Soc Am. 1961;33(8):993–1007. doi: 10.1121/1.1908935. [DOI] [Google Scholar]
- 36.Ayres FJ, Rangayyan RM. Design and performance analysis of oriented feature detectors. J Electron Imaging. 2007;16(2):023007. doi: 10.1117/1.2728751. [DOI] [Google Scholar]
- 37.Rangayyan RM, Ayres FJ. Gabor filters and phase portraits for the detection of architectural distortion in mammograms. Med Biol Eng Comput. 2006;44(10):883–894. doi: 10.1007/s11517-006-0088-3. [DOI] [PubMed] [Google Scholar]
- 38.Rangayyan RM, Zhu X, Ayres FJ: Detection of the optic disc in images of the retina using Gabor filters and phase portrait analysis. In Proceedings of 4th European Congress for Medical and Biomedical Engineering, IEEE, Antwerp, Belgium, November 23–27, 2008, pp 468–471