Computer-Aided Detection of Architectural Distortion in Prior Mammograms of Interval Cancer

Abstract

Architectural distortion is an important sign of breast cancer, but because of its subtlety, it is a common cause of false-negative findings on screening mammograms. This paper presents methods for the detection of architectural distortion in mammograms of interval cancer cases taken prior to the detection of breast cancer using Gabor filters, phase portrait analysis, fractal analysis, and texture analysis. The methods were used to detect initial candidates for sites of architectural distortion in prior mammograms of interval cancer and also normal control cases. A total of 4,224 regions of interest (ROIs) were automatically obtained from 106 prior mammograms of 56 interval cancer cases, including 301 ROIs related to architectural distortion, and from 52 prior mammograms of 13 normal cases. For each ROI, the fractal dimension and Haralick’s texture features were computed. Feature selection was performed separately using stepwise logistic regression and stepwise regression. The best results achieved, in terms of the area under the receiver operating characteristics curve, with the features selected by stepwise logistic regression are 0.76 with the Bayesian classifier, 0.73 with Fisher linear discriminant analysis, 0.77 with an artificial neural network based on radial basis functions, and 0.77 with a support vector machine. Analysis of the performance of the methods with free-response receiver operating characteristics indicated a sensitivity of 0.80 at 7.6 false positives per image. The methods have good potential in detecting architectural distortion in mammograms of interval cancer cases.

Introduction

Mammography is the most effective screening tool available for early detection of breast cancer. Early detection of breast cancer is crucial: mammographic screening has been shown to be effective in reducing mortality rates by 30% to 70%.¹ However, interpretation of screening mammograms is difficult, and the sensitivity of screening mammography is affected by image quality, the radiologist’s level of expertise, and the volume of the images to be assessed. Although double reading of screening mammograms has been shown to provide higher sensitivity than single reading,² the resources and expertise required for this purpose render such an approach impractical. Computer-aided diagnosis (CAD) could help in increasing the detection sensitivity and accuracy by providing a “second opinion” to the radiologist and could be almost as effective as double reading.^3,4

Architectural distortion, defined as distortion of the architecture of breast parenchyma without being accompanied by increased density or mass,⁵ is the third most common mammographic sign of nonpalpable breast cancer⁶ and is an important finding in interpreting the manifestation of breast cancer on mammograms.⁷ However, due to its subtlety and variability in presentation, this sign of abnormality is often missed during screening.⁶ The detection of architectural distortion is performed by a radiologist through the identification of subtle signs of abnormality such as the presence of spiculations and distortion of the normal oriented-textured pattern of the breast. CAD techniques and systems have been shown to be effective in detecting masses and microcalcifications with satisfactory performance, but have been found to fail in detecting architectural distortion with a high level of accuracy.⁸ Increasing the sensitivity and accuracy in the detection of architectural distortion could lead to an effective improvement in the prognosis of breast cancer patients⁹ and help in reducing the associated mortality rate.

Although a substantial record of research exists in the literature regarding CAD and classification of masses and calcifications, not many works have been reported so far on the detection of architectural distortion.^7,10–18 Furthermore, only a few studies have been reported on the detection of subtle abnormalities in mammograms acquired before the detection of cancer^16,19–22 to explore the possibilities of detection of early signs of breast cancer. In the context of a screening program, a mammogram on which cancer is detected is referred to as a “detection mammogram,” whereas a mammogram acquired at the last scheduled visit to the screening program prior to the detection of cancer is referred to as a “prior mammogram.”¹⁶ A case of cancer detected in a screening program is referred to as “screen-detected cancer.” The term “interval cancer” is used to indicate a case where breast cancer is detected outside the screening program in the interval between scheduled screening sessions. Studies on prior mammograms of interval cancer cases with the specific aim of detection of architectural distortion^21,22 could help in developing strategies for the detection and treatment of breast diseases at their early stages and lead to substantial improvement in the prognosis.

We hypothesize that screening mammograms obtained prior to the detection of breast cancer could contain subtle signs of early stages of breast cancer, in particular architectural distortion. In this paper, we present methods for the detection of sites of architectural distortion in prior mammograms of interval cancer cases in a screening program using several image processing and pattern classification methods,^21,22 including the artificial neural network (ANN) and the support vector machine (SVM). The image processing methods are based upon Gabor filters,²³ phase portrait analysis,^10–12,24 fractal analysis,^16,25,26 and Haralick’s texture features.^27,28

Detection of Architectural Distortion in Mammograms

Architectural Distortion

Architectural distortion is a common cause of false-negative findings on screening mammograms and is defined in BI-RADS²⁹ as follows: “The normal architecture (of the breast) is distorted with no definite mass visible. This includes spiculations radiating from a point and focal retraction or distortion at the edge of the parenchyma. Architectural distortion can also be an associated finding.” Focal retraction is considered to be easier to recognize than spiculated distortion within the breast parenchyma.⁵ Architectural distortion could be malignant or benign; the malignant category includes cancer, and the benign category includes scar and soft tissue damage due to trauma. Architectural distortion has been found to be associated with breast malignancy in one half to two thirds of the cases in which it is present.⁷ Architectural distortion could appear at the initial stages of the formation of a breast mass or tumor.⁷ Because architectural distortion may mimic the appearance of normal breast tissue overlapped in the projected mammographic image, its detection could be difficult. Specifically, architectural distortion accounts for 12% to 45% of breast cancer cases overlooked or misinterpreted in screening mammography.^30,31 In a study of cases of screening interval breast cancer, it has been found that architectural distortion is the most commonly missed abnormality in false-negative cases.³²

In a mammogram, the breast is seen as a directionally oriented-textured image³³ due to the presence of several piecewise linear structures such as ligaments, ducts, and blood vessels. The normal oriented-texture pattern, which typically converges toward the nipple, is changed in the presence of architectural distortion. Mudigonda and Rangayyan³⁴ explored the use of texture flow field to detect architectural distortion based on the local coherence of texture orientation. Ayres and Rangayyan^11,12,24,35 and Rangayyan and Ayres¹⁰ proposed methods based on the application of Gabor filters and phase portrait modeling to characterize subtle changes due to architectural distortion from a pattern recognition perspective. The methods were applied to two datasets, one set with 19 cases of architectural distortion and 41 normal mammograms from the Mammographic Image Analysis Society (MIAS) database³⁶ and another set with 37 cases of architectural distortion. Sensitivity rates of 84% at 4.5 false positives per image and 81% at 10 false positives per image were obtained from an analysis of the free-response receiver operating characteristics (FROC) for the two sets of images.¹²

Matsubara et al.^7,37 used morphological image processing techniques along with a concentration index to detect architectural distortion around the skin line and within the mammary gland; the sensitivity obtained was 94% with 2.3 false positives per image and 84% with 2.4 false positives per image, respectively. Ichikawa et al.³⁸ presented an automatic method for the detection of areas related to spiculated architectural distortion; suspicious areas were detected by means of a concentration index of linear structures obtained using the mean curvature of the given image. Discriminant analysis was performed with the nine features obtained for classification, and a sensitivity of 68% with 3.4 false positives per image was obtained. Hara et al.³⁹ used dynamic range compression as a preprocessing step before extracting the mammary gland by a combination of mean curvature and shape index; a sensitivity of 70% was achieved at 2 false positives per image. Matsubara et al.⁴⁰ proposed a modification of their previous method for the detection of architectural distortion using the mean curvature of images with a combination of two levels of resolution after dynamic range compression and improved the accuracy of extraction for thin mammary glands; at the final stage, they obtained a sensitivity of 75% at 2.9 false positives per image.

Guo et al.⁴¹ studied the characterization of architectural distortion using the Hausdorff fractal dimension (FD) and an SVM to perform classification of regions of interest (ROIs) exhibiting architectural distortion and those with normal mammographic patterns. A set of 40 ROIs was selected from the MIAS database,³⁶ including 19 ROIs with architectural distortion and 21 ROIs with normal tissue patterns. The best classification accuracy obtained was 72.5%. Guo et al.¹⁷ also used five different methods to estimate the FD and an SVM to differentiate masses and architectural distortion from normal parenchyma; using FD and lacunarity, the best result obtained for architectural distortion in terms of area under the receiver operating characteristics (ROC) curve (area under the curve, AUC) was 0.875 ± 0.055.

Sampat and Bovik⁴² and Sampat et al.^15,43 applied a linear filter to the Radon transform of the given image for the enhancement of spicules; the enhanced image was filtered with radial spiculation filters to detect spiculated masses and architectural distortion marked by converging lines or spiculation. Using a set of 45 images with spiculated masses and another set of 45 images with architectural distortion, the sensitivity achieved was 91% at 12 false positives per image and 80% at 14 false positives per image, respectively. Özekes et al.⁴⁴ used several distance thresholds to detect architectural distortion and reported an accuracy of 89.02%.

Tourassi et al.¹⁴ investigated the use of FD to distinguish between normal tissue patterns and architectural distortion in mammographic ROIs. The FD was estimated using the circular average power spectrum technique.^25,26 The method was applied to a dataset of 1,500 ROIs, including 112 ROIs with architectural distortion and 1,388 ROIs exhibiting normal tissue patterns. The best performance achieved was 0.89, in terms of AUC. Tourassi et al. observed that the presence of architectural distortion disrupts the self-similarity properties of breast parenchyma and that the average FD of the ROIs with architectural distortion was significantly lower than that of normal ROIs.

Eltonsy et al.⁴⁵ developed a method to detect masses and architectural distortion by locating points surrounded by concentric layers of image activity. A set of 80 images was used to evaluate the technique, including 13 masses, 38 masses with architectural distortion, and 29 images with only architectural distortion. An overall sensitivity of 91.3% with 9.1 false positives per image was obtained. A sensitivity of 93.1% was obtained in the detection of architectural distortion at the same rate of false positives.

Nakayama et al.⁴⁶ performed a multiresolution analysis by decomposing the original digitized image into several sub-images at three scales by a novel filter bank based on wavelets and the Hessian matrix. With six objective features obtained from automatically detected ROIs at three scales, the sensitivity and the number of false positives were 71.3% (57 out of 80 images) and 3.01 per image, respectively.

Nemoto et al.⁴⁷ proposed a method to detect architectural distortion. Validation was performed using 25 computed radiography digital mammograms, each of which had a single area with architectural distortion including radiating spiculation. The methods are based on the observation that the lines corresponding to spiculation related to architectural distortion differ in characteristics from lines in the normal mammary gland. The likelihood of spiculation was computed and a modified point convergence index weighted by the likelihood was calculated to enhance architectural distortion. After the classification step, a sensitivity of 80.0% was obtained at 0.80 false positive per image.

Detection of Architectural Distortion by CAD Systems

A few studies have been reported on analysis of the performance of commercial CAD systems in the detection of architectural distortion. Burhenne et al.⁴⁸ studied the performance of a commercial CAD system for mammography and obtained a sensitivity of 75% in the detection of masses and architectural distortion at 1 false positive per image. Evans et al.⁴⁹ investigated the ability of a commercial CAD system to mark invasive lobular carcinoma of the breast and obtained a sensitivity of 91% with screening mammograms demonstrating biopsy-proven cancer and 77% with the corresponding prior mammograms. Birdwell et al.⁵⁰ studied the performance of a commercial CAD system used for marking the signs of cancer that were overlooked by radiologists; the system was able to detect five out of six cases of architectural distortion and 77% of the previously missed lesions at 2.9 false positives per image. Baker et al.⁸ evaluated the performance of two commercial CAD systems in detecting architectural distortion; fewer than 50% of the 45 cases of architectural distortion were detected, with a lower image-based sensitivity of 38%, or 30 out of 80 images, at 0.7 false positive per image.

Analysis of Mammograms Acquired Prior to the Detection of Breast Cancer

Screening mammography has limited sensitivity⁵¹; it has been observed that subtle signs of abnormality can be identified in a significant portion of prior mammograms of screen-detected¹⁶ or interval cancer cases.^19–22 Such cases of abnormality include subtle or hard-to-detect features or patterns that can indicate early signs of breast cancer. Only a few studies have been reported on the analysis of prior mammograms to explore the possibilities of detection of early signs of breast cancer.

Rangayyan et al.¹⁶ used phase portraits, FD, and texture features for the detection of architectural distortion in prior mammograms of screen-detected cancer and achieved a sensitivity of 79% at 8.4 false positives per image with a set of 14 prior mammograms.

Sameti et al.⁵² evaluated the structural differences between regions related to subsequent development of malignant masses and other normal areas in the last screening mammograms prior to the detection of tumors. Circular ROIs were manually identified and transformed into their optical density equivalent images. The selected ROIs were further divided into three types of regions representing low, medium, and high optical density, and photometric and texture features were extracted. In 72% of the 58 cases of breast cancer studied, differences were observed between regions related to malignant tumors and normal tissues in the prior mammograms. Sameti et al.²⁰ also reported an average classification rate of 72% using six selected texture and photometric features computed from manually marked regions on the last screening mammograms prior to the detection of breast cancer.

Burnside et al.⁵³ evaluated the effect of the availability of prior mammograms on the clinical outcomes of diagnostic and screening mammography and reported that incorporating prior mammograms improved the specificity of screening mammography significantly but did not improve the sensitivity. However, the approach increased the sensitivity of diagnostic mammography. Sumkin et al.⁵⁴ assessed and compared the benefit of using images acquired 1 or 2 years previously during the interpretation of current mammograms; it was found that the sensitivity was not significantly affected by the availability of the prior mammograms, but the specificity was improved. Varela et al.⁵⁵ found that the use of prior mammograms as reference could significantly increase the accuracy of classification between benign and malignant masses.

Zheng et al.⁵⁶ analyzed a method for the detection of masses in current and prior mammograms in two situations: one with the algorithm optimized using the current mammograms and the other with the algorithm optimized using the related prior mammograms. The method included three steps: difference of Gaussian filtering and thresholding for the initial selection of potential sites of lesions; adaptive region growing and topological analysis of the suspicious regions to eliminate false positives; and feature extraction (including shape, histogram, and texture features) and classification using an ANN. A database of 260 pairs of consecutive mammograms was used where the latest image showed one or two masses, and the prior image had been originally classified as negative or probably benign. The first two steps of the method were applied to both the latest and prior images, resulting in a set of 1,449 suspicious ROIs which were classified according to the true mass location in the corresponding latest mammograms. The ROIs were classified into the normal and mass categories using the third step of feature extraction and classification. Training the ANN with the latest mammograms resulted in AUC = 0.89 ± 0.01 and 0.65 ± 0.02 when classifying ROIs from the latest and prior mammograms, respectively. When the ANN was trained with ROIs from the prior mammograms, the classification performance was AUC = 0.81 ± 0.02 and 0.71 ± 0.02 with ROIs from the latest and prior mammograms, respectively. The results demonstrate the importance of incorporating knowledge about the particular features of early signs of breast cancer.

Petrick et al.⁵⁷ studied the effectiveness of their method for the detection of benign and malignant masses as applied to the related regions in prior mammograms. A set of 92 images, including 54 malignant and 38 benign lesions from 37 cases (22 malignant and 15 benign), was used. The methods achieved a “by film” mass detection sensitivity of 51% with 2.3 false positives per image; a slightly better accuracy of 57% was achieved in the detection of malignant tumors. The detection scheme segmented salient densities via region growing after contrast enhancement; such intensity-based segmentation algorithms may not be adequately robust to detect developing densities with poor contrast in prior mammograms.

Garvican and Field⁵⁸ evaluated the performance of a commercial CAD system with prior mammograms of interval cancer cases; the system was found to over-prompt normal areas and under-prompt cancer in the difficult cases analyzed. Ikeda et al.⁵⁹ analyzed the performance of a commercial CAD system using prior mammograms of 172 cases of cancer with subtle findings; the system was able to detect 42% of the findings. Ciatto et al.⁶⁰ compared single, double, and CAD-assisted reading of negative prior mammograms in cases of interval cancer and concluded that CAD-assisted reading is significantly more specific and almost as sensitive as double reading. However, in a study conducted on CAD-assisted analysis of cases of interval cancer by Moberg et al.,⁶¹ it was found that despite the high sensitivity of the CAD system on its own, the system had no effect on the sensitivity or the specificity of the radiologists.

Simultaneous analysis of current and prior mammograms is recommended for use by radiologists in the detection of breast cancer;^54,55,62 the same approach could enhance the performance of CAD systems. Complementary to systems designed for the detection of well-developed masses or calcifications, the development of CAD systems designed specifically for the detection of subtle signs of breast cancer, such as architectural distortion in prior mammograms, is important and could improve the prognosis by facilitating the detection of breast diseases at their early stages.

Methods

Detection of Potential Sites of Architectural Distortion

The methods proposed in the present work include the analysis of oriented-texture patterns with the application of Gabor filters and phase portrait models¹² for the detection of architectural distortion in prior mammograms. At first, the breast portion of a given mammogram was segmented by applying Otsu’s thresholding method.⁶³ The morphological opening filter⁶⁴ with a disk-shaped structuring element of radius 25 pixels (5 mm at 200 μm per pixel) was used for smoothing the edges. The method for the detection of architectural distortion was applied to the segmented breast portion in a given mammogram, including the stages of extraction of the orientation field using Gabor filters, selection of curvilinear structures (CLS), filtering and downsampling of the orientation field, modeling of phase portraits, and detection of potential sites of architectural distortion.^12,16

Gabor Filters for the Detection of Oriented Patterns

Gabor filters are a category of filters obtained by the modulation of a sinusoidal function (real or complex) by a Gaussian envelope.⁶⁵ The Gabor function has been recognized as a useful tool in computer vision and image processing, especially for texture analysis, due to its optimal localization properties in both the spatial and frequency domains. In image processing applications, Gabor filters may be used as line detectors or detectors of oriented features.^{10,23,33,66,67}

The real Gabor filter kernel oriented at the angle 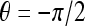is given as^10,23:

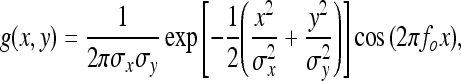1

where σ_x and σ_y are the standard deviation values in the x and y directions and f_o is the frequency of the modulating sinusoid. Kernels at other angles are obtained by rotating this kernel using coordinate transformation as:

where (x′, y′) is the set of coordinates rotated by the angle α. We use a set of 180 kernels with angles spaced evenly over the range 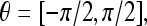. The parameters in Eq. 1 were derived by taking into account the size of the lines or CLS to be detected, as follows¹⁰:

• Let τ be the full width at half-maximum of the Gaussian term in Eq. 1 along the x-axis. Then, .

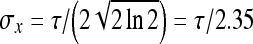• Let the period of the cosine term be τ; then, f = 1/τ.

• The value of σ_y is defined as σ_y = lσ_x, where l determines the elongation of the Gabor filter in the y direction as compared to the extent of the filter in the x direction.

• In the present work, we use τ = 4 pixels (corresponding to a thickness of 0.8 mm at the pixel size of 200 μm) and l = 8.

For each image, a magnitude response and an orientation field were obtained using the response and angle of the Gabor filter with the highest response at each pixel. The CLS of interest (spicules and fibroglandular tissue) were separated from confounding structures (edges of the pectoral muscle and parenchymal tissue, breast boundary, and noise) using the orientation field, the gradient field, the nonmaximal suppression technique, and additional conditions.¹² The selected core CLS pixels and the orientation field were filtered with a Gaussian filter and downsampled by a factor of 4, to an effective resolution of 800 μm/pixel, to reduce noise and further computational requirements.^10,23,24

Phase Portrait Analysis

The phase portrait diagram of a system of two linear, first-order differential equations depicts the possible trajectories of the state variables for different initialization values.⁶⁸ Rao and Jain⁶⁹ developed a method for the analysis of oriented texture which relies on the association of an image presenting an oriented-texture pattern with the appearance of a phase portrait diagram.

Let p(t) and q(t), 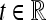, denote two differentiable functions of time t, related as:

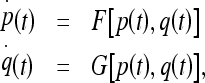2

where 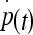and indicate the first-order derivatives with respect to time and F and G represent functions of p and q.¹⁰ Given initial conditions p(0) and q(0), the solution (p(t), q(t)) can be viewed as a parametric trajectory or streamline of a hypothetical particle in the (p, q) plane placed at (p(0), q(0)), at time t = 0, and moving through the (p, q) plane with the velocity . The (p, q) plane is referred to as the phase plane of the system; the phase portrait is a graph of the possible streamlines in the phase plane. A fixed point is a point in the phase plane where and ; a particle left at a fixed point remains stationary. When the system is affine, we have:

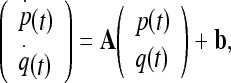3

where A is a 2 × 2 matrix and b is a 2 × 1 column matrix. The center (p₀, q₀) of the phase portrait is given by the fixed point as:

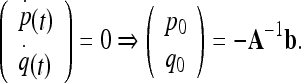4

Associating the functions p(t) and q(t) with the x and y coordinates of the Cartesian (image) plane, we can define the orientation field as:

5

which is the angle of the velocity vector with the x-axis at (x, y) = (p(t), q(t)).

In the model described above, there are three types of phase portraits: node, saddle, and spiral; the type of phase portrait is determined by the nature of the eigenvalues of A.^10,23,68,69 The orientation field of a textured image can be described by determining the type of the phase portrait that is most similar to the orientation field. Because spiral patterns are not of interest in the present work, matrix A was constrained to be symmetric, resulting in only two phase portrait maps: node and saddle. Further conditions were also placed on the distance between the fixed point and the position of the corresponding analysis window. Because a mammogram could exhibit several patterns, a sliding analysis window of size 10 × 10 pixels (at 800 μm/pixel) was used with 1 pixel per step. For each position of the window, a vote was cast at the node position given by the corresponding fixed point. Instances of matrix A with the condition number >3.0 were rejected so as to ignore patterns not associated with architectural distortion.¹² The peaks in the node map are expected to indicate potential sites of architectural distortion. Hence, the node map was analyzed to detect peaks related to the sites of architectural distortion; however, the procedure also results in the detection of a number of false-positive sites.

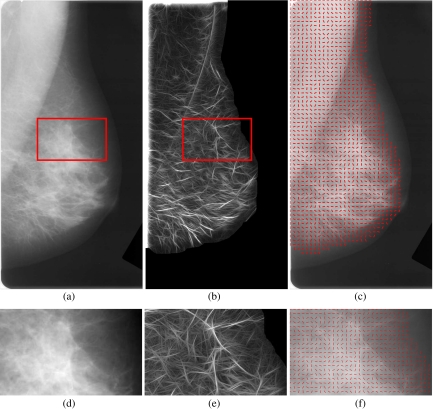
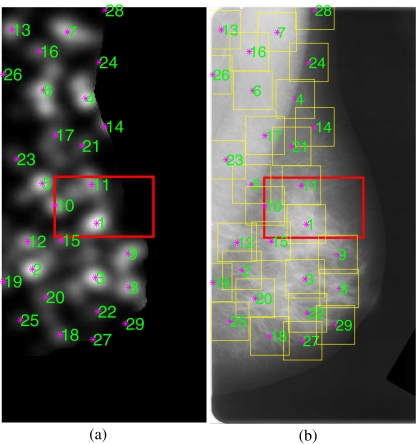
The results of application of the methods are illustrated in Figure 1 for a prior mammogram of an interval cancer case. In part a, the rectangle shows the area of architectural distortion identified by a radiologist (J.E.L.D.). The magnitude image and the orientation field resulting from the Gabor filters are shown in parts b and c, respectively. The node map is shown in part a of Figure 2; the most dominant peak is evident within the site of architectural distortion.

Fig. 1.

a Prior mammogram of an interval cancer case. The rectangle is of size 65 × 39 mm and indicates the region of architectural distortion identified by a radiologist. The size of the full image is 1,372 × 675 pixels at 200 μm per pixel. b Magnitude response obtained using a bank of 180 real Gabor filters. c Orientation field angle superimposed on the mammographic image; needles are drawn for every 12th pixel. d Zoomed view of the rectangular area shown in a. e Magnitude response zoomed. f Orientation field zoomed; needles are drawn for every sixth pixel for clarity.

Fig. 2.

a Node map at 800 μm/pixel for the mammogram in Figure 1a. Each asterisk mark corresponds to a peak position detected automatically in the node map. The numbers next to the asterisk marks indicate the peaks in descending order of magnitude. b The 29 ROIs obtained automatically using the peaks detected in the node map. The size of each ROI is 128 × 128 pixels at 200 μm per pixel (except at the edges).

Feature Extraction

The statistical measures of texture proposed by Haralick et al.^27,28 were used in the present work for the analysis of texture and feature extraction. Haralick’s texture measures are based upon the moments of a joint probability density function that is estimated using the joint occurrence or co-occurrence of gray levels, known as the gray level co-occurrence matrix (GCM), and may be computed for various directions and distances.³³

The GCM P_(d,θ)(l₁, l₂) represents the probability of occurrence of the pair of gray levels (l₁, l₂) separated by the given distance d at the angle θ. In the present work, four normalized GCMs were computed with unit pixel distance for the angles of 0°, 45°, 90°, and 135°. The four GCMs were averaged to obtain a single GCM for computation of Haralick’s 14 texture features, as listed in Table 1.

Table 1.

List of Features Used

Feature type	Feature number	Feature name
Haralick’s texture	1	Energy
	2	Contrast
	3	Correlation
	4	Sum of squares
	5	Inverse difference moment
	6	Sum average
	7	Sum variance
	8	Sum entropy
	9	Entropy
	10	Difference variance
	11	Difference entropy
	12 and 13	Information theoretic measures of correlation
	14	Maximal correlation coefficient
Fractal measure	15	Fractal dimension
Node map	16	Node value

Although many measures or estimates of fractal properties have been proposed,^17,70 FD is the most frequently used measure in medical imaging; see Rangayyan and Nguyen.⁷¹ In diagnostic imaging, the power spectrum estimation method has gained attention because it appears to provide the most accurate and robust estimate of FD.^25,26 Aguilar et al.²⁶ proposed a new frequency analysis method, known as fractal analysis by circular average, and an image replication procedure to produce accurate measurements of FD of surfaces and profiles.

To estimate FD, the 2D Fourier power spectrum of the ROI being processed was obtained, including the application of the von Hann window and zero padding to the size of 256 × 256 pixels. The 2D spectrum was mapped to the radial (f, θ) space from the Cartesian (u, v) space by resampling and taking weighted average of the four neighbors of each point for radial distances ranging from zero to half the sampling frequency and over the range of angles [0, 179°]. Then, the 2D spectrum in the (f, θ) space was transformed into a 1D function S(f) by averaging as a function of the radial distance or frequency f from the zero frequency point over the range [0, 179°] in angle. The spectrum S(f) is considered to be related to the radial frequency f according to the model 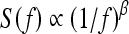.^72–75 Linear regression was applied to a limited frequency range of the 1D spectrum on a log–log scale, excluding points in selected low-frequency and high-frequency regions, to estimate the slope β of the fitted line. The estimated slope is related to FD as^14,16,25,26 FD = (8 − β)/2. Selected low- and high-frequency regions were excluded so as to remove the effects of the low-frequency components related to the overall appearance of the image and the large structures present in the image, as well as to prevent the effects of high-frequency noise. In the present work, the range of f used to fit the linear model is [6, 96] pixels or [0.117, 1.875] mm⁻¹, where the range of [1, 128] pixels corresponds to the discrete representation of the frequency range [0, 2.5] mm⁻¹.

Feature Analysis, Selection, and Classification

Feature selection^76–78 can be performed by evaluating the performance of each feature or combinations of several features based on the p values,⁷⁹ AUC values,^80,81 statistical or distance measures, deviation or error measures, discriminant analysis, genetic programming or algorithms, classification accuracy using a training set,^77,82 or through exhaustive search. The conventional statistic for measuring the significance of a difference of means is the Student’s t test.^79,83 Once a t value is determined, a p value can be found using the table of values from Student’s t distribution. The smaller is the p value, the stronger is the evidence against the null hypothesis.

ROC analysis^80,81 is commonly used to assess the performance of a radiologist or a CAD system in detecting abnormalities in medical images. The ROC curve depicts the sensitivity versus the false-positive rate (complement of the specificity) for various values of the decision threshold. The AUC (or A_z) could be used as a measure of performance of the decision-making system or individual. In FROC analysis,^84,85 the sensitivity is plotted on the ordinate, and the mean number of false-positive responses per image is shown on the abscissa.

Logistic classification is a statistical technique based on a logistic regression model that estimates the probability of occurrence of an event.^33,86 The technique is designed for problems where patterns are to be classified into one of two classes. When the response variable is binary, theoretical and empirical considerations indicate that the response function is often curvilinear. The typical response function is shaped as a forward or backward tilted “S” and is known as a sigmoidal function. The function has asymptotes at 0 and 1. The main approaches of logistic classification are: forward selection, which involves starting with no variables in the model, trying out the variables one by one, and including them if they are statistically significant; backward selection, which involves starting with all candidate variables, testing them one by one for statistical significance, and deleting those that are not significant; and methods that are a combination of the above, testing at each stage for variables to be included or excluded. Stepwise logistic regression includes regression models in which the choice of the predictive variables is carried out by an automatic procedure.⁸⁶ Each step consists of one step of forward selection and one step of backward elimination. These two tasks are repeated until no features can be added or removed.

Feature selection through stepwise regression iteratively varies the number of features used in the classification step by entering features into or removing features from the group of selected features based on a selection criterion using F statistics.⁷⁷

Fisher linear discriminant analysis (FLDA) is based on linear projection of the given L-dimensional feature data onto a line.⁷⁶ The expectation is that such projections onto a line will be well separated by class. Thus, the line is oriented to maximize class separation.⁸⁷ Bayesian decision theory is a fundamental statistical approach to the problem of pattern classification⁷⁶ based on quantifying the trade-offs between various classification decisions using prior probabilities, likelihood functions, and the costs that accompany the decisions.

In many practical problems, we may have no knowledge of the prior probabilities of patterns belonging to one class or another. In such situations, conventional pattern classification methods may not be well suited for the classification of pattern vectors. ANNs could be effective in solving such classification problems.⁸⁸ In general, three fundamentally different classes of network architecture can be identified as single-layer feedforward (SLFF), multilayer feedforward, and recurrent networks. The training of an ANN classifier is typically achieved by the back-propagation algorithm.⁸⁸

The radial basis function (RBF) neural network⁸⁸ is a major class of neural network models in which the activation of a hidden unit is determined by the distance between the input vector and a prototype vector. RBF neural networks can be viewed as a nonlinear mapping between a set of inputs and a set of outputs. Because the mapping functions are nonlinear, it is not necessary to have more than one hidden layer to model any function: a sufficient number of RBF units will approximate the target function. To combine the outputs of the hidden radial units into the network’s outputs, a linear combination of the outputs (i.e., a weighted sum of the Gaussian RBFs) may be used to model any nonlinear function. The standard RBF has an output layer containing dot-product units with identical activation functions.⁸⁸ RBF neural networks can be regarded as linear-in-the-parameters models which have some unique computational advantages over other architectures of neural networks.

A generalized regression neural network (GRNN)⁸⁹ has a radial basis layer and a special linear layer and is often used to approximate a regression function. It is usually faster to train a GRNN than a multilayer perceptron (MLP) network. A GRNN is often more accurate than an MLP; a GRNN is also relatively insensitive to outliers in the data provided.

The SVM is a learning tool based on modern statistical learning theory⁹⁰ and gives useful bounds on the generalization capacity of machines for learning tasks. The SVM algorithm constructs a separating hypersurface in the input space; it maps the input space into a higher dimensional feature space through a nonlinear mapping operation.^90–93 SVMs are a set of related supervised learning methods used for classification and regression. Viewing input data as two sets of vectors in an n-dimensional space, an SVM constructs a separating hyperplane in that space so as to maximize the margin between the two datasets. To calculate the margin, two parallel hyperplanes are constructed, one on each side of the separating hyperplane. Intuitively, a good separation is achieved by the hyperplane that has the largest distance to the neighboring data points of both classes. In general, the larger is the margin, the lower is the generalization error of the classifier.

Experimental Setup and Database

Database of Mammograms

For the present study, mammographic images were obtained from a database of 1,745 digitized mammograms of 170 subjects from Screen Test: Alberta Program for the Early Detection of Breast Cancer.^94,95 Ethics approval of the project was obtained from the Conjoint Health Research Ethics Board, Office of Medical Bioethics, University of Calgary and the Calgary Regional Health Authority. The film mammograms were digitized at the spatial resolution of 50 μm and grayscale resolution of 12 bits per pixel using the Lumiscan 85 laser scanner (Lumisys, Sunnyvale, CA).⁹⁴

All cases of interval cancer in the database for which prior mammograms are available are included in the present study. Mammograms acquired in the last scheduled visit to the screening program prior to the detection of cancer were included in the dataset for the present study and labeled as prior mammograms. The mammograms on which cancer was detected (i.e., detection mammograms) were not available for the present study. In this manner, a total of 106 prior mammographic images of 56 individuals diagnosed with breast cancer were obtained. All but two of the 106 prior mammograms had been declared to be free of signs of breast cancer at the time of their original acquisition and interpretation in the screening program; the two mammograms had been referred for biopsy although there were no signs of malignancy. The time span between the detection and prior mammograms ranged from 1.5 to 24.5 months, with an average of 15 months and standard deviation of 7 months.

The 106 prior mammograms of interval cancer cases were reviewed independently by a radiologist specialized in screening mammography (J.E.L.D.). The radiologist indicated that 38 of the 106 prior mammographic images had visible architectural distortion, and the remaining 68 images had questionable or no visible architectural distortion; regardless, all of the 106 images have been included in the present study. Parts of the images related to or suspected to contain architectural distortion were marked using rectangular boxes based on the reports available on subsequent imaging, biopsy, or by detailed inspection of the prior mammograms. One rectangular part per image was marked by the radiologist. The average width, height, and area of the 106 parts of images marked by the radiologist are 56 mm, 39 mm, and 2,274 mm², with standard deviation of 11.8 mm, 11.6 mm, and 1073.9 mm², respectively.

Biopsy and other reports of subsequent imaging were available only for 33 out of the 56 cases of interval cancer. According to the subsequent imaging or biopsy reports, 23 cases were detected with masses occasionally accompanied by architectural distortion, calcification, or other signs of cancer, and ten cases were detected with calcification occasionally accompanied by architectural distortion or other signs of cancer.

No BI-RADS ranking²⁹ of breast density or subtlety of the lesions was provided in the reports from the screening program or the diagnostic clinics.

In addition to the above, all normal cases in the database with at least two visits to the screening program were identified. The mammograms of the penultimate screening visits of the normal cases at the time of preparation of the database were obtained and labeled as prior mammograms of the normal cases. In this manner, 52 prior mammographic images of 13 normal control cases were obtained for the study.

Detection of ROIs

The image processing methods proposed by Ayres and Rangayyan¹² for the detection of architectural distortion (see “Detection of Potential Sites of Architectural Distortion”) were applied to the 158 images obtained as described in “Database of Mammograms.” The images were filtered and downsampled to 200 μm/pixel and 8 bits/pixel before applying Gabor filters for the detection and analysis of oriented patterns. The resulting orientation field was filtered and downsampled to an effective resolution of 800 μm/pixel to facilitate efficient phase portrait modeling. From the 158 mammograms in the study, a total of 4,224 ROIs (2,821 ROIs from the 106 prior mammograms of interval cancer cases with 301 ROIs related to the parts with architectural distortion and 1,403 ROIs from the 52 normal prior mammograms) of size 128 × 128 pixels at 200 μm/pixel (except at the edges of the images) were automatically obtained. ROIs were labeled at the locations indicated by the peaks in the node maps, in decreasing order of the value of the peak, up to a maximum of 30 ROIs per mammogram. The automatically detected ROIs with their centers within the parts of architectural distortion identified by the radiologist were labeled as true-positive ROIs; the others were labeled as false-positive ROIs. Phase portrait analysis did not detect any true-positive ROI in one prior mammogram of the interval cancer cases; the radiologist had indicated that the corresponding image had no visible architectural distortion.

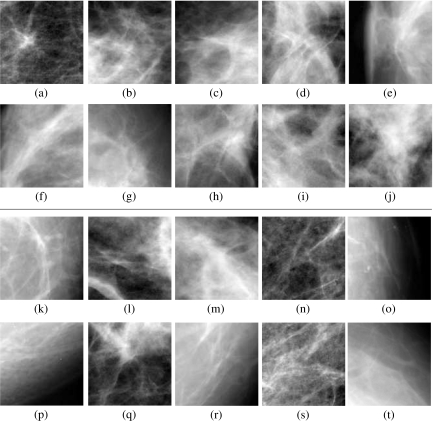
Figure 2b shows the ROIs obtained for the image illustrated in Figure 1. Figure 3 shows examples of true-positive and false-positive ROIs obtained from several cases included in the study. Table 2 gives the details of the dataset prepared for further analysis.

Fig. 3.

Examples of true-positive (a–j) and false-positive (k–t) ROIs detected. Each ROI is of size 128 × 128 pixels at 200 μm/pixel, or 25.6 × 25.6 mm.

Table 2.

Number of Prior Mammograms and ROIs in the Dataset

Dataset	Number of individuals	Number of prior mammograms	Number of automatically detected ROIs	Number of true-positive ROIs	Number of false-positive ROIs
Normal control cases	13	52	1403	0	1,403
Interval cancer cases	56	106	2821	301	2,520
Total	69	158	4224	301	3,923

In order to reduce the number of false positives, first, ROIs were selected from each mammographic image using the peak positions in the corresponding node map as the centers. Then, fractal and texture analysis was applied to the resulting ROIs (see “Feature Extraction”). The ROIs were classified using the feature selection and pattern classification techniques described in “Feature Analysis, Selection, and Classification.”

Feature Selection

Feature selection and pattern classification were performed for two distinct situations: one with the interval cancer cases only and the other with the full dataset of interval cancer cases and the normal control cases. Feature selection was performed based on stepwise logistic regression⁸⁶ and stepwise regression.⁷⁷ The AUC value of each of the features was also studied. In addition, the t test was applied to obtain the p value to evaluate the statistical significance of the difference between the values of a given feature for the true-positive and false-positive ROIs. Table 3 lists the AUC and p values obtained for the features and datasets used in the study. The individual AUC and p values of each of the features are presented for two situations: one with only the interval cancer cases and the other with the full dataset including normal control cases. The ranking of the features based on AUC value is also shown.

Table 3.

List of Features with AUC and P value

Feature no.	Feature name	With interval cancer cases only			With the full dataset including the normal control cases
		AUC	p value	Ranking	AUC	p value	Ranking
1	Energy	0.59	7.2E−7	5	0.59	7.2E−7	4
2	Contrast	0.51	4.2E−5	15	0.55	9.8E−5	7
3	Correlation	0.52	7.4E−5	11	0.53	1.0E−5	10
4	Sum of Squares	0.51	7.6E−2	13	0.51	3.3E−2	12
5	Inverse difference moment	0.61	4.1E−10	2	0.56	2.6E−4	6
6	Sum average	0.61	3.3E−9	1	0.63	6.9E−13	1
7	Sum variance	0.51	7.7E−2	14	0.51	3.4E−2	13
8	Sum entropy	0.53	9.6E−3	9	0.53	1.2E−2	9
9	Entropy	0.55	1.9E−4	6	0.54	2.9E−3	8
10	Difference variance	0.53	8.7E−6	10	0.57	4.9E−5	5
11	Difference entropy	0.55	3.0E−3	7	0.51	7.5E−1	14
12	Information theoretic measures of correlation1	0.53	2.8E−1	8	0.50	4.3E−1	15
13	Information theoretic measures of correlation2	0.51	1.6E−3	16	0.52	1.3E−4	11
14	Maximal correlation coefficient	0.52	1.3E−3	12	0.50	7.5E−4	16
15	Fractal dimension	0.60	1.5E−4	4	0.59	1.9E−4	3
16	Node value	0.61	5.0E−9	3	0.61	1.8E−9	2

Ranking is shown in terms of AUC values

The 2,821 ROIs obtained from the 106 prior mammograms of the interval cancer cases were used for feature selection and classification. Stepwise logistic regression resulted in the selection of five features: inverse difference moment, sum average, difference variance, entropy, and node value. The features selected by stepwise logistic regression have high AUC values and low p values. Stepwise regression analysis resulted in the selection of six features: inverse difference moment, sum average, node value, information theoretic measure of correlation,¹ FD, and difference entropy.

The 4,224 ROIs obtained from the full dataset of the interval cancer cases and the normal control cases were also studied separately for feature selection and classification. Stepwise logistic regression led to the selection of six features: sum average, energy, difference variance, node value, FD, and entropy. Again, the features selected by stepwise logistic regression have high AUC values and low p values. Stepwise regression analysis resulted in the selection of five features: sum average, sum entropy, node value, difference variance, and FD. The features selected by logistic regression and stepwise regression were used independently to perform classification.

Pattern Classification

The ROC and the FROC procedures were used to test and evaluate the classification accuracy using several classifiers. For ROC analysis, FLDA, the Bayesian classifier, the ANN based on an SLFF neural network with a single neuron in the hidden layer and a logistic activation function, the MLP with two hidden layers (the first hidden layer with three neurons and the second with one neuron) and the tangent sigmoid activation function, and the RBF were used. In addition, the SVM with an RBF kernel was also used to obtain a discriminant value. In training and testing the FLDA and Bayesian classifiers, the leave-one-out (LOO) method was used. The ROI to be classified was excluded from the training set. For classification using ANNs with the SLFF, MLP, and RBF and the SVM with an RBF kernel, 50% of the true-positive and 50% of the false-positive ROIs were randomly selected to generate the training and the testing sets, and the procedure was repeated 100 times. The flowchart shown in Figure 4 gives an overview of the whole procedure described above.

Fig. 4.

Flowchart of the procedures used to detect architectural distortion in prior mammograms. The steps in the dashed box labeled in a are shown in detail in b. The connecting lines and the boxes in dotted lines indicate options to be selected. CLS curvilinear structure, ROI region of interest, FLDA Fisher linear discriminant analysis, ANN artificial neural network, SLFF single-layer feedforward network, MLP multilayer perceptron, RBF radial basis function, SVM support vector machine.

FROC analysis was used to assess the false-positive rate for a given level of sensitivity when classification of the ROIs was placed in the context of detection of architectural distortion in full mammograms. The GRNN and the ANN based on the SLFF, MLP, and RBF were used for classification using the leave-one-image-out method: the features of all ROIs belonging to the image being analyzed were removed from the dataset during the training step of the classifier.

For implementation of the SVM with an RBF kernel, the MATLAB® Bioinformatics Toolbox (The MathWorks, Natick, MA) was used. The discriminant values of the SVM^91–93 were obtained using quadratic programming optimization. Because the GRNN is fast in function approximation, it was also used for FROC analysis. All the parameters required for the classifiers used in the present study were selected empirically; because of dependence on the specific datasets, they are not reported in the present paper. The AUC values were obtained using ROCKIT, a widely used software package developed at the University of Chicago, IL.⁹⁶ The p values were obtained by using the two-tailed t test⁷⁹ in MATLAB.

Results

The classification performance of the node value and FD was evaluated using ROC analysis. With the node value, the AUC obtained was 0.61 with the interval cancer mammograms; the same AUC value was obtained with the full dataset including the normal control cases. The AUC obtained with the FD was 0.60 with the interval cancer mammograms and 0.59 with the normal control cases included. The results indicate that the node value and FD, on their own, are not adequate for efficient detection of architectural distortion in prior mammograms; regardless, node analysis serves as an important preprocessing step to select candidate ROIs for further analysis.

Interval Cancer Cases Only

With the interval cancer cases only, the features selected by stepwise logistic regression and with the leave-one-ROI-out method, the same AUC value of 0.73 was obtained using FLDA and the Bayesian classifier. The features selected by stepwise regression resulted in AUC values of 0.73 and 0.74 using FLDA and the Bayesian classifier, respectively. The use of all the 16 features (see Table 1) resulted in poorer performance with AUC values of 0.67 with FLDA and 0.52 with the Bayesian classifier.

The results of FROC analysis with the selected features obtained by stepwise logistic regression and stepwise regression are illustrated in Figure 5 for the ANN-RBF classifier with the leave-one-image-out method. The FROC curve obtained using the node value only (i.e., the starting point of this study) is also shown for reference. The selected features demonstrate considerable improvement of performance over the node value. With 80% sensitivity as the reference point, the ANN-RBF classifier with the selected features based on stepwise logistic regression and stepwise regression resulted in lower false-positive rates of 8.6 and 7.5 per image, respectively; on the contrary, the node value produced 9.6 false positives per image at the same level of sensitivity.

Fig. 5.

FROC curves for the dataset of only the prior mammograms of the interval cancer cases with the selected features using the ANN-RBF classifier and the leave-one-image-out method. The FROC curve generated using the node value only is also shown for reference. Sensitivity=true-positive fraction.

Interval Cancer Cases and Normal Control Cases

The results obtained using several classifiers with the selected features based on stepwise logistic regression and stepwise regression are shown in Table 4 for the whole dataset including normal control cases. An SVM with the RBF kernel resulted in an average AUC value of 0.77 over 100 trials using the features selected by stepwise logistic regression and stepwise regression. The ANN-RBF resulted in an average AUC value of 0.77 using the features selected by stepwise logistic regression and 0.76 using the features selected by stepwise regression. The classification performance of the full set of 16 features was also evaluated in terms of ROC analysis, with FLDA and the Bayesian classifier and using the leave-one-ROI-out procedure; the corresponding AUC values obtained were 0.68 and 0.57, respectively.

Table 4.

Results Obtained in Terms of AUC Using the Selected Features Based on Stepwise Logistic Regression and Stepwise Regression

Classifier	Six features from stepwise logistic regression	Five features from stepwise regression
FLDA	0.73	0.72
Bayesian	0.76	0.76
SLFF	Mean 0.75, SD 0.03	Mean 0.74, SD 0.04
MLP	Mean 0.73, SD 0.11	Mean 0.72, SD 0.13
RBF	Mean 0.77, SD 0.01	Mean 0.76, SD 0.02
SVM	Mean 0.77, SD 0.03	Mean 0.77, SD 0.03

The dataset includes the prior mammograms of the interval cancer cases as well as the normal control cases. The mean and SD values are presented for 100 trials in each case of the ANNs and SVM

FLDA Fisher linear discriminant analysis, SLFF single-layer feedforward neural network, MLP multilayer perceptron, RBF radial basis function, SVM support vector machine

The results of FROC analysis are presented in Table 5 for several classifiers with the leave-one-image-out method. The FROC curves using four classifiers with the features obtained by stepwise logistic regression and stepwise regression are shown in parts a and b of Figure 6. With the sensitivity of 0.8 as the reference point, the selected features based on stepwise logistic regression showed the best performance at 7.6 false positives per image using the SLFF-ANN and 7.7 false positives per image using an ANN-RBF.

Table 5.

Results Obtained Using Several Classifiers and the Leave-One-Image-Out Method with FROC Analysis

Classifier	Six features from stepwise logistic regression	Five features from stepwise regression
SLFF	7.6	8.3
MLP	11.4	11.3
GRNN	7.7	7.8
RBF	7.7	8.0

The dataset includes the prior mammograms of the interval cancer cases as well as the normal control cases. The results are in terms of false positives per image at 80% sensitivity

SLFF single-layer feedforward neural network, MLP multilayer perceptron, RBF radial basis function, GRNN generalized regression neural network

Fig. 6.

FROC curves: a using four classification techniques with the leave-one image-out method and the features obtained by stepwise logistic regression, b using four classification techniques with the leave-one-image-out method and the features selected by stepwise regression analysis. The dataset includes the prior mammograms of the interval cancer cases as well as the normal control cases.

To facilitate further detailed comparative analysis, the results of FROC analysis with the selected features obtained by stepwise logistic regression and stepwise regression are illustrated in Figure 7 for the ANN-RBF classifier with the leave-one-image-out method; the FROC curve obtained using the node value (i.e., the starting point of this study) is also shown for reference. At 80% sensitivity, the node value produced 10.3 false positives per image, whereas the selected features using stepwise logistic regression with the ANN-RBF classifier provided better performance with a lower false-positive rate of 7.7 per image.

Fig. 7.

FROC curves for the full dataset including the prior mammograms of the interval cancer cases and normal control cases. The curves are shown for the ANN-RBF classifier and the leave-one-image-out method using the features obtained by stepwise logistic regression and stepwise regression. The FROC curve generated using the node value only is also shown for reference. Sensitivity=true-positive fraction.

Discussion and Conclusion

Referring to the ROC performance presented in Table 4 using the features selected by stepwise logistic regression and stepwise regression, the results were expected to be better with ANN-based classification as compared to FLDA and the Bayesian method. However, because of random subsampling for cross-validation, the results are biased and dependent on the sample size, the randomly selected samples, and their statistical distribution.⁷⁷ Furthermore, the AUC values obtained with the ANN-based classifiers are pessimistically biased because the ratio of the total number of available samples per class to the number of available features is >5.⁷⁷ The results could be improved by using the LOO method with these classifiers; however, the associated computational requirements are high.

In a related previous study,¹⁶ ROC analysis with FD of the 14 prior mammograms of seven screen-detected cases provided good classification performance with AUC = 0.74. Texture measures resulted in a poorer performance of AUC = 0.70 with the prior mammograms. Using feature selection and the Bayesian classifier, the best classification performance achieved was AUC = 0.80 for the prior mammograms. In addition, FROC analysis with the detection mammograms indicated a sensitivity of 0.79 at 13.7 false positives per image with the selected features. The same sensitivity of 0.79 was achieved at a lower rate of 8.4 false positives per image using the selected set of features with the prior mammograms. The dataset used was small, with only 14 prior mammograms and 14 detection mammograms and with no normal control cases. Contrary to the present study, the detection mammograms were available for reference to the radiologist when labeling the parts with architectural distortion on the prior mammograms.

However, in the present study on interval cancer cases, including normal control cases, the detection or diagnostic mammograms were not available to aid the process of localization of the sites of architectural distortion on the prior mammograms. Biopsy and other reports of subsequent imaging were available only for 33 out of the 56 cases of interval cancer. These factors could have affected the size and positional accuracy of the rectangular parts drawn by the radiologist to delineate the suspicious areas on the prior mammograms. Although some of the automatically detected ROIs were ranked low in the step of node map analysis, they were marked as true positives (if their centers were within the related area delineated by the radiologist) and contained only small portions of the spiculations due to architectural distortion; such ROIs could increase the ambiguity and complexity in pattern classification. Moreover, there exist as many as 68 images with questionable or no visible architectural distortion (as determined by the radiologist) in the dataset used in the present study. Even with a larger dataset, increased ambiguity, and a number of normal control cases included, the rates of sensitivity obtained in the present study are comparable to those obtained in a related previous study¹⁶ without a substantial increase in the number of false positives per image. The proposed methods have demonstrated the ability to detect early signs of breast cancer 15 months ahead of the time of clinical diagnosis, on average, for interval cancer cases, with a sensitivity up to 99%, albeit at a high false-positive rate of 18 per image; at a lower but still substantial sensitivity of 80%, the false-positive rate is correspondingly lower, at 7.7 per image. In the context of the results of the works on architectural distortion reviewed in “Detection of Architectural Distortion in Mammograms,” the results obtained in the present work on prior mammograms of interval cancer cases including normal control cases are comparable and encouraging. However, detailed comparative analysis is difficult because of variation in the datasets used.

The results of FROC analysis in the present study indicate that the false-positive rate in the detection of architectural distortion in prior mammograms, at a given level of sensitivity, may be reduced by the application of a trained ANN-based classifier. The SLFF, GRNN, and RBF classifiers have all provided comparable results, with substantial reduction in the false-positive rate as compared to the particular MLP architecture used and phase portrait analysis. Establishment of the statistical significance of the differences between the several FROC curves derived is beyond the scope of the present study. Reliable techniques for testing the significance of differences between FROC curves are not yet well established.⁹⁷ Although some methods have been proposed for this purpose,⁹⁸ their robustness has not been established.⁹⁷ Future studies should include detailed and objective analysis of FROC curves.

The programs for Gabor filtering, phase portrait modeling, fractal analysis, and texture analysis were written in MATLAB and took about 70 min to process a mammogram, on average (with an average size of 1,300 × 800 pixels at 200 μm/pixel resolution). The classification time using the several classifiers studied was not recorded. The computer used is a Dell workstation with dual Intel Xeon processors operating at 1.50 GHz, with 2 GB of RAM. Conversion of the code to the C or C++ language and the use of multiple processors in parallel could lead to faster computation of the results for application in a practical setting.

The results obtained in the present study with the prior mammograms are important and encouraging and indicate that Gabor filters, phase portraits, fractal analysis, and texture features can be used to achieve early detection of subtle signs of breast cancer in mammograms, specifically architectural distortion. Further reduction in the false-positive rate is desirable; detection and removal of the pectoral muscle⁹⁹ in mediolateral oblique views and additional conditions at the edges of the fibrograndular disk¹⁰⁰ could reduce the number of false positives. Nonlinear phase portrait analysis¹⁰¹ and multifractal analysis¹⁰² could be explored to derive features with improved discriminant capability.

The development of CAD techniques for the detection and localization of architectural distortion in prior mammograms may lead to efficient detection of early signs of breast cancer.