Torque-induced deformations of charged elastic DNA rods: thin helices, loops, and precursors of DNA supercoiling

Abstract

We study the deformations of charged elastic rods under applied end forces and torques. For neutral filaments, we analyze the energetics of initial helical deformations and loop formation. We supplement this elastic approach with electrostatic energies of bent filaments and find critical conditions for buckling depending on the ionic strength of the solution. We also study force-induced loop opening, for parameters relevant for DNA. Finally, some applications of this nano-mechanical DNA model to salt-dependent onset of the DNA supercoiling are discussed.

Introduction

Several approaches exist in the literature for analysis of buckling instability of neutral elastic rods under applied torque and end stretching forces [1–5]. Looping of twisted and stretched charged filaments has attracted less attention because of long-range electrostatic (es) interactions between segments of a polyelectrolyte chain [6–8]. The inter-charge repulsions along the filament affect its final geometrical shape, particularly in the limit of weak screening by electrolytes. Applications of such polyelectrolyte buckling models could, however, help to rationalize a number of biologically important salt-dependent phenomena, such as DNA supercoiling [9–14] and protein-induced DNA looping [15–18].

In this paper, we treat particular deformations of charged semiflexible elastic filaments. We concentrate on filament shape and energetics, neglecting the effects of thermal fluctuations that is applicable for filaments shorter than 1–2 bending persistence lengths. In applications to DNA, we use the standard elastic [19] and es [20] DNA parameters at physiological conditions. In the last section, we apply the model results for the polyelectrolyte rings/loops under tension to a description of the initial stages of DNA supercoiling.

Thin helix deformations

In this section, we study the initial helical deformations of a charged elastic rod under torque Γ and applied end stretching forces F (Fig. 1). We show that below some critical stretching force F_helix the helical deformations of the filament are energetically favorable. Physically, forming a helix, the excess twist energy in the filament is exchanged for mechanical bending energy, work against the end forces, as well as the excess es energy of the helix. We analyze the dependence of this critical transition force on relevant parameters.

Fig. 1.

Cascade of deformation transitions upon increase of the applied twist, from left to right: thin helix, one-helix-turn loop, and rotated loop state

We use the energy of one turn of a helix with length L_p, small radius R, pitch P, curvature K, and torsion KP/(2πR) [21]. The helix’s total energy is the sum of bending, twisting, es energy and work against the end forces F, i.e., we get 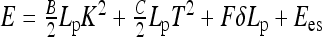. Here, B and C are the rod elastic moduli and δL_p is the end displacement upon helix formation (slack per pitch). Fixing the helix length per pitch L_p, and using the persistence lengths for filament bending l_p and twisting l_tw, we obtain

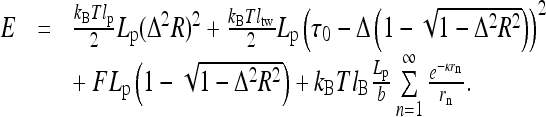1

Here, τ₀ is the initial twist rate on a straight rod and parameter Δ ≡ 2π/L_p.

The last energy term is the Debye-Hückel es repulsive energy in the simplest model of discrete equidistant charges positioned on the filament. It contains the separations of charges i and i + n on a helix, 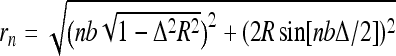, the inter-charge distance on a straight rod, b, and the Bjerrum length l_B ≈ 7.1 Å (in water at room temperature). The Debye screening length in electrolyte solution is λ_D = 1/κ, about 1 nm at 0.1 M NaCl. For highly charged rods, we account for the Manning counterion condensation [22, 23], renormalizing the separations between unit charges along the contour down to b = l_B. This gives ≈75% charge neutralization for the case of B-DNA in 1:1 salt solution. We neglect possible attractive forces between DNA segments that can be potentially induced by condensed cations [24]. See the discussion of DNA charged models in [17].

For uncharged filaments, expanding the energy of thin helices up to R⁴-terms, one gets for the optimal helix radius

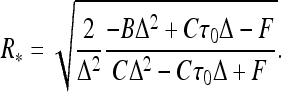2

This provides an accurate description for radii of thin helices. As the helix radius grows, this expression starts to deviate from the exact solution, as can be seen by comparing the thin dotted and solid blue curves in Fig. 2. Helix stability follows from the condition 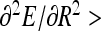0 [25] that requires that 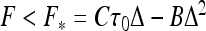. The maximal force the helices can sustain is reached at an optimal 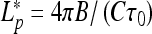value. This force is equal to the Greenhill buckling instability force [26],

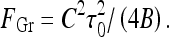3

The radius of these thin helices grows with the filament slack and decreases with twist rate, namely 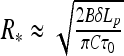, as one can show using 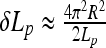with 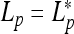. The helix of zero pitch is realized at .

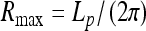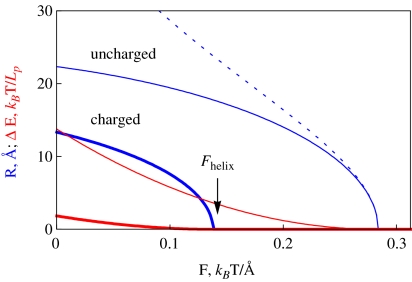
Fig. 2.

Optimal radius of a thin helix R and energy profit upon helix formation, ΔE. Thin and thick curves correspond to uncharged and charged filaments. The dotted curve is the analytical solution (2) for R_∗. F_helix is defined as the force at which R → 0. The es summation over charges within 10 λ_D from a particular charge on the helix is performed. Parameters: τ₀ = 0.2 τ_DNA, 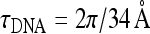, B = 500k_BT Å, C/B = 3/2, L_p = 150 Å, 1/κ = 100 Å

For thin charged helices, the optimal radius is found numerically. Physically, the es energy of a helix is larger than that of a straight rod with the same charge-charge separation b. This es penalty for helix formation gives rise to the fact that (at the same external twist rate τ₀) the radius of the helix decreases as compared to uncharged filaments (Fig. 2). As κ grows upon addition of screening electrolyte, the es effects are diminished.

This es penalty also reduces the critical force F_helix below which helix formation is energetically favorable. Upon decrease in salt concentration, es repulsions within the helix accumulate progressively and the value of F_helix decreases (Fig. 3). We could not find, however, a simple scaling for this F_helix (κ) decrease. For smaller excess twist energy in the filament (i.e., smaller τ values), no helices might be formed below a critical κ value (at this point, F_helix → 0).

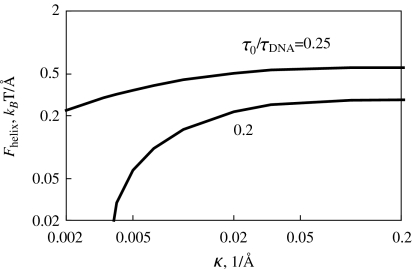
Fig. 3.

Maximal force F_helix that still allows helix formation on a charged filament. It decreases at lower salt concentrations and grows with the twist rate applied. For large κ values, F_helix approaches the values for an uncharged rod. Parameters are the same as in Fig. 2

In es DNA models, the polyelectrolyte bending persistence undergoes es stiffening 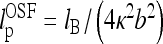[27–29], while the twisting persistence l_tw is almost insensitive to the salt concentration [30, 31]. The renormalized Greenhill force 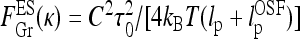however, does not describe the entire dependence of F_helix(κ) obtained from numerical solution.

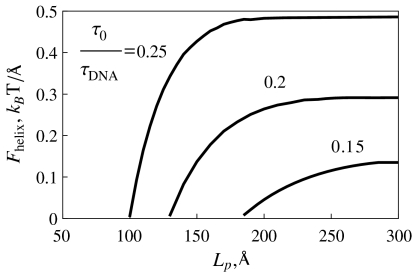
At a fixed κ value, F_helix increases with the twist rate τ₀ applied. In this case, the excess twist energy grows, and the filament can perform larger work against terminal forces upon helix formation. Also, the F_helix value increases with L_p at a fixed twist rate. The physical reason is that at a fixed stretching force, the helical deformations with longer helical repeat length L_p can be formed at smaller τ₀ values (Fig. 4), and have typically larger helix radius. Also, smaller L_p values imply larger linear densities of the filament elastic energy.

Fig. 4.

Maximal helix formation force grows with the twist rate imposed. Parameters are the same as in Fig. 2

Loop formation

Neutral filament

As the amount of twist stored in the filament increases, thin helices might no longer describe a stable equilibrium and a single loop can emerge instead. The model below studies the loop evolution, when its shape can be approximated by a single turn of a helix with radius R and small pitch P ≡ 2πRλ, where parameter λ < < 1 (Fig. 1). The helical axis is now perpendicular to the applied force and we follow the procedure suggested in [32].

For a neutral filament with the residual twist rate τ forming such a loop, the elastic energy and work against end forces can be written as

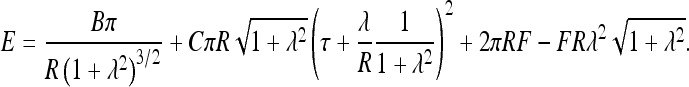4

We expand the energy up to λ³-terms, equate the derivatives over R and λ to zero, and find the optimal loop radius

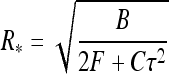5

and pitch

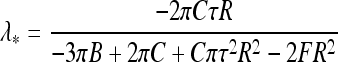6

(here λ_∗ > 0 by definition).

Equation 5 shows that loops are tightened when larger torques Γ = Cτ are applied. At F = 0 the loop radius is maximal and it defines the maximal “slack” the filament can tolerate without looping

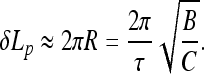7

Therefore, torsionally stiffer filaments sustain less slack, as one could expect, because twist energy is traded for bending energy upon looping. Also, at larger τ values smaller cable end displacement towards the center will trigger filament looping. Note that exact homoclinic solution for looping instability predicts for maximal sustainable slack 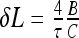[33].

The loops are stable at 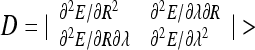0, which for small λ_∗ values yields 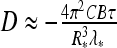. This indicates that for λ_∗ > 0 the helical loops are unstable because the D and λ_∗ have opposite signs. Stable loops would thus need “unphysical” negative λ_∗ values, indicating that a loop rotation around the contact point can be required to reach the energy minimum. Condition D > 0 for optimal loop dimensions at R → R_∗, λ → λ_∗ reduces to

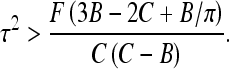8

This shows that stable loops can exist if they are twist-less, i.e., if τ = 0 (D and τ have opposite signs) and planar, i.e., if λ_∗ = 0. Their radius is then given by 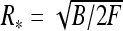provided

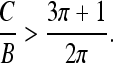9

This last inequality means that large C and small B values favor filament looping, as one could expect, because the excess twist energy is easier converted into loop bending. For B-DNA, the ratio of these two moduli is C/B ≈ 3/2 that is, slightly smaller than the critical ratio. Yet, for conditions favoring small B values, such as the presence of multivalent cations in solution or tight DNA bending [34], stable DNA planar twist-less loops can be formed.

Charged filament: untwisted ring

To study the es effects on formation of small planar untwisted rings predicted above to be stable under tension, we supplement the ring mechanical elastic energy E_el = πB/R + 2πRF with es energy of ring formation, ΔE_es. The latter is the difference between the es energy of a ring and a straight rod of the same length 2πR, given, following [35], by

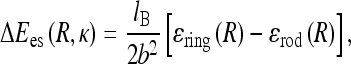10

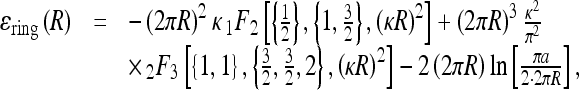11

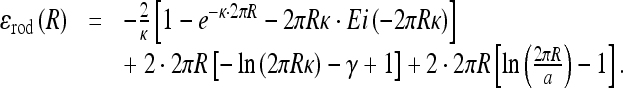12

Here, b ≈ l_B is the charge-charge separation on the polyelectrolyte after counterion condensation, a is a short-range cut-off used for counting es interactions, Ei(x) is the exponential integral, γ is the Euler constant, and _iF_j(x) are the generalized hyper-geometric functions.

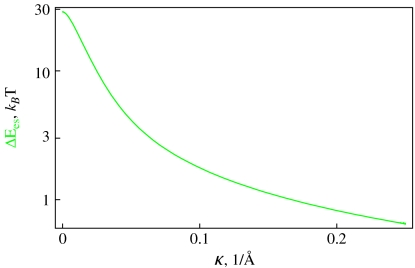
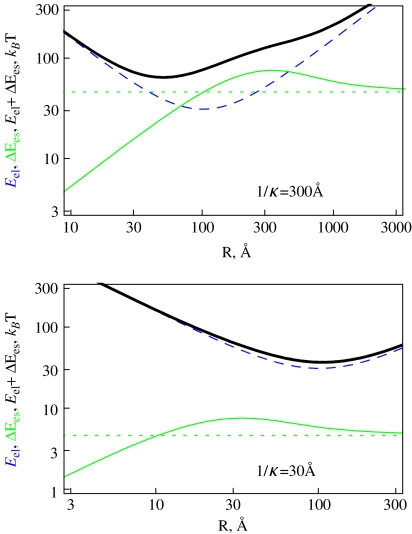
Ring es formation energy [36] decays fast with κ due to electrolyte shielding (Fig. 5). Plotting the ring energy as a function of its size, one can see that the elastic energy minimum at

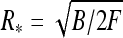13

interferes with the maximum of the es energy for the ring size of R ∼ 1/κ (Fig. 6). For large R, the ring es energy asymptotes to the polyelectrolyte end closure energy,

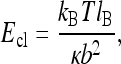14

while it approaches zero for small R values. In the latter case, at R < < 1/κ, the inter-charge interactions are unscreened and the actual conformation of polyelectrolyte is of little relevance for its ΔE_es value.

Fig. 5.

The decay of the es energy of formation of 100 bp long polyelectrolyte rings with DNA parameters of B = 500 k_BT Å, C/B = 3/2 calculated at b = l_B, a = 1 Å, τ = 0

Fig. 6.

Elastic, es, and total energies as a function of the ring radius, plotted for two values of κ corresponding to different directions of the total energy minimum shift. The es closure energy E_cl is the dotted green curve. Parameters are the same as in Fig. 5 and F = 1 pN

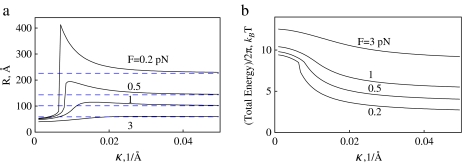
Intuitively, one would expect that es repulsions should always lead to expansion of energy-optimal polyelectrolyte rings. The effect is however, more complex due to a maximum in E_es(R) dependence. The shift of the total energy minimum of the charged rings depends on the F and κ values. Namely, if the R ∼ 1/κ value for the es energy maximum is larger (smaller) than R_∗ for the elastic energy minimum, the optimal rings shrink (expand), as shown in Fig. 6. The shift in optimal R value induced by es ring closure energy is diminished by addition of salt because the es energy decreases. The effect is also impeded at large filament stretching forces, when the ring mechanical energy dominates. For small forces and small κ values, when the total ring energy attains a double-well shape, an abrupt transition in R(κ) dependence is observed, as shown in Fig. 7a. This first-order transition is accompanied by a change in energy derivative (Fig. 7b).

Fig. 7.

Optimal radius (a) and total energy (b) of DNA-like polyelectrolyte rings stretched by the force F. Transition from ring shrinkage to ring expansion takes place for ring size R ∼ 1/κ. Dashed blue lines indicate 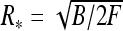values. Parameters are the same as in Fig. 5

Note here that when the loops do possess a residual twist, the ring-like shapes might no longer describe the energy minimum. The loops can rotate by an angle Φ to relax the excess twist, see Ref. [25] forming a precursor of plectonemic structures (Fig. 1).

Loop re-opening by force

A finite physical diameter d of the filament prevents the formation of ideally planar loops predicted above to be stable. For instance, in the model of a one-helix-turn loops, the minimal pitch d defines the critical

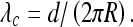15

For λ_c > λ_∗ the loops tend to reopen as the force increases, displacing the system from an unstable equilibrium at λ = λ_∗, where λ_∗(τ, F, R) according to Eq. 6. This equality defines the critical loop radius R_open below which the loops will reopen. The F(R) dependence of λ_∗ is extracted from the equilibrium of a polyelectrolyte ring under tension (Fig. 7a). It shows that at a fixed κ, as the optimal ring radius decreases, the end force required to keep the ring stable increases. For rings on neutral chains, we use 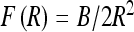. The critical opening radius defines a critical force 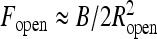above which these nearly circular loops will reopen, see also Ref. [46].

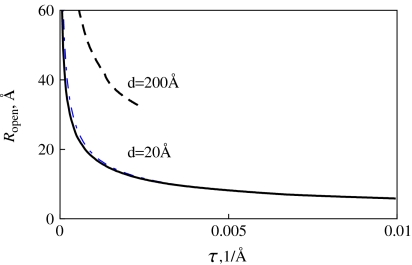
We obtain that R_open grows with d and decreasing residual twist in the filament (Fig. 8). Both DNA’s physical (d = 20 Å) and effective es (d ∼ 200 Å at 1/κ = 100 Å in ∼0.001 M of 1:1 salt [37]) diameters were used in Fig. 8 to evaluate the re-opening radius of tight DNA loops. The effective DNA diameter mimics the inter-segmental interactions that tend to avoid close contacts in structures formed by a self-repelling DNA polyelectrolyte chain.

Fig. 8.

Loop re-opening radius for DNA-like filaments. Black curves correspond to charged rings; the blue dashed curve is plotted for neutral loops. Parameters are the same as in Fig. 5 and 1/κ = 100 Å

We observe that for d = 20 Å the presence of charges on rings has almost no effect on the opening radius R_open. On the contrary, for much larger effective DNA diameters realized at low salt, a dramatic increase of the opening radius and a decrease in the opening force are observed (Fig. 8). Thus, an effective DNA es “thickening” at low salt favors DNA loop re-opening and prevents loop tightening by the force and possible DNA kinking. Note that for large d values a maximal τ exists that defines the validity domain of this procedure (obtained from the λ < 1 condition). Above this critical twist we do not show the results for the opening radius, see dashed curve in Fig. 8. Typical twist rates in Fig. 8 are τ = 0.01/Å corresponding to a DNA supercoiling degree of σ ≈ 0.055.

Onset of salt-dependent DNA supercoiling

The process of DNA supercoiling has been investigated in a number of excellent experimental and theoretical studies (the list is too long to cite). We solely rationalize here the recent salt- and force-dependence data on initial stages of DNA supercoiling.

In the magnetic tweezers experiments, a DNA of typically several kilo-base-pairs in length is held under constant tension F being rigidly attached by the ends to a surface and to a magnetic bead. Bead rotation by an external magnetic field imposes some torque onto the DNA. Initially, the DNA end-to-end extension decreases slightly with the torque, indicative of some (probably helical) DNA deformations taking place, that are more pronounced at smaller stretching forces.

After a critical number of DNA end rotations, the DNA “buckles” and its extension starts to vary linearly with the torque. At the buckling point, the DNA extension varies either smoothly or abruptly, according to recent magnetic and optical tweezers measurements [38–41]. The magnitude of these jumps decreases with the force applied (see Fig. 3a in Ref. [38]), it increases with NaCl concentration (Fig. 1a in Ref. [39]), and probably also depends on DNA length. The jumps become more pronounced in the high salt limit and they disappear below 20 mM NaCl [39], rendering the supercoiling curve into a classical shape.

The entire supercoiled DNA, including the terminal loop, can in some limits be described within a simple model as an array of connected rings, the so-called circular model, see Eq. 25 in Ref. [42]. The change in DNA extension upon formation of one circle is then 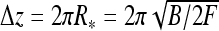and the buckling torque is

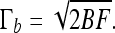16

At the transition point, the energy of extended and looped DNA states are nearly equal, allowing for a fast inter-conversion between the two DNA states. This process has been visualized for DNA held at a constant tension close to the buckling point (Fig. 3b in Ref. [38] and Fig. 2 in Ref. [39]). The optical tweezers study has shown that (independent of DNA length) the discontinuous jumps in DNA extension follow a 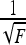, as shown in Fig. 3a Ref. [38], as for a circular loop in Eq. 13 above. The jump magnitude is, however, far from the one predicted by a simple circular model for terminal DNA loops. A recent magnetic tweezers investigation has revealed that, on the contrary, the jumps are sensitive to DNA length and exhibit a different force-dependence, as shown in Fig. 5a in Ref. [39]. Other magnetic tweezers measurements at small stretching forces do not exhibit any jumps in DNA extension at all upon increasing the torque imposed on the DNA [43].

After buckling, the torque Γ_b on the DNA remains nearly constant [43] and DNA extension decreases linearly with the number of DNA axial turns [44]. The slope of this decrease is faster for smaller applied forces (Fig. 1a in Ref. [40]) and lower salt concentrations (Fig. 1a in Ref. [39]).

Force- and salt-dependence of critical buckling torque Γ_b required to trigger DNA supercoiling have been systematically measured by magnetic tweezers in Ref. [43]. This torque separates the regime of nearly constant DNA extension at small σ and a linear decrease in extension with torque at large σ values. The DNA first accumulates the twist energy, relaxing it later into writhe via plectoneme formation. The critical torque exhibits an increase with applied force F and decreasing concentration of NaCl (Fig. 3 in Ref. [43]).

The salt-dependence of the post-buckling DNA torque and DNA supercoiling slopes have recently been quantitatively rationalized in the es-mechanical model of dense DNA plectonemes [40], see also Ref. [45]. Initial stages of DNA supercoiling still however, pose some theoretical challenges. For instance, the analysis of the width of buckling transitions suggests [39] that instead of forming a single loop as a “nucleus of supercoiling”, an extended DNA stem of a couple of DNA turns might be created, as shown in Fig. 1c. Experimental data for abrupt changes in DNA extension thus cannot be used to extract directly the size of terminal DNA loops, for varying forces and salt conditions. The initial stage of DNA coiling is likely to be more energetically costly than subsequent DNA ply formation.

The es effects for DNA terminal loops have not been considered in detail. A recent theoretical study argues that the role of es in the DNA initial loop is smaller than in subsequent DNA ply [39], due to larger DNA–DNA distances in the loop. The model suggested that below some salt concentration, only the initial loops are formed on the DNA and thus no abrupt buckling transition takes place, similarly to the experimental situation.

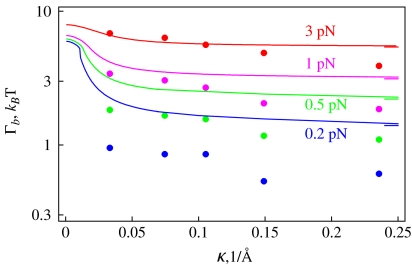
We concentrate below on es effects in the initial DNA loop and the experimental data of Ref. [43] for the onset of DNA supercoiling. To describe the salt-dependence of Γ_b measured, we utilize the model of energy-optimized polyelectrolyte rings under tension from Section 3.2. A simple model of DNA circles forming a plectoneme is known to substantially overestimate the Γ_b as shown in Fig. 4b in Ref. [38]. In Fig. 9 we thus use a reduced value of DNA bending persistence, setting B = 200 k_BTÅ, that provides a satisfactory agreement with experimental data. We supplement the bending energy and work against end forces upon initial DNA ring/loop formation with the excess es energy ΔE_es. The energy difference at the looping transition is connected to the critical buckling torque as

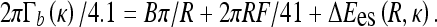17

Here, Γ_b is measured in pN·nm and F is in pN. The right-hand side is evaluated for the optimal ring radius in the minimum of the total energy. The known results for neutral loops [42] are obtained when neglecting the es term. The decay of the critical torque with added salt originates from ΔE_es(κ)-dependence and the outcomes are consistent with a DNA neutralization degree of ≈75%.

Fig. 9.

Salt- and force-dependence of the critical buckling torque for DNA supercoiling. Dots are the measured values taken from Fig. 3 of Ref. [43], solid curves are the model predictions with B = 200 k_BT Å. At large κ values, the torques predicted approach the no-salt value of Eq. 16 marked as ticks on the right. Other parameters are the same as in Fig. 5

Note that at large κ values the measured Γ_b(κ)-dependence is stronger than predicted in the model. A salt-dependence of B neglected in this model might help to rationalize this torque decrease with salt concentration. Another way to reduce the influence of DNA’s elasticity on the buckling torque is to introduce a DNA “stretching factor” prior to buckling, that is smaller than unity, see Eq. 16 in Ref. [39].

Discussion and conclusions

We have studied several types of elastic deformations of a charged filament clamped on the ends induced by applied torques and tensions. We analyzed the effect of es repulsions on the buckling instability threshold. In particular, the radius of thin helical deformations and the critical force below which they occur were shown to be reduced by repulsions within the polyelectrolyte filaments, as compared to uncharged ones. For tightening of circular loops, the optimal rings had a non-monotonic dependence on electrolyte concentration, favoring a compression of charged rings at low salt. This counterintuitive behavior originates from a peculiar shape of the es ring formation energy.

We have applied these results to analyze DNA buckling instability at the onset of the DNA supercoiling transition. The model of semiflexible polyelectrolyte rings under tension, with a reduced elastic bending modulus and self-consistently determined radius of the terminal loop, has provided a qualitative agreement with experimental data for critical DNA buckling torque as a function of salt concentration and DNA stretching force.