Physical aspects of precision in genetic regulation

Abstract

The process by which transcription factors (TFs) locate specific DNA binding sites is stochastic and as such, is subject to a considerable level of noise. TFs diffuse in the three-dimensional nuclear space, but can also slide along the DNA. It was proposed that this sliding facilitates the TF molecules arriving to their binding site, by effectively reducing the dimensionality of diffusion. However, the possible implications of DNA sliding on the accuracy by which the nuclear concentration of TFs can be estimated were not examined. Here, we calculate the mean and the variance of the number of TFs that bind to their binding site in reduced and partially reduced diffusion dimensionality regimes. We find that a search process which combines three-dimensional diffusion in the nucleus with one-dimensional sliding along the DNA can reduce the noise in TF binding and in this way enables a better estimation of the TF concentration inside the nucleus.

Introduction

One of the primary means by which cells adapt to new conditions is by modulating the expression of genes. Gene expression is controlled by transcription factors (TFs) which bind specific binding sites along the DNA to regulate the expression of adjacent genes. TFs must, therefore, recognize their specific binding site in the promoter and the occupancy of the promoter by the TF will ultimately determine the extent of regulation.

The dependence between regulation and promoter occupancy suggests that the number of molecules of a specific TF inside the nucleus will define the level of expression of the regulated gene. It follows that in order to achieve precision in gene expression, TF concentration inside the nucleus must be measured accurately by the cell. However, this concentration is inferred based solely on promoter occupancy. As binding site localization is likely to be a diffusion-limited process, promoter occupancy will be subject to diffusional noise. Therefore, this source of noise must be overcome by the cell if regulation is to be accurate.

It has long been postulated that reducing the dimensionality of diffusion of bulk-phase reactants from three dimensions to two or one dimensions can theoretically enhance the rate by which these molecules interact with a nearby trap [1]. The concept was also borrowed for the analysis of the search of a TF for its specific DNA binding site [2–4]. It was also shown that the time of this search can be minimized by a strategy that combines two phases of motion: three-dimensional (3D) diffusion in bulk and one-dimensional (1D) diffusion along the DNA [5, 6]. The 1D diffusion phase provides thorough scanning of close-by sites. At long distance, however, this 1D motion is slow due to energy barriers of unbinding from each site, and is thus effective only locally. On the other hand, the 3D phase is fast and enables effective translocation between distant regions. Consequently, 3D motion interspersed by 1D events comprises the most effective search strategy in terms of search-time minimization. This view, albeit with modifications, has been accepted by several groups and further elaborated [7–12].

While facilitation of the search process by reduction of diffusion dimensionality has been well studied, the potential ability of such a diffusional scheme to promote precision in the process of transcriptional regulation has not been demonstrated. In this study we evaluate the implications of reduced diffusion dimensionality on the noise in TF-DNA binding. We first calculate the current of molecules arriving at the cognate site using a simple model that involves a minimal collection of measurable parameters, and derive a new expression for this current. We then assess noise levels associated with the search process and show that a combined diffusion dimensionality scheme can reduce noise levels and measurement time.

Noise in concentration measurement by a perfect absorber

We start by calculating the noise associated with a naive diffusional search process, consisting of 3D diffusion in the nucleus. Importantly, we do not make any assumptions regarding the nature of the distribution of the number of molecules arriving at the binding site.

We consider a large volume V of space where a collection of point-like particles with average concentration 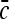perform diffusion with a diffusion coefficient D. It is assumed that the collection is dilute and that the particles’ diffusion is independent.

At the origin a perfectly absorbing receptor is placed which registers the number of particles reaching the boundary of its volume V_i. We assume that once the particles reach the boundary they are counted once and not counted again later. This assumption corresponds to assuming that the instrument boundary is an absorbing wall.

We consider the statistics of the number of particles N registered by the instrument during the time interval T. Since diffusion of each particle is independent of all other particles, the problem is reducible to a single-particle problem. Therefore, one first considers the following problem: given a particle located initially at some x⁰ (outside the instrument volume) what is the probability that it survives during the time T? As is well known [13] the survival probability P_s(x⁰) can be found by considering the solution to the diffusion equation

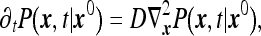1

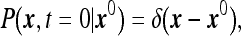2

in the volume outside the instrument with the boundary condition that P vanishes at the instrument boundary. Then P_s(x⁰) can be written as

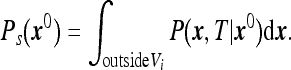3

To pass to the problem of interest we assume that N₀ particles are initially scattered independently over the volume V ≫ V_i with the average density 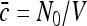. The particles’ coordinates at t = 0 are 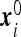. At t > 0 the particles perform independent diffusion. Particles that occasionally reach the instrument boundary get absorbed by that boundary. It follows that the probability P_T (N) that N particles were absorbed during the time interval T is given by the sum of probabilities of mutually exclusive events that N particles with initial coordinates 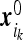were absorbed while the rest were not. We find

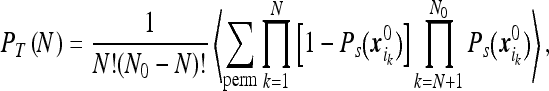4

where the averaging is over the initial positions of the particles. The above sum is over all permutations of N indices and the factorials are intended so as to prevent counting twice the event of the same N particles absorbed by the instrument. Since the initial particles’ positions are independent and identically distributed we find that all summands are equal and

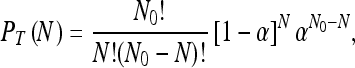where

5

It is useful to define the generating function G(λ) via

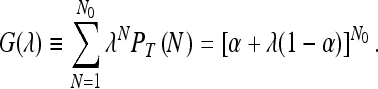6

Clearly the normalization condition 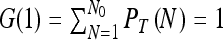is satisfied. The moments of N can be obtained by differentiating G(λ) and setting λ = 1. For example

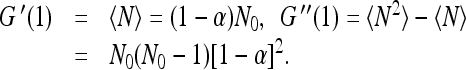7

For the dispersion Δ, we have

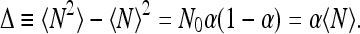8

Thus, the problem is reduced to the calculation of α. We will be interested in the limit of large volume V. Firstly, let us note that at large distances from the instrument P_s(x) tends to unity. It follows immediately that

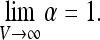9

It is the correction to the above expression, 1 − α, that determines 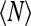in the limit of large V. We have

10

The RHS of the above equation has finite limits proportional to 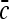as it must on the basis of physical considerations. For the dispersion, to leading order we have just

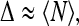11

as one would expect from the Poisson distribution. Thus, in the limit of large volume we need to solve (1) and (2) in the infinite space and, based on the solution, find the coefficient β defined by

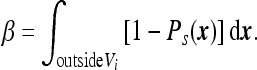12

Since β times the average concentration is the total number of absorbed particles, then the coefficient β can be interpreted as the effective volume from which the particles are absorbed within time T while particles outside survive. We thus calculate β (see Appendix A) and find

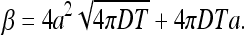13

At large times 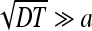we have

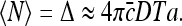14

Note that the above expression is dimensionless, as it should be. For the relative dispersion, we find

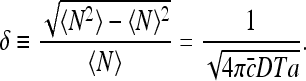15

Equation 15 is an exact solution of the dispersion in the number of molecules arriving at the specific binding site, that does not rely on assumptions regarding the distribution of TF arrival events. However, the result implies that these events obey a Poisson distribution with a mean molecular flux identical to the von Smoluchowski equation J = 4πDac [14]. Therefore, this result indicates that the noise in TF arrival can be derived directly from the current of TF molecules arriving at the specific binding site.

Reduction of diffusion dimensionality in binding site localization

The result in (15) suggests that noise in TF-DNA binding can be reduced by a search strategy that increases the current of newly arriving molecules at the cognate site. One way of possibly increasing this current is 1D sliding on DNA. In the following, we analyze a model that combines 3D diffusion with 1D sliding on DNA, and examine an optimal strategy to minimize noise in TF-DNA binding.

Combined three-dimensional diffusion in the nucleus and one-dimensional sliding of TF on DNA—formulation of the model

In order to obtain an expression for the current of molecules arriving at a specific DNA binding site by sliding on the DNA, and from it deriving the associated noise level in TF-DNA binding, we consider the sliding process as diffusion in one dimension. We assume that the TF interacts specifically (with high affinity) with a particular DNA site, x_site, and non-specifically (with lower affinity) with every other site, x. Accordingly, we model the DNA as consisting of one perfectly absorbing specific binding site, while all other sites are identical with respect to their non-specific interaction with the protein.

The motion of every protein includes two phases: 3D diffusion in the bulk of the nucleoplasm and 1D diffusion along the DNA. It follows that the number of protein molecules occupying a typical site, x, at a certain time, t, is the sum of the contributions of molecules arriving from the nucleoplasm, landing directly on the site, and molecules that have originated from the two adjacent sites on the DNA, arriving at the site via 1D diffusion. Let φ be the probability of a molecule that is (non-specifically) bound to the DNA to escape the DNA back to 3D diffusional motion, rather than transferring to one of the two neighboring sites through 1D diffusion. At every given time, a molecule either transfers to one of its adjacent sites or otherwise escapes the DNA. Therefore, the population of molecules at every site, consisting of 3D and 1D contributions, is constantly renewed. It follows (see Appendix B) that the rate of change in (non-specific) site occupancy can be expressed in the form:

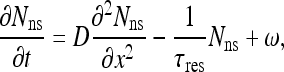16

where τ_res is the typical residence time a molecule spends on the DNA during every encounter, before it dissociates back to the nucleoplasm, D is the 1D diffusion coefficient and ω is the current of molecules arriving at a site from 3D diffusion alone. The steady state solution of (16), assuming the total length of the DNA to be much larger than the length of a typical binding site, is:

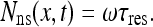17

This solution was verified numerically. The equation above implies that:

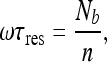18

where N_b is the total number of molecules bound to the DNA and n is the number of sites comprising the DNA. In addition, according to the steady state assumption, we have the following relation:

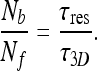19

Here N_f is the number of molecules that are free in the nucleoplasm, not bound to DNA, and τ_3D represents the typical time a molecule spends in 3D diffusion between an event of dissociation from the DNA and subsequent re-association. Substituting N_f with N_T − N_b, where N_T is the total number 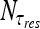of searching protein molecules in the nucleus, together with (18), we obtain the following expression for ω:

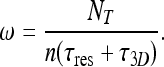20

Calculation of the molecular current in a 3D + 1D diffusion profile

We now have the means for deriving an explicit expression for the total current of molecules arriving at the specific binding site, assuming 3D and 1D diffusion in the target site search process. Due to the perfect absorbing nature of the site, the total number of new molecules arriving at the site during time 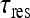—can be calculated by the first passage time (FPT) of molecules originating from all sites, i.e., summing up all contributions from all sites. This is conducted by using the probability density function for the FPT on a semi-infinite one-dimensional medium [15]. The resulting expression is:

Multiplication by 2 is a consequence of having treated the intervals [0, x_site] and [x_site, n] as two separate semi-infinite axes (assuming comparable contributions of the two intervals). Δx is the length of a binding site. The solution is:

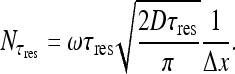21

After substitution of ω from (20) and dividing by τ_res, we obtain the current of new molecules:

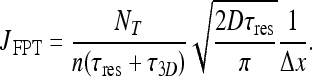22

Differentiating with respect to τ_res shows that the result peaks at τ_res = τ_3D, similar to the result obtained by [5]. In Fig. 1 the current is plotted for different values of τ_res. Evidently, combined diffusion dimensionality enhances the current of molecules, compared with 3D or 1D diffusion alone.

Fig. 1.

Current of molecules arriving at the specific binding site, as a function of τ_res. The number of molecules arriving per second is calculated according to (22); N_T = 200, n = 66,000 nm (corresponding to 50,000 binding sites of 1.32 nm each), τ_3D = 0.04, 0.06, 0.1, 0.12, 0.14 ms (a) or τ_3D = 0.1 ms (b), D = 30 nm²/ms (a) or D = 30,40,60,70,80 nm²/ms (b). τ_3D, D and τ_res were approximated according to [16]. The two limits of short and long residence times correspond to pure 3D and pure 1D diffusion, respectively. Combined 3D + 1D diffusion produces a peak at τ_res = τ_3D

Comparison of the FPT current with previous analysis

We would now like to compare the result in (22) with the current in a system of pure 3D diffusion search, i.e., no non-specific binding. The diffusion current of molecules searching in 3D for an absorbing receptor of linear dimension a is 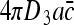, where D ₃ is the 3D diffusion coefficient and 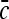is the concentration of the searching species in the surrounding solution. The current should obey:

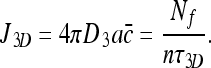23

The rightmost expression comes from the fact that N_f molecules arrive at the DNA every τ_3D time units, and distribute themselves evenly among n sites. Furthermore, because N_f = N_T for the pure 3D case (because N_b = 0) we obtain:

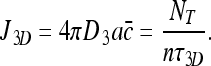24

For the sake of comparison, we rewrite our result (22), obtained by FPT calculation, in the form:

25

and

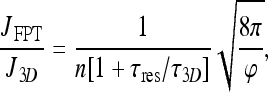which makes clear the relation between the FPT result and the expression for the pure 3D search current.

Noise levels accompanying the diffusional search process

Finally we use the expression for the current in order to determine the noise accompanying the search process of a TF for its DNA binding site. As in the analysis for the pure 3D diffusion scheme, we define noise as the standard deviation over the mean number of TF molecules arriving at the cognate site during time T. By consequence of taking the FPT of molecules in the cognate site, the obtained current J _FPT represents the number of new, uncorrelated arrivals at the site, therefore justifying their contribution to noise reduction [17]. It follows that the noise (relative dispersion) in a combined 3D+1D diffusional scheme should be:

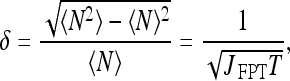26

where T is the time available for measurement (averaging time).

In order to test this prediction, we constructed a Monte Carlo simulation of the search process, which individually tracks the location of every protein molecule at every time it resides on the DNA. DNA was considered as a 1D axis consisting of 50,000 binding sites, out of which one site, at a random location, was defined as the specific binding site. The simulation ran 50 cells in parallel, corresponding to 50 nuclei, each cell containing 200 independently searching molecules.

At time t = 0, all molecules are given an initial random position on the DNA. Molecules are given a probability φ to escape the DNA, once bound, corresponding to a certain residence time. Once escaping, the molecule is assigned a random position on the DNA after a time step τ_3D. Alternatively, a bound molecule can diffuse to one of two neighboring sites during a time step τ. However, a molecule that has reached the specific binding site cannot diffuse in 1D diffusion to neighboring sites, but can only detach from the DNA. Thus, unlike previous simulations of the search process, our simulation ensures that only newly arriving molecules are counted and can therefore contribute to noise reduction.

Deterministic time steps of τ = 0.01 ms and τ_3D = 0.1 ms were simulated. Each molecule was set to run for a total time of T = 300 s, during which the number of times the molecule has arrived at the specific binding site was counted. The number of arrivals at the specific binding site was summed over all molecules of each cell. Multiple values of escape probability were simulated. Finally, the whole simulation of 50 cells was repeated 60 times, yielding 3,000 independently running cells. Standard deviation and mean of arrivals at the specific binding site per second, among the 3,000 entries, were obtained to give the simulated noise (26).

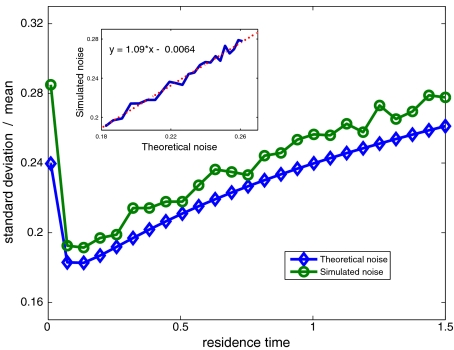
A comparison between the predicted noise (26) and that measured by simulation (Fig. 2) displays good agreement. We find that intermediate values of TF residence time on DNA, during a single 1D event, corresponding to a combined 3D+1D diffusion profile, results in reduction of noise levels in arrival events, compared with 3D or 1D diffusion schemes.

Fig. 2.

Noise (standard deviation over mean) of promoter occupancy by newly arriving TF molecules. Theoretically predicted noise was calculated according to (22) and (26), NT = 200 molecules, n = 50,000 sites, τ_3D = 0.1 ms; 0.01 < τ_res < 1.5 ms, corresponding to 0.0067 < φ < 1, T = 300 s; Simulated noise was obtained by taking the standard deviation over the mean of 3,000 independent entries, for each value of τ_res that was simulated. Inset Simulated vs. theoretically predicted noise in occupancy of the cognate binding site, with a linear fit showing good agreement

In addition to possible reduction of noise levels, this analysis also has implications for the averaging time available for concentration measurement. If the limit of precision required is set and the current of molecules is known, the minimum averaging time necessary can be determined.

Discussion

In this study we calculate the level of noise in the binding of TFs to their cognate DNA binding site. We first calculate the noise that is associated with a naive diffusional motion, consisting only of 3D diffusion in the nucleus. We then calculate the noise in a process that combines 3D diffusion in the nucleus with 1D sliding on DNA. We compare the analytical results we obtained with noise generated by numerical simulations of the search process.

The overall noise that is associated with TF-dependent regulation of gene expression consists of two components. First, transcription is initiated by the binding of TFs to their specific DNA binding site. This process is noisy with respect to the number of TFs arriving at the site, because the search process is diffusion-limited. Calculation of this noise was the focus of our study. The second component stems from the relationship between the actual physical entity that is being measured—promoter occupancy—and its translation into gene expression (input–output relation). This second component may or may not contribute to the overall noise. For instance, if gene expression is linear with the number of TFs arriving at the promoter site, then only the diffusional search process will contribute to the noise. However, in the presence of non-linearities resulting from other stochastic processes accompanying gene expression, noise will increase. Our calculations thus represent the lower limit of noise accompanying concentration measurement.

The notion that the search process of TFs after their cognate site on DNA may be facilitated by a combination of 3D diffusion in the nucleus and 1D diffusion along the DNA is well established. However, reduction of noise by a combined diffusion dimensionality scheme has not been demonstrated (cf. [18]). We show that this reduction is made possible by the enhancement of the current of TF molecules arriving at the promoter. As we demonstrate by comparison of the analytical result ((22) and (26)) with simulation, noise in promoter occupancy is inversely proportional to the current of molecules arriving at the promoter. Therefore, noise reduction by a combined diffusion dimensionality search process is consequential to enhancement of the current by this search scheme.

Importantly, in our analysis we have avoided any correlations between arrival events at the site, either due to the local nature of 1D diffusion or by recently detached molecules that did not wander off before re-attaching. These correlations were circumvented by taking the FPT in the mathematical model, and by treating the specific DNA binding site as a sink in the simulations.

In our analysis, we have assumed spherical symmetry of the binding site. Considering the shape of a DNA binding site, it might seem that an elongated geometry of an ellipsoidal cigar-shaped receptor would be more appropriate. The current of molecules to an adsorbing cigar-shaped receptor with semi-axes a > b = c is 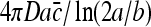[19]. This expression differs from that of a spherical receptor by the term (ln(2a/b)) in the denominator. However, considering the dimensions of a DNA binding site, this term is approximately unity, therefore justifying the spherical assumption.

In conclusion, in this study we have shown that facilitating the diffusion of TFs in the nucleus by combining 3D diffusion in the nucleus with 1D sliding on the DNA can reduce noise levels in the process of transcriptional regulation. Additional biological systems that perform computational tasks via factors binding to specific DNA sites may exhibit diverse input–output relations that (possibly) contribute differently to the overall noise in these processes. These contributions should be added to the basal physical limits of precision which we have assessed here.

Appendix A: Calculation of β

Since we are only interested in the calculation of the integral β, one can use the shape symmetry of the instrument to simplify the calculation. For a spherical instrument, we may consider, from the very start, P_s(x) integrated over the angles, that is, consider

27

where we consider the physical, three-dimensional situation. In terms of this function we have

28

where a is the instrument radius. The angle-averaged function can be written as

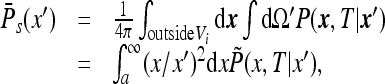29

where we introduce

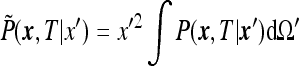30

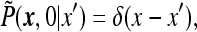31

and notice that 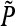depends on 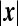only. This follows from the fact that 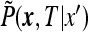obeys the diffusion equation in x that preserves the spherical symmetry of the initial conditions thanks to the spherical symmetry of the boundary conditions. The function 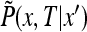obeys the diffusion equation in spherical coordinates

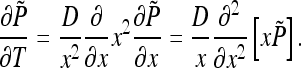32

The above equation is solved in the interval (a, ∞ ) with the boundary condition 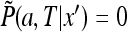and the initial condition (31). The equations are simpler in terms of the function 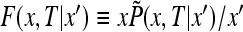. We have

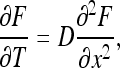33

supplemented by

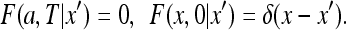34

The shifted function 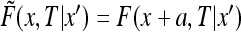obeys the diffusion equation with the conditions

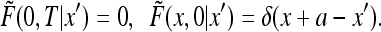35

The solution can be found by the method of images by noting that the solution to the above problem is the same as the restriction to the interval (0, ∞ ) of the solution to the diffusion equation with the initial condition δ(x + a − x′) − δ(x − a + x′). Indeed, the initial condition is odd and so the solution is odd at all times and vanishing at x = 0. We conclude that

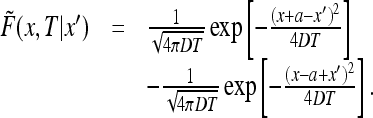36

We find

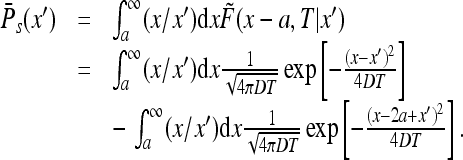Passing, in the first integral, to the variable x − a and in the second to x − 2a + x′ we find

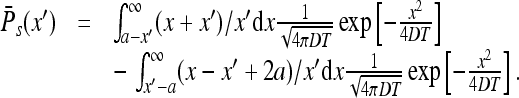We are interested in the domain x′ > a (see (28)). Using the fact that the integrand is odd one has

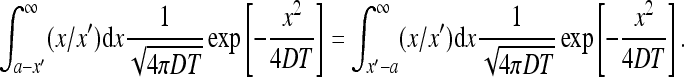Also one notes that

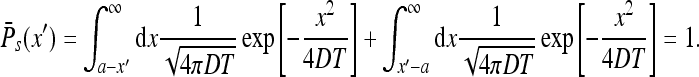Using the above we find

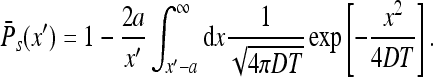The above formula describes the decay of survival probability with time. At times where the particles’ initial location x′ is much farther from a than the diffusive spreading length 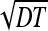, that is, , the survival probability is close to one. At times satisfying 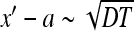the probability decays and at 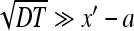the survival probability reaches its saturation value (cf. [17]):

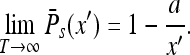It follows that the particle has a finite probability to “live forever”, i.e., escaping to infinity and never returning. The situation would be different in d = 1 and d = 2, where the particle always returns to where it was and the saturated probability would be equal to unity.

For the constant β we find

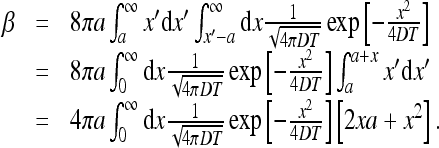The integrals above can be found easily,

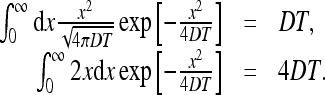37

We obtain

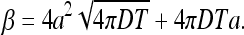38

Appendix B: Derivation of the differential equation describing the search process

As in the main text, let φ be the probability of a molecule that is (non-specifically) bound to the DNA to escape the DNA back to 3D diffusional motion, rather than transferring to one of the two neighboring sites through 1D diffusion; and let the time duration of a 1D diffusion step be Δt. Every Δt time units, a molecule either transfers to one of its adjacent sites or otherwise escapes the DNA. Therefore, during every time interval Δt, the population of molecules at every site, consisting of 3D and 1D contributions, is renewed. We can therefore express the number N(x,t + Δt) of molecules at any site x and time t + Δt by the equation:

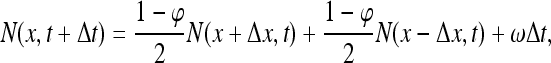39

where ω is the current of molecules arriving at the site just from 3D diffusion. The first two terms on the right-hand side represent the contribution of 1D motion to site occupancy while the third term is the 3D contribution. The leading order differential approximation to the equation above is

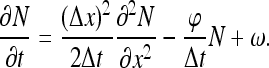40

This equation reproduces (16) from the main text with D = (Δx)²/2Δt and τ_res = Δt/φ.