Automatic Colon Segmentation with Dual Scan CT Colonography

Abstract

We present a fully automated three-dimensional (3-D) segmentation algorithm to extract the colon lumen surface in CT colonography. Focusing on significant-size polyp detection, we target at an efficient algorithm that maximizes overall colon coverage, minimizes the extracolonic components, maintains local shape accuracy, and achieves high segmentation speed. Two-dimensional (2-D) image processing techniques are employed first, resulting in automatic seed placement and better colon coverage. This is followed by near-air threshold 3-D region-growing using an improved marching-cubes algorithm, which provides fast and accurate surface generation. The algorithm constructs a well-organized vertex-triangle structure that uniquely employs a hash table method, yielding an order of magnitude speed improvement. We segment two scans, prone and supine, independently and with the goal of improved colon coverage. Both segmentations would be available for subsequent polyp detection systems. Segmenting and analyzing both scans improves surface coverage by at least 6% over supine or prone alone. According to subjective evaluation, the average coverage is about 87.5% of the entire colon. Employing near-air threshold and elongation criteria, only 6% of the data sets include extracolonic components (EC) in the segmentation. The observed surface shape accuracy of the segmentation is adequate for significant-size (6 mm) polyp detection, which is also verified by the results of the prototype detection algorithm. The segmentation takes less than 5 minutes on an AMD 1-GHz single-processor PC, which includes reading the volume data and writing the surface results. The surface-based segmentation algorithm is practical for subsequent polyp detection algorithms in that it produces high coverage, has a low EC rate, maintains local shape accuracy, and has a computational efficiency that makes real-time polyp detection possible. A fully automatic or computer-aided polyp detection system using this technique is likely to benefit future colon cancer early screening.

COLORECTAL CANCER is the second leading cause of cancer-related death in the United States.¹ Optical colonoscopy (OC) screening on a 10-year interval, as recommended by the American Cancer Society for people over 50, would substantially reduce mortality because most detected benign polyps can be removed before converting to carcinoma.¹ Computerized tomographic colonoscopy (CTC or virtual colonoscopy) promises to become a routine screening procedure for colorectal cancer because it improves patient comfort has no risk of perforation, and provides diagnostic accuracy that continues to close the gap with the current gold standard, OC.^2-5 At present, clinically acceptable CTC interpretation is provided by experienced radiologists who interpret two-dimensional (2-D) images slice by slice or virtually fly through the inner colon using three-dimensional (3-D) visualization software. Besides the significant learning curve, the procedure is time consuming, and the accuracy is currently lower than OC.² Effective computer-aided polyp detection (CAPD) systems potentially could supplement or even replace the radiologists’ interpretation to provide faster, more objective, and more accurate detection, as currently published CAPD methods^6-10 have reported encouraging results. The segmentation of the colon lumen surface as boundary (vicinity) voxels or a surface mesh is required for most CAPD schemes, and the segmentation performance directly affects polyp detection capability.

In CTC, theoretically it should not be difficult to distinguish the air in the colon from colon wall and outer soft tissues because the linear attenuation of air and soft tissue are theoretically about -1000 Hounsfield units (HU) and 50 HU, respectively; however, difficulties in automated segmentation occur for several reasons:

1. Partial volume effect (PVE) and the low 3-5 mm z-axis resolution degrade sharp edges. The colon wall is likely to be missed if the threshold is set incorrectly, as in the case of two adjacent loops of air-filled colon (Fig. 1a).

2. Residue fluid has similar attenuation to soft tissue and may mimic and subsequently hide the colon wall. Although we may ignore colon areas distorted by residue fluid, it is still an issue because the fluid might fill the lumen and thus block the colon segmentation, especially in some U-shaped areas (Fig. 1b).

3. Many patients have parts of their colons that are not well distended. (Fig. 1c).

There are many algorithms^{6, 7, 11-15} for 3-D colon lumen segmentation, most of which could be categorized as using region-growing,^{6, 7, 15} statistical classification,^{11, 12} or combination.^{13, 14} Geometric connectivity is one of the most important features for all these algorithms; however, for the reasons mentioned above, improper connectivity can occur. Consequently, missing colon segments or including unexpected non-colon structures, especially the small bowel, are problematic. Wyatt et al¹⁵ present a segmentation algorithm that includes a high number of extra-colonic (EC) structures and requires considerable computation. In recent colon segmentation work, Chen et al¹² perform a local volume statistical analysis followed by a high level EC structures removal, which also involves electronic bowel cleansing. Lakare et al¹¹ describe an electronic cleansing algorithm using segmentation rays with a very high fluid/soft tissue contrast in the CTC images. The algorithms in eg. (13) and eg. (14) segment the neighboring voxels that encompass the colon wall, combining anatomic-based extraction and colon-based analysis to improve results. Our CAPD system, including segmentation and polyp detection, has been folly automated to take raw DICOM data and produce a report of detected polyps. Three-dimensional segmentation is the basis for the system’s success and is the focus of this paper.

Figure 1.

Typical 2-D CT slice with segmentation difficulties. The rectangular frame regions in (a) show thin walls with air on both sides; (b) has a part of colon buried in the residue fluid, which is highlighted with the dashed line. The rectangular frame regions in (c) are the collapsed parts in sigmoid colon.

Our clinical protocol specifies dual CT scans, and we independently segment the prone and supine scans, a method that has been used for almost all radiologist-based CTC diagnosis and that has been shown to improve significantly polyp detection.^{16, 17} Similarly, we combine both scans to improve the colon coverage in computerized segmentation. Colon deformation between the two positions makes surface registration difficult at best. Fortunately, the specific situation and the clinical purpose of CTC leave registration unnecessary because, if a polyp shows in either or both scans, the patient would be forwarded to OC. Considering clinical practice, we implicitly stress the preference of patient-based accuracy over polyp-based accuracy. Even at the polyp level, instead of registering the two surfaces, we provide a rough registration of the detected polyps according to their locations; however, much remains to be done in the area of polyp registration.

Automatic and exhaustive search on seed allocation based on 2-D image analysis has been emphasized in our scheme to obtain optimal coverage. For region-growing based segmentation schemes, single or multiple seeds^{6, 7, 15} do not adequately result in optimal colon coverage. Seed-on-demand approaches^{13, 14} also encounter this problem as a result of colon path variation and the collapsed colon regions during the performance of segmentation checking. We use near-air thresholding in our region-growing, which avoids leaking and tends to retain local shape for polyp detection rather than attempting to locate the exact boundary.

We have developed an unproved marching-cubes algorithm that efficiently produces a direction-encoded triangle mesh of the colon lumen and a hash-searching algorithm that efficiently removes the vertex redundancy of the mesh. The output of the segmentation is a well-organized vertex-triangle-structure that represents the colon lumen. Our prototype polyp detection¹⁸ is entirely based on the geometric features of the well-segmented lumen surface produced from the procedures outlined above.

We continue by describing the proposed segmentation algorithm and the evaluation scheme in the methods section; scanning protocol and data acquisition are introduced in the Data Section, followed by the Results. In the Discussion we explore the pitfalls and possible improvements of the algorithm, and we then present our conclusions.

METHODS

The goal of our segmentation is the best combination of overall coverage, EC rate, shape accuracy, and execution speed. Our method comprises two parts: (1) automatic seed placement produces multiple seeds for the following 3-D region growing to ensure the coverage all colon fragments, which is complicated by residual fluid, bad distention, and distortion; therefore, high overall coverage is achieved; (2) using the seeds from part 1, 3-D region-growing is performed simultaneously with surface generation. An overview of the segmentation process is provided in Fig. 2.

Figure 2.

Flow diagram of the segmentation. The two parts of the algorithm are separated by the double line.

Automatic Seed Placement

Manual seed placement is time consuming, operator dependent, and error prone, and it is impractical for a reader to place seeds in every colon segment in every slice. Furthermore, placing seeds in such a way to ensure optimal colon coverage by the subsequent segmentation algorithm would be difficult. Instead, we use a 2-D segmentation technique and anatomical knowledge of the colon to locate seeds in an automated seed-placement process. From the statistics of the 50 subjects, we found that a segmented colon has from 1 to 10 fragments with an average of 2.4. The ideal seed-selection process should select one 3-D point in each isolated colon fragment. As a practical alternative, we collect more seeds than the number of fragments to ensure coverage. Of the hundreds of slices, most contain more than one intersection with the colon because of the path variation and haustral folds. The seeds from a small portion of these intersections are enough for covering all fragments. Based on 2-D region-growing, we have designed a colon segment detector that exhaustively searches for colon segments specific to our 3-D region-growing method and that requires high specificity and trades off sensitivity. The average number of seeds generated by the algorithm is 42 per scan.

Our 2-D automated seed-placement algorithm uses all originally collected (not interpolated) slices to obtain maximum coverage. A standard 2-D region-growing method¹⁹ is performed on these slices with the seeds automatically generated by scanning each slice. Therefore, all the air-inflated areas in these 2-D slices are segmented as colon-segment candidates for the classifier described below, which includes size and shape filters. We then place seeds at the centers of all the segments determined to be colon. The segmentation is designed for high specificity. The underlying assumption is that any isolated colon fragment would have at least one segment that is well distended, and seeds are identified in the intersections of slices and well-distended colon areas. Redundant seeds for an isolated colon fragment are inevitable but do not affect segmentation as they are absorbed by region-growing from another seed in the fragment. The important objective of the method is to largely reduce the possibility of placing seeds in non-colonic, air-inflated structures. Our 2-D segmentation is performed for each original slice by using an experimentally set threshold (-650 HU) that is high enough to connect the lung area as one region but would disqualify the region due to a size criterion defined below. Anatomical knowledge of the air-inflated colon, EC components, and background can be summarized as follows, (see also Fig. 3):

1. The background is very large or non-oval shape.

2. The 2-D tomographic sections of lung are very large (far from bottom), or shaped like a hook (at the bottom).

3. The small bowel sections produce tomographic segments similar to the colon, but their size is much smaller than a well-distended colon segment.

4. Some of the segments of a well-distended colon are oval shaped and almost convex.

We translate this anatomic knowledge into several strict, algorithmically based criteria integrated in two filters (see Table 1) that efficiently remove most segments of EC structures: size filtering, shape filtering, and seed placement.

Figure 3.

The anatomical features in 2-D CTC slices: (a) shows a non-bottom slice of lungs. The lung segments are large when small nodules and bronchioles are removed with an appropriate threshold, such as -650 HU. Background regions are shown in (a)-(c), and they are either too large or non-oval in shape; (b) shows a bottom slice of lungs, and (c) is in the rectum section. No big air-inflated anatomic structures are apparent, and the axes of the colon are relatively large.

Table 1.

Anatomic-Based Parameters Used in 2-D Shape Analysis

	Parameters		Value	Effective size
Size filter	Max area		6500	Area (mm2)	3185-6500
	Min area		1000		490-1000
Shape filter	Regular slices	Max axis	14.14	Radii (mm)	17.1-24.5
		Min axis	10		12.1-17.3
	Last 100 slices	Max axis	17.3		21-30
		Min axis	10		12.1-17.3
	Eccentricity		1.73:1
	Almost-convex shape		Refer to (1)

Size filtering

The area should be less than 6500 pixels to remove background area and the non-bottom part of the lungs and should be larger than 1000 pixels to remove most of the small bowel and image artifacts.

Shape filtering

Principal component analysis (PCA)²⁰ is performed to determine the main axes of a 2-D colon candidates. The equivalent radii are about 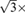main axes, because the main axes are the standard deviations of the points in the area in the principal directions. To remove the small bowel, both axes must be larger than 10 pixels, and the effective size is about 12.1-17.3 mm depending on the in-plane resolution. To remove the lungs or stomach, we set the upper limit for both axes to 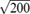pixels. Rectum sections of the colon often have larger diameters, and we set the upper limit for these axes pixels. We predefine the rectum location to the last 100 slices. Air-inflated, non-colon structures with large diameters are not likely to appear in these locations. To account for the oval shape of the colon, we remove segments whose aspect ratios are larger than 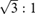, which will remove the bottom of the lungs and some isolated small background sections. The almost-convex shape requirement is added to remove the C- or S-shaped small bowel that would have similar size and axes ratio and is defined as

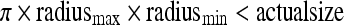We specifically have chosen to use the pixel as the unit for in-plane 2-D processing-as it reflects the size of the patients. The field of view (FOV) for a given scan is visually set according to the patient size appearing in the scout scan, and the FOV determines the pixel size that varies from 0.70 mm to 1.00 mm in our data sets. It is reasonable to assume that a larger patient has larger anatomic structures and is suitable for increased linear criteria that are implicated by using pixel units.

Seed placement

We place the seeds in the geometric centers of the segments that passed both filters. Therefore, the seeds are still valid for the lower threshold in 3-D region-growing. Because there are ~100 original slices for each scan, and the number of generated seeds (~42/scan) is much larger than the average number of isolated colon fragments, 2.4/scan, having seeds in each fragment is highly probable despite the low sensitivity of the 2-D classification. In the examples in Fig. 4, there are ~30 isolated, air-inflated segments in the slices. The isolated dark segments belong to colon, and the brighter segments with arrows are small bowel or artifacts. Background areas in black are easily removed because of oversize or elongation. Of 14 colon segments in these slices, only 5 well-distended segments pass both the size and shape filters.

Figure 4.

The result of the 2-D segmentation. The short arrows indicate the small air chambers or artifacts, and the long arrows are small bowel segments. The thick long arrow in (b) points out a C-shaped small bowel segment. In (a) and (b), the dark regions are the segments of the colon, only five of which pass the filters and result in the seeds shown at the cross points.

3-D Segmentation and Surface Generation

Theoretically, the colon has no CT detectable airway connection to other air inflated structures; therefore, an appropriate threshold should detect the entire colon wall for most cases. In our 3-D region growing method, an empirically determined near-air threshold is used to avoid leaking to EC structures such as small bowel. A subsequent elongation test lowers the EC rate even more. In previous colon segmentation work that incorporates mesh representation, segmentation and surface generation are normally separated. That is, a 3-D region-growing algorithm selects all inner voxels followed by a marching-cubes or ray-tracing method to generate a mesh surface. We perform the region-growing described above simultaneously with an improved marching-cubes algorithm; the computational efficiency for surface generation is remarkably improved.

Fast Region-Growing with Near-Air Threshold

A general region-growing algorithm uses a fixed or adaptive threshold around the middle of the intensities of the two categories forming the boundary. Although locally approaching the real boundaries, choosing centrally based thresholds encounters the serious problem of EC inclusion in CTC segmentation. Therefore, we set the threshold at near-air intensity to reduce the probability of growing into unexpected regions, and the near-air threshold practically keeps the local shape variations that carry the dominant features for subsequent polyp detection. To determine this threshold, we analyzed the histogram of the voxel values of middle range slices that have a higher rate of colon appearance. Figure 4 shows the histogram from all patients’ data ignoring the white background voxels outside the FOV. The two dominant peaks correspond to air and soft tissues (see Fig. 5). To avoid possible PVE voxels, we take -814 HU at the bottom of the air peak. The threshold was chosen from the near-air intensities, from -834 to -714 with 5 HU increments. Each one was tested on the first 20 data sets for the best coverage and EC rate. The optimal thresholds were found in the range of -814 ? 5 HU, and this value was used for subsequent scans.

Figure 5.

The histogram of middle-range slices from all data sets.

Figure 6 shows the segmented surfaces for centrally based (for example, -574 HU) and near-air (-814 HU) thresholds. Although -574 HU is much lower than the theoretical air/tissue interface (around -475 HU), the colon still grows into small bowel because of PVE and the 5-mm collimation. Therefore, the near-air threshold is necessary to avoid leaking and to reduce EC rate.

Figure 6.

Surface difference between high and low thresholds: (a) uses near-air threshold, -814 HU; (b) uses a median threshold, -574 HU, but includes significant parts of small bowel.

Although the lower threshold may generates a rougher surface, our experience tells us that significant size polyps are still visible. Figure 7 shows the surface of a 5-mm polyp area (confirmed by both CTC and OC) using two different thresholds, both of which show the polyp with the higher threshold producing a smoother surface. Beside visual inspection, the prototype detection results show that the algorithm effectively maintains the local shape accuracy.

Figure 7.

Comparison of polyp (about 5-mm) areas segmented using different thresholds: (a) uses -814 HU, and (b) uses -574 HU. Both clearly show the polyp.

We grow the region in 3-D from the first seed in the list, marking all voxels in the region. Voxels whose 8 vertices are not all inside or outside the colon are boundary voxels. An improved marching-cubes algorithm, described next, is performed on each boundary voxel, and the generated triangles are pushed into the surface triangle lists. We do not need to save the information from the inner voxels or even all the boundary ones; only the final surface triangles are saved for future use. We then retrieve the next unmarked seed and repeat the procedure until the end of the seed list; therefore, redundant seeds are ignored and will not affect segmentation speed. This simple thresholding keeps the most clinically important geometric features of the colon lumen surface and is computationally efficient. EC structures are few in our segmentation and can be categorized as upper abdomen stomach due to error seeds and small bowel due to leaking. A region elongation test based on the growing depth¹⁵ is performed on all isolated segment in the upper half of the volume and successfully removes most of the EC components in stomach.

Improved Marching Cubes Method

Traditional marching-cubes methods²¹ check a table for all 15 possible boundary cube models such as the one in Figure 8 by rotating the given cube or voxel and matching it with all the models in the table. To avoid this computationally intensive process, we take advantage of the marching-cubes algorithm in²² and incorporate some substantial improvements. To present the details of the algorithm, we provide the following definitions. An iso-point is the point on a cube edge whose nodes’ values are not both above or not both below the threshold, for example, A-F in Fig. 8. It is actually one vertex of the final surface, and the position of the iso-point on the edge is determined by interpolation according to the edge nodes’ values. The associate node of an iso-point is the edge node whose value is lower than the threshold. In Fig. 8, c is the associate node for F, G, and H. We have incorporated three major improvements into our marching-cubes algorithm. First, we keep triangles as the surface element units to avoid extra computation in polyp detection, whereas the referenced algorithm would introduce polygons. Second, we set the order of the 3 vertices of each triangle so that the surface normal of the triangle points toward the lumen. Third, we merge the iso-points into the voxel vertices where the distances from the iso-points to the vertices are small enough so that the merging does not degrade the surface. In our case, the merging distance is 0.05 mm. This last improvement greatly reduces the number of triangles of the segmented surface because many iso-points are very close, smaller than 0.5 mm, to their neighboring vertex due to interpolation and floating-point calculation. Based on the framework of the compact iso-contour algorithms presented by D. Moore et al,²³ the process reduces the number of triangles by 40% to 60%. Thus the time for the feature calculation for any subsequent polyp detection can be substantially reduced. Pseudo-code for the improved marching cubes algorithm on a boundary voxel is provided in the Appendix.

Figure 8.

An example of marching-cubes: Points A-H are iso-points. Triangles of the marching-cubes are shown in gray.

A careful reader will find that there is ambiguity for different starting iso-points. In Fig. 8, if we start with C, the triangle list would be, C-D-E, C-E-A, and C-A-B, whereas if we start from A, we get a list of A-B-C,_A.-C-D, and A-D-E. The sub-voxel variation does not affect the detection of significant size polyps and is consequently ignored.

Universal Hash Table to Remove Duplicate Vertices

The triangles of the mesh are uniquely generated while the cube is marching in the volume data from voxel to voxel. The mesh vertices composing these triangles are, however, repeatedly recorded because adjacent cubes share some edges and iso-points. The lists of both unique vertices and unique triangles are required for fast calculation of curvatures at all vertices on the surface. The vertex-triangle-structure provides instant reference to surrounding triangles of a given vertex as well as the 3 vertices composing a triangle. A linear search method for removing the duplicity of the vertices would takes hours for an entire colon surface, which comprises one about million triangles. Instead we use a hash table²⁴ and construct the vertex-triangle-structure at the same time. The hash function is the determining factor for the efficiency of the search. We take the summation of the 3 coordinates of a given vertex and the origin coordinates as the hash key such that

where (x, y, z) are the world coordinates of the given vertex, and (x₀, y₀, z₀) are the coordinates of the origin of the data set. The hash function is selected as

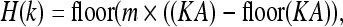where m is the size of the hash table, and A is the number recommended in,²⁵

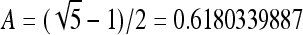The time for sorting a one-million triangle surface with our algorithm takes only 1.5 min on a PC Linux system (Linux 9.0 RedHat Inc.). The high speed is possible by setting m as large as the system memory capacity allows. In addition, the vertex-triangle structure is easily exported as OOGL files that are used in the Geomview²⁶ surface visualization software with GNU license. All colon surface images provided in this article are generated using Geomview.

Subjective Evaluation of Colon Coverage

In previous work, objective evaluation was performed to show algorithm repeatability¹² or improvement of one computerized algorithm over another ¹⁴. Objective evaluation of colon coverage is problematic; however, we provided a reliable subjective evaluation method. All segmented colon surfaces were converted to 3-D visual reality modeling language (VRML) and shrunk for easy manipulation without losing any anatomic structures. Two radiologists used a VRML viewer (Computer Associates International, Inc. Islandia, NY.) and quantitatively estimated the percentage of coverage over the entire colon for each scan and the combination of dual scans with respect to the scout images of lateral and posterior-anterior (P-A) positions. Using the scout images in conjunction with the 3-D visualization software improves the radiologists’ estimation of segmentation coverage.

DATA

Data for 50 subjects were collected using a multi-detector⁴ helical CT scanner (GE LightSpeed QX/I, General Electric Medical Systems, Milwaukee, WI.), operating at 120 KVp, 5 mm collimation, and a pitch of 3:1. Each subject had two studies performed, the first without oral contrast and the second with oral contrast, and each study comprised a supine and a prone scan performed at 180 mA and 80 mA, respectively. With continuous CO₂ insufflation, scanning started after 2-3 liters of CO₂ were administered. The CO₂ insufflator continually delivers a constant pressure (25 mmHg) to compensate for the absorption across the gut mucosa until patient tolerance is met. Scan time is about 20 s using a single breath-hold for each subject. Images are reconstructed and interpolated to 1 mm slice thickness and comprise approximately 500, 512 × 512 voxel slices. OC was performed the same day, after the second CT study. The oral contrast studies were performed for a special clinical trial, and we did not differentiate them in our computerized algorithm. Therefore, we have 100 dual scan data sets regardless of oral contrast.

RESULTS

For all subjects, our seed-placement algorithm satisfied the high specificity requirement, providing an average of 42 seeds per scan based on the results of the 100 dual scan data sets. Twelve of the 100 data sets resulted in a total of 45 seeds in EC components. Therefore, the algorithm provides a high specificity at 1-45 (42 ? 100 ? 2) = 99.5%. All error seeds fell in the air inflated stomach fragments.

Using the subjective evaluation described above (see Subjective Evaluation of Colon Coverage), 42% of supine scans are fully segmented, as are 21% of prone scans. Combining the supine and prone scans results in 57% fully segmented colons. The results for the 100 data sets show an average coverage for supine scans of 81.8% and 55.4% for the prone scans. Figure 9a illustrates the coverage distribution of the 100 data sets and compares results among supine, prone, and dual scans. Supine scans are generally better than prone scans, partially because the increased pressure from the inner body for the prone scan collapses parts of the colon. Nevertheless, the prone segmentation covers some parts that are missed by the supine scan. Consequently, we get an average coverage of 87.5% for dual scans, demonstrating that dual scan segmentation improves coverage of lumen surface. The interobserver agreement indicated by the Pearson correlation coefficients, 0.85/prone, 0.80/supine, and 0.70/dual scan, validates our evaluation algorithm. Results for no-contrast and contrast scans are shown in Fig. 9b and 9c, respectively.

Figure 9.

Percent coverage of the segmentation result on 100 dual scan studies. The results for supine scans better than for prone scans and obviously improved while using both: (a) shows the results from all scans; (b) shows the results of no-contrast scans; and (c) shows the results from contrast scans.

The dual scan provides a solution for residue fluid because most of fluid-covered surface in one scan is revealed in the other. However, for collapsed colon fragments, which are the main reason for the missing sections, we doubt there is a solution based solely on CTC. Fortunately, gas distention only fails on a small portion of subjects and only on a small percentage of the entire colon, especially for the sigmoid colon, and is comparable to the inaccessible percentage (5% to 15%² in OC.

The elongation test substantially reduces EC components in the upper abdomen, decreasing the EC rate from 15% to 6%. Among the six data sets generating EC components, one includes the stomach with an air-inflated fragment longer than 80 mm, the elongation limit; three are due to an unclosed ileocecal valve; and two result from leaking at a missing wall.

In Fig. 10, we present segmentation examples, (a) is a 100% segmentation of an entirely well-distended colon; (b) is a fully segmented colon with some small artifacts; (c) and (d) is an example that shows the coverage improvement with dual scan. (c) is the supine position, and (d) is the corresponding prone position. The lost hepatic and splenic flexures in (c) appear in (d), and most of the surface hidden in residue fluid of (c) is revealed in (d). The radiologists’ estimates are 97% for the dual scan, yet only 65% for the prone and 75% for the supine scans. Image (e) shows a case that fails to fully cover the colon. The vertical box is the supine segmentation, which covers the ascending colon, the rectum, and a small part of sigmoid colon, whereas the horizontal box is the prone segmentation, which covers the two flexures, part of the transverse colon, and the descending colon. The estimated coverage using both scans is 45%. Image (f) shows a segmentation result with EC components, and the leak point is indicated by an arrow.

Figure 10.

Surface view of the segmentation results: (a) is a well-inflated colon that is fully segmented under a single scan; (b) shows another case of a fully segmented colon, which has thinner sigmoid, descending, and transverse sections and a small spike of artifact at the arrow position; (c) and (d) show a 97% segmentation by combining the two scans; (e) shows 45% coverage using dual scan; (f) shows a segmentation that includes small bowel due to missing wall.

Polyp detection based on an algorithm that uses the principal geometric features, maximum and minimum curvatures, further validates the segmentation algorithm.¹⁸ Without parametric training, the prototype system using a multi-plane linear discriminant function method provides encouraging patient-based accuracy, as shown in Table 2. The improved sensitivity proved the effectiveness of the method when using both scans, and we anticipate better specificity after parametric training with a polyp database.

Table 2.

Patient-Based Accuracy of the Prototype Polyp Detection Algorithm Comparing to Optical Colonoscopy Results with the Cut-Off Size of 6 mm

	No contrast data sets			Contrast data sets			All data sets
	Supine	Prone	Both	Supine	Prone	Both	Supine	Prone	Both
True positives	8	9	12	11	11	12	19	20	24
False positives	21	19	27	16	13	21	37	32	48
Total positives	13	13	13	13	13	13	26	26	26
Total negatives	37	37	37	37	37	37	74	74	74
Sensitivity	61.54%	69.23%	92.31%	84.62%	84.62%	92.31%	73.08%	76.92%	92.31%
Specificity	43.24%	48.65%	27.03%	56.76%	64.86%	43.24%	50.00%	56.76%	35.14%

The speed for the segmentation procedure is reasonable for real-tune detection. For a complete colon, it takes 6 min on a 900 MHz Sun Blade 2000 workstation (Sun Microsystems Inc., Santa Clara, CA) with a 1 GByte memory and less than 5 min on the Linux PC that is powered by a 1 GHz AMD CPU, 1 GByte memory, and a 5400 rpm 80 GByte hard drive with 2-MByte cache. The segmentation in¹⁴ takes about 7.5-13 min on a dual AMD 1.2 Ghz CPU, while the algorithm in¹² takes less than 9 min on a dual CPU SGI/Octane 250 MHz. The algorithm in¹⁵ while more sophisticated, takes an hour for an entire colon.

DISCUSSION AND CONCLUSIONS

We simply take the scans with and without contrast as two different data sets and do not consider the oral contrast in our algorithm because: (1) oral contrast requires intake of large amount of fluid, which increases patient discomfort in CTC and it is still under experimental trials; (2) most residual fluid-covered regions are revealed in the counterpart scans; (3) the CT intensities of the enhanced fluid regions in our scans are not consistent throughout the colon; and (4) the fluid/wall boundary contrast is much lower than that of air/wall boundary in our data sets, and the detected boundary would be sensitive to the PVE and acquisition noise. An electronic cleansing algorithm is useful for improving coverage when high fluid/wall contrast is achievable.¹¹ At present, we use a 4-detector helical scanner with 5-mm slice thickness so that an entire colon scan within a single breath-hold is possible. A 16-slice CT scanner can complete the scan in less time and provides better z-axis resolution. Accordingly, we could use a higher threshold in region-growing and produce a smoother and more accurate colon lumen, which should provide higher accuracy in polyp detection and benefit smaller lesion detection. Segmentation performance is anticipated to be highly improved if better z-axis resolution, 1-mm, were used.

The 3-D segmentation algorithm described is fast and efficient on real data. Considering the existing problems for colon segmentation, our algorithm globally obtains high colon coverage (87.5%), low EC inclusion (6%), and locally retains surface shape accuracy enough for detecting significant size polyps. The automatic segmentation using dual scans improves the coverage of the segmented colon, which will benefit the polyp detection. Improved resolution, possible with today’s scanners, would make the algorithm even more effective.

APPENDIX: Pseudo-code for the improved marching cube algorithm

1: A cube is set up on the given boundary voxel.

2: for each of cube’s edge

3: if a boundary edge*

4: We get an iso-point;

5: Calculate the position of the iso-point by interpolation

6: if the position near either nodes

7: Take the node as the position of this iso-point;

8: endif

9: Put the iso-point in the list

10: Record its associate node

11: endif

12: endfor

13: for each unmarked iso-point in the list;

14: set this point as current point, and mark it;

15: setfirst_point = NULL;

16: Find next iso-point in the list by the following conditions:

17: a AND b AND (c OR d OR e).

18: -a. next iso-point are not marked;

19: -b. next iso-point lies on the same cube face as the current;

20: -c. the current and the next share an associate node.

21: -d. the current and the next iso-points’ associate nodes share a cube edge.

22: -e. the cube face that contains the current and the next iso-points has 3 nodes that have values above the threshold.

23: if no such point

24: setfirst_point = NULL;

25: goto line 13;

26: endif

27: iffirst_point = NULL

28: if the direction from the current iso-point to the next is reversed

29: Swap the current and the next iso-points

30: endif

31: Open a new triangle with its first two vertices being the current and the next iso-point.

32: setfirst_point = the current point;

33: endif

34: if the current and the next are not at same position

35: if the current triangle is closed*

36:* Open a new triangle with its first two vertices as first point and the next iso-point.

37: else

38:* Close the current triangle by setting the next iso-point as the third vertex.

39: endif

40: endif

41: set the next iso-point as current, and mark it.

42: goto 16.

43: endfor

Notes

3*: To be a boundary edge, it must have one of its node values above the threshold and the other node value below the threshold.

27-33*: This code section provides the required direction for the triangles. From the code, we can see that all the triangles starting from one iso-point have the same normal direction. Therefore, only the direction from the first iso-point to the second is checked to ensure the directions for all the following triangles from the same first iso-point.

36, 38*: Opening a triangle is the procedure to assign the first two vertices of the triangle, whereas closing a triangle provides the third vertex.