Depth-resolved blood oxygen saturation measurement by dual-wavelength photothermal (DWP) optical coherence tomography

Abstract

Non-invasive depth-resolved measurement of hemoglobin oxygen saturation (SaO₂) levels in discrete blood vessels may have implications for diagnosis and treatment of various pathologies. We introduce a novel Dual-Wavelength Photothermal (DWP) Optical Coherence Tomography (OCT) for non-invasive depth-resolved measurement of SaO₂ levels in a blood vessel phantom. DWP OCT SaO₂ is linearly correlated with blood-gas SaO₂ measurements. We demonstrate 6.3% precision in SaO₂ levels measured a phantom blood vessel using DWP-OCT with 800 and 765 nm excitation wavelengths. Sources of uncertainty in SaO₂ levels measured with DWP-OCT are identified and characterized.

1. Introduction

Tissue oxygenation is an important physiological parameter. Abnormal oxygenation of tissues and blood has been implicated in a number of diseases preceding irreversible tissue damage including cancer, inflammatory and infectious processes, diabetic retinopathy, choroidal disorders, stroke and vascular dementia among others [1]. Tissue oxygenation levels have been measured invasively and non-invasively.

Optical methods have recently attracted significant interest for non-invasive assessment of SaO₂ levels due to the inherent ability to provide high temporal and spatial resolution. Distinct differences in the absorption spectra between oxy- and deoxy-hemoglobin in the visible and infrared (IR) spectral regions underlie spectroscopic methods for non-invasive assessment of in vivo hemoglobin oxygen saturation levels [2–11]. Because these spectroscopic methods provide mean arterial and venous [2–8] and arterial [9–11] SaO₂ levels averaged over a relatively large volume of tissue, longitudinal and lateral spatial specificity to identify a damaged tissue volume is compromised. Assessment of in vivo SaO₂ levels with higher longitudinal and lateral spatial specificity is required for early diagnosis and longitudinal monitoring of many diseases including cancer of epithelial tissues, local inflammatory and infectious processes, retinopathy, choroidal eye disorders and stroke. For example, the human retina is only 200-300 µm thick and consists of many well defined physiological longitudinal layers and has two independent vascular oxygen supplies (retina and choroid). Because the choroidal vascular supply provides a ten-fold higher blood flow than the retinal supply, methods without longitudinal or depth-resolved specificity can provide SaO₂ levels that are difficult to interpret.

Spectral Fourier Domain Optical Coherence Tomography (FD OCT) [12,13] can provide simultaneously high depth-resolved specificity and temporal resolution and has been applied for assessing blood oxygenation levels [14–18]. Although SaO₂ measurements with Spectral OCT in the visible range was reported in phantoms where absorption of hemoglobin is maximal [17], in the near infrared spectrum, which provide increased depth penetration, only a correlation with SaO₂ levels has been demonstrated [16,18]. Spectral OCT in the visible range is limited to probing superficial tissue depths of a few hundred microns and faces technical challenges to monitor ocular disorders due to high sensitivity of retinal photoreceptors and stimulation of the occipital lobe of the cerebral hemisphere. Challenges to apply spectral OCT to measure SaO₂ levels are: 1) relatively low absorption of infrared light by oxy-/deoxy-hemoglobin (6% energy absorption through a 300 µm diameter blood vessel at the isobestic 800 nm wavelength); 2) trade-off between spectral and depth-resolved resolutions [13,19]; and 3) high signal variability due to speckle interference effects.

Instrumentation where phase changes in a sample are induced by absorption of single-wavelength excitation light and measured with phase sensitive (PhS) OCT [20–23] are known as Photothermal OCT [24–27]. Photothermal OCT was used for detection of contrast agents in vitro [25], in live cells [26] and in ex vivo tissues [24,27] for early cancer [26,27] and atherosclerotic plaques [24] diagnosis. In this paper, we introduce a Dual-Wavelength Photothermal OCT (DWP-OCT) that uses excitation and probe light in the near infrared spectral region for depth-resolved SaO₂ monitoring in tissue phantoms. Our approach was applied to depth-resolved measurement of graded SaO₂ levels in phantoms and does not suffer from the high signal variability of spectral OCT approaches.

2. Materials and Methods

The experimental setup for our DWP-OCT (Fig. 1 ) system to measure SaO₂ levels contains three major components: 1) excitation laser (800 nm or 765 nm) and fiber delivery system to induce nanometer-scale optical pathlength changes in the blood sample; 2) sample consisting of a non-absorbing polytetrafluoroethylene (PTFE) conduit containing blood with variable graded SaO₂ levels; and 3) Phase Sensitive (PhS) OCT system [23] to measure SaO₂-dependent optical pathlength changes induced by excitation laser light.

Fig. 1.

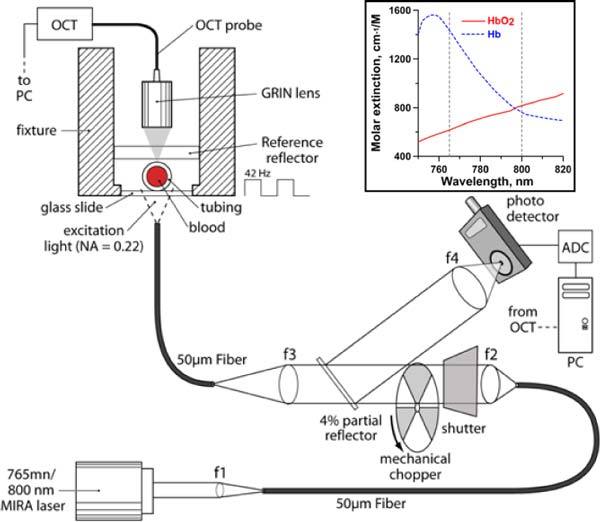
Dual Wavelength Photothermal (DWP)-OCT. A tunable Ti:Al₂O₃ laser was utilized as an excitation source (765 and 800 nm). Excitation laser light was intensity modulated at 42 Hz with a mechanical chopper and delivered to the blood sample through a multimode 50 µm core-diameter fiber (NA = 0.22). Relative intensity of excitation laser light on the blood sample was calibrated with a 4% partial reflector. Probe OCT light (1328 nm) emitted from a single mode fiber was focused on the blood sample from the topside with a GRIN lens. A reference reflector (5%) provides the OCT reference optical signal. Inset in the upper right corner shows absorption spectra of oxy- and deoxy-hemoglobin. Dashed lines indicate laser excitation wavelengths (765 nm and 800 nm) utilized in the reported experiments.

The ability of PTFE tubing to maintain a constant blood oxygenation level was tested using a commercial avoximeter (ITC, 1000E, Edison, NJ). Blood with SaO₂ = 97.6% was placed in the PTFE tubing at room temperature for 230 min; after removal, avoximeter-measured SaO₂ level showed a 1.7% decrease to 95.9%.

Phase measurements provided by DWP-OCT are associated with optical pathlength (op) changes in response to dual-wavelength (765 nm and 800 nm) excitation of a blood sample. Optical pathlength changes (op = φλ/(4π)) in the sample are induced by light absorption of oxy- and deoxy-hemoglobin in blood, where φ is measured phase change at a specific depth and λ = 1328 nm is central wavelength of the DWP-OCT system. Measurement of op at 765 nm and 800 nm laser excitation wavelengths is used to compute SaO₂ levels in blood using an analytical model described in section 2.5 below.

2.1 Sample Preparation

Fresh porcine arterial blood was collected, placed in a sealed container and stored at 4°C. To prevent clotting, 50 units of heparin per 50 ml of blood were added immediately after collection. To prepare the samples with graded SaO₂ levels for DWP-OCT measurement we divided blood into two equal parts and added to one portion 5 mg of Sodium Dithionite per 1 ml of blood to achieve a sample with SaO₂ = 0%. Oxygenated arterial blood was mixed with the 0% SaO₂ blood in different proportions to achieve intermediate SaO₂ levels of 18.5%, 58.4%, 84.1% and 92.8%. Blood samples with desired SaO₂ levels were kept at room temperature (22°C) in 2.5 ml sealed cuvettes for at least 20 min prior to DWP-OCT measurement to avoid small drifts in oxygenation [28]. The PTFE conduit with a 330 µm inner diameter and 480 µm outer diameter (SUBL-190, Braintree Scientific Inc.) was fastened to the surface of a 1 mm thick glass slide using epoxy and filled with blood at a prepared SaO₂ level using a 1 ml syringe. Remaining blood in the syringe was utilized for simultaneous reference measurement of SaO₂ by the avoximeter. Manufacturer specified SaO₂ measurement precision of the avoximeter is 1%. After DWP-OCT measurement of each blood sample, the phantom vessel was flushed with distilled water and dried with forced air.

2.2 Laser Excitation

A Mira 900 Ti:Al₂O₃ laser system (Coherent Inc., Santa Clara, CA) was used in continuous wave mode to induce optical pathlength (op) changes in blood samples (Fig. 1). First, the laser was tuned to oscillate at 765 nm as verified by an optical spectrometer (USB2000, Ocean Optics, Dunedin, FL). Light emitted from the laser was coupled into a 0.22 NA 50 µm core-diameter multimode fiber using an optical collimator (f = 11.23 mm). Light output from the fiber was collimated with a bi-convex lens (f = 25.4 mm) and intensity modulated (f_o = 42 Hz) with a mechanical chopper. A small fraction (4%) of excitation light was utilized as an intensity reference and coupled into a Si photodetector (2032, New Focus, Irvine, CA) using a thin glass cover slip and lens (Fig. 1). The intensity reference signal from the Si photodetector was digitized with a 14-bit analog-to-digital converter (USB-6009, National Instruments, Austin, TX) at 100 S/s and stored in computer memory for computation of SaO₂ levels.

The end face of the excitation laser output fiber was placed 1 mm below the glass slide underlying the blood sample giving a 900 µm beam-diameter on the vessel phantom. The relatively wide excitation beam diameter allowed easy co-registration of OCT and laser excitation beams. Light from the MIRA laser was blocked with a shutter when DWP-OCT data was not being recorded. To simultaneously irradiate the blood sample and record the intensity reference signal, the shutter was opened for 15-20 seconds and DWP-OCT data was recorded while excitation light (765 nm) impinged on the blood sample for 4-6 seconds. The measurement procedure using 765 nm excitation light was repeated three to five successive times for each blood sample. The MIRA laser was then tuned to 800 nm and the measurement procedure was repeated for the same blood sample as with 765 nm excitation. Following laser excitation at 765 nm and 800 nm, blood in the phantom vessel was removed, the lumen cleaned and replaced with blood prepared at another SaO₂ level. The measurement procedure was repeated by exciting the blood sample at 765 nm and 800 nm and recording both DWP-OCT and laser excitation intensity reference data. The average laser excitation power at each blood sample was fixed at 23 mW (765 nm) and 51 mW (800 nm). The higher power at 800 nm was due to limited emission capability of the MIRA laser at 765 nm.

2.3. Phase Sensitive OCT system

A phase sensitive (PhS) OCT system (Fig. 1) was used to measure nanometer and sub-nanometer scale changes in optical pathlength in the sample in response to laser excitation. The PhS-OCT system has been described in detail previously [23]. Briefly, the PhS-OCT system uses a 20 kHz swept source laser with a central wavelength of 1328 nm and bandwidth of 100 nm (HSL-2000, Santec USA Corp., Hackensack, NJ) and employs a common-path geometry. The system provides excellent phase stability (65 pm at a 280 µm depth) and low degradation of optical pathlength sensitivity with depth (0.16 nm/mm). Acquisition and display of M-mode data uses a real-time uniform-frequency clock signal. A diagram of the blood phantom, M-mode intensity map, intensity A-scan and M-mode phase map of the phantom vessel filled with blood is shown in Fig. 2A , Fig. 2B, Fig. 2C and Fig. 2D respectively.

Fig. 2.

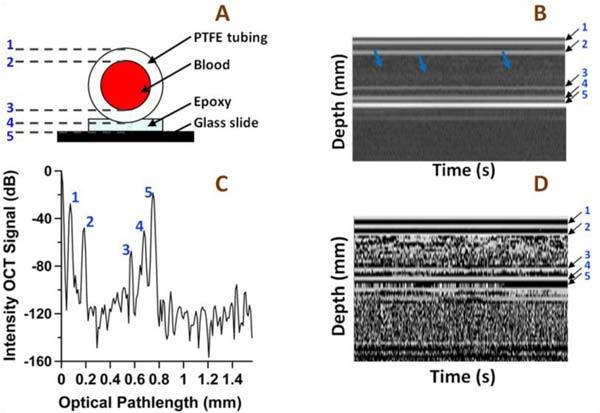
A) Blood vessel phantom geometry, B) M-mode intensity map, C) intensity OCT A-scan, and D) M-mode phase map. The lines of constant phase in the M-mode phase map and spikes on the intensity OCT map and A-scan correspond to: 1 – the upper air-vessel interface (optical pathlength, op = 73 µm), 2 – upper vessel-blood interface (op = 187 µm), 3 – lower blood-vessel interface (op = 572 µm), 4 – vessel-epoxy interface (op = 676 µm), 5 - epoxy-glass slide interface (op = 749 µm). The blue arrows in the Intensity map indicate boundary between RBC poor blood plasma and RBC dense layer due to sedimentation.

2.4. Depth-resolved Photothermal OCT signal

Depth-resolved Photothermal OCT signals corresponding to variation of optical pathlength (op) was measured at five depths in the blood sample (Fig. 2): 1 – the upper air-vessel interface (op = 73 µm), 2 – upper vessel-blood interface (op = 187 µm), 3 – lower blood-vessel interface (op = 572 µm), 4 – vessel-epoxy interface (op = 676 µm), 5 - epoxy-glass slide interface (op = 749 µm). The intensity signal-to-noise ratio (SNR), magnitude of op change induced by excitation laser light near the isobestic point (800 nm) and SNR of the detected op at the five depths are summarized in Table 1 .

Table 1. Typical signal and noise levels at five depths (SaO₂ = 18%) shown in Fig. 2. Here dB is computed as 20•Log₁₀(SNR).

		765 nm			800 nm
Depth	Intensity SNR (dB)	OP amplitude ( nm)	OP SNR (dB)		OP amplitude ( nm)	OP SNR (dB)
1	70.4 ± 2.6	0.15 ± 0.0048	36.6 ± 1.1		0.24 ± 0.020	40.6 ± 1. 5
2	50.3 ± 2.7	0.21 ± 0.11	12.5 ± 4.4		0.20 ± 0.059	12.9 ± 2.5
3	32.1 ± 4.0	1.21 ± 0.23	21.2 ± 0.96		1.70 ± 0.10	26.0 ± 4.4
4	48.3 ± 4.1	1.26 ± 0.065	36.5 ± 5.8		1.70 ± 0.071	43.1 ± 0.91
5	79.7 ± 3.78	1.29 ± 0.027	39.0 ± 7.8		1.74 ± 0.048	47.4 ± 1.2

Measured OP changes at a given sample depth were the result of an accumulation of optical pathlength changes of probe light propagating through overlying layers [24]. To measure SaO₂ levels in a blood sample, influence of optical pathlength changes in overlying layer(s) must be excluded and requires measurement of differential optical pathlength (Δop) between two longitudinal points. To measure SaO₂ levels in the phantom vessel, Δop between the lower blood-vessel interface (depth 3) and the upper vessel-blood interface (depth 2) was computed. The computed value represents SaO₂ level of blood in the vessel lumen. For reference, SaO₂ levels were also computed from Δop between depths 1 and 5 which provide higher SNR OCT signal intensities (Table 1). DWP-OCT data was acquired for 8-12 seconds. Within the DWP-OCT data acquisition time period the shutter was opened to expose the blood sample with laser radiation for 4-6 seconds. A one-second time interval of DWP-OCT data including laser excitation of the sample was used for calculations of SaO₂ levels. The 1 second segment time interval was at least 1 second following opening of the shutter to remove transient effects. After subtracting the linear trend, the 1 second time-interval of DWP-OCT data (Fig. 3A ) was Fourier transformed to compute the amplitude of differential optical pathlength at 42 Hz (Δop(f_o = 42Hz), Fig. 3B).

Fig. 3.

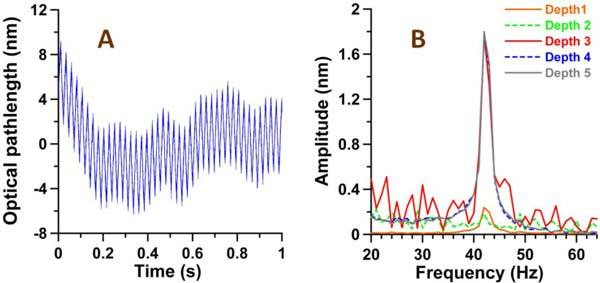
A) Optical pathlength (op) variation at depth 5 (linear trend subtracted) in response to laser excitation (blood-gas SaO₂ = 18.5%, excitation at 800 nm at 42 Hz). B) Amplitude of op variation at depths 1-5 vs laser excitation modulation frequency (grey trace in Fig. 3B is magnitude of fast Fourier transform of op depicted in A).

2.5. Blood Oxygenation (SaO₂) Levels

Photothermal OCT is capable of measuring laser-induced variation in op on the nanometer scale in scattering objects such as human tissues [24–27]. In DWP-OCT, two laser excitation wavelengths are used to induce optical pathlength (op) changes in the sample. Difference in the absorption spectra between oxy- and deoxy-hemoglobin in two spectral regions (765 nm and 800 nm, see inlet in Fig. 1) may be utilized by DWP-OCT to determine blood oxygenation levels (SaO₂).

Since magnitude of op variation in response to clinically relevant excitation laser irradiance levels (mW and tens of mW) is small (0.2 nm – 2 nm), a linear relationship exists between differential optical pathlength (Δop) and fluence of excitation light absorbed by blood over a half-period (τ = 1/2f_o) of laser excitation:

$$\Delta o{p}_1=k\tau I_1\left(1-e^{-{\mu }_{a1}l}\right),$$  

$$\Delta o{p}_2=k\tau I_2\left(1-e^{-{\mu }_{a2}l}\right),$$ (1)

where l is the vessel diameter, Δop₁₍₂₎ is the differential optical pathlength between depths 2 and 3 (blood vessel) due to laser excitation (subscript 1 denote laser excitation at λ₁ = 765 nm and subscript 2 denotes laser excitation at λ₂ = 800 nm), k - is a constant coefficient, I₁₍₂₎τ – fluence of excitation light on the phantom vessel, τ = 1/2f_o = 0.012 second is half period of modulation of laser excitation light, I₁₍₂₎ is intensity amplitude of excitation light incident on the phantom vessel, µ_a1(2) – is absorption coefficient of the blood sample at 765 nm(1) and 800 nm(2). Neglecting absorption in blood by any constituent except for hemoglobin, gives algebraic expressions for the absorption coefficients of blood at 765 nm and 800 nm:

$${\mu }_{a1}={\alpha }_{d1}{c}_d+{\alpha }_{o1}{c}_o,$$  

$${\mu }_{a2}={\alpha }_{d2}{c}_d+{\alpha }_{o2}{c}_o,$$ (2)

where c_o is concentration of oxygenated hemoglobin (mM), c_d is concentration of deoxygenated hemoglobin (mM), α_o1(2) is tabulated molar extinction of oxygenated hemoglobin (cm⁻¹mM⁻¹, see inlet in Fig. 1), α_d1(2) is tabulated molar extinction of deoxygenated hemoglobin (cm⁻¹mM⁻¹). Equation (2) may be rewritten in terms of oxygen saturation (SaO₂ = c_o/(c_o + c_d)) and total hemoglobin concentration (THb = c_o + c_d):

$${\mu }_{a1}=THb\left[Sa{O}_2\left({\alpha }_{o1}-{\alpha }_{d1}\right)+{\alpha }_{d1}\right],$$  

$${\mu }_{a2}=THb\left[Sa{O}_2\left({\alpha }_{o2}-{\alpha }_{d2}\right)+{\alpha }_{d2}\right].$$ (3)

When absorption length of excitation light is much longer than the vessel diameter (${\mu }_{a1,2}l<<1$), differential optical pathlength (Eq. (1) simplifies to

$$\Delta o{p}_1=k\tau I_1{\mu }_{a1}l,$$  

$$\Delta o{p}_2=k\tau I_2{\mu }_{a2}l.$$ (4)

Blood oxygen saturation level (SaO₂) obtained from the ratio $\Delta o{p}_1/\Delta o{p}_2$ using Eqs. (3) and 4 is written as

$$Sa{O}_2=\frac{{\alpha }_{d1}-{\chi }_{12}{\alpha }_{d2}}{{\alpha }_{o2}+{\alpha }_{d1}-{\alpha }_{d2}-{\alpha }_{o1}},$$ (5)

where

$${\chi }_{12}=\frac{\Delta o{p}_1{I}_2}{\Delta o{p}_2{I}_1}.$$ (6)

By measuring differential optical pathlength (Δop) in blood at two wavelengths normalized by incident excitation light intensities, SaO₂ levels can be computed directly.

3. Results and Discussion

The dependence of op and Δop magnitude per 1 mW of excitation power on reference avoximeter oxygenation for 765 nm and 800 nm at different depths is shown in Fig. 4 . The magnitude of op at the upper air-vessel interface (depth 1) was equivalent (within experimental error) to that at the upper vessel-blood interface (depth 2) and magnitude of op at the lower blood-vessel interface (depth 3) was equivalent (within experimental error) to that at the epoxy-glass slide interface (depth 5) and vessel-epoxy interface (depth 4). Depth 4 was not shown in Fig. 4 since it was not used for calculation of SaO₂ levels. Typical op magnitude at depth 4 for a specific SaO₂ (18%) can be found in Table 1. Note the magnitude of op at depths 3, 4 and 5 are 8-10x larger than those at depths 1 and 2. The order of magnitude increase of op for probe light double passed through the blood as compared with op values for light not propagating through blood is discussed below.

Fig. 4.

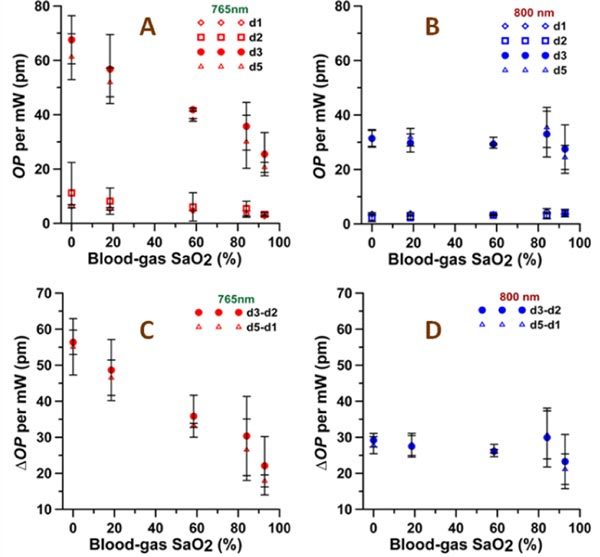
Optical path (op) variation amplitude per 1 mW power of excitation light vs. reference avoximeter readings. OP variations are at depths 1, 2, 3, 5 for A) 765 nm and B) 800 nm excitation light. ΔOP variations between depths 3 and 2 (Δop₃₂) and between depths 5 and 1 (Δop₅₁) that was used for calculating of SaO₂ levels for C) 765 nm and D) 800 nm excitation light. Error bars are mean ± SD, n = 3-5.

As observed in Fig. 4, op for all depths decreased significantly with increasing SaO₂ for excitation at 765 nm and was almost independent of SaO₂ at 800 nm. The relative change in op magnitude with SaO₂ increasing from 0% to 100% was estimated using a linear fit of the data in Fig. 4. At 765 nm excitation (Fig. 4A), the relative decrease of op was 2.2 - 2.9, times, whereas the Hb absorption coefficient is 2.3 times higher than the HbO₂ absorption coefficient at 765 nm (Table 2 ). At 800 nm excitation (Fig. 4B), the relative change of op over the tested range of SaO₂ levels was within ± 10% as expected (i.e., Hb absorption is 1.08 times lower than HbO₂ absorption) except for depth 2. At depth 2, the relative increase in op magnitude was 1.4x versus 1.08x expected due to a lower op signal-to-noise ratio (SNR OP, Table 1).

Table 2. Major parameters used in results and discussion section.

Parameter	Fluence* (J/cm2)	HbO2 molar extinction (cm−1mM−1)	Hb molar extinction (cm−1mM−1)	HbO2 absorption coefficient** (mm−1)	Hb absorption coefficient** (mm−1)
765 nm	Φ01 = 0.043	αo1 = 0.616	αd1 = 1.435	µao1 = 0.11	µad1 = 0.25
800 nm	Φ02 = 0.096	αo2 = 0.816	αd2 = 0.762	µao2 = 0.14	µad2 = 0.13

*Calculated using half period of modulation of laser excitation light τ = 0.012 second

**Calculated suggesting SaO₂ = 100% for HbO₂ and SaO₂ = 0% for Hb and using typical concentration of hemoglobin in porcine blood THb = 1.77 mM (11.4 g/dL, hemoglobin molecular weight MW = 64500 g/mole) [30].

SaO₂ levels were computed using Δop between depths 3 and 2 (Δop₃₂) and between depths 5 and 1 (Δop₅₁). For 765 nm excitation Δop was estimated to decrease with increasing SaO₂ levels (from 0% to 100%) by 2.5 for Δop₃₂ and 2.9 times for Δop₅₁ (Fig. 4C). For 800 nm excitation Δop was almost constant with increasing SaO₂ levels (from 0% to 100%) and decreased slightly (by 1.1x) for both Δop₃₂ and Δop₅₁ (Fig. 4D). Note the standard deviations for Δop₃₂ at 765 nm excitation were much higher (3.7 times in average) than standard deviations for Δop₅₁ due to low OP SNR at depths 2 and 3 for high SaO₂ levels where the hemoglobin absorption is small (Table 2). For 800 nm excitation, the standard deviations for Δop₃₂ and Δop₅₁ were very close since excitation power was more than 2 times greater than that at 765 nm and smallest hemoglobin absorption coefficient at 800 nm (SaO₂ = 0%) is 20% greater than the smallest absorption coefficient for 765 nm light (SaO₂ = 100%).

Average deviation of SaO₂ levels (Eq. (5) in the blood sample measured with DWP-OCT using Δop₃₂ from depths 2 and 3 differ from the reference avoximeter values by less than 10.1% while SaO₂ values determined from depths 1 and 5 differ by less than 6.3% (Fig. 5 ). Higher precision SaO₂ measurements using Δop₅₁ between depths 5 and 1 as compared to depths 3 and 2 is due to higher SNR of op amplitude at depth position 5 compared to 3 and depth position 1 compared to 2 (Fig. 5). The results demonstrated application of DWP-OCT to measure depth-resolved SaO₂ in a phantom blood vessel.

Fig. 5.

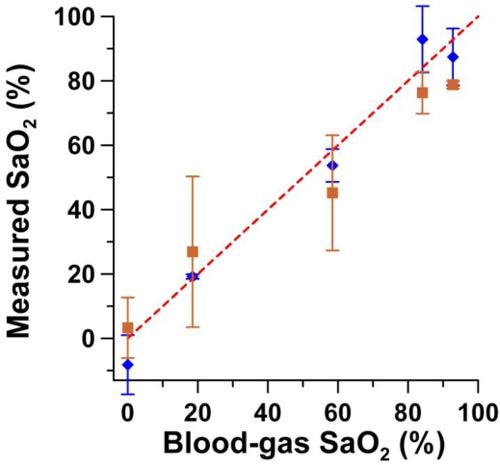
SaO₂ levels measured with DWP-OCT (765 nm and 800 nm excitation light) vs. reference avoximeter readings. DWP-OCT SaO₂ levels were calculated from measured Δop₅₁ between depths d5-d1 (diamonds) and Δop₃₂ between depth d3-d2 (squares) Error bars are mean ± SD, n = 3-5.

The sensitivity of SaO₂ measurements was correlated with signal-to-noise-ratio of op amplitude (Table 1, column 4 (OP SNR) for 765 nm excitation wavelength and column 6 (OP SNR) for 800 nm). To facilitate interpretation, data in Table 1 is presented in graphical form (Fig. 6 ). OP SNR at a given depth was dependent on the combined effect of OCT intensity SNR and op amplitude. Highest OP SNR (purple in Fig. 6) was achieved at depth 5 where large-value intensity SNR was coupled with large-value (nanometer-scale) op amplitude. Lowest OP SNR was achieved at depth 2 where medium-value intensity SNR was coupled with low-value (subnanometer-scale) op amplitude. Large value OP SNR was achieved at depths 1 and 4. At depth 1 large-value intensity SNR was coupled with low-value op amplitude while at depth 4 medium-value intensity SNR was coupled with large-value op amplitude. Finally, medium-valued OP SNR was achieved at depth 3 where low-value intensity SNR was coupled with large-value op amplitude.

Fig. 6.

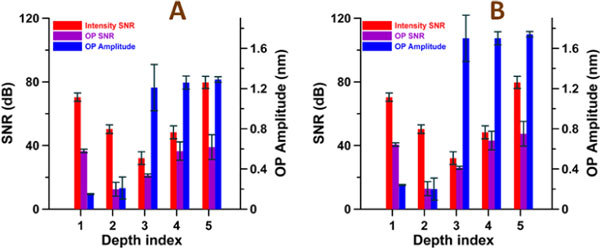
OCT Intensity SNR, op SNR and op amplitude measured at five depths indicated in Fig. 2. The op SNR and op amplitude was measured at A) 765 nm and B) 800 nm excitation wavelengths.

Two levels of measured op magnitude are observed (Figs. 4 and 6 and Table 1) in response to laser excitation: op in the subnanometer range (0.15 nm - 0.24 nm) at depths 1 and 2, and op in nanometer range (1.21 nm – 1.74 nm) at depths 3, 4 and 5. Additionally, within experimental error, op magnitudes are equivalent for depths 1 and 2 (in the subnanometer range) and for depths 3, 4 and 5 (in the nanometer range). Thus, only two mechanisms result in op variation: one for depths 1 and 2 and another for depths 3, 4 and 5. In general, the thermally induced op variations can be represented by a sum of thermoelastic expansion (dL/dT) and thermorefractive effect (dn/dT) [24]. Since op magnitude is of the same order for depth 1 (where probe light did not pass through the phantom wall) and depth 2 (where probe light propagated double pass through the phantom wall) negligible absorption of excitation light occurred in the phantom wall and op variation at these depths were induced dominantly by thermoelastic expansion of the vessel wall. OCT probe light reflected from depths 3, 4 and 5 propagates double-pass through the blood while OCT probe light returned from depths 1 and 2 do not propagate through the blood. Therefore the 8-10x larger op variation observed at depths 3-5 as compared with depths 1 and 2 are due to a thermorefractive effect in blood. In conclusion, at depths 3-5 both thermoelastic and thermorefractive effects were present and effected op, at depths 1 and 2 only a thermoelastic effect due to expansion of blood was present. Thermorefractive effect contributed a 7-9x greater op variation than that due to thermoelastic effect.

The model proposed here assumes: a) ${\mu }_{a\max }l<<1$, where ${\mu }_{a\max }$ is maximum absorption coefficient in the working range of excitation light and SaO₂ levels; b) excitation wavelengths are sufficiently close so that optical throughput into the blood vessel at the two wavelengths is equal. Conditions a) and b) are satisfied here: a) if SaO₂ levels are measured in a blood vessel with l = 300 µm, maximal absorption coefficient µ_amax = µ_ad1 = α_d1THb = 0.25 mm⁻¹ (Table 2), where${\alpha }_{d1}=$1.435 cm⁻¹mM⁻¹ [29] and typical values in porcine blood of THb = 1.77 mM (11.4 g/dL) [30] give µ_amaxl = 0.075 <<1 consistent with assumption a; b) optical throughput of 765 nm and 800 nm light into the blood vessel is equivalent because light diffraction and scattering are nearly equal.

Additionally the model assumes that heat produced by light absorption of hemoglobin is confined within the heating volume over a half period of excitation light (τ = 1/2f_o = 12 ms). Therefore, for the static phantom blood vessel utilized in experiments reported here, thermal relaxation time τ_th should be longer than τ. This condition was satisfied since τ_th = d²/(16α) = 62 ms and is 5.2 times longer than τ = 12 ms. Here α = 1.1•10⁻³ cm²s⁻¹ [31] is thermal diffusivity of blood and d = 0.33 mm is diameter of the phantom blood vessel. The thermal confinement condition may be broken if blood in the vessel is flowing. In the case of flowing blood, the method requires half period of excitation light τ is shorter than the time for blood to flow through the beam diameter (b_d = 0.9 mm) of excitation light (τ_f = b_d/v_b,) where v_b is the blood flow velocity. This condition is satisfied in the experimental setup described here if the blood flow velocity is significantly less than 75 mm/s.

Estimated temperature increase over a half period (on-time) of laser excitation is [32]

$$\Delta T=\frac{{\mu }_{ad2}{\Phi }_{02}}{{\rho }_c}=0.033\text{}K$$ (7),

where ΔT is the maximal temperature increase due to absorption of excitation light by hemoglobin in the blood sample; ρ_c = c_p•ρ = 3.8 J•cm⁻³•K⁻¹ is volumetric heat capacity of blood, c_p is specific heat capacity of blood [33], ρ = 1060•10⁻⁶ kg⁻¹•cm⁻³ is density of the blood [34]. Parameters ${\mu }_{ad2}$ and Φ₀₂ = I₀₂τ are shown in Table 2.

Additional to temperature oscillations at the excitation frequency as described in Eq. (7), the cumulative effect of light absorption was responsible for the observed slow temperature increase (Fig. 7 ). The effect was observed in photothermal OCT studies using nanoparticles reported by Adler et al. [25] and Skala et al. [26]. To estimate temperature increase ΔT_1s over a 1 second time period due to the cumulative effect of light absoprtion, average optical pathlength Δop_1s over one second and Δop_τ over half period (on-time) of laser excitation were calculated:

Fig. 7.

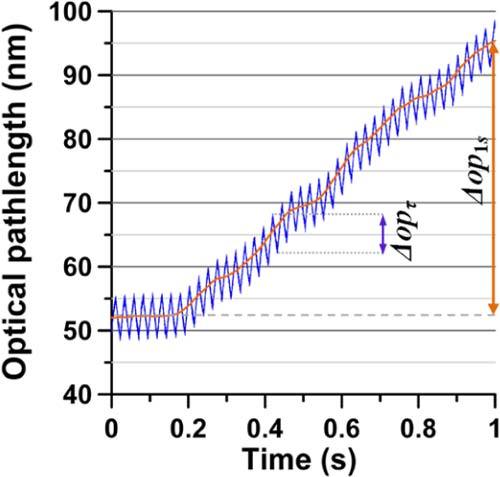
Optical pathlength (op) variation at depth 5 shown in Fig. 3 where linear trend is not subtracted in response to laser excitation (blood-gas SaO₂ = 18.5%, excitation at 800 nm at 42 Hz). The orange line without oscillations is a running average over one period of oscillations.

$$\Delta T_{1s}=\frac{\Delta o{p}_{1s}}{\Delta o{p}_{\tau }}\Delta T=\left(0.16\pm 0.073\right)\text{\hspace{0.05em}}K.$$ (8).

To estimate the average drift Δop_1s, from the original signal the running average over the period of excitation light was applied and Δop_1s was calculated as Δop_1s = op_1s- op_0s as shown in the Fig. 7, where op_0s is the optical pathlength at the beginning and op_1s at the end of the 1 second time segment. Since the temperature increase in the experiments was well below 1 K as following from Eqs. (7) and (8) no structural modifications are believed to occur in blood.

Equations (5) and (6) indicate that measurement of SaO₂ requires that ratio of excitation light intensities (I₂/I₁) be monitored accurately. Since differential optical pathlength at the two laser excitation wavelengths (Δop₁ and Δop₂) was measured at f_o = 42 Hz, I₁ and I₂ were monitored by a Si photodetector at 42 Hz. Error of DWP-OCT measured SaO₂ levels (ΔSaO₂) depends on the SaO₂ level, relative errors in optical pathlength variation ($\delta \left[\Delta o{p}_{1,2}\right]$) and relative uncertainty in laser excitation intensities (δΙ) at the blood sample:

$$\Delta Sa{O}_2=\delta {\chi }_{12}\left(\frac{{\alpha }_{d1}}{{\alpha }_{o2}+{\alpha }_{d1}-{\alpha }_{d2}-{\alpha }_{o1}}-Sa{O}_2\right),$$ (9)

where α_o1, α_d1, α_o2 and α_d2 are taken from Table 2 and $\delta {\chi }_{12}=\delta \left[\Delta o{p}_1\right]+\delta \left[\Delta o{p}_2\right]+2\delta I$ is the relative error in parameter χ₁₂. Here relative error in optical pathlength δ[Δop₁] = (2.7 ± 2.4)% and δ[Δop₂] = (0.4 ± 0.2)% were derived from op measurements. Using measured SaO₂ values and their variation from reference values, relative uncertainty for 765 nm and 800 nm laser excitation intensities was assumed equal and is estimated from Eq. (9) at δI = (2.1 ± 2.1)%.

Previous studies of non-invasive depth-resolved blood oxygenation measurements using intensity based spectral OCT revealed a number of challenges due to the scattering properties of blood including multiple scattering [35], highly forward scattering by RBC’s [36], Brownian movement of the scattering centers [37–39] and blood sedimentation in phantoms [40]. Light scattering is unpredictable due to dynamic intra- and inter-subject changes, and large variation in detected intensity due to speckles. Boyer et al. [41] showed and Skala et al. confirms [26] that photothermal approach is insensitive to scattering. Accordingly, in our studies we did not observe significant op noise in the signal bandwidth due to fluctuations in scattering. OP signals recorded here depend primarily on light absorption and excitation fluence in the irradiated sample volume. Differential modification of fluence at the two excitation wavelengths (765 nm and 800 nm) by scattering in the irradiated sample was not observed. As noted by Tuchin et al. [40] we also observed some blood sedimentation (the boundary between plasma and RBC indicated by arrows on the Fig. 2B) but this effect did not influence the op measurements.

Influence of Brownian movement of RBC was noted as a slow modulation of the 42 Hz signal (“radio”) frequency of the op (Fig. 3A and Fig. 7). The effect introduced additional noise onto the op amplitude at 42 Hz. The influence was small, however, since the modulation frequency was approximately an order of magnitude faster than the slow modulation due to Brownian movement.

Precision of DWP-OCT SaO₂ measurements can be improved by: 1) decreasing relative uncertainty of laser excitation intensity (δI) incident on the sample; 2) decreasing relative error in optical pathlength (δ[Δop]) by utilizing a higher modulation frequency of laser excitation thus detuning from low-frequency phase drift artifacts; 3) increasing number of laser excitation wavelengths to more than two; or 4) increasing number of op measurements in the vessel wall at each laser excitation wavelength.

In conclusion, we introduced DWP-OCT to measure SaO₂ levels in a blood vessel phantom. The approach was demonstrated in a vessel phantom containing stationary blood and provides good agreement with an established reference technique. Compared to existing techniques, DWP-OCT provides some important features for SaO₂ measurement including depth-resolved measurements and capability to measure SaO₂ levels in discrete vessels. DWP-OCT is based on detection of optical pathlength (op) changes in response to absorption of excitation light and is therefore free from high variation of depth-resolved scattering-based spectral OCT approaches [15,19]. Moreover, scattering properties of blood do not influence the accuracy of DWP-OCT SaO₂ measurements and spectral- and depth-resolution provided by DWP-OCT are not compromised. Moreover, the model equation (Eq. (6) developed to determine DWP-OCT SaO₂ levels avoids computationally intensive Monte Carlo simulations utilized in previous approaches. High sensitivity of DWP-OCT to measure optical pathlength (op) changes in blood allows application of relatively low-level laser excitation intensities. The demonstrated results suggest that further investigation of DWP-OCT in pre-clinical models is warranted.