Rapid and accurate determination of tissue optical properties using least-squares support vector machines

Abstract

Diffuse reflectance spectroscopy (DRS) has been extensively applied for the characterization of biological tissue, especially for dysplasia and cancer detection, by determination of the tissue optical properties. A major challenge in performing routine clinical diagnosis lies in the extraction of the relevant parameters, especially at high absorption levels typically observed in cancerous tissue. Here, we present a new least-squares support vector machine (LS-SVM) based regression algorithm for rapid and accurate determination of the absorption and scattering properties. Using physical tissue models, we demonstrate that the proposed method can be implemented more than two orders of magnitude faster than the state-of-the-art approaches while providing better prediction accuracy. Our results show that the proposed regression method has great potential for clinical applications including in tissue scanners for cancer margin assessment, where rapid quantification of optical properties is critical to the performance.

1. Introduction

Noninvasive optical techniques, such as diffuse reflectance spectroscopy (DRS), have been extensively researched for quantitative tissue characterization and disease diagnosis [1–6]. Specifically, DRS provides an assessment of scattering of sample (which is primarily a function of density and scattering cross sections of internal structures) as well as absorber composition (hemoglobin and beta-carotene). This wealth of information has led to several applications of DRS including microcirculation monitoring [7,8], pre-cancer and cancer detection [9] and intra-operative tumor margin assessment [10].

One of the major challenges of such diagnosis is the accurate and robust analysis of the spectral data, namely the extraction of the absorber concentration and scatterer information, over a variety of sample optical properties and excitation-collection (optical probe) geometries. To this end, diffusion-approximation based solutions of the radiative transport equations [1] and their variants [2] have been employed due to their analytical approach and simplicity of application. However, these methods are unsuitable for application in tissues where absorption is high in comparison to scattering (e.g. in cancer angiogenesis) and where the source detector-separation is small. To overcome these difficulties, several investigators have proposed sophisticated computational techniques such as inverse Monte Carlo models [11] and higher-order analytic approximations [4]. Additionally, specialized probe geometries [12] and multiple source-detector separation [13] have been successfully used for determination of optical properties from tissue.

Recently, a novel look-up table (LUT) approach based on experimental measurements from physical tissue models was reported to provide high accuracy in optical property determination even at high absorption levels [14,15]. The primary advantage of the LUT approach is that it does not require modeling of the probe-sample geometry (which is a major challenge for the aforementioned analytical and computational approaches). It also does not necessitate the alteration of the conventional optical probes or measurement at multiple source-detector separation distances. However, the LUT approach involves iterative fitting of the spectra using a non-linear optimization routine, which is computationally expensive (the typical fit time is of the order of a few seconds). This is particularly problematic when the algorithm is deployed in a spectral imaging platform [10], where data may need to be routinely acquired and processed from a few thousand points. Clearly the speed of the prediction algorithm is critical to the success of imaging platform applications including the investigation of full tumor margins in intra-operative cancer assessment.

In this article, we propose an alternate optical property determination approach based on a non-linear multivariate calibration (MVC) framework. Specifically, we demonstrate the effectiveness of least-squares support vector machines (LS-SVM) in providing rapid and accurate diagnostic information from diffuse reflectance spectra. Previously, empirical models using multivariate calibration (MVC) schemes, including partial least squares (PLS) [16] and neural networks [17,18], have been employed for analysis of reflectance spectra. However, PLS does not provide accurate predictions as it is unable to account for the intrinsic nonlinear relationships in light transport problems [19]. Furthermore, the proposed LS-SVM approach, which provides a class of kernel machines for non-linear regression, results in a unique and reproducible global solution in contrast to neural networks [20]. Using reflectance spectra collected from physical tissue models over a wide range of optical properties, we compare the prediction accuracy and computation time of LS-SVM with that of PLS and the LUT-approach of Tunnell and associates. Here, PLS is chosen for comparison because of its similarity in approach (MVC) with the proposed scheme and fast computation time, whereas LUT is selected for its superior prediction performance. Our results suggest that the dual advantage of speed and accuracy of the LS-SVM approach makes it ideally suited for application in tissue imaging platforms.

2. Theory

Support vector machines, and their recent derivative LS-SVM, have been described extensively elsewhere in the literature for generic applications [21,22] as well as with respect to spectroscopic data sets [23]. Here, we provide a brief summary of the key aspects of LS-SVM for orientation. Similar to conventional linear regression modeling, LS-SVM estimation between the regressors (x) and the dependent variable (y) can be expressed as:

$$y=w^{T}x+b$$ (1)

in which w is the regression coefficient and b represents the bias. Analogous to the ridge regression solution of ill-posed problems, LS-SVM constructs a trade-off in the objective function (Q_LS-SVM) between the regression error (e) and the minimization of the regression coefficients for the N training samples (to enhance model robustness):

$$Q_{LS-SVM}=\frac{1}{2}{\Vert w\Vert }^2+\gamma {\displaystyle \sum _{i=1}^N{e}_i{}^2}\text{\hspace{1em}where\hspace{0.17em}}{e}_i=y_i-w^T{x}_i-b$$ (2)

where the relative weight of the two penalties is mediated by the regularization parameter, γ, and ||w|| represents the 2-norm of the vector of regression coefficients. The critical step in LS-SVM is the subsequent formulation of Lagrangian function by incorporating the regression error using Lagrangian multipliers (α_i). Solving the resultant Lagrangian problem, it can be shown that the regression problem reduces to the following:

$$y={\displaystyle \sum _{i=1}^N{\alpha }_i\langle x_i,x\rangle }+b\text{\hspace{1em}where\hspace{0.17em}}{\alpha }_i={\left(\langle x_i,x_i\rangle +{\left(2\gamma \right)}^{-1}\right)}^{-1}\left(y_i-b\right)$$ (3)

Here, the notation 〈.,.〉 denotes the inner product of the vectors. In essence, the Lagrangian multipliers mediate the relative importance of the individual training samples to the overall model and subsequent prediction. This linear formulation can be readily extended to solve non-linear problems if the inner product is replaced with appropriate kernel functions (K) that satisfy Mercer's conditions [24]. The problem is then modified to:

$$y={\displaystyle \sum _{i=1}^N{\alpha }_{i}K\langle x_i,x\rangle }+b$$ (4)

A polynomial function or a radial basis function is commonly used for LS-SVM based regression. Clearly, the application of such a function allows a higher-dimensional modeling, where the dependent variable estimation of the prediction sample is dependent on the distance of its corresponding regressor from that of the calibration samples in the database.

The kernel functions are parameterized allowing for adjustments with respect to the training data, i.e. the kernel parameter(s) and γ are hyper-parameters specific to the problem data set. It is worth mentioning that implementation of LS-SVM requires the solution of linear equations as opposed to quadratic optimization for SVM, which makes the former implementation faster. Furthermore, only two parameters need to be optimized for LS-SVM in contrast to three for classical SVM regression, thereby reducing the probability of overfitting the calibration data set.

In our case, the diffuse reflectance spectra are input as the regressors (x) to the model whereas the scattering and absorption coefficients are treated as dependent variables (y). Specifically, two models are constructed to predict the scattering and absorption coefficients, respectively, as detailed below.

3. Materials and methods

For characterizing the effectiveness of the LS-SVM approach in extracting the optical properties, diffuse reflectance data sets, previously acquired by Rajaram et al. (at The University of Texas at Austin), are employed [14]. Briefly, a custom-built reflectance system was used to acquire steady-state spectra (350-700 nm) from a set of 24 physical tissue models (tissue phantoms) with varying absorption (µ_a, 0.5 to 3.79 mm⁻¹) and reduced scattering (µ_s', 0.44 to 6.74 mm⁻¹) coefficients. A pulsed xenon flash lamp was used as the excitation source and an imaging spectrograph-CCD combination was used for spectral acquisition. A classical six-around-one fiber-optic probe was used for delivery and collection of light by placing it in close proximity (~300 µm) of the samples. The tissue phantoms were fabricated by adding 1 µm polystyrene spheres and India ink to water solutions to simulate typical absorption and scattering properties of biological tissue [25]. Three spectral acquisitions from each sample were averaged for enhanced SNR prior to off-line spectral processing for background correction and normalization using a reflectance standard. The spectral resolution of the system was observed to be approximately 0.78 nm.

For our investigations, the experimental data set, consisting of 24 samples in all, is split into calibration (23) and prediction (1). A leave-one-out protocol is employed to estimate the average prediction error from the 24 samples. For each such splitting, LUT, PLS and LS-SVM models are first generated on the calibration set, by optimizing the model parameters. The optimization of each of these models is performed by an inner cross-validation within the calibration data set. The developed calibration models are then used prospectively on the prediction data point to determine the absorption (µ_a) and reduced scattering (µ_s') coefficients. Specifically, for all results presented in this paper, we assumed the following functional form for the reduced scattering coefficient: µ_s'(λ) = µ_s'(λ₀).(λ/λ₀)^-B, where λ₀ is a reference wavelength (630 nm) and B represents the wavelength dependence of the scattering coefficient. Since the same scatterers were used in the tissue phantoms, the B parameter (which depends on the shape/size and relative refractive index of the scatterers [2]) remains constant for all samples. Additionally, for our data set, the computation of the absorption coefficient is identical to that of the India ink concentration due to the lack of other significant absorbers. Thus, our computations involved the extraction of the following two values, namely µ_s'(λ₀) and absorber concentration (which can be directly translated to the absorption spectra by multiplying the intrinsic absorption spectrum of India ink). It is worth mentioning that the B parameter can be readily determined from the computation of the scattering coefficient at a wavelength different from λ₀ using an additional model.

To create the LUT model, the diffuse reflectance values (at all wavelengths) are mapped onto a two-dimensional space constituted by the optical properties at the corresponding wavelengths. Prediction is then performed by executing a non-linear optimization routine which minimizes the error in fitting the sample spectra onto the calibration LUT space (inverse mapping). In contrast to the LUT approach, which creates a single coupled model of the relevant parameters (reflectance values, absorption and scattering coefficients), for the PLS and SVM calculations two separate models for scattering and absorption are constructed. For the PLS regression analysis, the regression vectors for prediction are constructed by employing the number of loading vectors which corresponds to the minimum error in inner cross-validation in the calibration data set. In all cases, the number of factors is observed to vary between 4 and 7, which ensures that the rank of the calibration model is more than three times smaller than the size of the calibration data set [26]. Finally, the LS-SVM computations are performed using a LS-SVM MATLAB toolbox [27]. Here, a RBF kernel with a typical Gaussian profile ($K(x_i,x_j)=\exp (-{\Vert x_i-x_j\Vert }^2/2{\sigma }^2)$) is used for non-linear regression. As the reflectance spectra are previously normalized using a reflectance standard, further intensity scaling is not required. It is worth mentioning that the normalization step is critical to the reduction of skewed behavior of specific pixel intensity values that reside in greater numeric ranges over those having smaller numeric values. The optimal model parameters γ and σ² that provide the smallest error in inner cross-validation are determined by performing a grid search over the range of 1 to 10000 (γ) and 0.01 to 10 (σ²), respectively.

In addition to the prediction errors, the average computation time for the prediction step is noted for comparison of LUT, PLS and LS-SVM schemes. The time taken for model building is not included as the calibration model is developed prior to clinical application. All computations are performed on an Intel Celeron(R) CPU 2.00 GHz and 3GB RAM computer.

4. Results and discussion

The first goal of this study is to assess the feasibility of LS-SVM approach to optical property determination, especially in highly attenuating biological media. The absorption and scattering coefficients and the corresponding fits (using all the three modeling approaches) from a representative tissue phantom is shown in Fig. 1 . From Fig. 1, one can observe that all the three approaches are valid and can achieve a high level of accuracy. This is also evidenced by the absence of significant features in the accompanying residual plots. However, it is also clear that compared to LUT and LS-SVM based predictions, PLS provides inferior prediction results, especially for absorption.

Fig. 1.

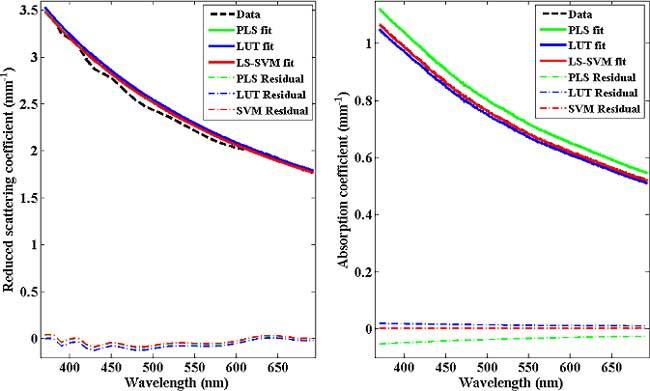
Reduced scattering and absorption coefficients as a function of wavelengths. The dashed line indicates the raw data and PLS, LUT and LS-SVM model fits are shown with green, blue and red solid lines, respectively. For this representative phantom, PLS (green) and LS-SVM (red) fits for the reduced scattering coefficient are nearly coincident. Similarly, the raw data (black) and LS-SVM (red) fit coalesce for the absorption coefficient plot.

To investigate this in greater details, we have performed a leave-one-out validation strategy, as mentioned before, to obtain an average estimate of the prediction errors over the whole range of tested optical properties. It is worth mentioning that the limited number of samples of tissue phantoms (24) does not allow us to create a true prospective prediction set. Nevertheless, the presence of an outer loop for validation of the calibration models provides a measure of the ability of the model(s) to generalize relationship between the spectra and optical properties beyond the specific data of the calibration set. Figure 2 shows the box plot results of validation error percentage values obtained for the absorption and scattering coefficients. Here, we compute the percentage error (|actual-predicted|/actual*100) instead of the absolute errors due to the large variations in absolute values of these parameters. The mean prediction error percentages for the reduced scattering coefficient are 9.73%, 2.57% and 0.79% for the PLS, LUT and LS-SVM models, respectively. Similarly, the mean prediction error percentages for absorption coefficients are 29.03%, 7.94% and 3.77% for the PLS, LUT and LS-SVM models respectively. Evidently, both the approaches substantially improve prediction accuracy as compared to PLS modeling. Furthermore, there is also a corresponding reduction in the standard deviation of the error percentages for both scattering and absorption parameters on application of LS-SVM regression.

Fig. 2.

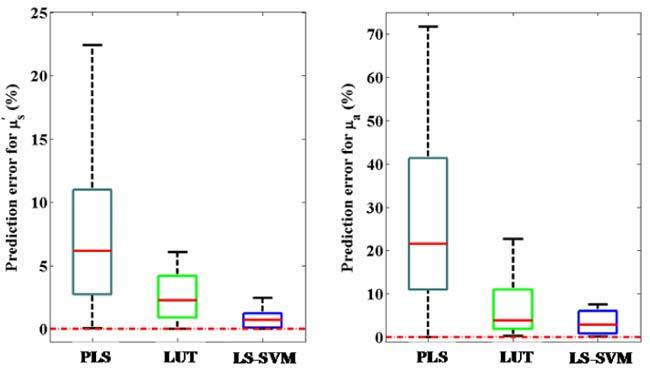
Box plot of prediction error percentages for reduced scattering (µ_s') and absorption (µ_a) coefficients using PLS, LUT and LS-SVM regression models. The red dotted line indicates the position where the observed values are equal to the reference values in the samples.

Our results suggest that PLS is clearly inadequate for modeling of diffuse reflectance spectral data sets, especially in highly attenuating media. This is not surprising given the intrinsic nonlinear relationship between diffuse reflectance and absorption and scattering properties, as noted in the literature [28], even under assumptions of semi-infinite media. The specific geometry of the probes, including the source detector separation distance, adds another layer of complexity which necessitates to consideration of nonlinear approaches. It should be noted that curved effects can be modeled by linear multivariate calibration methods such as PLS, but these necessitate the retention of a larger number of factors, with the subsequent risk of inclusion of irrelevant sources of variance in the model [29]. In contrast, LS-SVM based regression is able to address the presence of curved effects, similar to that observed for Raman spectra acquired in turbid media [30].

Importantly, we observe statistically significant improvements in prediction accuracy on application of LS-SVM over the LUT model for both reduced scattering (p<10⁻⁵) and absorption (p = 0.028) coefficients. This may be attributed to the ability of support vector machines to distinguish between important and irrelevant training samples by assigning corresponding weights (Lagrangian multipliers) to them. This provides the necessary flexibility to deal with outliers, which unduly influence least squares methods (an integral part of the nonlinear fitting routine in the LUT prediction step) [31,32]. The small prediction errors of the LS-SVM model can be largely attributed to the uncertainty in optical property estimation (based on the gold standard measurement) in the calibration samples and the imperfect construction of the tissue phantoms.

The second goal of this work is to examine the computation time taken by the models to predict the tissue optical properties. Figure 3 gives the computation time in milliseconds for the three modeling approaches employed in this study. Clearly, the time taken by the LUT approach is greater than that of PLS and LS-SVM models by more than two orders of magnitude. Although appropriate utilization of the memory cache can reduce the computation time of the LUT approach, nevertheless this remains a major challenge for imaging of large sections of biological tissue. Additionally, in contrast to the PLS and LS-SVM schemes, there is an inherent tradeoff between the prediction accuracy and the computation time of the prediction step in the LUT approach. Specifically, construction of a larger LUT (i.e. with finer resolution) provides improved prediction accuracy at the cost of increased computation time.

Fig. 3.

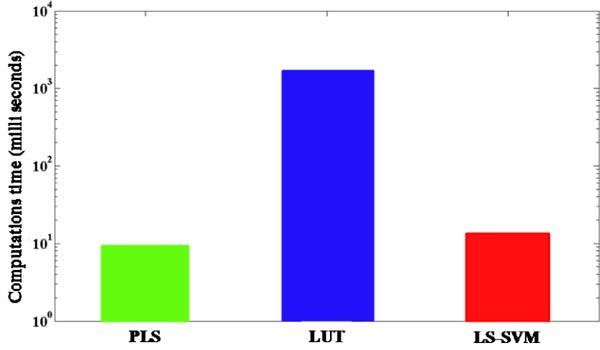
Bar plot of average computation time for the prediction step of PLS, LUT and LS-SVM algorithms.

It is worth noting that PLS is marginally faster than LS-SVM based regression in predicting tissue optical properties but this advantage is heavily outweighed by its poor prediction performance. In summary, we can conclude that LS-SVM provides the best combination of accuracy and computation time for the determination of tissue optical properties.

5. Conclusions

This work demonstrates that LS-SVM provides a promising alternative for the rapid and accurate determination of tissue optical properties. Our results indicate that the LS-SVM regression models are able to maintain a high degree of prediction accuracy over a wide range of tissue properties, which is particularly advantageous for the characterization of highly absorbing tissue - a surrogate marker for tumor growth. While our studies have been performed in simplified tissue phantom models the approach can be extended to the estimation of tissue optical property without further modification. Given the necessity for faster algorithms for tissue imaging applications we anticipate that the proposed approach will be extensively employed in histo-pathological assessment including the detection of tumor margins in breast cancer and cervical pre-cancer diagnosis. Clearly this approach is adaptable to a wide array of tissue properties and probe geometries. Our work here can also be extended to direct determination of absorber concentration, without a priori knowledge of the presence of other absorbers, in applications where the concentration of the analyte of interest (specific absorber) is known in the training samples (implicit calibration).