Abstract
We investigated differences between healthy tissue and metastatic tumor from ex vivo human partial liver resections using diffuse optical spectroscopy with a fiber optic probe. We extracted various physiological and morphological parameters from the spectra. During evaluation of the residual between the measurements and a fit model based on diffusion theory, we found that bile is an additional chromophore absorbing in the visible wavelength range that was missing in our model. Consistency of the residual with the absorption spectrum of bile was noticed. An accurate measurement of the absorption coefficient of bile from various human bile samples was performed and implemented into the fit model. Having the absorption coefficient of bile as a priori knowledge in the model showed a clear improvement in terms of reducing the fitting discrepancies. The addition of this chromophore yields significantly different estimates of the amount of blood. Furthermore, the estimated bile volume fraction and reduced scattering amplitude turned out to be two main relevant discriminators between normal and metastatic liver tissues.
OCIS codes: (170.6935) Tissue characterization, (300.6170) Spectra, (170.3660) Light propagation in tissues, (170.1610) Clinical applications
1. Introduction
Incidence and mortality rates of primary and secondary liver cancer have progressively increased worldwide over the last two decades [1]. In the western world, malignant lesions of the liver are generally metastases from other organs. Tumors of the gastro-intestinal tract, such as primary colorectal cancer, preferentially metastasize to the liver.
For liver metastases of colorectal origin, resection is the only accepted treatment with curative intent. However, radiofrequency ablation (RFA) is an increasingly practiced treatment modality for patients with liver malignancy that are not suitable for surgery [2–4].
The main negative prognostic factor for survival after liver surgery is a positive surgical margin [5,6]. Histological analysis to determine the surgical margin is still considered to be the golden standard. However, intra-operative margin analysis would allow direct surgical intervention of a positive surgical margin, therefore reducing the chance of post-operative loco-regional recurrence.
Patients treated with RFA have demonstrated prolonged survival compared to patients treated with chemotherapy alone [7,8]. Nevertheless, localization of the ablative needle and monitoring of the ablation process are important steps for optimal treatment of liver malignancies with RFA, since incidence of loco-regional disease recurrence due to ineffective ablation ranges from 3.6% to 60% [9]. Therefore, real-time intra-operative needle localization and ablation monitoring could improve ablation efficacy and disease-free survival.
Diffuse optical spectroscopy with fiber optic probes is a widely used technique to estimate the optical properties of tissue [10–15]. Concomitantly, several models have been developed to extract the absorption and reduced scattering coefficients from the measured spectra which are subsequently converted into physiological parameters. Such parameters are very useful to discriminate between healthy tissue and tumors in different organs. Indeed, several ex vivo and in vivo clinical studies were performed in the last decade showing the potential of optical spectroscopy to discriminate between healthy and tumor samples. However, only a few studies have focused on estimating tissue optical properties from spectroscopy measurements in liver [16–18] compared to other organs such as breast [11,19–21], cervix [22,23], lung [10,24,25] and skin [26–28].
In the present paper, we report on an ex vivo clinical study of healthy and metastatic human liver tissue where we measured the diffuse optical spectra in the 500-1600 nm wavelength range. From the acquired spectra, several physiological and morphological parameters of clinical relevance were extracted, using a widely accepted analytical model developed by Farrell et al. based on the diffusion theory [29]. Recently, we have shown the applicability of the model to wavelength ranges extended to 1600 nm where additional absorption features of water and lipids appear [30,31]. Parameters that were also obtained by fitting the model to the measurements are blood, water, lipid volume fractions, average vessel radius, oxygen saturation level in blood and tissue scattering properties. Accurate analysis of the measured spectra suggested that bile is an important chromophore in the liver because it significantly absorbs in the visible wavelength range. This chromophore should therefore be included in the fitting model. The difference between healthy and tumor ex vivo human liver tissue was investigated based upon the parameters extracted from these measurements.
2. Materials and methods
2.1. Patients and liver tissue handling
The presented pilot study on ex vivo liver was conducted at the Netherlands Cancer Institute in Amsterdam (NKI-AVL) under approval from the internal review board committee. Spectra were collected from liver surgical specimens after partial liver hepatectomy. Before resection of the specimen, the hepatic vessels that provide the blood supply to the part of the liver containing the tumor were clamped up to one hour before the resection started. Directly after resection, tissue was transported to the pathology department for further processing. After gross inspection by the pathologist, the optical spectra were collected from macroscopic normal and malignant tissue samples. Spectroscopy measurements were performed on freshly excised tissue before formalin fixation within two hours after the resection. In order to ensure that the measurements were at the tumor location, the samples were cut by the pathologist such that the tumor would be exposed in the most optimal way for measurements. All tumors were colorectal metastases and none were primary tumors. At the measurement sites, tissue was collected for conventional histopathology and the slides were analyzed at the pathology department. The pathological findings were correlated with the optical measurements.
Several spectra were measured on liver tissues from 14 enrolled patients. In average, 15 spectra at different sites were taken from each of the fourteen healthy and metastatic tumor samples, respectively. All the measurements taken from the 14 samples were included in the study and compiled with the results from the pathological report. All measurements were performed by the same operator and care was taken to ensure the same measuring conditions on all the samples.
2.2. Instrumentation and calibration
The spectra were collected from the different samples with an instrument which was used in our previous study [31]. The setup consists of a halogen broadband light source with an embedded shutter, an optical probe with three fibers and two spectrometers that can resolve light from 400 to 1100 nm (silicon detector) and 800 to 1700 nm (InGaAs detector), respectively. A filter that rejects light for wavelengths below 465 nm was mounted in front of the spectrometers to reject second order light at the detectors. The 1.3 mm diameter probe has a fiber connected to the light source and two other fibers each connected to a spectrometer. The center-to-center distance between the emitting and collecting fibers is 2.48 mm, where the tip of the probe has an angled bevel. All optical fibers are low-OH fibers of 200 microns core diameter. The spectrometers are controlled by custom-made software to acquire the data. Figure 1 depicts a schematic of the full setup.
Fig. 1.
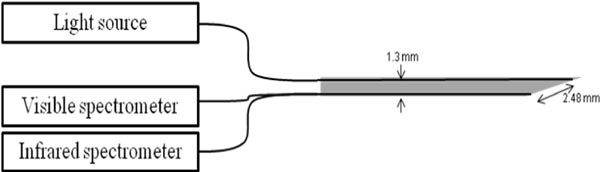
Schematic of the optical setup and the design of the optical probe.
The system was calibrated prior to each measurement on the tissue samples. The calibration consisted of several steps. First, the detectors were cooled down to −40°C. Once the temperature was stable, a wavelength calibration was performed to assign a wavelength value to each pixel of both detectors, fitting a second order polynomial to a set of atomic lines from argon and mercury light sources with peaks at known wavelengths. The second steps consisted of calibrating the system with a white reflectance standard measurement to compensate for the spectral shape of the light emitted by the lamp and the wavelength-dependent sensitivity of the detectors. Subsequently, a background measurement was carried out. Each spectrum was acquired by measuring simultaneously with both spectrometers. The analyzed spectra corresponded to tissue measurements corrected for the spectral shape of the light source, and the spectral response of the detectors measured on a white standard reference measurement as described in detail in our previous studies [30,31].
The simultaneously acquired spectra in the 400-1100 nm range and in the near-infrared 800-1700 nm range were combined to a single spectrum, using the 950-1000 nm range to scale the near-infrared spectrum to the visible spectrum. For the spectral analyses we have used the 500-1600 nm spectral range, where the 500 to 1000 nm and 1000 to 1600 nm correspond to the data collected with the silicon and InGaAs detectors, respectively [31].
2.3. Mathematical modeling of the diffuse optical spectra
The measured diffuse optical spectra were fitted, using the method of Farrell et al. [29] where the reduced scattering coefficient, the absorption coefficientand the center-to-center distance between the emitting and collecting fibers at the tip of the probe are input arguments for the model. The spectra were fitted over the wavelength range of 500-1600 nm, using a non-constrained linear least squares fitting algorithm. The validation of this method with the setup and optical probe described in section 2.2 was performed in our previous work based on an extensive phantom and in vivo animal studies [30,31]. Briefly, we demonstrated that the fiber distance separation that is used is large enough in order not to infringe the diffusion theory assumptions. An extensive phantom study with different absorption and reduced scattering properties was performed to investigate the robustness of the fit. It was also shown that the model is suitable to properly estimate chromophore concentrations independently from the reduced scattering profile which was varied by changing the particle size distribution in the phantoms. The confidence intervals of the estimated parameters that derive from the covariance matrix were also used to investigate the reliability of the fits from the phantom measurements.
The wavelength dependant reduced scattering coefficient is expressed by a double power law
| (1) |
where the wavelength λ is expressed in nm and is normalized to a wavelength value of = 800 nm. The reduced scattering coefficient is expressed as the sum of a Mie and a Rayleigh scattering where is the Mie-to-total reduced scattering fraction and b corresponds to the slope of the Mie reduced scattering. The total reduced scattering amplitude at is denoted a.
We adopted the formulation of the absorption coefficient that is described in our previous study [31] where the absorption, due to chromophores present in the measured tissue, is expressed as
| (2) |
where corresponds to the absorption by blood and corresponds to absorption by water and lipid in the probed tissue. The blood related absorption coefficient is given by
| (3) |
where and are the absorption coefficient of oxygenated hemoglobin and deoxygenated hemoglobin Hb, respectively. The parameter corresponds to the blood volume fraction for a concentration of hemoglobin in whole blood of 150 mg/ml and corresponds to the oxygen saturation of the blood in the probed volume. The factor C is a wavelength dependant correction factor known as a pigment packaging factor [32] and is given by
| (4) |
with R the average vessel radius expressed in cm; note however that its value is reported in microns throughout this paper. The absorption due to the presence of water and lipid in the measured tissue is defined as
| (5) |
with and being the absorption coefficient of water and lipid (density of 0.86 g/ml [31]), respectively. The parameters and correspond to the total volume fraction of water and lipid in the tissue and the lipid fraction within this volume, respectively. Describing the absorption due to water and lipid as in Eq. (5) has the advantage that the covariance between and is smaller compared to the sum of the absorption of water and lipid separately weighted by corresponding volume fractions [31]. However, throughout this paper and are converted to water and lipid fractions and reported as such because of their clinical relevance for interpretation.
When inspecting the measured spectra, it was observed that there was a missing absorber in the visible wavelength range i.e. between 500 and 750 nm. The assumption was that bile would be the missing absorber in the fit model, since it is an endogenous compound which is abundant in liver [33]. Absorption by bile was included by incorporating it into Eq. (2) so that the total absorption is expressed as
| (6) |
where and are the volume fraction and absorption coefficient of bile, respectively. The absorption coefficient was determined by measuring bile freshly obtained from the gallbladder of two patients who underwent a cholecystectomy as part of the liver resection operation. The bile was poured in cuvettes of different thickness (1, 2, 5 and 10 mm) and the optical transmission was measured in a spectrophotograph (Lambda 900 Spectrometer, Perkin Elmer) with a resolution of 1 nm. The bile absorption is depicted in Fig. 2 (circle-marked curve) and it corresponds to the measured absorption coefficients from 300 to 1600 nm. In the near-infrared, the bile absorption is similar to the water absorption coefficient [33]. This is due to the fact that bile is mainly composed of water. In the visible, bile has a local maximum at 409 nm, a local minimum at 350 nm and a large absorption peak centered at 605 nm. Additionally, Fig. 2 shows the absorption coefficient in a logarithmic scale of fully oxygenated hemoglobin [34], deoxygenated hemoglobin [34], lipid [30] and water [30] from 400 to 1600 nm.
Fig. 2.
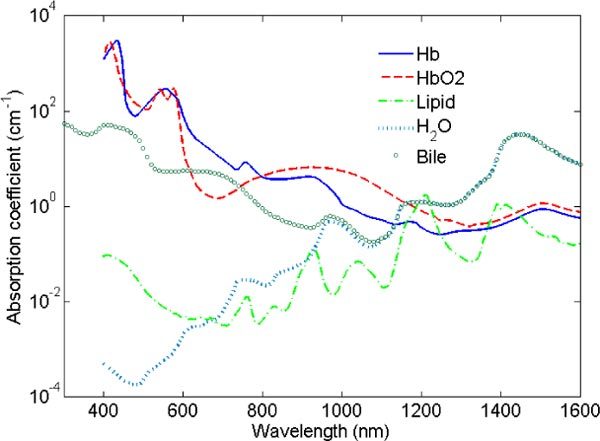
Absorption coefficients of deoxygenated hemoglobin (solid line), oxygenated hemoglobin (dashed line), lipid (dashed-dotted line) and water (dotted line) from 400 to 1600 nm .Absorption coefficient of bile (circle-marked line) from 300 to 1600 nm. The absorption coefficient axis is in a logarithmic scale.
In the model, we have used the bile absorption coefficient as the measured bile absorption coefficient from which the water absorption coefficient was retrieved. Figure 3 depicts the normalized absorption coefficients of bile, oxygenated and deoxygenated hemoglobin starting from 500 nm (starting wavelength of the fit). Bile has a large absorption peak at 605 nm of 5.4 cm−1 and its value does not change more than 5% between 550 and 650 nm. This large absorption peak can significantly change the spectral shape in the visible range of a measurement where bile is present in the tissue.
Fig. 3.

Normalized absorption coefficients of deoxygenated hemoglobin (dashed line), oxygenated hemoglobin (dotted line), and bile (solid line) between 500 and 1000 nm.
From the acquired spectra the following parameters a, b, , R, , , , , and are determined. For each of these fit parameters, the confidence intervals were computed from the square root of the diagonal of the covariance matrix for a critical value of 0.05 [35]. A statistical F-test was performed to evaluate the improvement when bile is added to the model. The F-test is based on analyzing the difference between the sum-of-squares of the model with and without the bile absorption component. From the number of data points within the wavelength range where the fit was performed and the number of fit parameters for the models with and without the bile component, an F-ratio is computed from which a p-value can be extracted. If the p-value is smaller than the specific significance level chosen to be 0.05, the model with the bile component leads to a better description of the measured spectra. Statistical comparison of the parameters estimated from the healthy and metastatic tumor measurements was performed, using the Kruskal-Wallis non-parametric test with significance determined by computed p-values [36].
3. Results
3.1. Mathematical model applied to the healthy liver tissue measurements
Figure 4 shows a measured spectrum from 500 to 1600 nm of a healthy liver sample (dotted line), the corresponding fit curve without the bile component added into the model (solid line) and the 95% confidence bounds (dashed lines) [37]. For the measurement shown in Fig. 4, the parameters and the corresponding confidence intervals obtained from the fit are = 4.4 ± 0.3%, = 22 ± 8%, R = 76 ± 13μm, = 91 ± 2%, = 17 ± 2%, and a reduced scattering amplitude of 14.2 ± 0.3 cm−1 at 800 nm with a Mie-to-total reduced scattering fraction of 19 ± 4%. When investigating the residual (χ2 = 0.238) and the confidence bounds, a large deviation between the measurement and the fit curves was observed around the deoxygenated hemoglobin peak at 758 nm.
Fig. 4.
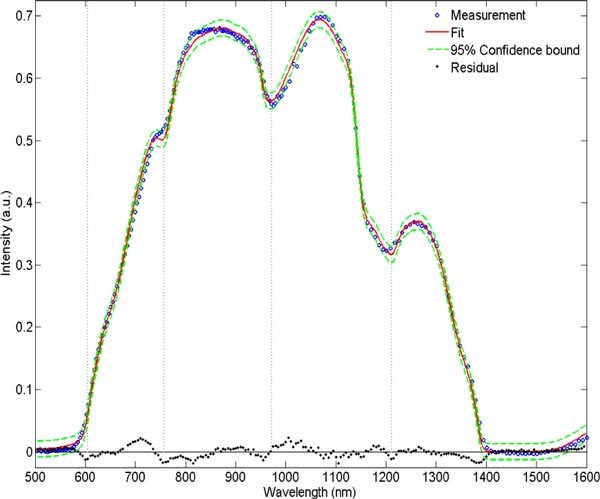
Reflectance measurement (dotted line) from a normal ex vivo tissue sample and its fit (solid line) without bile absorption coefficient implemented in the model and the corresponding 95% confidence bound (dashed lines). The vertical dotted lines at 605, 757, 972 and 1211 nm correspond to the absorption peaks location of bile, deoxygenated hemoglobin, water and lipid, respectively.
By adding the absorption coefficient of bile to the model, the large deviation around 758 nm significantly reduced while the confidence bounds narrowed towards the fit curve. The measurement curve in Fig. 5 is the same than the one depicted in Fig. 4 with a fit including the bile absorption coefficient in the model. For the measurement shown in Fig. 5, the estimated values and the corresponding confidence intervals are = 3.9 ± 0.7%, = 3.5 ± 0.3%, = 37 ± 8%, R = 56 ± 13μm, = 93 ± 2%, = 19 ± 1%, and a reduced scattering amplitude of 14.5 ± 0.3 cm−1 at 800 nm with a Mie-to-total reduced scattering fraction of 25 ± 7% were found. The residual decreased to a value of χ2 = 0.206. In comparison to the outcome of the model without bile, the oxygen saturation level is higher, indicating that the bile absorption was compensated by deoxygenated hemoglobin. Similar results can be seen in Table 1 which shows comparison of the mean and standard deviation of the parameters obtained from all the spectra measured on the 14 normal human liver tissue samples. Based on the confidence intervals, the model with bile showed for each sample that the parameters were estimated more reliably compared to the model without bile. Another observation in Fig. 5 is that the 95% confidence bound is closer to the fit curve, especially in the wavelength range between 500 and 800 nm where a bile absorption peak is present.
Fig. 5.
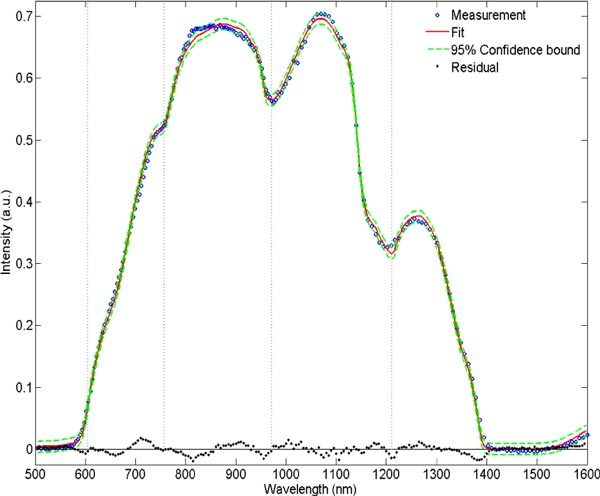
Reflectance measurement (dotted line) from a normal ex vivo tissue sample and its fit (solid line) with bile absorption implemented in the model and the corresponding 95% confidence bound (dashed line). The vertical dotted lines at 605, 757, 972 and 1211 nm correspond to absorption peaks location of bile, deoxygenated hemoglobin, water and lipid, respectively.
Table 1. Mean and standard deviation of the estimated values of the physiological and morphological parameters of healthy liver tissues obtained from the fitting model without and with bile absorption coefficient.
| Parameters | Fit without bile | Fit with bilea |
|---|---|---|
| Bile (%) | - | 6.6 ± 4.5 |
| Blood volume fraction (%) | 4.8 ± 0.3 | 3.4 ± 2.0 |
| Blood oxygenation level (%) | 6 ± 8 | 8 ± 14 |
| Average vessel radius (microns) | 67 ± 28 | 50 ± 22 |
| Water volume fraction (%) | 77 ± 7 | 76 ± 7 |
| Lipid volume fraction (%) | 17 ± 11 | 19 ± 11 |
| Reduced scattering at 800 nm (cm−1) | 17 ± 2 | 17 ± 3 |
| Mie slope | 0.5 ± 0.3 | 1.0 ± 0.5 |
| Mie-to-total scattering fraction (%) | 19 ± 10 | 37 ± 19 |
aAccording to a statistical F-test with p<0.05, 95% of the data showed improvement on the fitting when bile is added to the model.
In order to depict the imprint of bile absorption on the measured spectra, a forward calculation of the spectrum with the estimated parameters can be computed by setting the bile volume fraction to 0%. Figure 6 shows another example of a healthy liver spectrum and the corresponding fits where the estimated bile volume fraction is 10.4%. Additionally, the forward computation of the spectrum by using the estimated parameters as input arguments and setting the bile volume fraction to 0% is plotted and the area comprised between the generated curves and the fitted curves is illustrated and highlights the spectral changes that result from bile absorption.
Fig. 6.
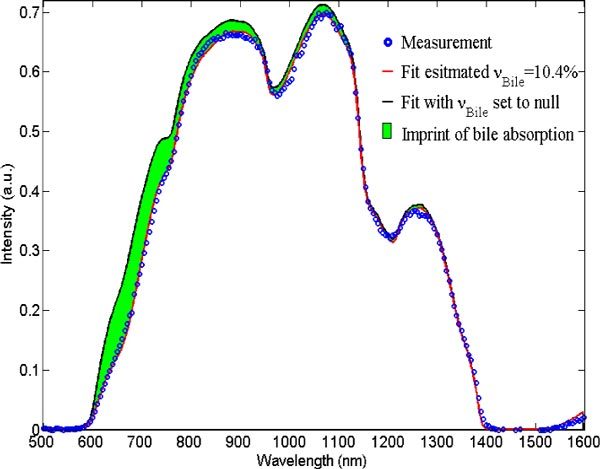
Tissue measurement from a normal tissue sample (dotted line) with an estimated bile volume fraction estimated from the fit (red solid line) of 10.4%. The colored area indicates the imprint of bile absorption obtained by comparison with a forward computation of the diffuse reflectance spectrum where the bile volume fraction is set to 0% (black solid line).
In order to mathematically evaluate whether bile is the missing absorber in the model, a statistical F-test was applied to all the data acquired at healthy sites in the liver [37]. P-values were computed from the F-ratios to evaluate if the model with bile absorption improved the fits. In total, 95% of the data have shown that the model including bile described best the measured spectra with a p-value below 0.05.
3.2. Comparison of healthy and metastatic tumor liver tissue
Figure 7 shows a typical spectrum (dotted line) from both healthy and metastatic tumor liver tissues with the corresponding fit curves (solid line) including bile. Major differences between the two typical spectra correlated with a difference in the estimated parameters.
Fig. 7.
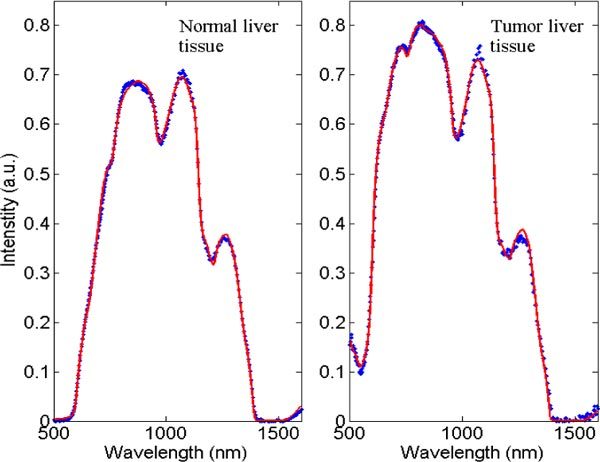
Reflectance measurement of healthy and metastatic tumor liver tissues (dotted line) and their corresponding fits (solid line).
From the typical metastatic tissue measurement depicted in Fig. 7, the estimated parameters and the corresponding confidence intervals are = 0 ± 0%, = 1.5 ± 0.1%, = 3 ± 5%, R = 31 ± 3μm, = 101 ± 2%, = 10 ± 1%, and a reduced scattering amplitude of 9.8 ± 0.3 cm−1 at 800 nm with a Mie-to-total reduced scattering fraction of 76 ± 4%.
Table 2 summarizes all the median and standard deviations derived from the interquartiles of the various fit parameters for all the measurements performed in the fourteen samples of healthy and metastatic liver tissues. The advantage of reporting the median and the standard deviation derived from interquartiles instead of the mean and standard deviation is that the data cannot be described by a parametric distribution, hence we used a non-parametric statistical Kruskal-Wallis test instead of a t-test to find which parameters show significant difference between the two types of tissue, as was also done in previous studies [10,12,13,19,20,22,24,25]. The blood oxygenation was not reported, due to the fact that the study was conducted on ex vivo samples. Therefore this parameter does not reflect the actual oxygenation level as it would be in vivo. According to the Kruskal-Wallis statistical test, the values that showed most significant differences between healthy and metastatic tissues with p<0.01 were bile, the reduced scattering amplitude and the water volume fraction.
Table 2. Median and standard deviation of the various morphological parameters estimated from ex vivo measurements performed on normal and metastatic tumor tissues in liver.
| Parameters | Normal liver (14 samples) | Metastatic tumor (14 samples) |
|---|---|---|
| Bile (%)a | 5.5 ± 2.3 | 1.0 ± 1.1 |
| Blood volume fraction (%) | 3.2 ± 1.6 | 0.8 ± 2.4 |
| Blood oxygenation level (%) | 8 ± 14 | 45 ± 44 |
| Average vessel radius (microns) | 53 ± 20 | 67 ± 82 |
| Water volume fraction (%)a | 76 ± 4 | 93 ± 17 |
| Lipid volume fraction (%) | 16 ± 3 | 12 ± 6 |
| Reduced scattering at 800 nm (cm−1) a | 17 ± 3 | 10 ± 3 |
| Mie slope | 1.2 ± 0.7 | 0.5 ± 0.5 |
| Mie-to-total scattering fraction (%) | 44 ± 25 | 57 ± 15 |
aIndicates significant differences with p<0.01 for the Kruskal-Wallis test.
Figure 8 shows a picture of a tumor and the surrounding healthy liver tissue. It is visually clear that the tumor is less rich in blood than the healthy liver tissue. All the measured tumors were at least a centimeter in diameter and rather white in appearance.
Fig. 8.
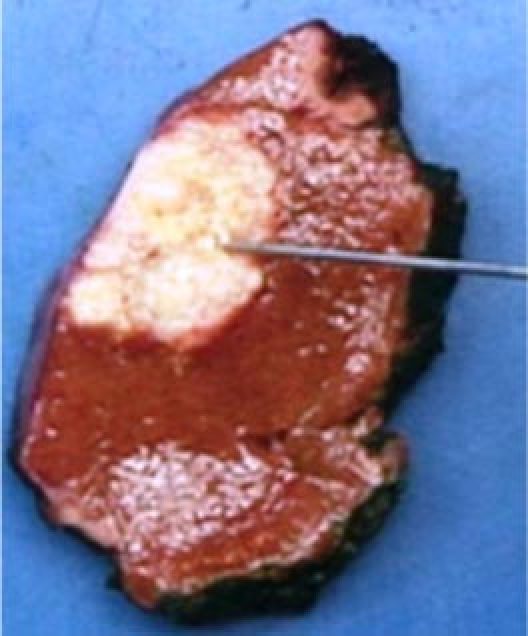
Picture of a tumor surrounded by healthy liver tissue. The optical probe is directed towards the tumor site.
4. Discussion
A paucity of studies has investigated the absorption coefficient of bile. Maitland et al. [33] measured the absorption coefficient of bile from 350 to 2450 nm and stated that bile has its main absorption peaks at 400, 1450 and 1900 nm. The latter two most likely correspond to absorption due to the presence of water in bile, whereas the peak at 400 nm corresponds to an actual absorption peak of bile. After measuring the absorption coefficient of bile, we observed a broad absorption peak between 550 and 650 nm with a local maximum of 5.4 cm−1 at 605 nm. Our measurement also suggests that there is a higher absorption peak at 409 nm, whereas the maximum reported by Maitland et al. is at 400 nm [33]. The presented bile absorption coefficients in this paper can therefore be considered as an updated measurement of the one reported by Maitland et al. [33].
This study demonstrated the necessity to incorporate the bile absorption coefficient into the model when fitting spectroscopic measurements in liver tissue. In 95% of the measured healthy tissue data, including bile in the fitting model provided a better fit according to a statistical F-test. The fit parameters that were mainly altered when the bile was not added to the model were the blood volume fraction and the average vessel radius. For the 14 measured normal samples, the blood volume fraction decreased on average from 4.8 ± 1.7% to 3.4 ± 2.0%, whereas no significant changes were observed for the oxygenation level of blood. Figure 2 and 3 illustrates a higher absorption for deoxygenated hemoglobin than for oxygenated hemoglobin between 550 and 750 nm. The main absorption of bile is between these wavelengths. The resulting fit model without bile compensates for the residual by overestimating the deoxygenated hemoglobin yielding higher blood volumes with unchanged oxygen saturation levels. Moreover, this discrepancy is observed between the measurement and the fit curves depicted at 758 nm in Fig. 4 where no bile was taken into account in the model. It is important to note that deoxygenated-hemoglobin has a distinct spectral absorption peak at 758 nm (cf. Fig. 2) resulting in an inflection point in the fits that is not present in the measured liver spectra. Furthermore, changes are observed in the Mie slope and Mie-to-total reduced scattering fractions, whereas the reduced scattering amplitude remains unchanged. Finally, no effects on the estimation of water and lipid fractions is seen when bile is not present in the model. This is expected since there are no overlapping absorption features between these two biological parameters.
It is important to note that the bile that was used to measure its absorption coefficients comes from patients suffering from metastatic colorectal cancer. Therefore the pigmentation concentration in the bile can vary from one person to another, resulting in slightly different absorption coefficients; hence the presence of a significant residual around 800 nm when bile is added in the model (cf. Fig. 5). However, this is not the case in all patients. Another remark with respect to the residual is the small deviation between the measurement and the fits around 1211 nm which is most probably due to changes in water absorption coefficients with temperature. Indeed, the tissue measurements were performed ex vivo after resection, and hence the temperature of the samples decreased from body temperature down to the room ambient temperature when brought to the pathology department. We have shown elsewhere [30] that water absorption coefficient is temperature dependant and that it is prone to significant variation in absorption in the vicinity of 1200 nm, hence the small residual around this wavelength.
The analysis of the diffuse optical spectra showed significant differences according to the Kruskal-Wallis non-parametric test with a critical value of 0.01 for bile and water volume fractions, as well as the reduced scattering amplitude and the oxygenation saturation of blood.
The study by Kitai et al. [16] measured the optical properties before and after clamping the left branches of the hepatic pedicle, including the portal vein and hepatic artery, during 60 minutes. Their study showed that the oxygenation level in blood equals 75% just before clamping the vessels and drops down to 8% one hour after clamping. The median oxygenation values in the healthy tissues and tumors presented in Table 2 are 8% and 45%, respectively. In our study, the blood vessels of the resected specimens were clamped up to one hour before the resection was completed and the samples were transported within a time frame of two hours after resection to the pathology department. Therefore, there was no more blood flow and perfusion to the liver tissue in the ex vivo samples yielding to a decrease in oxygenation levels when the samples were delivered for measurements. It is therefore difficult to draw any conclusions by comparing the estimated oxygenation levels in healthy tissues and the tumors measured ex vivo.
The reduced scattering amplitude and the bile volume fraction showed the most significant differences (p<0.0001) between healthy and metastatic liver tissues. As shown in Table 2, healthy tissue has more than five times more bile than tumors whereas the reduced scattering amplitude is almost twice as high. Healthy liver tissue is mainly constituted of hepatocytes which are cells that are arranged as very thin plates separated by fine vascular sinusoids where blood flows; allowing perfusion of the bile throughout the liver [38]. In the tumor, this structure is lost, causing a different perfusion of the bile and an alteration of the cell structures yielding to a different light scattering. This observation is consistent with the fact that the tumors in liver are metastases of colorectal cancer with different structural composition. The tumor consists therefore of abnormal colorectal tissue cells embedded in collagenous cellular stroma induced by the epithelial tumor cells. Such tumors are almost completely devoid of stroma. Therefore, hardly any bile is expected in the tumor cells from colorectal origin.
The reduced scattering amplitude is 1.7 times higher in healthy tissue than in tumors. Germer et al. measured the absorption coefficient, scattering and anisotropy of human liver tissues and colorectal liver metastases in vitro at 850, 980 and 1064 nm [39]. They found that scattering in human liver tissues is in average 1.7 times higher than in the metastases tissues. However, the large difference in anisotropy yields to reduced scattering of 9.5 and 11 cm−1 at 800 nm (extrapolated values) for normal and metastatic liver tissue, respectively [39]. Therefore, the reduced scattering amplitude of the metastatic tumor reported in Table 2 is very comparable to the value reported in ref [39], whereas the value in healthy liver tissue is much higher.
The water volume fraction showed significant difference between both types of tissue with higher water content in tumor. There is a multitude of factors that could explain this observation. In particular, the fact that water is attracted to necrotic tissue which is also abundantly present in most colorectal liver metastases, the high water content of collagenous stroma in general, and tumor induced stroma could play a role.
From Table 2, one can observe a low Mie scattering contribution in liver compared to other organs. The reported Mie-to-total scattering fraction in healthy tissue and tumors are 44% and 57%, respectively. Optical properties such as the absorption coefficient, scattering coefficient and anisotropy of porcine liver were measured with a double integrating sphere setup by Fritz et al. [40] where it is clearly shown that the anisotropy of liver tissue steeply increases from 0.75 to 0.9 between 400 and 600 nm and is constant at a value of 0.93 beyond 600 nm up to 1600 nm. By applying the double power law for reduced scattering as expressed in Eq. (1) to the data of Fritz et al. up to 1600 nm, the Mie-to-total reduced scattering contribution is as low as 59% which is comparable to the values reported in Table 2. This is a result of the high gradient of the anisotropy below 600 nm. Rayleigh scattering occurs due to the interaction of light with sub-micron structures, such as thin fibers, in tissue and it was proven that it is necessary to include a Rayleigh term in the reduced scattering model beyond 500 nm [41]. Liver is very rich in sub-micron reticular fibers in the perisinusoidal space separating hepatocytes from sinusoids, likely yielding high Rayleigh scattering [38].
Table 2 reports a median value of blood volume fraction in healthy and metastatic tissue of 3.2% and 0.8%, respectively. However, despite this large difference, there is statistically no significant difference (p<0.05) between the two types of tissue because the standard deviation for tumor tissue is very large. The reason is that in two of the fourteen tumor samples, which were large necrotic samples, high amounts of blood were present. Indeed it is known that most tumors have a vascular network of higher density than most normal tissues. However, the opposite is true for colorectal liver metastases, as normal liver tissue is extremely well vascularized to fulfill its many functions related to metabolism, detoxification, bile production, etc. The absorption coefficient of the human liver measurements in Ref. [39] was found to be higher in the liver than in the metastases for the wavelengths of interest which in fact means that more blood is present in healthy liver tissue than in metastatic tumors which corroborates with the estimated blood volume fraction in Table 2.
Given the distance between the emitting and collecting fibers, the amount of light that is collected below 600 nm is in some cases close to the noise level because of the high blood amount (above roughly 5%) in the liver. The high amount of blood causes a decrease in the amount of light that is collected. In order to enhance the reliability of the estimated parameters of the blood and bile, one could measure below 500 nm where additional absorption peaks of these chromophores exist (cf. Fig. 2) by using a smaller distance separation between the emitting and collecting fibers.
5. Conclusion
In conclusion, this paper presents the first study in which bile, water and lipid are included in addition to oxygenated and deoxygenated hemoglobin in the discrimination between healthy and metastatic tumors tissues in human liver with diffuse optical spectroscopy. The absorption spectrum of bile was accurately measured and integrated in the model in order to estimate the concentration of this chromophore in the liver. We have demonstrated that bile should be included when analyzing diffuse optical spectroscopy data, because of its presence in the liver bile ducts. Our results illustrate that discrimination between healthy and metastatic liver cancer tissues seems possible based on the estimated bile volume fraction and reduced scattering amplitude obtained from diffuse optical spectra measured on both types of tissue. Compared to healthy tissue, tumors have around five and two times lower bile and reduced scattering amplitude values, respectively. This method can also be applied during real-time intra-operative needle localization and ablation monitoring to improve ablation efficacy and hence disease-free survival.
Acknowledgments
The authors would like to thank the pathology department staff at the Netherlands Cancer Institute (NKI-AVL) and Philips Research project members. Furthermore, the authors thank Gert‘t Hooft, Susanne van der Berg, and Willem Verkruijsse for their valuable feedback when preparing the manuscript and Walter Bierhoff and Jeroen Horikx for improving the hardware and making the probes. This work is supported by a European Commission Marie Curie contract MEST-CT-2004-007832.
References and links
- 1.Am. Canc. Org. 2010 official stats website: http://www.who.int/mediacentre/factsheets/fs297/en/index.html
- 2.Tsim N. C., Frampton A. E., Habib N. A., Jiao L. R., “Surgical treatment for liver cancer,” World J. Gastroenterol. 16(8), 927–933 (2010). 10.3748/wjg.v16.i8.927 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kemeny N., “The management of resectable and unresectable liver metastases from colorectal cancer,” Curr. Opin. Oncol. 22(4), 364–373 (2010). 10.1097/CCO.0b013e32833a6c8a [DOI] [PubMed] [Google Scholar]
- 4.Shimada H., Tanaka K., Endou I., Ichikawa Y., “Treatment for colorectal liver metastases: a review,” Langenbecks Arch. Surg. 394(6), 973–983 (2009). 10.1007/s00423-009-0530-8 [DOI] [PubMed] [Google Scholar]
- 5.Muratore A., Ribero D., Zimmitti G., Mellano A., Langella S., Capussotti L., “Resection margin and recurrence-free survival after liver resection of colorectal metastases,” Ann. Surg. Oncol. 17(5), 1324–1329 (2010). 10.1245/s10434-009-0770-4 [DOI] [PubMed] [Google Scholar]
- 6.Pawlik T. M., Scoggins C. R., Zorzi D., Abdalla E. K., Andres A., Eng C., Curley S. A., Loyer E. M., Muratore A., Mentha G., Capussotti L., Vauthey J. N., “Effect of surgical margin status on survival and site of recurrence after hepatic resection for colorectal metastases,” Ann. Surg. 241(5), 715–724, discussion 722–724 (2005). 10.1097/01.sla.0000160703.75808.7d [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bhardwaj N., Strickland A. D., Ahmad F., Dennison A. R., Lloyd D. M., “Liver ablation techniques: a review,” Surg. Endosc. 24(2), 254–265 (2010). 10.1007/s00464-009-0590-4 [DOI] [PubMed] [Google Scholar]
- 8.Ruers T. J., Joosten J. J., Wiering B., Langenhoff B. S., Dekker H. M., Wobbes T., Oyen W. J., Krabbe P. F., Punt C. J., “Comparison between local ablative therapy and chemotherapy for non-resectable colorectal liver metastases: a prospective study,” Ann. Surg. Oncol. 14(3), 1161–1169 (2007). 10.1245/s10434-006-9312-5 [DOI] [PubMed] [Google Scholar]
- 9.Wong S. L., Mangu P. B., Choti M. A., Crocenzi T. S., Dodd G. D., 3rd, Dorfman G. S., Eng C., Fong Y., Giusti A. F., Lu D., Marsland T. A., Michelson R., Poston G. J., Schrag D., Seidenfeld J., Benson A. B., 3rd, “American Society of Clinical Oncology 2009 clinical evidence review on radiofrequency ablation of hepatic metastases from colorectal cancer,” J. Clin. Oncol. 28(3), 493–508 (2010). 10.1200/JCO.2009.23.4450 [DOI] [PubMed] [Google Scholar]
- 10.Bard M. P., Amelink A., Hegt V. N., Graveland W. J., Sterenborg H. J. C. M., Hoogsteden H. C., Aerts J. G. J. V., “Measurement of hypoxia-related parameters in bronchial mucosa by use of optical spectroscopy,” Am. J. Respir. Crit. Care Med. 171(10), 1178–1184 (2005). 10.1164/rccm.200501-046OC [DOI] [PubMed] [Google Scholar]
- 11.Volynskaya Z., Haka A. S., Bechtel K. L., Fitzmaurice M., Shenk R., Wang N., Nazemi J., Dasari R. R., Feld M. S., “Diagnosing breast cancer using diffuse reflectance spectroscopy and intrinsic fluorescence spectroscopy,” J. Biomed. Opt. 13(2), 024012 (2008). 10.1117/1.2909672 [DOI] [PubMed] [Google Scholar]
- 12.Cerussi A. E., Shah N., Hsiang D., Durkin A., Butler J., Tromberg B. J., “In vivo absorption, scattering and physiologic properties of 58 malignant breast tumors determined by broadband diffuse optical spectroscopy,” J. Biomed. Opt. 11(4), 044005 (2006). 10.1117/1.2337546 [DOI] [PubMed] [Google Scholar]
- 13.Brown J. Q., Wilke L. G., Geradts J., Kennedy S. A., Palmer G. M., Ramanujam N., “Quantitative optical spectroscopy: a robust tool for direct measurement of breast cancer vascular oxygenation and total hemoglobin content in vivo,” Cancer Res. 69(7), 2919–2926 (2009). 10.1158/0008-5472.CAN-08-3370 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zonios G., Perelman L. T., Backman V. M., Manoharan R., Fitzmaurice M., Van Dam J., Feld M. S., “Diffuse reflectance spectroscopy of human adenomatous colon polyps in vivo,” Appl. Opt. 38(31), 6628–6637 (1999). 10.1364/AO.38.006628 [DOI] [PubMed] [Google Scholar]
- 15.Reif R., A’Amar O., Bigio I. J., “Analytical model of light reflectance for extraction of the optical properties in small volumes of turbid media,” Appl. Opt. 46(29), 7317–7328 (2007). 10.1364/AO.46.007317 [DOI] [PubMed] [Google Scholar]
- 16.Kitai T., Miwa M., Liu H., Beauvoit B., Chance B., Yamaoka Y., “Application of near-infrared time-resolved spectroscopy to rat liver--a preliminary report for surgical application,” Phys. Med. Biol. 44(8), 2049–2061 (1999). 10.1088/0031-9155/44/8/314 [DOI] [PubMed] [Google Scholar]
- 17.Kitai T., Nishio T., Miwa M., Yamaoka Y., “Optical analysis of the cirrhotic liver by near-infrared time-resolved spectroscopy,” Surg. Today 34(5), 424–428 (2004). 10.1007/s00595-003-2721-1 [DOI] [PubMed] [Google Scholar]
- 18.Hsu C. P., Razavi M. K., So S. K., Parachikov I. H., Benaron D. A., “Liver tumor gross margin identification and ablation monitoring during liver radiofrequency treatment,” J. Vasc. Interv. Radiol. 16(11), 1473–1478 (2005). [DOI] [PubMed] [Google Scholar]
- 19.van Veen R. L. P., Amelink A., Menke-Pluymers M., van der Pol C., Sterenborg H. J. C. M., “Optical biopsy of breast tissue using differential path-length spectroscopy,” Phys. Med. Biol. 50(11), 2573–2581 (2005). 10.1088/0031-9155/50/11/009 [DOI] [PubMed] [Google Scholar]
- 20.Zhu C., Breslin T. M., Harter J., Ramanujam N., “Model based and empirical spectral analysis for the diagnosis of breast cancer,” Opt. Express 16(19), 14961–14978 (2008). 10.1364/OE.16.014961 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bigio I. J., Bown S. G., Briggs G., Kelley C., Lakhani S., Pickard D., Ripley P. M., Rose I. G., Saunders C., “Diagnosis of breast cancer using elastic-scattering spectroscopy: preliminary clinical results,” J. Biomed. Opt. 5(2), 221–228 (2000). 10.1117/1.429990 [DOI] [PubMed] [Google Scholar]
- 22.Chang V. T., Cartwright P. S., Bean S. M., Palmer G. M., Bentley R. C., Ramanujam N., “Quantitative physiology of the precancerous cervix in vivo through optical spectroscopy,” Neoplasia 11(4), 325–332 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mourant J. R., Bocklage T. J., Powers T. M., Greene H. M., Bullock K. L., Marr-Lyon L. R., Dorin M. H., Waxman A. G., Zsemlye M. M., Smith H. O., “In vivo light scattering measurements for detection of precancerous conditions of the cervix,” Gynecol. Oncol. 105(2), 439–445 (2007). 10.1016/j.ygyno.2007.01.001 [DOI] [PubMed] [Google Scholar]
- 24.Kanick S. C., van der Leest C., Djamin R. S., Janssens A. M., Hoogsteden H. C., Sterenborg H. J. C. M., Amelink A., Aerts J. G. J. V., “Characterization of mediastinal lymph node physiology in vivo by optical spectroscopy during endoscopic ultrasound-guided fine needle aspiration,” J. Thorac. Oncol. 5(7), 981–987 (2010). [DOI] [PubMed] [Google Scholar]
- 25.Kanick S. C., van der Leest C., Aerts J. G. J. V., Hoogsteden H. C., Kascáková S., Sterenborg H. J. C. M., Amelink A., “Integration of single-fiber reflectance spectroscopy into ultrasound-guided endoscopic lung cancer staging of mediastinal lymph nodes,” J. Biomed. Opt. 15(1), 017004 (2010). 10.1117/1.3290822 [DOI] [PubMed] [Google Scholar]
- 26.Zonios G., Dimou A., “Modeling diffuse reflectance from semi-infinite turbid media: application to the study of skin optical properties,” Opt. Express 14(19), 8661–8674 (2006). 10.1364/OE.14.008661 [DOI] [PubMed] [Google Scholar]
- 27.Zonios G., Bassukas I., Dimou A., “Comparative evaluation of two simple diffuse reflectance models for biological tissue applications,” Appl. Opt. 47(27), 4965–4973 (2008). 10.1364/AO.47.004965 [DOI] [PubMed] [Google Scholar]
- 28.Zonios G., Dimou A., “Light scattering spectroscopy of human skin in vivo,” Opt. Express 17(3), 1256–1267 (2009). 10.1364/OE.17.001256 [DOI] [PubMed] [Google Scholar]
- 29.Farrell T. J., Patterson M. S., Wilson B., “A diffusion theory model of spatially resolved, steady-state diffuse reflectance for the noninvasive determination of tissue optical properties in vivo,” Med. Phys. 19(4), 879–888 (1992). 10.1118/1.596777 [DOI] [PubMed] [Google Scholar]
- 30.Nachabé R., Hendriks B. H. W., Desjardins A. E., van der Voort M., van der Mark M. B., Sterenborg H. J. C. M., “Estimation of lipid and water concentrations in scattering media with diffuse optical spectroscopy from 900 to 1,600 nm,” J. Biomed. Opt. 15(3), 037015 (2010). 10.1117/1.3454392 [DOI] [PubMed] [Google Scholar]
- 31.Nachabé R., Hendriks B. H. W., van der Voort M., Desjardins A. E., Sterenborg H. J. C. M., “Estimation of biological chromophores using diffuse optical spectroscopy: benefit of extending the UV-VIS wavelength range to include 1000 to 1600 nm,” Biomed. Opt. Express 1(5), 1432–1442 (2010). 10.1364/BOE.1.001432 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Verkruysse W., Lucassen G. W., de Boer J. F., Smithies D. J., Nelson J. S., van Gemert M. J. C., “Modelling light distributions of homogeneous versus discrete absorbers in light irradiated turbid media,” Phys. Med. Biol. 42(1), 51–65 (1997). 10.1088/0031-9155/42/1/003 [DOI] [PubMed] [Google Scholar]
- 33.Maitland D. J., Walsh J. T., Jr, Prystowsky J. B., “Optical properties of human gallbladder tissue and bile,” Appl. Opt. 32(4), 586–591 (1993). 10.1364/AO.32.000586 [DOI] [PubMed] [Google Scholar]
- 34.W. G. Zijlstra, A. Buursma, and O. W. Van Assendelft, Visible and Near Infrared Absorption Spectra of Human and Animal Haemoglobin (VSP Publishing, Utrecht, The Netherlands, 2000). [Google Scholar]
- 35.Amelink A., Robinson D. J., Sterenborg H. J. C. M., “Confidence intervals on fit parameters derived from optical reflectance spectroscopy measurements,” J. Biomed. Opt. 13(5), 054044 (2008). 10.1117/1.2982523 [DOI] [PubMed] [Google Scholar]
- 36.Kruskal W. H., Wallis W. A., “Use of ranks in one-criterion variance analysis,” J. Am. Stat. Assoc. 47(260), 583–621 (1952). 10.2307/2280779 [DOI] [Google Scholar]
- 37.H. Motulsky, Intuitive biostatistics (Oxford University Press, 1995). [Google Scholar]
- 38.B. Young, J. Lowe, A. Stevens, and J. Heath, Wheater’s functional histology (Churchill Livingstone, 2006). [Google Scholar]
- 39.Germer C. T., Roggan A., Ritz J. P., Isbert C., Albrecht D., Müller G., Buhr H. J., “Optical properties of native and coagulated human liver tissue and liver metastases in the near infrared range,” Lasers Surg. Med. 23(4), 194–203 (1998). [DOI] [PubMed] [Google Scholar]
- 40.Ritz J. P., Roggan A., Isbert C., Müller G., Buhr H. J., Germer C. T., “Optical properties of native and coagulated porcine liver tissue between 400 and 2400 nm,” Lasers Surg. Med. 29(3), 205–212 (2001). 10.1002/lsm.1134 [DOI] [PubMed] [Google Scholar]
- 41.Saidi I. S., Jacques S. L., Tittel F. K., “Mie and Rayleigh modeling of visible-light scattering in neonatal skin,” Appl. Opt. 34(31), 7410–7418 (1995). 10.1364/AO.34.007410 [DOI] [PubMed] [Google Scholar]


