Quantitative investigation of the effect of the extra-cerebral vasculature in diffuse optical imaging: a simulation study

Abstract

Diffuse optical imaging (DOI) is a non invasive technique allowing the recovery of hemodynamic changes in the brain. Due to the diffusive nature of photon propagation in turbid media and the fact that cerebral tissues are located around 1.5 cm under the adult human scalp, DOI measurements are subject to partial volume errors. DOI measurements are also sensitive to large pial vessels because oxygenated and deoxygenated hemoglobin are the dominant chromophores in the near infrared window. In this study, the effect of the extra-cerebral vasculature in proximity of the sagittal sinus was investigated for its impact on DOI measurements simulated over the human adult visual cortex. Numerical Monte Carlo simulations were performed on two specific models of the human head derived from magnetic resonance imaging (MRI) scans. The first model included the extra-cerebral vasculature in which constant hemoglobin concentrations were assumed while the second did not. The screening effect of the vasculature was quantified by comparing recovered hemoglobin changes from each model for different optical arrays and regions of activation. A correction factor accounting for the difference between the recovered and the simulated hemoglobin changes was computed in each case. The results show that changes in hemoglobin concentration are better estimated when the extra-cerebral vasculature is modeled and the correction factors obtained in this case were at least 1.4-fold lower. The effect of the vasculature was also examined in a high-density diffuse optical tomography configuration. In this case, the difference between changes in hemoglobin concentration recovered with each model was reduced down to 10%.

1. Introduction

Optical imaging has seen significant developments in the last two decades mainly due to its clinical potential. Optical neuroimaging includes a variety of methods enabling its use across species including human from premature newborn [1] to elderly [2], nonhuman primate [3], cat [4, 5] and rodent [6]. Diffuse optical imaging studies in human are non-invasive and can be monitored continuously at bedside, in intensive care units for newborn, children and elderly, avoiding moving critically ill patients.

Diffuse optical imaging employing near infrared spectroscopy (NIRS) in human has been utilized in the past during visual stimulation to monitor visual cortical function [7] and estimate evoked brain activity and tissue oxygenation [8–10]. For example, in [9, 11], the authors measured regional changes in hemoglobin concentrations using an optode array placed 10 mm to the right of the midline to minimize the sagittal sinus effect. Changes in hemoglobin concentrations were also assessed when they were induced by a decrease in neuronal activity [12]. While almost all functional retinototopic mappings of the visual cortex were investigated using intrinsic optical imaging in monkey [3], cat [5] and rat [6] visual cortex, recent work proposed to use high-density diffuse optical tomography (DOT) approaches to reveal phase-encoded mapping of the human visual cortex's retinotopic organization [13]. In particular, the authors employed a multi-distance high-density optical grid to show that diffuse optical tomography is able to measure complex organized structures in the visual cortex. In [14], the authors demonstrated, using the same methodology, resting-state functional connectivity in the human brain. This approach enabled the recovery of two-dimensional maps of changes in oxygenated [HbO] and deoxygenated [HbR] hemoglobin concentrations with a 1 cm lateral and cortical depth resolutions. In all cases, the optical array configuration was horizontally centered near the inion.

The localization of focal hemodynamic activation in the brain is non accurate and recovered hemoglobin concentrations suffer from significant partial volume errors due to the diffusive nature of the propagation of light in biological tissues [15]. These errors originate from the limited depth sensitivity of DOI, leading to an underestimation of changes in hemoglobin concentration. The partial volume error depends on the position and the magnitude of the activation (in terms of absorption change) and is sensitive to the optical properties of tissues [16]. Photon propagation theory demonstrates that the trajectory of light in tissue is longer than the source-detector distance and that a multiplicative factor can account for this difference. This factor is known as the differential pathlength factor [17, 18] and varies with the wavelength of light. However, in functional study, only a fraction of the light travels in the activated regions of the brain and this phenomenon is known to create partial volume error.

In order to use NIRS data in vascular modeling [19] to compute metabolic parameters, NIRS measurements must first be corrected for partial volume errors. This correction is needed as the absolute changes occurring in the cortex during cerebral activity are required in the modeling process [20] and can be achieved using numerical simulations [21]. When NIRS measurements are performed over a region where the contribution of extra-cerebral vasculature is negligible, the numerical simulation can use a segmented head model containing the following tissue types of the human head: scalp, skull, cerebrospinal fluid (CSF) and brain tissue (including the white and the gray matters). However, when measurements are performed over an area in the vicinity of large pial vessels such as the sagittal sinus, additional partial volume errors might arise due to the high sensitivity of DOI to blood. These structures contain whole blood, both oxy- and deoxyhemoglobin, which strongly absorb light in the near-infrared (NIR) spectrum. The goal of this study is to quantify the influence of the extra-cerebral vasculature on DOI measurements. A similar effect was previously explored on blood flow measurements [22, 23] and on hemoglobin oxygenation measurements with time-resolved reflectance spectroscopy [24]. As far as we know, this is the first study in which the effect of the extra-cerebral vasculature on DOI measurements is quantified.

In this study, the influence of the extra-cerebral vasculature on DOI measurements was investigated by including this vasculature in the 3D anatomical head model. The geometrical structure of these vessels was obtained from a 3D phase contrast angiography MRI sequence. Light propagation was modeled using a numerical Monte Carlo (MC) approach and simulations were carried out in two specific anatomical models. The first model included the extra-cerebral vasculature while the second was build with only the typical tissues: scalp, skull, CSF and brain. Optical properties of the extra-cerebral vasculature were assigned to those of whole blood. Brain activation was simulated by applying a change in the absorption coefficient in a specific and limited region of the brain tissue. The changes in hemoglobin concentration recovered with each model were compared and correction factors accounting for the difference between the recovered and the simulated changes were computed. This procedure was repeated for different optical arrays and regions of activation located in the proximity of the sagittal sinus. This technique was finally applied in the context of a high-density diffuse optical tomography.

2. Methods

2.1. MR imaging technique

The images were acquired on a 3T Trio TIM MR device (Siemens Healthcare, Erlangen, Germany). One volunteer was scanned using a 12-channel matrix head coil. Written consent was obtained from the subject prior to the study and the subject received financial compensation.

The structural image was acquired with a 3D MPRAGE. Imaging times were TE/TR/TI = 4.18/2300/900 ms and the field of view (FOV) was 256 × 224mm² with partial Fourier 6/8 and an acceleration factor of 2 with GRAPPA (Generalized Autocalibrating Partially Parallel Acquisition) reconstruction. 176 slices were acquired with a thickness of 1 mm for isotropic voxel volume (1 mm³) and a bandwidth of 150 Hz/px.

A phase contrast (PC) technique was selected because we required a high spatial resolution brain peripheral veins angiography without contrast agent injection [25]. This sequence allowed good stationary tissue suppression and easy venous blood signal selection using a velocity encoding (VENC) approach. Improved sensitivity was obtained by making the sequence sensitive to venous blood in three perpendicular spatial directions [26] leading to a clear identification of the venous path in 3D. A saturation band was also applied below the volume of interest in the superior-inferior direction to suppress arterial blood signal. The saturation band was 110 mm thick below the volume of interest and perpendicular to the carotid arteries. The PC sequence was based on a high resolution 3D gradient recalled echo scheme. The sequence parameters were: FOV = 200.0 × 168.8 × 129.6mm³, matrix = 256 × 216 × 144 to obtain a nearly isotropic voxel volume (Vvoxel = 0.78 × 0.78 × 0.90mm³). The selected VENC was 5 mm/s for the plane described by the right-left and anterior-posterior encoding. The total sequence duration was 11 min and 40 sec. The bandwidth was 300 Hz/px and imaging times were TR/TE = 80.9/10.3 ms. The flip angle was set to 15° and an image GRAPPA with acceleration factor of 2 with 24 integrated reference scans over one average were used for reconstruction.

2.2. Anatomical head models

Two specific anatomical head models were created from MRI data segmented with SPM5 (Wellcome Trust Centre for Neuroimaging, UCL, London, UK) and FSL (Analysis Group, FMRIB, Oxford, UK) softwares. Both models were segmented in the following tissue types: scalp, skull, CSF, gray (GM) and white (WM) matters. The first model included the extra-cerebral vasculature and was derived by the co-registration of the 3D PC angiography in the structural T1-weighted image space, while the second did not incorporate the vasculature. Dimensions for both models were 155 × 214 × 130 mm³ of isotropic voxels of 1 mm³.

2.3. Optical properties

The baseline optical properties used in the MC simulations for scalp, skull, CSF, gray and white matters were taken from [21] at two specific wavelengths (λ) of 690 and 830 nm in the NIR spectrum (see Table 1). To compute the absorption coefficient in the extra-cerebral vasculature, we assumed that oxy- and deoxyhemoglobin were the only chromophores with concentrations C_HbO and C_HbR, respectively. Baseline absorption coefficients ${\mu }_{a_0}^{\lambda }$ were computed from

Table 1. Optical coefficients for anatomical models described in section 2.2 including baseline absorption coefficients ${\mu }_{a_0}$ [mm⁻¹], scattering coefficients µ_s [mm⁻¹], anisotropic factors g and refractive indexes n; Note that brain tissue included gray and white matters [21].

Tissue	λ = 690 nm				λ = 830 nm
	${\mu }_{a_0}$	µs	g	n	${\mu }_{a_0}$	µs	g	n
Scalp	0.0159	8.0	0.9	1.4	0.0191	6.6	0.9	1.4
Skull	0.0101	10.0	0.9	1.4	0.0136	8.6	0.9	1.4
CSF	0.0004	0.1	0.9	1.4	0.0026	0.1	0.9	1.4
Brain	0.0178	12.5	0.9	1.4	0.0186	11.1	0.9	1.4
Vasculature	0.5745	74.5	0.985	1.4	0.4758	67.5	0.992	1.4

$${\mu }_{a_0}^{\lambda }=2.303({\mathrm{\xi }}_{\mathrm{HbO}}^{\mathit{\lambda }}{C}_{\mathrm{HbO}}+{\mathrm{\xi }}_{\mathrm{HbR}}^{\lambda }{C}_{\mathrm{HbR}})$$ (1)

where ξ^λ_HbO and ξ^λ_HbR are the extinction coefficients for HbO and HbR, respectively.

The NIR absorption is higher in the vasculature than in other tissues because the content is mainly whole blood. In the following, it is assumed that oxygenated blood is composed of 150 grams (g) of hemoglobin per liter (ℓ) of blood with a hemoglobin molar mass of 66500 g/Mol [27]. Sinuses are large veins having a baseline oxygen saturation of approximately 60% [28] and their baseline optical absorption coefficients were computed with Eq. (1) leading to ${\mu }_{a_0}^{690}$ = 0.5745 and ${\mu }_{a_0}^{830}$ = 0.4758 mm⁻¹. Scattering coefficients, anisotropy factors and refractive indexes were taken from literature [29] and are provided in Table 1.

2.4. Optical array configuration

A set of one optical source and two optical detectors were placed in a horizontal configuration forming a simple optical array. The distances between the source and the two detectors were set to 30 and 45 mm, respectively. The optical array was positioned at three locations with respect to the sagittal sinus (Fig. 1). From configuration 1 to 3, the optical array was translated by 10 mm. The same optical array was also positioned in a vertical configuration at 20 mm to the right of the midline [10]. Finally, a high-density grid was built and horizontally centered near the inion to cover the occipital cortex and was composed of 24 sources and 28 detectors [30].

Fig. 1.

Horizontal optical arrays 1–3, vertical array (V) and high density (HD) grid superimposed on a 3D coronal view of the anatomical head model including the extra-cerebral vasculature (black) and the gray matter (GM). Sources and detectors are represented by red and blue dots, respectively.

2.5. Region of activation

Three different positions of the activation region were simulated (Fig. 2). Regions of activation had a diameter between 25 and 30 mm and were located in the right hemisphere. For the high-density DOT study, regions of activation were flipped to the left hemisphere and vertically centered with respect to the HD grid (see Fig. 5(a)–5(c)). The distances between the sagittal sinus and the center of regions A, B and C were 10, 20 and 30 mm, respectively. All activations were located at a depth between 15 and 17 mm from the skin.

Fig. 2.

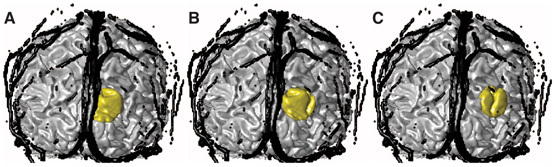
3D coronal view of the anatomical head model including the extra-cerebral vasculature (black), gray matter (GM) and the region of activation (gold). The distance between the midline and the center of regions A, B and C were 10, 20 and 30 mm, respectively.

Fig. 5.

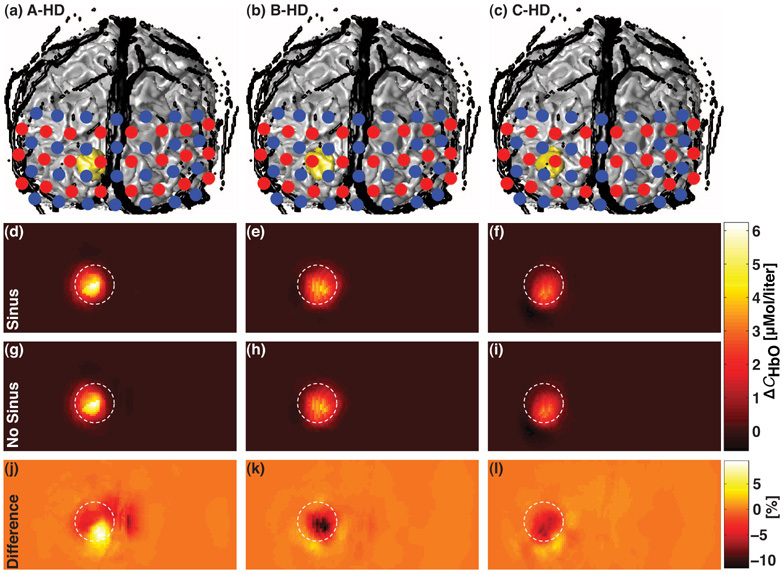
(a)–(c) 3D coronal views of the anatomical head model including the extra-cerebral vasculature (in black) and the regions of activation A, B and C (in gold) superimposed with the HD grid. Sources and detectors are represented by red and blue dots, respectively. A true change ΔC_HbO = 9µMol/ℓ was simulated in the region of activation. (d)–(f) Corresponding recovered changes in oxyhemoglobin concentration ΔC^Sinus_HbO estimated with the model including the extra-cerebral vasculature (Sinus). (g)–(i) Corresponding recovered ΔC^NoSinus_HbO estimated when the vasculature was not modeled (No Sinus). (j)–(l) Corresponding normalized differences in percentage between ΔC_HbO reconstructed from the two anatomical models. All images were posterior coronal projections of a cortical shell of 1 cm of thickness and represent the field of view of the HD grid when removing the scalp and the skull [13]. The white dashed circle superimposed on each 9 reconstruction maps indicated the diameter of the region of activation.

Regions of activation were set in both gray and white matters voxels [21]. Assuming that [HbO] increases by 9 µMol/ℓ and [HbR] decreases by 3 µMol/ℓ during cerebral activity [31], changes in the absorption coefficient Δμ^λ_a were computed using Eq. (1) leading to Δμ⁶⁹⁰_a = −0.00062 and Δμ⁸³⁰_a = 0.00155 mm⁻¹ for 690 and 830 nm, respectively. The hemoglobin content in the vasculature was assumed to remain constant during cerebral activity.

2.6. Monte Carlo simulations

Light propagation modeling can be accurately achieved by the use of the radiative transport equation (RTE) and numerically implemented via probabilistic MC methods [32]. Photon propagation can also be modeled by the so-called diffusion equation being the first approximation (DA) of the RTE [33], which is inaccurate in non- or low-scattering regions as the cerebrospinal fluid and in the vicinity of the light source. Because of these limitations, several approaches were developed, including the hybrid radiosity diffusion finite element model [34] and a coupled RTE-DA approximation model [35]. In this study, the Monte Carlo framework was selected to provide quantitative synthetic measurements. Propagation rules and code were adapted from [32]. All simulations were performed at a zero modulation frequency for both 690 and 830 nm. Photon fluences were computed for two specific states: activation and baseline. Fluence during activation state was evaluated with respect to an absorption perturbation Δμ^λ_a defined in the region of activation while baseline fluence was computed using homogeneous optical absorption coefficients described in Table 1. Photon propagations were all simulated with 100 millions photon packets.

2.7. Synthetic measurements and recovery of changes in hemoglobin concentration

The Beer-Lambert law [18, 36] is used to describe the exponential attenuation of light in tissue for a specific wavelength λ. It is expressed as

$$\frac{\mathrm{\Phi }}{{\mathrm{\Phi }}_0}=\exp (-{\mu }_a^{\lambda }{\mathrm{DPL}}^{\lambda })$$ (2)

where Φ and Φ₀ are the detected and initial light intensities, respectively, and DPL is the differential pathlength [17, 18]. The MC method allowed tracking each photon in each tissue type providing quantitative and accurate DPL computations. Using the modified Beer-Lambert law [37], the change in optical density ΔOD between the baseline (B) and the activated (A) state at a specific wavelength λ is related to the change in absorption Δμ^λ_a through the equation

$$\mathrm{\Delta }{\mathrm{OD}}^{\lambda }=-\ln \left(\frac{{\left[\frac{\mathrm{\Phi }}{{\mathrm{\Phi }}_0}\right]}_{\mathrm{A}}}{{\left[\frac{\mathrm{\Phi }}{{\mathrm{\Phi }}_0}\right]}_{\mathrm{B}}}\right)=\mathrm{\Delta }{\mu }_a^{\lambda }{\mathrm{DPL}}_{\mathrm{B}}^{\lambda }.$$ (3)

In the following, the subscript “Sinus” will refer to a quantity obtained from the model containing the extra-cerebral vasculature while “NoSinus” will design a quantity obtained from the second model in which the vasculature is not described. For each wavelength, a synthetic measurement ΔOD^λ_Sinus (Eq. (3)) was first generated from the quantities [Φ/Φ₀]_A,Sinus and [Φ/Φ₀]_B,Sinus simulated with the model including the extra-cerebral vasculature (both from Eq. (2)). (Note: here, the subscript “Sinus” simply emphasizes the fact that the synthetic measurement is generated from the model including the extra-cerebral vasculature. There is no ΔOD^λ_NoSinus quantity.)

For each wavelength, change in absorption coefficient Δμ^λ_a was then recovered using three different baseline optical pathlengths: (1) the partial pathlength (PPL) of detected light only within the brain (gray and white matters) [21] with the model including the vasculature (Sinus-PPL), (2) the partial pathlength (PPL) of detected light only within the brain with the model in which the vasculature was not described (NoSinus-PPL), and (3) the total differential pathlength (DPL) of detected light within all the tissues with the model with no vasculature (NoSinus-DPL). These three quantities were then used to recover changes in absorption such that

$${\mathrm{\Delta }}_{a,\mathrm{Sinus-PPL}}^{\lambda }=\frac{\mathrm{\Delta }{\mathrm{OD}}_{\mathrm{Sinus}}^{\lambda }}{{\mathrm{PPL}}_{\mathrm{B},\mathrm{Sinus}}^{\lambda }},$$ (4)

and

$$\mathrm{\Delta }{\mu }_{a,\mathrm{NoSinus}-\mathrm{PPL}}^{\lambda }=\frac{\mathrm{\Delta }{\mathrm{OD}}_{\mathrm{Sinus}}^{\lambda }}{{\mathrm{PPL}}_{\mathrm{B},\mathrm{NoSinus}}^{\lambda }},\mathrm{and}\mathrm{\Delta }{\mu }_{a,\mathrm{NoSinus}-\mathrm{DPL}}^{\lambda }=\frac{\mathrm{\Delta }{\mathrm{OD}}_{\mathrm{Sinus}}^{\lambda }}{{\mathrm{DPL}}_{\mathrm{B},\mathrm{NoSinus}}^{\lambda }}.$$ (5)

The optical pathlengths were computed as weighted averages with all detected photons. The weights were computed by summing the intensity of each individual photon at the detector and took into account the absorption coefficient in each tissue. Changes in absorption from Eq. (4) and Eq. (5) were then converted in changes in hemoglobin concentration ΔC_HbO and ΔC_HbR using Eq. (1) for λ = [690,830].

Here, the PPL was computed only within the brain as opposed to the traditional definition in which the pathlength is evaluated only within a given region of activation [38]. The rationale for this consideration is justified by the fact that in functional NIRS study, the spatial location of this focal “region of activation” is generally unknown. Thus, the PPL computed only within the brain is reflecting a more realistic approximation when no a priori information such as simultaneous fMRI activation map is available to provide localization of the activated area.

2.8. Spatial reconstruction of changes in hemoglobin concentration

High-density diffuse optical tomography combines multiple measurements collected at multiple source-detector separations in order to improve the localization and the quantification of cerebral activity. A high-density grid similar to that of [30] was simulated to investigate the effect of the extra-cerebral vasculature in a diffuse optical tomography application. The HD grid yielded a total of 212 first- and second-nearest neighbor measurements (Fig. 1). The corresponding source-detector distances were 13 and 30 mm [13, 30].

Light propagation was modeled for the two anatomical head models using the same Monte Carlo approach described in section 2.6. Sensitivity matrices of each measurement was truncated at 60 dB of magnitude signal loss [13, 32]. A randomly distributed Gaussian noise was added to the generated measurements. The variance was selected from an in vivo experiment involving the occipital lobe [39] and the noise to signal ratio was set to 0.15% [40]. All measurements were linearly regressed by removing a global signal contribution due to the first-nearest neighbor measurements [30]. Resulting measurements were then used for reconstruction.

Spatial reconstruction of change in absorption coefficient was carried out using a Moore-Penrose regularization approach [41]. The inverse problem consisted of estimating the vector of change in absorption Δμ_a = [Δμ⁶⁹⁰_a, Δμ⁸³⁰_a]^T assuming the knowledge of the light sensitivity matrix M and the vector of measurements y = [y₆₉₀, y₈₃₀]^T for wavelength λ = [690,830], such that

$$M\mathrm{\Delta }{\mu }_a=y\mathrm{with}M=[M_{690},M_{830}]\mathrm{and}{M}_{\lambda }=\underset{i=1}{\overset{N_{\mathrm{mea}}}{\mathrm{\Sigma }}}\underset{j=1}{\overset{N_{\mathrm{vox}}}{\mathrm{\Sigma }}}{\mathrm{\Phi }}_0(r_{s,i},r_j,\lambda ){\mathrm{\Phi }}_0(r_j,r_{d,i},\lambda )$$ (6)

where r_s,i and r_d,i are the source and detector positions, respectively. This formulation was possible by the use of the Rytov approximation [33]. The problem is typically ill-posed because the number of measurements N_mea is much less than the number of estimates (number of voxels N_vox). The Moore-Penrose approach helps inverting M from Eq. (6) by writing the solution such that

$$\Delta {\mu }_a=\underset{P}{\underbrace{M^T{(M{M}^T+\gamma I)}^{-1}}}\Delta y\mathrm{with}I=\frac{1}{\sqrt{\mathrm{diag}\left(M{M}^T\right)+\beta }}$$ (7)

where Δy was the difference between activated and baseline measurements, and γ = 10⁻⁵ and β = 10⁻² were regularization parameters [40]. The Moore-Penrose inverse matrix was defined by the variable P from Eq. (7).

A realistic measurement Δy_Sinus was simulated with the model including the vasculature (Sinus) and the vector Δμ_a from Eq. (7) was then recovered using the two head model inverse matrices (Sinus and NoSinus), i.e.

$$\mathrm{\Delta }{\mu }_{a,\mathrm{Sinus}}=P_{\mathrm{Sinus}}\mathrm{\Delta }{y}_{\mathrm{Sinus}}\mathrm{and}\mathrm{\Delta }{\mu }_{a,\mathrm{NoSinus}}=P_{\mathrm{NoSinus}}\mathrm{\Delta }{y}_{\mathrm{Sinus}}.$$ (8)

Changes in absorption from Eq. (8) were then converted in changes in hemoglobin concentration ΔC_HbO and ΔC_HbR using Eq. (1) for λ = [690,830]. All reconstruction images were created in a 2mm³ resolution [13] and re-interpolated in the original volume (1mm³). Images consisted of posterior coronal projections of a particular cortical shell of 1 cm of thickness, where the scalp and the skull have been removed [13]. The final images were restricted in the sagittal and axial planes to correspond with the field of view of the HD grid.

The reconstruction images recovered with and without extra-cerebral vasculature were compared and the absolute difference between the two images was also computed. An image representing this difference in percentage was generated by normalizing the initial absolute difference image by a constant. This constant was given by the difference between averaged values of voxels located inside and outside the region of activation. These voxels were extracted from the image reconstructed from the model including the extra-cerebral vasculature.

3. Results

Recovered values for ΔC_HbO are illustrated in Fig. 3 for different positions of the optical array and in Fig. 4 for different positions of the region of activation. In both figures, panel (a)–(d) shows 3D coronal views of the anatomical head model including the extra-cerebral vasculature (in black) and the region of activation (in gold) superimposed with the optical arrays. Sources and detectors are represented by red and blue dots, respectively. The corresponding recovered changes in oxyhemoglobin concentration ΔC_HbO are illustrated in bar graphs in histograms (e) and (f) for source-detector distances of 30 and 45 mm, respectively. The results are shown for the three recovery procedures: (1) using the anatomical model including the extra-cerebral vasculature (cyan: Sinus-PPL), (2) using the anatomical model where the extra-cerebral vasculature was not modeled and based on brain partial pathlengths (yellow: NoSinus-PPL), and (3) with total differential pathlength (dark red: NoSinus-DPL). The corresponding correction factors computed as the ratio between the true and recovered hemoglobin changes are listed in Table 2. Recovered values for ΔC_HbR were similar and are not shown.

Fig. 3.

(a)–(d) 3D coronal views of the anatomical head model including the extra-cerebral vasculature (in black) and the region of activation A (in gold) superimposed with optical arrays 1, 2, 3 and V, respectively. Sources and detectors are represented by red and blue dots, respectively. (e)–(f) Corresponding recovered changes in oxyhemoglobin concentration ΔC_HbO for source-detector distances of 30 and 45 mm, respectively. Four values are represented and correspond to: (blue) true change (9µMol/ℓ) simulated in the region of activation, (cyan: Sinus-PPL) change recovered using the anatomical model including the extra-cerebral vasculature and the partial pathlength, (yellow and dark red) changes recovered using the head model with no vasculature and the partial pathlength (NoSinus-PPL), and the total differential pathlength (NoSinus-DPL).

Fig. 4.

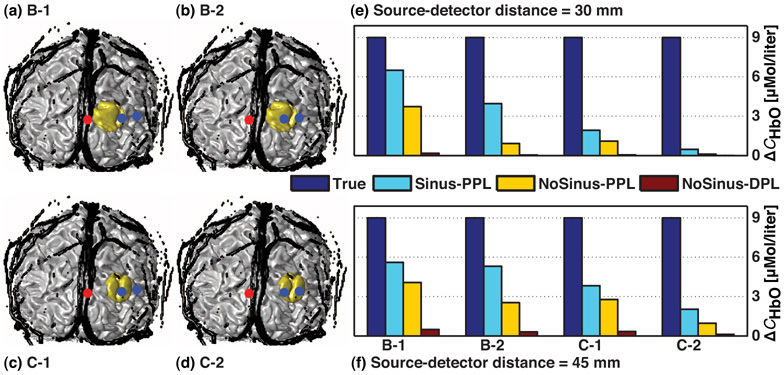
(a)–(d) 3D coronal views of the anatomical head model including the extra-cerebral vasculature (in black) and the regions of activation B and C (in gold) superimposed with optical arrays 1 and 2, respectively. Sources and detectors are represented by red and blue dots, respectively. (e)–(f) Corresponding recovered changes in oxyhemoglobin concentration ΔC_HbO for source-detector distances of 30 and 45 mm, respectively. Four values are illustrated and correspond to: (blue) true change (9µMol/ℓ) simulated in the region of activation, (cyan: Sinus-PPL) change recovered using the head model containing the extra-cerebral vasculature and the partial pathlength, (yellow and dark red) changes recovered when the vasculature was not taken into account and using the partial pathlength (NoSinus-PPL), and the total differential pathlength (NoSinus-DPL).

Table 2. Correction factors [no unit] for ΔC_HbO computed by the ratio between the true and the recovered change.

Config.	Sinus-PPL		NoSinus-PPL		NoSinus-DPL
	30 mm	45 mm	30 mm	45 mm	30 mm	45 mm
A-1	1.3	2.1	2.2	2.9	46.9	23.5
A-2	1.5	1.6	6.4	3.2	123.4	26.5
A-3	6.2	2.2	29.5	4.5	576.2	38.5
A-V	3.7	2.5	3.9	3.0	49.7	21.4
B-1	1.4	1.6	2.4	2.2	51.5	18.1
B-2	2.3	1.7	9.7	3.5	186.1	29.0
C-1	4.7	2.3	8.1	3.2	173.5	26.7
C-2	19.1	4.4	81.8	9.3	1567.4	75.6

Hemoglobin concentration changes recovered with the model including the extra-cerebral vasculature (Sinus-PPL) at 30 mm varied between 21 and 81% of the true value (9µMol/ℓ), which corresponded to correction factors starting at 4.7 and decreasing to 1.3, respectively. In simulation A-3 (Fig. 3(c)), where the optical array entirely overlapped the sagittal sinus, and C-2 (Fig. 4(d)), where the region of activation was located at 30 mm from the midline, the correction factors were higher (6.2 and 19.1, respectively). The concentration changes recovered with the model including the vasculature (Sinus-PPL) at 45 mm were all between 23 and 64% of the simulated change, which corresponded to correction factors ranging from 4.4 and decreasing to 1.6, respectively.

The concentration changes recovered with no vasculature and using partial pathlength (NoSinus-PPL) were lower and reached not more than between 1 and 45% of the true change for 30 and 45 mm, respectively. The correction factors for source-detector distance of 30 mm ranged from 2.2 to 9.7 while 2.2 to 3.5 for 45 mm (excluding A-3 and C-2). The correction factors obtained with no vasculature and using total differential pathlength (NoSinus-DPL) were markedly higher and are listed in Table 2. When considering the extra-cerebral vasculature in the head model, the correction factors were at least 1.4-fold lower than the values computed with no vasculature (except for A-V: at least 1.1-fold). In the absence of the extra-cerebral vasculature, the correction factors computed using partial pathlength (NoSinus-PPL) were at least 7-fold lower than the values computed with total differential pathlength (NoSinus-DPL).

Baseline brain partial (PPL) and total differential (DPL) pathlengths [mm] of all cases presented in Fig. 3 and Fig. 4 are compiled in Table 3 for both wavelengths of 690 and 830 nm as well as for both head models (Sinus and NoSinus). For the head model including the vasculature (Sinus), PPL vary from 1.6 to 30.5 mm. Case A-V presents higher pathlength values since the optical arrays is positioned parallel to the sagittal sinus (vertical position). When the extra-cerebral vasculature is not described, PPL vary from 6.8 to 35.8 mm while total DPL from 146.2 to 282.5 mm. Pathlengths have higher values in this configuration (NoSinus) because of the absence of the vasculature. Baseline pathlengths from cases B-1 and C-1 are identical to that of case A-1 while cases B-2 and C-2 to case A-2 because of the identical optical arrays used to propagate light at 690 and 830 nm.

Table 3. Baseline Brain partial (PPL) and total differential (DPL) pathlengths [mm].

		Sinus				NoSinus
		690 nm		830 nm		690 nm		830 nm
		30 mm	45 mm	30 mm	45 mm	30 mm	45 mm	30 mm	45 mm
A-1	PPL	4.7	22.2	3.9	22.0	8.7	35.2	6.8	29.7
	DPL	-	-	-	-	176.9	282.5	146.3	245.2
A-2	PPL	2.3	17.6	1.9	13.7	10.9	33.2	7.9	29.1
	DPL	-	-	-	-	187.8	278.5	153.6	236.9
A-3	PPL	1.8	15.0	1.6	12.6	10.1	29.3	7.6	26.0
	DPL	-	-	-	-	181.8	262.8	149.0	221.5
A-V	PPL	13.4	30.5	10.9	27.2	14.2	35.8	11.3	32.9
	DPL	-	-	-	-	176.2	264.5	146.2	231.1

Table 4 shows correction factors computed when considering the partial pathlength with detected photons having traveled only in the given region of activation (Fig. 2), i.e. where the change in absorption was introduced [21, 38], as opposed to brain PPL used to calculate correction factors from Table 2. Correction factors are presented for the four cases of Fig. 3 in which the traditional partial pathlength, noted “tPPL” for the purpose of this study, was considered. As expected, the recovery is much more accurate for the two head models, especially for the model including the extra-cerebral vasculature in which values almost reach the true value of 9µMol/ℓ. Correction factors are close to 1 for the Sinus model while higher for the head model without vasculature. Case A-V shows the lower values (1.11 and 1.34 for 30 and 45 mm, respectively).

Table 4. Correction factors [no unit] when recovering ΔC_HbO with traditional partial pathlength (tPPL) of detected photons within only the given region of activation for cases described in Fig. 3; Cases from Fig. 4 yield similar results.

Config.	A-1		A-2		A-3		A-V
	30 mm	45 mm	30 mm	45 mm	30 mm	45 mm	30 mm	45 mm
Sinus	1.02	1.02	1.02	1.02	1.02	1.03	1.02	1.02
NoSinus	1.64	1.48	3.92	1.92	9.55	2.12	1.11	1.34

Results of the simulations with the HD grid are illustrated in Fig. 5. Panel (a)–(c) depicts 3D coronal views of the anatomical head model including the extra-cerebral vasculature (in black) and the regions of activation (in gold) superimposed with the HD grid. The sources and the detectors are represented by red and blue dots, respectively. The recovered changes in hemoglobin ΔC^Sinus_HbO estimated with the model including the extra-cerebral vasculature (Sinus) are illustrated in panel (d)–(f) for different activation regions. Panel (g)–(i) shows corresponding recovered ΔC^NoSinus_HbO estimated when the vasculature was not taken into account (No Sinus). Finally, panel (j)–(l) shows corresponding normalized differences (in percentage) between reconstructed ΔC_HbO from the two anatomical models. The white dashed circle superimposed on each 9 sub-figures was drawn to indicate the diameter of the region of activation. Both anatomical head models shown similar reconstruction maps of ΔC_HbO varying from 0 to 6µMol/ℓ while a change of 9µMol/ℓ was simulated. Both methods were able to reconstruct the change in hemoglobin concentration with a good spatial accuracy. The difference between the two reconstructions was less than 10% and decreased as the distance between the simulated activation and the midline increased (panel (j)–(l)).

4. Discussion

4.1. Vasculature model improves the recovery

Figure 3 and Fig. 4 together with Table 2 and Table 4 illustrate the benefit of recovering changes in hemoglobin concentration with the model including the extra-cerebral vasculature (Sinus-PPL). The values recovered with this model were closer to the true value of 9µMol/ℓ than with the model in which the extra-cerebral vasculature was not described (NoSinus-PPL). The correction factors that quantify the accuracy of the recovery were at least 1.4 times lower when using the model describing the vasculature (except for A-V: at least 1.1-fold). This result indicates the necessity of taking into account the extra-cerebral vasculature to compute the partial pathlength of the photons in brain tissues. The blood contained in the vasculature absorbs an important quantity of the light emitted by the laser source. Modeling the vasculature helps to prevent considerable biases in the partial pathlength calculation.

When using the model with no vasculature, the hemoglobin concentration changes recovered using partial pathlength (NoSinus-PPL) were closer to the true value than using the total differential pathlength (NoSinus-DPL). The correction factors obtained were at least 6 times lower when using partial pathlength computation. This improvement confirms the use of partial pathlength to separate the contribution from the superficial tissues [42, 43].

4.2. Error reduced using the high-density approach

Increasing the number of sources and detectors leads to an increase in the number of measurements and the possibility to use a multi-distance approach to distinguish superficial and cortex responses. The high-density tomography approach generally allows for a higher spatial resolution and a better quantification of change in hemoglobin concentration than the traditional single source-detector separation method. In this study, the use of a high-density grid to recover changes in hemoglobin concentration was beneficial for reducing the partial volume error. This improvement was clearly shown when comparing ΔC_HbO estimated with the Beer-Lambert law from Fig. 3 and Fig. 4, and with the high-density spatial reconstruction shown in Fig. 5(d)–5(i). Nevertheless, the effect of the extra-cerebral vasculature was still visible but reconstruction maps computed from the two head models differed by less than 10% (Fig. 5 (j)–(l)). For all reconstructions, the use of the linear regression from short separations [30] produced similar benefits of computing partial pathlength [38] in the quantification of ΔC_HbO from the Beer-Lambert law. Both methods helped improving the recovery by isolating the signal originated from the cortex.

4.3. Lateral vs. vertical array configuration

Positioning the optical array parallel to the sagittal sinus at a distance of 2 cm [10] helped to recover hemoglobin concentrations and appears to be sufficient to avoid the major effect of the sagittal sinus. In this case, correction factors computed when the vasculature was not taken into account (NoSinus-PPL) were similar to those computed when considering the extra-cerebral vasculature in the head model (Sinus-PPL).

4.4. Brain vs. traditional PPL

In this study, we computed the baseline partial pathlength with detected light within the brain as opposed to the traditional calculation [21, 38] in which only the region of activation is considered. The motivation behind this approach was justified by the fact that in the majority of functional NIRS studies, the spatial description of the region of activation is unknown. Recovering hemoglobin concentrations with brain PPL represents a good compromise between traditional PPL and total DPL computations and offers realistic correction factors. In addition, total DPL evaluated from the head model in which the vasculature was not described provide similar values than published work from literature such as [44].

4.5. Effect of the activation region location

The recovered hemoglobin concentration decreased as the distance between the source and the region of activation increased. This trend was shown in Fig. 4 when comparing cases B-1 and C-1, and B-2 and C-2, respectively. In both comparisons, changes in hemoglobin concentration were lower when the region of activation was moved from 20 to 30 mm from the midline. This decrease was due to a lower sensitivity to the change in the absorption coefficient as the region of activation was moved away from the source.

4.6. Limitations and future studies

The study was conducted in the occipital lobe because of the size of the sagittal sinus and the recent use of a high-density diffuse optical tomography approach in the visual cortex [13,14,30,45,46]. The quantification of the effect of the extra-cerebral vasculature would be reproducible in other cortical areas in which this vasculature is present. However, as the optical probe is moved toward the forehead, the extent of this effect would probably be lower because the size of the sagittal sinus decreases as it passes from posterior to anterior regions.

It is also important to precise that the pathlengths and recovered hemoglobin changes provided by this study are only valid for this particular anatomical structure and for the set of optical properties given in Table 1, as well as for the optical arrays used to simulate light propagation. Indeed, any changes in these parameters will modify the light distribution and then the detected optical fluences. However, for the same set of parameters described in this study, we think that correction factors would be similar from another adult head structure but should not be used for correcting neonatal or pediatric measurements. The physiology and the composition of the developing brain as well as the size and shape of the infant's head will affect considerably the measurements, e.g. the effect produced by the curvature of the head.

In this study, we assumed that oxygen saturation in the sagittal sinus remained constant during cerebral activity. The simulations demonstrated the screening effect due to the additional amount of light blocked by the sagittal sinus during diffuse optical imaging. However, past works have studied the influence, mainly from fMRI measurements, of a change in oxygen saturation in the sinus during cerebral activity. Blood oxygen level dependent (BOLD) signal used in fMRI to image contrast response to a cognitive task is mainly due to paramagnetic properties of [HbR]. For this reason, the potential problem of BOLD signal alterations in the visual cortex produced by the proximity of the sagittal sinus has been investigated [47]. For instance, Boxerman and colleagues [48] developed a method to quantify BOLD contrast from extra-vascular contributions using a MC model to improve mapping of neuronal activity. Other studies have contributed using various fMRI techniques to reduce large vein effects [49, 50].

In [51], the authors demonstrated more elevated or shifted [HbR] and [HbO] contrasts in the vicinity of the sagittal sinus using DOT during electrical stimulations of the rat somatosensory cortex. In particular, these observations suggested that oxygen saturation changes occur in the sagittal sinus during cerebral activity while the volume remains constant. This phenomenon would produce a small additional variation in blood volume [HbT] but significant additional ΔC_HbO and ΔC_HbR due to the sagittal sinus. This phenomenon is well-known and named the washout effect of deoxyhemoglobin and could be studied in future works with biomechanical modeling of the neurovascular coupling [19,52,53] by introducing a compartment representing the sagittal sinus. In order to simulate the washout of [HbR] in the sinuses, blood volume would remain constant while oxygen saturation would be free to experiment a variation in the extra-cerebral compartment. In particular, a recent study [54] shown that a major componet of the low frequency oscillations detected by both DOI and fMRI arises from the propagation of endogenous global blood flow and oxygenation fluctuations through the cerebral vasculature, rather than from local variations in neuronal activation (i.e. not related to the task or resting state connectivity) or localized cerebral blood flow changes. The need of methods for quantifying the signal contribution from extra-cerebral tissues is still justified [23, 43].

5. Conclusion

In this study, we investigated the effect of the extra-cerebral vasculature on DOI measurements. The results shown that the sagittal sinus influenced the recovery of changes in hemoglobin concentration. We tested several realistic optical configurations in which the effect of the sagittal sinus was quantified. We demonstrated that modeling the extra-cerebral vasculature in the recovery procedure reduced the partial volume error by at least a factor of 1.4. The effect of the extra-cerebral vasculature was also investigated in the context of a high-density diffuse optical tomography. In this case, the effect of the vasculature was lower and the difference between the two head models was less than 10% confirming the ability of HD tomography procedure to remove the signal contribution originated from superficial tissues.