Influence of non-Newtonian Properties of Blood on the Wall Shear Stress in Human Atherosclerotic Right Coronary Arteries

Abstract

The objective of this work is to investigate the effect of non-Newtonian properties of blood on the wall shear stress (WSS) in atherosclerotic coronary arteries using both Newtonian and non-Newtonian models. Numerical simulations were performed to examine how the spatial and temporal WSS distributions are influenced by the stenosis size, blood viscosity, and flow rate. The computational results demonstrated that blood viscosity properties had considerable effect on the magnitude of the WSS, especially where disturbed flow was observed. The WSS distribution is highly non-uniform both temporally and spatially, especially in the stenotic region. The maximum WSS occurred at the proximal side of the stenosis, near the outer wall in the curved artery with no stenosis. The lumen area near the inner wall distal to the stenosis region experienced a lower WSS during the entire cardiac cycle. Among the factors of stenosis size, blood viscosity, and flow rate, the size of the stenosis has the most significant effect on the spatial and temporal WSS distributions qualitatively and quantitatively.

1 Introduction

Atherosclerosis is a disease of large- and medium-size arteries. There are various systemic risk factors involved in atherogenesis, such as environmental, genetic, biologic, and biomechanical factors. Atherosclerotic lesions preferentially develop in certain regions like bifurcations, branches, and bends. A possible explanation for such a preferential localization of atherosclerosis is that the geometry of the vessel influences the blood flow pattern [1], which suggests that biomechanical factors, such as blood pressure, flow velocity, wall shear stress, blood viscosity, etc. may be responsible for the initiation and progression of atherosclerosis [2]. It is now well established that the WSS plays a significant role in the endothelial homeostasis and the focal distribution of atherosclerotic lesions. The WSS is one of the most decisive factors, among the local biomechanical factors [3–7]. A detailed hemodynamic evaluation of disturbed flow and the spatial and temporal WSS distributions may give additional insight to understanding the progression of atherosclerosis and may have useful clinical value, such as early detection of a highly stenosed artery segment, prediction of future disease progression, and treatment planning [8].

During the last two decades, many research studies, including clinical observations, in vitro experiments, and numerical simulations, have been conducted to study the WSS distribution pattern and to investigate the correlation between the WSS and the localization of lesions and the intima-media thickness [3–7, 9–13]. Some efforts have also been made to quantify the correlation and to simulate the growth of the atherosclerotic plaque using the equations obtained from quantitative angiography studies [14, 15]. Friedman et al. [4] and Nerem et al. [10] have performed experiments that showed an accelerated occurrence of atherosclerosis in human subjects. Ku et al. [7] and Zarins et al. [13] have estimated shear stress with laser-Doppler anemometry and found that the intimal thickening bears an inverse relationship to both the maximum shear stress and the minimum shear stress. Gibson et al. [9] investigated the relation between vessel wall shear stress and the rate of atherosclerosis progression by means of quantitative angiography. Their results showed that there was a significant correlation between the low shear stress and an increased rate of atherosclerosis progression. Tang et al. [15] investigated the correlation between the human carotid atherosclerotic plaque progression with the plaque wall stress and the fluid shear stress based on in vivo patient tracking MRI data. They found that the wall thickness increase correlates negatively with the flow wall shear stress calculated from the previous observation time and positively with the flow wall shear stress calculated from the current observation time (time interval: 18 months). In their computational analysis on blood flow in a left coronary artery, He and Ku [16] concluded that the low and oscillatory WSS correlates strongly with the localization of atherosclerosis. Soulis et al. [17] conducted similar studies and found that the lateral walls of the bifurcation are more susceptible to atherosclerosis and the systolic period, rather than the diastolic one, favors the development and progression of atherosclerosis. Krams [6] and Van Langenhove et al. [18] used angiographically-guided intravascular ultrasound and computational fluid dynamics to reconstruct the local haemodynamics in a coronary artery, and an inverse relationship between the shear stress and the wall thickness was demonstrated. Nosovitsky et al. [11] studied the Newtonian flow in a coronary artery model of several degrees of stenosis-like obstruction, where the artery was occluded from all surfaces for higher degree of stenosis. Their results showed that coronary artery curvature exerts an important impact on the intraluminal flow and shear stress in the presence or absence of a luminal obstruction. They also concluded that at higher stenoses laminar flow separation occurs and the inner wall is exposed to shear stresses that vary widely, both temporally and specially.

Many numerical investigations have been conducted on examining the non-Newtonian effect on the pattern and distribution of the blood flow in a variety of human arteries, mostly focused on bifurcations, branches and grafts [8, 17, 19, 20], and some on right coronary arteries and curved tubes [21, 22], but a few on stenotic right coronary arteries [23]. Some studies found non-Newtonian rheology important [21, 23], while others suggested that under normal physiological conditions, the non-Newtonian effect may not be significant [19, 22, 24, 25]. Yang and Tang [26] studied the effects of model difference, including the comparisons of Newtonian with non-Newtonian and FSI with wall-only/fluid-only models, on the computational predictions for flow and stress/strain behaviors. Perktold et al. [24] investigated the effect of non-Newtonian viscosity on the blood flow in a bifurcation with an aneurysm. They found that there was no essential difference between the Newtonian and non-Newtonian simulations under the normal physiological conditions. Johnston et al. [22] compared the effects of different blood viscosity models on the wall shear stress distributions in healthy right coronary arteries during the cardiac cycle. Their study showed that the use of a Newtonian blood model is a reasonably good approximation when studying the wall shear stress distribution for transient blood flow in large arteries. After studying non-Newtonian blood flow in an end-to-side anastomosis, Ballyk et al. [19] pointed that non-Newtonian blood rheology has a significant effect on the steady flow wall shear stress, but no significant effect on the unsteady flow wall shear stress.

The purpose of the present paper is to examine the effect of non-Newtonian blood property, stenosis size and flow rate on spatial and temporal WSS distribution during the cardiac cycle in a stenotic right coronary artery. The remainder of this paper is organized as follows: Section 2 briefs the mathematical models used, including the boundary conditions, blood properties, and parameter settings; Section 3 presents results obtained from the computer simulations; Section 4 gives the discussions on the numerical results and conclusions.

2 Mathematical models and parameter settings

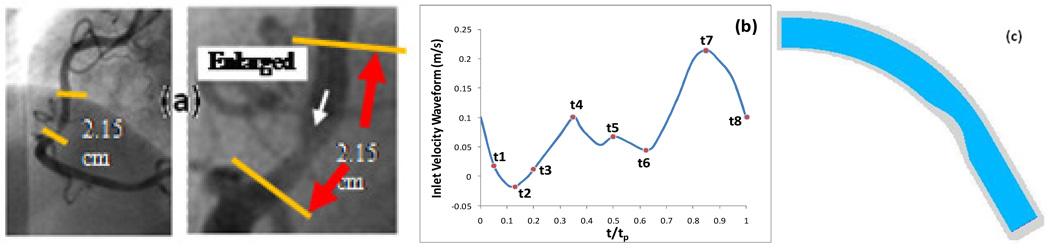
In this study, the blood flow in a right coronary artery is assumed to be laminar, incompressible and unsteady. The artery wall is treated to be inelastic and impermeable. The flow is governed by the three-dimensional Navier-Stokes equations. The computational domain is a simplified geometry [Fig. 1 (c)], re-constructed from the in vivo intravascular ultrasound (IVUS) image of a patient [27] shown in Fig. 1 (a). The radius of the cross section at the inlet boundary is 0.00145m. The area stenosis severity is 50%. The boundary conditions imposed are as follows. At the inlet boundary, a fully developed flow with a physiological human right coronary waveform [Fig. 1(b)] is prescribed:

$$u=\mathit{\text{Qf}}(\mathit{x})w(t),$$ (1)

where f has a standard parabolic profile changing between 0 and 1; Q is a scale which can be chosen as different values in the computation such that Qf(x)w(t) yields different mean flow rates; The waveform w(t) is re-produced using curve-fitting based on Fig. 4(a) in [28], consisting of a brief systolic phase and a longer diastolic phase with a small increase and a large peak in flow rate. This waveform has been widely cited in the medical literature [22, 29]. A no-slip condition is applied to the velocities at the wall boundary. The outlet boundary is treated as an open boundary, with normal derivative of the flow velocity set to zero. The initial conditions for the velocity and pressure are obtained by solving the system of steady state Navier-Stokes equations.

Fig. 1.

(a) Angiography of a human coronary plaque sample providing information for vessel geometry [27], (b) Pulsatile coronary inlet velocity waveform, (c) Geometry of the computational domain.

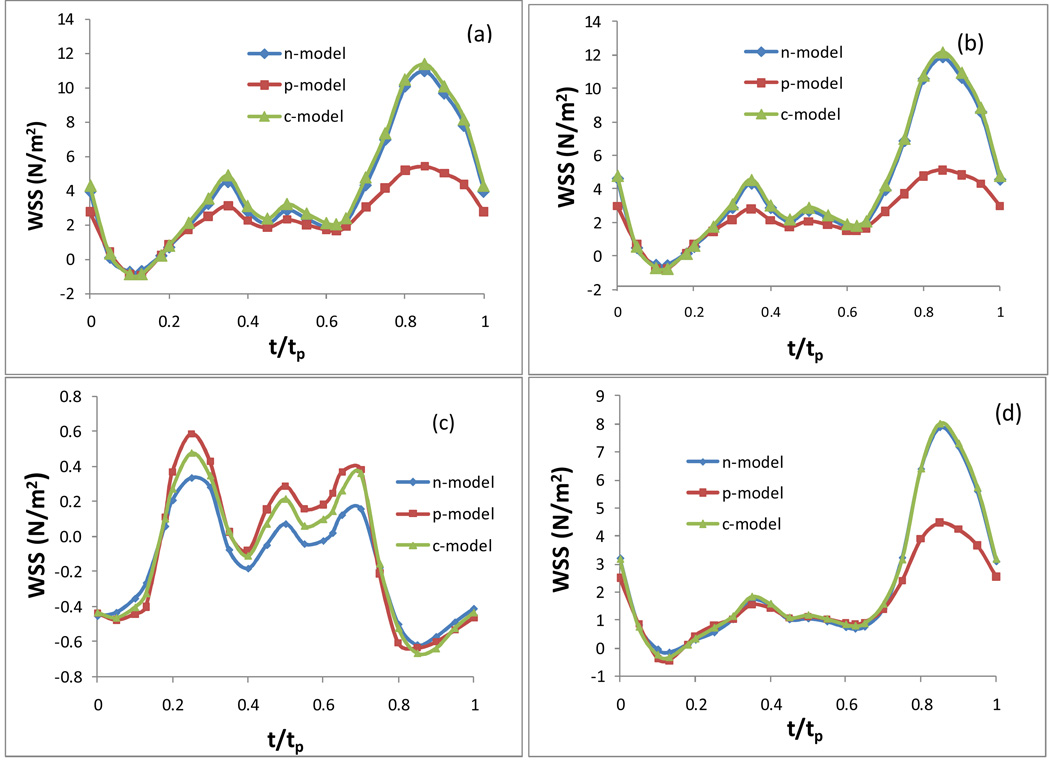
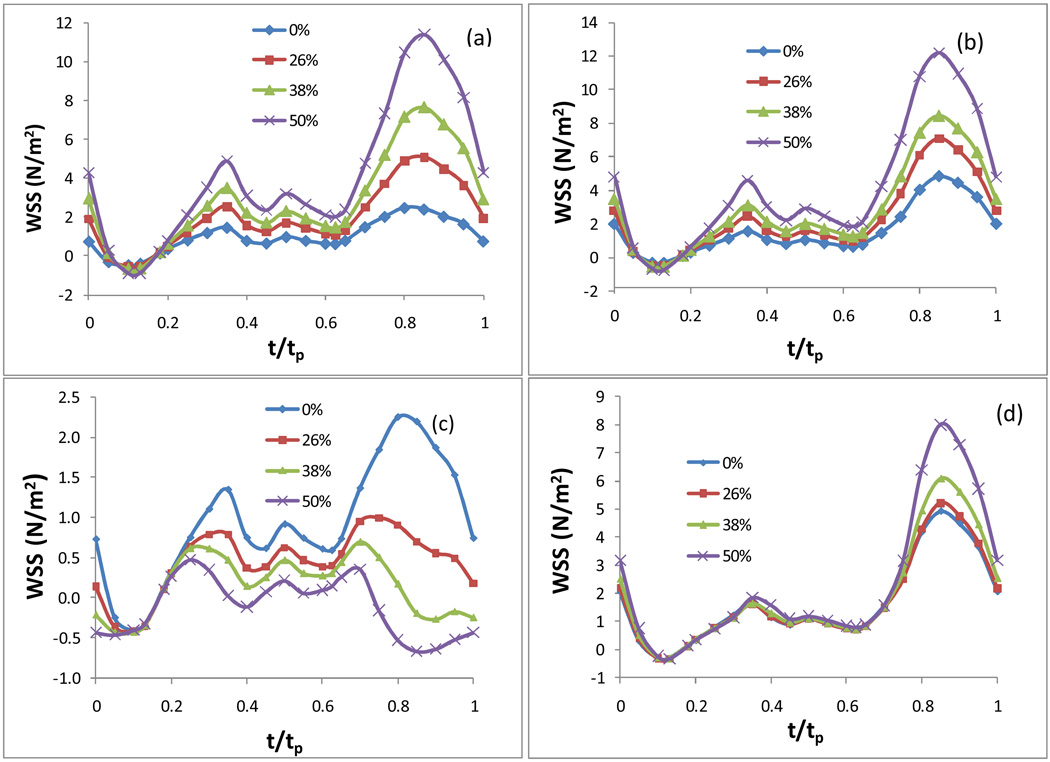
Fig. 4.

The temporal variation of the WSS in an entire cardiac cycle at various locations: a) on the inner wall at the neck of the stenosis; b) on the outer wal l at the neck of the stenosis; c) on the inner wall in the post stenosis, d) on the outer wall in the post stenosis, in an artery with 50% stenosis, Carreau model.

The blood is treated as a non-Newtonian fluid obeying the non-Newtonian Carreau model with the viscosity-shear rate relation:

$$\eta ={\eta }_{\mathrm{\infty }}+({\eta }_0-{\eta }_{\mathrm{\infty }}){[1+{(\lambda \dot{\gamma })}^2]}^{\frac{n-1}{2}},$$ (2)

where η₀ = 0.056 Pa·s is the zero shear rate viscosity, η_∞ =0.00345 Pa·s is the infinite shear rate viscosity, λ =3.313s is a parameter, and n = 0.3568 is a dimensionless parameter [20, 22, 23]. To investigate the influence of blood viscosity properties on the distribution of the WSS, computer simulations are also performed using other two models: 1) considering the blood as a Newtonian fluid with a constant viscosity 0.00345 Pa·s; 2) considering the blood as a non-Newtonian fluid obeying the Power Law with the viscosity-shear rate relation:

$$\eta ={\eta }_0{(\dot{\gamma })}^{n-1},$$ (3)

where η₀ = 0.035 Pa·s, and the Power Law index n equals to 0.6 [22, 23]. All of the three models have been commonly used to simulate blood flows in recent years. Even though many non-Newtonian models of blood rheology have been used in blood research, no one model is universally accepted.

In the computations, the blood density ρ is assumed to be constant at 1050kg/m³. When examining the effect of the inlet flow rate on the WSS, the scale Q is chosen as 1.8, 2.1, 2.4, and 2.7, respectively. When examining the effect of the blood viscosity with different models the scale Q for the inlet flow rate is fixed as 2.4, which yields a time averaged flow velocity of 0.199 m/s at the centre-line. The WSS is defined as the tangential force per unit area that is exerted by the flowing blood on the surface of the artery wall. For incompressible fluids and non-slip conditions applied at the arterial wall, the spatial wall shear stress is calculated as

$${\tau }_w=-\eta \frac{\partial u_t}{\partial n}{|}_{\mathit{\text{wall}}}$$ (4)

where η is the dynamic viscosity, u_t is the tangential to the wall velocity, and n⃑ is the outward normal unit vector at the artery wall boundary.

3 Numerical results

Computations were carried out on the blood flow simulations in coronary arteries with or without stenosis using both Newtonian and non-Newtonian models. The Navier-Stokes equations were solved with the finite element method using piecewise quadratic functions for velocity and piecewise linear functions for pressure over a tetrahedral mesh. Numerical computations were mainly performed using the Comsol software. Four consecutive cardiac cycles were simulated to ensure that the flow is truly periodic and the computations were repeated over different meshes to confirm the independence of the numerical solutions on spatial mesh. The numerical results presented here were obtained based on an unstructured finite element mesh containing about 40,000 tetrahedrons and having the number of degrees of freedom around 200,000. Computations were carried out with various values of physiological parameters to reveal the detailed local spatial and temporal distributions of the WSS in stenotic coronary arteries and to examine the influences of the flow rate, blood viscosity, and stenosis size on the WSS pattern.

3.1 Comparison of Newtonian and non Newtonian models

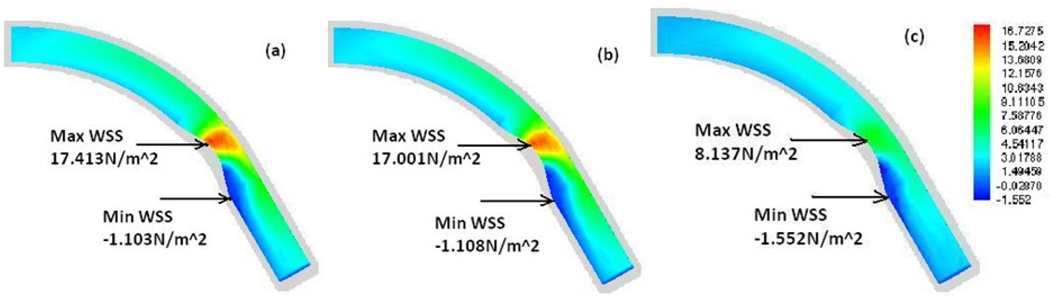
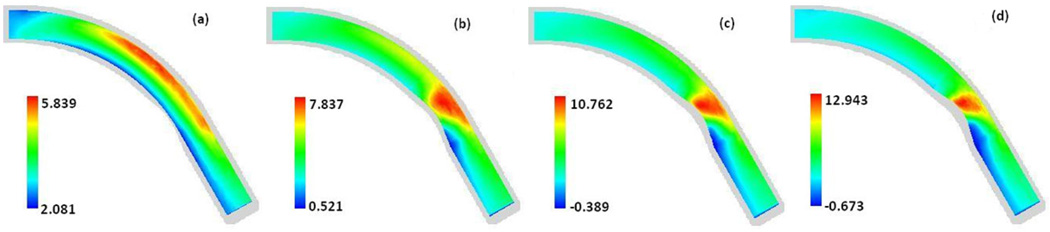
Fig. 2 presents contour plots of the WSS on the lumen surface for the baseline stenotic artery (with 50% stenosis by area) at the maximum flow rate (peak in diastole, t/t_p=0.85) based on (a) Carreau model, (b) Newtonian model, and (c) Power Law model, respectively. It shows that all three models reveal basically the same spatial pattern of the WSS: The maximum WSS occurs at a point near the inner wall at the proximal side of the stenosis and the minimum WSS occurs at the inner wall distal to the stenosis region. But the magnitude of the WSS varies between models. The maximum WSS from the Carreau and Newtonian models are almost the same; however, they are about 100% higher than that from the Power Law model.

Fig. 2.

Contour plots of the WSS (N/m²) along the wall at the maximum flow rate (t/t_p=0.85) (a) Carreau model, (b) Newtonian model, (c) Power Law model.

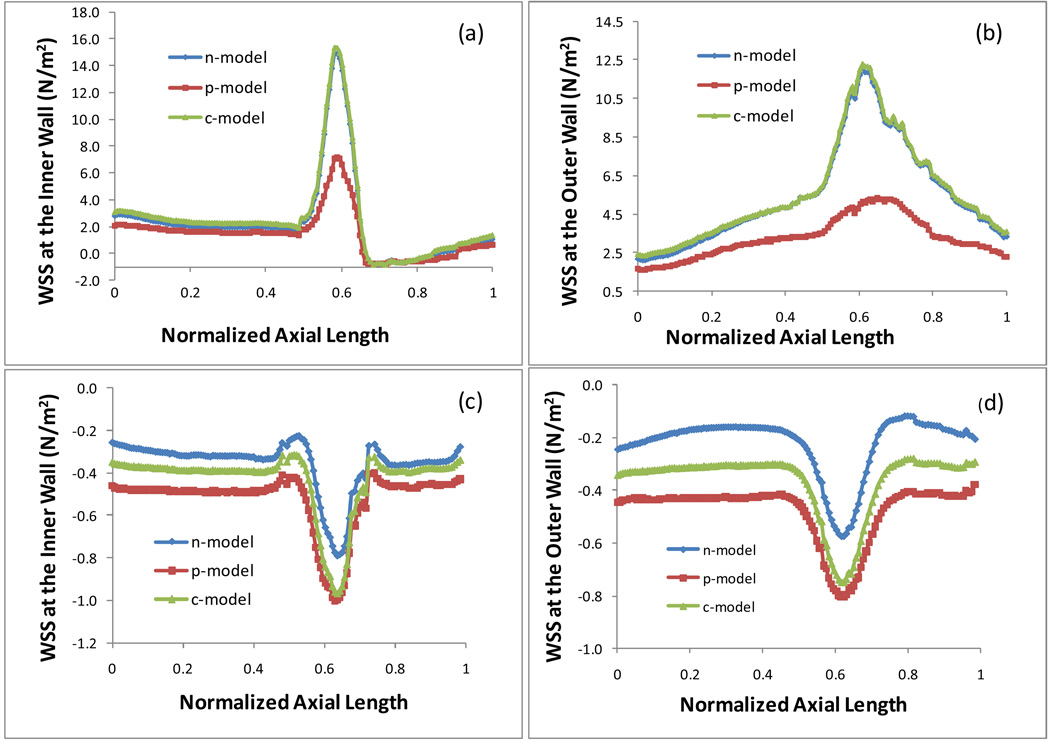
Fig. 3 plots the WSS on the inner wall and outer wall at the maximum and minimum flow rate in an artery with 50% stenosis based on the Newtonian and two non-Newtonian models. The maximum flow rate occurs at the peak in diastole when t/t_p = 0.85, labeled as t7 in Fig. 1 (b). The minimum flow rate occurs at the end of the deceleration in the systolic phase with a reverse flow when t/t_p = 0.13, labeled as t2 in Fig. 1 (b). Fig. 3 (a) and (c) present the WSS on the inner wall at the maximum and minimum flow rate, respectively; Fig. 3 (b) and (d) present the WSS on the outer wall at the maximum and minimum flow rate, respectively. Here n-, p-, c-represent the Newtonian, Power Law, and Carreau models respectively. The horizontal axis is the normalized axial length of the artery. The neck of the stenosis is at x = 0.62. The time averaged inlet flow velocity is 0.199 m/s. Fig. 4 presents the temporal variation of the WSS in an entire cardiac cycle at various locations on the artery wall: a) on the inner wall at the neck of the stenosis; b) on the outer wall at the neck of the stenosis; c) on the inner wall distal to the stenosis, d) on the outer wall distal to the stenosis, in an artery with 50% stenosis based on the three different models.

Fig. 3.

Plots of the WSS on the inner and outer wall at the maximum (t/t_p = 0.85) and minimum flow rate (t/t_p = 0.13) in an artery with 50% stenosis, (a) WSS on inner wall, max flow rate; (b) WSS on outer wall, max flow rate; (c) WSS on inner wall, min flow rate; (d) WSS on outer wall, min flow rate.

From Fig. 3 and Fig. 4 we can see that the Newtonian model and Carreau model show a good agreement quantitatively in the WSS along the inner wall and the outer wall at the maximum flow rate (t/t_p = 0.85) [see Fig. 3 (a) & (b)]. At the points on the neck of the stenosis and on the outer wall downstream, the numerical results of the WSS obtained based on the Newtonian and Carreau models are very close during the entire cardiac cycle [see Fig. 4 (a), (b) and (d)]. There is a minor difference on the WSS between Newtonian and Carreau models at the minimum flow rate (t/t_p = 0.13) along the inner and outer walls [see Fig. 3 (c) & (d)] and at the inner wall in the post stenosis during the middle of the cardiac cycle [see Fig. 4 (c)]. However, the Power Law model shows more discrepencies from the other two models. The significant difference occurs where and when the WSS is relatively high. The Power Law model results in much smaller values of the WSS than those from the other two models along the outer wall and around the neck of the stenosis on the inner wall at the maximum flow rate ((t/t_p = 0.85) [see Fig. 3 (a) & (b)]. As for the difference of the Power Law model from the other two models on the temporal variation of the WSS during the cardiac cycle, we observe the similar pattern at three points: on the inner wall and outer wall at the neck of stenosis and on the outer wall downstream [see Fig. 4 (a), (b) and (d)]. The Power Law model results in a much lower WSS at peaks, especially towards the end of the cardiac cycle (when t/t_p> 2/3).

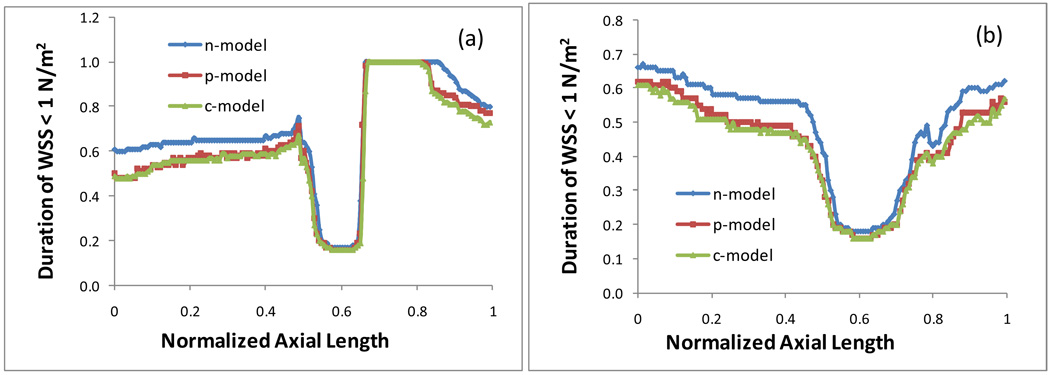
Vessel segments with low WSS or highly oscillatory WSS is believed to be at high risk for the development of atherosclerosis. Evidence from in vitro and in vivo studies suggests that intimal thickening likely occurs when the average WSS is below 1 N/m² (=10 dynes/cm²), which presents an inverse hyperlasia with respect to the shear stress [30]. Therefore, it is of special interest to know the size of the region on the surface of the artery wall where the WSS is lower than 1 N/m² and to examine the duration of the low WSS area in a cardiac cycle. At each point on the inner wall or on the outer wall, we calculated how long the location experiences a low WSS less than 1 N/m² (including the negative WSS resulted from the reverse flow or flow recirculation) in a cardiac cycle. Figure 5 plots the duration of the WSS < 1 N/m² at each point on the inner wall (a) and on the outer wall (b) in a cardiac cycle for three different blood property models. A point with a value of 1.0 on the graph indicates that the WSS at this point is lower than 1 N/m² anytime during the entire cardiac cycle. Fig. 5 shows that on both of the inner wall and the outer wall in the stenotic region and the post stenotic region all three models predict approximately the same duration of the low WSS. However, in the rest of the artery segment the Newtonian model results in a longer period of the duration of the WSS < 1 N/m², while the Power Law gives a shorter period of the duration.

Fig. 5.

Duration of the WSS < 1 N/m² at each point on the inner wall (a) and on the outer wall (b) in a cardiac cycle.

3.2 Effect of stenosis size on distribution pattern of the WSS

Fig. 6 is a set of contour plots of the WSS at the maximum flow rate (t/t_p = 0.85) along the walls of four arteries with stenosis sizes of 0%, 26%, 38%, and 43%, respectively. Fig. 6 shows the change of the spatial distribution pattern of the WSS along the wall at the different stages of the growth of stenosis. Both Fig. 2 and Fig. 6 demonstrate that the WSS distribution is highly non-uniform spatially. The region with low WSS occurs near the inner wall. The area of this low WSS is getting larger in the post stenotic region expanding towards the downstream direction and the minimum WSS value is getting lower as the size of the stenosis increases. We also investigated the location and the value of the global minimum WSS over the whole surface of the artery wall at 30 different times spread throughout the entire cardiac cycle (plots not included in this paper) and find that the minimum WSS always occurs at the location near the inner wall in the post stenosis region. Fig. 6 also shows that the maximum WSS occurs near the outer wall in the curved artery with no stenosis. As the stenosis at the inner wall grows, the location of the maximum WSS gradually shifts towards the inner wall at the proximal side of the neck and the maximum WSS value increases rapidly.

Fig. 6.

Contour plots of the WSS (N/m²) along the wall at the maximum flow rate (t/t_p=0.85) in arteries with 0%, 26%, 38%, 43% stenosis, respectively. Carreau model was used.

Fig. 7 plots the WSS in an entire cardiac cycle at various points on the artery wall: a) on the inner wall at the neck of the stenosis; b) on the outer wall at the neck of the stenosis; c) on the inner wall in the post stenosis region; d) on the outer wall in the post stenosis region (Q=2.4, Carreau model). Fig. 7 demonstrates the variation of the local WSS during an entire cardiac cycle at the four locations of most interest: two around the neck of stenosis and two in the post stenosis region. Other than the area on the inner wall in the post stenosis region, the local WSS at any point basically experiences the same fluctuation as that of the flow waveform at the inlet: a dip with negative WSS value caused by the reverse flow in systole followed by two small peaks and a large elevation in diastole [see Fig. 7 (a), (b) and (d)].

Figure 7.

The temporal variation of the WSS in an entire cardiac cycle at various locations: a) on the inner wall at the neck of the stenosis; b) on the outer wall at the neck of the stenosis; c) on the inner wall in the post stenosis, d) on the outer wall in the post stenosis, in an artery with various sizes of stenosis, Carreau model was used.

3.3 Factors affecting the WSS

Plots in Fig. 6 and Fig. 7 also show the effect of the size of stenosis on the WSS along the wall at different times in the cycle. It is apparent that the size of the stenosis has a significant effect on the WSS both qualitatively and quantitatively. As mentioned above in section 3.2, the location of the spatial maximum WSS on the surface of the artery shifts corresponding to the size change of the stenosis. More importantly, in a coronary artery with no stenosis, the variation of the WSS in a cardiac cycle at each point on the inner wall in the post stenosis region has the same shape as that of the inlet velocity waveform, i.e. the local WSS also experiences a relatively higher WSS temporally towards the end of the diastole (t/tp=0.85) even though this location is where the WSS assumes global minimum spatially. As the size of the stenosis increases, the WSS on the inner wall in the post stenosis region during the second half of the cycle (in diastole) starts getting lower [see Fig. 7 (c)]. This indicates that the WSS in this area stays at a constant low level through the entire cardiac cycle.

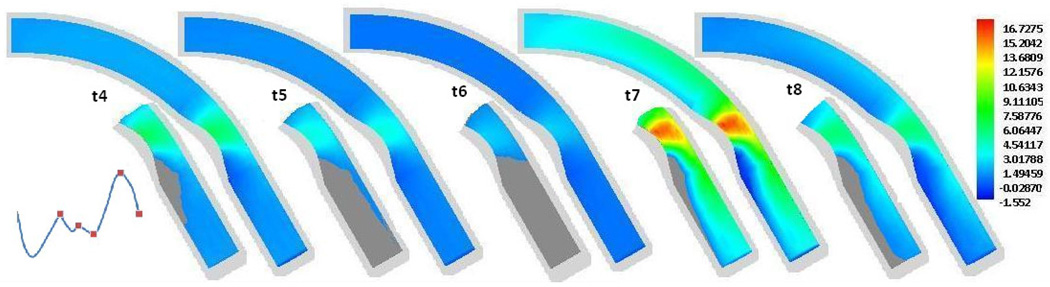
To examine the size of this low WSS area on the inner wall distal to the stenosis, we included in Fig. 8 the contour plots of the WSS along the wall at five different times in a cardiac cycle, labeled as t4 through t8 in Fig. 1 (b). t4, t5, …, t8 correspond to t/t_p = 0.35, 0.19, 0.625, 0.85, and 1, respectively. At each time, on the second half of the artery (from the stenosis region to the outlet) the WSS contour is also plotted by replacing the area of the WSS < 1 N/m² with the dark grey color. The contour plots of the WSS at times t1, t2 and t3 are not included since the WSS along the entire artery wall is lower than 1 N/m². From Fig. 8 we can see that the WSS in the area on the inner wall distal to the stenosis is lower than 1 N/m² in the entire cardiac cycle. The size of this low WSS area is minimum at the peak of the diastole (t/t_p =0.85).

Figure 8.

Contour plots of the WSS at different times in a cardiac cycle with grey area showing the size of region with the WSS < 1 N/m². t4, t5, …, t8 corresponding to t/t_p = 0.35, 0.190.625, 0.85, and 1, respectively.

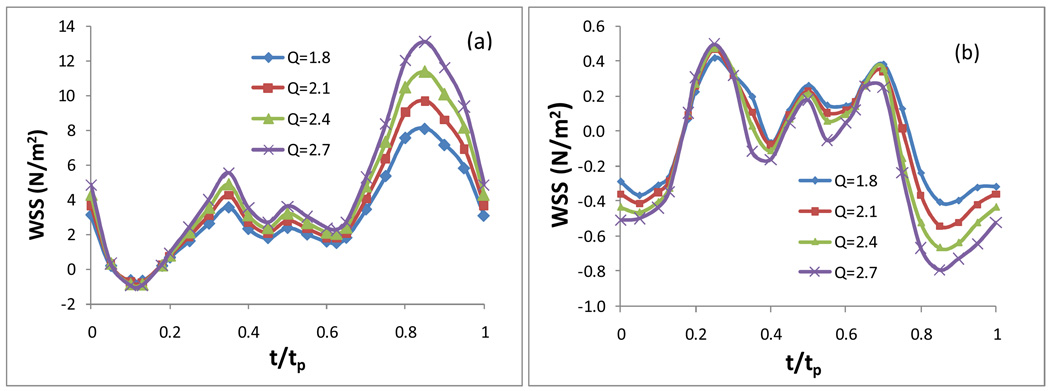
Fig. 9 presents the WSS in an entire cardiac cycle on the inner wall a) at the neck of the stenosis, b) in the post stenosis region (Q = 1.8, 2.1, 2.4, and 2.7, respectively, which correspond to the time-averaged centre-line flow velocities of 0.149 m/s, 0.174 m/s, 0.199 m/s, and 0.224 m/s, respectively. Carreau model, 50% stenosis). It shows the effect of the change of the scale Q for the velocity boundary condition at the inlet on the WSS. As the inlet flow rate changes with the scale Q varying from 1.8 to 2.7, the peak Reynolds number varies from 170 to 255. Here the Reynolds number is calculated by R_e = ŪDρ/η, where Ū is the mean inlet velocity at the peak time and D is the diameter of the artery at the inlet boundary. Fig. 9 shows that increasing the scale factor of the inlet velocity boundary condition does not affect the WSS fluctuation pattern at the neck of the stenosis and in the post stenosis on the inner wall, it only mainly increases the magnitude of the WSS during the diastole.

Figure 9.

Effect of the flow rate at the inlet boundary: the WSS in an entire cardiac cycle on the inner wall a) at the neck of the stenosis; b)in the post stenosis region, 50% stenosis, Carreau model was used.

4 Discussion and conclusion

In the current work, computer simulations of blood flow in the stenotic right coronary arteries have been conducted to investigate the spatial and phasic variation in the WSS. Two non-Newtonian blood models and the usual Newtonian blood model are compared in the stenotic right coronary arteries to quantify the differences between the models. We observed that under the physiological conditions considered in the current work, the blood viscosity properties do not affect the spatial and temporal distribution pattern of the WSS qualitatively. However, the blood viscosity properties have considerable effect on the magnitude of the WSS, especially where disturbed flow is observed. When the magnitude of the WSS is relatively small (< 1 N/m²) on the inner wall distal to the stenosis or at the minimum flow rate, the Newtonian model gives an underestimated WSS (smaller in absolute value), while the Power Law model results in the greatest WSS in absolute value compared to the other two models. Over all, the Newtonian model and Carreau model show a good agreement quantitatively in the WSS during the cardiac cycle. In brief, in the stenotic coronary artery at a centre-line velocity of 0.199m/s considerated in this paper, the Power Law model gives a relatively lower WSS value compared to the Carreau model and the Newtonian model when or where the shear stress is relatively high (> 2 N/m²). This observation is consistent with that made by Johnson et al. in the healthy right coronary arteries [22] and by other researchers [8, 17, 31], who reported that at low inlet velocities, the WSS produced by the Power Law model is higher than that from the Carreau and Newtonian models. As the inlet velocity becomes large, the Carreau and Newtonian models are very similar, while the Power Law model produces much lower values of shear stress. It has been suggested [22, 23, 32] that the Power Law model could artificially mimic this behaviour by assuming a constant viscosity of 0.004 Pa·s if the shear rate is greater than 226.5 s⁻¹.

The WSS is an important factor of atherogenesis and rupture of atherosclerotic plaques. The alterations of blood flow velocity and viscosity might contribute to the WSS modifications and, as a result, to arterial wall thickness [1]. Based on the computational results presented in this paper, we can see that the WSS distribution is highly non-uniform both temporally and spatially, especially in the stenotic region. The WSS along the inner wall elevates in the stenotic region, reaches the maximum at the neck of the stenosis, drops sharply in the post stenotic region, and then recovers gradually downstream in a stenotic coronary artery. The area near the inner wall in the post stenosis region is subject to relatively low WSS during the entire cardiac cycle. This might be one of the dynamic causes to why stenosis tends to grow more downwards. The lower WSS and the larger area with the low WSS might promote further expansion of the stenosis downwards. Evidently, low WSS values are associated with low local velocity, which increases residence time and interaction between blood lipoproteins and vessel endothelium. Long residence time with endothelium results in an increased lipoprotein intake and therefore the final outcome might be the thickening of the arterial vessel wall. In vitro experiments have demonstrated that any change in the WSS stimulates the endothelial cells to release and synthesize vasoactive substances: vasodilators, like NO and prostacyclin, when it increases, and vasocontrictors, like endothelin-1, when it decreases, in order to restore basal WSS values [33]. Smedby [34] did an angiographic study in the femoral artery on the direction of growth of plaques, participated by 237 patients with slight or moderate atherosclerosis. The results suggested that the growth in the downstream direction was significantly more frequent than the growth in the upstream direction.

The higher blood velocity and the higher WSS upstream in front of the neck of a large sized stenosis might prevent the particles from further deposition and might slow down the rate of the wall thickness increase in arteries with larger stenosis. Stone et al. [35] performed serial quantitative angiography three years apart with 26 patients to determine changes in both absolute measurements of the luminal diameter and relative percent stenosis. They found that obstructed arteries with a larger initial minimal diameter and presumably milder disease progressed more rapidly than did those with a smaller diameter. The least severely obstructed segments were most likely to progress. The Familia Atherosclerosis Treatment Study [36] and the Lifestyle heart Trial [37] also suggest that lesions with < 50% stenosis progress more rapidly than do those with ≥ 50%.