Continuous-Time Random Walk Models of DNA Electrophoresis in a Post Array: II. Mobility and Sources of Band Broadening

Abstract

Using the two-state, continuous-time random walk model, we develop expressions for the mobility and the plate height during DNA electrophoresis in an ordered post array that delineate the contributions due to (i) the random distance between collisions and (ii) the random duration of a collision. These contributions are expressed in terms of the means and variances of the underlying stochastic processes, which we evaluate from a large ensemble of Brownian dynamics simulations performed using different electric fields and molecular weights in a hexagonal array of 1 μm posts with a 3 μm center-to-center distance. If we fix the molecular weight, we find that the collision frequency governs the mobility. In contrast, the average collision duration is the most important factor for predicting the mobility as a function of DNA size at constant Péclet number. The plate height is reasonably well-described by a single post rope-over-pulley model, provided that the extension of the molecule is small. Our results only account for dispersion inside the post array and thus represent a theoretical lower bound on the plate height in an actual device.

1 Introduction

Continuous-time random walk (CTRW) models are a powerful tool for understanding, at a fundamental level, the sources of dispersion and concomitant band broadening during electrophoresis in a gel [1–4] or a microfabricated post array [5–8]. We focus here on the latter system, which has the potential for rapid separations of long DNA [9–13]. Modeling DNA transport in post arrays benefits from their ordered geometries and the insights gained from studies of the collision with a small, isolated post [14–16]. Thus, we are optimistic that a predictive model for DNA electrophoresis in post arrays, based on CTRW theory, ultimately will allow us to engineer such devices.

The existing CTRW models for DNA electrophoresis in a post array [5–8] only qualitatively capture the mobility and band broadening seen in experiments and simulations. In Part I of this series [17], we investigated the microscale probability densities of the existing models using a combination of videomicroscopy experiments and Brownian dynamics (BD) simulations. We found that the probability density for the unhooking time is reasonably well captured by the standard rope-over-pulley microscale model [15], provided that we correct for the finite size of the post. In contrast, the distance between collisions is much harder to predict. In particular, the existing models for the distance between collisions [5–8] account for neither the electric field strength (apart from the chain extension during the collision) nor the local variations in electric field in an electrically insulating post array. The extant microscale models for the transport between collisions thus require significant modifications before they can be used for engineering purposes.

In Part II of this series, we take a different approach to CTRW modeling of DNA electrophoresis in a post array. Rather than start from some microscale model, we use a two-state CTRW model [18] to develop expressions for the mobility and the plate height in a post array that delineate the contributions due to the unhooking time and the distance between collisions. These are generic results that do not depend on any particular microscopic model. We used Brownian dynamics simulations to study both contributing factors as a function of the electric field strength and molecular weight for a given array geometry. Our approach permits a deeper insight into the transport process than we could obtain by simply computing the dispersivity (or plate height) alone [19, 20]. Moreover, as the two-state model subsumes prior CTRW models [2, 5–8, 18] and expresses the mean velocity and dispersivity in terms of moments of the pertinent microscale processes, the approach here represents the proper starting point for future modeling efforts.

2 Methods and Materials

2.1 Two-State Continuous-Time Random Walk

Weiss derived the asymptotic results for a two-state continuous-time random walk [18] in which a given cycle of the walk leads to a displacement over a random distance x = x₁ + x₂ during a random time t = t₁ + t₂. In a post array, we define the first state as the translation between hooking events (x₁ = x, t₁ = t_T) and the second state as the hooked state (x₂ = 0, t₂ = t_H). If the moments of x and t are finite, the above model leads to the mean velocity [18]

$$\langle x\rangle =\overline{U}\langle t\rangle ,$$ (1)

with 〈t〉 = 〈t_H〉 + 〈t_T〉 . The dispersivity [18],

$$2\overline{D}\langle t\rangle ={\sigma }_x^2+{\overline{U}}^2\left({\sigma }_{t_H}^2+{\sigma }_{t_T}^2\right)-2\overline{U}{\rho }_{xt},$$ (2)

includes a contribution due to the space-time correlation,

$${\rho }_{xt}=\langle {xt}_T\rangle -\langle x\rangle \langle t_T\rangle .$$ (3)

In the latter equations, 〈 · · · 〉 represents the average over many cycles and ${\sigma }_i^2$ is the variance of i over many cycles. For example, ${\sigma }_x^2=\langle x^2\rangle -{\langle x\rangle }^2$.

Using this approach, we calculated the dimensionless mobility from previous simulation data [19] finding that the two-state model gives an excellent prediction of the mobility. The predictions of the two-state model and two of the previous CTRW models [6–8] are shown against the simulation data [19] in Supporting Information Fig. A1.

2.2 Brownian Dynamics Simulations

We simulated DNA transport in a regular hexagonal post array of 1 μm diameter posts with a = 3 μm center to center spacing using Brownian dynamics (BD) in a non-uniform electric field to generate trajectories of the DNA in the post array. From the BD simulation results, we extract the random variables used in the CTRW calculation. While we used a 2 μm high channel in Part I to aid visualization [17], we used a 4.5 μm high channel here to reflect the deeper channels used in separation experiments to increase the signal [10, 13, 21]. The simulation algorithm is described elsewhere [19]. Briefly, we used N_b beads connected by Marko-Siggia wormlike chain springs [22]. Excluded volume interactions were modeled with a soft potential [23]. Interactions between DNA and boundaries were handled by the Heyes-Melrose algorithm [24]. The key differences between the simulations used here and our prior work [19] are (i) the electric field is computed using a finite element solution; (ii) the code is vectorized in Fortran 95; and (iii) the post boundary is implemented as a continuous curve rather than an 448-sided polygon.

The ratio of convective forces to thermal fluctuations in the simulation was tuned by the Péclet number, defined as

$$\text{Pe}=\frac{{\mu }_{0}E\xi l}{k_{B}T},$$ (4)

where ξ is the bead drag coefficient, l = 0.5833 μm is the maximum extension of a spring, k_BT is the thermal energy, μ₀ is the free solution mobility, and E is the applied electric field. We simulated the trajectory of a molecule over 1 mm of the post array for Péclet numbers ranging from Pe = 0.523 to Pe = 20 and sizes ranging from N_b = 12 to N_b = 42, where N_b = 37 beads represents λ DNA.

Although we found a conversion between the simulation and experiment in Part I [17], the latter was obtained using data for a 2 μm deep channel. To estimate the electric field corresponding to a given Péclet number in a 4.5 μm deep channel, we experimentally measured the diffusion coefficient of λ DNA in a 4.5 μm channel containing 1 μm diameter posts using the particle tracking method in Part I [17]. The corresponding diffusion coefficient, D = 0.46 μm²/s, is the same as the bulk diffusion coefficient to within experimental error [25]. If we assume that the in-array mobility (i.e., when the DNA is not interacting with a post), μ₀ = 1.45 ×10⁻⁴ cm²/Vs, is unchanged from its value in the 2 μm deep channel [17] and the chain is freely-draining, these parameters lead to a Péclet number Pe = 1.14 being equivalent to an electric field E = 23 V/cm in the 4.5 μm deep channel. In what follows, we use this Péclet number for the constant Pe case.

The following analysis is based on ensembles of 100 non-interacting molecules for each value of N_b and Pe. The data were analyzed using the same algorithms as in Part I [17]. Each data point thus consists of hundreds (or even thousands) of collisions. To estimate the error in our measurement, we calculated the standard error of each statistic. Since the standard error scales with the inverse of the square root of the number of collisions, the sampling error is very small. For example, for N_b = 26 the error of the plate height is between 1% and 2%. This error is smaller than the size of the symbols in the following plate height figures, and thus is not displayed. The error in the mobility calculation is significant and thus is included in the corresponding figures.

3 Results and Discussion

3.1 Limiting Cases

The current model captures the extant CTRW models [5–8], which were based on the partially separable Scher-Lax CTRW [26]. The models [5–8] assume that the translation between collisions occurs at the uniform rate U = μ₀E, where μ₀ is the free-solution electrophoretic mobility and E is the electric field strength. As a result, x = Ut_T, which implies that ${\sigma }_{t_T}^2={\sigma }_x^2/U^2$ and ${\rho }_{xt}={\sigma }_x^2/U$. The two-state dispersivity given by Eq. (2) then reduces to

$$2\overline{D}\langle t\rangle ={\sigma }_x^2{\left(1-\frac{\overline{U}}{U}\right)}^2+{\overline{U}}^2{\sigma }_{t_H}^2.$$ (5)

The term (1−Ū/U ) represents the delay caused by the hooking collisions and multiplies the variance in distance between collisions. Thus, Eq. (5) shares some semblance with the lever-rule [27].

All of the existing CTRW models [5–8] assume a probability ρ of colliding in a given row of the array after an exclusion region of size n* = L/a, where L is the length of the chain during unhooking and a is the spacing between posts. The corresponding expectation for the distance of a cycle is 〈x〉 = a(n* + ρ⁻¹ − 1) and the variance is ${\sigma }_x^2=a^2({\rho }^{-2}-{\rho }^{-1})$. If we include a pre-averaged unraveling of the chain during the collision [2, 5–7], then the expectation and variance for the holdup time are 〈t_H〉 = 3L/(2U) and ${\sigma }_{t_H}^2=L^2/(4U^2)$. If we do not include the pre-averaged unraveling [8], then we subtract its deterministic contribution L/U from the expectation to give 〈t_H〉 = L/(2U). Since the unraveling time is pre-averaged, the variance in the holdup time is unchanged.

Inserting these expectations and variances in Eqs. (1) and (5) readily leads to the mobility and dispersivity formulae reported in previous Scher-Lax CTRW models [5, 7, 8]. We have also confirmed, through significant algebra, that the Scher-Lax CTRW model of transport in a post array is equivalent to the present two-state model. We recall that the model of Ref. [5] with ρ = 1 leads to the geometration model [2], which is itself a Montroll-Weiss CTRW [28]. Thus, the two-state model [18] that we adopt here is indeed a generalization of the existing CTRW models.

In the limit of zero posts, the dispersivity of the DNA should limit to the molecular diffusivity. However, this result cannot be recovered from Eq. (2) because the latter result was based on finite moments for x and t [18]. As the distance between collisions grows, the moments for x and t_T become unbounded and we reach an anomalous diffusion regime. (When a collision occurs, we would still expect the moments of t_H to remain bounded.) While results exist for unbounded moments in x [29], we have two reasons to believe this limit will not be of much interest for separations. First, the experimental data reported in Part I of this series [17] indicate that the distance between collisions decays exponentially and thus has bounded moments. Second, a system with large distances between collisions will have very low separation resolution. Nevertheless, if the distance between collisions were to decay algebraically then the mathematical tools are available to modify the present analysis.

3.2 Electrophoretic Mobility

3.2.1 Constant DNA Size

For each ensemble of molecules, we calculated the dimensionless electrophoretic mobility (μ/μ₀) according to

$$\frac{\mu }{{\mu }_0}=\frac{\langle x\rangle }{{\mu }_{0}E(\langle t_T\rangle +\langle t_H\rangle )}.$$ (6)

We simulated 26 bead DNA at Péclet numbers from 0.523 to 4.83 and 12 bead DNA at Péclet numbers from 0.523 to 20 to measure the dependence of the mobility on the electric field.

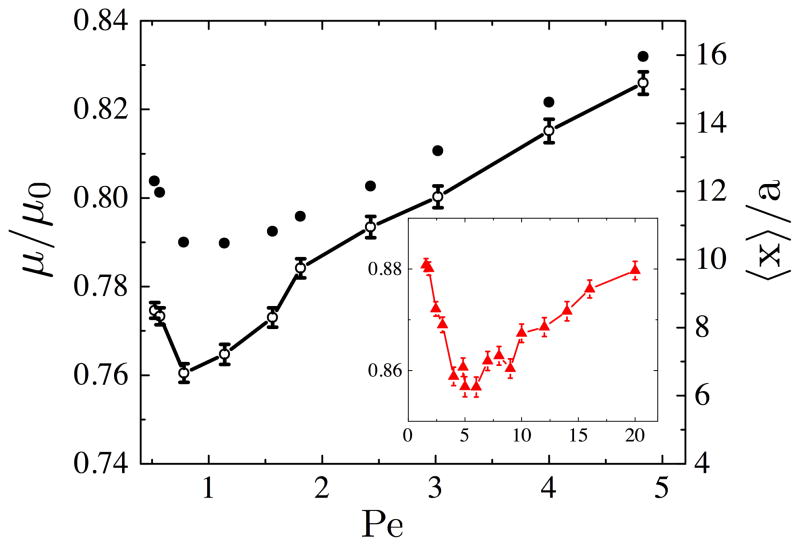
The dimensionless electrophoretic mobility is shown as a function of Pe for N_b = 26 beads in Fig. 1. At low Pe, the mobility decreases with increasing Pe until a critical Péclet number, Pe*, is reached, after which the mobility increases with increasing Pe. These two regimes in DNA mobility have been reported elsewhere [20, 30]. For Pe < Pe*, the number of collisions is limited by the relatively small stretching force when the chain collides with the post; the DNA is not pulled from its equilibrium coil state into a hairpin around the post. Indeed, we found many more molecules experience roll-off collisions at lower Pe numbers. As Pe increases in this low Pe regime, the number of collisions increases until the critical Pe* is reached. At the critical Péclet number, we observed the highest frequency of collisions and the lowest mobility. Scaling arguments suggest that Pe* occurs at Pe*N_b ≈ 20 [20], in agreement with our 26 bead DNA data. However, as seen in the inset of Fig. 1, Pe* occurs at significantly higher Pe than scaling laws predict for the 12 bead case. Note that the post diameter in our simulations is 1 μm, while the previous studies used 0.15 μm posts [20] or an asymptotically thin post [30]. The 26 bead DNA is large enough that the force required to stretch the molecule around a 1 μm diameter post is similar to the force required to stretch the molecule around a thin post. However, the force required to hook the 12 bead DNA is larger; thus Pe* is also larger.

Figure 1.

Dimensionless mobility (open circles) and mean distance between collisions (closed circles) as a function of Pe for 26 bead DNA. The inset shows the dimensionless mobility of the 12 bead DNA plotted against Pe. Error bars show the sampling error.

For Pe > Pe*, the number of collisions decreases with increasing Pe, resulting in an increase in mobility. In this high Pe regime, the collision frequency is limited by (i) the relaxation of the chain after a collision [19] and (ii) the lateral diffusion of the chain to a position in front of a subsequent post. These diffusive processes are largely independent of the applied electric field. Thus, at a higher Pe, the molecule bypasses more rows of posts before the subsequent collision.

Using the two state model, we can determine whether the change in mobility as a function of the electric field is dominated by the hooked state or the translating state. Since the hold-up time in the simulation scales linearly with Pe, we converted the hold-up time to a distance by x_H = U〈t_H〉, similar to Eq. 1. This x_H is interpreted as the distance lost by the molecule because of the collision [31]. We found that x_H increases slightly in the low Pe regime, then reaches a constant value of 5.47± 0.20 μm above Pe*. In contrast, the distance traveled during the translating state, 〈x〉, exhibits a strong dependence on Pe that mimics the trend of the mobility data, as seen in Fig 1. We note that our simulations were run for a constant distance of 1 mm and thus 〈x〉 is inversely proportional to the number of collisions and the collision probability. Thus, the distance between collisions controls the change in mobility as a function of the electric field.

3.2.2 Constant Péclet Number

While the study of a single size of DNA at varying Pe reveals interesting physics behind the transport process, DNA separation occurs at a single Pe for many DNA sizes. To study the transport of a mixture of DNA, we simulated DNA sizes between 15 ≤N_b ≤42 at Pe = 1.14.

We found that the mobility decreases monotonically with the DNA size as expected from prior experiments in post arrays [16]. As in the constant Pe case, the mobility decreases as the number of collisions increases. The range of DNA sizes spans both transport regimes [Pe < Pe*(N_b) and Pe > Pe*(N_b)] discussed in the previous section. In both regimes, larger molecules form more hooking collisions. At low Pe, the applied force required to form a hooking conformation is smaller for a longer chain; at high Pe, the collision probability is proportional to the size of the molecule in the direction perpendicular to the field, which is larger for a longer molecule. Thus, mobility should decrease with increasing size in both regimes.

We can again use the two-state model to determine the key factor governing the mobility. Here, it is convenient to invert the dimensionless mobility to clearly separate the two contributions:

$$\frac{{\mu }_0}{\mu }=\frac{U\langle t_T\rangle }{\langle x\rangle }+\frac{U\langle t_H\rangle }{\langle x\rangle }.$$ (7)

We found that the translation time and the distance traveled during translation are related by 〈x〉 = [f(Pe)U] 〈t_T〉, where f(Pe) accounts for the difference between the mean velocity and the instantaneous velocity of the molecule as it moves in the non-uniform electric field in the post array. In the previous CTRW models [5–8], f = 1. Here, we simply assume that this parameter is independent of molecular weight. For the sizes studied here, linear regression to the data furnishes f(Pe = 1.14) = 0.89 (R² = 0.999). A plot of U〈t_T〉 versus 〈x〉 is shown in Supporting Information Fig. A2. Since the translation time and the distance traveled during translation exhibit a linear relationship, the first term of Eq. (7) is constant with changing DNA size.

According to the rope-over-pulley model of unhooking dynamics [8, 15, 32], the hold-up time scales with the extension of the chain during the collision, L. To leading order, the extension of the chain depends linearly on the chain size; again using linear regression, we found that L = 0.33lN_b (R² = 0.999, Supporting Information Fig. A3). We therefore postulate that 〈t_H〉 dominates the second term of Eq. (7), and thus U〈t_H〉/〈x〉 has a linear dependence on N_b. With the plausible assumption that 〈t_H〉 ~ N_b, we can find an equation for the inverse mobility using linear regression, then invert the result to obtain

$$\frac{\mu }{{\mu }_0}=\frac{1}{1.0+0.010N_b}(R^2=0.961).$$ (8)

For N_b =26 beads, the dimensionless mobility from Eq. (8) is 0.794, a 4% difference from the raw data. The discrepancy between the data and Eq. (8) is due to error in the regression. The original data, along with a plot of Eq. (8), is shown in Supporting Information Fig. A4. We find that Eq. (8) provides a better fit to the data than the $\mu /{\mu }_0\sim N_b^{-3/2}$ scaling for single DNA-post collisions [20, 33]. Thus, at a constant Péclet number the dependence of the mobility on size is governed by the variable hold-up times of the different chains. While we certainly expected the mobility to depend on the collisions, our analysis shows that it is the duration, rather than the frequency, of the collisions that governs the separation. This contrasts with the constant size case, where the variation in the mobility is dominated by the number of collisions (or, equivalently, the frequency of collisions).

3.3 A van Deemter-like Equation

The general two-state model in § 2.1 suggests a way to isolate the different sources of dispersion during electrophoresis in a post array. From a conceptual standpoint, our approach is analogous to the van Deemter equation for chromatography [34]. In the latter, the contributions to the plate height are apportioned to longitudinal molecular diffusion, eddy dispersion, and mass transfer. In the case of a post array, the dispersion comes from the random distance between collisions and the random collision time. The random distance between collisions takes dispersion and molecular diffusion into account, while the random collision time is analogous to the mass transfer term in the van Deemter equation.

We recast the two-state CTRW results in terms of the plate height,

$$H=\frac{2\overline{D}}{\overline{U}}=H_1+H_2.$$ (9)

The first term is the contribution due to the fluctuations in the distance between collisions,

$$H_1=\frac{{\sigma }_{x-{\overline{U}t}_T}^2}{\langle x\rangle },$$ (10)

while the second term is the contribution due to the fluctuations in the holdup time,

$$H_2=\frac{{\overline{U}}^2{\sigma }_{t_H}^2}{\langle x\rangle }.$$ (11)

In the following, we use H₁ and H₂ to investigate the various contributions to the plate height as a function of molecular weight and electric field.

3.3.1 Constant DNA Size

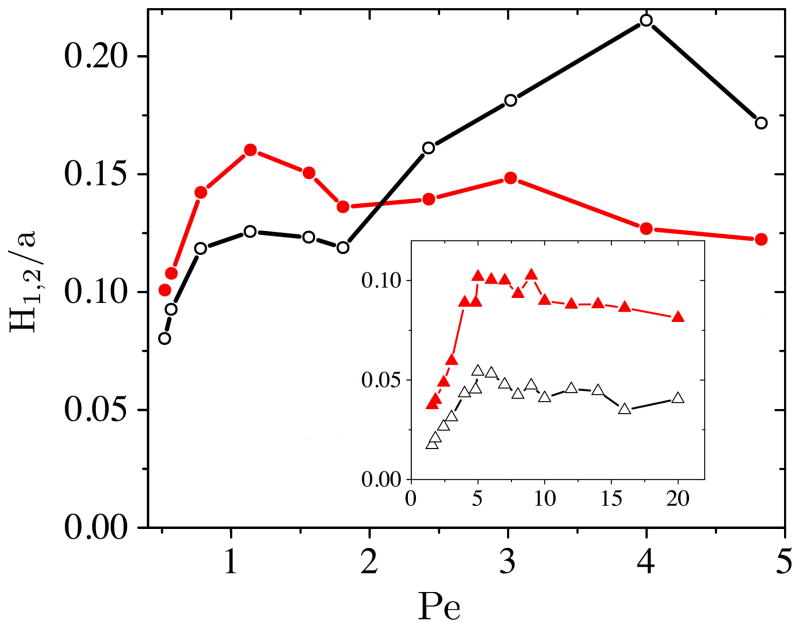
The contributions to the plate height for N_b = 26 are shown in Fig. 2. The band broadening from state 1 (translation) is due to the random distance between collisions and the local velocity fluctuations caused by the non-uniform electric field. We found a piecewise linear relationship between the variance of the distance between collisions and the variance of the translation time as shown in Supporting Information Fig. A5:

$${\overline{U}}^2{\sigma }_{t_T}^2=\{\begin{array}{cc}1.0{\sigma }_x^2-17a^2(R^2=0.999),& \text{Pe}<{\text{Pe}}^{\ast }\\ 0.86{\sigma }_x^2-7.6a^2(R^2=0.999),& \text{Pe}>{\text{Pe}}^{\ast }.\end{array}$$ (12)

Figure 2.

Plate height contributions from each state as a function of Pe for N_b = 26. Filled circles are H₁ and open circles are H₂. The inset shows the plate height contributions for N_b = 12 as a function of Pe, where filled triangles are H₁ and open triangles are H₂.

Since the variance of the travel time and the variance of the distance between collisions are linearly related, ${\sigma }_{x-\overline{U}{t}_T}^2$ is nearly independent of Pe; it depends only on the relation between Pe and Pe*. The distance between collisions, rather than the local velocity fluctuations, is the dominant contributor to H₁, with H₁ ~ 1/〈x〉 .

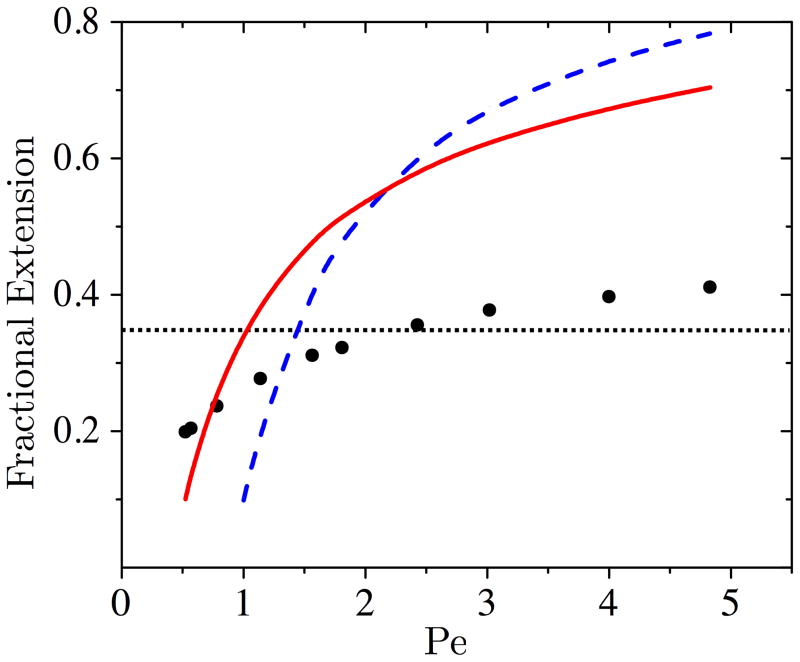
The plate height due to the colliding state, H₂, is dependent on the hold-up time of the collision. For a rope-over-pulley collision, the hold-up time is proportional to the extension of the chain during the collision, L [8, 15]. Indeed, we find that this relation is a reasonable description for the range of Pe studied here; linear regression provides U〈t_H〉 = 0.55L + 0.83a (R² = 0.839, Supporting Information Fig. A6). The average maximum extension of the 26 bead DNA is shown in Fig. 3. At the lowest Pe, L increases rapidly leading to an increase in H₂. At higher Pe, we see a drastic increase in H₂ once the extension of the molecule becomes greater than twice the row spacing. At this high extension, a single arm of the molecule can interact with multiple rows of posts, leading to an increase in the variance of the hold-up time, and thus an increase in H₂.

Figure 3.

Fractional extension of the molecule in the field direction as a function of Pe for N_b = 26 (filled circles) plotted against the predictions of the stem-flower model [6, 7] (blue, dashed line) and the Marko-Siggia worm-like chain interpolation formula [8] (red, solid line). The horizontal dotted line is at an extension equal to twice the row spacing for this molecular weight.

The extension of the chain can be estimated from the Marko-Siggia worm-like chain interpolation formula [8, 22, 35],

$$L=l(N_b-1)\left[1-{\left(\frac{N_b\text{Pe}A}{l}\right)}^{-1/2}\right],$$ (13)

where A = 53 nm is the persistence length of double-stranded DNA. Alternatively, we can model the extension of the chain during collision using the stem-flower model [6, 7, 36],

$$L=l(N_b-1)\left(1-\frac{4l}{\text{P}e{N}_b{l}_k}\right),$$ (14)

where l_k is the Kuhn length. Equations (13) and (14) are plotted with the simulation data in Fig. 3. Both models overestimate the extension of the molecule. Also, they predict multipost interactions at much lower Pe. As a result, these models only qualitatively capture the influence of the electric field on the likelihood of multi-post interactions in the array. The worm-like chain and stem-flower models were originally developed for DNA interactions with an isolated post. In an array of insulating posts, the non-uniform electric field causes compressional forces on the molecule based on its location in the array. The posts also act as physical barriers to chain extension. Thus, we might expect the chain extension in the array to be smaller than for an isolated tethered chain.

The inset of Fig. 2 shows the contributions to the plate height for N_b = 12. The band broadening from state 1 follows the same trend as the 26 bead case; H₁ increases with increasing Pe for Pe < Pe*, then decreases above the critical Péclet number. The plate height from state 2 (unhooking) only follows the trend of the 26 bead case below Pe*. The difference between the two constant N_b cases for Pe > Pe* is due to L; the average maximum extension during a collision for the 12 bead DNA is L = 3.79 ± 0.54 μm and occurs at Pe = 20. Even at this extension, multi-post interactions are not important, and thus H₂ remains relatively constant above Pe*. Indeed, due to the relatively short collision times for this short DNA, the variance in the distance between collisions is the larger contributor to the plate height for all Peclet numbers.

3.3.2 Constant Péclet Number

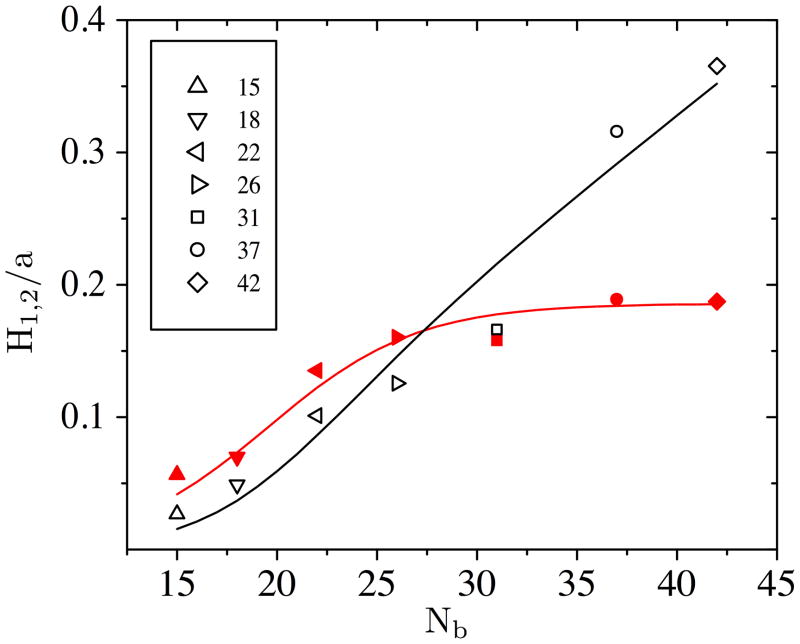
In the case of a constant Péclet number, the plate height contribution from the translating state, H₁, is still driven by the number of collisions. We used linear regression to obtain

$$H_1=\frac{1.4a^2}{\langle x\rangle }(R^2=0.952).$$ (15)

The fit of H₁ is shown in Fig. 4 along with the simulation data. While DNA-post collisions cause a decrease in mobility and thus are necessary for separation, they also increase the band broadening in the array.

Figure 4.

Contributions to plate height for changing DNA size. H₁ is shown in filled (red) symbols, and H₂ is shown in open (black) symbols. The lines are the model equations for H₁ [Eq. (15)] and H₂ [Eq. (17)]. The legend shows the number of beads corresponding to each symbol.

Based on the rope-over-pulley model of unhooking [8, 15], the hold-up time scales with L, and thus t_H ~ N_b. We found that a good phenomenological fit to the data is

$$\langle x\rangle =b_{1}exp[b_2{N}_b]+b_3,$$ (16)

where b_i are constants; this fit is shown in Supporting Information Fig. A7. Using Eq. (16) we are able to fit the simulation data for 〈x〉 with b₁ = 4400, b₂ = −0.27 and b₃ = 22 (R² = 0.999). We can then express the plate height due to hold-up as a function of N_b by combining Eqs. (8, 16), and using ${\sigma }_{t_H}^2\sim t_H^2\sim N_b^2$,

$$H_2={\left(\frac{N_b}{1.0+0.010N_b}\right)}^2\frac{c_{1}a}{b_1\mathit{exp}[b_2{N}_b]+b_3},$$ (17)

where c₁ is the scaling coefficient. Using least squares minimization, we find c₁ = 9.3×10⁻³ (R² = 0.958). This fit is shown in Fig. 4 along with the simulation data. While Eq. (17) is a phenomenological model, it allows us to easily identify how the size of the DNA affects the second contribution (unhooking) to the plate height.

For Pe = 1.14, we found that the extension L remains smaller than the distance between posts for N_b ≤26. As a result, we might expect this regime to correspond to the dispersion due to repetitive collisions with isolated posts. However, we found that the dispersivity in this regime scales like $\overline{D}\sim N_b^{2.2}$. This result differs from the dispersivity scaling from simulations of DNA collisions with a single post, $\overline{D}\sim N_b^{5/2}$ [20]. However, we note that dispersion calculated from simulations in a random array of posts also exhibited a weaker dependence on chain length than the $N_b^{5/2}$ scaling [20], in agreement with our results.

4 Conclusions

Our analysis, based on a two-state model of DNA transport in a post array, allowed us to decouple the effects of (i) translation between collisions and (ii) hold-up during a collision on the electrophoretic mobility and the plate height. We found that the mobility of a fixed DNA size over a range of Pe depends primarily on the number of collisions experienced by the molecule, and that the number of collisions also predicts the observed mobility minimum. In this case the hold-up time is of secondary importance because t_H ~ 1/E. When the Péclet number is held constant and the size of the DNA is varied, the change in mobility is governed by the hold-up time of the collisions rather than the change in their frequency. Thus, the state that dominates the change in the electrophoretic mobility depends on whether we consider mobility as a function of Pe, or mobility as a function of DNA size.

Using a van Deemter-like equation we calculated the plate height due to the different states of the molecule. The plate height due to translation between collisions scales with the number of collisions. The plate height due to the variable hold-up time of a collision is well predicted by the single post rope-over-pulley unhooking model for small molecules and low Pe. However, large molecules under a strong electric field have such a large extension that the effects of multiple posts become important. Since these multi-post effects increase the variance in the hold-up time [19], they increase the plate height.

Our results make clear the usefulness of the two-state model [18], since it allows us to interpret the various factors contributing to the mean velocity and band broadening. We should also point out that the mathematics required to produce meaningful results from the two-state model are trivial compared to those required for the equivalent Scher-Lax treatment [5]. In the latter approach, one begins with the probability density ψ(x,t) for moving a distance x in a time t and computes the asymptotes of the first two moments from the solution to the random walk [26]. In the context of a post array model, the steps include inverting the microscale model for the holdup time (which can only be done with certain limiting assumptions [2]) and extensive algebra. In contrast, the two-state model given by Eqs. (1)–(3) allows a rapid calculation of the mean velocity and dispersivity from the moments of the microscale processes. Importantly, these moments are obtained without inverting the holdup time model. Thus, we posit that the two-state model provides the ideal starting point for any future CTRW studies of DNA electrophoresis in a post array.

Abbreviations

CTRW

continuous-time random walk

BD

Brownian dynamics