Clustering to identify RNA conformations constrained by secondary structure

Abstract

RNA often folds hierarchically, so that its sequence defines its secondary structure (helical base-paired regions connected by single-stranded junctions), which subsequently defines its tertiary fold. To preserve base-pairing and chain connectivity, the three-dimensional conformations that RNA can explore are strongly confined compared to when secondary structure constraints are not enforced. Using three examples, we studied how secondary structure confines and dictates an RNA’s preferred conformations. We made use of Macromolecular Conformations by SYMbolic programming (MC-Sym) fragment assembly to generate RNA conformations constrained by secondary structure. Then, to understand the correlations between different helix placements and orientations, we robustly clustered all RNA conformations by employing unique methods to remove outliers and estimate the best number of conformational clusters. We observed that the preferred conformation (as judged by largest cluster size) for each type of RNA junction molecule tested is consistent with its biological function. Further, the improved quality of models in our pruned datasets facilitates subsequent discrimination using scoring functions based either on statistical analysis (knowledge based) or experimental data.

RNA is an important molecule in gene regulation both in the presence and absence of proteins (1). The paradigm that “structure affects function,” so commonly used on proteins, can also be applied to RNAs, which adopt intricate three-dimensional structures that depend strongly on their in vivo environment. The plethora of RNA types, ranging from small-interfering RNA to ribozymes and riboswitches, points to a need for a strong understanding of how RNA folds in order to better elucidate how RNA functions (2, 3).

One test of our understanding of RNA folding is the extent to which we can predict RNA tertiary structure from sequence, a challenging problem that recent research has tackled in a variety of ways (4). Some of the approaches to predicting RNA tertiary structure include assembling RNA fragments from native-like RNA fragment libraries (5–7) or sampling RNA chains using discrete molecular dynamics (8). Such prediction methods are confined to small molecules or require coarse-graining of bases due to the difficulty associated with sufficiently complete all-atom conformational sampling of larger, more complex RNA systems.

The sampling process can be simplified because most RNAs fold in a hierarchical fashion (9–11), in which the RNA sequence determines its secondary structure, or the base-pairing within the RNA (Fig. 1A). These base-pairing interactions are preserved during folding to a specific three-dimensional (3D) structure. Therefore, each RNA can generally be regarded as comprising of helical regions (simplified as uniform cylinders) connected by single-stranded junction regions in 3D (Fig. 1B). Hence every RNA molecule is made up of helix-junction-helix motifs.

Fig. 1.

Representations of an RNA molecule. (A) The secondary structure of tRNA with each base-paired segment differently colored and simplified as a cylinder (of radius 11 Å) shown in three-dimensions (B). A reference helix (black) is arbitrarily chosen to define a reference coordinate system. The other helices are color-coded. (C) Each helix axis is projected on the reference coordinate system to give two angles (θ_h and ϕ_h). The vector pointing from the origin of the reference helix to the helix origin (defined as position closest to the junction) is also projected giving θ_o and ϕ_o. Each projection can be represented as x, y, and z-axes scaled direction cosines (labeled l_x, l_y, and l_z for the helix orientation projection). These scaled direction cosines and the origin coordinates, were used as the clustering metric.

It is common, therefore, to make use of RNA secondary structure to facilitate sampling of RNA tertiary structure (12, 13). Recent work (14) compared the quality of RNA structure prediction in the absence and presence of native secondary structure and showed that in the latter case, RNA conformations were both less diverse, and more similar to the native state. Understanding the degree to which secondary structure affects the range of 3D conformations an RNA can take may improve our ability to effectively sample, predict, and identify folding pathways of different complex RNA systems. Such information may further elucidate evolutionary behavior of junctions and conservation of sequences not directly involved in tertiary contacts or binding pockets.

Bioinformatics approaches to study RNA junctions focused on static, native-folds (15–18). Consequently, these studies do not provide information on how an RNA’s secondary structure affects its 3D conformational search during a folding process. Also, such approaches are heavily affected by other stabilizing influences; it is unclear if the observed RNA conformation for a given secondary structure is a consequence of constraints from secondary structure, or the presence of tertiary contacts and/or ion or ligand binding.

Here we sampled RNA with native-like secondary structure using MC-Sym (7), which does not have an explicit scoring function to filter out nonnative conformations. The absence of scoring and the inability to sample tertiary contacts without added information (4) give us the opportunity to study RNA conformations that are constrained by secondary structure alone, without complicating effects. Even with this simple geometrical constraint, RNAs can adopt a wide variety of shapes and sizes, with the most interesting ones falling within sampling basins: regions of high conformational density. Other less well sampled conformations are outliers that skew our perception of the sampling landscape.

To identify sampling basins and remove outliers, we introduce a simple but unique clustering scheme, which also estimates the number of basins that fit the data. We describe our procedure, and use it on three different types of RNA structures: tRNA and the aptamer domains of adenine and thiamine pyrophosphate (TPP) riboswitches.

Visual inspection of the clusters of conformations for these three RNA types indicated that the preferred conformations corresponding to large sampling basins were generally consistent with the biological function of the RNA respectively. This preliminary study suggests that the constraints imposed by secondary structure alone may play a pivotal role in dictating the RNA’s possible tertiary folds, and/or guide its folding mechanism.

Clustering is also commonly used to facilitate identification of near-native conformations (19). Each cluster is typically represented by the structure closest to its centroid. We found that in all three RNA molecules we looked at, our clustering and outlier removal scheme improved the quality—defined by root-mean-squared deviation (rmsd) to the native structure—of these representative models. This result suggests that when used in combination with a good scoring scheme, our approach will improve the selection of a useful representative model.

Results

RNA Conformations Confined by Secondary Structure.

We generated tRNA^phe conformations consistent with its native secondary structure using MC-Sym (see Materials and Methods, and Fig. 1A). The geometry of each RNA secondary structure can be defined by representing each base-paired helix by its origin, as well as the orientation of its helix axis (Fig. 1C). A reference helix is selected (shown as black in Fig. 1A) to define an internal coordinate system (see Materials and Methods). In this system, both the helix origin and orientation can be defined with respect to the internal coordinate system either as two polar angles and a length or as three direction cosines and a length. For the helix origin, its direction cosines scaled by distance are identical to its internally defined Cartesian coordinates. This coordinate system was only used for visualization, and to evaluate a metric for clustering; no conformational restrictions beyond secondary structure were imposed in sampling.

The distributions of tRNA conformations consistent with its native secondary structure are shown in Fig. 2. Fig. 2A shows the positions of the helix origins with the same color scheme as in Fig. 1A. The allowed helix positions depend on the connectivity defined by secondary structure, consistent with one’s intuition. For instance, the yellow helix is directly connected with no intervening unpaired nucleotide to the reference, and hence takes on more constrained locations about the end of the reference helix (Fig. 2A) compared to the blue helix (connected by two unpaired nucleotides to the reference helix), or the green helix (not directly connected to the reference helix). The number of intervening single-stranded nucleotides also dictates the possible orientation of the helices (Fig. 2B), which explains why the orientation of the yellow helix is localized, while the green helix has the most orientational flexibility. The blue helix shows an intermediate range of helix orientations, lying between the extremes of the yellow and green helices. Similarly, Figs. S1 and S2 summarize the diversities of structures obtained for the aptamer domains of the adenine and TPP riboswitches sampled.

Fig. 2.

Distributions of the origins and orientations of the helices of tRNA. (A) The helix origins for the blue, green, and yellow helices as defined in Fig. 1A and the corresponding scatter and contour plots (shown in sinusoidal projections) show distributions of θ_o and ϕ_o. (B) Similar to (A) but of the orientation of the helix axes (θ_h and ϕ_h). In contour maps, the native helix positions and orientations are indicated as white points. Comparing (A) with (B), the helix orientations show greater diversity than do their positions. For clarity, only 5,000 randomly selected models are shown, and in (B) the nonreference helices are represented as thin cylinders.

Consistent Clustering of RNA Models.

We clustered the diverse set of tRNA models (as elaborated in Fig. S3; see Materials and Methods) using multiple iterations of the k-means clustering algorithm. Each k-means clustering run leads to different results that depend on the initial choice of the conformation associated with the center of each cluster. We used this lack of consistency to our advantage and assumed that models belonging to a well defined conformational basin should be clustered together more consistently, regardless of cluster center initialization. Therefore, clustering similarities from multiple k-means clusterings help us identify RNA models in such basins.

By analyzing 100 independent k-means clustering runs, we observed that the tRNA models show more consistent clustering compared to a control set with random helix positions and orientations (Random Orientation Set; see Fig. S4). This observation suggests that physical requirements of avoiding steric clashes and preserving chain connectivity lead to distinct nonrandom conformational clusters of tRNA.

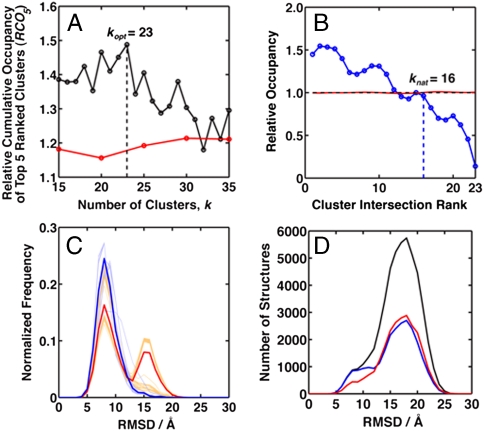
The workings of our procedure are best seen in the plots in Steps 7 and 8 (Fig. S3). The value of the Relative Cumulative Occupancy (RCO₅) for the tRNA dataset varies with the number of clusters, k, and peaks around 23 while that for the Random Orientation Set shows almost no dependence on k (Fig. 3A). Hence we estimated the optimal number of clusters (k_opt) for the complete tRNA dataset (Full Set) as k_opt = 23, meaning that the Full Set needs to be sorted into 23 clusters for effective removal of sampling outliers. A subset of models (Selected Set) was chosen based on each model’s propensity to be in cluster intersections (Fig. S4). The number of “natural” clusters (k_nat) for this subset was estimated as k_nat = 16 (Fig. 3B) indicating that the Selected Set should cluster to approximately 16 bins. In comparison, a random subset (Random Set) of the Full Set shows no variation in relative occupancy with Cluster Intersection Rank (cluster intersections sorted by size).

Fig. 3.

Clustering tRNA. (A) The optimal k (k_opt) is selected using the relative enhancement in the population of the top five clusters (RCO₅) of the Selected Set compared to the Full Set (black). The control analysis of randomly oriented helices (Random Orientation Set, red) shows little variation with k. (B) The relative occupancy of clusters for the Selected Set compared to the Full Set drops steadily below 1.0 at the 16th cluster, giving an estimate of the “natural” number of clusters, k_nat = 16, for the Selected Set. There is no significant variation of relative occupancy for the Random Set of tRNA models (red). (C) Both the Selected Set and Random Set were reclustered to 16 bins using 100 k-means clustering runs: the Selected Set is clustered more consistently than the Random Set. We show results for the cluster for which the structure closest to its centroid is most like the native structure. The difference between the rmsd histograms for all clustering runs is smaller for the Selected Set (light blue, each clustering run shown as a line; most overlap) than the Random Set (orange). The mean of all 100 clustering runs’ rmsd distributions for the Selected Set and Random Set are shown in blue and red respectively. The Selected Set also has a stronger peak of low rmsd models. (D) The C4′ backbone rmsd histograms of all the models in the Selected Set (blue), Random Set (red), and Full Set (black) of the tRNA models. Almost all of the low rmsd (< 10 Å) models in the Full Set are found in the Selected Set, indicating MC-Sym samples a near-native basin for tRNA. Removing sampling outliers strongly enhanced the likelihood of selecting a good structural model in the absence of any scoring function.

To obtain a sense of consistency in the reclustering of the Selected Set into 16 bins, we compared its clustering results for all 100 k-means clusterings to that for the Random Set. To easily match clusters, we focused on the cluster whose structure closest to the centroid has the lowest rmsd to the native state. As expected (Fig. 3C), clustering of the Selected Set is more consistent, with all members in this particular chosen cluster for 100 independent clustering runs showing very similar rmsd distributions (light blue lines). This consistency was not seen for the Random Set, which had a greater run-to-run diversity (Fig. 3C, orange). Other RNA systems also illustrated the same improvement in clustering consistency (Figs. S5 and S6). Interestingly, the mean rmsd distribution for the Selected Set (Fig. 3C, blue) was narrower than that for the Random Set (Fig. 3C, red), with a lower average rmsd, indicating that our clustering approach has very effectively removed sampling outliers close to the basin of good tRNA models. This narrowing of the rmsd distribution was also seen for the adenine riboswitch, and to a lesser extent the TPP riboswitch studied (Figs. S5 and S6).

Removal of Sampling Outliers.

If conformational sampling is effective and results in a highly populated basin close to the native state, then removing sampling outliers should accentuate the population of low rmsd models—exactly what we observe for tRNA (Fig. 3D). Almost all the low rmsd models (rmsd < 10 Å) were found in the Selected Set. This low rmsd enrichment in the Selected Set population is not reproduced for other RNA systems tested here (adenine and TPP riboswitches; see Figs. S5 and S6), likely because in these cases there were much fewer low rmsd models sampled, possibly a consequence of sampling these riboswitches with only native secondary structure, but without any ligand or tertiary contact information. Conversely, the tight four-way junction topology in tRNA helps to better constrain RNA sampling towards native-like conformations.

Improving Selection of Representative RNA Models.

Clustering is commonly used in protein and RNA structure prediction to reduce the effects of sampling and scoring outliers (19). In an average structure scoring and selection procedure, each cluster is represented by the model closest to its cluster centroid. We therefore examined the rmsd distributions of these representative models for all clusters in all 100 independent k-means clustering runs. In all three RNA cases looked at, we consistently found more representative structures in the lower rmsd regions for the Selected Set than the Random Set (Table 1 and Fig. S7). Making use of the Selected Set (at least for the RNAs tested here) improves the quality of the representative model chosen for any reasonable scoring function. These observed improvements are dependent on the quality of structural sampling (and consequently the flexibilities of junctions), and may well be less pronounced if incomplete or suboptimal secondary structures are used.

Table 1.

Summary of results for the tRNA, adenine riboswitch, and TPP riboswitch systems

	Number of bases	Set type	Percentage of structures closest to centroid with rmsd below					rms with p -value < 0.01 (in Å) (13)	Min. rmsd sampled	Min. rmsd cluster
			6 Å	7 Å	8 Å	9 Å	10 Å
tRNA	76	selected	1.7	4.1	7.9	9.1	9.7	10.3	4.21	6.7 ± 1.0
		random	0	0.19	4.6	6.3	6.8		4.53	7.7 ± 0.3
Adenine riboswitch	71	selected	0	0	1.1	2.9	3.7	9.5	5.97	8.5 ± 0.8
		random	0	0	0.037	0.41	2.6		6.14	10.0 ± 1.0
TPP riboswitch	77	selected	0	0	0	0	0	10.5	9.04	12.8 ± 0.4
		random	0	0	0	0	0		8.84	13.7 ± 0.8

Compared to the Random Set, the Selected Set shows a consistent increase in percentage of low rmsd structures closest to the centroid.

Discussion

Improved RNA Clustering.

We have developed a unique outlier removal cum clustering process to effectively cluster RNA conformations in order to understand the correlations between different helix positions and orientations for a given secondary structure. Our protocol is based on the premise that a combination of clusterings from weak, unsophisticated clustering algorithms is better than the individual clusterings themselves. There is extensive research in this field of combining cluster ensembles, and one such subfield is the concept of evidence accumulation (20, 21). A simple and intuitive way to consolidate information from multiple different clusterings is to generate a coassociation matrix between each element with one another based on how often they are clustered together. Such an approach scales poorly with number of models (20). In our work we instead adopted cluster-to-cluster comparison. Rather than comparing each model with one another, only the number of instances each model is found in cluster intersections is recorded.

Unique to our protocol is the incorporation of outlier removal with evidence accumulation and estimation of k_nat. Outliers were identified by their lower frequency of occurrence in cluster intersections—an intuitively simple definition. We also tried outlier removal by approximate k-centers clustering—shown to identify sampling states for large protein datasets (22)—by filtering out structures in low density clusters. Although this worked well (data not shown), we were unable to determine the best number of clusters for the remaining data. Our protocol estimates k_nat from the occupancies of clusters before and after outlier removal.

One limitation of our analysis is that cluster comparisons were done by one-to-one matching, hence requiring different clusterings to have the same k. Therefore it is less practical for comparing clusterings from different clustering algorithms (unless the same k can be fixed), which could lead to bias from k-means’ preference for hyper-spherical clusters. However, analysis work by Fred et al. has shown that if the k used is high enough, the limitations of k-means’ preference for hyper-spherical clustering can be overcome by evidence accumulation (23). Further, due to the nature of our k_opt optimization, only the largest clusters show meaningful, consistent clustering. Depending on the user’s preference for this number, one can change the metric (RCO_i) in step 7 of the protocol.

Preferred RNA Conformations Constrained by Secondary Structure.

Once noisy data were removed, and the remaining structures clustered to their respective sampling basins, we made use of cluster sizes to give us an indication of the preferred sampled RNA conformations constrained by native secondary structure only. Fig. 4 illustrates the three most frequent conformations for tRNA and the aptamer domains of adenine and TPP riboswitches.

Fig. 4.

The structures closest to the centroids of the three largest clusters for the Selected Sets of tRNA, adenine riboswitch, and TPP riboswitch. The C4′ rmsds to the native are shown. The clusters were sorted based on their size, and the percentages shown indicate the degree of consensus for the particular cluster being in the top three largest of each clustering run (see Materials and Methods). For tRNA and the adenine riboswitch, one of the three largest clusters has similar conformation to that of the native state, with similar global folds and/or interhelical orientations. The clusters for TPP riboswitch, instead favor extended conformations, different from that of the native TPP-bound state, consistent with the fact that the TPP riboswitch only folds to the compact form in the presence of its ligand, while the adenine riboswitch adopts identical global conformations in the presence and absence of ligand. These observations suggest that sampling and clustering RNA junction conformations gives insight into function and dynamics.

As described earlier, the yellow helix of tRNA has highly localized orientations relative to the reference helix: the three largest clusters for tRNA show the consistent coaxial stacking of the yellow and reference helices. This placement of the yellow helix constrains the blue and green helices to be further away from the reference helix, while still preserving chain connectivity. For tRNA, the third most frequent conformation is most native-like. It is likely that specific ion bindings and tertiary interactions between the loops would favor this set of native-like conformations. The constrained junction topology may guide folding by facilitating the distant motif interactions found in the native structure.

In the case of the aptamer domain of the adenine riboswitch, while the lowest representative rmsd structure (∼8 Å) is not in the three largest clusters, the largest cluster has similar global conformations as the native, adenine-bound form, with two of its helices coming together in almost parallel fashion. Adenine riboswitch (24) is a Type I riboswitch, which undergoes local conformational changes upon ligand binding (25–29, 46). Our results suggest that the adenine riboswitch (constrained only by secondary structure) preferentially samples a global fold similar to its adenine-bound state, consistent with its riboswitch type classification.

The TPP riboswitch (30, 31), on the other hand, is a Type II riboswitch which undergoes a large conformational change in the presence of ligand (31, 32, 46). This classification might be why the three largest clusters of the TPP riboswitch all have extended conformations. It appears that the aptamer domain of the TPP riboswitch under native secondary structure geometric constraints preferentially explores extended forms. TPP is required to orient the bases within the junctions to fold the riboswitch into its TPP-bound compact form.

Further work is necessary to investigate the generality of our observations on more types of RNA junctions, and to probe the effects of alternate secondary structures on conformational search space for a particular RNA. Nonetheless, our preliminary observations suggest that we might be able to elucidate some features of an RNA’s behavior just by exploring the conformational space geometrically allowed by its constraining native secondary structure, consistent with extensive work on the hairpin ribozyme, where altering the RNA’s junction has significant effects on the docking behavior of the RNA (33–36). The four-way junction of the naturally occurring hairpin ribozyme is highly constrained, and this appears to favor the native-like docked conformation, allowing docking to proceed more effectively than with a two- or three- way variant. Recent thermodynamic work on simple nucleic acid junctions illustrated the effects of RNA junctions on RNA conformations (37): certain tertiary contact locations are not energetically favorable due to chain connectivity constraints. In addition, experimental and simple modeling work on the transactivation response element (TAR) RNA by Bailor et al. (38) showed that RNA dynamics are strongly dependent on its secondary structure.

New Sampling Algorithm Needed for Thermodynamic Dissection to Guide RNA Structure Prediction.

Our current study does not provide us with a systematic analysis of the contributing factors of how an RNA’s junctions dictate its tertiary topology. The observed results could be a consequence of junction order, base-identity, and/or length of single-stranded regions within a junction. Further, the effects of bias from using native RNA fragments are unclear and electrostatic effects—crucial in RNA systems—are only implicitly captured using native RNA fragments. A rigorous and systematic thermodynamic dissection of these various contributions to RNA junction topologies will improve our physical understanding of RNA folding. This dissection in turn is insightful to guide RNA folding predictions and RNA design. Even though the preferred RNA conformations we identified are likely to be related to entropically favored states, the nonphysical, sequential, and cyclic fragment assembly by MC-Sym fails to generate a thermodynamic ensemble for this energetic dissection.

A general and physical RNA sampling approach that preserves secondary structure is needed to study the different contributions of RNA junctions on 3D conformational search space. We are currently working on such sampling methods that may lead to the development of more effective RNA scoring functions and sampling potentials for secondary structure constrained systems, and so improve methods in RNA structure prediction, particularly for large RNA systems.

Materials and Methods

Generating RNA Models with Defined Secondary Structures.

Decoy structures were generated using MC-Sym (7) run locally. Input information used was the RNA sequence and native secondary structure (defined from the respective X-ray structures), with no additional distance or interaction constraints. To minimize bias from different assembly directions, the reference helix was always built first, and subsequent helices added clockwise for half of the dataset and anticlockwise for the other. Junction regions were made up of single-stranded fragments of two, three, or four bases.

Because fragment assembly does not preserve chain connectivity, the models were energy minimized (up to 100 steps) with the AMBER 99 force-field (39) and Generalized Born treatment (40) of electrostatics with an inverse Debye-Hückel length of 0.19 Å^-1 as implemented in Nucleic Acid Builder (NAB) (41). A small number of steps was chosen to reduce computational time per structure, and also to correct broken bonds—a consequence of fragment assembly—while not moving the atoms too much, ensuring that we are looking at sampling features of MC-Sym, not that of the force-field. In addition, the base-pairing defined in MC-Sym is preserved. Models were rejected when steric clashes (based on high van der Waals energy) were not completely removed by this energy minimization. After these steps, there remained about 50,000 models for each of the three systems: tRNA (PDB id: 1EHZ), adenine riboswitch (1Y26) and TPP riboswitch (2CKY) tested here.

Verifying Minimal Sampling Bias from Native Fragments.

It is unclear how the native RNA fragment libraries affect sampling of the RNA systems considered here. Specifically, there are both native tRNA and adenine riboswitch fragments in the MC-Sym fragment libraries but as libraries are constantly updated, it is impossible to know if any TPP-riboswitch fragments were present when our models were generated (42). To check for sampling bias, we aligned each fragment to its corresponding region in the native structure. Excessive sampling bias from native fragments should result in a strong peak of low rmsd fragments used. We found no significant dependence of fragment rmsd distributions on RNA type (Fig. S8), suggesting that sampling bias is minimal.

Distance Measure Based on Interhelical Angles.

Interhelical angles are natural measures of RNA structure, for a given secondary structure. rmsd can overemphasize differences in the helical backbone and depend on the relative alignment of structural models. Therefore clustering based on atomistic rmsd can lead to misleading and ineffective results.

Each helical region of the RNA was superimposed [using C4′, C2, C4, and C6 atoms for each nucleotide; implemented in NAB (41)] to a perfect A-form helix (from http://structure.usc.edu/make-na/server.html) whose helix axis was evaluated using 3DNA (43, 44). The axis of the reference helix (colored black in Fig. 1B) defined the z-axis of the model, while the O3′ of the terminal base in the helix defined the direction of the x-axis. The y-axis was then defined as orthogonal to the x- and z- axes. The choice of reference helix did not significantly affect results (Figs. S9 and S10).

Once the internal axes were defined, the direction cosines (scaled by length) of each helix and Cartesian coordinates of each helix origin were used for the distance metric in clustering. Direction cosines were used to avoid the degeneracy of angles. The helix rotation about its own axis was ignored in our clustering: each helix is represented by only six distances.

For clustering, the Euclidean distance is taken as (Distances_ij)² = Σ_n>1[(x_orient,nj - x_orient,ni)² + (y_orient,nj - y_orient,ni)² + (z_orient,nj - z_orient,ni)² + (x_origin,nj - x_origin,ni)² + (y_origin,nj - y_origin,ni)² + (z_origin,nj - z_origin,ni)²], where x_orient,ni, y_orient,ni, and z_orient,ni are scaled (by helix length) x, y, and z direction cosines of the nth helix orientation of the ith structure and x_origin,ni, y_origin,ni, and z_origin,ni are the Cartesian coordinates of the nth helix origin of the ith structure. n_helices is the number of helices in the RNA system. Because the first helix was used for reference, for a n_helices system, there are 6(n_helices-1) dimensions to cluster.

Clustering RNA Models.

The clustering protocol we developed is described as follows, and summarized pictorially in Fig. S3.

Step 1:

Generate a set of RNA three-dimensional structures constrained by secondary structure.

Step 2:

The 10th percentile of the cumulative intermodel distances is used to estimate a threshold distance. Models within this threshold distance from the ith model are summed to give Neighbors_i; an initial estimate for k = Σ_i1/(Neighbors_i + 1) (45). If the initial estimate is too small, clusters would be merged, yielding less insightful interpretations. If k is too large, all clusters will be small and clustering noisy, with low consistency.

Step 3:

100 independent k-means runs are conducted, with the initial value of k. Each k-means clustering result is slightly different, depending on the initialization of cluster centers. While our approach can be extended to other clustering methods, the criteria are that there must be run-to-run variation between the clustering results, and the same k is used in all runs. k-means was chosen for its speed and ease of use. The objective is to identify structures that are often clustered together (or equivalently belonging to cluster intersections, as defined below), under the premise that they belong to well defined sampling basins.

Step 4:

Each cluster run is compared with one another to evaluate their similarities. For each comparison of a pair of clustering runs the k clusters are matched and ranked based on the number of common cluster members, which are said to belong to the cluster intersection of the matched clusters.

Step 5:

The full dataset of structures (referred to as the Full Set) are then scored and sorted by how often they occur in cluster intersections. The top 50% (Selected Set) are chosen—a reasonable compromise between noise removal and good statistics.

Step 6:

When matching clusters, the cluster intersections are further sorted by their size to give a size rank. For each model, the rank of the intersection it occupies is recorded. Next, the cumulative occupancy of each Cluster Intersection Rank is compiled. The cumulative occupancy differs for the Selected Set from that of the Full Set, a natural consequence due to our selection criterion.

Step 7:

Optimization of the k value is based on the Relative Cumulative Occupancy (RCO) of the differently ranked clusters. The optimal value of k (k_opt) was chosen to maximize the relative occupancy of the top five ranked clusters (RCO₅) for the RNA sets, and the averaging process helps to ensure a more robust k_opt is determined. RCO₅ refers to the ratio of the sum of occupancies of the top five ranked clusters in the Selected Set to the Full Set (Step 7 in Fig. S3 uses RCO₃ for illustrative purposes).

Step 8:

The Selected Set is clustered again, this time using k_nat number of clusters. k_nat is usually smaller than k_opt because a higher value of k_opt is required for the identification of noisy data (23). k_nat was estimated by observing when the relative occupancy of each cluster rank steadily fell below one.

All k-means clustering was done using the kmeans function in Matlab, with “onlinephase” set to “off” and a maximum of 500 iterations using the distance measure described above.

Identifying Largest RNA Clusters.

Even after outlier removal, independent k-means clusterings of models in the Selected Set to k_nat bins were slightly different. To identify the largest RNA clusters, we had to identify the consensus large clusters from all clustering runs. In each clustering run, the structures closest to the centroids of the three largest clusters were recorded. Out of this nonunique total of 3 × 100 representative structures, the three occurring most frequently were selected, and taken as representatives for the consensus top three largest clusters (labeled in main text as “three largest clusters”) and illustrated in Fig. 4. All molecular figures were generated using Pymol (Version 1.2r3pre, Schrödinger, LLC).

Generation of the Randomly Oriented RNA Helices Dataset.

Our cluster analysis approach sorts models based on their percentage of time in cluster intersections. As sorting is relative, we would still find “clusters” for perfectly random data. To check that results are not dominated by noise, we generate a synthetic dataset with randomly oriented RNA helices relative to the reference by using uniformly distributed points on a unit sphere to describe the end points of helices. The same was done for helix origins, with scaling length randomly selected from distance distributions in the real dataset. We then conducted the clustering analysis with the same clustering dimensions so as to have a reference to compare our real dataset to.