Frustration, specific sequence dependence, and nonlinearity in large-amplitude fluctuations of allosteric proteins

Abstract

Proteins have often evolved sequences so as to acquire the ability for regulation via allosteric conformational change. Here we investigate how allosteric dynamics is designed through sequences with nonlinear interaction features. First, for 71 allosteric proteins of which two, open and closed, structures are available, a statistical survey of interactions using an all-atom model with effective solvation shows that those residue contact interactions specific to one of the two states are significantly weaker than are the contact interactions shared by the two states. This interaction feature indicates there is underlying sequence design to facilitate conformational change. Second, based on the energy landscape theory, we implement these interaction features into a new atomic-interaction-based coarse-grained model via a multiscale simulation protocol (AICG). The AICG model outperforms standard coarse-grained models for predictions of the native-state mean fluctuations and of the conformational change direction. Third, using the new model for adenylate kinase, we show that intrinsic fluctuations in one state contain rare and large-amplitude motions nearly reaching the other state. Such large-amplitude motions are realized partly by sequence specificity and partly by the nonlinear nature of contact interactions, leading to cracking. Both features enhance conformational transition rates.

Proteins have evolved sequences that allow them to meet many requirements. For enzymes, two obvious requirements are foldability and catalytic ability. In the cellular context, a third requirement is regulation: Many proteins need to turn their activities on and off by changing conformation upon binding to their regulatory molecules or by posttranslational modification, i.e., the allosteric effect (1, 2). What are the design principles for meeting these requirements? It has been understood that foldability can be accomplished by having an overall funnel-like energy landscape: the principle of minimum frustration (3). Catalytic requirements seem to arise case-by-case, but precise spatial arrangement of catalytic residues is clearly of central importance. As for the third requirement of regulation, however, how sequences and structures are designed to facilitate conformational change is less clear. To enable conformational changes, proteins need to make relatively large-amplitude fluctuations toward specific directions. Here, we address the design principles for rotein allostery using an all-atom-based simplified force field.

In native-basin dynamics, it has been well established that the quasi-harmonic fluctuations are encoded largely in the three-dimensional architecture, as illustrated by the structure-based elastic network models (ENMs) (4–8). The relative root mean square fluctuations (RMSF) in the native state can be accurately reproduced by the Gaussian network model (5), a member of the ENM family. The direction of conformational change from the open (apo) state can usually be represented well by a few low-frequency modes of the anisotropic network model (6), another version of the ENM family, constructed at the open state.

Mounting evidence, however, suggests that protein architecture alone is not sufficient, but that sequence specificities also play crucial roles in encoding motions (9–11). Some mutations that do not modify catalysis or the native structure alter functional behavior dramatically (11, 12). A recent theoretical study has shown that the interactions within a protein can be locally frustrated due to the restraints imposed by functions (13), suggesting that functional requirements on the sequence may conflict with the optimal conditions for folding. Indeed, a survey of allosteric proteins shows that hinge regions are located near regions of high frustration according to a residue-based simplified energy function (14). Clearly, functional dynamics is indeed modulated by the detailed physicochemical features of the specific sequences.

Protein motions modeled by elastic network models are harmonic, but the large-amplitude fluctuations required for chemically relevant conformational change are anharmonic (15). We expect nonlinear effects come into play to facilitate large-amplitude fluctuations in the native-basin dynamics, especially for the allosteric proteins. Clearly when proteins pass through their transition states for rearrangement, nonlinearity should be of central importance.

To address these issues, technically we need a simulation model that can take into account sequence-specific and nonlinear interactions and that is efficient enough to simulate large-amplitude fluctuations for many proteins. Conventional all-atom force-field models can be used, but their application to large-amplitude motions for many proteins is difficult. On the other hand, the perfect funnel model (often called Go models) (16–18), developed based on the energy landscape theory (3), can efficiently simulate large-amplitude fluctuations, but normally it does not take into account the chemical nature of interactions. Here, combining an all-atom description with the perfect funnel model, we develop a coarse-grained (CG) model that explicitly uses atomic interactions obtained via a multiscale protocol.

In this work, we start with a statistical survey of residue-pairwise interaction energies computed from an all-atom model with implicit solvation both for a set of single-domain proteins and for a set of allosteric proteins. For the latter, we find a simple but robust feature in the distribution of interaction energies, which facilitates conformational changes. This observation parallels results obtained with a simplified residue-level model (14). Then, to take into account this feature, we developed an atomic-interaction-based coarse-grained (AICG) model via a multiscale method. We verify that this model can predict both the native-basin mean fluctuations and the orientation of conformational change more accurately than either ENMs or the standard pure-structure-based models do. Using adenylate kinase as an example, we find that nonlinear effects and cracking allowed by the pairwise contact interactions, together with the above-mentioned local frustration, enables allosteric proteins to exhibit rare and large-amplitude fluctuations nearly up to the opposite state basin.

Result and Discussions

Specificity in Contact Energies.

We start with statistical surveys of residue-pairwise interaction (contact) energies. To estimate contact energies at the native structure, we employed an energy decomposition scheme with the AMBER force field and an implicit solvent model (19) (see Materials and Methods).

First, for a set of 40 single-domain proteins (termed the training set), we calculated the contact energies for every residue pair. We find that the energy distribution clearly exhibits an exponential distribution up to the lower bound -15 kcal/mol (Fig. 1A and SI Appendix, Fig. S1A). The precise origin of such simple exponential distribution law, however, is unclear, although it may reflect the selection temperature (20). We also note that the contact energies are only weakly correlated with the number of atomic contacts between the residue pairs (Fig. 1A, Inset) and the Cα–Cα distances (SI Appendix, Fig. S1B).

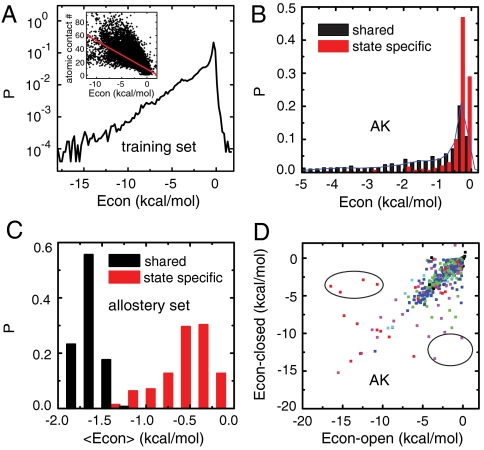
Fig. 1.

Statistical survey of contact energies. (A) Distributions of the contact energies for all the single-domain proteins in the training set. The inset shows the correlation between the contact energies and the number of atomic contacts. (B) Distributions of the contact energies for the state-specific contacts (red) and the shared contacts (black) in adenylate kinase (PDB ID 1AKE and 4AKE). The blue line is the same distribution as A. (C) Distributions ofthe averaged contact energies for the state-specific contacts (red) and the shared contacts (black) among the allosteric proteins in the allostery set. (D) Correlation between the contact energies for the shared contacts in the open and closed states for adenylate kinase. The contacts showing the most distinct energies between the two states are circled in black. Red, contacts between residues with opposite charges; pink, charged-polar contacts; green, charged-apolar contacts; cyan, polar-polar contacts; blue, polar-apolar or apolar-apolar contacts; black, contacts between residues with identical charges.

Next, we performed the same statistical survey for a set of 71 allosteric proteins (termed the allostery set) which have at least two well-defined states: the open and the closed states. We classified the contacts into two categories, the contacts formed only in one of the two states (state-specific contacts) and those contacts formed in both states (shared contacts). Fig. 1B shows the contact energy distributions of the two sets of contacts for adenylate kinase, a model allosteric protein (10–12, 21–28). To address the effects of sequence specificity unambiguously, we did not include interactions with ligands or substrates throughout this work. Interestingly, the state-specific contacts (red bars) are significantly weaker than the shared contacts (black bars). The shared contacts have a long-tailed energy distribution essentially the same as that for single-domain proteins (blue curve). In contrast, the state-specific contact energies are nearly always weak. Apparently, this feature facilitates conformational change because the state-specific contacts need to be broken upon conformation change.

This pattern is seen not only for adenylate kinase, but also for all the proteins in the allostery set, as illustrated in Fig. 1C, which gives the distributions of the contact energies averaged for each protein in the set. For each protein, the averaged shared contact was always stronger than the averaged state-specific contacts. Such a simple but robust interaction feature would provide a general principle of sequence design via evolution for allosteric proteins. Moreover, for the case of F₁-ATPase (29) which takes the three distinct conformations of αβ-subunits, we see the same tendency extended to the three categories (SI Appendix, Fig. S2).

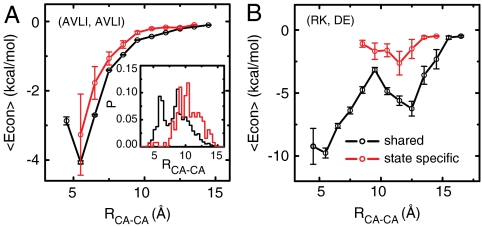
One may argue that the difference between the shared and the state-specific contact energies may come directly from the different compositions of amino acids in the two sets. This argument is partly true in that the amino acid compositions are indeed biased as in the SI Appendix, Fig. S3; hydrophobic (charged) pairs are more frequent in the shared (state-specific) contacts. Similarly, one can argue that the Cα–Cα distances may distribute in different ways in the two contact sets. This argument is also partly true, as shown in the inset of Fig. 2 and SI Appendix, Fig. S4. Yet, importantly, even for the same type of amino acid pairs and at the same Cα–Cα distance, the average contact energies are different between the shared and the state-specific contact sets (Fig. 2 A and B and SI Appendix, Fig. S5). Thus, the weak contact energies for the state-specific pairs are encoded by multiple means, the amino acid compositions, the Cα-Cα distances, and more detailed side-chain interactions.

Fig. 2.

(A) Average of contact energies as a function of Cα–Cα distances for the shared contacts (black) and state-specific contacts (red) formed between the aliphatic residues (A, V, L, I). The corresponding distance distributions are given in the inset. (B) The average of contact energies as a function of Cα–Cα distances for the shared contacts (black) and state-specific contacts (red) formed between the oppositely charged residues.

Finally, we address the enzymatic functional aspect for adenylate kinase. Among the shared contact pairs, some contact energies are quite different in the open and closed states (Fig. 1D). Many of these contacts involved charged residues which are often functionally relevant. The contacts that showed the most distinct energies between the two states (marked by the black circles) involved at least one of the residues D54, K200, D158, E167, E162, K50, and D61. All of these are responsible for the substrate binding, the hinge motion, or the catalysis. These results are in harmony with the observation of the local frustrations in ref. 13, which are useful for functioning. Contact energies optimal for the stability in one state can be structurally frustrated in the other state, which is required for functioning. It is helpful for sculpting the functional dynamics, so as to make only part of the protein movable, like a macromachine.

Modeling Protein Motions with Specific Contact Energies and Nonlinearity.

Now we use the above-characterized atomic-interaction (AI) based contact energies to model the dynamics of protein motions. We employed a CG model where each amino acid was simplified as a bead located at its Cα position, and a potential function form of refs. 16–18 that is based on the energy landscape theory and has been applied (26, 27, 30–32). In contrast to the homogeneous contact strength used in refs. 16–18, which is represented by a single coefficient in the nonlocal term of the native interaction, here we generalized the energy function so that the coefficients depend on residues. The coefficients were determined by referring to the energies and dynamics of the all-atom model via a multiscale protocol (SI Appendix Text and Fig. S6) (33–35). Strengths of contact energies are proportional to AI contact energies obtained by the AMBER energy decomposition, and are therefore able to capture the specificity of the contact energies discussed in the first subsection. Moreover, for the local potentials, i.e., the angle term and the dihedral term, the coefficients are dependent on the secondary structure of the residue. The local and nonlocal interaction weights were tuned to fit the native-basin mean fluctuations by CG simulations with those by the all-atom simulations for the 23 proteins in the training set (the training set sub) (SI Appendix Text and Tables S1 and S2). We call the resulting CG model the AICG model. Compared with the ENM, the AICG incorporates chemical specificity and nonlinearity based on the full all-atom force field.

Mean Fluctuations in the Native Basin.

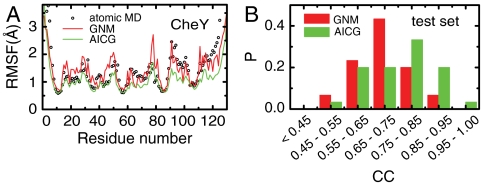
We first test the AICG model by comparing the native-state mean fluctuations calculated by the AICG with those found by the all-atom (AA) simulations. We estimated the RMSF along the sequence and calculated the correlation coefficient (CC) between the RMSFs by CG simulations and those by AA simulations. Using a protein CheY (PDB ID 1E6K) as an example, Fig. 3A shows the RMSFs predicted by the AICG and by the Gaussian network model, which is known to be the best version among the ENM family for the RMSF calculation, together with those by AA simulations. Both the Gaussian network model and AICG approximate the AA RMSFs reasonably well. Quantitatively, AICG (CC = 0.84) can approximate the RMSFs somewhat better than the Gaussian network model (CC = 0.72). This result is not so surprising because we have more parameters in the AICG. For the statistics, we compared the RMSFs for the 30 test-set proteins, which are exclusive from the training-set proteins. As shown in Fig. 3B (the distribution) and Table 1 (the average), we see that the AICG outperforms the Gaussian network model and the anisotropic network model in predicting the RMSFs. Such improvements probably arise from the atomic-based estimate of contact energies as well as the anharmonic nature of the pairwise energy terms.

Fig. 3.

(A) RMSFs as a function of residue number calculated by AA MD simulations (black), Gaussian network model (GNM) (red), and AICG (green) for protein CheY. The RMSFs by the GNM are scaled to match the average to that of the AA MD simulations. (B) Distribution of the CC for the GNM (red) and the AICG (green) for the test set.

Table 1.

Average CC and SE between the RMSFs derived by AA MD and by different CG models, including Gaussian network model (GNM), anisotropic network model (ANM), and AICG model

Models	GNM	ANM	AICG
CC	0.694	0.648	0.758
SE	0.018	0.031	0.021

Conformational Change Direction.

We move on to the investigation of the conformational change of allosteric proteins. Many years ago, Tama et al. pointed out that the directions of conformational change from the open state to the closed state can often be well represented by a few low-frequency normal modes defined in the open state (36). Combining this observation with the success of ENMs to approximate low-frequency normal modes suggests that the structure alone can encode the conformational change direction of allosteric proteins to a certain extent. Interestingly, however, the same analysis often fails in the opposite direction; using the low-frequency modes in the closed state, one cannot well predict the directions of conformational change from the closed to the open states (36).

We tested whether the AICG can predict the direction of conformational change for the 71 proteins in the allostery set. Quantitatively, the overlaps between the identified low-frequency modes and the experimentally observed structural difference between the two states can be used to evaluate the model predictions (SI Appendix). Following ref. 8, we used the maximal overlap and cumulative overlap among the first several modes for the assessment. We illustrate the simulation results for adenylate kinase by AICG as well as by the ENM (specifically, the anisotropic network model) (Fig. 4 A and B). When the open (apo) state is used as the reference, both the ENM (red in Fig. 4D) and the AICG (green in Fig. 4D) worked equally well; the lowest frequency mode represents ∼80% of the conformational change. Whereas, when the closed (holo) state is used as the reference, AICG (green) outperformed the ENM (red, Fig. 4C) (e.g., the cumulative overlap is improved by around 15.0%).

Fig. 4.

Structures and low-frequency modes of adenylate kinase. (A and B) Crystal structures of adenylate kinase in the closed state (A) and the open state (B). (C and D) Overlaps between the distance vector and the low-frequency modes predicted by anisotropic network model (ANM) (red), homogeneous AICG (homo AICG) (black), and full AICG (green) using the closed (C) or open (D) structures as the reference. The cumulative overlaps are also shown by the solid line (with the same color code). Only the first 10 lowest-frequency modes are shown.

The improvement was not limited to adenylate kinase, and a statistical survey for the proteins in the allostery set showed systematic improvement of the averaged overlaps by the AICG over the results by the ENM (Table 2 and SI Appendix, Fig. S7). Table 2 shows that the average maximal overlap by the AICG was larger than that by the ENM by around 8.6% (8.5%) when the closed (open) structure is used as the reference.

Table 2.

Average maximal overlap (MO) and cumulative overlap (CO) among the first five modes by anisotropic network model (ANM), full AICG model (full), homogeneous AICG model (homo), and heterogeneous-nonlocal AICG model (hete-nloc) based on the allosteric proteins in allostery set

		ENM	AICG
Models		ANM	Full	Homo	Hete-nloc
Open → closed	MO	0.471 (0.028)	0.556 (0.027)	0.528 (0.029)	0.549 (0.029)
	CO	0.594 (0.030)	0.675 (0.028)	0.647 (0.029)	0.657 (0.029)
Closed → open	MO	0.429 (0.025)	0.515 (0.027)	0.469 (0.027)	0.499 (0.028)
	CO	0.555 (0.028)	0.643 (0.028)	0.604 (0.029)	0.629 (0.030)

Corresponding SEs are listed in the brackets.

This improvement by the AICG over the ENM may have several sources: sequence specificity in contact energies, specificity in the local rigidity, or nonlinearity in the contact potential. To identify each contribution, we tested some intermediate models (SI Appendix, Table S3). The homogeneous AICG model is one where both contact strengths and local potentials are homogeneous (essentially the same as the standard off-lattice Go model; ref. 16). The heterogeneous-nonlocal AICG model is one where only the contact strengths are heterogeneous. The (full) AICG has both heterogeneous contact strengths and heterogeneous local potentials. From Table 2, we see that the heterogeneity of the local interaction contributes to the functional fluctuations in both the open and closed states, whereas the heterogeneity in the contact interactions is more crucial for the functional fluctuations in the closed state. This result suggests that fluctuations around the closed state involve the breaking of the state-specific contacts, which is sensitive to the chemical nature of the residues. The prominent difference between the homogeneous AICG and the ENM (Fig. 4 and Table 2) comes from the nonlinearity in the pairwise contact as opposed to the linear network force and the linear approximation of the normal mode analysis of the ENM, directly suggesting the dominant role of local unfolding, or cracking, for the dynamics around the functional states. We note that the ENM can also be improved by introducing interaction heterogeneity to the force constants of the ENM energy function, as in Yang et al. (8).

Rare and Large-Amplitude Fluctuations of Adenylate Kinase.

We next focus on rare and large-amplitude fluctuations of allosteric proteins. We illustrate them for the fluctuations in the closed state of adenylate kinase. Fig. 5A plots the rmsds from the closed (x axis) and from the open (y axis) states of simulated samples by heterogeneous-nonlocal AICG (black dots). Because it is an ensemble for the closed state, the majority of samples had small rmsds (∼2 Å) from the closed state, whereas the mean rmsd from the open state was ∼7 Å. Importantly, the mean fluctuations by AICG agree with those by AA results in absolute scale (similar to Fig. 3A). In Fig. 5A, we observe that the large-deviation data are highly biased toward the open state (decreases in the rmsd from the open state up to ∼4 Å). Generally, the conformation space of a given rmsd is exponentially growing with the rmsd value and thus random fluctuations always tend to increase rmsds, and thus the fluctuations biased to lower rmsd here is highly nontrivial. We note that the AICG was constructed purely using the closed, but not the open, state structural information. Quantitatively, the probability distribution calculated by an umbrella sampling (37) shows that, with the probability 10^-6, the protein can approach ∼3.5 Å from the open state (Fig. 5B) (SI Appendix).

Fig. 5.

Rare and large-amplitude fluctuations in closed state of adenylate kinase. (A) Scattering plot of the rmsd from the closed state (x axis) and rmsd from the open state (y axis) with harmonic AICG (harmonic) (red), homogeneous AICG (homo) (blue), and the heterogeneous-nonlocal AICG (hete-nloc) (black). (B) Distribution of the rmsd from the open state by the three models. (C) Average rmsds from the open and closed states as a function of the strength of the pulling potential. The results with the randomly heterogeneous interactions were also shown (dashed lines). (D) Distributions of the fraction of native contacts Q for the NMP (red), LID (blue), and core domains (black) by using the homogeneous AICG (dashed lines) and heterogeneous-nonlocal AICG (solid lines). The green arrow in A indicates the direction of the conformation change from the closed to open states.

Next, we address what features cause such biased large-amplitude fluctuations. We employed a variant of AICG with a harmonically truncated contact potential (SI Appendix Text and Fig. S8) (harmonic AICG, red dots in Fig. 5A) as well as the homogeneous AICG (blue dots), of which the local potentials are identical to that of the heterogeneous-nonlocal AICG. The harmonic AICG exhibited markedly reduced fluctuations (rmsd only reach 5.8 Å with the probability 10^-6). The homogeneous AICG, which allows cracking, shows modest fluctuations (rmsd reaches 5 Å with the probability 10^-6), which are larger than those of the harmonic AICG, but are much smaller than those predicted by heterogeneous-nonlocal AICG. These results indicate that both the nonlinearity and the sequence specificity contribute to the observed large-amplitude fluctuations.

We further monitor large-amplitude motions of the protein by investigating the response to an applied perturbation. Here, for the closed state of adenylate kinase, we applied a pulling potential toward the open state, and observed the mean rmsds as a function of the strength of the pulling potential (SI Appendix). The mean rmsd curves show marked differences (Fig. 5C). The heterogeneous-nonlocal AICG (black curve) shows a transition from the closed state to nearly open states at the smallest strength of the pulling potential, and the homogeneous AICG (blue) followed it at a larger strength, whereas the harmonic AICG does not make any transition at all, of course (red). If the interaction heterogeneity is introduced randomly, the resulted transition curve was almost identical to that of the homogeneous AICG (dashed line in Fig. 5C), showing the importance of specifically designed sequence heterogeneity that promotes the rapid breaking of state-specific contacts.

We also looked into the structural aspects of fluctuations of adenylate kinase, which has three domains, core domain, ATP binding domain (called LID), and AMP binding domain (called NMP), linked by two hinges (Fig. 4 A and B). The free energy surface described in terms of the two hinge angles (SI Appendix, Fig. S9) shows the degree of fluctuation in the two hinge motions. First, it shows that fluctuations in the closed state are markedly smaller than those in the open state. Second, both the nonlinear nature and sequence-specific features in the heterogeneous-nonlocal AICG enhance hinge motions. Fluctuations in the closed state obtained by the heterogeneous-nonlocal AICG and the homogeneous AICG, but not by the harmonic AICG, are inherently larger in the LID-core hinge than in the NMP-core hinge. The free energy surface indicates that upon closing, two pathways are possible, but the pathway in which the LID domain closes first is more favorable, which is consistent with Lu and Wang (27, 28). In contrast, upon opening, the LID domain always opens before the NMP domain. Fig. 5D plots fluctuations in each domain by homogeneous AICG and heterogeneous-nonlocal AICG models, showing that sequence specificity, but not the structure alone, makes the NMP domain more fragile than the LID domain. The core domain is, as expected, more rigid primarily by its structure. This result is reminiscent of recent experimental work which shows that the thermal adaptations of the catalytic activity of adenylate kinase from Bacillus are mainly contributed by the sequence changes in the LID and NMP domains instead of the hinge or core domain (12).

The same analysis in the open state of adenylate kinase shows similar trends, but sequence-specific and nonlinear effects are much weaker (SI Appendix, Fig. S10). Thus, fluctuations in the open state are dominated by quasi-harmonic normal modes that are mostly determined by the open structure.

A trajectory that exhibited large-amplitude fluctuations is shown as a series of snapshots in SI Appendix, Fig. S11 and as in Movie S1 and suggests a particular cracking pattern. The local unfolding for the contacts between the NMP and core domains is coupled to the opening of the LID domain to some extent (SI Appendix, Figs. S11 and S12).

Sequence Specificity in Conformational Hopping.

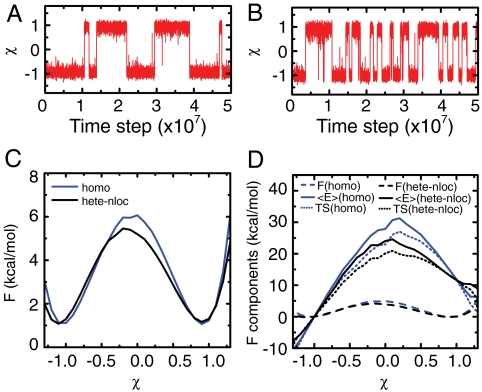
So far we have reported on the fluctuations in one basin. Now we address how such sequence-designed large-amplitude fluctuations in each basin promote the complete conformational transitions between the two basins. We implemented the AICG in the multiple-basin potential (30) (SI Appendix) and simulated reversible conformational transitions for adenylate kinase (Fig. 6). We see that the heterogeneous-nonlocal AICG enables more frequent transitions than does the homogeneous AICG (Fig. 6 A and B), suggesting that sequence specificity indeed does facilitate conformational transitions. Decomposing the free energy into energy and entropic contribution, we see that a lower free energy barrier predicted by the heterogeneous-nonlocal AICG (Fig. 6C) arises from the reduction in energy contribution to the barrier by ∼8.0 kcal/mol (Fig. 6D), which is thus a designed sequence feature. Partial unfolding as monitored by the entropy increase is also reduced for the designed sequence (Fig. 6D). The interactions designed by the specific sequence lead to more frequent conformation transitions and simultaneously allow for relatively well-defined transition pathways. Such a feature may contribute to the efficiency and robustness of the functional dynamics.

Fig. 6.

Conformational transition of adenylate kinase. (A and B) Representative trajectories with homogeneous AICG (homo) (A) and heterogeneous-nonlocal AICG (hete-nloc) (B). (C) Free energy curves by homogeneous AICG (blue) and heterogeneous-nonlocal AICG (black). (D) Free energies (dashed line) and their components, the average energy 〈E〉 (solid line), and the product of temperature and entropy TS (dotted line) by homogeneous AICG (blue) and by heterogeneous-nonlocal AICG (black). The χ is a reaction coordinate monitoring the conformation transition (SI Appendix).

Materials and Methods

Energy Decomposition.

The contact energies were calculated by the energy decomposition strategy (34, 35, 38), where the atomistic energy of a protein is decomposed into the interactions between the atom pairs. The residue–residue contact energies were calculated by summing the corresponding interactions of the atom pairs. The AMBER force field ff99SB and the generalized Born/surface area implicit solvation model were used for the calculations of the atomistic energies (19, 39). For more details, refer to the SI Appendix, in which we also discussed the possibility to model the contact energies based on the regressions of atomic contact features (SI Appendix, Fig. S13 and Table S4).

Atomic-Interaction-Based Coarse-Grained Model.

The energy function of the AICG was taken from the perfect funnel model (16–18). The nonlocal interactions were weighted according to the contact energies calculated by the energy decomposition. The average strength of the local interactions and the nonlocal interactions were optimized by matching the fluctuations calculated by the all-atom simulations (33, 34) (SI Appendix Text, Figs. S6 and S14–S16).

Simulation Details.

Here, all CG simulations were conducted by CafeMol (http://www.cafemol.org/). The all-atom simulations were conducted by AMBER 10 (19). The details for simulation method and data analysis are in the SI Appendix.

Dataset.

Four protein datasets were used, the training set (40 single-domain proteins), the training set sub (23 proteins from the training set), the test set (30 proteins), and the allostery set (71 allosteric proteins, each with two functional states). The details can be found in the SI Appendix.