Skip to main content
NCBI home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2011 Jan 28;108(9):3526–3529. doi: 10.1073/pnas.1012551108

Word lengths are optimized for efficient communication

Steven T Piantadosi 1,1, Harry Tily 1, Edward Gibson 1
PMCID: PMC3048148  PMID: 21278332

Abstract

We demonstrate a substantial improvement on one of the most celebrated empirical laws in the study of language, Zipf's 75-y-old theory that word length is primarily determined by frequency of use. In accord with rational theories of communication, we show across 10 languages that average information content is a much better predictor of word length than frequency. This indicates that human lexicons are efficiently structured for communication by taking into account interword statistical dependencies. Lexical systems result from an optimization of communicative pressures, coding meanings efficiently given the complex statistics of natural language use.

Keywords: information theory, rational analysis

One widely known and apparently universal property of human language is that frequent words tend to be short. This law was popularized by Harvard linguist George Kingsley Zipf, who observed that “the magnitude of words tends, on the whole, to stand in an inverse (not necessarily proportionate) relationship to the number of occurrences” (1).

Zipf theorized that this pattern resulted from a pressure for communicative efficiency. Information can be conveyed as concisely as possible by giving the most frequently used meanings the shortest word forms, much like in variable-length (e.g., Huffman) codes. This strategy provided one key exemplar of Zipf's principle of least effort, a grand “principle that governs our entire individual and collective behavior of all sorts, including the behavior of our language” (2). Zipf's idea of assigning word length by frequency can be maximally concise and efficient if words occur independently from a stationary distribution. However, natural language use is highly nonstationary as word probabilities change depending on their context. A more efficient code for meanings can therefore be constructed by respecting the statistical dependencies between words. Here, we show that human lexical systems are such codes, with word length primarily determined by the average amount of information a word conveys in context. The exact forms of the frequency–length relationship (3, 4) and the distribution of word lengths (5) have been quantitatively evaluated previously. In contrast, information content offers an empirically supported and rationally motived alternative to Zipf's frequency–length relationship.

A lexicon that assigns word lengths based on information content differs from Zipf's theory in two key ways. First, such a lexicon would not be the most concise one possible as it would not shorten highly informative words, even if shorter distinctive wordforms were available. Second, unlike Zipf's system, assigning word length based on information content keeps the information rate of communication as constant as possible (6). A tendency for this type of “smoothing out” peaks and dips of informativeness is known as uniform information density and has been observed in choices made during online language production (7–10). Formally, uniform information density holds that language users make choices that keep the number of bits of information communicated per unit of time approximately constant. For instance, more informative syllables are produced with longer durations than less informative syllables, meaning that speech rate is modulated to prevent communicating too many bits in a short period (7). This idea can be generalized to the design of lexical systems (11, 6): the amount of information conveyed by a word should be linearly related to the amount of time it takes to produce—approximately, its length—to convey the same amount of information in each unit of time. A constant information rate can make optimal use of the speech channel by maximizing the amount of information conveyed, without exceeding the channel capacity of speech or our cognitive systems (12, 13). Thus, lexical systems that assign length according to information content can be communicatively more efficient than those that use frequency.

Importantly, the amount of information conveyed by an instance of a word depends on its context. To formalize this, we can consider two random variables, C for contexts and W for words, with a joint distribution P(C, W) given by the natural statistics of language use. The average amount of information conveyed by a particular word w is given by the following (14):

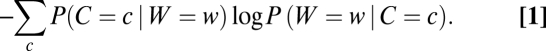graphic file with name pnas.1012551108eq1.jpg

Intuitively, this measure corresponds to the expected information conveyed by a randomly chosen instance of w from a large corpus. To see this, note that an instance of w will occur in context C = c with probability P(C = c|W = w), and will there convey an amount of information given by −log P(W = w|C = c). When estimated from a corpus, this measure is simply the mean negative log probability of tokens of w:

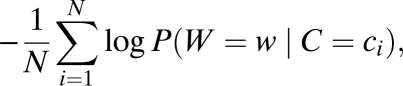graphic file with name pnas.1012551108uneq1.jpg

where ci is the context for the ith occurrence of w and N is the total frequency of w in the corpus.

In general, there are many variables that may count as part of the “context” for the purposes of language processing, including discourse context (15–20), local linguistic context (21–26), syntactic context (27, 28), and more global world knowledge (29–31). All these variables likely influence the probability of any word w, but they are not easily quantified. We chose to approximate P(W|C) by using a standard quantitative probabilistic model, an N-gram model, which treats C as consisting only of the local linguistic context containing the previous N − 1 words. This simplification allows Eq. 1 to be estimated cross-linguistically from large corpora, and is an approximation to the true information content of a word that has been used extensively in psycholinguistics. In addition, there are several possible ways to measure word length. Here, we primarily use orthographic length because it is readily available from corpora and tends to be highly correlated with both phonetic length and production time. However, we also present results in English, German, and Dutch measuring length in number of phonemes and number of syllables.

With these measures, we tested whether average information content or frequency is a better predictor of word length by computing the information conveyed by each word in Czech, Dutch, English, French, German, Italian, Polish, Portuguese, Romanian, Spanish, and Swedish. In each language, we computed Spearman rank correlations between (i) information content and length and (ii) frequency and length. This measure allowed us to test correlations without making assumptions about the parametric form of the relationship.

Results

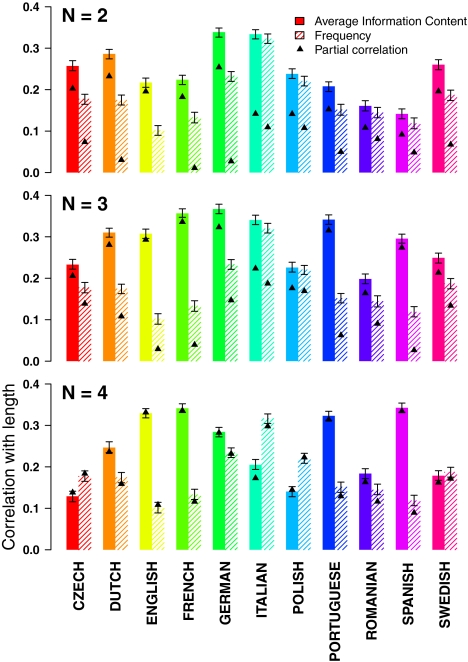
The solid and striped bars in Fig. 1 show correlations in the 11 languages between orthographic length and frequency, and orthographic length and information content, as measured by two-gram, three-gram, and four-gram models. Because of the size and form of the Google dataset, these N-gram models were not smoothed (although see SI Text). Statistical significance was assessed by using Z-tests on bootstrapped estimates of the difference between within-language correlations. In the two-gram model, information content is more strongly correlated with length than frequency across all 11 languages (P < 0.01, Z > 2.58 for each language). The three-gram models show similar patterns, showing significant effects in the predicted direction for 10 of the 11 languages (P < 0.001, Z > 3.30), with the exception of Polish, in which the trend is not significant (P > 0.47, Z = 0.71). The four-gram results show effects in the predicted direction for seven of 11 languages; all differences are significant (P < 0.001, |Z| > 4.91) except for Swedish (P = 0.29, Z = 1.05). The decreasing consistency of results for higher N-gram sizes likely results from increased estimation error caused in part by our use of Google N-gram counts, as information content in large N-gram models is more difficult to estimate than frequency, and estimation error deflates correlations (Table S1). In general, we take three-gram data—with 10 of 11 languages showing the predicted result—as the most representative finding, because the three-gram results have the highest overall correlations.

Fig. 1.

Fig. 1.

Open in a new tab

Correlations between information content and word length (solid) and between frequency (negative log unigram probability) and word length (striped) for two-gram, three-gram, and four-gram models. Error bars show bootstrapped 95% confidence intervals. Triangles show partial correlations (frequency and length partialing out information content; information content and length partialing out frequency).

Because frequency and information content are not independent, we also computed how well each variable predicts length controlling for effects of the other. The triangles in Fig. 1 show partial correlations: frequency and length, partialing out information content; and information content and length, partialing out frequency. In several languages, the partial correlation of frequency is close to zero, meaning that the effect of frequency is largely a result of the fact that it is correlated with information content. In most languages, the partial correlation of length with information content, controlling for frequency, is larger even than the absolute correlation between length and frequency.

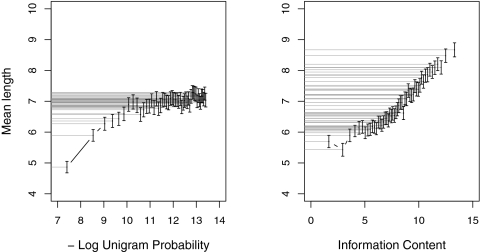
Information content and frequency exhibit qualitatively different relationships with length. Fig. 2 shows the mean length for (binned) frequency and information content in English, which is typical of the languages here with large effect sizes. The spread in the gray lines illustrate that length is more predictable from information content than from frequency. Frequency does not predict word length substantially for lower-frequency words: words in low unigram probability bins have approximately the same average length. In contrast, length varies as a function of information over almost its entire range of values, with the exception of just the few words with the very lowest information content. This pattern is observed in 11 of 11 languages and indicates that information content is not a good predictor of length for the 5% to 20% least informative (and typically also most frequent) words. This is potentially caused by the fact that, in text on the Internet, many long words occur in highly predictable collocations such as “all rights reserved.” These long words are highly predictable, conveying little information, and thus increase the mean length of the least informative words.

Fig. 2.

Fig. 2.

Open in a new tab

Relationship between frequency (negative log unigram probability) and length, and information content and length. Error bars represent SEs and each bin represents 2% of the lexicon.

To ensure that the results were not driven by artifacts of the Google dataset, we replicated this study in English by using the British National Corpus (BNC) (32), state-of-the-art N-gram smoothing techniques, and separate training corpora for P(W = w|C = c) and P(C = c|W = w). This was not possible in all languages because large enough corpora are not available.† In these data, the correlation between frequency (negative log unigram probability) and length was 0.121. The correlation for information content was 0.161 with the use of two-gram models and 0.168 with the use of three-gram models. Both N-gram correlations were significantly higher than the frequency correlation (P < 0.001, Z > 9.49). Interestingly, this analysis reveals no partial effects of frequency: the correlation of frequency partialing out information content was negative (−0.009 for two-gram and −0.009 for thee-gram models), but not significantly so (P > 0.13, Z < −1.48 for each comparison). The correlations for two-gram and three-gram models partialing out frequency were 0.106 and 0.117, respectively, both of which were significantly greater than zero (P < 0.001, Z > 16.90). These results show qualitatively similar results to the Google data. The numerical pattern of correlations differs somewhat from the Google data, likely because the BNC contains only 100 million words, only one 10,000th the size of the Google dataset for English.

In English, German, and Dutch, detailed phonetic information is available from the CELEX database (34). For these languages, we also computed the correlations measuring length in number of phones and also number of syllables. This resulted in two comparisons between information content and frequency for each language and each N-gram model. For two-gram and three-gram models, eight of eight English and Dutch correlations all are significant in the predicted direction (P < 0.001, Z > 9.19 for each comparison), with information content a better predictor of length than frequency. For German, phonetic length and syllable length trend in the right direction for two-gram models, but only the latter is statistically significant (P < 0.001, Z = 5.22). For three-gram models, German is significant in the wrong direction for length measured in phones (P < 0.001, Z = −4.42), but not significant for length measured in syllables (P = 0.29, Z = 1.04). Like the orthographic results, the four-gram results are more mixed, with two of two significant effects in the predicted direction for English (P < 0.001, Z > 12.43), zero of two significant effects in the predicted direction for German (P < 0.001, Z > −5.49), and marginally significant effects each way for Dutch. In general, these result show similar patterns to the orthographic measure of length used here earlier. Indeed, in several of the other languages studied (e.g., Spanish, Italian, Portuguese), there is a close relationship between the orthography and phonetics, meaning that these results likely generalize to phonetic length as well.

Discussion

Our results indicate that information content is a considerably more important predictor of word length than frequency. These results hold across languages with varying degrees of morphological inflection, indicating that the results are generally true regardless of how languages use morphemes to encode information. We expect that our basic theory—that information content predicts word length—should generalize to languages with a more free word order, although it is not clear that N-gram contexts could be used to estimate information content in such languages.

One likely mechanism for how the lexicon comes to reflect predictability is that information content is known to influence the amount of time speakers take to pronounce a word: words and phones are given shorter pronunciations in contexts in which they are highly predictable or convey less information (7, 13, 27, 28, 35–38). If these production patterns are lexicalized, word length will come to depend on average informativeness.

Our results show significant partial effects of frequency, and it may be that lexicons assign word lengths based on the effective information content for the language processing system. People's expectations about upcoming words are influenced by word frequency, even controlling for information content and other relevant factors (39). This means that a communication system which is optimal for people's probabilistic expectations may include frequency effects. Alternatively, the frequency effects might be illusory: a model of information content that takes into account more than N-gram contexts—for instance, global discourse context or world knowledge—may explain all the variance frequency explains.

In general, we take these results to necessitate a revision of Zipf's view of frequency and lexical efficiency. The most communicatively efficient code for meanings is one that shortens the most predictable words—not the most frequent words. Human lexicons are these types of information—theoretically efficient codes for meaning, constructed to respect the interword statistical dependencies of normal language use.

Materials and Methods

In Fig. 1, we approximated the information content of each word by using an unsmoothed N-gram model trained on data from Google (40). The size and form of the Google dataset makes standard smoothing techniques infeasible and also likely unnecessary, as we study only the most frequent words and these would not be highly affected by smoothing. To uniformly define lexicons across languages, we extracted the 25,000 most frequent strings in the Google dataset for each language that also occurred in the OpenSubtitles section of the OPUS Corpus (41). This was necessary because the Google dataset was gathered from the internet and contains many frequent strings that are not words (e.g., “aaaaa” and “aaaaaa”). The most frequent words in the dataset were used because information content can be estimated reliably only from a large number of occurrences. For each language, we computed the Spearman correlation between frequency (negative log unigram probability‡) and length, information content and length, and the corresponding partial correlations. We present Spearman correlations because length is related nonlinearly to frequency and information content, although Pearson correlations give nearly identical results.

For our replication on the BNC (32), we estimated Eq. 1 by splitting the BNC into two halves. The first half was used to train an N-gram model for computing P(W = w | C = c) by using the SRILM toolkit (42) with modified Kneser–Ney smoothing (43). The N-gram model was evaluated on the second half of the corpus to estimate Eq. 1. As with the Google data, we evaluated the 25,000 most frequent words that also occurred in the OpenSubtitles section of the OPUS Corpus.

Supplementary Material

Supporting Information
supp_108_9_3526__index.html (628B, html)

Acknowledgments

We thank Roger Levy and Florian Jaeger for helpful discussion about this work. This work was supported by a National Science Foundation graduate research fellowship and a Social, Behavioral & Economic Sciences Doctoral Dissertation Research Improvement Grant (to S.T.P.), as well as National Science Foundation Grant 0844472 (to E.G.).

The authors declare no conflict of interest.

*This Direct Submission article had a prearranged editor.

This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1012551108/-/DCSupplemental.

†Europarl (33), for instance, contains only approximately 50 million words per language-approximately one 2,500th the size of the non-English Google dataset. Bootstrapping revealed this to be too small to yield reliable estimates of information content.

‡This transformation puts frequency on the same scale as information content, bits, and corresponds to a measure of the information conveyed by a word if its context is not known.

References

  • 1.Zipf G. The Psychobiology of Language. London: Routledge; 1936. [Google Scholar]
  • 2.Zipf G. Human Behavior and the Principle of Least Effort. New York: Addison-Wesley; 1949. [Google Scholar]
  • 3.Sigurd B, Eeg-Olofsson M, van de Weijer J. Word length, sentence length and frequency–Zipf revisited. Studia Linguistica. 2004;58:37–52. [Google Scholar]
  • 4.Strauss U, Grzybek P, Altmann G. Word length and word frequency. In: Grzybek P, editor. Contributions to the Science of Text and Language: Text, Speech and Language Technology, Vol. 31. Berlin: Springer; 2006. pp. 277–294. [Google Scholar]
  • 5.Grzybek P. History and methodology of word length studies. In: Grzybek P, editor. Contributions to the Science of Text and Language: Text, Speech and Language Technology, Vol. 31. Berlin: Springer; 2006. pp. 15–90. [Google Scholar]
  • 6.Manin D. Experiments on predictability of word in context and information rate in natural language. J Inform Processes. 2006;6:229–236. [Google Scholar]
  • 7.Aylett M, Turk A. The smooth signal redundancy hypothesis: A functional explanation for relationships between redundancy, prosodic prominence, and duration in spontaneous speech. Lang Speech. 2004;47:31–56. doi: 10.1177/00238309040470010201. [DOI] [PubMed] [Google Scholar]
  • 8.Jaeger TF. Stanford, CA: Stanford University; 2006. Redundancy and syntactic reduction in spontaneous speech. PhD thesis. [Google Scholar]
  • 9.Levy R, Jaeger TF. Speakers optimize information density through syntactic reduction. In: Schölkopf B, Platt J, Hoffman T, editors. Advances in Neural Information Processing Systems 19. Cambridge, MA: MIT Press; 2007. pp. 849–856. [Google Scholar]
  • 10.Jaeger TF. Redundancy and reduction: Speakers manage syntactic information density. Cognit Psychol. 2010;61:23–62. doi: 10.1016/j.cogpsych.2010.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Piantadosi S, Tily H, Gibson E. The 31st Annual Meeting of the Cognitive Science Society (CogSci09) Austin, TX: Cognitive Science Society; 2009. The Communicative Lexicon Hypothesis; pp. 2582–2587. [Google Scholar]
  • 12.Frank AF, Jaeger TF. Speaking rationally: Uniform information density as an optimal strategy for language production. In: Love BC, McRae K, Sloutsky VM, editors. The 31st Annual Meeting of the Cognitive Science Society. Austin, TX: Cognitive Science Society; 2008. pp. 939–944. [Google Scholar]
  • 13.van Son R, Pols L. How efficient is speech? Proc Inst Phonetic Sci. 2003;25:171–184. [Google Scholar]
  • 14.Cohen Priva U. Using information content to predict phone deletion. In: Abner N, Bishop J, editors. Proceedings of the 27th West Coast Conference on Formal Linguistics. Somerville, MA: Cascadilla Proceedings Project; 2008. pp. 90–98. [Google Scholar]
  • 15.Altmann G, Steedman M. Interaction with context during human sentence processing. Cognition. 1988;30:191–238. doi: 10.1016/0010-0277(88)90020-0. [DOI] [PubMed] [Google Scholar]
  • 16.Altmann G, Garnham A, Dennis Y. Avoiding the garden path: Eye movements in context. J Mem Lang. 1992;31:685–712. [Google Scholar]
  • 17.Tanenhaus MK, Spivey-Knowlton MJ, Eberhard KM, Sedivy JC. Integration of visual and linguistic information in spoken language comprehension. Science. 1995;268:1632–1634. doi: 10.1126/science.7777863. [DOI] [PubMed] [Google Scholar]
  • 18.Spivey MJ, Tanenhaus MK. Syntactic ambiguity resolution in discourse: Modeling the effects of referential context and lexical frequency. J Exp Psychol Learn Mem Cogn. 1998;24:1521–1543. doi: 10.1037//0278-7393.24.6.1521. [DOI] [PubMed] [Google Scholar]
  • 19.Kaiser E, Trueswell JC. The role of discourse context in the processing of a flexible word-order language. Cognition. 2004;94:113–147. doi: 10.1016/j.cognition.2004.01.002. [DOI] [PubMed] [Google Scholar]
  • 20.Grodner D, Gibson E, Watson D. The influence of contextual contrast on syntactic processing: evidence for strong-interaction in sentence comprehension. Cognition. 2005;95:275–296. doi: 10.1016/j.cognition.2004.01.007. [DOI] [PubMed] [Google Scholar]
  • 21.Frazier L. On Comprehending Sentences: Syntactic Parsing Strategies. Storrs, CT: Univ of Connecticut; 1979. [Google Scholar]
  • 22.Jurafsky D. A probabilistic model of lexical and syntactic access and disambiguation. Cogn Sci. 1996;20:137–194. [Google Scholar]
  • 23.Gibson E. Linguistic complexity: Locality of syntactic dependencies. Cognition. 1998;68:1–76. doi: 10.1016/s0010-0277(98)00034-1. [DOI] [PubMed] [Google Scholar]
  • 24.McDonald SA, Shillcock RC. Eye movements reveal the on-line computation of lexical probabilities during reading. Psychol Sci. 2003;14:648–652. doi: 10.1046/j.0956-7976.2003.psci_1480.x. [DOI] [PubMed] [Google Scholar]
  • 25.Frisson S, Rayner K, Pickering MJ. Effects of contextual predictability and transitional probability on eye movements during reading. J Exp Psychol Learn Mem Cogn. 2005;31:862–877. doi: 10.1037/0278-7393.31.5.862. [DOI] [PubMed] [Google Scholar]
  • 26.Levy R. Expectation-based syntactic comprehension. Cognition. 2008;106:1126–1177. doi: 10.1016/j.cognition.2007.05.006. [DOI] [PubMed] [Google Scholar]
  • 27.Gahl S, Garnsey S. Knowledge of grammar, knowledge of usage: Syntactic probabilities affect pronunciation variation. Language. 2004;80:748–775. [Google Scholar]
  • 28.Tily H, et al. Syntactic probabilities affect pronunciation variation in spontaneous speech. Lang Cognition. 2009;1:147–165. [Google Scholar]
  • 29.Trueswell J, Tanenhaus M, Garnsey S. Semantic influences on parsing: Use of thematic role information in syntactic ambiguity resolution. J Mem Lang. 1994;33:285–318. [Google Scholar]
  • 30.Altmann GT, Kamide Y. Incremental interpretation at verbs: Restricting the domain of subsequent reference. Cognition. 1999;73:247–264. doi: 10.1016/s0010-0277(99)00059-1. [DOI] [PubMed] [Google Scholar]
  • 31.Kamide Y, Altmann G, Haywood S. The time-course of prediction in incremental sentence processing: Evidence from anticipatory eye movements. J Mem Lang. 2003;49:133–156. [Google Scholar]
  • 32.Clear J. The British National Corpus. Cambridge, MA: MIT Press; 1993. [Google Scholar]
  • 33.Koehn P. Proceedings of the 10th Machine Translation Summit (MT Summit) Aichi, Japan: Asia-Pacific Association for Machine Translation; 2005. Europarl: A parallel corpus for statistical machine translation; pp. 79–86. [Google Scholar]
  • 34.Baayen HR, Piepenbrock R, Gulikers L. The CELEX Lexical Database. (Release 2) Philadelphia: Univ of Pennsylvania; 1995. [Google Scholar]
  • 35.Lieberman P. Some effects of semantic and grammatical context on the production and perception of speech. Lang Speech. 1963;6:172–187. [Google Scholar]
  • 36.Jespersen O. Language: Its Nature, Development, and Origin. New York: Henry Holt; 1922. [Google Scholar]
  • 37.Fowler C, Housum J. Talkers signaling of new and old words in speech and listeners’ perception and use of the distinction. J Mem Lang. 1987;25:489–504. [Google Scholar]
  • 38.Gregory M, Raymond W, Bell A, Fosler-Lussier E, Jurafsky D. Chicago Linguistics Society 35 (CLS-99) Chicago: Univ of Chicago; 1999. The effects of collocational strength and contextual predictability in lexical production; pp. 151–166. [Google Scholar]
  • 39.Demberg V, Keller F. Data from eye-tracking corpora as evidence for theories of syntactic processing complexity. Cognition. 2008;109:193–210. doi: 10.1016/j.cognition.2008.07.008. [DOI] [PubMed] [Google Scholar]
  • 40.Brants T, Franz A. Web 1T 5-Gram, 10 European Languages, Version 1. Philadelphia: Linguistic Data Consortium; 2009. [Google Scholar]
  • 41.Tiedmann J. News from OPUS - a collection of multilingual parallel corpora with tools and interfaces. In: Nicolov N, Bontcheva K, Angelova G, Mitkov R, editors. Recent Advances in Natural Language Processing. Vol V. Amsterdam: John Benjamins; 2009. pp. 237–248. [Google Scholar]
  • 42.Stolcke A. Proceedings of the Seventh International Conference on Spoken Language Processing. Vol. 3. Denver: ICSLP/Interspeech; 2002. SRILM - an extensible language modeling toolkit; pp. 901–904. [Google Scholar]
  • 43.Chen SF, Goodman J. An empirical study of smoothing techniques for language modeling. Comput Speech Lang. 1999;13:359–393. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
supp_108_9_3526__index.html (628B, html)
1012551108_pnas.201012551SI.pdf (35.6KB, pdf)

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES