State-space decoding of primary afferent neuron firing rates

Abstract

Kinematic state feedback is important for neuroprostheses to generate stable and adaptive movements of an extremity. State information, represented in the firing rates of populations of primary afferent neurons, can be recorded at the level of the dorsal root ganglia (DRG). Previous work in cats showed the feasibility of using DRG recordings to predict the kinematic state of the hind limb using reverse regression. Although accurate decoding results were attained, reverse regression does not make efficient use of the information embedded in the firing rates of the neural population. In this paper, we present decoding results based on state-space modeling, and show that it is a more principled and more efficient method for decoding the firing rates in an ensemble of primary afferent neurons. In particular, we show that we can extract confounded information from neurons that respond to multiple kinematic parameters, and that including velocity components in the firing rate models significantly increases the accuracy of the decoded trajectory. We show that, on average, state-space decoding is twice as efficient as reverse regression for decoding joint and endpoint kinematics.

1. Introduction

Proprioception, or the sensation of movement and position, results from the integration of afferent inputs in the central nervous system (CNS). It provides vital information about the state of the limb during movement and serves as feedback during motor control to create stable and accurate movements. In applications where functional electrical stimulation (FES) is used to restore limb functions such as gait, posture or foot drop, it is important to be able to include feedback information to be able to cope with perturbations, muscle fatigue and non-linear behavior of the effected muscles (Matjacic et al. 2003, Winslow et al. 2003, Weber et al. 2007). Accessing and decoding the activity in native afferent signaling pathways would be a natural way to determine the kinematic state (i.e. position and velocity) of the controlled extremity (Haugland & Sinkjaer 1999). Feasibility of this approach has been demonstrated by controlling the ankle angle in a closed loop controller using the compound afferent input recorded from LIFE electrodes by Yoshida (Yoshida & Horch 1996). However, a larger and more diverse population of primary afferent recordings is needed to attain a more complete estimate of limb state. One solution is to record at the dorsal root ganglia where all proprioceptive information converges into the central nervous system. Recording at this site with multi-electrode arrays grants access to a wide variety of state information distributed across many individual neurons (Stein, Weber, Aoyagi, Prochazka, Wagenaar & Normann 2004, Weber et al. 2006, Weber et al. 2007).

Although it is generally accepted that proprioception is evoked by a variety of primary afferent (PA) inputs, including muscle, cutaneous, and joint receptors, the muscle spindle afferents are believed to be the main contributor (Gandevia et al. 1992). Various models with increasing complexity have been proposed for the muscle spindle firing rate (Matthews 1964, Poppele & Bowman 1970, Prochazka & Gorassini 1998, Mileusnic et al. 2006). These models are able to provide accurate predictions of spindle firing rates as a function of muscle length and presumed gamma drive inputs. While it might be desirable to invert these models to decode muscle length or limb-state from the firing rates of muscle spindles, such an inversion is not trivial because the models are non-linear, and position and velocity components of the firing rate are confounded. Similar limitations are applicable for including cutaneous afferents as they are often related to limb kinematics in a non-linear fashion.

To date, decoding efforts have avoided these difficulties by directly modeling each of several kinematic variables as independent functions of the afferent firing rates (Stein, Weber, Aoyagi, Prochazka, Wagenaar & Normann 2004, Weber et al. 2006). These studies used separate regression models to estimate the kinematic state of the hind limb as a weighted sum of the firing rates in a population of PA neurons recorded in the dorsal root ganglia (DRG) of cats during passive and active movements. In this paper, we refer to this approach as reverse regression since the natural relationships between the dependent and explanatory variables are reversed. We will discuss the limitations of that approach and propose an alternative decoding approach that does have these limitations. This method consists of modeling the firing rates of the primary afferents as functions of the kinematic parameters, and inverting these models via a state-space procedure to decode simultaneously all limb kinematics. Preliminary results were presented in (Wagenaar et al. 2009). In this paper, we extend the methods proposed in Wagenaar et al (2009) to include time-derivatives of the kinematic variables (velocities) and allow for decoding multiple correlated kinematic variables. We compare the efficiencies of the resulting estimates with those predicted using reverse regression (Stein, Weber, Aoyagi, Prochazka, Wagenaar & Normann 2004, Weber et al. 2006) and discuss the feasibility of using natural feedback decoding in neuroprostheses.

Finally, the coordinate frame in which limb kinematics are decoded has typically been based on polar coordinates of the endpoint of the limb or the individual joint angles (Weber et al. 2007, Bosco et al. 2000). Scott et al. (1994), found no evidence for a particular coordinate frame based on modeling studies of muscle spindle distributions (Scott & Loeb 1994). Stein et al. (2004), also found no significant difference in correlation coefficients when comparing PA firing rates to kinematic state in polar endpoint coordinates and joint angle space (Weber et al. 2007, Stein, Aoyagi, Weber, Shoham & Normann 2004). We included both endpoint and polar coordinates in the analysis of this paper since both representations are relevant for implementation in neural prostheses.

2. Methods and data

2.1. Surgical procedures

All procedures were approved by the Institutional Animal Care and Use Committee of the University of Pittsburgh. Two animals were used in these procedures. Both were anesthetized with isoflurane (1–2%) throughout the experiment. Temperature, end tidal CO2, heart rate, blood pressure, and oxygen saturation were monitored continuously during the experiments and maintained within normal ranges. Intravenous catheters were placed in the forelimbs to deliver fluids and administer drugs. A laminectomy was performed to expose the L6 and L7 dorsal root ganglia on the left side. At the conclusion of the experiments, the animals were euthanized with KCL (120 mg/kg) injected IV.

2.2. The experiment

A custom frame was designed to support the cat’s torso, spine, and pelvis while allowing the hind limb to move freely through its full range of motion (figure 1). A stereotaxic frame and vertebrae-clamp were used to support of the head and torso, and bone screws were placed bilaterally in the iliac crests to tether the pelvis with stainless steel wire (not shown in figure 1).

Figure 1.

The animal was positioned in a custom designed frame to support the torso and pelvis, enabling unrestrained movement of the left hind limb. The foot was attached to a robotic arm and active markers were placed on the hind limb to track the hind limb kinematics. A 90 channel micro-electrode array was inserted in the L6/L7 DRG and the neural activity was recorded using a programmable real-time signal processing system (TDT RZ2).

Hind limb kinematics were recorded with a high speed motion capture system (Impulse system, PhaseSpace Motion Capture, USA). Active LED markers were placed on the iliac crest (IC), hip, knee, ankle, and metatarsophalangeal (MTP) joints. During post-experiment analysis, the knee position was inferred from the femur and shank segment lengths and the hip and ankle markers because skin slip at the knee marker rendered position tracking based on the knee marker unreliable (Stein, Weber, Aoyagi, Prochazka, Wagenaar & Normann 2004, Weber et al. 2006). Synchronization between neural and kinematic data was ensured by recording a time-stamp in the neural recording system for every captured kinematic frame.

A robotic arm (VS6556E, DENSO Robotics, USA) was used to move the left foot in the parasagittal plane. The foot was strapped in a custom holder attached to the robot via a pivoting joint that allowed free rotation of the foot in the parasagittal plane (figure 1). The robot was programmed to generate center-out and random movement patterns occupying most of the motion range for the foot. Center-out patterns were ramp and hold displacements of 4cm in eight directions from a center position. Random movements, defined by a uniform distribution of limb positions and velocities within the workspace, were approximated by manually manipulating the hind limb through the entire workspace over a period of 5 minutes. During this time, cameras recorded the trajectory and programmed the robotic manipulator to mimic this trajectory. The robot was then used to manipulate the hind limb during the remainder of the trials. This ensured that we could generate the same random movement in a reliable fashion and optimally use the entire workspace of the hind limb.

Penetrating microelectrode arrays (1.5mm length, Blackrock Microsystems LLC, USA) were inserted in the L7 (50 electrodes in 10×5 grid) and L6 (40 electrodes in 10×4 grid) dorsal root ganglia. The neural data was sampled at 25kHz using an RZ-2 real-time signal processing system from Tucker Davis Technologies, USA. The neural data was band-pass filtered between 300 and 3000 Hz. A threshold was manually determined for each channel and spike events were defined as each instance the signal exceeded this threshold. Spike waveform snippets, 32 samples in length (1.2ms) were stored each time a spike event occurred, resulting in a time series of spikes and their corresponding waveforms per channel. Spike waveforms were sorted manually during the post-experiment analysis (Offline Sorter, TDT, Inc.).

2.3. Current decoding paradigm: reverse regression

Let X = (X_k, k = 1, …, K) be the vector of K kinematic variables we want to decode, based on the firing rates FR = (FR_i, i = 1, …, I) of I neurons. In this paper, X is the limb state expressed in one of two different reference frames, a joint-based frame with state vector (A_k, k = 1, 2, 3) that represents intersegmental angles for the hip, knee, and ankle joints, and an endpoint frame with state vector (R, θ) that represents the toe position relative to the hip in polar coordinates. We let Ẋ = (Ẋ_k, k = 1, …, K) denote the velocities of the kinematic variables, and Z = (X, Ẋ) the combined vector of limb kinematics and their velocities. A subscript t added to any variable means that we consider the value of that variable at time t. The methodologies described below can be applied to firing rates FR that are either raw or smoothed spike counts. Here, we computed smoothed instantaneous firing rates by convolving the spike events with a one-sided Gaussian kernel (σ = 50ms) to ensure causality (Stein, Weber, Aoyagi, Prochazka, Wagenaar & Normann 2004).

Reverse regression consists of modeling the mean of each kinematic variable X_k as a function of the spike-activity,

$$E(X_k)=f_k(\mathbf{FR}),k=1,\dots ,K,$$ (1)

where f_k is some function deemed appropriate, for example a linear function as in (3). An estimate f̂_k of f_k is obtained by least squares or maximum likelihood regression using a training set of simultaneously recorded values of X and FR. Then, given the observed neurons’ firing rates $\mathbf{F}{\mathbf{R}}_t^{\mathit{obs}}$ at time t, the prediction of X_k at t is

$$X_{kt}^{\ast }={\widehat{f}}_k(\mathbf{F}{\mathbf{R}}_t^{\mathit{obs}}),k=1,\dots ,K.$$ (2)

The resulting decoded trajectories { $X_{kt}^{\ast }$, t = 1, 2, …}, k = 1, …, K, are typically much more variable than a natural movement, so they are often smoothed to fall within the expected response frequencies (typically < 20 Hz).

Reverse regression was used by (Weber et al. 2006) and (Stein, Weber, Aoyagi, Prochazka, Wagenaar & Normann 2004) to predict joint and endpoint kinematics. They took f_k in (1) to be a linear function of spike activity, so that

$$X_k={\beta }_{k0}+\sum _{i\in S_k}{\beta }_{ki}F{R}_i+{\epsilon }_k,$$ (3)

where S_k indexes the set of neurons whose firing rates correlate most strongly with X_k (Stein, Weber, Aoyagi, Prochazka, Wagenaar & Normann 2004), and ε_k are uncorrelated random errors. We adopt the same approach with our data: we apply reverse regression with the linear model in (3) to decode joint angles (A_k, k = 1, 2, 3) and limb end point position (R, θ), and smooth the decoded trajectories by convolving the result with a gaussian kernel (σ = 75ms) to improve the decoding results.

One advantage of reverse regression is its simplicity: kinematic variables X_k are decoded separately and require just one equation each. However, the method does not allow physiologically meaningful modeling of the relationships between firing rates and kinematic variables. Indeed, not only do neurons often encode several kinematic variables simultaneously, the manner in which they encode these variables is not necessarily linear or additive. For example, many muscles in the hind limb span two joints, so that PA neurons code for multiple joint angles simultaneously. Such a neuron was shown in (Wagenaar et al. 2009): its firing rate depended both on ankle and knee angles, the relationship between firing rate and ankle angle was clearly non-linear, and the relationship changed for different values of knee angle, which suggested the existence of an interaction between the two joint angles. Such effects cannot be modeled in reverse regression. It is also possible for neurons to encode not only for kinematic variables but also for their derivatives; muscle spindle primary afferents (Ia) are such neurons. In that case it is possible to decode X_kt based on the relationship between its velocity Ẋ_kt ≈ (X_kt − X_k(t−δt))/δ_t and the neurons’ firing rates, by applying reverse regression with X_k replaced by Ẋ_k in equations (1) and (2). Based on a linear function f_k, this prediction is

$$X_{kt}^{\ast }=X_{k(t-{\delta }_t)}^{\ast }+{\delta }_t\left({\widehat{\alpha }}_{k0}+\sum _{i\in S_k}{\widehat{\alpha }}_{ki}F{R}_{it}^{\mathit{obs}}\right),$$ (4)

which is different than predicting $X_{kt}^{\ast }$ from (3). Stein et al (2004) offered an ad-hoc method of combining these two predictions. However, because it is not motivated by a principle that guarantees superior results over either separate predictions, we did not consider this method for our data.

2.4. Firing rate models and likelihood decoding

Reverse regression is easy to apply, but it does not make efficient use of the information in the data since effects such as interactions or effects of derivatives cannot be accounted for. In contrast, a likelihood approach can account for such effects, and is further known to be efficient when the models involved are appropriate (Kass et al. 2005).

The likelihood approach is based on models that describe the physiological dependencies of firing rates on limb state, which restores the natural relationship between X_k and FR_i that are swapped in the reverse regression approach. That is, the mean firing rates FR_i of each neuron are now modeled as functions of the kinematic variables Z = (X, Ẋ),

$$E(F{R}_i)=g_i(\mathbf{Z}),i=1,\dots I,$$ (5)

where the functions g_i are selected to accommodate any suspected effects between covariates, such as interactions. Sections 2.4.1 and 2.4.2 summarize the functions g_i we considered for our data. Although we could let g_i also depend on higher order derivatives of X, such as acceleration, we did not consider that option because PA neurons are known to encode primarily for muscle lengths and their velocities (Prochazka et al. 1977, Loeb et al. 1977, Mileusnic et al. 2006), and previous work using reverse regression methods failed to generate accurate estimates of acceleration (Weber et al. 2007). The maximum likelihood estimates ĝ_i of g_i i = 1, …, I, are obtained based on a training set of simultaneously recorded values of Z and FR, and on an assumed distribution for FR_i. Here we used the Gaussian distribution since FR_i are smooth firing rates, but the Bernoulli or Poisson distributions could be used instead if FR_i were raw spike trains (i.e. unfiltered spike counts). Then, given the observed firing rates $\mathbf{F}{\mathbf{R}}_t^{\mathit{obs}}$ at time t, the prediction of Z is obtained by solving the system of I equations

$$F{R}_{it}^{\mathit{obs}}={\widehat{g}}_i({\mathbf{Z}}_t^{\ast })+{\epsilon }_{it},i=1,\dots I$$ (6)

for ${\mathbf{Z}}_t^{\ast }$. Note that all components of Z are decoded simultaneously, whereas they are decoded separately in reverse regression. When the firing rates are not modulated by the velocities, so that the g_i’s are functions only of X, solving (6) amounts to performing standard least square estimation when the g_i’s are linear functions of their inputs; see the appendix. Otherwise, it can be challenging. In particular, (6) should be solved subject to the constraint that the derivatives of the decoded positions match the decoded velocities.

We did not use likelihood decoding in this paper, partly because of the technical difficulties just mentioned, but mostly because state-space models (section 2.5) are superior. We nevertheless provided details because the likelihood is a component of the state-space model, and decoding under the two approaches are related.

2.4.1. Firing rate models in joint angle frame

We considered hind limb biomechanics to guide our choice of physiologically plausible firing rate models in (5), as follows. We know that the firing rates of muscle spindle afferents depend primarily on the kinematic state of one or two adjacent joints since the host muscles are either mono or bi-articular. For example, a muscle spindle in the medial gastrocnemius muscle encodes movement of both ankle and knee, while a muscle spindle in the soleus muscle encodes only the movements of the ankle. Cutaneous afferent neurons are not so tightly linked to joint motion, but our previous work shows that even they exhibit responses that vary systematically with limb motion (see figure 3 in Stein, JPhysiol, 2004). Therefore we considered functions g_i in (5) that include the effect of a single joint, s(A_j) with j = 1, 2 or 3, or the additive effects of two adjacent joints, s(A_j) + s(A_k) with (j, k) = (1, 2) (ankle/knee) or (j, k) = (2, 3) (knee/hip). The notation s(A) signifies that a non-parametric smoother is applied to the covariate A, which models the potentially non-linear effect of A on the neuron’s firing rate. Here, we took s(.) to be splines with 4 non-parametric degrees of freedom, but other smoothers could be used. Figure 3 in (Wagenaar et al. 2009) also suggested that interactions between joints might be present, so we also considered the addition of interaction effects, which we denote by s(A_j): s(A_k), (j, k) = (1, 2) or (2, 3). We also know that muscle spindle primary afferents and possibly many rapidly adapting cutaneous afferents exhibit a velocity dependent response. Hence we allowed the addition of velocity terms s(Ȧ_j), s(Ȧ_j) + s(Ȧ_k), or s(Ȧ_j) * s(Ȧ_k) = s(Ȧ_j) + s(Ȧ_k) + s(Ȧ_j): s(Ȧ_k) in the model for g_i in (5). Finally, we also included the interactions s(A_j): s(Ȧ_j) between joints and their respective velocities, because we expect the velocity of a joint to get smaller when it is close to full extension or full flexion.

Table 1 contains the list of firing rate models we considered for our data. All models were fitted to all neurons by maximum likelihood using a standard statistical package (R, http://www.R-project.org), and the best model for each neuron was selected by the Bayesian information criterion (BIC) (Schwarz 1978).

Table 1.

List of the 33 models considered to describe the effect of the three joint angles A_k, k = 1, 2, 3 on the firing rates of neurons. The notation s(.) is a spline basis with 4 non-parametric degrees of freedom. The notation s(A_j) * s(A_k) means that the main effects s(A_j), s(A_k), and their interaction s(A_j): s(A_k) are included in the model.

Index	Model description	Variations
1	gi = β0i
2–4	gi = β0i + s(Aj)	j = 1, 2, 3
5–6	gi = β0i + s(Aj) + s(Ak)	(j, k) = (1, 2), (2, 3)
7–8	gi = β0i + s(Aj) * s(Ak)	(j, k) = (1, 2), (2, 3)
9–11	gi = β0i + s(Ȧj)	j = 1, 2, 3
12–14	gi = β0i + s(Aj) * s(Ȧj)	j = 1, 2, 3
15–18	gi = β0i + s(Aj) * s(Ȧj) + s(Ak)	(j, k) = (1, 2), (2, 1), (2, 3), (3, 2)
19–22	gi = β0i + s(Aj) * s(Ak) + s(Ȧk)	(j, k) = (1, 2), (2, 1), (2, 3), (3, 2)
23–25	gi = β0i + s(Aj) + s(Ȧj)	j = 1, 2, 3
26–27	gi = β0i + s(Aj) * s(Ȧj) + s(Ak) * s(Ȧk)	(j, k) = (1, 2), (2, 3)
28–31	gi = β0i + s(Aj) + s(Ȧj) + s(Ak)	(j, k) = (1, 2), (2, 1), (2, 3), (3, 2)
32–33	gi = β0i + s(Aj) * s(Ak) + s(Ȧj) + s(Ȧk)	(j, k) = (1, 2), (2, 3)

2.4.2. Firing rate models in limb end point frame

We took a similar approach to select models for the relationship between firing rates and limb end point (MTP, or toe marker) defined by the polar coordinates (R, θ), where R is the distance from the hip marker to the MTP marker and θ the angle between the horizontal and the vector spanned by the hip and MTP markers. For each neuron, we considered functions g_i in (5) that include either s(R), s(θ), or both, and possibly their interaction. We also considered the addition of velocity terms s(Ṙ), s(θ̇), s(Ṙ)+ s(θ̇), and their interaction, as well as s(R): s(Ṙ) and s(θ): s(θ̇), the interactions between effects and their respective velocities. For each neuron, the best model was determined by BIC.

2.5. State-space models

The firing rate models (5) describe the relationships between kinematic variables and spiking activity. Newer decoders provide significant improvements in decoding performance by supplementing the firing rate models with a probabilistic model that describes the intrinsic behavior of kinematic variables, such as constraints on velocity and trajectory smoothness. For example, (Brockwell et al. 2007) suggest the a priori random walk model

$${\mathbf{Z}}_t=\left(\begin{array}{c}{\mathbf{X}}_t^T\\ {\stackrel{.}{\mathbf{X}}}_t^T\end{array}\right)=\left(\begin{array}{cc}{I}_{K\times K}& \delta \times I_{K\times K}\\ 0& I_{K\times K}\end{array}\right)\left(\begin{array}{c}{\mathbf{X}}_{t-1}^T\\ {\stackrel{.}{\mathbf{X}}}_{t-1}^T\end{array}\right)+\left(\begin{array}{c}0\\ {\epsilon }_t\end{array}\right),$$ (7)

where ε_t, t = 1, 2, …, are independent vectors with mean 0 and K × K variance-covariance matrix Σ. For all k = 1, …, K, (7) specifies that Ẋ_kt = Ẋ_k(t−1) plus some perturbation ε_kt, which forces the velocities to change smoothly over time if the perturbations are taken to be small enough. Equation (7) also specifies that X_kt = X_k(t−1) plus the velocity Ẋ_k(t−1) multiplied by the size of the decoding window, δ msec. This not only forces the positions to be consistent with their respective velocities, but also induces the position paths to be smooth when the velocity paths are smooth. Alternatively, one can assume the more general random walk model

$$\left(\begin{array}{c}{\mathbf{X}}_t^T\\ {\stackrel{.}{\mathbf{X}}}_t^T\end{array}\right)=\mathbf{B}\left(\begin{array}{c}{\mathbf{X}}_{t-1}^T\\ {\stackrel{.}{\mathbf{X}}}_{t-1}^T\end{array}\right)+{\epsilon }_t,$$ (8)

where ε_t, t = 1, 2, …, are independent vectors with mean 0 and 2K × 2K variance-covariance matrix Σ, and estimate B and Σ by maximum likelihood according to

$$\begin{array}{l}\mathbf{B}=\sum _{t=2}^n{\mathbf{z}}_t{\mathbf{z}}_{t-1}^T{\left(\sum _{t=2}^n{\mathbf{z}}_{t-1}{\mathbf{z}}_{t-1}^T\right)}^{-1}\\ \mathbf{\sum }=\frac{1}{n-1}\left(\sum _{t=2}^n{\mathbf{z}}_t{\mathbf{z}}_t^T-\mathbf{B}\sum _{t=2}^n{\mathbf{z}}_{t-1}{\mathbf{z}}_t^T\right),\end{array}$$

as in (Wu et al. 2004), where z_t, t = 1, …, n, is a training set of kinematic data. We describe the specific kinematic models we used for our data in section 2.5.1, and until then use the generic notation

$${\mathbf{Z}}_t=h({\mathbf{Z}}_{t-1})+{\epsilon }_t.$$ (9)

Once the firing rate and kinematic models are fitted to data, as described in this and the previous sections, decoding follows a recursive scheme. Let ${\mathbf{Z}}_t^{\mathit{post}}$ be the prediction of Z at time t; ${\mathbf{Z}}_t^{\mathit{post}}$ is a random variable since the kinematic prior model in (9) is stochastic, so the actual prediction ${\mathbf{Z}}_t^{\ast }$ is usually taken to be the mean of ${\mathbf{Z}}_t^{\mathit{post}}$. Initially ${\mathbf{Z}}_1^{\ast }$ is set to the initial hind limb state of the encoding dataset. At time (t + 1), we first use the current prediction ${\mathbf{Z}}_t^{\mathit{post}}$ together with the kinematic model in (9) to obtain the a priori distribution of the next value of Z,

$${\mathbf{Z}}_{(t+1)}^{\mathit{prior}}=h({\mathbf{Z}}_t^{\mathit{post}})+{\epsilon }_t.$$

Then we use the observed firing rate vector $\mathbf{F}{\mathbf{R}}_{(t+1)}^{\mathit{obs}}$ at time (t + 1) with the firing rate models in (5) to update that prior into the posterior distribution of ${\mathbf{Z}}_{(t+1)}^{\mathit{post}}$, and finally take its mean to be the predicted kinematic state vector ${\mathbf{Z}}_{(t+1)}^{\ast }$. Depending on the forms of the firing rate and kinematic models, the posterior calculation is carried out by Kalman or particle filtering; these methods are described in detail in (Brockwell et al. 2004, Wu et al. 2006, Brown et al. 1998). Here we use particle filtering because the firing rate model in (5) involves splines. The resulting trajectories for X are typically smooth enough and do not require additional smoothing.

2.5.1. Kinematic models

For our data, we assumed the general random walk model (8) and used a training set of kinematic data to estimate B. We obtained

$$\mathbf{B}\approx \left(\begin{array}{cc}{I}_{3\times 3}& 0.05\times I_{3\times 3}\\ 0& I_{3\times 3}\end{array}\right)$$

for the three joint angles (A₁, A₂, A₃), and

$$\mathbf{B}\approx \left(\begin{array}{cc}{I}_{2\times 2}& 0.05\times I_{2\times 2}\\ 0& I_{2\times 2}\end{array}\right)$$

for the limb end-point kinematic variables (R, θ), which are precisely the a priori kinematic models suggested by Brockwell, Kass and Schwartz (2007) in equation (7), with our decoding window of δ = 0.05 msec.

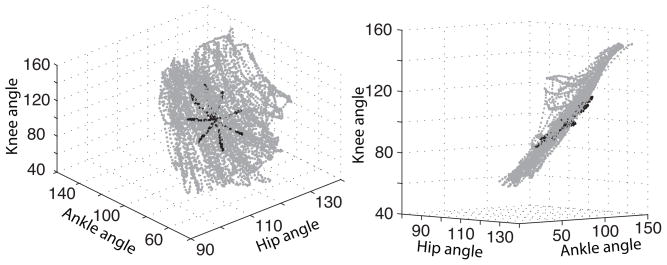
The kinematic model for (A₁, A₂, A₃) can further be improved by taking into account the physical constraints between these angles. These constraints are seen in figure 2, which shows a 3D scatter plot of (A₁, A₂, A₃) in two movement patterns: a center out path (black) and a random path (gray). We see that hip and ankle angles are highly inter-dependent, as was already observed in (Weber et al. 2006, Bosco et al. 2000), since the data lie almost entirely on a 2D manifold. This explains why, when decoding via reverse regression, neurons that encode for hip could be used to decode the ankle angle as well, and vice versa. In all experiments, the limb was made to move by controlling only its foot position. Therefore, figure 2 displays the relative positions that the three angles assume naturally during imposed movement of the foot. Moreover, these natural positions appear consistent across experiments, since the data from the random and center-our experiments lie within the same sub-space. It is thus reasonable to assume that all passive movements share the constraints between joint angles displayed in figure 2. We could include this prior information in the kinematic model by forcing the random walk in (8) to evolve within the envelope of the points in figure 2. However, this envelope is probably too tight since we did not observe all possible movements, so we will instead force the random walk to evolve near, rather than inside, the envelope, as follows.

Figure 2.

Observed trajectories of the three joint angles of the hind limb during random (gray) and a center-out (black) passive movements. The joint angles are clearly inter-dependent.

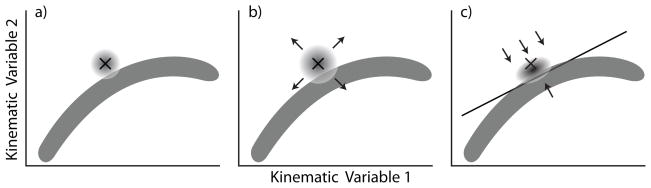
Let ${\mathbf{A}}_t^{\ast }=(A_{1t}^{\ast },A_{2t}^{\ast },A_{3t}^{\ast })$ be the predicted value of the joint angles at time t, depicted as × in figure 3a; as mentioned earlier, ${\mathbf{A}}_t^{\ast }$ is the mean of ${\mathbf{A}}_t^{\mathit{post}}$, whose distribution is depicted as the circular gray area in figure 3a. We identify the quarter of the points in figure 2 that are closest to ${\mathbf{A}}_t^{\ast }$, and obtain the 2D plane spanned by their first two principal components, depicted as the straight line in figure 3c; the most natural limb positions near ${\mathbf{A}}_t^{\ast }$ should be close to that plane. To obtain the prior distribution of A at time (t + 1), we first use the kinematic model in (9) to transform the posterior distribution of A at time t into an intermediate prior for A at time (t + 1) (circular gray area in figure 3b), and we orthogonally project it half the distance towards the principal component plane (see figure 3c). This modified random walk loosely mimics or ’accommodates’ the natural constraints on the joint angles. In particular, by using only a quarter of the training data to obtain the projection plane, we enable the prior model to follow the curvature of the cloud of points in figure 2. The polar coordinates appeared to be independent so we did not include any additional constraints in their kinematic model.

Figure 3.

Depiction of the random walk prior model for the joint angles, in 2D rather than 3D to improve visibility. a) Location of the current predicted state (×), posterior distribution of the state (small gray circular area, whose relative size represents the relative uncertainty of the current position), and kinematic data manifold (dark curved gray area). b) transformation of the posterior into the intermediate prior for the next state prediction, based on the kinematic model in (9). c) projection of the intermediate prior towards a locally defined plane representing the shape of the kinematic range of motion.

2.6. Decoding efficiency

We assessed the quality of decoded trajectories by the integrated squared error (ISE), defined as the squared difference between decoded and actual trajectories, integrated over all decoded time bins. The ISE is a combined measure of bias and variance, which typically decreases proportionally to the inverse of the number of neurons used to decode. Hence, when comparing two decoding methods, the ISE has the following interpretation: the accuracy of reverse regression, based on n_RR neurons, will be comparable to the accuracy of state-space decoding, based on n_SS neurons, if n_RR = n_SS (ISE_RR/ISE_SS). This means that if the ISE ratio ISE_RR/ISE_SS is one, the two methods are equally efficient; if the ratio is 1.5, reverse regression needs 50% more neurons to be as efficient as state-space decoding; etc. Therefore, two decoding methods can be compared by computing the ratio of their respective ISEs. Because ISE ratios vary from dataset to dataset in repeated simulations, we summarized their distributions using violin plots.

Violin plots are close cousins of boxplots; both show the distributions of several variables side by side, and are therefore particularly well suited to compare these distributions. The better known boxplot does not display full distributions, but only side by side summaries in the form of boxes with edges marking the quartiles. Violin plots do not reduce the distributions to be compared to a small number of features, but instead plot the full distributions and their mirror images vertically. They also include a marker for the medians of the distributions.

3. Results

The data from two animals are included in the analysis of this paper. Spike sorting the neural data resulted in 158 and 116 classified neurons for each animal respectively. From these 274 neurons, 171 neurons (115 and 56 respectively) were included in the analysis based on the criteria described in section 3.1. Section 3.1 describes an analysis of the firing rate models to give insight into how well each of the various state variables and their interactions are represented in the PA ensemble. Analysis of decoded trajectories in joint angle space and endpoint space are presented in sections 3.2 and 3.3 respectively.

3.1. Encoding models

In the methods section, we argued that a decoding method that involves firing rate models would use the data more efficiently than reverse regression because it can account for effects of multiple joint angles and their derivatives. Here, we assess if such effects are present in our data.

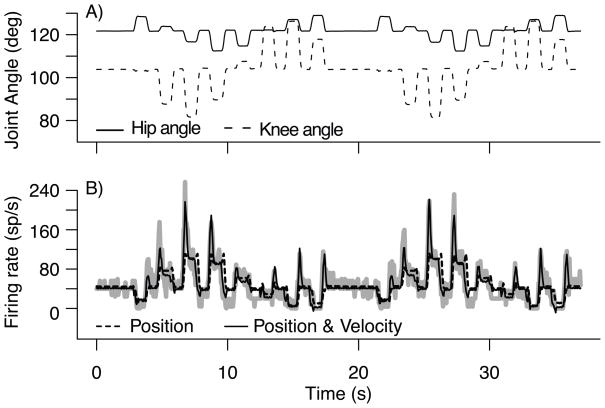
Figure 4 shows the observed firing rate response of a primary muscle spindle during a center-out passive movement (thick gray curve). We fitted all the models in table 1 to that neuron and selected the best model by BIC. That model has an adjusted R² of 0.82; it includes terms for the hip and knee joint angles, terms for their respective velocities, and interactions terms between positions and velocities (models 26–27 in table 1). Figure 4B shows that the firing rate predicted by that model (solid curve) closely follows the observed firing rate, and provides a particularly good fit to the sharp firing rate increases that occur when the joint angles shift to different positions. Figure 4B also shows the fit of the best model with all the velocity terms omitted (dashed curve). The adjusted R² dropped to 0.49 and the accuracy of the fit during the rapid movements degraded markedly. This shows that the PA neuron used in figure 4 encodes not only for joint angles, but also for their velocities.

Figure 4.

A) Kinematic trajectories of hip and knee angle during a center-out passive movement. B) Firing rate of a PA neuron during passive movement of the hind limb (thick gray curve). Overlayed are the predicted firing rates using models that include position of hip and knee angles(dashed curve) and position + velocity components (solid curve).

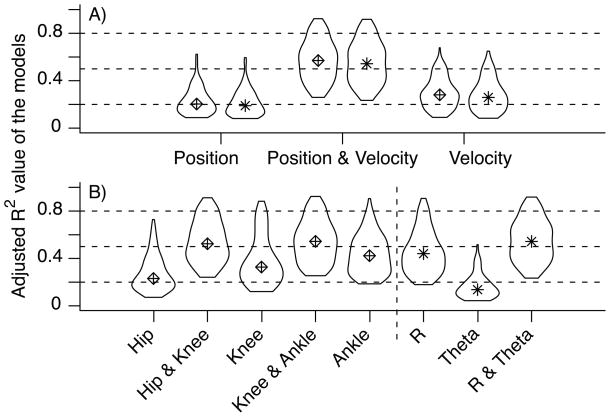
To evaluate the overall importance of the combined position and velocity models in the population of neurons for each neuron, we collected the adjusted R² value of three models; the best model involving only joint angles, the best model involving only joint angle velocities, and the overall best model. Figure 5-A shows the violin plots of the R² values of the three types of models. To clarify the plot, we dropped the neurons which achieved a maximum R² value less than 0.25, since they were deemed to encode little kinematic information. Velocity models outperform position models, which suggests that a large number of neurons encode information about joint angle velocity. Figure 5-A shows that the majority of the neurons are best modeled by a combination of joint angle positions and velocities (mean R² = 0.68 ± 0.12), which agrees with a previous report on the encoding properties of PA neurons (Stein, Weber, Aoyagi, Prochazka, Wagenaar & Normann 2004).

Figure 5.

A) Summary of the accuracy of firing rate models comparing position, velocity and the combination of position and velocity. Models were trained and tested on random-pattern datasets. B) Summary of the accuracy of firing models comparing various kinematic explanatory variables in joint angle space and endpoint space. Each distribution contains the R² value of the fitted trajectories of 162 firing rate models.

Next, we assessed which kinematic variables were represented in the neural population. We considered joint angle kinematic variables as well as polar coordinates of the MTP (i.e. toe position relative to the hip). For each neuron, we collected the adjusted R² value of 5 firing rate models (hip, hip&knee, knee, knee&ankle and ankle) and 3 polar coordinate models (R, θ and R & θ). Figure 5B shows the violin plots of the R² distributions where we excluded neurons which achieved maximum R² values less than 0.25. Models that include two joint angles generally outperform models that include only one. Similarly, including both R and θ increases the R² value on average. Note that θ is represented poorly in the neural population. We can also see that the combination of R and θ results in R² values that are on par with the best joint angle models.

The results displayed in figure 5 suggests that most neurons encode for a combination of angles, and their velocities. In fact, after applying the firing rate model selection procedure outlined in section 2.4.1, we found that 90% of the neurons have firing rates that are best modeled by models 26–27 in table 1. This indicates that the firing rates of these neurons depend on multiple joint angles, on interactions between the joint angles, and on their velocities. The neurons were equally distributed between hip/knee and knee/ankle neurons. This makes sense since the neurons were recorded from the L6 and L7 DRG, which cover the proximal and distal portions of the hind limb (Aoyagi et al. 2003). Similarly, in endpoint space, over 90% of the best models include R, θ, Ṙ, θ̇ and their interactions; R:Ṙ and θ:θ̇.

3.2. Decoding joint angles

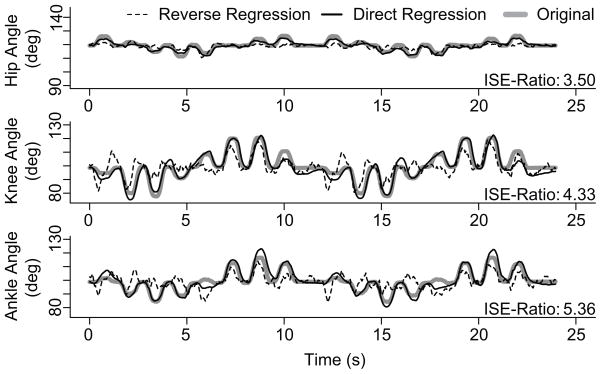
To compare the different decoding methods, we decoded limb kinematics using randomly selected groups of neurons. Performance results are in Figure 7. We first show in Figure 6 an example where the same 23 randomly selected units were used to decode the three joint angles using reverse regression and state-space modeling. In this case it is clear that state-space decoding is more accurate than reverse regression decoding. The ISE ratios for the three joint angles are 3.5, 4.3 and 5.4 respectively, which means that to obtain the same accuracy as the state space approach, reverse regression needs approximately 4 to 5 times more neurons. The reverse regression estimates have large errors particularly during periods of rapid displacement, which is presumably due to the lack of velocity integration. State-space decoding integrates the velocity components of the firing rates and thus tracks more closely the kinematics trajectories.

Figure 7.

The ISE ratios plotted as a function of the number of neurons that are used for decoding. The distribution of the ratio is plotted for groups of 3, 8, 13, 18, 23, and 28 neurons. The included data is comprised of decoded trajectories from 50 center-out and 50 random trials per animal per distribution. Therefore, each violin plot is based on 200 simulations. Firing rate models were fit to data comprised of a combination of center-out and random trials. The median of the distribution is indicated with a dot. A ratio greater than 1 favors the state-space decoding method. A ratio of 2 means that twice the amount of neurons are needed with reverse regression to attain the same accuracy as the state-space method.

Figure 6.

Example of hip, knee, and ankle joint angle trajectories decoded with the state-space and reverse regression models. This result was generated as one of the simulations with 23 randomly selected neurons. We filtered the decoded trajectory of the reverse regression post-decoding to to smooth the resultant estimates. The ISE ratio’s are displayed for each of the kinematic variables.

We repeated the analysis of joint angle decoding based on 50 sets of 3, 8, 13, 18, 23 and 28 randomly selected neurons, for each of two animals. The two passive movement patterns described in section 2.2 were decoded separately using each set. The ISE values of the decoded trajectories for the two animals were combined, resulting in 200 ISE ratios per decoding method and per data set size. Figure 7 summarizes these results as a function of the size of the neural population used for decoding. It shows that our state-space model is clearly superior to reverse regression, especially in decoding the knee angle. When using 28 randomly selected neurons, the median ISE ratio is 1.6, 2.5 and 2.1 for the hip, knee and ankle angles respectively. This means that reverse regression needs approximately twice as many neurons to produce results as accurate as the state-space approach on average. The proportionally large increase in accuracy for the knee angle estimates is probably due to the fact that 96% of the firing rate models include the knee joint and/or its derivative as one of the explanatory variables. During decoding, this translated into a large number of neurons contributing to the prediction of the knee angle.

Our motivation for using small groups of neurons in Figure 7 is two-fold. First, we are interested in comparing the two decoding methods when only a limited number of neurons are available for decoding, since it may not always be possible in practice to collect a large population of neurons from which a set of good decoding neurons can be extracted. Second, we need to use groups that are significantly smaller than the population available, so that the variability observed across the repeat simulations is comparable to the variability one would observe in practice; we have only 56 good neurons from the second animal, so we capped at 56/2 = 28 the decoding population size. Note however that when we used more than 28 neurons for decoding (not shown), the variability of the decoding efficiency decreased across datasets, so that the violin plots became very short, which is to be expected since neurons are drawn from a comparatively small population; however the mean decoding improvement of the particle filter remained constant and similar to using 28 neurons, with median ISE ratios approximately 1.6, 2.5 and 2.1 for the hip, knee and ankle angles respectively.

Finally, it is interesting to note that reverse regression does a little better on average when very few neurons are available for decoding (n = 3). However, the actual ISE values are very high, meaning that neither method performs well. The relatively better performance achieved by reverse regression can be explained by the direct relation between the decoded trajectory and the constant coefficient in (3): in the absence of any kinematic information in the neural response, the decoded trajectory is predicted to be the constant coefficient of the regression. In contrast, the state-space method is unable to produce meaningful predictions since there is insufficient information in the neural data.

3.3. Decoding endpoint coordinates

The decoding efficiency of polar coordinates of the endpoint were analyzed in a similar manner. The firing rates were modeled as functions of R and θ as described in section 2.4.2. We found that over 90% of the models included both kinematic variables, their derivatives and the interaction between the variable and their derivatives.

Figure 8 shows the efficiency results of decoding in polar coordinates, based on the same sets of neurons and trajectories used to produce figure 7. We see that state-space decoding significantly outperforms reverse regression for R, but does not show similar improvements for θ. The problem with θ is that it is poorly encoded by the neurons, as was shown in figure 5B. The consequence is that both methods decode θ poorly. Reverse regression tends to predict a constant for θ, so the estimate is biased with low variability, while the state-space model produced a highly variable estimate due to lack of information about θ.

Figure 8.

The ISE ratios plotted as a function of the number of neurons that are used for decoding. The distribution of the ratio is plotted for groups of 3, 8, 13, 18, 23, and 28 neurons. The included data is comprised of decoded trajectories from 50 center-out and 50 random trials per animal per distribution.

As a final remark, note that the trajectories for R and θ could also be inferred from the trajectories of ankle, knee, and hip angles when the segment lengths between the hip, knee, ankle and MTP marker are known. We found that the reverse regression trajectories were particularly poor compared to state-space decoding, presumably because the three angles are decoded separately so that their prediction errors accumulate.

4. Discussion

This paper addresses the problem of estimating limb state from the firing rates of an ensemble of PA neurons recorded simultaneously in the DRG. It is an extension of previous studies that used linear decoding models to estimate each of several kinematic variables as a weighted sum of firing rates in the PA ensemble. In those studies, a reverse regression approach was taken to build decoding models, which provided estimates of hind limb motion during both passive (Stein, Weber, Aoyagi, Prochazka, Wagenaar & Normann 2004) and active (Weber et al. 2006, Weber et al. 2007) movements. However, reverse regression has some apparent limitations in decoding the activity of PA neurons, motivating a change to maximum likelihood estimation methods such as state-space decoding. A comparison between reverse regression and state-space decoding is provided below. We also discuss implications of this and related work for developing a neural interface to provide limb-state feedback for control of FES systems.

4.1. State-space decoding methods of primary afferent activity

We showed that state-space decoding performs significantly better than reverse regression. The main limitation of reverse regression is that it is based on modeling the variations of each state variable as functions of neural activity, i.e state = f(rate), when in reality PA neurons are the true dependent variables modulated by one or usually multiple state variables and their time derivatives (i.e. velocities). The representations state = f(rate) do not allow such multivariate dependencies to be modeled, with the consequence that the information in the firing rates cannot be used efficiently. Previously published results show that reverse regression is capable of producing decent estimates of limb kinematics with, as few as, 5 of the ’best tuned’ neurons (Weber et al. 2007, Stein, Weber, Aoyagi, Prochazka, Wagenaar & Normann 2004). One of the key characteristics of reverse regression that enables this accuracy is that, despite the use of linear regression, the firing rates of individual neurons do not necessarily need to be linearly related to the kinematics. By reversing the actual dependencies, reverse regression merely assumes that each kinematic variable is a linear combination of the included PA neuron firing rates.

On the other hand, the state-space framework relies on modeling the actual dependencies on the state variables that drive the neuron’s firing rate, i.e. rate = f(state). It accommodates effects such as multivariate dependencies and interactions and thus makes the most efficient use of information embedded in the firing rate. In this paper, we modeled the physiological encoding properties of PA neurons by fitting their firing rates to non-linear functions of one or more state variables, and applied model selection to ensure that the natural encoding properties of each PA neuron were represented accurately. Previously, (Stein, Aoyagi, Weber, Shoham & Normann 2004) showed that non-linear functions could improve the accuracy of encoding models; a cubic polynomial was used there to account for regions where the firing rates saturated (i.e. at firing rates = 0 and the maximum discharge rate). In this paper, we used non-parametric functions consisting of moving lines with 4 non-parametric degrees of freedom to produce a more general non-linear fit to the firing rate models.

The state-space approach also involves a probabilistic model that describes the intrinsic behavior of the state variables. Standard models typically account for the fact that realistic state trajectories, eg. trajectory of the limb, should be smooth. In this paper, we not only accounted for trajectories smoothness, but also for the apparent inter-dependencies between the state variables in the joint angle frame (see figure 2). Specifically, we designed a kinematic model that forces the decoded trajectories to comply with the observed kinematic constraints. Note that with reverse regression, the effect of kinematic dependencies is that some neurons are included in multiple state decoding models. For example, the ankle and hip movements tend to be highly correlated, and thus, neurons that encode primarily for hip joint angle can also be used to estimate motion of the ankle joint. In contrast, the state-space approach maintains the physiological relationships between the state variables and the resulting PA firing rates.

We found that including velocity in the firing rate models improved the overall efficiency of the decoder, and simultaneous decoding of all kinematic variables results in lower prediction errors than decoding the joint angles individually. State-space decoding minimized the prediction error over the complete limb state, whereas reverse regression minimized it for each variable; i.e. state-space decoding provides the most likely limb posture given the firing rates and associated encoding models for a population of PA neurons. Similarly, Wu et al. found that simultaneous decoding of the full behavioral state vector (i.e. 2D position, velocity, and acceleration for the hand expressed in Cartesian coordinates) yielded the best performance in decoding neural activity in primary motor cortex.(Wu et al. 2006)

Loeb and also Prochazka (Prochazka et al. 1976) pioneered the development of techniques that enabled the first recordings of muscle spindle activity in awake, behaving animals. Both groups used microwires implanted chronically in the DRG to record simultaneously from PA neurons in locomoting cats. Data from these experiments was useful for developing computational models for estimating the firing rate of muscle spindle afferents as a function of muscle length, stretch rate, and fusimotor drive to the spindles (Prochazka & Gorassini 1998, Mileusnic et al. 2006). However, these mechanistic models of spindle function have not yet been used to decode limb kinematics from muscle spindle recordings, likely because the models are nonlinear and difficult to invert. State-space decoding could be combined with these more physiologically accurate models to generate estimates of muscle length and stretch rate. One more step would be required to convert the muscle-state estimates into joint angular positions and velocities, but this would be rather straightforward given knowledge of musculoskeletal biomechanics, such as described for the cat hind limb in (Goslow et al. 1973).

Our last comment concerns the aggregation of information across neurons. Stein et al. (Stein, Weber, Aoyagi, Prochazka, Wagenaar & Normann 2004) noted that, with reverse regression, optimal decoding performance could be achieved with approximately five ’best-tuned’ neurons having the highest correlations with a kinematic variable, and that including additional neurons that correlate well with kinematic variables did not necessarily improve decoding performance. This means that the performance of reverse regression is highly dependent on particular neurons, and that the method fails to incorporate the information provided by other neurons. This is likely to be an issue in realistic applications, when a limited set of recorded neurons might not yield a large enough crop of ’best-tuned’ neurons. In contrast, the state-space approach appropriately aggregates the information contained in all firing rate models via the likelihood function, and thus makes it possible to obtain accurate decoding from a non-select set of recorded neurons.

4.2. Natural feedback for FES control

Microelectrode recordings of PA activity can be used to provide feedback for controlling FES-enabled movements. Yoshida and Horch (Yoshida & Horch 1996) recorded muscle spindle activity in the tibialis anterior and lateral gastrocnemius muscles in response to ankle extensions generated by stimulating the medial gastrocnemius muscle with a longitudinal intrafascicular electrode (LIFE) in the tibial nerve. Ankle joint angle estimates from the decoded LIFE recordings were used as feedback for a FES controller programmed to reach and maintain a range of fixed and time-varying joint position targets (Yoshida & Horch 1996). Another study used the Utah Slant Electrode Array (USEA) to establish a peripheral nerve interface for both stimulating and recording activity in motor and sensory fibers in the sciatic nerve of anesthetized cats (Branner et al. 2004). This technology was advanced recently by incorporating a telemetry chip into the array assembly to create a fully implantable, wireless neural interface capable of recording and transmitting 100 channels of unit activity (i.e. spike-threshold crossings) from peripheral nerve or cerebral cortex (Harrison et al. 2008). Thus, the technology for establishing high-bandwidth neural interfaces with motor and sensory nerves is advancing rapidly and holds great promise for FES applications, as well as basic research.

To be suitable in a medical device application, the neural interface must remain viable and stable for several years, longevity that has yet to be demonstrated with any microelectrode interface in peripheral nerve. To date, long-term recording stability with penetrating microelectrode arrays in either peripheral nerve or DRG has not been demonstrated, and more work is needed to establish reliable, long-lasting neural interfaces (Weber et al. 2006, Rousche & Normann 1998). An alternative to penetrating microelectrodes is to use nerve cuff electrodes, which measure the combined activity of many nerve fibers passing through the cuff. However, attempts at providing graded measurements of limb-state (e.g. ground reaction force or joint position) with nerve cuff recordings have had limited success (Jensen et al. 2001). In general, research towards the use of nerve cuff recordings for continuous joint-angle estimation has been limited to a single isolated joint, typically the ankle, and tested only in anesthetized animals (Cavallaro et al. 2003, Jensen et al. 2001, Jensen et al. 2002, Micera et al. 2001). Cavallaro et al. (Cavallaro et al. 2003) sought to improve continuous state estimation from nerve cuff recordings and tested several advanced signal processing methods, but reported difficulty in achieving generalization, especially for movements with large joint angular excursions. However, newer nerve cuff electrode designs such as the flat intrafascicular nerve electrode (FINE) contain a higher density of electrodes and are designed to reshape the nerve to improve alignment and access to central fascicles (Leventhal & Durand 2003). Finite element modeling studies have shown that FINE electrodes may be capable of resolving compound nerve activity within individual fascicles using beam-forming techniques, an approach that may greatly increase the quality of information that can be extracted from nerve cuff recordings. (Durand et al. 2008).

As further improvements towards chronically stable neural interfaces proceed, focus will shift towards interpreting the recorded signals. Advanced decoding methods, such as the state-space decoder discussed here, will enable us to extract meaningful information from PA firing rates and take us a step closer to incorporating afferent feedback in closed loop neuroprostheses.

5. Conclusions

The results of the present study and those reviewed above demonstrate the potential for using PA neuronal activity to generate estimates of limb-state, which would be useful feedback for controlling FES systems. Using-state space decoding is a principled and accurate method for decoding kinematics based on population recordings of PA neurons in the DRG. Because of its ability to efficiently use all neural responses to predict limb state, fewer neurons are needed to attain a similar accuracy as reverse regression, and multijoint dependencies are correctly incorporated in the neural models. The resulting accuracy of decoding these ensembles of PA neurons provides significant information about limb state and is well-suited for incorporation in a neural interface. However, the stability and reliability of the neural interface needs to be addressed before these decoding efforts can successfully be used to provide limb state feedback for controlling neural prostheses.

Appendix A. State space algorithm for decoding limb state

The state space model applied in this work is an extension of the particle filter described in Brockwell et al. (Brockwell et al. 2004). A thorough explanation of the particle filter can be found in the appendix of that work. In this appendix we summarize the procedure and indicate where our method diverges from the algorithm in Brockwell et al.

The objective of state space decoding is to estimate the state of the hind limb, X = (X_k, k = 1, …, K), based on the input firing rates of I neurons, FR = (F R_i, i = 1, …, I). It relies on an iterative algorithm which updates the posterior distribution of limb state (and therefore the mean of that posterior, which is used as the estimate of limb state) as new observations of spike counts/firing rates arrive. A Kalman filter calculates that posterior distribution analytically, a particle filter by simulation. In this paper, we used a particle filter with m = 3000 particles to approximate the posterior distribution, which means that a histogram of the m particles approximates that posterior. Below we explain how to update the particle cloud, and thus the limb state posterior distribution, at each time step.

1. Initial prior distribution for the limb state: we have no information about limb state when we start the algorithm, so we generate the m initial particles ${\stackrel{\sim }{x}}_0^{(j)}$, j = 1, 2 …, m from a prior distribution that has mean at the center of the limb state space, and a large variance to reflect the lack of information about limb state. This prior can be adjusted if there is prior information about the limb state.

   Set t = 1.

2. Let ${\stackrel{\sim }{x}}_{t-1}^{(j)}$, j = 1, 2 …, m denote the particle cloud at time t − 1, and ẑ_{t − 1} the limb state prediction at t − 1. To obtain the limb state prediction at time t, we first collect the vector of observed firing rates $\mathbf{F}{\mathbf{R}}_t^{\mathit{obs}}$.

3. We advance all particles ${\stackrel{\sim }{x}}_{t-1}^{(j)}$ by simulating the state model one step forward as per (9). The resulting particles, $x_t^{\mathit{prior}(j)}$ say, estimate the prior distribution of the kinematic state at time t. Equation (9) simply consists of adding Gaussian random noise to all the particles, with aim to increase the spread of the particle cloud so that it can envelop all possible limb states at t, given the current state ẑ_{t − 1}. Adding too much noise results in particles being able to capture highly unlikely limb states, while adding too little prevents the algorithm from tracking fast movements. To avoid making an arbitrary decision, we estimated the variance-covariance matrix of the random noise from training data, as described section 2.5.

4. The next step is specific to the kinematic model used in this paper for the joint angles: project each particle $x_t^{\mathit{prior}(j)}$ towards the physiologically plausible kinematic space. To do that, we determine the quarter of the points in the training data set that are closest to the current state estimate ẑ_{t − 1}, and express the coordinates of each particle as a linear combination of the 3 principle components spanning that quarter data. The first two PCs span a local approximation of the 2D plane of the physiologically plausible kinematic space, while the third PC is the orthogonal distance from that plane to the predicted state variable. Hence to project the particle $x_t^{\mathit{prior}(j)}$ towards the physiologically plausible space, we simply scale the third PC by ζ ∈ [0, 1]. This operation reduces by a factor of ζ the orthogonal distance of each particle to the kinematic plane.

5. We compute a weight $w_t^{(j)}$ for each particle as

   $$w_t^{(j)}=p\left(\mathbf{F}{\mathbf{R}}_t^{\mathit{obs}}\mid x_t=x_t^{\mathit{prior}(j)}\right),$$ (A.1)
   which is the probability of observing the firing rate vector $\mathbf{F}{\mathbf{R}}_t^{\mathit{obs}}$ if the kinematic variable takes value $x_t^{\mathit{prior}(j)}$. In this paper, we assumed that each firing rate F R_i has a Gaussian distribution with mean ĝ_i (Z) and variance $s_i^2$, both estimated in the encoding stage (6), and we assumed that the neurons were independent, so that the weights reduce to

   $$w_t^{(j)}=\prod _{i=1}^I\frac{1}{\sqrt{2\pi s_i^2}}exp\left(-\frac{{\left(F{R}_{it}-{\widehat{g}}_i\left(x_t^{\mathit{prior}(j)},{\stackrel{.}{x}}_t^{\mathit{prior}(j)}\right)\right)}^2}{2s_i^2}\right).$$ (A.2)

   Then we normalize the weights $w_t^{(j)}$ so they sum to one.

6. We create the new particle cloud by sampling the current prior particles $x_t^{\mathit{prior}(j)}$ with weights $w_t^{(j)}$ and with replacement. Hence particles that have low weights are unlikely to be sampled, while particles that have high weights might be sampled several times. We call the new particles ${\widehat{x}}_t^{(j)}$, j = 1, 2 …, m. This new particle cloud estimates the posterior distribution of the limb at time t. We take the estimate of the limb state at time t to be the sample mean of the particles,

   $${\widehat{z}}_t=\frac{1}{m}\sum _{j=1}^m{\widehat{x}}_i^{(j)}$$ (A.3)

7. Set t to t + 1 and go back to step (ii).

In summary, the estimate of the limb state evolves over time as new observations of the firing rates arrive. The estimate at t depends on the state estimate at the previous time point t − 1 and on the observed firing rates at time t. Since the limb state can only exist within a confined region of the space spanned by the kinematic inputs, we constrain the kinematic model to evolve close to that space.

Appendix B. Details for solving eq.6

When the firing rates are not modulated by the velocities, so that the g_i’s are functions only of X, solving (6) amounts to performing standard least square estimation when the g_i’s are linear functions of their inputs. Indeed in that case, (6) reduces to

$$F{R}_{it}^{\mathit{obs}}={\widehat{\beta }}_{0i}+\sum _{k=1}^K{\widehat{\beta }}_{ki}{X}_{kt}^{\ast }+{\epsilon }_{it},i=1,\dots I,$$

where the ε_it are independent Gaussian random variables with mean 0, and the β̂_ki are known: they were estimated in the encoding stage. Therefore (6) is a linear regression model where the dependent variables are the $F{R}_{it}^{\mathit{obs}}$, the role of the dependent variables are played by the β̂_ki and the parameters to be estimated are the $X_{kt}^{\ast }$. This regression can be fitted using any statistical software. Eq.6 can still be solved, although not quite as trivially, if the g_i functions are non-linear or involve derivatives of X.