Abstract
Despite its frequent use to assess effects of environmental and pharmacological variables on short-term memory, little is known about the development of delayed matching-to-sample (DMTS) performance. This study was designed to examine the dimensions and dynamics of DMTS performance development over a long period of exposure to provide a more secure foundation for assessing stability in future research. Six pigeons were exposed to a DMTS task with variable delays for 300 sessions (i.e., 18,000 total trials; 3,600 trials per retention interval). Percent-correct and log-d measures used to quantify the development of conditional stimulus control under the procedure generally and at each of five retention intervals (0, 2, 4, 8 and 16-s) individually revealed that high levels of accuracy developed relatively quickly under the shorter retention intervals, but increases in accuracy under the longer retention intervals sometimes were not observed until 100–150 sessions had passed, with some still increasing at Session 300. Analyses of errors suggested that retention intervals induced biases by shifting control from the sample stimulus to control by position, something that was predicted by observed response biases during initial training. These results suggest that although it may require a great deal of exposure to DMTS prior to obtaining asymptotic steady state, quantification of model parameters may help predict trends when extended exposure is not feasible.
Keywords: delayed matching-to-sample, conditional discrimination, response bias, extended exposure, steady state, memory, key peck, pigeons
The study of memory has captivated researchers since the conception of a science of psychology, as evidenced by a myriad of experimental techniques designed for both human and nonhuman animals. One of the most commonly employed recognition tasks that is used to test remembering is delayed matching-to-sample (e.g., Berryman, Cumming, & Nevin, 1963; Blough, 1959; Cumming & Berryman, 1965; Mackay, 1991; Weinstein, 1941; White, 1985). In a delayed matching-to-sample (DMTS) procedure, a subject is presented with a sample stimulus. Completion of an observing response to the sample stimulus terminates sample presentation and initiates a delay (usually called the retention interval) between sample offset and the onset of comparison stimuli. In the case of identity matching, a response to the comparison stimulus that matches some physical property (e.g., hue) of the previously presented sample stimulus results in the delivery of reinforcement, and responses to a comparison stimulus that does not match the sample results in a timeout.
Despite its frequent use to assess environmental and pharmacological effects on memory, however, little is known about the acquisition and development of DMTS performance with multiple delays in each testing period, especially how performance under various retention intervals develops individually and interacts collectively. That is, although a great deal of inquiry and analyses have been devoted to experimental manipulations following some characterization of steady-state performance, we know of no study that has explicitly and extensively explored the development of stable performance during DMTS in its own right.
An early study by Berryman et al. (1963) serves as one of the only examinations of DMTS acquisition. In this study, immediately after pigeons were trained to peck response keys, they were exposed to a DMTS task with trials of simultaneous matching-to-sample (i.e., sample remains on with comparisons) 0, 1, 2, 4, 10, and 24 s delay values alternating in a quasirandom sequence. After nine sessions of exposure, no evidence of accurate performance acquisition was observed in any of the subjects. A subsequent phase of exposure to the simultaneous trials only resulted in the development of near-perfect accuracy. After that was established, subjects were returned to the conditions of the first phase, and DMTS performance developed with the now robust finding of the inverted relationship between delay value and accuracy. These results are primarily responsible for the current standard experimental practice of training simultaneous matching-to-sample performance to high accuracies prior to exposure to DMTS conditions. A second finding of observed position biases was common in all conditions. Both findings, however, were discussed briefly and only in broad descriptive terms. Unfortunately, no detailed follow up on these important dimensions of early acquisition and development of DMTS performance was conducted.
Nevertheless, the DMTS procedure has been widely used in studies with several species. Recent investigations using DMTS as a procedure to assess short-term remembering include studies with rats (e.g., Seif, Clements, & Wainwright, 2004), pigeons (e.g., Urcuioli, DeMarse, & Lionello, 1999), nonhuman primates (e.g., Sawaguchi & Yamane, 1999), humans with developmental disabilities (e.g., Williams, Johnston, & Saunders, 2006), and typically developing humans (e.g., Critchfield & Perone, 1990). In addition, the DMTS procedure has been repeatedly employed to assess pharmacological effects on short-term remembering of several drugs including amphetamine (e.g., Baron & Wenger, 2001), cocaine (e.g., Branch & Dearing, 1982), ethanol (e.g., Girard, Xing, Ward, & Wainwright, 2000), MDMA (e.g., Harper, Hunt, & Schenk, 2006), and nicotine (e.g., Elrod, Buccafusco, & Jackson, 1988).
A common dependent measure of the DMTS procedure is percent correct, with values plotted across different retention intervals to determine a forgetting function for a subject. Another measure of performance accuracy under the DMTS procedure is log d (e.g., McCarthy & White, 1985; White, 1985; White & Wixted, 1999). Log d stems from an extension of a signal-detection model based on the generalized matching law devised by Davison and Tustin (1978) and provides a bias-free measure of discriminability of the sample stimuli at the time the discriminative behavior is being emitted and thus is consistent with the assumption that remembering is behavior under the control of temporally extended discriminative stimuli (Branch, 1977). To calculate log d under a two-stimulus task, for example red (r) and green (g) key lights, the geometric mean of the ratios of correct (c) to error (e) responses following each sample is assessed under each retention interval (t) to determine the forgetting function:
Because there are cases, especially under zero-delay trials, where no errors may be observed, 0.25 can be added to all response totals before log ratios are calculated to avoid instances of indeterminate log ratios, as recommended by Brown and White (2005).
Although changes in accuracy as a function of increased retention intervals reveal a similar pattern with both percent correct and log d calculations, there are two primary virtues of log d relative to percent correct. First, calculations result in a measure of discriminability that is free from response bias (which is measured by a related model described below) due to the reinforcer differential by which stimulus control is established (White, 1985). Second, unlike percent correct, because the range of log d values is related to the sample size of the ratios, it is not bounded at 1.0 and thus less susceptible to the ceiling effects that can mask differences at high levels of accuracy (White & Wixted, 1999).
Previous findings (see White, 2001, for a review) have also suggested that fitting a negative exponential function of the retention interval (t) in the following manner accounts for a large amount of the data's variance:
where log do is the level of discriminability at a zero-delay retention interval and serves as the ordinate-intercept, and b is the rate of exponential decay (i.e., a time constant with dimensions of t−1). This function has been demonstrated not only to account for the data well, but also to reveal more nuanced characteristics of remembering. For example, the decay parameter of the function is thought to characterize the rate of forgetting and to be modulated by variables in the experimental preparation that influence forgetting, while the ordinate-intercept is thought to measure initial discriminability, with no delay, of the stimuli. These parameters have been empirically demonstrated to be reliable and sometimes independent. For example, in a study with pigeons engaging in a DMTS task in an operant conditioning chamber, White (1985) controlled whether the houselight was on during the retention interval and discovered that the forgetting functions had a steeper slope (i.e., larger b) when the houselight was on during the retention interval relative to when it was off, but there was little change in intercept. In another experiment he found that increasing the response requirement (i.e., number of responses) on the sample before initiating the delay increased the intercept without changing the slope. These parameters, therefore, not only offer a means to quantify values of different components of the DMTS procedure, but also help illuminate experimental variables to be manipulated.
Despite the sophisticated DMTS measurement tactics described above, there nonetheless remains a dearth of data on DMTS development. This state of affairs may be responsible for the fact that although several common techniques have been used to assess stability of baseline DMTS performance, a standard practice has yet to be adopted. Stable baselines, however, are fundamental to the experimental analysis of behavior, and to the identification of reproducible and generalizable behavioral processes in individual subjects (Sidman, 1960). A review of the literature suggests that although there has not been a formal investigation of DMTS stability during extended exposure, there are several common methods used to assess stability. We examined the Methods sections of 122 peer-reviewed publications with the keywords delayed matching-to-sample and pigeons. Studies were reviewed specifically for their characterization of stability criteria used in multiple-delay DMTS performance prior to investigation of other variables. Although several methods were employed across the articles, three common methods of determining stability were more frequently observed. One common criterion required some minimum number of consecutive sessions in which predefined accuracy measures were reached or exceeded (e.g., Hartl & Fantino, 1996; Roitblat & Scopatz, 1983; Santi, 1991; Teal & Evans, 1982; Wixted & Gaitan, 2004; Zentall, Roper, & Sherburne, 1995; Zentall & Sherburne, 1994). A second common criterion required some minimum number of sessions be experienced (e.g., Jones & White, 1992; Karas, Picker, & Poling, 1986; Nevin & Grosch, 1990; Picker, White, & Poling, 1985; Spetch & Treit, 1986). A third criterion relied on visual inspection of data for minimal variability with no increasing or decreasing trends (e.g., Poling, Picker, Polder, & Clark, 1986; Spetch & Wilkie, 1983). Interestingly, even comparable methods of analysis tended to vary considerably across experiments, such as the minimum-percentage stipulations (85% to 95% for the same retention interval) and consecutive-session requirements (e.g., 2, 5, or 10).
These inconsistencies in stability criteria directly result in high variability of baseline training exposure prior to subsequent manipulations, both across subjects in an experiment as well as across experiments. Because the DMTS procedure is a discrete-trials task, one important unit of analysis for exposure is number of trials, and although the total number of DMTS training trials could not be derived from most of the articles reviewed, it is clear that this measure of baseline exposure varied considerably across experiments. For example, the study in our review reporting the largest amount of extended DMTS exposure during baseline was by Nevin and Grosch (1990) who employed a minimum of 15,000 trials in a DMTS task prior to pharmacological and nonpharmacological stimulus interference tests. This was an extreme outlier in our analysis, however, as numerous studies have used fewer than 2,000 training trials (e.g., Grant, 1991; Hogan, Edwards & Zentall, 1981; Pastenak, 1977; Spetch & Treit, 1986; Spetch & Wilkie, 1983).
Therefore, the purpose of the present study was to identify some characteristics of the development and mechanics of DMTS performance. To accomplish this, each subject was exposed to 300 daily sessions (18,000 total trials; 3,600 of each retention interval) under a typical multiple-delay, identity DMTS procedure to allow for retrospective analyses to capture the dynamics of development of DMTS performance generally and under each retention interval specifically.
METHOD
Subjects
Six experimentally naïve White Carneau pigeons (Columba livia), approximately 1 year old, were obtained from Double-T Farms, Glenwood, Iowa, and were maintained at approximately 85% of their free-feeding weights by postsession feeding as needed. The animals were housed in individual cages, in a temperature- and humidity-controlled colony room, with exposure to a 16:8-hr light/dark cycle. Water and grit were available continuously in the birds' home cages. Sessions were conducted 7 days a week at approximately the same time each day.
Apparatus
The experiment was conducted in a sound- and light-attenuating BRS/LVE pigeon operant conditioning chamber with inside dimensions measuring 35 cm high, 30 cm long, and 35 cm deep. One side wall (the intelligence panel) contained a houselight, three horizontally arrayed response keys (2.5 cm in diameter) and a 6-cm by 5-cm opening for access to a solenoid-operated hopper filled with mixed grain. The opening was located 10 cm above the floor directly below the center key. During each feeder operation, the aperture was illuminated, and all other lights in the chamber were extinguished. The center key was horizontally centered on the intelligence panel 25 cm above the floor. The houselight was centered 7 cm above the center key. The two side keys were located 8 cm to the left and right of the center key (middle of center key to middle of side key). Each key could be transilluminated red, green, or white, and a peck with a force of at least 0.15 N counted as a response and was accompanied by a 30-ms feedback tone (2900 Hz) via the operation of a Mallory Sonalert™. To mask extraneous sounds, white noise at approximately 95 dB was present in the room in which sessions were conducted. Scheduling of experimental events and data collection were controlled via a dedicated computer system (Palya & Walter, 1993) operating with a resolution of 1 ms.
Procedure
Each pigeon was first trained to eat food from the hopper and then trained by shaping (see Catania, 1998) to peck the center key (illuminated white). After the pigeon reliably pecked the center key when it was lit, shaping was employed to induce it to peck the right and left keys (illuminated white). After the pigeon was pecking reliably all three keys when they were lit, trials were arranged in which one of the three keys was illuminated red or green and pecks to the illuminated key resulted in access to grain. Additional shaping was used if necessary, and training trials continued until the pigeon reliably pecked each of the three keys when it was illuminated either red or green.
Matching-to-sample
Subjects were next trained on the matching-to-sample (MTS) task using a simultaneous MTS procedure. Specifically, discrete trials began with the illumination of the houselight and the center (sample) key with either a red or green hue. One response to the sample key illuminated the two side (comparison) keys with matching and nonmatching hues so that sample and comparison keys were illuminated simultaneously. One response to the side key illuminated with the same color as the sample key (i.e., the correct match) turned off the houselight, the sample key, both comparison keys, and raised the food hopper for 3 s followed by a 10-s intertrial interval (ITI). An ITI was employed because previous research has shown that ITIs improve accuracy of pigeon MTS performance (e.g., Thomas, 1979; White, 1985). A response to the nonmatching comparison key (i.e., the incorrect response) turned off all lights in the chamber and initiated a 13-s ITI.
A two-color (red [R] and green [G]), two-comparison MTS procedure yields four possible trial configurations—R–R–G, G–R–R, R–G–G, G–G–R (left comparison–sample–right comparison) in a three-key chamber. The computer arranged the presentation of these configurations on each trial in a quasirandom order. Specifically, each of the four configurations was presented before any configuration could be repeated (i.e., random selection without replacement). This procedure guarantees that the maximum number of consecutive identical trials is two, the maximum number of consecutive trials on which the same comparison color is correct is four, and the maximum number of consecutive trials on which the same side key is correct is also four.
Subjects engaged in the simultaneous MTS task for 30 daily sessions with 48 trials per session. One problem that often occurs during early simultaneous MTS training is the development of position or stimulus biases (e.g., Berryman et al., 1963; Cumming & Berryman, 1961; Mackay, 1991). A recent investigation in our laboratory addressed this and empirically validated a correction procedure (i.e., repeating a trial if an error was made) designed to eliminate these biases (Kangas & Branch, 2008). If following 30 sessions of exposure to the MTS procedure trial configuration analyses suggested biases (which occurred for 2 of the subjects), the correction procedure was employed as follows. Each time a subject made an incorrect response (i.e., pecked the nonmatching comparison), the trial configuration was repeated, after the ITI, until a correct response was made. For example, if the pigeon pecked the right key in the presence of an RRG configuration, the 13-s ITI would begin and the RRG configuration would be presented again on the subsequent trial, and would continue to be presented after each ITI until the pigeon pecked the correct (i.e., left) comparison key. Each session under correction ended upon completion of 48 correct matches, and the correction procedure was programmed until 10 consecutive sessions with 85% or greater accuracy (i.e., six or fewer error trials repeated) were observed prior to exposure to the DMTS procedure.
Delayed matching-to-sample
The general structure and consequences of the DMTS procedure was the same as that of the simultaneous MTS procedure described above with three exceptions. First, five responses to the sample stimulus were required; second, the sample stimulus was terminated after completion of the response requirement; and third, a variable delay was programmed between the offset of the sample stimulus and the onset of the comparison stimuli. The retention intervals programmed were 0, 2, 4, 8, and 16 s. Each 60-trial session consisted of four trials (one of each trial configuration: R–R–G, G–R–R, R–G–G, G–G–R) of each of the five retention intervals (0, 2, 4, 8, and 16 s) alternating in a random-selection-without-replacement fashion three times.
In an attempt to capture fully all dynamics of development of DMTS performance generally and under each retention interval individually, each subject was studied for an extended number of sessions. To accomplish this, a fixed time-interval stability criterion (Perone, 1991; Sidman, 1960) was employed such that each subject was studied for 300 daily sessions with 60 trials per session (i.e., 18,000 total trials; 3,600 trials per retention interval).
RESULTS AND DISCUSSION
Initial MTS Training
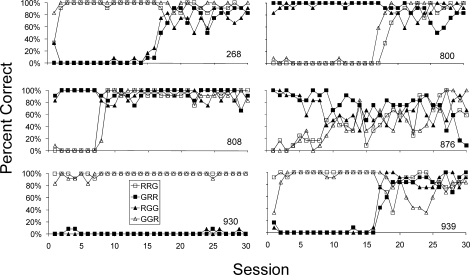
All 6 subjects learned to eat from the hopper and peck all three keys first illuminated white and then either red or green within approximately 1 hr of training. No systematic between-subject differences were noted, but each subject took a different amount of time before key pecks were reliably observed. Figure 1 shows percent correct measures by trial configuration during the 30 sessions of simultaneous MTS training. That is, the number of trials ending with a correct comparison response under each trial configuration: R–R–G, G–R–R, R–G–G, G–G–R (left comparison–sample–right comparison) was divided by the total number of trials of each configuration per session (i.e., 12). As frequently observed during early MTS training, all 6 subjects initially displayed a position bias (a left-key bias for Subjects 268, 930, and 939, and a right-key bias for Subjects 800, 808, and 876). Four of the 6 subjects (Subjects 268, 800, 808, and 939), however, engaged in the simultaneous MTS task with high accuracy and no observed bias following extended exposure (upwards of 20 sessions) to the contingencies. Two of the subjects (Subjects 876, 930), however, exhibited a prolonged bias (Subject 930) or highly variable and inaccurate performance (Subject 876) both resulting in low daily session accuracy. These 2 subjects were then exposed to the correction procedure described above that resulted in highly accurate performance. (Baseline performance of these 6 subjects served as the control group in Kangas & Branch, 2008. See that paper for additional details of the correction procedure and initial baseline for these subjects.)
Fig 1.
Accuracy by trial configuration, as indicated in the legend, of simultaneous MTS performance during the 30 sessions of baseline exposure. Open symbols indicate the left comparison stimulus was correct, filled symbols indicate the right comparison stimulus was correct.
DMTS Development
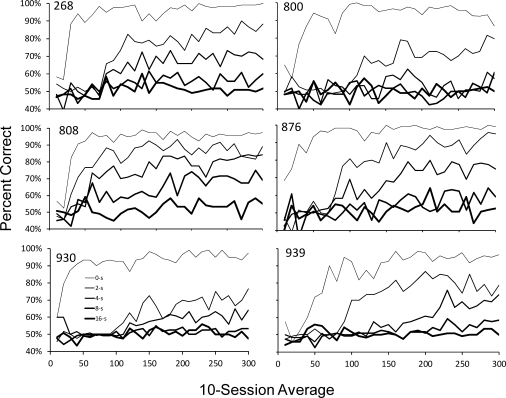
Figure 2 presents accuracy data from the 300 sessions of DMTS exposure. Specifically, the figure shows percent-correct measures of DMTS performance development under each retention interval—0, 2, 4, 8, and 16 s. In this figure, the retention interval is related to the width of the data series line with the thinnest representing 0 s and the thickest representing 16 s. Each measure was assessed using a 10-session block average across the 300 sessions of DMTS exposure. For example, for each measure the average accuracy obtained for sessions 1–10 produce the leftmost value; the average of the accuracies for sessions 11–20 result in the second value, and so on. This averaging was done to minimize some of the session-to-session variability to make it easier to assess patterns of development with visual inspection. As the figure shows, although the specific rate of development under each retention interval varied among the subjects, the general relationship was consistent. High accuracies under the 0-s delay emerged relatively quickly, within a few sessions for Subject 876 and 930, and by session 25 for the other 4 subjects. In addition, there was a highly consistent inverse relationship between the retention interval and accuracy for all subjects during baseline exposure. By the end of the extended baseline exposure (i.e., 300 sessions) generally steady-state performance was evident upon visual inspection, but it should be noted that even at Session 300 (i.e., 18,000 total trials of exposure—3,600 at each retention interval) there was some evidence of upward trends in accuracy (e.g., 2-s data series of Subjects 800 and 876; 4-s data series for Subject 939).
Fig 2.
Block averages (10-session) of accuracy under each of the five retention intervals during the 300-session DMTS baseline. The thickness of the line is related to the value of the retention interval with the thinnest representing 0 s and the thickest representing 16 s.
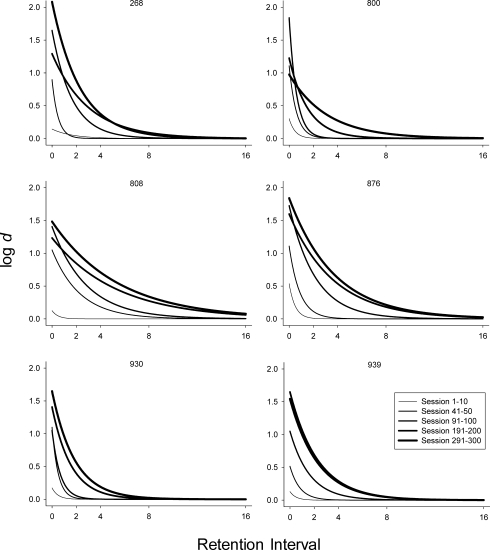
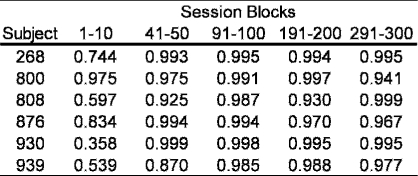
Figure 3 presents the development of DMTS performance in a standard forgetting-function form using the log d measure of discriminability described above (Equation 1). Specifically, log d was calculated using the summed response frequencies of correct and error responses following each sample under each retention interval across five 10-session blocks across the extended exposure (i.e., from Sessions 1–10, 41–50, 91–100, 191–200, and 291–300). Negative exponential functions using Equation 2 were fitted to the data of each of the 10-session blocks. In Figure 3, the temporal position of the block is related to the width of the data series line, with the thinnest representing the average from Sessions 1–10 and the thickest representing the average of Sessions 291–300. To make the five functions in each panel of Figure 3 more easily interpretable and comparable upon visual inspection, the data points to which the functions were fitted were removed. It is important to note, however, that the negative exponentials accounted for most of the total variance in four of the five curves evidenced by the R2 values presented in Table 1. As Figure 3 shows, additional exposure changed the forgetting function in systematic ways for all 6 subjects. The plots for the first block, which was composed of initial exposure to the DMTS contingencies, indicate accuracy levels near chance, with the exception of that on zero-delay trials. The successive curves presented in each panel of Figure 3 also show, consistent with Figure 2, that with increased exposure to the DMTS task log d values for shorter retention intervals increased first, and for longer retention intervals increased later. Accuracy under the longest retention interval (i.e., 16 s) remained at near-chance levels (i.e., log d of approximately 0.0) throughout. Accuracy under the trials with moderate retention intervals systematically increased as a function of extended trials of exposure systematically in order of retention interval, that is, first 2 s, then 4 s, then 8 s. This resulted in upward shifts in the forgetting function across each of the 10-session blocks in Figure 3. Interestingly, the magnitude of these upward shifts systematically decreased as a function of exposure time for 5 of the 6 subjects.
Fig 3.
Log d forgetting functions under each of the five retention intervals during five 10-session blocks across the 300 sessions of DMTS exposure. The thickness of the line is related to the temporal sequence across the 300 sessions exposure with the thinnest representing the average of Sessions 1–10 and the thickest representing the average of Sessions 291–300.
Table 1.
Total variance accounted for (R2) in each 10-session-block forgetting function shown in Figure 3.
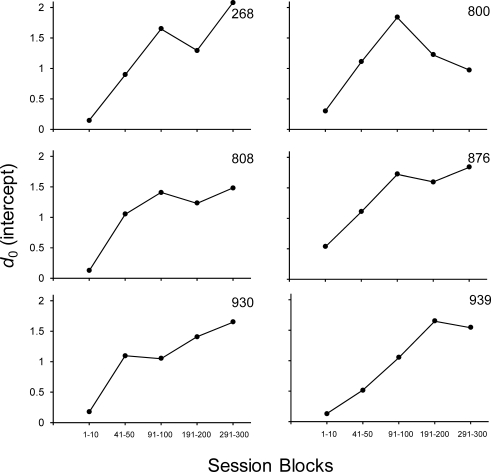
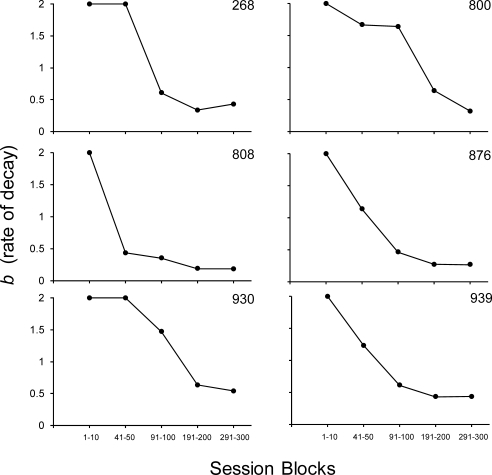
Because development of performance as measured by a negative exponential forgetting function involves changes in both intercept and rate of decay, we quantified the development of enhanced performance generally, and the intermediate values specifically, by examining changes in intercept (d0) and the rate-of-decay parameter (b) of the negative exponential function (Equation 2). Figure 4 shows the intercept values (d0) of Equation 2 across the five blocks of sessions used to compute the curves in Figure 3. Again, the intercept of the negative exponential function is an empirically derived fixed parameter representing the level of discriminability at a zero-delay retention interval (t0). As Figure 4 indicates, upward trends in intercept values are observed across the extended exposure revealing that performance even under zero-delay trials was continually improving, even at Session 300 for 4 of 6 subjects. To quantify performance improvement more generally across the retention intervals, Figure 5 shows the rate-of-decay parameter (b) of Equation 2 across the five blocks of sessions used to compute the curves in Figure 3. Because very rapid decay was observed for all subjects during the first 10 sessions of exposure as accuracy under the 0 s retention interval values was high and all others were at chance, a b of 2 was used for the first fit. The best-fit b-parameter subsequently decreased systematically across the extended exposure because accuracy under the intermediate retention intervals also increased, with the end point of the function remaining approximately the same, making the overall function more linear. Some of the changes, after what might normally be considered a sufficient amount of baseline exposure (e.g., 100 sessions), were substantial. For example, for Subjects 800 and 930, the decay parameter decreased by 61% and 57%, respectively, from Sessions 91–100 to Sessions 191–200. Even Subject 808, which showed the least overall change, showed a 47% decrease from Sessions 91–100 to 191–200. Changes in the decay parameter from Sessions 191–200 to Sessions 291–300 varied more across subjects with a 30% increase for one subject (268) and decreases observed with the other 5 subjects, Subject 800 showing the largest decrease (50%). The fact that the rate of decay was lower at Session 300 relative to Session 200 in 5 of 6 subjects provides additional evidence that performance did not reach steady-state by Session 200.
Fig 4.
Change in the intercept (d0) of the negative exponential function (Equation 2) across the five blocks of sessions used to determine the curves in Figure 3.
Fig 5.
Change in the rate of decay parameter (b) of the negative exponential function (Equation 2) across the five blocks of sessions used to determine the curves in Figure 3.
These systematic decay-parameter changes comport well with both the empirical evidence and theoretical tenets of the negative exponential function that suggest stimulus control declines at a constant rate (White, 2001). Additional exposure to the contingencies appeared to decrease that constant rate. Therefore, analyses of percent decreases in the decay parameter may provide an additional means by which to quantify the extent of performance stability. The consistency of the decreases in the rate-of-decay parameter (b) across each of the 10-session blocks shown in Figure 3 is evident for all 6 subjects. In addition, the fitted forgetting functions across each of the blocks shifted upward for all 6 subjects at each of four opportunities to shift (p < 5.96 × 10−8, exact binomial probability), providing evidence that the subjects continued to improve across the 300 sessions of extended exposure.
Data from the present study suggest that researchers employing the DMTS task and using a forgetting function as a baseline dependent variable to measure changes observed following exposure to some independent variable may be assessing effects against a moving target. When considering the typical baseline exposure time in the DMTS literature summarized above, no studies provided as much exposure as the present study, and thus upward shifts of the function unrelated to the independent variable may have occurred. It is also important to note, however, that when considering issues of practicality involved in the cost of time and money in nonhuman animal research, it is clear that spending upwards of a year simply to achieve some semblance of steady-state performance may not always be feasible. It is not our intention to emphasize the futility of achieving stability under the DMTS procedure, but to provide a means to estimate the extent to which the effects of extended exposure may play a role in observed shifts in a forgetting function following introduction of an independent variable. Assessments of observed changes in the intercept and decay parameter and predictions based on decelerating upward shifts in the forgetting function may help to achieve that objective.
Matching Errors
The loss of stimulus control as a function of temporally extending discriminative stimuli is evidenced in the DMTS procedure by incorrect responses. Although it is well known that incorrect responses systematically increase as a function of longer retention intervals (as systematically replicated in all 6 subjects of the present experiment), further characterizing subjects' errors may prove illuminating and inform understanding of these decrements in stimulus control. For example, does increasing the retention interval induce random responding to comparison stimuli? Or does it shift control by the sample stimulus to something else?
One way to determine the role of control by variables other than the sample stimulus is to assess potential sources of response bias. Here too, modifications of equations rooted in signal detection theory (Davison & Tustin, 1978; see also McCarthy, 1983) can serve to quantify measures of response bias that is also related to the discriminability measure in Equation 1. Because there are at least two primary sources of response bias—stimulus bias and position bias, two equations are needed to distinguish between them. Stimulus color bias in the context of this experiment can be quantified by the following:
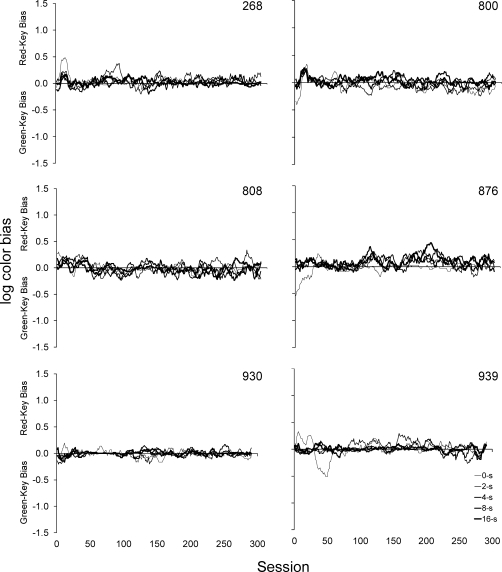
where cs is the number of trials with a correct red-key response following a red sample, et is the number of trials with an incorrect green-key response following a red sample, eu is the number of trials with an incorrect red-key response following a green sample, and cv is the number of trials with a correct green-key response following a green sample. Figure 6 shows the log color bias measure across the 300 sessions of exposure smoothed with a 10-session moving-window average. The width of the data series line is related to the retention interval. For reference, because each log color bias value comes from a session-wide sample size of 12 (i.e., 12 trials per session of each retention interval), log color biases with a range of 1.11 to −1.11 were possible with positive values indicating red-key bias, negative values indicating green-key bias, and zero indicating no bias. As the figure shows, with only a few minor deviations, no systematic color biases were observed for any of the subjects throughout the 300 sessions of extended exposure to the DMTS contingencies.
Fig 6.
Moving-window average (10-session window) of log color bias data calculated with Equation 3 under each of the five retention intervals during the 300 sessions of DMTS exposure. The thickness of the line is related to the value of the retention interval with the thinnest representing 0 s and the thickest representing 16 s. Positive values indicate red-key bias, negative values indicate green-key bias, and zero indicates no bias.
To examine and quantify the role of position biases under this framework, Equation 3 is modified in the following way:
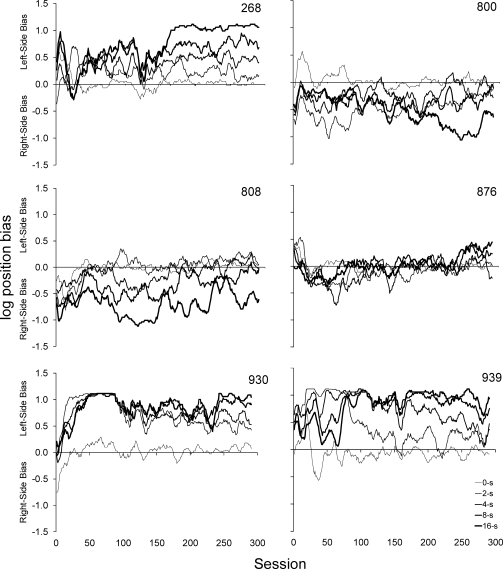
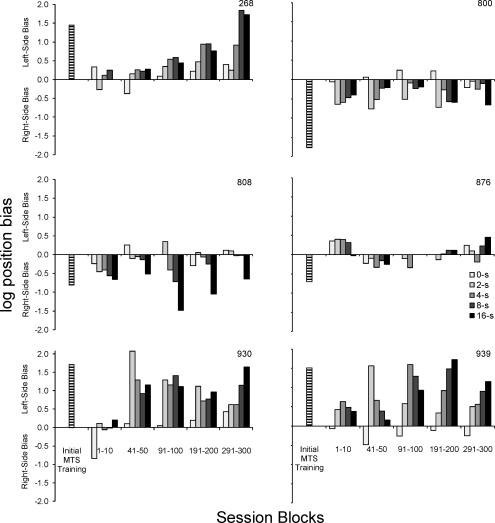
where cw is the number of trials with a correct left-key response if the correct comparison stimulus was on the left, ex is the number of trials with an incorrect right-key response if the correct comparison stimulus was on the left, ey is the number of trials with an incorrect left-key response if the correct comparison stimulus was on the right, and cz is the number of trials with a correct right-key response if the correct comparison stimulus was on the right. Figure 7 displays log position bias where positive values indicate left-side bias and negative values indicate right-side bias, with all other features exactly as Figure 6. Position biases were evident in all 6 subjects throughout the 300 sessions of exposure. Furthermore, although the data series in Figure 7 are not as systematically differentiated as those in Figure 2, there appears to be a moderate positive relationship between the retention interval and the severity of position bias.
Fig 7.
Moving-window average (10-session window) of log position bias data calculated with Equation 4 under each of the five retention intervals during the 300 sessions of DMTS exposure. The thickness of the line is related to the value of the retention interval with the thinnest representing 0 s and the thickest representing 16 s. Positive values indicate left-key bias, negative values indicate right-key bias, and zero indicates no bias.
In a revealing juxtaposition, Figure 8 presents analyses of log position bias based on response frequencies summed across the five 10-session blocks (i.e., the functions presented in Figure 3) with the log position bias of the initial 10 sessions of simultaneous MTS performance presented in Figure 1. As Figure 8 shows, subjects' observed biases under each retention interval throughout the DMTS procedure comport with those observed during the initial training of simultaneous MTS performance. That is, biases observed during the sessions of MTS training perfectly predicted biases related to DMTS errors observed almost 1 year later, despite the fact that they were matching at near-perfect accuracy prior to DMTS exposure. Therefore, it appears that the breakdown of stimulus control induced by increased retention intervals shifted control from the sample stimulus to previously observed control by position. Interestingly, even the relatively variable log position bias values observed for Subject 876 corresponds well to the similarly high amount of variability in accuracy observed during simultaneous MTS training in Figure 1.
Fig 8.
Log position bias based on response frequencies summed across the five 10-session blocks (i.e., the functions presented in Figure 3) with the log position bias of the initial 10 sessions of simultaneous MTS performance presented in Figure 1. Bias is shown individually for each delay. Positive values indicate left-key bias, negative values indicate right-key bias, and zero indicates no bias.
Despite the highly systematic results for all 6 subjects in the present experiment, the ubiquity of this phenomenon of stimulus control transfer from sample stimuli to other previously observed nonsample sources of control currently remains unclear, although, interestingly, position biases in DMTS performance were noted in the literature very early on (e.g., Berryman et al., 1963). Nevertheless, the data do appear to correspond well with a remembering as delayed stimulus control account. That is, action at a temporal distance may be less effective at obtaining all possible reinforcers, especially after long retention intervals, but decrements in stimulus control from a previously presented sample stimulus probably does not result in an absence of stimulus control, but rather a shift from one stimulus (or likely stimulus complex) to another. These log bias models effectively draw out and quantify the relative sources of bias and strongly suggest that, at least under these conditions, not all incorrect responses are created equal.
Conclusion
As experimental techniques prove effective in obtaining orderly and reliable data, their use tends to increase in prevalence. Increased prevalence requires examination of their procedural components as well as verification of the standard practice more generally. The results of the present study indicate that achieving asymptotic steady-state performance under a typical DMTS procedure requires a great deal of extended exposure. Whether such development is dependent on the specific parameters of the present experiment, for example, number of trials per session or range of delay values, remains to be determined. Additionally, it remains unclear if pigeons ever fail to continue to improve their accuracy under these conditions. Perhaps the rate of enhanced performance evidenced by ever-increasing accuracy simply decreases, yet never quite ceases given ever larger amounts of training. Practically speaking, of course, no baseline can be conducted indefinitely, so assessments of intercept and decay-parameter changes as well as decelerating upward shifts in the forgetting function, for example, may serve to identify effects not related to the independent variable(s) of a typical DMTS experiment.
The present findings also emphasize that assessment of error responses can add importantly to the account of performance development and mechanics. Analyses of errors serve to link the empirical results into the larger theoretical framework of remembering as delayed stimulus control. That is, remaining aware that errors are behavior under stimulus control makes clear that memory tasks involve competing sources of stimulus control. Because error responses are a necessary feature of comprehensive parametric assessments of remembering capabilities (i.e., effective action at a temporal distance), a complete account must also include the determinants of error responses specifically and how they change as a function of performance development more generally.
Acknowledgments
This research was supported by USPHS Grants DA004074 and DA014249 from the National Institute on Drug Abuse. The authors are grateful to K. Geoffrey White for comments on a previous draft of this manuscript and Anne Macaskill, David Maguire, Julie Marusich, and Matthew Weaver for assistance conducting this study.
REFERENCES
- Baron S.P, Wenger G.R. Effects of drugs of abuse on response accuracy and bias under a delayed matching-to-sample procedure in squirrel monkeys. Behavioural Pharmacology. 2001;12:247–256. doi: 10.1097/00008877-200107000-00003. [DOI] [PubMed] [Google Scholar]
- Berryman R, Cumming W.W, Nevin J.A. Acquisition of delayed matching in the pigeon. Journal of the Experimental Analysis of Behavior. 1963;6:101–107. doi: 10.1901/jeab.1963.6-101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blough D.S. Delayed matching in the pigeon. Journal of the Experimental Analysis of Behavior. 1959;2:151–160. doi: 10.1901/jeab.1959.2-151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Branch M.N, Dearing M.E. Effects of acute and daily cocaine administration on performance under a delayed-matching-to-sample procedure. Pharmacology, Biochemistry, and Behavior. 1982;16:713–718. doi: 10.1016/0091-3057(82)90223-4. [DOI] [PubMed] [Google Scholar]
- Branch M.N. On the role of memory in the analysis of behavior. Journal of the Experimental Analysis of Behavior. 1977;28:171–179. doi: 10.1901/jeab.1977.28-171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown G.S, White K.G. The optimal correction for estimating extreme discriminability. Behavior Research Methods. 2005;37:436–449. doi: 10.3758/bf03192712. [DOI] [PubMed] [Google Scholar]
- Catania A.C. Learning. (4th ed.) New Jersey: Prentice Hall; 1998. [Google Scholar]
- Critchfield T.S, Perone M. Verbal self-reports of delayed matching to sample by humans. Journal of the Experimental Analysis of Behavior. 1990;53:321–344. doi: 10.1901/jeab.1990.53-321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cumming W.W, Berryman R. Some data on matching behavior in the pigeon. Journal of the Experimental Analysis of Behavior. 1961;4:281–284. doi: 10.1901/jeab.1961.4-281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cumming W.W, Berryman R. The complex discriminated operant: Studies of matching-to-sample and related problems. In: Mostofsky D.I, editor. Stimulus generalization. Stanford, CA: Stanford University Press; 1965. pp. 284–330. (Ed.) [Google Scholar]
- Davison M.C, Tustin R.D. The relation between the generalized matching law and signal-detection theory. Journal of the Experimental Analysis of Behavior. 1978;29:331–336. doi: 10.1901/jeab.1978.29-331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elrod K, Buccafusco J.J, Jackson W.J. Nicotine enhances delayed matching-to-sample performance in primates. Life Sciences. 1988;43:277–287. doi: 10.1016/0024-3205(88)90318-9. [DOI] [PubMed] [Google Scholar]
- Girard T.A, Xing H.C, Ward G.R, Wainwright P.E. Early postnatal ethanol exposure has long-term effects on the performance of male rats in a delayed matching-to-place task in the Morris water maze. Alcoholism: Clinical and Experimental Research. 2000;24:300–306. [PubMed] [Google Scholar]
- Grant D.S. Symmetrical and asymmetrical coding of food and no-food samples in delayed matching in pigeons. Journal of Experimental Psychology: Animal Behavior Processes. 1991;17:186–193. [Google Scholar]
- Harper D.N, Hunt M, Schenk S. Attenuation of the disruptive effects of (+/−)3,4-methylene dioxymethamphetamine (MDMA) on delayed matching-to-sample performance in the rat. Behavioral Neuroscience. 2006;120:201–205. doi: 10.1037/0735-7044.120.1.201. [DOI] [PubMed] [Google Scholar]
- Hartl J.A, Fantino E. Choice as a function of reinforcement ratios in delayed matching to sample. Journal of the Experimental Analysis of Behavior. 1996;66:11–27. doi: 10.1901/jeab.1996.66-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hogan D.E, Edwards C.A, Zentall T.R. Delayed matching in the pigeon: Interference produced by the prior delayed matching trial. Animal Learning and Behavior. 1981;9:395–400. [Google Scholar]
- Jones B.M, White K.G. Sample-stimulus discriminability and sensitivity to reinforcement in delayed matching to sample. Journal of the Experimental Analysis of Behavior. 1992;58:159–172. doi: 10.1901/jeab.1992.58-159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kangas B.D, Branch M.N. Empirical validation of a procedure to correct position and stimulus biases in matching-to-sample. Journal of the Experimental Analysis of Behavior. 2008;90:103–112. doi: 10.1901/jeab.2008.90-103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karas C.A, Picker M, Poling A. Effects of phenobarbital in combination with phenytoin or valproic acid on the delayed-matching-to-sample performance of pigeons. Pharmacology, Biochemistry and Behavior. 1986;25:929–932. doi: 10.1016/0091-3057(86)90409-0. [DOI] [PubMed] [Google Scholar]
- Mackay H.A. Conditional stimulus control. In: Iversen I.H, Lattal K.A, editors. Techniques in the behavioral and neural sciences: Vol. 6. Experimental analysis of behavior (Part 1, pp. 301–350) Amsterdam: Elsevier; 1991. (Eds.) [Google Scholar]
- McCarthy D. Measures of response bias at minimum-detectable luminance levels in the pigeon. Journal of the Experimental Analysis of Behavior. 1983;39:87–106. doi: 10.1901/jeab.1983.39-87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarthy D, White K.G. Behavioral models of delayed detection and their applications to the study of memory. In: Commons M.L, Mazur J.E, Nevin J.A, Rachlin H, editors. Quantitative analyses of behavior: Vol. 5 Reinforcement value: The effect of delay and intervening events. Cambridge, MA: Ballinger; 1985. (Eds.) [Google Scholar]
- Nevin J.A, Grosch J. Effects of signaled reinforcer magnitude on delayed matching-to-sample performance. Journal of Experimental Psychology: Animal Behavior Processes. 1990;16:298–305. [Google Scholar]
- Palya W.L, Walter D.E. A powerful, inexpensive experiment controller for IBM PC interface and experiment control language. Behavior Research Methods, Instruments & Computers. 1993;25:127–136. [Google Scholar]
- Pasternak T. Delayed matching performance after visual Wulst lesions in pigeons. Journal of Comparative and Physiological Psychology. 1977;91:472–484. doi: 10.1037/h0077350. [DOI] [PubMed] [Google Scholar]
- Perone M. Experimental design in the analysis of free-operant behavior. In: Iverson I.H, Lattal K.A, editors. Experimental analysis of behavior: Part I. Amsterdam: Elsevier; 1991. pp. 135–172. (Eds.) [Google Scholar]
- Picker M, White W, Poling A. Effects of phenobarbital, clonazepam, valproic acid, ethosuximide, and phenytoin on the delayed matching-to-sample performance of pigeons. Psychopharmacology. 1985;86:494–498. doi: 10.1007/BF00427915. [DOI] [PubMed] [Google Scholar]
- Poling A, Picker M, Polder D, Clark R. Chronic effects of ethosuximide, phenytoin, clonazepam, and valproic acid on the delayed-matching-to-sample performance of pigeons. Psychopharmacology. 1986;88:301–304. doi: 10.1007/BF00180828. [DOI] [PubMed] [Google Scholar]
- Roitblat H.L, Scopatz R.A. Sequential effects in pigeon delayed matching-to-sample performance. Journal of Experimental Psychology: Animal Behavior Processes. 1983;9:202–221. [PubMed] [Google Scholar]
- Santi A. The effects of associative congruence and dimensional similarity of samples in delayed matching by pigeons. Behavioural Processes. 1991;24:9–19. doi: 10.1016/0376-6357(91)90083-C. [DOI] [PubMed] [Google Scholar]
- Sawaguchi T, Yamane I. Properties of delay-period neuronal activity in the monkey dorsolateral prefrontal cortex during a spatial delayed matching-to-sample-task. Journal of Neurophysiology. 1999;2:2070–2080. doi: 10.1152/jn.1999.82.5.2070. [DOI] [PubMed] [Google Scholar]
- Seif G.I, Clements K.M, Wainwright P.E. Effects of distraction and stress on delayed matching-to-place performance in aged rats. Physiology and Behavior. 2004;82:477–87. doi: 10.1016/j.physbeh.2004.04.051. [DOI] [PubMed] [Google Scholar]
- Sidman M. Tactics of scientific research. New York: Basic Books, Inc; 1960. [Google Scholar]
- Spetch M.L, Treit D. Does effort play a role in the effect of response requirements on delayed matching to sample. Journal of the Experimental Analysis of Behavior. 1986;45:19–31. doi: 10.1901/jeab.1986.45-19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spetch M.L, Wilkie D.M. Subjective shortening: A model of pigeons' memory for event duration. Journal of Experimental Psychology: Animal Behavior Processes. 1983;9:14–30. [Google Scholar]
- Teal J.J, Evans H.L. Effects of DDAVP, a vasopressin analog, on delayed matching behavior in the pigeon. Pharmacology, Biochemistry and Behavior. 1982;17:1123–1127. doi: 10.1016/0091-3057(82)90106-x. [DOI] [PubMed] [Google Scholar]
- Thomas J.R. Matching-to-sample accuracy on fixed-ratio schedules. Journal of the Experimental Analysis of Behavior. 1979;32:183–189. doi: 10.1901/jeab.1979.32-183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Urcuioli P.J, DeMarse T.B, Lionello K.M. Sample-duration effects on pigeons' delayed matching as a function of predictability of duration. Journal of the Experimental Analysis of Behavior. 1999;72:279–297. doi: 10.1901/jeab.1999.72-279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinstein B. Matching-from-sample by rhesus monkeys and children. Journal of Experimental Psychology. 1941;31:195–213. [Google Scholar]
- White K.G. Characteristics of forgetting functions in delayed matching to sample. Journal of the Experimental Analysis of Behavior. 1985;44:15–34. doi: 10.1901/jeab.1985.44-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White K.G. Forgetting functions. Animal Learning & Behavior. 2001;29:193–207. [Google Scholar]
- White K.G, Wixted J.T. Psychophysics of remembering. Journal of the Experimental Analysis of Behavior. 1999;71:91–113. doi: 10.1901/jeab.1999.71-91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams D.C, Johnston M.D, Saunders K.J. Intertrial sources of stimulus control and delayed matching-to-sample performance in humans. Journal of the Experimental Analysis of Behavior. 2006;86:253–267. doi: 10.1901/jeab.2006.67-01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wixted J.T, Gaitan S.C. Stimulus salience and asymmetric forgetting in the pigeon. Learning & Behavior. 2004;32:173–182. doi: 10.3758/bf03196018. [DOI] [PubMed] [Google Scholar]
- Zentall T.R, Roper K.L, Sherburne L.M. Most directed forgetting in pigeons can be attributed to the absence of reinforcement on forget trials during training or to other procedural artifacts. Journal of the Experimental Analysis of Behavior. 1995;63:127–137. doi: 10.1901/jeab.1995.63-127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zentall T.R, Sherburne L.M. Role of differential sample responding in the differential outcomes effect involving delayed matching by pigeons. Journal of Experimental Psychology: Animal Behavior Processes. 1994;20:390–401. [PubMed] [Google Scholar]