Counting peptide-water hydrogen bonds in unfolded proteins

Abstract

It is often assumed that the peptide backbone forms a substantial number of additional hydrogen bonds when a protein unfolds. We challenge that assumption in this article. Early surveys of hydrogen bonding in proteins of known structure typically found that most, but not all, backbone polar groups are satisfied, either by intramolecular partners or by water. When the protein is folded, these groups form approximately two hydrogen bonds per peptide unit, one donor or acceptor for each carbonyl oxygen or amide hydrogen, respectively. But when unfolded, the backbone chain is often believed to form three hydrogen bonds per peptide unit, one partner for each oxygen lone pair or amide hydrogen. This assumption is based on the properties of small model compounds, like N-methylacetamide, or simply accepted as self-evident fact. If valid, a chain of N residues would have approximately 2N backbone hydrogen bonds when folded but 3N backbone hydrogen bonds when unfolded, a sufficient difference to overshadow any uncertainties involved in calculating these per-residue averages. Here, we use exhaustive conformational sampling to monitor the number of H-bonds in a statistically adequate population of blocked polyalanyl-six-mers as the solvent quality ranges from good to poor. Solvent quality is represented by a scalar parameter used to Boltzmann-weight the population energy. Recent experimental studies show that a repeating (Gly-Ser) polypeptide undergoes a denaturant-induced expansion accompanied by breaking intramolecular peptide H-bonds. Results from our simulations augment this experimental finding by showing that the number of H-bonds is approximately conserved during such expansion⇋compaction transitions.

Introduction

The quantitative assessment of H-bond strength dates back to Schellman's early work on urea dimer formation.¹ During ensuing years, the reaction in which a peptide H-bond is formed has been represented as either

(1a)

or

(1b)

and interpreted variously as a strict enthalpy of formation (1a) or a free energy of formation that may or may not include contributions from the entropy of released water (1b) and/or the total solvation free energy of amide hydrogens and carbonyl oxygens (1a,b).²

Biochemical thermodynamics is grounded in the measurement of energetic differences between defined states. To capture the difference between reactants and products in equations such as (1a,b), Fersht introduced the notion of an H-bond inventory.³ However, it was soon realized that simple counting leads to an “apples vs. oranges” comparison²: the reactants in (1b) involve the loss of two solvation free energies, not two H-bond energies, and these are being equated to the gain of one H-bond energy, which is different in kind. Further damage to the approach was inflicted by later work demonstrating that the H-bond inventory fails to capture experimentally determined solvation enthalpies of simple amides like N-methylacetamide (NMA).^4,5

Nevertheless, we adopt a strict H-bond inventory type of approach in this article, arguing that the preceding deficiencies have little bearing on our present topic of principal interest, which is to count the number of peptide:water H-bonds in unfolded polypeptide chains. The long tradition of using data from simple model systems to assess complex protein energetics often leads to unsuspected erroneous conclusions: see “Seven decades of hydrogen bonding history” in Ref.6. In particular, amides like NMA are inappropriate models because they fail to take into account two characteristic features that differentiate the polypeptide backbone from simple models. (i) Apart from chain termini, neighboring residues impede solvent-access to backbone units in polypeptide chains, whereas a simple amide is “all ends.” (ii) H-bonding in a polypeptide chain is conformation-dependent,^4,7 unlike a simple amide. Consequently, although the H-bond inventory is insufficient to account for the solvation enthalpies of simple amides, its failure involves deficiencies that may not be an issue in longer chains. Furthermore, the objection that mismatched energetic quantities are being equated in Eq. (1b) is obviated by separating differences in the number of H-bonds from differences in their corresponding energies.

When counting H-bonds, the native state (N) is commensurate with a numerical census, but the H-bond population in the unfolded state (U) can only be described by a distribution. Our main objective is to evaluate the distribution of peptide:water H-bonds in U. However, even the presumably straightforward task of counting H-bonds in proteins of known structure is not without ambiguity. Database surveys of hydrogen bonding in high resolution X-ray structures have often identified a significant number of backbone polar groups that ostensibly lack H-bond partners. This finding seems questionable because a completely unsatisfied donor or acceptor in N that could have been satisfied by water in U would come at an energetic cost of ∼3–5 kcal/mol, rivaling the entire free energy difference between N and U.^8,9 To cite just one contrary example, the database has many conformers that resemble β-turns but with unacceptable H-bond geometry. Almost all can be minimized into near-ideal turn geometry with only minor shifts in atomic coordinates (<< 1 Å), resulting in an apparent 13% increase in the population of H-bonded β-turns.¹⁰ Accordingly, we estimate the number of hydrogen bonds in N to be at least two per peptide unit: one for each amide hydrogen and one for each carbonyl oxygen.

Turning now to the main focus of this article, we calculated distributions of chain:water and chain:chain H-bonds by generating a statistically meaningful population of blocked polyalanyl six-mers, all in allowed regions of φ,ψ-space and free of steric overlap (Fig. 1). This population was then Boltzmann-weighted according to solvent quality, which was allowed to range from poor to good. In a poor solvent, chain solubility is reduced and chain-chain interactions are enhanced at the expense of chain-solvent interactions, and the root-mean-squared radius of gyration, <R_G>, of the population contracts. Conversely, in a good solvent, chain solubility is increased, chain-solvent interactions predominate, and the <R_G> of the population expands. In this study, as in our previous work,¹¹ a blocked six-mer is judged to be of sufficient length. Solvent quality was parameterized using a scalar parameter, ɛ, used to Boltzmann-weight the influence of intra-peptide hydrogen bond strength on the population of six-mers (see Methods). This parameter was varied incrementally, ranging from a value that favors chain:chain H-bonds (poor solvent) to one that favors chain:solvent H-bonds (good solvent).

Figure. 1.

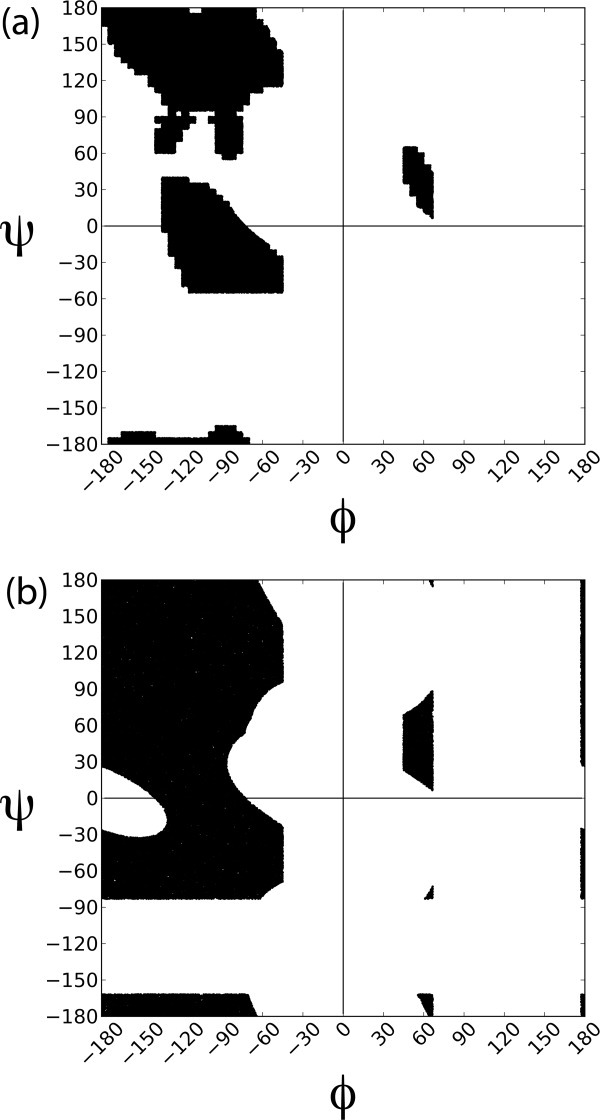
The Ramachandran plot. (a) Updated sampling region derived from the coil library.^44,45 (b) Conventional plot¹²; shaded region is sterically allowed.

Several technical issues required particular attention in the course of this work, as described in Methods. The φ,ψ-map was refined and hydrogen bonding criteria were improved based on data from ultra-high resolution protein structures (156 nonredundant structures with resolution ≤ 1 Å). Unlike the classical Ramachandran map found in textbooks,¹² the φ,ψ−map derived from these structures [Fig. 1(a)] is unpopulated in the large region between −180 < φ < −125° and −60° < ψ < 0°, as noted in both a database survey¹³ and a density functional calculation.¹⁴ To assess the sensitivity of our results to the choice of atomic and water radii, two separate populations were generated: one with accepted radii and another with atomic radii scaled by 0.95 and water by 0.90.

At any given value of solvent quality, the distribution of H-bonded waters per amide hydrogen or lone pair oxygen can be determined by Boltzmann-weighting the parent population. The averages extracted from these distributions describe sigmoidal curves that reach a plateau at the extremes of either high or low solvent quality values. Consequently, robust minimax averages can be evaluated in the plateau regions.

In good solvent, we find that an average of approximately two, not three, water molecules form hydrogen bonds to the middle peptide units in a blocked polyalanyl six-mer. In poor solvent, this number decreases to 1.0. Experimental data indicate that in terms of either enthalpy^15,16 or free energy,⁸ an intramolecular H-bond stabilizes protein structure in comparison with the corresponding H-bond to water. Therefore, if the number of H-bonds is approximately the same in N and U but the enthalpy per H-bond is stronger in N, then hydrogen bonding provides enthalpic stabilization for the native state.

Results

To inventory the unfolded state, the number of hydrogen-bonded waters was averaged over the entire conformational ensemble by Boltzmann-weighting the solvent quality parameter, ɛ [Fig. 2(a,c)]. Using normal/relaxed criteria, the average describes a sigmoidal-shaped decrease from 1.50/2.08 waters per residue in good solvent to a minimum of 1.02/1.08 waters in poor solvent. On average, 0.48/1.00 hydrogen bonded waters per residue are lost when the peptide is transferred from unfolding to folding conditions. This per-residue average was further decomposed into individual site probabilities at the three backbone sites (N—H, O1, and O2) [Fig 2(b,d)]. Both N—H and O2 describe sigmoidal-shaped curves because poor solvent conditions (i.e., ɛ > 0) favor contracted conformers, which restrict water access to these two sites. The probability profile of the O1 site is less variable [Fig. 2(b,d)] and increases with poor solvent conditions because diminished water access to the N—H site reduces the correlative likelihood of interference with water access to the O1 site.

Figure. 2.

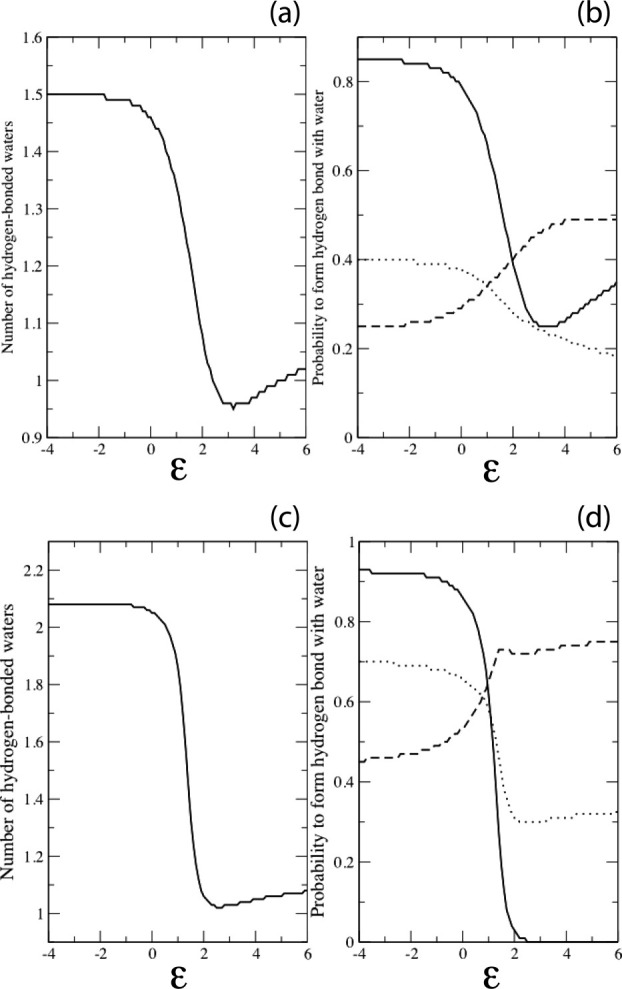
Hydrogen-bonded water molecules as a function of solvent quality. (a) Average number per residue and (b) individual site probability using normal criteria. (c) Average number per residue and (d) individual site probability using relaxed criteria. Negative values of ɛ correspond to good solvent, positive values to poor solvent. Site probabilities in (b) and (d) are annotated as a continuous line (N—H), dashed line (O1) or dotted line (O2). With relaxed criteria, the O1 site probability peaks at ɛ = 2, then diminishes slightly as further chain contraction results in an increased frequency of steric clashes at this site.

To inventory representative folded conformers, the probability of finding hydrogen bonded waters at the three backbone sites was evaluated for the four repetitive secondary structures: α-helix, parallel, and antiparallel β-strand, and polyproline II helix (P_II). Results are given in Table I, derived from 5000 independent water placement attempts at each backbone site (described in Methods). To rationalize the numerical results shown in Table I, probe waters were placed in randomly chosen H-bonding orientations at the N—H, O1, and O2 positions in the middle residue of a blocked polyalanine 7-mer, as illustrated in Figure 3. In the antiparallel β-strand, a severe steric clash occurs between the probe waters on the N—H and O1 positions [Fig. 3(a)]. This clash can be relieved and the O1 satisfied by a bridging water that H-bonds to both groups simultaneously, in agreement with earlier grand canonical ensemble Monte Carlo simulations in explicit water.⁷ In an α-helix, the low probability of water H-bonded to the N—H and O2 positions results from a steric clash with the carbonyl oxygen at i − 4 and the amide nitrogen at i + 4, respectively [Fig. 3(c)]. In a longer helix, the N—H(i) donor would H-bond to the O=C(i – 4) acceptor, but a 7-mer is too short to form this bond, and in this case the N—H remains vacant, freeing the O1 position to accept a water. In a polyproline II (P_II) helix, there is a comparatively high probability of finding waters H-bonded to the N—H and O1 positions, but a reduced probability at the O2 position owing to a potential collision with N(i + 2) [Fig. 3(d)].

Table I.

Water:Peptide Hydrogen Bonds to Repetitive Secondary Structures

	φ	Ψ	N—H	O1	O2	Overall	Maximum
α-helix	−60°	−45°	0.00/0.03	0.34/0.61	0.01/0.05	0.35/0.68	1.00
Anti-parallel β-strand	−140°	135°	0.93/1.00	0.05/0.02	0.51/0.89	1.49/1.91	3.00
Parallel β-strand	−120°	115°	1.00/1.00	0.11/0.43	0.51/0.88	1.62/2.31	3.00
PII	−75°	150°	1.00/1.00	0.19/0.68	0.19/0.56	1.38/2.24	3.00

The probability of water:peptide hydrogen bonds to the central residue of a blocked polyalanyl 7-mer in each of the four repetitive secondary structures. Two probabilities (separated by a slash), derived using either stringent or relaxed criteria, were calculated as described in the text. Columns 4–6 list these probabilities for the amide hydrogen donor and both lone pair oxygen acceptors, column 7 is the summed probability for all three sites, and column 8 is the maximum number. The lone pair acceptors O1 and O2 point either toward or away from the α-carbon, respectively, as illustrated in Figure 3.

Figure. 3.

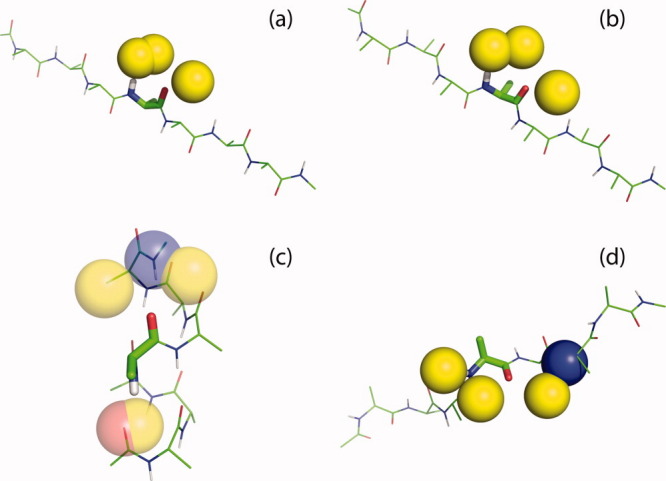
Probe waters in hydrogen-bonding positions on the central residue of a blocked polyalanyl-7-mer, evaluated for each of the four repetitive secondary structures: (a) anti-parallel β-strand; (b) parallel β-strand; (c) α-helix; (d) polyproline II helix. Waters are shown as yellow spheres, situated at an ideal distance 2.90 Å from their peptide partners (N or C=O). The peptide is displayed in wireframe, with atoms in the central residue as sticks. Peptide atoms that clash with a probe water are shown as spheres. Color code: oxygen: red; nitrogen: blue; hydrogen: white; and carbon: green.

The most probable number of hydrogen bonded waters at backbone sites is reckoned by summing the three individual site probabilities in Table I. In summary, the α-helix, which forms intrasegment H-bonds, has a low value, while the most probable number for the extended conformers, β-strand and P_II helix, is ∼2 waters per residue, under relaxed criteria. Although much less probable, it is nevertheless possible for the extended conformers to form water:peptide H-bonds at all three backbone sites simultaneously (Table I and Fig. 4).

Figure. 4.

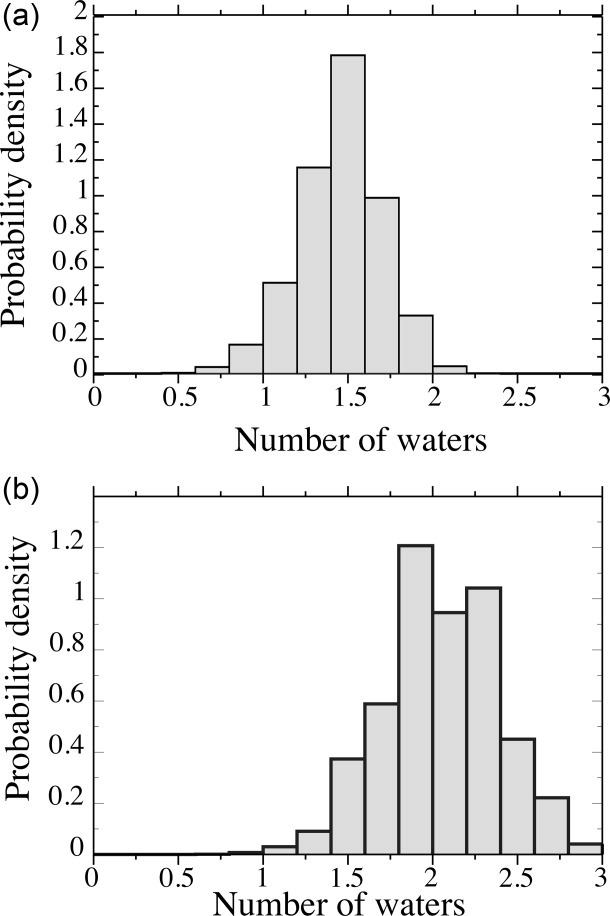
Probability density of water molecules at backbone sites in good solvent using (a) normal criteria and (b) relaxed criteria.

The average number of hydrogen-bonded waters for extended conformers [Table I; Fig. 3(a,b,d)] are in satisfying agreement with the corresponding number (∼2) in ensemble-derived data under good solvent conditions (Figs. 2 and 4). To analyze the basis for this agreement in further detail, Boltzmann-weighted Ramachandran density maps were constructed as solvent quality was varied from ɛ = −2 to ɛ = 2 (Fig. 5). Reassuringly, the unweighted map (ɛ= 0; Fig. 5) recapitulates the allowed sampling space [Fig. 1(a)] rather closely, with a dense population in the northwest quadrant and a sparse population between −120° < φ < −90° and 0° < ψ < 30°. As solvent quality increases [ɛ= −1, −2; Fig. 5(b,a)], the population in the inverse gamma turn region is depleted, while the remainder of the northwest quadrant persists. This solvent-induced selective winnowing accounts for the agreement between the number of hydrogen bonded waters in good solvents (Fig. 2) and the number in extended conformations, β-strand and P_II (Table I). Conversely, as solvent quality decreases [ɛ = 1, 2; Fig. 5(d,e)] most of the northwest quadrant is depleted progressively. However, the inverse gamma turn region is an exception: this region gains population at ɛ = 1 but is then depleted as solvent quality approaches ɛ = 2, overtaken by the α-helix with its stronger intrapeptide hydrogen bond.¹¹ At sufficiently poor solvent quality, when intrapeptide H-bonds are paramount, α-helical conformations outweigh other alternatives. The punctate appearance of Figure 5 is a consequence of this small but heavily weighted population that predominates as high ɛ-values are attained. Of course, such conditions would not be feasible under typical experimental conditions in aqueous solvent, although they can be attained readily in simulations.

Figure. 5.

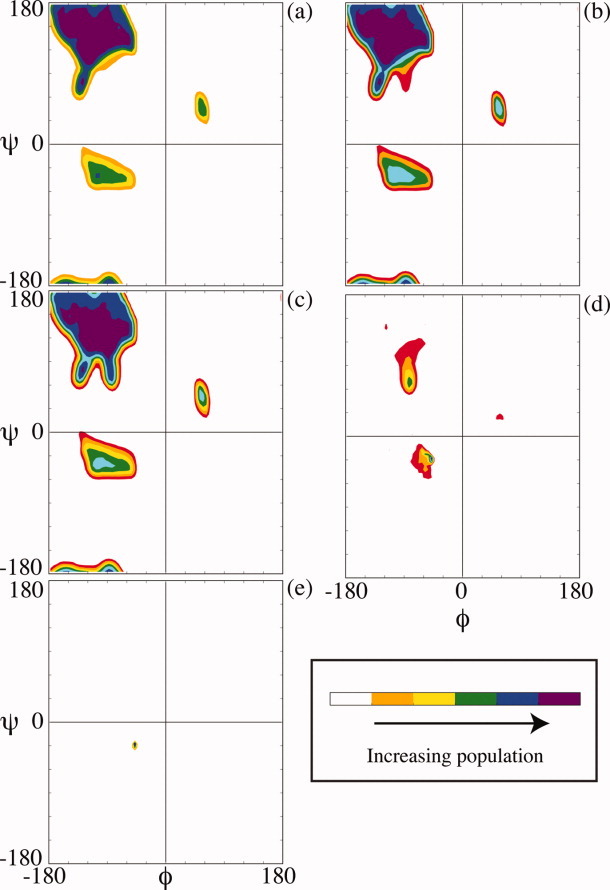
Ramachandran density plots from the Boltzmann-weighted conformational ensemble, sampled at ɛ = (a) −2; (b) −1; (c) 0; (d) +1; (e) +2. Colors refer to the population density, as indicated by the color bar to the right of each figure.

Discussion

We find an average of approximately two water molecules per backbone unit for a polypeptide chain subjected to unfolding conditions in good solvent. However, our simulations also indicate that the hydrogen bond inventory given by Eq. (1) is oversimplified because water molecules are not distributed uniformly between the N—H and C=O groups. Nevertheless, the anchoring assumption of the hydrogen bond inventory still holds. Essentially every N—H donor or C=O acceptor that is sequestered from solvent upon folding will form a compensatory intrapeptide hydrogen bond because, if left unsatisfied, the energy penalty would rival a typical protein's entire free energy of stabilization.⁹

Protein folding involves at least two H-bond-related inventory items—number and energy—with differing “bottom lines.” According to our simulations, the number of backbone hydrogen bonds remains approximately the same between U and N, and, in fact, it may even increase slightly upon folding [Fig. 2(a)]. However, the corresponding energy changes markedly: the formation of intra peptide H-bonds at the expense of peptide:water H-bonds is enthalpically favored by ∼1 kcal/mol/H-bond.^15,16 For even a small protein, one or two intrapeptide H-bonds per peptide unit summed over the entire chain would contribute substantially to native state stabilization. Additionally, the entropy of water release on intrapeptide H-bond formation makes a further contribution to chain stabilization.¹⁷ Taken together, these contributions are consistent with experiments indicating that H-bonding is a major driving force that favors the folded state.^18,19

To model the polypeptide chain in the unfolded state, Kiefhaber and colleagues used poly(Gly-Ser) peptides,²⁰ highly flexible, polar chains that can undergo a denaturant-induced expansion. Specifically, a (Gly-Ser)₁₆ chain expands by 11.6 Å between denaturant-free buffer and 8M GdmCl, as determined by FRET measurements.

The end-to-end distance of a blocked 6-mer is the length-equivalent of an 8-mer, and the length of a Kiefhaber peptide with added FRET probes is the length-equivalent of an 34-mer. Upon scaling by a factor of 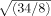, an Ala₆-mer contracts somewhere between 5.0 Å or 11.7 Å (using either normal or relaxed criteria, respectively, in poor solvent; Fig. 6), bracketing the observed value for a Gly-Ser peptide. A 32-mer is well beyond the persistence length of the peptide chain, and chain flexibility will increase the population of contracted conformers; this contribution cannot be captured by scaling the blocked 6-mer. Moreover, a glycine-based peptide has more opportunities to form intramolecular H-bonds than an alanine-based peptide of equal length. Furthermore, the FRET-based measurements range from 8M GdmCl to buffer, while ensemble-derived calculations continue into a protecting solvent regime, as though adding a compatible osmolyte like TMAO.^18,19 Yet, despite these differences, a qualitative comparison between FRET-based measurements and our ensemble-derived calculations is made possible by the fact that the end-to-end distance in good solvent attains a plateau in both systems, providing a comparable end-point (Fig. 6).

Figure. 6.

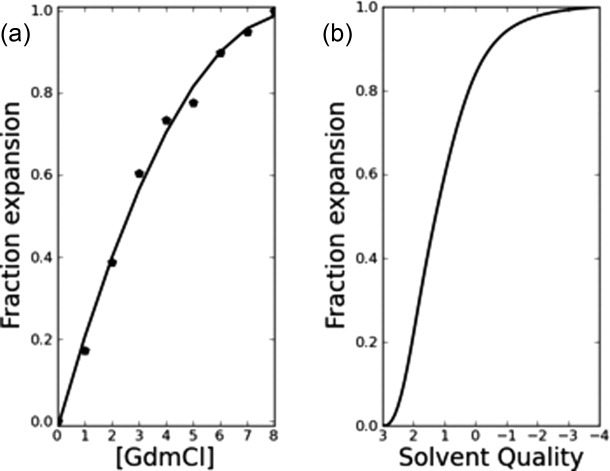
Solvent-induced expansion⇋compaction transition in unfolded chains. (a) The <end-to-end> distance of a (Gly-Ser)₁₆ chain increases by11.6 Å between denaturant-free buffer and 8 M GdmCl, as determined by FRET.²⁰ Experimentally determined data points are indicated by (•); the second-degree polynomial of best-fit to these points is shown to guide the eye. (b) Using normal criteria, the <end-to-end> distance of a scaled, blocked polyalanyl 6-mer increases by 5.0 Å between poor solvent and good solvent, as determined by simulation.

In principle, a complete energetic description of the expansion⇋compaction transition described by the Kiefhaber peptides or by the U ⇋ N transition during protein folding could be obtained by calculating differences in solvation free energy as the polypeptide chain ranges from expanded to contracted to fully folded. An obstacle to this goal is the fact that conventional forcefields, which neglect atomic polarizability, fail to capture either the correct strength²¹ or the correct geometry (Marshall et al., Unpublished) of the peptide H-bond. This deficiency may soon be overcome with the advent of next generation forcefields.²² Meanwhile, by taking an H-bond inventory as described here, we show that solvent quality has little effect on the number of H-bonds, and therefore the primary effect is on their energy.²¹

According to a computational model of Goldenberg,²³ an unfolded protein can visit collapsed states readily, and a substantial fraction of the solvent accessible surface is buried in some of these states (Fig. 9 in Ref.23). In this model, chain conformations are restricted solely by sterics, and some collapsed conformers may have unsatisfied H-bonding groups.⁹ Even so, results can be compared with a corresponding plot from our sterically allowed, H-bond satisfied, blocked 6-mers (Fig. 7), where a similar trend is observed.

Figure. 9.

Contour plots of water:backbone interaction geometry extracted from 157 ultrahigh (<1 Å) resolution protein structures. (a) N—H-water angle vs. donor–acceptor distance and (b) C=O-water angle vs. acceptor–donor distance. Red boxes surround areas that are sampled in simulations.

Figure. 7.

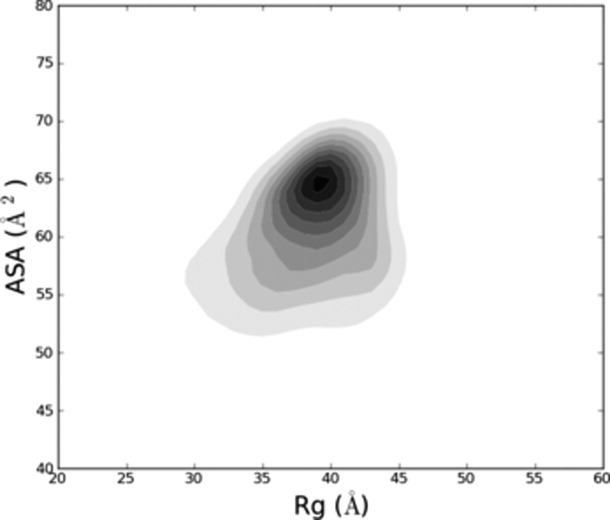
Distribution of expanded⇋contracted polyalanyl 6-mers. The root-mean-squared radius of gyration <R_G> vs. average backbone accessible surface area (ASA) of the two middle residues is contoured for 5.2 × 10⁶ H-bond satisfied, clash-free polyalanyl 6-mers, simulated using normal criteria. Populations are proportional to shading; the largest population corresponds to the darkest gray. A subpopulation of these 6-mers is contracted, and many bury a substantial fraction of available solvent accessible surface, similar to the distribution seen in Fig. 9 of Ref.23.

Recalcitrant data from proteins is often quite accessible in simple model systems. However, as mentioned above in introductory paragraphs, extrapolation from the simple to the complex often comes with cryptic issues that confound a direct H-bond inventory. Hydrogen-bonding groups (N—H and C=O) are far more solvent accessible in simple amides, like N-methylacetamide (NMA), than in corresponding groups incorporated within longer peptides (Fig. 8). Further, the hydrogen bond inventory incorrectly equates hydrogen bonding to water with the total solvation free energy.² In contrast, the H-bond inventory, as defined here, is limited to counting backbone H-bonds, not measuring their energies or exchange reactions.

Figure. 8.

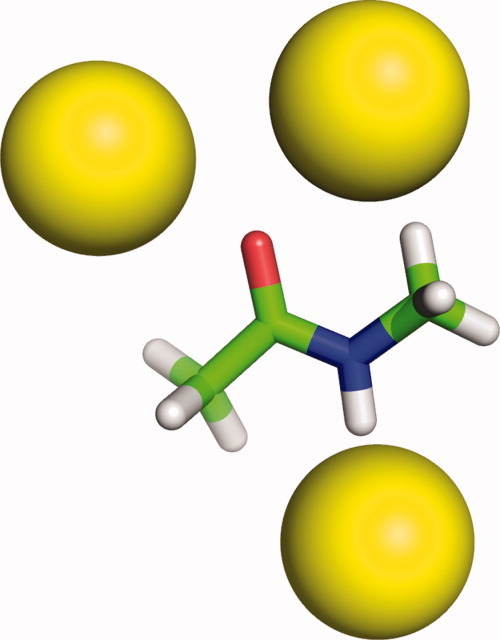
H-bonded water molecules at polar sites of N-methylacetamide using the same criteria and descriptors as in Fig. 3. Water access to the polar sites of simple model compounds is unhindered, unlike the situation in longer chains.

How does solvent quality influence chain dimensions?

A motivation for our analysis is the fundamental question of whether water is a good solvent or a poor solvent for proteins.^6,24 Intuitively, one might expect that water is a good solvent if, on average, residue backbones have three water-accessible sites in U but only two sites in N. However, the supposition of three water binding sites is a misleading extrapolation from model compounds like NMA because additional steric constraints emerge at longer chains lengths, as shown here.

Experimental investigation of this question has focused on the extent to which solvent quality affects chain dimensions as the unfolded population re-equilibrates upon changing to folding conditions. Detailed insight into solvent influences on folding can be extricated from chain properties during the elusive time interval following the onset of solvent quality-induced changes but preceding the rate limiting barrier for native structure formation. During this interval, does the radius of gyration, R_g, collapse toward N? And if collapse occurs, is it specific or nonspecific? That is, does identifiable structure emerge at this stage, or instead is the population a broad mixture of structures with no specific experimentally detectable signature?

Available experimental data come largely from either time-resolved energy transfer probes or small angle X-ray scattering (SAXS). In principle, the latter technique enables R_g to be measured directly. Many studies report a nonspecific coil-globule collapse preceding the rate-limiting step after the protein is transferred to folding conditions, as expected in poor solvent.⁶ In donor–acceptor energy transfer experiments, nonspecific collapse was detected under these conditions,^25–29 in agreement with many,^30–32 but not all,^33,34 SAXS results. An example will illustrate the difficulty in interpreting such data: an extreme test case, with almost the entire chain (∼92%) locked into its native structure but with a small number of hinge points (∼8%) distributed throughout the remaining structure, still retains a root-mean-squared radius of gyration and a Kratky plot that resemble those of the denatured protein (Fig. 6 in Ref.35).

What is the physical-chemical basis for nonspecific collapse? Given that no covalent bonds are made or broken during the re-equilibration process, changes in R_g must be caused by the solvent-induced reweighting of conformational biases among weak interactions (see Fig. 5). It is often assumed that a nonspecific coil-globule transition is synonymous with hydrophobic collapse. Contrary to this assumption, Doniach, Kiefhaber and colleagues, who studied the refolding of lysozyme over a broad time range (14 msec –2 sec) using time-resolved SAXS, found that hydrophobic side chains are still highly solvent accessible following the major chain collapse (representing 50% of the total change in R_g between U and N) that occurs in the dead time of mixing.³¹ Assuming their result is general, it seems unlikely that the hydrophobic effect is primarily responsible for the shift toward compact species. Why then do protein chains collapse in poor solvent prior to the formation of native structure?

Two recent studies concluded that formation of hydrogen-bonded secondary structure plays an organizing role during folding,^18,19 but these are equilibrium studies, and the time step at which H-bond-based compaction emerges is indeterminate. At an extreme, some have argued that organizing electrostatic^36,37 or hydrophobic³⁸ interactions are already realized in the unfolded state, and they induce compaction by gathering strength after shifting to folding conditions.

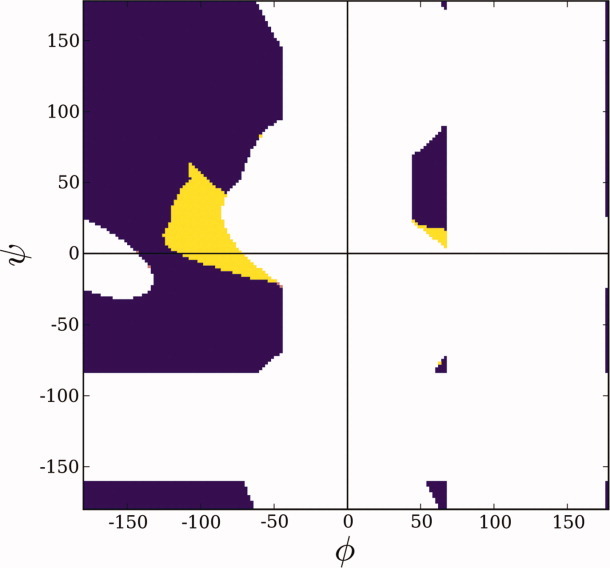
Unlike these explanations, we hypothesize that nonspecific chain collapse is primarily an entropic effect, a proposition that challenges intuitive expectations. A recent finding³⁹ indicates that solvent quality modulates occupancy of the bridge region in a conventional Ramachandran plot.¹² The bridge region is the locus of the penultimate residue of a four-residue, H-bonded type I β-turn,⁴⁰ far and away the most common type of nonglycine turn in proteins.⁴¹ This region is readily accessible in a poor solvent, where intrapeptide H-bonds are favored (like those in a type I turn), but it is significantly abridged in a good solvent because a backbone amide is deprived of an H-bonding partner under these conditions. In greater detail, when the ith residue is situated in the abridged region (Fig. 10), the amide hydrogen of the (i + 1)st residue is shielded from solvent access, and, in good solvent where intramolecular H-bonds are disfavored,⁶ that N—H would lack an H-bonding partner. The high energetic penalty of an unsatisfied backbone polar group⁹ would shift the thermodynamic population toward other energetically favored conformers and away from the abridged region, depleting its population. Consequently, accessible φ,ψ-space would be enlarged upon shifting from good solvent conditions to poor solvent conditions, with newly accessible backbone conformations centered in the region that facilitates type I β-turn formation, thereby increasing globularity by providing more opportunities for changes in overall chain direction. This entropic rationale for chain collapse is entirely consistent with the previously mentioned study of poly(Gly-Ser) peptides by Kiefhaber and colleagues, who concluded that “rapid collapse of polypeptide chains during refolding of denaturant-unfolded proteins … can, at least in part, be ascribed to nonspecific intramolecular hydrogen bonding.”²⁰

Figure. 10.

The Ramachandran plot. For a blocked peptide unit, steric clash alone winnows allowed conformational space to the regions shown in color (purple and yellow), as shown by Ramachandran et al.¹² The bridge is defined as the narrow isthmus on the left side of the plot (φ < 0), situated around ψ = 0. The addition of hydrogen-bonding constraints eliminates a minor segment of φ,ψ-space in α_L (yellow) and a major segment in the bridge (yellow).³⁹ The penultimate residue of a type I β-turn (φ,ψ = −90°, 0°)⁴⁰ is situated in this latter yellow segment.

Methods

Simulating the unfolded state ensemble

Consistent with previous work,¹¹ clash-free, hydrogen bond-satisfied polyalanine conformers, N-acetyl-(Ala)₆-N-methylamide, were generated with backbone φ,ψ-torsions that sampled all sterically allowed regions in the Ramachandran map uniformly and ω-angles chosen at random from a normal distribution with a mean of 180° ± 5°. Bond lengths and angles were held constant at typical values.^42,43 The “allowed” region of the Ramachandran map was updated (Fig. 1) based on an analysis of the protein coil library^44,45 to adjust for the observation that two classically allowed regions are, in fact, unpopulated,^13,14 as described in the text. Two ensembles were generated, one with standard van der Waals radii and a water radius of 1.4 Å (normal criteria), and the other with atomic radii scaled by 95% and a water radius of 1.25 Å (relaxed criteria). In either case, conformers were accumulated until the conformational entropy of the ensemble reached equilibrium¹¹ and conformational strings¹¹ of at least 95% of the previous 1000 newly generated conformations had already been sampled. Using this convergence protocol, 5.2 × 10⁶ conformers were generated with normal criteria and 7.5 × 10⁶ conformers were generated with relaxed criteria. Atomic radii, from⁴² were: C(sp²) = 1.5 Å, C(sp³) = 1.65 Å, O(sp²) = 1.35 Å, O(sp³) = 1.5 Å, N(sp²) = 1.35 Å, and H = 1.1 Å.

Probability of hydrogen-bonded waters

Each peptide unit was considered to have three possible water H-bonding sites: an N—H donor and two oxygen lone pair acceptors, designated O1 and O2. Waters were modeled as spheres. Trial waters were placed along a unit vector calculated as follows:

1. N—H vector: origin at H and colinear with the N→H bond vector

2. C=O vectors: origin at O in the peptide group plane, 130° angle with the C→O vector.

Trial waters were placed at a donor (N—H) or acceptor (O) distance between 1.80-2.10 Å or 2.60-3.10 Å, respectively, and at an angle between the unit vector and the H→water or O→water vector that was varied by up to 20°. These distance and angle ranges are based on protein:solvent data from ultra-high resolution proteins (resolution ≤ 1 Å), summarized in Figure 9.

To assess concerted interactions among H-bonded waters, water placement at the three sites was evaluated in terms of conditional probabilities. Specifically, waters were placed at N—H, O1, and O2 in three successive steps, with clash-free placement at a given step taken into account in remaining steps. For example, a water placed successfully at the N—H position would be included when evaluating the O1 position, and results from both sites would be included when evaluating the O2 position. These three successive steps constitute one trial.

Water placement was attempted in 100 trials at each site, and a clash-free trial was scored as a success. The fraction of successes was taken to be the probability, p_i, of finding a water at the ith site, [p_i = successes_i/100 (i = 1,2,3)]. These site probabilities were summed to give the most probable number of waters at a given residue, [Σp_i, (i = 1,2,3)]. Values of p_i and Σp_i were averaged over the two middle residues of each blocked 6-mer, and the ensemble mean was calculated by averaging over all Boltzmann-weighted conformers, as described next.

The Boltzmann-weighted ensemble average

A physical property of interest, X, (e.g., radius of gyration, hydrogen bond energy, number of hydrogen-bonded waters, etc.) was calculated for each conformer, with the ensemble average of this property given by

(2)

where β = 2≈1/RT (kcal/mol)⁻¹ at room temperature, H_i is the intrapeptide hydrogen bond energy of the ith conformer, and ɛ is the value of the solvent quality dial. The intrapeptide bond energy, H_i, attains a maximum value of 1.00 kcal/mol^15,16 when all geometric criteria are satisfied completely (donor–acceptor distance ≤ 3.5 Å, N—H—O scalar angle ≥ 100°, H—O—C scalar angle ≥ 90°). This term is scaled linearly beyond a donor–acceptor distance of 3.5 Å, reaching 0.00 at 5 Å. A large positive value of the solvent quality parameter, ɛ, corresponds to poor solvent conditions, which favor intrapeptide H-bonds, while a large negative value of ɛ corresponds to good solvent conditions, which favor peptide:water H-bonds. The unweighted average is obtained at ɛ = 0.

To compile the Ramachandran density maps in Figure 5, the probability P of φ and ψ in a region of interest was calculated as

(3)