Molecular Evolution, Mutation Size and Gene Pleiotropy: A Geometric Reexamination

Abstract

The influence of phenotypic effects of genetic mutations on molecular evolution is not well understood. Neutral and nearly neutral theories of molecular evolution predict a negative relationship between the evolutionary rate of proteins and their functional importance; nevertheless empirical studies seeking relationships between evolutionary rate and the phenotypic role of proteins have not produced conclusive results. In particular, previous studies have not found the expected negative correlation between evolutionary rate and gene pleiotropy. Here, we studied the effect of gene pleiotropy and the phenotypic size of mutations on the evolutionary rate of genes in a geometrical model, in which gene pleiotropy was characterized by n molecular phenotypes that affect organismal fitness. For a nearly neutral process, we found a negative relationship between evolutionary rate and mutation size but pleiotropy did not affect the evolutionary rate. Further, for a selection model, where most of the substitutions were fixed by natural selection in a randomly fluctuating environment, we also found a negative relationship between evolutionary rate and mutation size, but interestingly, gene pleiotropy increased the evolutionary rate as . These findings may explain part of the disagreement between empirical data and traditional expectations.

THE evolutionary rate of amino acid substitutions in a gene depends upon the fitness consequences of such substitutions. A pattern accepted early in molecular evolutionary biology is that functionally less important molecules or parts of a molecule evolve faster than more important ones, which was considered one of the few principles of molecular evolution (Kimura and Ohta 1974; Kimura 1983; Ohta and Gillespie 1996), hereafter the Kimura–Ohta principle of molecular evolution. Early examples of this principle in proteins were centered on the structural constraints of a few proteins (Dickerson 1971), but recently there have been relevant efforts aimed at obtaining systematic patterns from a large number of genes and for different measures of a biological role (reviewed in Pál et al. 2006; Camps et al. 2007). The functional importance of a protein has been measured as dispensability (Wall et al. 2005), lethality in RNAi experiments (Castillo-Davis and Hartl 2003), expression level (Pál et al. 2001; Subramanian and Kumar 2004; reviews in Zhang and He 2005; Pál et al. 2006), multifunctionality (Salathé et al. 2006), position in the protein interaction network (Makino and Gojobori 2006), times of interaction with the protein's partners (Hahn et al. 2004; Fraser 2005), and connectivity (Fraser et al. 2002; Chen and Xu 2005). Nevertheless, the results of those approaches have not been conclusive (Pál et al. 2006; Camps et al. 2007). It is particularly surprising that, with few exceptions (e.g., Hahn and Kern 2005; He and Zhang 2006), studies have not found support for a negative relationship between the pleiotropy of a given gene (protein) and its rate of evolution, measured as the ratio of nonsynonymous to synonymous substitutions (d_N/d_S) (Bloom and Adami 2003; Jordan et al. 2003; Hahn et al. 2004; Fraser 2005; Ericson et al. 2006; Salathé et al. 2006; Cooper et al. 2007; Jovelin and Phillips 2009; Podder et al. 2009). For example, Salathé et al. (2006) studied the relation between the rate of molecular evolution and pleiotropy of genes in Saccharomyces cerevisiae. Pleiotropy was measured as the number of biological processes in which a gene is involved, according to the Gene Ontology project (Gene Ontology Consortium 2002). The authors expected to find a negative correlation between evolutionary rate and pleiotropy (see also Otto 2004; Pál et al. 2006) but they found only a very weak correlation and concluded that their results did not support the notion that multifunctionality limits a gene's rate of evolution. Similarly using data from a study that quantified pleiotropy on the basis of phenotypic effects on growth in different environments (Dudley et al. 2005), Salathé et al. (2006) concluded again that pleiotropy has a limited impact on a gene's rate of evolution.

According to Camps et al. (2007), these and other similar results (e.g., Jordan et al. 2003; Hahn et al. 2004) imply notable inconsistency with the neutral and nearly neutral theories of molecular evolution. In fact, the Kimura–Ohta principle has been considered one of the strongest pieces of evidence for the neutral and nearly neutral theories of molecular evolution (Kimura and Ohta 1974; Kimura 1983; Ohta and Gillespie 1996; Hughes 2007). The reason is that if, as the neutralist theories claim, effectively advantageous mutations (s > 1/N) are very rare, only mutations with neutral or nearly neutral effect should be fixed. Thus, important proteins would evolve slowly because more mutations would have a severe and detrimental impact on fitness (s < −1/N) and fewer mutations would be neutral or nearly neutral. By contrast, less important proteins would evolve faster because more mutations would be neutral or nearly neutral.

Contrary to this widely accepted argument, in the current study we suggest that the Kimura–Ohta principle of molecular evolution is not incompatible with a selection model (i.e., an evolutionary model where the majority of substitutions are fixed by positive natural selection; see Gillespie 1994). Indeed, on the basis of his geometrical model, Fisher (1930) argued that positive selection tends to favor the less important changes and disfavors the important ones because mutations with greater phenotypic effects (hereafter larger “mutation size”) have a lower probability to be advantageous; thus processes of positive selection could apparently predict the same behavior as that associated with the neutral theories (Clarke 1971, 2001). Kimura and Ohta (1974) argued that the principle cannot be explained by positive natural selection because smaller advantageous mutations are less likely to be fixed by selection (see also Jukes and King 1971); thus selection disfavors smaller and favors larger advantageous mutations. This argument was incorporated by Kimura (1983) into Fisher's geometrical model (FGM), reaching the result that the distribution of advantageous mutations fixed by natural selection must have a peak at an intermediate mutation size, which led him to state that evolutionary processes dominated by natural selection predict a “maximum evolutionary rate occurring for an intermediate mutational effect” (Kimura 1983, p. 155). Later, Orr (1998) showed that Kimura's distribution was misleading because he did not consider the complete bout of adaptation experimented by a population, but only the first step of the adaptive walk. Orr (1998, 1999) estimated the distribution of sizes of factors fixed in a complete bout of adaptation and found that it is roughly exponential. Although the rate of substitution was not an aim of Orr's studies, the decreasing exponential distribution found in his studies suggests that a model considering adaptive processes in the FGM in theory could also predict the Kimura–Ohta principle of molecular evolution. In fact, adaptive bouts favor the fixation of a higher number of small phenotypic changes; thus if positive natural selection has been pervasive, proteins whose mutations have little effect on the phenotype should evolve faster than those with more effect. If this is the case, the principle cannot be considered evidence for the neutral and nearly neutral theories as has been traditionally assumed.

To gain insight into these complex and perhaps contradictory theoretical frameworks and empirical results, we developed a model of molecular evolution on the basis of the FGM to study the relationship between evolutionary rate and both the size of mutational effects of proteins and gene pleiotropy. The FGM is particularly useful to study the evolutionary consequences of the complexity of mutational effects. In the FGM a mutation is represented as a vector in an n-dimensional space, where the number of dimensions represents the number of traits that can be affected by the mutation and the magnitude of the vector represents the size of the phenotypic mutational effect. Gene pleiotropy can be understood as the capacity of a gene to affect multiple phenotypic characters and can be modeled as the number of dimensions in Fisher's multidimensional space (Gu 2007a,b). Thus, in the FGM it is possible to differentiate between the average phenotypic size of gene mutations (the average magnitude of vectors) and gene pleiotropy (the number of dimensions of the multidimensional space).

In contrast to the previous FGM-based models of Gu (2007a,b) and Su et al. (2010), here we show that there is no negative relationship between pleiotropy and gene evolutionary rate when the size of mutational effects is controlled. Our simulations also reveal that the negative association between mutation size and evolutionary rate is predicted by both a nearly neutral model with stable environment and a selection model with random environmental change. Furthermore, we suggest that a selection model could explain the weak empirical correlation observed between pleiotropy and gene evolutionary rate.

METHODS

Model assumptions:

Our model was inspired by Gu's (2007a,b), but has some substantial differences. Following Gu (2007a,b; see also Hartl et al. 1985), we assume that genes differ in the average phenotypic effect of their mutations (average mutational size) and the number of traits that are affected (gene pleiotropy). Gene pleiotropy is characterized by n distinct functional components of a gene (protein) that may affect the fitness of the organism independently, henceforth “molecular phenotypes” (Gu 2007a,b). The possible effects of mutations on the gene are represented as a multidimensional space of orthogonal phenotypic components. A strong assumption of the model is that a protein has a single optimum in each molecular phenotype.

Usually the evolutionary process in the FGM is modeled as a bout of adaptation produced after a sudden, recent optimum shift caused by an environmental change, after which the optimum is maintained static (Orr 1998, 1999, 2000; Welch and Waxman 2003). However, the unavoidable fate of an adaptive bout is to reach to a balanced steady state away from the optimum, where molecular evolution does not stop (Hartl and Taubes 1996). Properties of the balanced steady state have been studied, also maintaining a fixed optimum (Hartl and Taubes 1998; Poon and Otto 2000; Sella and Hirsh 2005; Tenaillon et al. 2007; Sella 2009), which is a very unrealistic scenario (Orr 1998, 2005a). Thus in our simulations we modeled evolution under both a static and a randomly shifting optimum [which would be produced either by environmental changes or by internal physiological compensation for the previously fixed mutations (Gu 2007b; Su et al. 2010]. In the former scenario the evolutionary process is characterized by a balanced steady state, but in the latter the evolutionary process is an alternation between adaptive bouts and balanced steady states that will be determined by the extent of the variability of environmental changes.

We made two methodological improvements with respect to previous FGM-based molecular evolutionary models (Gu 2007a,b; Su et al. 2010). First, the stabilizing selection model of Gu (2007a) is based on the assumptions of the shift model (Ohta 1977; Kimura 1979), and thus it considers only deleterious mutations. This leads to two important problems. On one hand, the shift model has been severely criticized (Tachida 1991; Ohta 1992; Gillespie 1995; Ohta and Gillespie 1996). For example, when a deleterious mutation becomes fixed, all subsequent mutations must be less fit than the fixed mutation, which makes no biological sense (Tachida 1991; Ohta 1992; Gillespie 1995; Ohta and Gillespie 1996). On the other hand, the model of Gu (2007a) has the additional inconvenience that the population remains always at the optimum peak even though slightly deleterious mutations are permanently fixed, which also does not make biological sense. The later microadaptation model of Gu (2007b) extends Gu's (2007a) stabilizing selection model (Gu 2007b, p. 1813) and uses some of his previous results, with the result that the microadaptation model is reduced to the stabilizing selection model when there is not optimum variation (Gu 2007b, p. 1816). Consistently, in the microadaptation model mutational random vectors have a static distribution centered at the origin. This kind of static distribution has been criticized and replaced by a distribution that changes with each substitution, in the house-of-cards model (Ohta and Tachida 1990; Tachida 1991, 1996). This assumption is more reasonable but makes analytical tractability very difficult because the effects of each substitution affect subsequent substitutions by changing the fitness of the population, and the population fitness fluctuates as a result of mutant fixations (e.g., Ohta and Tachida 1990; Tachida 1991, 1996, 2000; Gillespie 1995; Ohta and Gillespie 1996). Gu's assumptions allow one to obtain analytical results, as in the shift model (Ohta 1977; Kimura 1979). In our model, the distribution of mutations is centered on the position of the population phenotype, which changes with each substitution, implying a model with two coupled stochastic processes that make the analytical estimation of evolutionary rates intractable, as in the house-of-cards model, which is developed via simulations (see Ohta and Tachida 1990; Tachida 1991, 1996, 2000; Gillespie 1995).

Second, Gu (2007a,b) used a bottom–up approach for the generation of mutational random vectors (Poon and Otto 2000), in which the magnitude of vectors increases as the number of dimensions increases (Appendix 2 of Orr 2000). Thus, the previous approaches cannot distinguish separately the effect of mutation size and the effect of pleiotropy in the substitution rate of a gene. To differentiate between the influence of mutation size and pleiotropy, it is critical to use a top–down approach (Poon and Otto 2000). That is, our second improvement was to specify explicitly the magnitude distribution of the vector, which implies that the magnitude distribution of vector components along each axis is left unspecified. Thus a change in the number of dimensions does not affect the magnitude of mutational effects, guaranteeing that gene pleiotropy is not correlated with mutation size.

The distribution of magnitude used was uniform, implying that in each axis the magnitude distribution of vector components is leptokurtic in correspondence with the empirical evidence (see Keightley 1994; Lynch et al. 1999). We studied molecular evolution as the ratio between the rate of substitutions and the rate of mutations (k/u), which is usually measured empirically as d_N/d_S, under the assumption that synonymous substitutions are almost neutral. We modeled asexual populations under weak mutation (Nu ≪ 1); thus the evolutionary process is depicted as a succession of fixations and neglects the dynamic of polymorphisms.

Simulations:

Simulations represented two conditions, one with a fixed optimum and the second with a shifting optimum. All simulations were made using Monte Carlo methods in which random vectors r_j were generated into an n-dimensional phase space. Random vectors representing mutations were generated by a top–down approach (Poon and Otto 2000) according to a uniform distribution of vector magnitudes (from 0 to r) (following Kimura 1983 and Orr 1998). The total effect of a gene mutation on a number of quantitative traits (Wagner et al. 2008) or mutation size r_j = |r_j| was measured as the Euclidean distance 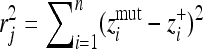, where is the value of coordinate i of the mutant, 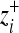is the value of the wild type, and i = 1, … , n. Fitness values were determined by the Gaussian function 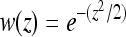, where z is the distance to the optimum. Selection coefficients were defined as 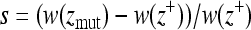, where is the distance to the optimum of the mutant and 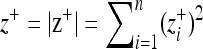is the distance to the optimum of the wild type. Mutations are fixed in the population according to the probability function , where N is the effective population size and s is the selection coefficient of the mutation (Crow and Kimura 1970).

We obtained the ratio between the substitution rate and mutation rate (k/u) for different conditions, determined by the following parameters: degree of pleiotropy (number of dimensions, n), average mutational size (average vector magnitude, 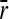), population size (N), and amplitude and variability of optimum shifts due to environmental change.

In those simulations that involved environmental changes, random optimum shifts were simulated as a Poisson process such that 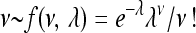, where ν and λ are the number and the expected number of changes in a time interval, respectively. Time intervals between consecutive changes (t) followed an exponential distribution 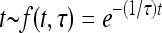, where τ = 1/λ is the expected time between environmental changes. If the mutation rate per gene per individual per generation (u) is constant, the expected time between environmental changes can be measured as the number of generations 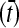according to 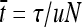. To compare processes with different effective population sizes in variable environments we then set τ ∝ N. The amplitudes of environmental changes were calculated by a bottom–up approach as 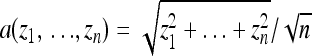, where z_i are the coordinates of the new optimum that were randomly chosen from a Gaussian distribution centered at the origin of the n-dimensional space, 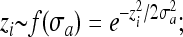and the denominator 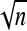is to guarantee that any relationship between evolutionary rate and pleiotropy will be due to the effect of dimensionality itself and not because of a correlation between dimensionality and amplitude of environmental changes.

We differentiate between effectively advantageous, effectively neutral, and effectively deleterious substitutions according to the selection coefficient of the substitution (s_s). Effectively advantageous substitutions are defined as substitutions that satisfied s_s > 1/N, i.e., advantageous substitutions fixed by positive selection; effectively neutral substitutions are defined as |s_s| < 1/N, i.e., substitutions mainly fixed by random drift; and effectively deleterious substitutions are defined as s_s < −1/N, i.e., deleterious substitutions fixed by drift despite the strong negative selection against them.

RESULTS

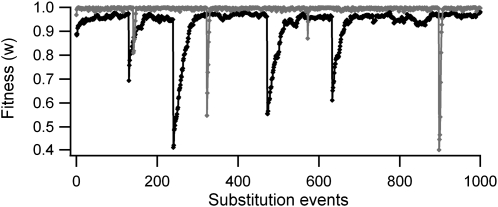
In Figure 1 we show two trials of the substitution process simulated with random environmental variability, where the time scale is measured in substitution events, i.e., the substitution of a newly arisen mutation. After an optimum shift due to environmental change, the population undergoes a burst of adaptive substitutions, raising its fitness until it attains a balanced steady state. In this state, the population remains around a suboptimum equilibrium fitness that is lower for a greater number of dimensions (Figure 1; see also Poon and Otto 2000; Tenaillon et al. 2007). The number of substitutions required to attain the steady state is larger for more pleiotropic genes (solid curve in Figure 1).

Figure 1.—

Trials of the sequence of fitness changes in a population due to substitutions in a gene in a randomly fluctuating environment. The shaded line corresponds to substitutions in a gene with pleiotropy of n = 3 (τ = 10⁵); the solid line corresponds to n = 30 (τ = 3 × 10⁵). Environmental variability values (τ) were chosen for visual convenience. General parameters used were effective population size N = 200, average mutational size 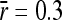, and environmental amplitude of changes σ_a = 0.85.

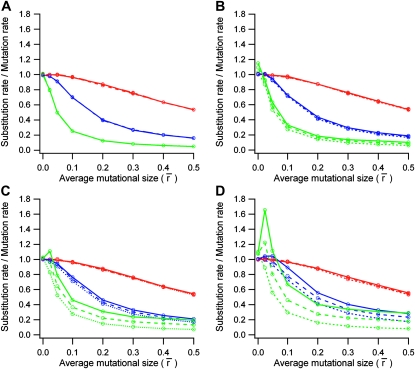
In all studied conditions, processes dominated by natural selection (|Ns| > 1) showed a negative relationship between evolutionary rate (k/u) and average mutational size (Figure 2). This negative relationship was lost for greater environmental changes only when the average mutational size was so small that the process was strongly dominated by genetic drift (|Ns| < 1) and thus the evolutionary rate tended to 1 (Figure 2, C and D). Larger effective population sizes produced lower evolutionary rates when the amplitude of optimum shifts (σ_a) was null (Figure 2A) or low (Figure 2B). This pattern was attenuated for higher shift amplitudes (see green lines in Figure 2, C and D).

Figure 2.—

Ratio between substitution rate and mutation rate (k/u) according to the average mutational size (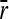) in (A) a static environment (σ_a = 0) and (B–D) variable environments with parameters (B) σ_a = 0.85, τ = 500 × N, (C) σ_a = 0.425, τ = 100 × N, and (D) σ_a = 0.85, τ = 100 × N. General parameters used were population sizes N = 10 (red lines), N = 100 (blue lines), and N = 1000 (green lines) and dimensions n = 2 (dotted lines), n = 10 (dashed lines), and n = 20 (solid lines). Each point corresponds to a simulation yielding 25,000 substitutions.

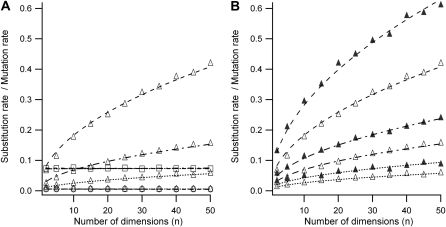
For smaller effective population sizes the evolutionary rate was less sensitive to environmental variability (red and blue lines in Figure 2), but populations with greater size increased their evolutionary rate considerably with the amplitude and variability of environmental changes (green lines in Figure 2, B–D). This increase in evolutionary rate was greater for more pleiotropic proteins (Figure 3; note the difference in the green lines in Figure 2C and 2D). This increase was due to effectively advantageous substitutions, while effectively neutral and deleterious substitutions were insensitive to the degree of gene pleiotropy (Figure 3A). When the optimum was maintained constant (static environment), the majority of substitutions were effectively neutral (|s_s| < 1/N) and the degree of pleiotropy did not affect the evolutionary rate (Figure 3A, solid horizontal curves).

Figure 3.—

(A) Ratio between substitution rate and mutation rate (k/u) for effectively advantageous (triangles), effectively neutral (squares), and effectively deleterious (circles) substitutions for different numbers of dimensions (n). Different curves correspond to different variability of environmental shifts with their respective curve fittings: from lower to higher variability, lines are solid (stable environment), dotted (τ = 10⁶, 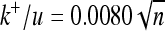), dotted-dashed (τ = 3 × 10⁵, 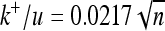), and dashed (τ = 10⁵, 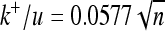). Parameters used were average mutational size 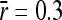, population size N = 1000, and amplitude of environmental variability σ_a = 0.85. (B) Ratio between strictly advantageous substitution rate and mutation rate plotted in A (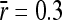, open triangles) compared with the result for an average mutational size of 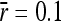(shaded triangles, with fitted curves, from lower to higher variability, 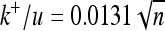, , 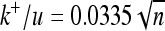and 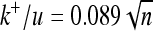, respectively). Each point corresponds to a simulation yielding 20,000 substitutions.

The rate of effectively advantageous substitutions 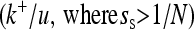satisfied ∼ 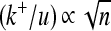and became greater than the rate of effectively neutral mutations for dimensions above a critical value (n_c ≈ 2 for τ = 10⁵ and n_c ≈ 12 for τ = 3 × 10⁵ in Figure 3A); this effect was greater for more variable environments (see green lines in Figure 2, B–D). This implies that more pleiotropic proteins in variable environments (e.g., with a mean time between shifts of 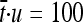, 500, and 1000 generation times in Figure 2, B–D) were ruled by a selection model, meaning that the majority of substitutions were advantageous mutations fixed by natural selection. The increase of effectively advantageous substitution rates with number of dimensions was greater for smaller mutation sizes (Figure 3B).

DISCUSSION

In this study we investigated the effect of mutation size and gene pleiotropy on protein evolution. As discussed above, the Kimura–Ohta principle of molecular evolution predicts that more important proteins evolve at a slower rate than less important proteins. As mentioned in the Introduction, protein importance can be understood as the mean size of the phenotypic effect of protein mutations. Under this interpretation our model shows that the principle is satisfied under a wide range of conditions (Figure 2). In the absence of environmental change a population remains in a dynamic balanced steady state, a state commonly understood as a nearly neutral evolutionary process (Hartl and Taubes 1996; Sella and Hirsh 2005; Sella 2009), which is in some aspects similar to the house-of-cards nearly neutral model (Ohta and Tachida 1990; Tachida 1991, 1996). Under this condition we found the expected negative relationship between evolutionary rate and mutation size according to the Kimura–Ohta principle (Figure 2A). Interestingly, this pattern was found both for a nearly neutral condition where most of the substitutions are fixed by random drift and for a selective condition in a randomly fluctuating environment where most of the substitutions are fixed by positive natural selection (e.g., Figure 2D, green lines). Thus, a confirmation of the Kimura–Ohta principle applied to differences among protein evolutionary rates is not necessarily evidence in favor of the neutral or nearly neutral theories, as has been traditionally claimed (Kimura and Ohta 1974; Kimura 1983; Ohta and Gillespie 1996; Hughes 2007). In our model, selective processes led to the Kimura–Ohta principle, making sense of two biological points. First, for any fixed distance to the optimum, an increase in mutation size increases the number of deleterious mutations, as predicted by Fisher (1930). Second, although the probability of fixation of advantageous mutations by natural selection increases with mutation size, the fixation of large advantageous substitutions in an adaptive bout occurs for a low proportion of mutations and for a short time period relative to the complete bout. Indeed, when the protein progressively approaches the optimum, the same mutations that would have been advantageous at the beginning become deleterious with time (in accordance with the exponential distribution found by Orr 1998). These findings are in strong opposition to Kimura's (1983) FGM-based prediction that under pervasive positive natural selection there would be a maximum evolutionary rate occurring for intermediate mutational effects. As is shown in Figure 2, under pervasive positive natural selection there is a negative relationship between evolutionary rate and average mutational size; peaks appeared only for greater environmental changes and very small (not intermediate) mutational size; thus mutations attain the limit at which almost all mutations are substituted by genetic drift and the evolutionary rate tends to one (Figure 2, C and D). As a matter of fact, these findings may be model and parameter specific. It is possible to construct other models of adaptive substitution where this is not fully met (e.g., with coevolution or a gradually and continuously moving optimum).

Note that in our model we considered only intragenic compensatory mutations. The effect of intergenic compensatory mutations should increase the evolutionary rate of more pleiotropic proteins because more pleiotropic proteins affect a greater number of phenotypes and therefore a greater number of genes affecting the same phenotypes are possible. Thus, more pleiotropic proteins should be less constrained to evolve due to intergenic compensatory mutations, for example, that ameliorate functions previously deteriorated by slightly deleterious substitutions in the protein and thus allow new slightly deleterious substitutions to occur in the protein.

The protein importance of a protein has also been understood as the degree of gene pleiotropy (see Otto 2004; Pál et al. 2006; and references in the Introduction). We found that gene pleiotropy, i.e., the number of orthogonal molecular phenotypes affected by the mutations in a protein, does not affect the rate of substitutions in a nearly neutral, environmentally stable condition (Figures 2A and 3A). This could explain the very weak correlation found between evolutionary rate and pleiotropy in empirical studies (Bloom and Adami 2003; Jordan et al. 2003; Hahn et al. 2004; Salathé et al. 2006; Ericson et al. 2006; Camps et al. 2007; Cooper et al. 2007; Podder et al. 2009). This result contrasts with the fact that in the FGM the probability that a mutation of a given phenotypic size is advantageous decreases with the number of dimensions, and the probability that it is deleterious increases (Fisher 1930; Orr 1998). Interestingly, in the balanced steady state, this fact affects only the mean equilibrium fitness [which is lower for a higher number of dimensions (Hartl and Taubes 1998; Poon and Otto 2000; Tenaillon et al. 2007)]; but when the equilibrium is attained, the rate of substitutions is not affected by the number of dimensions; i.e., protein evolution is not affected by gene pleiotropy. This is explainable because, while the equilibrium fitness is lower for higher dimensions, the number of advantageous mutations increases since the population is further away from the optimum (Fisher 1930; Orr 1998; Poon and Otto 2000). Thus the effect of the dimensionality is compensated by the effect of the distance from the optimum.

In our model we differentiated the effect of gene pleiotropy and the average size of the mutational effects such that gene pleiotropy was not correlated with the average mutational size. It is likely that this is not the case in nature, and it is to be expected that the greater the gene pleiotropy is, the greater the overall phenotypic effect of gene mutations. For example, Wall et al. (2005) found in S. cerevisiae a negative (although weak) correlation between dispensability of proteins (measured as the growth rate of a strain in which this gene was knocked out) and the number of biological processes in which they are involved (Salathé et al. 2006). Similarly, Chen and Xu (2005) found a positive correlation between the average value of fitness and gene connectivity in the protein–protein interaction network (see also Cooper et al. 2007). This positive relationship between pleiotropy and fitness effects would imply an expected negative correlation between pleiotropy and evolutionary rate, due to its indirect effect on mutation size. The lack of empirical support for this prediction (Pál et al. 2001; Fraser et al. 2002; Bloom and Adami 2003; Fraser 2005; Wall et al. 2005; Salathé et al. 2006; Camps et al. 2007; Cooper et al. 2007; Jovelin and Phillips 2009; Podder et al. 2009) could be explained in our model when environmental variability was incorporated. Our results showed that the substitution rate increases with gene pleiotropy in variable environments (Figure 3). This could produce an attenuation of the expected negative correlation between substitution rate and gene pleiotropy. Thus, although mutations in more pleiotropic proteins tend to generate a phenotypic effect of greater size (and therefore a lower evolutionary rate), their more pleiotropic nature tends to increase the evolutionary rate above the expected rate, according to their expected average mutational size. This effect should be even stronger for smaller mutation size (Figure 3B), which could make it more important in nonessential genes (Thatcher et al. 1998; Ericson et al. 2006). Therefore if positive natural selection is pervasive in protein evolution, as a number of studies suggest (e.g., Fay et al. 2002; Bierne and Eyre-Walker 2004; Eyre-Walker 2006; Bachtrog 2008), our findings suggest a plausible explanation for the apparent difficulty of observing the Kimura–Ohta principle with respect to gene pleiotropy. Consistent with the selection model's prediction, Fraser (2005) and Jovelin and Phillips (2009) found a significantly higher evolutionary rate of proteins with signals of higher pleiotropy, viz. interaction with different partners at different times, and centrality in the protein–protein interaction and metabolic network, respectively.

Due to their formal nature, our results on the influence of gene pleiotropy on molecular evolution may be related to the “cost of complexity” also developed in the FGM framework (Orr 2000; Welch and Waxman 2003). From a geometric point of view, our results on the substitution rate of more pleiotropic proteins could be interpreted as results about the genomic substitution rate of more complex organisms (i.e., organisms with a higher number of traits subjected to mutational change and selection). Thus, more complex organisms should suffer a higher genomic rate of substitutions (total rate and rate of strictly advantageous) than less complex organisms. This result is coherent with the cost of complexity, one of the most interesting results obtained from the FGM (Orr 2005b). Orr (2000) demonstrated that as the number of characters (i.e., complexity) increases, there is a significant reduction (cost) in the rate of adaptation. Welch and Waxman (2003) showed that Orr's finding is robust to many modifications of the model's assumptions. Consistently, in our model more pleiotropic genes take longer to attain the steady state (Figure 1). Surprisingly, the lower rate of adaptation in more complex organisms has induced the expectation that “beneficial mutations should be less frequent in complex organisms” (Martin and Lenormand 2006, p. 893), and the equivalent FGM-based reasoning at the protein level can be found in other studies (e.g., Hahn and Kern 2005; Ericson et al. 2006; He and Zhang 2006; Pál et al. 2006; Cooper et al. 2007). In contrast to this expectation, our simulations showed that the rate of advantageous mutations increases with complexity (n) (Figure 3). However, this is not inconsistent with the cost of complexity, but on the contrary is a direct consequence of it. More complex organisms have a lower rate of adaptation in part because favorable mutations of a given size travel shorter mean distances to the optimum (Orr 2000; Welch and Waxman 2003). Thus, our finding of an increased evolutionary rate of advantageous substitutions for greater complexity is due to the fact that a greater number of substitutions are necessary to travel the same distance toward the optimum. Analogously, more pleiotropic proteins would spend more time in adaptive processes than less pleiotropic proteins, accumulating a larger number of small-sized advantageous substitutions (see Figure 1). Consequently the increase of the strictly advantageous substitution rate with the number of dimensions is stronger for smaller mutation sizes (Figure 3B).

Recently, Gu (2007a,b) and Su et al. (2010) theoretically found a strong negative relationship between evolutionary rate and gene pleiotropy. Nevertheless, these findings can be explained by their bottom–up approach to the random vector generation (Appendix 2 of Orr 2000; Poon and Otto 2000). In this approach, the distribution and magnitude of mutational effects are specified for each axis and the total magnitude of mutation is left unspecified. Thus under the bottom–up approach the magnitude of vectors increases as the number of dimensions increases (Appendix 2 of Orr 2000). Therefore, in Gu's model higher pleiotropy decreases the evolutionary rate simply because pleiotropy increases the size of mutations (see also Wagner et al. 2008); thus it does not allow one to study the evolutionary consequences of gene pleiotropy independently of its impact on the size of its mutational effects (other criticisms applicable to the approach used by Gu 2007a,b can be found in Appendix 2 of Orr 2000).

Overall, the status of the Kimura–Ohta principle of molecular evolution is well established for nonsynonymous vs. synonymous or intronic substitutions (“parts of a molecule” sensu Kimura and Ohta 1974) in the same loci, and it provides strong support for the neutral model of the evolution of synonymous nucleotide sites (Hughes 2007). However, the applicability of the principle to protein comparisons has been questioned (Camps et al. 2007). Part of the discrepancy between empirical studies and the traditional expectation may be explained because the measures of the biological role or functional centrality of a protein (connectivity, dispensability, multifunctionality, essentiality, and expression level, among others) may be related to the number of molecular phenotypes affected by the protein (gene pleiotropy). For example, connectivity in a protein network could be related to the pleiotropy of proteins (Camps et al. 2007). Therefore, more connected proteins could have a higher substitution rate than the expected rate according to their impact on fitness, weakening the expected negative correlation between substitution rate and connectivity (e.g., Fraser et al. 2002). Similarly, Wagner et al. (2008) found that the total effect of a mutation in mouse skeletal QTL increases with pleiotropy; thus the effect of gene pleiotropy on the evolutionary rate may be strongly counteracted by its correlation with the mutation size. Therefore, we think that further studies of the Kimura–Ohta principle of molecular evolution applied to proteins should (1) clarify and define precisely the different properties denoted by the notion of gene “importance,” (2) analyze the specific molecular evolutionary effect of each property, and (3) study the relationship between these properties and their combined effect on the protein evolutionary rate.