CAG-Repeat Length and the Age of Onset in Huntington Disease (HD): A Review and Validation Study of Statistical Approaches

Abstract

Background

CAG-repeat length in the gene for HD is inversely correlated with age of onset (AOO). A number of statistical models elucidating the relationship between CAG length and AOO have recently been published. In the present article, we review the published formulae, summarize essential differences in subject sources, statistical methodologies, and predictive results. We argue that unrepresentative sampling and failure to use appropriate survival analysis methodology may have substantially biased much of the literature. We also explain why the survival analysis perspective is necessary if any such model is to undergo prospective validation.

Methods

We use prospective diagnostic data from the PREDICT-HD longitudinal study of CAG-expanded participants to test conditional predictions derived from two survival models of age of onset of HD.

Principal Findings

A prior model of the relationship of CAG and AOO originally published by Langbehn et al. yields reasonably accurate predictions, while a similar model by Gutierrez and MacDonald substantially overestimates diagnosis risk for all but the highest risk subjects in this sample.

Conclusions/Significance

The Langbehn et al model appears accurate enough to have substantial utility in various research contexts. We also emphasize remaining caveats, many of which are relevant for any direct application to genetic counseling.

Introduction

Huntington Disease (HD) is an inherited neuropsychiatric illness caused by polyglutamine expansion in the gene for the protein huntingtin (HTT),. (Huntington’s Disease Collaborative Research Group 1993). Almost immediately upon discovery of this gene, it was recognized that the mean age of clinical onset was strongly related to length of the CAG trinucleotide expansion that codes for the polyglutamine repeat (Duyao et al., 1993; Stine et al., 1993). Since then, numerous statistical models have been published that fit relationships between CAG length and clinical onset. We begin by reviewing the various published models, focusing on substantive differences between these studies and potential methodological explanations for those differences. We then test the prospective validity of two models that lend themselves to such examination, focusing on a model previously reported by Langbehn et al.(Langbehn et al., 2004). We do this using data from a prospective longitudinal study of the development of HD, PREDICT-HD (Paulsen et al., 2006; Paulsen et al., 2008).

Methodological Issues for Regression Formulae of CAG length and HD onset

The majority of published models (Andresen et al., 2007b; Andrew et al., 1993; Aylward et al., 1996; Lucotte et al., 1995; Squitieri et al., 2000; Stine et al., 1993) have been based on some form of linear regression. A sample of people with previously diagnosed HD have been used and their age of onset has been fit by least-squares regression to CAG repeat length. In many cases, (Andrew et al., 1993; Lucotte et al., 1995; Ranen et al., 1995; Rubinsztein et al., 1997; Squitieri et al., 2000) researchers have noted a better model fit if the logarithm of onset age is fit, and in one recent report (Andresen et al., 2007b), further piece-wise fitting of log(age) ¹ provided a better description of onset for extremely long (and rare) CAG lengths. (Note that fitting logarithms in a linear regression results in exponential functions for predicting the original outcome variable.)

These regression models suffer from a significant potential weakness, well-described in the introductory chapters of survival analysis texts (Cox and Oakes 1984; Kalbfleisch and Prentice 2002; Lawless 2003). Unless a well-defined sample is completely followed until the point where all members have “failed” (i.e., in the context of this paper, “failure” means manifesting with HD), conventional regression models based only on the failures will provide a biased and generally inappropriate estimate of the true distribution of failure times. This defect chiefly arises for two closely related reasons. First, members of a sample who do not fail (or who are lost to follow-up) are not accounted for in such an analysis. If subjects do not reach the point of onset of HD diagnosis, they are ignored. Such subjects will typically have a later onset age than those whose ages are recorded. Second, there may have been no provision for observation of such non-failing subjects in the first place. If a model is based only on cases with onset that have come to clinical attention, then it cannot be expected to generalize well to a broader population that may also include longer-term survivors. These issues are of critical practical importance because an important (although controversial) application of such models has been provision of healthy-life expectations to those who are known to carry the HD mutation. The above biases have a substantial potential to provide unduly pessimistic estimates of age of onset. This is especially relevant for shorter CAG repeat lengths, where onset may be quite late or not occur at all during a normal lifespan (Brinkman et al., 1997; Falush et al., 2001; Langbehn et al., 2004; Maat-Kievit et al., 2002; Rubinsztein et al., 1996).

Survival Analysis

The mathematical modeling techniques particular to Survival Analysis address one of the two biases discussed above. Subjects who are part of the sample but who are not observed to fail are accounted for . Such subjects are said to be “censored”. By various mathematical approaches, we may operationalize this concept in HD research so that it applies to a person who is known to have reached at least their age of last observation without yet having onset of HD. The second bias source, failure to include such subjects in the sample when they represent a significant part of the target population, is ideally addressed by more representative sampling. This is a difficult issue in HD research. Population genetic models (Falush et al., 2001; Warby et al., 2009) strongly suggest a relatively widespread prevalence of nonsymptomatic CAG expansions in the 36 to 40 range, but subjects in this range are rare in clinical samples. Pedigree sampling from index cases would probably not solve this problem, as a substantial portion of these cases are thought to arise from earlier generations with intermediate (27–35) CAG expansions and no previous family HD history (Almqvist et al., 2001). An alternative to modeling biased clinical samples of such subjects is extrapolation from CAG repeat ranges where ascertainment is arguably nearly complete. The validity of doing so is of course subject to a strong assumption that the relationships can be extended to this under-observed CAG range.

We are aware of four research reports that have used survival analysis to estimate HD onset distributions: Brinkman et al. (Brinkman et al., 1997), Gutierrez and MacDonald (Gutierrez and Macdonald 2002; Gutierrez and Macdonald 2004), Langbehn et al. (Langbehn et al., 2004) and Maat-Kievit et al. (Maat-Kievit et al., 2002). Brinkman et al. modeled a subset of the data described below that was eventually used in Langbehn et al. They reported separate, nonparametric survival models for each CAG length, but no mathematical formulation linking CAG-length influences together in a parametric relationship. Gutierrez and MacDonald fit gamma distributions (using least squares criteria) to the nonparametric survival curves reported by Brinkman et al. The parameters of the Gamma distribution were functions of CAG length.

Our previously reported model (the Langbehn et al model) (Langbehn et al., 2004) was developed using a database of 2,913 subjects (2,298 who had received a diagnosis and 615 who had not) contributed by 40 HD centers worldwide. Many of these centers followed HD families and provided genetic testing services and therefore could provide data for those with and without a diagnosis. We directly modeled onset age distribution for CAG lengths 41–56 using a nonstandard parametric Survival model and offered extrapolations for the 36 to 40 range. We review additional details of the Langbehn et al and Gutierrez and MacDonald models, relevant to prospective validation, in the Methods section.

Maat-Kievit et al. was based on a national Dutch register of CAG-tested subjects from HD families. They performed Kaplan-Meir nonparametric survival analyses for individual CAG lengths and Cox proportional hazards modeling to estimate the CAG-length hazard ratio. They did not report the actual estimated survival functions from their analysis. In contrast, such linking formulae were estimated in Langbehn et al. (Langbehn et al., 2004) and Gutierrez and MacDonald (Gutierrez and Macdonald 2004).

The importance of modeling CAG-length-dependent shape and variance of age of onset distribution

Explicit modeling of the standard deviation of diagnosis age is a novel feature of the Langbehn et al. and Gutierrez and MacDonald models. Langbehn et al. found the lifetime distributions to be symmetrical and with wider variance for shorter CAG expansions. Both considerations play an influential role in translating lifetime models to age-conditional expectations of time to onset. Gutierrez and MacDonald (Gutierrez and Macdonald 2004) also imbedded a CAG-dependent variance function in the gamma distribution adopted for their model. They too explicitly considered symmetry of onset age and concluded that, for the data from Brinkman et al. (Brinkman et al., 1997), the slight asymmetry associated with these gamma distributions provided the best empirical fit. In contrast, linear regression models of age have assumed a constant, symmetrical variance of onset ages around the estimated means. The constancy appears clearly contrary to published data (Andresen et al., 2007b; Brinkman et al., 1997; Duyao et al., 1993; Langbehn et al., 2007; Lucotte et al., 1995; Maat-Kievit et al., 2002; Ranen et al., 1995; Snell et al., 1993; Squitieri et al., 2000; Stine et al., 1993; Trottier et al., 1994). In simple regression models using the logarithmic transformation, there is an implicit assumption that the variance decreases as the mean age of onset decreases. This was noted by both Lucotte et al. (Lucotte et al., 1995) and Andrew et al. (Andrew et al., 1993). However, no attempt to explicitly estimate this variability is evident in the reports of these log-transformed models. Further, the assumed symmetry of log transformed variance implies an asymmetrical distribution of diagnosis on the untransformed age scale. This implication does not seem to have been addressed as those models were developed.

Comparative Review of Mean Diagnosis Ages from the Various Formulae

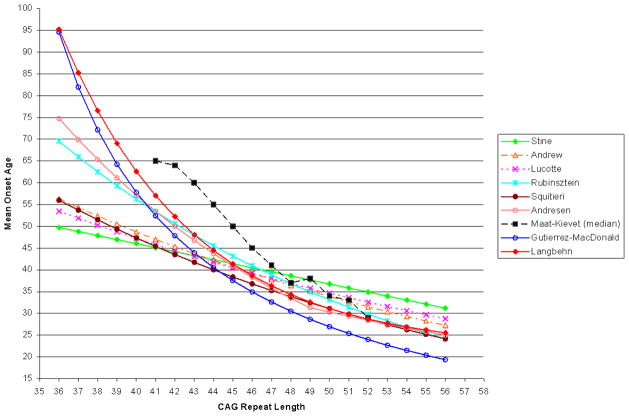
In Figure 1, we illustrate mean onset ages predicted by the various published formulae. The formulae and reported CAG ranges used in their estimation are summarized in Table 1. We have excluded most published reports where either no overall CAG formula was estimated (Brinkman et al., 1997) or, if estimated, not explicitly published (Ranen et al., 1995). We also exclude a formula reported by Aylward et al. (Aylward et al., 1996). This formula, onset age = 54.87 − 0.81*CAG + 0.51*(Parent’s onset age), defies direct comparison because of the need for parent age. We note that it was derived using linear regression and subject to the limitations and potential bias from that approach discussed earlier.

Figure 1.

Mean Onset Age as Estimated by Various Published Formulae

Table 1.

Various Proposed Formulae and Source Sample Characteristics for Age of onset of HD

Study	N	CAG Range	CAG Median	Formula for Mean Diagnosis Age
Stine et al.	114	36–82	48.41	83.1-0.927*CAG
Lucotte et al.	72	36–60	46	Exp(5.095-0.031*CAG)
Andrew et al.	360	38–121	44	Exp(5.3379-0.0363*CAG)
Rubinsztein et al	293	36–73	–	Exp(6.15-0.053*CAG)
Squitieri et al.	319	37–97	45	Exp(5.5413-0.0421*CAG)
Andresen et al. (HD MAPS )2	692	36–80	–	CAG < 50: Exp[4.046-(CAG-40)*0.067] CAG ≥ 50: Exp[3.443-(CAG-49)*0.032]
Gutierrez & MacDonald3	845	40–50	43	(48.1685-0.376508*CAG)/(−1.49681+0.051744*CAG)
Langbehn et al.	2913	41–56	44	21.54 + Exp( 9.556 – 0.1460 CAG)
Maat-Kievit et al.	755	38–71	45	Means estimated individually for each CAG length. No overall formula.

Notes: See text for full references. All formulae given to published precisions. Some formulae mathematically transformed for simplicity and uniformity of presentation.

¹This is themean CAG length. The median was not reported.

²For Andresen et al. (2007a), intercepts were estimated from published graphs.

³Gutierrez & MacDonald sample characteristics determined by cross reference to Brinkman et al (1997).

For CAG lengths of 43 to 46, Figure 1 reveals fairly good agreement among all formulae, with the exception of Maat-Kievit. Differences are more substantial outside of this range. For shorter CAG lengths, the regression formulae from Stine et al. (Stine et al., 1993), Lucotte et al. (Lucotte et al., 1995), Andrew et al. (Andrew et al., 1993), and Squitieri et al. (Squitieri et al., 2000) provide similar estimates that are substantially lower than those from the survival models¹. This is quite plausibly due to incomplete ascertainment. Models fit only to data that are known because onset has occurred may be substantially biased. These four models were fit using data extending down to 36 or 37 repeats. Therefore, inaccurate extrapolation from longer CAG lengths does not seem to be an alternative or additional explanation.

The argument that these estimates are too low may appear weakened by the fact that all survival analysis-based formulae extrapolate for CAG lengths of 40 or less. However, within this range, the data that was available and eventually rejected for probable bias in Langbehn et al. (Langbehn et al., 2004) yielded estimates from survival analyses that were still higher than those from any regression formulae except Andresen et al. (Andresen et al., 2007b) or Rubinsztein et al. (Rubinsztein et al., 1997)

The median CAG repeat length in most samples was around 44 (Table 1). Therefore, use of any of these biased formulae for genetic counseling means that ages-of-onset that are substantially too early would be predicted for nearly half of those potentially seeking such information. (This is even before considering the additional potential underestimate from failing to consider a person’s current age.) The negative impact of such seemingly authoritative misinformation is self-evident.

The point of best formulae agreement is CAG length 44. Interestingly, this is the minimum length at which Falush et al., (Falush et al., 2001), based on population models of mutation flow, felt confident that clinical ascertainment of the disease was typically close to 100%. For longer CAG lengths, the Stine et al., Lucotte et al., and Andrew et al. formulae estimate the highest mean onset ages. These relatively mild discrepancies may actually be due to a combination of biased observation in the shorter CAG lengths and the relative inflexibility of the mathematical functions (linear or log-linear) in these models. Biased early onset ages at low CAG repeat lengths have a “leverage” effect on fitting the entire line—not only pushing down estimated age of onset at low CAG lengths, but pushing upward the estimates for CAG lengths larger than the mean of the data (Neter et al., 1990).

The Andresen et al. and Langbehn et al. formulae show remarkable agreement for CAG lengths of 43 or greater. Divergence of the estimates for shorter CAG lengths (with Andresen et al. lower) is again possibly attributable to biased ascertainment in the clinical Andresen et al. data. Somewhat similarly, the Squitieri et al. and Rubinsztein et al. formulae also converge to very similar estimates for CAG lengths of 47 and above.

The CAG-age plot from the Gutierrez-MacDonald survival formula has a very similar shape to that from Langbehn et al (Figure 1). However, estimated means are lower in Gutierrez-MacDonald. Their model is based on the data from Brinkman et al. (Brinkman et al., 1997), which was also a subset of data used for Langbehn et al. We have therefore been able to examine the discrepancy is detail. The Langbehn et al. model is more flexible, but only because we found that it needed to be in order to fit our entire data well. The gamma-model approach used by Gutierrez-MacDonald does indeed fit the Brinkman et al. subset accurately. Different ranges of CAG lengths were used in the two analyses. Gutierrez and MacDonald used lengths of 40 to 50 (Gutierrez and Macdonald 2002) and Langbehn et al. used a range of 41 to 56, excluding 40 because of suspected underascertainment and including longer repeats because of additional data subsequently collected in that extended range. Despite these differences, inconsistencies between the two models appear primarily due to systematically lower diagnosis ages in the subset of data available to Gutierrez and MacDonald. The reason for this is unknown. We can not distinguish among differences in subjective thresholds of assessment of onset at the source sites, true differences in the source populations (perhaps from unknown secondary disease modifiers), or relatively biased sampling at these sites.

The Maat-Kievit et al. estimates, based on a Dutch population registry, show notably later onset ages for CAG lengths of 46 or less (Figure 1). This inconsistency also appears to be due to differences in the raw data. Possible reasons for the difference include those just mentioned above. These possibilities were discussed in detail but unresolved with the original report of that model (Maat-Kievit et al., 2002)

Age-Conditional Estimates of Time Until Future Onset

Thus far, we have discussed estimates based on the lifetime distribution of onset of HD. In practice, mutation expanded research volunteers are not followed from birth. Research for studies like PREDICT typically entails an entry requirement that an adult volunteer has not been diagnosed with HD, despite being at risk. We assume that these volunteers have further been tested and verified to have expanded CAG lengths. Thus they are known not to be “immune” to the outcome in question. (Potential immunity, if present, poses another significant obstacle to accurate modeling (Maller and Zhou 1996). This is relevant in studies of HD family members in the absence of mutation testing.) Under these circumstances, it is vital that we additionally account for the fact that the volunteer has reached his or her age at research entry without yet experiencing an onset. A lifetime distribution formula yields the probability that onset could have occurred. (Integrate over the probability distribution from birth to current age.) Via the calculus of conditional probability, we account for the fact that such earlier onset ages have become impossible events. We can then derive quantities such as the expected age of future onset, given that a subject has a certain CAG length and has not yet had onset of illness (Paulsen et al., 2008), or the probability that such a subject will have onset within some fixed future time period. Such calculations, conditional on both CAG length and current age are relevant to most issues in research and genetic counseling. These are also the types of estimates that can be checked prospectively ¹.

Prospective Validation

Despite the above-argued strengths of survival analysis estimates, there are nevertheless reasons to question the generalizability of formulae such as Langbehn et al. and Gutierrez and MacDonald. The data used were unlikely to have represented the whole CAG-expanded population. Only those electing to receive CAG tests were included. Appropriate balance of subjects with or without onset was ultimately a matter of conjecture. Familial data was not available that could potentially control atypical but correlated features within linked pedigrees (due, for example, to unknown secondary genetic or environmental factors). Further, in Langbehn et al,, it was not technically feasible to incorporate potential site-specific effects into the form of statistical model that we chose. (The only published survival model using such a correction is Maat-Kievit et al. (Maat-Kievit et al., 2002). All of these factors are potential sources of significant bias. Regarding sample representation, it might be better to argue that the data were representative of the population likely to come to attention for clinical research and eventual HD clinical trials—both for treatment and prevention. We would argue that generalization to even this more restricted population is of clinical and scientific relevance. In any event, these considerations support the need to prospectively test the validity of these formulae.

PREDICT-HD is an ongoing longitudinal observational study of volunteers known to have the HD CAG expansion but who, at study entry, have not received a diagnosis of HD (Paulsen et al., 2006; Paulsen et al., 2008). This international study, so far involving 1,003 participants, aims to develop a comprehensive, interrelated description of the early neurobiological phenotype of HD. A key goal is identification and development of quantifiable outcome measures for eventual clinical trial use. During annual follow-ups (up to 5 years at present), 81 of the volunteers have received HD diagnoses. We judged this to be an adequate number to conduct a validating test of key predictions derivable from the Langbehn et al. and Gutierrez and MacDonald formulae. (None of the other formulae reviewed here have been published with adequate detail to derive testable predictions of short-term onset probability.)

Results

Table 2 summarizes distribution information from the prospective PREDICT-HD data for Langbehn et al. and Gutierrez and MacDonald estimates of 2-year onset probability. It is helpful to bear these distributions in mind as we assess regions of relatively good and poor fit for the validation survival models. Median onset probability from the Langbehn et al. formula was 7.6%, whereas from the Gutierrez and MacDonald formula it was 11.9%. The Gutierrez and MacDonald formula generally yields higher estimated onset probabilities.

Table 2.

Distribution of estimated 2-year onset probability (%) in Predict-HD data (N = 610): Langbehn et al. and Gutierrez and MacDonald Formulae.

Quantile	Langbehn et al	Gutierrez & MacDonald
Minimum	0.1	0.1
25	2.7	4.4
50	7.6	11.9
75	16.0	20.1
95	28.6	32.2
Maximum	43.9	84.3

As described in the methods, we checked the calibration of these formulae by fitting log-logistic survival models to the prospective onset experience in the PREDICT-HD data. We fit separate models for each predictive formula, and in each model the logit transform of predicted onset probability was the only fixed–effect predictor. Table 3 lists the parameter estimates from these prospective models. Under perfect calibration, it can be shown that these estimates would have the following identities: intercept = log(2) ≈ 0.69 and the 2-year-logit coefficient/scale = − 1. The corresponding calibration plot of diagnosis probabilities would simply be a diagonal line through the intercept with slope 1 (i.e., predicted probability = observed probability). The joint deviation of the intercept and logit coefficient/scale parameters from their ideal values can be tested using the delta method transformations of the parameter estimate covariance matrix from the calibration fit. These tests give Chi Square = 7.36 (2 .d.f, p = .025) for the Langbehn et al. model and Chi Square = 20.83 (2 d.f., p < .0001) for the Gutierrez-MacDonald model. Thus Langbehn et al. predictions come closer to fitting the ideal calibration diagonal, but we would reject ideal calibration for both models at the p = .05 level.

Table 3.

Log-Logistic Survival Model Estimates Fitting 2-Year Predictions from the Langbehn et al. and Gutierrez & MacDonald Models to Huntington’s Disease Onset From the PREDICT-HD Data.

	Ideal Calibration	Langbehn et al.		Gutierrez & MacDonald
		Coefficient	S.E.	Coefficient	S.E.
Intercept	0.693a	0.278	0.223	0.5656	0.208
Logit of 2-year onset probability	–	−0.704	0.101	−0.826	0.124
Log (Scale coefficient)	_	−0.781	0.109	−0.777	0.109
Logit(2-year probability)/Scale	−1.000	−1.537	0.198	−1.796	0.207

^alog(2) ≈ 0.693.

Note: Inter- rater frailty was highly statistically significant for both models: Chi-square = 52.9, 24.1 df for Langbehn et al and chi square = 51.8, df = 24.1 for Gutierrez and MacDonald. p < .0001 in both cases.

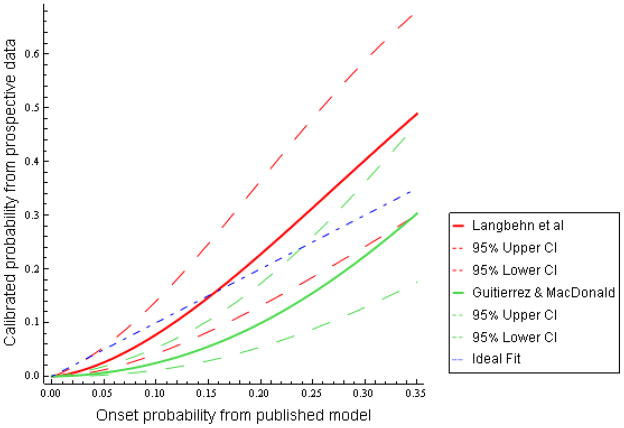
The actual fitted relationships for each formula versus observed onset probability are plotted in Figure 2. The x-axis range of 0 to 35% predicted probability includes nearly the whole range of observed data (Table 2). For the Langbehn et al. formula, the mild curvature of the fitted line indicates that observed onset rates are higher than predicted for those with the highest formula-estimated probabilities and slightly lower than predicted for those with the lowest predicted risk, up to about 16%. Nonetheless, the confidence intervals demonstrate that, allowing for a reasonable degree of statistical uncertainty, the 2-year onset estimates from Langbehn et al. are consistent with experience thus far in the PREDICT-HD study.

Figure 2.

Two-Year Probability of Onset, Predictions from Langbehn et al and Gutierrez and MacDonald versus Prospective Observed Results

In Figure 2, the plot for the Gutierrez and MacDonald formula forms a convex function with values substantially lower than the ideal fit throughout most of the observed data range. The corresponding 95% confidence interval excluded the ideal diagonal throughout much of the observed data range. This indicates that this formula consistently overestimates the observed 2-year probability of onset in our data. However, at the highest predicted onset probabilities (approximately 24% or greater, the 85^th percentile of predicted probabilities from this formula), the overestimate from Gutierrez and MacDonald was less severe and the confidence interval was consistent with the prospective data.

For fixed values on the x-axis of Figure 2, the Gutierrez and MacDonald plot has narrower confidence intervals than the Langbehn et al. plot. This may give the impression that Gutierrez and MacDonald could be calibrated more precisely. However, the narrower regions are due to the recalibrated probabilities (the y-axis) having lower values for Gutierrez and MacDonald. Roughly analogous to the situation with a simple Bernoulli or Binomial estimate, lower estimated probabilities have lower variances, all other things equal. The appropriate comparison is for predicted values from the two models that yield the same probabilities on the y-axis of Figure 2. Inspection of the figure then reveals that confidence intervals are similar for both models.

Discussion

The substantive question of this manuscript is whether observation and theory are in reasonable agreement for estimation of age of onset. We believe that the theoretical predictions from Langbehn et al. are usefully consistent with observations to date, and that this empirical verification is especially necessary and important, given the additional assumptions required to convert estimates of a lifetime distribution of onset to conditional estimates over a relatively short period of follow-up. As we have argued in the introduction, it is these conditional estimates that are of greatest relevance for most research applications. Further, they will frequently be more germane to the concerns of affected individuals, should these formulae be employed in genetic counseling.

The Gutierrez and MacDonald model also appears to provide reasonable estimates for those at highest risk. However, estimates from this model substantially overestimated the prospective rate of onset for 85% of the PREDICT-HD subjects at lower risk.

With regard to genetic counseling applications, we still have not shown the model to be free of referral and observation biases such that it is applicable to the general population. As evidence for this possibility, we note that we currently have no explanation to resolve the later ages of diagnosis seen in the Dutch register (Maat-Kievit et al., 2002). In addition to observation bias and variable diagnostic standards, we cannot discount the possible impact of secondary genetic factors, which in turn may have peculiar, specific population distributions. It has become clear that the huntingtin protein has diffuse biological interaction with additional proteins regarding, for example, multiple gene-transcription pathways (Cha 2007) and metabolism of the mutant huntingtin itself (Raychaudhuri et al., 2008). Genotypic variability in these other proteins may have an important influence on the distribution of diagnosis ages (Andresen et al., 2007a; Li et al., 2003; MacDonald et al., 1999; Metzger et al., 2008; Rubinsztein et al., 1996). Further, there are reports claiming possible effects from additional variation in the huntingtin protein itself, such as repeat variation in the CAG length of the non-expanded huntingtin allele (Djousse et al., 2003,) and CCG-repeat (Chattopadhyay et al., 2003) and Δ2642 polymorphisms (Vuillaume et al., 1998) adjacent to the CAG-repeat region in the affected allele.

Our model is in agreement with prospective data on subjects volunteering for HD research in North America, Australia, and parts of Europe. Further, we must emphasize that, while we can predict the future with some increased precision, we are still estimating probability distributions over which an event may occur. We can not use this information to predict any individual’s age of onset with certainty. However this data can be used to provide overall ranges and expected ranges of onset for any individual at a particular age.

This probabilistic prognosis has clear research utility. In the PREDICT-HD study, it serves as an independent benchmark by which candidate clinical measures of prognosis can initially be compared cross-sectionally. While no substitute for true longitudinal follow-up, it allows provisional identification of preclinical markers deserving greater scrutiny (Paulsen et al., 2008). It provides a relatively simple mechanism to incorporate both CAG length and age into structural equation models looking for possible biological mediators of the quantitative aspect of CAG repeat length risk. Finally, it allows the possibility for targeted enrollment of various prognostic groups (e.g., high risk vs. low-risk for onset within the next 5 years), should such targeting be deemed scientifically appropriate.

Generally, only models based on survival analyses can provide the age-conditional predictions appropriate for such applications. Similarly, the survival analysis paradigm is necessary for prospective validation of any such model. The longitudinal PREDICT-HD data have now provided a rare opportunity for such prospective validation, and our confidence in recommending the Langbehn et al. formula is substantially reinforced by the results.

Materials and Methods

Details of the Langbehn et al. Model

The mathematical form of the Langbehn et al model does not fall into a standard family of parametric survival models (Cox and Oakes 1984; Lawless 2003). Nonetheless, its derivation was straightforward. We began with three observations: (1) For all fixed CAG length between 41 and 56, the scatter of diagnosis ages was well-described by the logistic distribution (Kalbfleisch and Prentice 2002; Lawless 2003; Marshall and Olkin 2007). (2) The means of those distributions were closely approximated by an exponential function of CAG length. (3) The variances of the distributions were also described by a similar exponential function of CAG length. A synthesis of these assumptions leads to the model:

Let M[CAG] represent mean age of diagnosis, given CAG length. Let S[CAG] be the corresponding standard deviation. The lifetime probability distribution of diagnosis age for a given CAG length has a logistic density with

$$\begin{array}{l}\text{M}[\text{CAG}]=21.54+\text{Exp}(9.556-0.1460\text{CAG})\\ \text{S}[\text{CAG}]=\text{Sqrt}[35.55+\text{Exp}(17.72-0.3269\text{CAG})]\end{array}$$

where Exp(x) is the exponential function and Sqrt(x) is the positive square root function. As CAG length increases, there is not only a lower mean age of diagnosis, but also a narrowing in the standard deviation of diagnosis ages.

Details of the Gutierrez-MacDonald Model

This model was not derived from a direct parametric survival analysis of raw data, but rather results from least squares smoothing of a family of Gamma distributions to the nonparametric survival curves reported by Brinkman et al. (Brinkman et al., 1997). Within the CAG range of 40 to 50, the fitted gamma distribution (with θ as the scale parameter) was reported as

$$\theta =48.1685-{0.376508}^{\ast }\text{CAG},\alpha ={0.051744}^{\ast }\text{CAG}-\mathrm{1.49681.}$$

Prospective Validation

The current report is based on 610 subjects (36% male and 64% female), all with at least one year of follow-up in the PREDICT-HD study. Mean age at study entry was 41.4 years (s.d. = 9.75, median = 41.0, range 20–75). Mean CAG length was 42.4 (s.d. = 2.5). The median CAG length was 42 and all but two subjects fell in the range 38–51. The other two subjects had lengths in the 52–70 range and we did not judge them to be unduly influential outliers. As of October 2007 (the biannual data cut used in this analysis), there were 81 subjects who had received a HD diagnosis at some point in follow-up. However, in 12 of these cases (discussed below), the diagnostic rating reverted to a lesser category on the next follow-up visit.

All subjects gave informed consent for participation in PREDICT-HD, and the research methods were approved by the Human Subjects IRB at the University of Iowa and all local site institutions.

PREDICT -HD diagnostic methods

The Modified Unified Huntington’s Disease rating Scale (UHDRS99) is a detailed instrument widely used as a centerpiece in clinical HD research (Huntington Study Group Investigators 1996), including the PREDICT -HD study, where it is administered at each annual visit. The 17th item on this scale asks the clinician, after a detailed motor exam, to what degree he or she is confident that the research subject at risk for HD displays an unequivocal, otherwise unexplained extrapyramidal movement disorder. By standard convention, HD “diagnosis” is defined as the point at which the most severe score of 4 (“motor abnormalities that are unequivocal signs of HD, as least 99% confidence”) is first assigned.

Presumably, a given rater is unlikely to revise this diagnostic opinion on subsequent visits. However, we occasionally encountered inconsistent opinions regarding diagnosis on further follow-up. We describe statistical down-weighting of such diagnoses as part of the survival analysis methods below. A perhaps more substantial issue is the consistency among raters in calibrating the point at which an unequivocal diagnosis is called, given that HD is an insidiously developing disease. Preliminary analyses, beyond the scope of this paper, strongly suggested some notable rater inconsistency in this matter, and we will also describe our approximate statistical corrections for these inconsistencies shortly.

CAG length determination

Participation in PREDICT -HD requires that subjects have previously and voluntarily undergone HD gene testing for other purposes. No one is encouraged to receive the gene test so that they can participate in HD research, and the Huntington Study Group (HSG) makes alternative research opportunities available to those who do not wish gene testing. At study entry, all participants self-report the length of their CAG expansion based on previous testing. Additionally, subjects provide blood samples used to verify the CAG length. This verification is performed by Dr. Marcy MacDonald’s laboratory at Harvard University using quantitative autoradiograms of amplified CAG-repeat oligonucleotides (Warner et al., 1993). Verification data were unavailable for 101 (15.7%) of the sample used for these analyses and self-reported CAG length was used in these cases. We justify this on the basis of high concordance when both measures are available. (Lengths agree in 66.1% of verified cases, are within 1 repeat in 90.4%, and within 2 repeats in 95.5% of such cases. Disagreement directions are symmetrically distributed.)

Probability of diagnosis calculation

We discussed both the general principles of and the reasons for age- and CAG-conditional calculations in the introduction. The analyses here depend specifically on probabilities of diagnosis over a fixed future period of time, conditional on the fact that the subject has already reached their current age without receiving a HD diagnosis. Mathematically, this is expressed by a standard conditional probability identity. Let f(age| c) represent the lifetime probability distribution (density) of diagnosis age for a given CAG length c. Then

$$\text{probability}\text{of}\text{diagnosis}\text{in}t\text{years},\text{given}\hspace{0.17em}\text{age}a\text{and}\text{CAG}\text{length}c=\frac{\underset{a}{\overset{a+t}{\int }}\text{f}(\text{age}\mid c)\partial \text{age}}{\underset{a}{\overset{\infty }{\int }}\text{f}(\text{age}\mid \text{c})\partial \text{age}}.$$

This formula may be interpreted as follows: The probability, calculated at birth, that a subject would receive a diagnosis at some point between their age at study entry (a) and, say, t = 2 years in the future, is found by finding the area under the probability curve f(age| c) between age = a and age = (a + 2). To account for the additional fact that the subject is known to have reached age a without receiving a diagnosis, we divide this result by the total remaining area under the lifetime probability-of-diagnosis curve, given that their current age is a. (This represents the remaining theoretical sample space in which diagnosis may occur and we are renormalizing our probability calculation to this sample space. Inclusion of an infinite upper age limit may seem strange. However, we simply interpret this to mean that we are modeling the age of diagnosis of HD, assuming that a person lives long enough to acquire the disorder.)

Statistical analysis

The number and inter-correlation of parameters in the Langbehn et al. and Gutierrez-MacDonald models are such that far more prospective diagnoses than are currently available would be needed to test the original mathematical forms to any meaningful precision. Instead, we focus on simpler survival models that yield checks on age-conditioned probability of diagnosis derivable from both models.

After satisfying ourselves that reasonable goodness-of-fit was achievable, we chose to conduct this study using the standard family of parametric survival analysis distributions available in software packages such as SAS (Allison and SAS Institute 1995; Clark and SAS Institute 2004), S-Plus (Insightful Corporation 2007) and R (Venables et al., 2002). We fit our models using the S-Plus “survReg” method because of the availability of random effect (“frailty”) options for rater-specific effects on the diagnostic threshold (Therneau and Grambsch 2000). (Identical methods are also available in R.) We chose parametric families because the survival function for the “average” rater can be readily derived by setting the random rater effect to 0 in the estimated model. This is needed for model validation.

The survival regression models contained a transform of the CAG and age-based a priori probability of diagnosis, derived from either Langbehn et al. for Gutierrez-MacDonald, as the only fixed predictor. We determined the appropriate transform for each candidate model such that ideal validation would yield a linear plot of the a priori probability versus the observed probabilities with intercept 0 and slope of 1. (That is, the plot would reveal the two probabilities to be identical.) Using Aikake’s AIC criteria, we ultimately chose the log-logistic model from among candidate models (Akaike 1973; Akaike 1992; Burnham and Anderson 1998). For this model, the appropriate linear transformation of a priori diagnostic probability p is the logit function, log[p/(1 − p)]. We derived estimates of the corresponding standard errors from the covariance matrix of the survival regression parameters via the delta method (Knight 2000; Sen and Singer 1993), and used these standard errors to calculate normal theory point-wise confidence intervals for the logit of the fitted survival function (Lawless 2003; Marshall and Olkin 2007). Finally, we transformed these confidence intervals from the logit scale, where normality approximations have good accuracy, to the probability scale.

We present models based on 2-year diagnosis probabilities because this is the median follow-up time in the sample. Use of other time periods between 1 and 4 years yielded essentially identical conclusions.

Rater-specific diagnostic variability was treated as a normally distributed random (frailty) effect. This was estimated using the AIC option in S-Plus. Other possible distribution assumptions had trivial impact on the results. This random effect accommodated our assumption that the raters’ individual criteria for assigning diagnoses form a random distribution with non-negligible variance around a true (or at least an average) criterion for diagnosis. We also assume that the transition to a state that the rater would consider as “diagnosed” occurs at an unknown point between visits. To accommodate this, we adopted the technical assumption that diagnosis times were interval censored between visit dates (Kalbfleisch and Prentice 2002). The time scale for modeling was measured to the day, with 0 being the date of first PREDICT-HD evaluation.

In 12 cases, subjects subsequently reverted from a diagnosis in the opinion of the diagnostician. Among 27 instances of 2+ year follow-up after diagnosis (7.4%), there were 2 instances (7.4%) where this reversion occurred two years after the initial diagnosis. All other diagnostic reversions occurred at the next annual follow-up. In these 12 cases, we assumed that the initial diagnoses were possibly correct. For example, one could imagine an underlying threshold model where severity reaches a point that a given examiner might make the diagnosis on, say, 50% of possible visit days. We duplicated the data for each of these subjects. Only one of the two copies was considered diagnosed, and each copy was given an observation weight of 0.5 (Harrell 2001). Informally, we interpret this to mean that we assign a 50% probability of “true” diagnosis to these subjects at this point. While more detailed measurement error models can be formulated, this partial weighting scheme is an approximation that allows a much more straightforward presentation of results. Simulations incorporating a diagnostic measurement error model (which we do not present) suggested this approximation is sufficiently accurate for our purposes.

PREDICT-HD Investigators, Coordinators, Motor Raters, Cognitive Raters (October 2007 data cut)

David Ames, MD, Edmond Chiu, MD, Phyllis Chua, MD, Olga Yastrubetskaya, PhD, Phillip Dingjan, M.Psych., Kristy Draper, D.Psych, Nellie Georgiou-Karistianis, PhD, Anita Goh, D.Psych, Angela Komiti and Christel Lemmon (The University of Melbourne, Kew, Victoria, Australia);

Henry Paulson, MD, Kimberly Bastic, BA, Rachel Conybeare, BS, Clare Humphreys, Peg Nopoulos, MD, Robert Rodnitzky, MD, Ergun Uc, MD, BA, Leigh Beglinger, PhD, Kevin Duff, PhD, Vincent A. Magnotta, PhD, Nicholas Doucette, BA, Sarah French, MA, Andrew Juhl, BS, Harisa Kuburas, BA, Ania Mikos, BA, Becky Reese, BS, Beth Turner and Sara Van Der Heiden, BA and (University of Iowa Hospitals and Clinics, Iowa City, Iowa, USA);

Lynn Raymond, MD, PhD, Joji Decolongon, MSC (University of British Columbia, Vancouver, British Columbia, Canada);

Adam Rosenblatt, MD, Christopher Ross, MD, PhD, Abhijit Agarwal, MBBS, MPH, Lisa Gourley, Barnett Shpritz, BS, MA, OD, Kristine Wajda, Arnold Bakker, MA and Robin Miller, MS (Johns Hopkins University, Baltimore, Maryland, USA);

William M. Mallonee, MD, Greg Suter, BA, David Palmer, MD and Judy Addison, MA (Hereditary Neurological Disease Centre, Wichita, Kansas, USA);

Randi Jones, PhD, Joan Harrison, RN, J. Timothy Greenamyre, MD, PhD and Claudia Testa, MD, PhD (Emory University School of Medicine, Atlanta, Georgia, USA);

Elizabeth McCusker, MD, Jane Griffith, RN, Bernadette Bibb, PhD, Catherine Hayes, PhD and Kylie Richardson, B LIB (Westmead Hospital, Wentworthville, Australia);

Ali Samii, MD, Hillary Lipe, ARNP, Thomas Bird, MD, Rebecca Logsdon, PhD, Kurt Weaver, PhD and Katherine Field, BA (University of Washington and VA Puget Sound Health Care System, Seattle, Washington, USA);

Bernhard G. Landwehrmeyer, MD, Katrin Barth, Anke Niess, RN, Sonja Trautmann, Daniel Ecker, MD and Christine Held, RN (University of Ulm, Ulm, Germany);

Mark Guttman, MD, Sheryl Elliott, RN, Zelda Fonariov, MSW, Christine Giambattista, BSW, Sandra Russell, BSW, Jose Sebastian, MSW, Rustom Sethna, MD, Rosa Ip, Deanna Shaddick, Alanna Sheinberg, BA and Janice Stober, BA, BSW (Centre for Addiction and Mental Health, University of Toronto, Markham, Ontario, Canada);

Susan Perlman, MD, Russell Carroll, Arik Johnson, MD and George Jackson, MD, PhD (University of California, Los Angeles Medical Center, Los Angeles, California, USA);

Michael D. Geschwind, MD, PhD, Mira Guzijan, MA and Katherine Rose, BS, (University of California, San Francisco, California, USA);

Tom Warner, MD, PhD, Stefan Kloppel, MD, Maggie Burrows, RN, BA, Thomasin Andrews, MD, BSC, MRCP, Elisabeth Rosser, MBBS, FRCP, Sarah Tabrizi, MD, PhD and Charlotte Golding, PhD (National Hospital for Neurology and Neurosurgery, London, UK);

Roger A Barker, BA, MBBS, MRCP, Sarah Mason, BSC and Emma Smith, BSC (Cambridge Centre for Brain Repair, Cambridge, UK);

Anne Rosser, MD, PhD, MRCP, Jenny Naji, PhD, BSC, Kathy Price, RN and Olivia Jane Handley, PhD, BS (Cardiff University, Cardiff, Wales, UK);

Oksana Suchowersky, MD, FRCPC, Sarah Furtado, MD, PhD, FRCPC, Mary Lou Klimek, RN, BN, MA, and Dolen Kirstein, BSC (University of Calgary, Calgary, Alberta, Canada);

Diana Rosas, MD, MS, Melissa Bennett, Jay Frishman, CCRP, Yoshio Kaneko, BA, Talia Landau, BA, Martha Lausier, CNRN, Lindsay Muir, Lauren Murphy, BA, Anne Young, MD, PhD, Colleen Skeuse, BA, Natlie Balkema, BS, Wouter Hoogenboom, MSC, Catherine Leveroni, PhD, Janet Sherman, PhD and Alexandra Zaleta (Massachusetts General Hospital, Boston, Massachusetts, USA);

Peter Panegyres, MB, BS, PhD, Carmela Connor, BP, MP, DP, Mark Woodman, BSC and Rachel Zombor (Neurosciences Unit, Graylands, Selby-Lemnos & Special Care Health Services, Perth, Australia);

Joel Perlmutter, MD, Stacey Barton, MSW, LCSW and Melinda Kavanaugh, MSW, LCSW (Washington University, St. Louis, Missouri, USA);

Sheila A Simpson, MD, Gwen Keenan, MA, Alexandra Ure, BSC and Fiona Summers, DClinPsychol (Clinical Genetics Centre, Aberdeen, Scotland, UK);

David Craufurd, MD, Rhona Macleod, RN, PhD, Andrea Sollom, MA and Elizabeth Howard, MD (University of Manchester, Manchester, UK)

Kimberly Quaid, PhD, Melissa Wesson, MS, Joanne Wojcieszek, MD and Xabier Beristain, MD (Indiana University School of Medicine, Indianapolis, IN);

Pietro Mazzoni, MD, PhD, Karen Marder, MD, MPH, Jennifer Williamson, MS, Carol Moskowitz, MS, RNC and Paula Wasserman, MA (Columbia University Medical Center, New York, New York, USA);

Peter Como, PhD, Amy Chesire, Charlyne Hickey, RN, MS, Carol Zimmerman, RN, Timothy Couniham, MD, Frederick Marshall, MD, Christina Burton, LPN and Mary Wodarski, BA (University of Rochester, Rochester, New York, USA);

Vicki Wheelock, MD, Terry Tempkin, RNC, MSN and Kathleen Baynes, PhD (University of California Davis, Sacramento, California, USA);

Joseph Jankovic, MD, Christine Hunter, RN, CCRC, William Ondo, MD and Carrie Martin, LMSW-ACP (Baylor College of Medicine, Houston, Texas, USA);

Justo Garcia de Yebenes, MD, Monica Bascunana Garde, Marta Fatas, Christine Schwartz, Dr. Juan Fernandez Urdanibia and Dr. Cristina Gonzalez Gordaliza. (Hospital Ramón y Cajal, Madrid, Spain);

Lauren Seeberger, MD, Alan Diamond, DO, Deborah Judd, RN, Terri Lee Kasunic, RN, Lisa Mellick, Dawn Miracle, BS, MS, Sherrie Montellano, MA, Rajeev Kumar, MD and Jay Schneiders, PhD (Colorado Neurological Institute, Englewood, Colorado, USA);

Martha Nance, MD, Dawn Radtke, RN, Deanna Norberg, BA and David Tupper, PhD (Hennepin County Medical Center, Minneapolis, Minnesota, USA);

Wayne Martin, MD, Pamela King, BScN, RN, Marguerite Wieler, MSc, PT, Sheri Foster and Satwinder Sran, BSC (University of Alberta, Edmonton, Alberta, Canada);

Richard Dubinsky, MD, Carolyn Gray, RN, CCRC and Phillis Switzer (University of Kansas Medical Center, Kansas City, Kansas, USA).

Steering Committee

Jane Paulsen, PhD, Principal Investigator, Douglas Langbehn, MD, PhD and Hans Johnson, PhD (University of Iowa Hospitals and Clinics, Iowa City, IA); Elizabeth Aylward, PhD (University of Washington and VA Puget Sound Health Care System, Seattle, WA); Kevin Biglan, MD, Karl Kieburtz, MD, David Oakes, PhD, Ira Shoulson, MD (University of Rochester, Rochester, NY); Mark Guttman, MD (The Centre for Addiction and Mental Health, University of Toronto, Markham, ON, Canada); Michael Hayden, MD, PhD (University of British Columbia, Vancouver, BC, Canada); Bernhard G. Landwehrmeyer, MD (University of Ulm, Ulm, Germany); Martha Nance, MD (Hennepin County Medical Center, Minneapolis, MN); Christopher Ross, MD, PhD (Johns Hopkins University, Baltimore MD); Julie Stout, PhD (Indiana University, Bloomington, IN, USA and Monash University, Victoria, Australia).

Study Coordination Center

Steve Blanchard, MSHA, Christine Anderson, BA, Ann Dudler, Elizabeth Penziner, MA, Anne Leserman, MSW, LISW, Bryan Ludwig, BA, Brenda McAreavy, Gerald Murray, PhD, Carissa Nehl, BS, Stacie Vik, BA, Chiachi Wang, MS, and Christine Werling (University of Iowa)

Clinical Trials Coordination Center

Keith Bourgeois, BS, Catherine Covert, MA, Susan Daigneault, Elaine Julian-Baros, CCRC, Kay Meyers, BS, Karen Rothenburgh, Beverly Olsen, BA, Constance Orme, BA, Tori Ross, MA, Joseph Weber, BS, and Hongwei Zhao, PhD (University of Rochester, Rochester, NY.)

Cognitive Coordination Center

Julie C. Stout, PhD, Sarah Queller, PhD, Shannon A. Johnson, PhD, J. Colin Campbell, BS, Eric Peters, BS, Noelle E. Carlozzi, PhD, Terren Green, BA, Shelley N. Swain, MA, David Caughlin, BS, Bethany Ward-Bluhm, BS, Kathryn Whitlock, MS (Indiana University, Bloomington, Indiana, USA; Monash University, Victoria, Australia; and Dalhousie University, Halifax, Canada)

Recruitment and Retention Committee

Jane Paulsen, PhD, Elizabeth Penziner, MA, Stacie Vik, BA, (University of Iowa, USA); Abhijit Agarwal, MBBS, MPH, Amanda Barnes, BS (Johns Hopkins University, USA); Greg Suter, BA (Hereditary Neurological Disease Center, USA); Randi Jones, PhD (Emory University, USA); Jane Griffith, RN (Westmead Hospital, AU); Hillary Lipe, ARNP (University of Washington, USA); Katrin Barth (University of Ulm, GE); Michelle Fox, MS (University of California, Los Angeles, USA); Mira Guzijan, MA, Andrea Zanko, MS (University of California, San Francisco, USA); Jenny Naji, PhD (Cardiff University, UK); Rachel Zombor, MSW (Graylands, Selby-Lemnos & Special Care Health Services, AU); Melinda Kavanaugh (Washington University, USA); Amy Chesire, Elaine Julian-Baros, CCRC, Elise Kayson, MS, RNC (University of Rochester, USA); Terry Tempkin, RNC, MSN (University of California, Davis, USA); Martha Nance, MD (Hennepin County Medical Center, USA); Kimberly Quaid, PhD (Indiana University, USA); and Julie Stout, PhD (Indiana University, Bloomington, IN, USA and Monash University, Victoria, Australia).

Event Monitoring Committee

Jane Paulsen, PhD, William Coryell, MD (University of Iowa, USA); Christopher Ross, MD, PhD (Johns Hopkins University, Baltimore, MD); Elise Kayson, MS, RNC, Aileen Shinaman, JD (University of Rochester, USA); Terry Tempkin, RNC, ANP (University of California Davis, USA); Martha Nance, MD (Hennepin County Medical Center, USA); Kimberly Quaid, PhD (Indiana University, USA); Julie Stout, PhD (Indiana University, Bloomington, IN, USA and Monash University, Victoria, Australia); and Cheryl Erwin, JD, PhD (McGovern Center for Health, Humanities and the Human Spirit, USA).