DIRECTIONAL ASYMMETRY IN THE MEASURED N2O TIME-CONSTANT FOR MIDDLE EAR TRANSMUCOSAL GAS EXCHANGE

Abstract

Simple, two-compartment models of transmucosal gas exchange for the middle ear (ME) are useful for describing ME pressure behavior under a variety of conditions. The most well developed exchange models require input of an experimentally determined, lumped-parameter, exchange-constant for each represented gas species. Evidences from past studies suggest that the value of the exchange-constant for inert gases is specific to the direction of the extant pressure-gradient, an unexpected result. In this study, the N₂O transmucosal exchange-constant (time-constant) for 16 ears of 8 monkeys was measured for positive and negative ME-blood N₂O gradients using previously published methods. The results showed that the two time-constant measures were highly correlated, but that the ME-blood time-constant was approximately 13 times greater than the blood-ME time-constant. This directional effect depends on the value of a gradient-ratio (arterial-venous/arterial-ME) included as a parameter in the time-constant for perfusion-limited gas exchange. All values of that ratio not equal to 1 introduce directional asymmetry into the measured time-constant. The significance of this phenomenon to current models and as a lead to the development of more complex, distributed models of transmucosal gas exchange is discussed.

INTRODUCTION

The mechanism for exchange of gas between the middle ear airspace (ME) and mucosal blood determines the basal rate of ME pressure change and, under physiological conditions, the demand placed upon the Eustachian tube for gas supply (1). Because the exchange compartments (ME airspace, mucosa, local arterial and venous blood) are not accessible to direct measurement of the relevant exchange parameters (e.g. partial-pressures of the physiological gases, blood flow etc), mathematical models were developed with the specific goal of predicting ME pressure change under various extant conditions. Early models assumed a simple, diffusive exchange between two compartments, the ME airspace and local blood, and the exchange of all relevant gases was treated as diffusion-limited (2-5). However, the results of experiments showed that this assumption is invalid and that transmucosal exchange discriminates between inert and reactive gases, with the former being primarily perfusion-limited and the latter diffusion-limited (6-8). Despite the facts that the mechanism underling this discrimination was described and revised models that incorporate appropriately adjusted, gas specific, time-constants better simulate ME pressure behavior (7-17), the literature is replete with erroneous conclusions based upon expectations predicted by the more simple model assumptions (15-19).

However, even with inclusion of the diffusion/perfusion discrimination, the revised mathematical model of ME transmucosal gas exchange does not reproduce accurately the temporal dynamics for ME pressure when the established gradients are opposite to those under which the relevant time-constants were measured by experiment (9,10,20). In one study using monkeys, suggestive evidence for directional differences in the ratios of the time-constants for the physiological gases was reported (9). Also, in different experiments, the time-constant for inert gas exchange was measured to be greater for gas transfer in response to positive ME-blood gradients when compared to negative gradients (8,20). This directional asymmetry implies that, in present form, accurate mathematical descriptions of ME pressure change need to include different, gas-specific, directional time-constants.

In the present study, the transmucosal N₂O time-constant was measured in 16 ears of 8 monkeys under established positive and negative ME-blood gradients using methods previously published (7,20). The results documented a significant effect of gradient direction on the measured N₂O time-constant and showed that the equations for perfusion-limited gas exchange can be written in a form to predict this effect. A more complex geometry of the exchange system than that currently modeled is suggested to underlie the mechanistic explanation for this phenomenon.

METHODS

Protocol

Eight juvenile cynomolgus monkeys weighing between 2.8 and 3.9 kg were used in the experiments. Three test sessions were conducted at a minimum one-week interval, two with an established positive ME-blood gradient and one with an established negative gradient. For all experiments, the monkey was sedated with 30 mg Ketamine®, anesthetized with “monkey mix” (ketamine-10mg/kg, xylazine-2mg/kg, acepromazine-0.3mg/kg), intubated, and monitored over a 60 minute acclimation period (10 minute intervals) for ME pressure by tympanometry, body temperature by rectal probe and vital signs by cuff monitor. Then, the endotracheal tube was placed online to the output of a Harvard respirator (model 661, South Natick, MA. USA) that delivered 50 cc gas/stroke at 20 strokes/minute.

To establish negative ME-blood N₂O gradients, the gas intake to the respirator was placed online to a gas composition of 40% N₂O, 20% O₂, balance N₂ at ambient pressure. The animal was breathed with this gas mixture for 60 minutes during which time ME pressure was recorded bilaterally at 5-minute intervals using a clinical tympanometer (GSI-33 Middle Ear Analyzer, Model 1733, Littleton, MA USA). To establish positive ME-blood N₂O gradients, the intake to the respirator was room air and the ME was inflated bilaterally as previously described (modified Politzer maneuver) with a gas composition of 6 % CO₂, 6 %O₂, 20% N₂O, balance N₂. ME pressure was recorded bilaterally at 5 minute intervals for 100 minutes.

Throughout all experiments, vital signs and rectal temperature were recorded at regular intervals. At the termination of each experiment and after the monkey had recovered from the anesthesia, it was returned to the vivarium. This study was performed in accordance with the PHS Policy on Humane Care and Use of Laboratory Animals, the NIH Guide for the Care and Use of Laboratory Animals, and the Animal Welfare Act (7 U.S.C. et seq). The protocols were approved by the Animal Care and Research Committee at the Children’s Hospital of Pittsburgh.

Analytic Methods

Under certain restrictive conditions, the primary outcome variable for these experiments, rate of change in ME pressure, is equal to the rate of change in ME N₂O pressure. Below we present a mathematical description that defines these conditions and the methods for calculating the time-constant for transmucosal inert gas exchange.

The pressure of any closed, gas filled compartment such as the ME (m) between Eustachian tube openings is defined by the general gas law, or:

$${\mathrm{P}}^{\mathrm{m}}{\mathrm{V}}^{\mathrm{m}}={\mathrm{N}}^{\mathrm{m}}{\mathrm{RT}}^{\mathrm{m}}$$ EQ1

where P^m is pressure, V^m is volume, N^m is number of moles of gas and T^m is temperature for the ME, and R is the general gas constant. Total ME pressure is equal to the sum of the partial-pressures of the physiological gases and any represented, non-physiological gas-species (e.g. N₂O). The change in total ME pressure is equal to the sum of the changes in the partial-pressures of those gases, or:

$${\mathrm{\delta }\mathrm{P}}^{\mathrm{m}}{/\mathrm{\delta }\mathrm{t}=(\mathrm{\delta }\mathrm{P}}_{\mathrm{O}2}^{\mathrm{m}}{+\mathrm{\delta }\mathrm{P}}_{\mathrm{CO}2}^{\mathrm{m}}{+\mathrm{\delta }\mathrm{P}}_{\mathrm{H}2\mathrm{O}}^{\mathrm{m}}{+\mathrm{\delta }\mathrm{P}}_{\mathrm{N}2}^{\mathrm{m}}{+\mathrm{\delta }\mathrm{P}}_{\mathrm{g}}^{\mathrm{m}})/\mathrm{\delta }\mathrm{t}$$ EQ2

where P^m_g is the ME partial-pressure of a test gas. Under physiological conditions and at constant O₂ and CO₂ pressures in blood (as is true for the acclimated state), the ME-blood O₂ and CO₂ gradients are approximately 0 mmHg and the ME is saturated with water vapor (11,14). Because there is no gradient to drive the transmucosal exchange of these gases, δP^m_O2/δt = δP^m_CO2/δt = δP^m_H2O/δt = 0 pressure/time. Thus, for the ME of an acclimated, anesthetized animal with an established N₂O gradient between ME and blood, EQ2 reduces to:

$${\mathrm{\delta }\mathrm{P}}^{\mathrm{m}}{/\mathrm{\delta }\mathrm{t}=(\mathrm{\delta }\mathrm{P}}_{\mathrm{N}2}^{\mathrm{m}}{+\mathrm{\delta }\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{m}})/\mathrm{\delta }\mathrm{t}.$$ EQ3

Direct measurements in animals show that the change in ME N₂ pressure at extant ME-blood gradients as high as 50mmHg is not measurable in experiments lasting for 4 hours (7-9). Therefore, in relatively short duration experiments as described here, the effective N₂ exchange rate (δP^m_N2/min) is 0 pressure/time, and EQ3 becomes:

$${\mathrm{\delta }\mathrm{P}}^{\mathrm{m}}/\mathrm{\delta }\mathrm{t}\approx {\mathrm{\delta }\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{m}}/\mathrm{\delta }\mathrm{t}.$$ EQ4

For a simple two-compartment system, the change in the number of moles of N₂O in the ME compartment is equal to the extant difference between the number of moles of that gas in the local arterial (a) and venous (v) blood compartments, or:

$${\mathrm{\delta }\mathrm{N}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{m}}{=(\mathrm{N}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{a}}{-\mathrm{N}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{v}}).$$ EQ5

For blood (b), the number of moles of a gas is directly related to its partial-pressure (P^bg), solubility (S^bg), and the local blood volume (V^b); or for N₂O:

$${\mathrm{N}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{a},\mathrm{v}}{=\mathrm{V}}^{\mathrm{a},\mathrm{v}}{\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{a},\mathrm{v}}{\mathrm{S}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{a},\mathrm{v}}.$$ EQ6

Recognizing that N₂O solubility is the same for arterial and venous blood (S^a,v_N2O), substituting the expressions for pressure from EQs 1 and 6 for moles of gas in EQ5, and rearranging terms yields:

$${\mathrm{\delta }\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{m}}{=(\mathrm{RT}}^{\mathrm{m}}{\mathrm{S}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{b}})({\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{a}}{\mathrm{V}}^{\mathrm{a}}{-\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{v}}{\mathrm{V}}^{\mathrm{v}})/{\mathrm{V}}^{\mathrm{m}}.$$ EQ7

Dividing both sides of this equation by a time interval (δt) and noting, that by continuity, V^a/δt = V^v/δt = ME mucosal blood flow (Q^m), yields:

$${\mathrm{\delta }\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{m}}{/\mathrm{\delta }\mathrm{t}=(\mathrm{RQ}}^{\mathrm{m}}{\mathrm{T}}^{\mathrm{m}}{\mathrm{S}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{b}})({\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{a}}{-\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{v}})/{\mathrm{V}}^{\mathrm{m}}\text{.}$$ EQ8

Under the experimental conditions, the following inequalities relate extant ME N₂O pressure to the local arterial and venous blood N₂O pressures for positive (EQ9a) and negative ME-blood gradients (Eq9b):

$${\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{m}}\ge {\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{a}}\mathrm{and}{\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{m}}\ge {\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{v}},\mathrm{or}-{\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{m}}\le -{\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{v}}.$$ EQ9a

$${\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{m}}\le {\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{a}}\mathrm{and}{\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{m}}\le {\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{v}},\mathrm{or}-{\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{m}}\ge -{\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{v}}.$$ EQ9b

Adding P^a_N2O to both sides of EQ9 yields:

$${\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{a}}-{\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{m}}\le {\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{a}}-{\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{v}},\mathrm{or}{\mathrm{F}}_{\mathrm{N}2\mathrm{O}}^{+}({\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{a}}-{\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{m}})={\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{a}}-{\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{v}}$$ EQ10a

$${\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{a}}-{\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{m}}\ge {\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{a}}-{\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{v}},\mathrm{or}{\mathrm{F}}_{\mathrm{N}2\mathrm{O}}^{­}({\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{a}}-{\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{m}})={\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{a}}-{\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{v}}$$ EQ10b

where F⁺_N2O = (P^a_N2O – P^v_N2O)/(P^a_N2O – P^m_N2O), F^-_N2O is the inverse of that ratio and 1 ≥ F^-_N2O ≥ 0. Substituting the results from EQ10b into EQ8 and combining with EQ4 yields:

$${\mathrm{\delta }\mathrm{P}}^{\mathrm{m}}/\mathrm{\delta }\mathrm{t}\approx {\mathrm{\delta }\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{m}}/\mathrm{\delta }\mathrm{t}=({\mathrm{F}}_{\mathrm{N}2\mathrm{O}}^{+/­}{\mathrm{RQ}}^{\mathrm{m}}{\mathrm{T}}^{\mathrm{m}}{\mathrm{S}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{b}})({\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{a}}-{\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{m}})/{\mathrm{V}}^{\mathrm{m}}.$$ EQ11

This equation relates the rate of change in ME pressure (δP^m/δt, determinable from experimental data) to the change in ME N₂O partial-pressure which is the product of: the extant arterial-ME N₂O pressure-gradient (P^a_N2O - P^m_N2O, estimated from experimental data); the general gas constant (R); the inverse of ME volume (1/V^m, a constant for each ear); ME temperature (T^m, measured to be constant); N₂O solubility in blood (S^b_N2O, a constant); local volume blood flow (Q^m), and the gradient ratio defined by F^+/-_N2O. If Q^m and F^+/-_N2O are constants for each experiment, EQ11 is linear and the rate of change in ME pressure divided by the extant arterial-ME N₂O pressure-gradient is a time-constant (K^m+/-_N2O), such that:

$${\mathrm{K}}_{\mathrm{N}2\mathrm{O}}^{\text{m}+/­}=({\mathrm{\delta }\mathrm{P}}^{\mathrm{m}}/\mathrm{\delta }\mathrm{t})/({\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{a}}-{\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{m}})={\mathrm{F}}_{\mathrm{N}2\mathrm{O}}^{+/­}({\mathrm{RQ}}^{\mathrm{m}}{\mathrm{T}}^{\mathrm{m}}{\mathrm{S}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{b}})/{\mathrm{V}}^{\mathrm{m}}.$$ EQ12

Note that violation of these assumptions (i.e. within session changes in partial-pressures of other gases, Q^m or F^+/-_N2O) will be reflected as a non-linear relationship between the rate of ME pressure change (δP^m/δt) and gradient (P^a_N2O - P^m_N2O), and consequently linearity between those variables is a testable hypothesis of assumption validity.

Data Structure

The primary data for each experimental session consist of the repeated measurements of bilateral ME pressure after establishing a positive or negative ME-blood N₂O gradient. To calculate a time-constant for transmucosal N₂O exchange by EQ12, these data were transformed into estimates of the extant arterial-ME N₂O pressure-gradient and the rate of ME pressure change.

For the N₂O breathing experiments, arterial N₂O pressure (P^a_N2O) is assumed to be constant and was estimated by multiplying the physiological blood N₂ pressure (≈570mmHg at 760 mmHg ambient pressure) by the N₂O/(N₂ + N₂O) ratio for the breathing mixture (i.e. % substitution for N₂ by N₂O). At the onset of breathing the gas mixture (t=0 min), ME N₂O pressure (P^m_N2O) is 0 mmHg and, by EQ4 that partial-pressure at any time (t) can be estimated as the difference between ME pressure at that time (t=i) and ME pressure at t=0. These estimates were used to calculate the extant ME-blood N₂O pressure-gradient (G^(t=i)_N2O) as given by:

$${\mathrm{G}}_{\mathrm{N}2\mathrm{O}}^{(\mathrm{t}=\mathrm{i})}=-{\mathrm{P}}^{\mathrm{m}(\mathrm{t}=\mathrm{i})}.$$ EQ13

Because the gradient did not appreciably change during the course of the experiment, the time-constant was calculated as:

$${\mathrm{K}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{m}­}=\mathrm{\delta }{\mathrm{P}}^{\mathrm{m}(\mathrm{t}=\mathrm{i}­0)}/({\mathrm{G}}_{\mathrm{N}2\mathrm{O}}^{(\mathrm{t}=\mathrm{i}/2)}({\mathrm{T}}^{\mathrm{i}}­{\mathrm{T}}^0))$$ EQ14

or the change in ME pressure for an interval divided by the average interval gradient and the interval duration in minutes (units of /min). To allow for the blood N₂O pressure to reach steady state, we chose to analyze the data for the interval between 15 and 60 minutes after the onset of N₂O breathing.

For the N₂O inflation experiments, the gradient decays during the post-inflation period. There, EQ 12 can be rewritten as the linear function:

$$({\mathrm{\delta }\mathrm{P}}^{\mathrm{m}}{/\mathrm{\delta }\mathrm{t})=-\mathrm{K}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{m}+}{\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{m}}+{\mathrm{K}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{m}+}{\mathrm{P}}_{\mathrm{N}2\mathrm{O}}^{\mathrm{a}}$$ EQ15

where, for constant P^a_N2O, the time-constant is the slope of the line relating the rate of ME pressure change to extant ME pressure, which can be calculated by linear regression over all data recorded within a time interval. To allow for re-establishing negligible ME-blood gradients for O₂ and CO₂ that could have been disturbed by inflation, the data were analyzed for the post-inflation interval between 15 and 90 minutes (linear region of the rate-pressure function).

Data Reporting

The format, mean ± standard deviation is used consistently in data summaries, and the Pearson Correlation Coefficient is used when representing the relationships between paired data sets. Linear regression equations were fitted by the method of least squares. In comparing paired sets of time-constants, the paired Student’s t test was used and evaluated for significance at an alpha of .05.

RESULTS

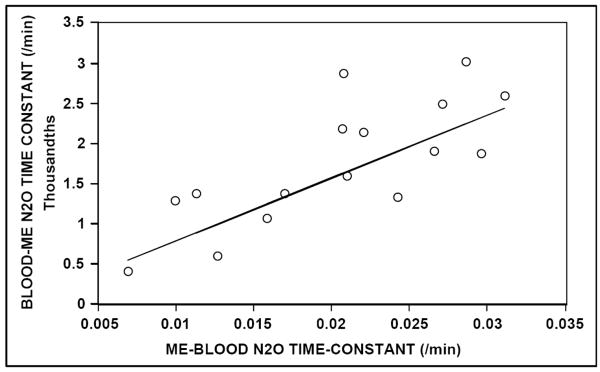
The Table reports the transmucosal N₂O time-constants calculated for both ears of all animals at the three test sessions, and the average and standard deviations of these measures for the left ear, right ear and total sample. For ME to blood exchange, the measured values of the N₂O time-constant were highly correlated for the two test sessions (r = .88) and for the two ears of each animal (r = .92). Figure 1 shows a scatterplot demonstrating the test-retest reproducibility of that estimate (regression equation: K^m+_{N2O est2} = 1.034 K^m+_{N2O est1} + 0.001 /min). For Blood to ME N₂O exchange, the average rate of change in MEP for the 45 minutes of analyzed data was 5.12 ± 2.14 mmH₂O/min and the estimated Blood to ME gradient for all experiments was approximately 2900 mmH₂O. As with the data for ME to Blood N₂O exchange, the measured values of the time-constant were highly correlated for the two ears of each animal (r = .99).

TABLE.

CALCULATED ME-BLOOD (ME-BD1,2) AND BLOOD-ME (BD-ME) TRANSMUCOSAL N2O TIME-CONSTANTS (/MIN) FOR BOTH EARS OF EACH ANIMAL (NO.)

NO.	LEFT			RIGHT
	ME-BD (1)	ME-BD (2)	BD-ME	ME-BD(1)	ME-BD (2)	BD-ME
37	0.0167	0.0173	0.0014	0.0160	0.0158	0.0010
38	0.0194	0.0220	0.0022	0.0280	0.0312	0.0019
39	0.0093	0.0106	0.0013	0.0083	0.0143	0.0014
40	0.0066	0.0072	0.0004	0.0172	0.0081	0.0006
41	0.0231	0.0188	0.0016	0.0235	0.0249	0.0013
44	0.0209	0.0206	0.0029	0.0242	0.0301	0.0025
46	0.0186	0.0254	0.0021	0.0264	0.0267	0.0019
47	0.0280	0.0292	0.0030	0.0285	0.0337	0.0026
AVG	0.0178	0.0189	0.0019	0.0215	0.0231	0.0017
STD	0.0066	0.0068	0.0008	0.0068	0.0081	0.0007
AVGT				0.0197	0.0210	0.0018
STDT				0.0068	0.0081	0.0007

FIGURE 1.

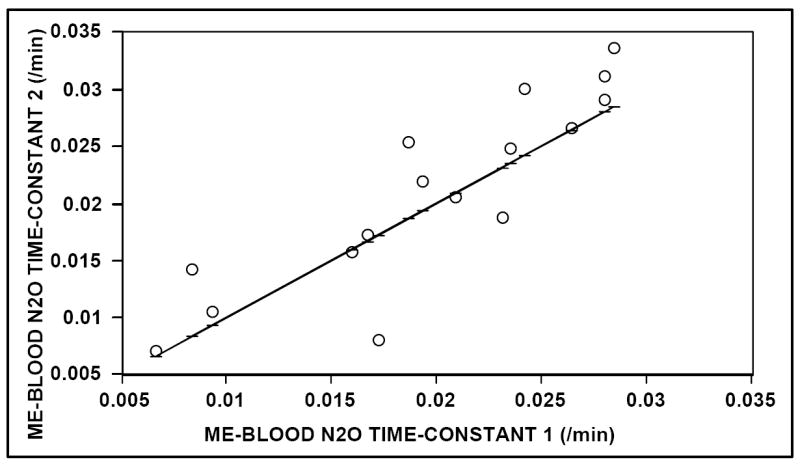
Scatterplot of the Middle Ear to Blood, transmucosal N₂O time-constant recorded at the second test session as a function of that recorded at the first session for both middle ears of the 8 animals. Solid line = identity for first session.

Figure 2 shows a scatterplot of the Blood to ME, N₂O time-constant as a function of the ME to Blood, N₂O time-constant (average of two measures) for both ears of all animals. Also shown is the solution to the regression equation relating those measures (K^m-_N2O = .079 K^m+_N2O + 0.000 /min). Time-constants for the two exchange directions were highly correlated (r = .767), but the magnitude of the measured ME to Blood time-constant was approximately 13 times greater than that of the respective Blood to ME time-constant (P<.001). These results document a significant directional asymmetry in the measured value of the transmucosal, N₂O time-constant for the ME.

FIGURE 2.

Scatterplot of the Blood to Middle Ear, transmucosal N₂O time-constant as a function of the average (for two sessions) Middle Ear to Blood transmucosal N₂O timeconstant for both middle ears of the 8 animals. Solid line = solution for the linear regression equation.

DISCUSSION

Appropriately calibrated mathematical models of transmucosal gas exchange for the ME can make an important contribution to predicting ME pressure behavior under various extant conditions (See Equation 2). As such, they can be used to describe the mechanism for maintaining near ambient ME pressure (i.e. adequate ME pressure regulation) as well as the circumstances under which that mechanism fails and consequently provokes ME pathology (1). At present, these models are not sufficiently detailed to include the fine-structure of the exchange system, and therefore, they treat gas exchange as bulk, gas-species flows between sequential exchange compartments (e.g. ME and blood). Existing two-compartment exchange models require as inputs: ME airspace volume, mucosal blood flow, the extant inter-compartment partial-pressure gradients and gas-specific, lumped-parameter, time-constants (1). Early mathematical descriptions of gas exchange between ME and blood estimated the ratios of the gas-specific, time-constants by assuming a diffusion-limited exchange for all represented gas-species (2-5) and used those ratios to calibrate the models. However, the results for simulations of ME pressure dynamics under different extant conditions using these models were not in agreement with experiment or clinical observation (6-14).

In contrast, our approach to modeling transmucosal ME gas exchange includes: experimental determination of the lumped-parameter, exchange-constant (i.e. the time-constant) for representative gases in an animal model; examining the values of that constant across gas-species for predictable mathematical relationships; interpreting those relationships with respect to underlying physiology, and then testing the accuracy of the calibrated model with respect to predicting ME pressure behavior for different experimental and clinical situations (1). Most simply, the exchange of gas between two adjoining compartments can be described by the Fick diffusion equations where volume gas flow between compartments is equal to the product of the inter-compartment, partial-pressure gradient and the gas-species conductance (21). The time-constant described in this report is an estimate of gas-species conductance for a simple, two-compartment system (i.e. ME and blood) and was shown in Equation 12 to be equal to F^+/-_g(RQ^mT^mS^b_g)/(V^m) for perfusion-limited gases. Consequently, the ratio of time-constants measured in the same ear for paired gas-species is equal to the respective F^+/-_gS^b_g ratios if the exchange of both gases is perfusion-limited. Previously, we reported that, compared to the respective ratios of gas solubility in blood/tissue, the measured ME to blood time-constant ratio was equal for inert gas parings (e.g. N₂O, N₂, Ar) and for reactive (e.g. O₂, CO₂, CO) gas pairings, but was much larger for reactive-inert gas pairings (6-9). Because the measured F^+/-_gS^b_g ratio for paired combinations of inert gases was equal to the respective S^b_g ratio, we hypothesized that F^+/-_g is gas-species independent, i.e. better represented as F^+/-.

We interpreted the difference in predicted time-constants between the two general classes of gas as reflecting a diffusion-limited exchange for reactive gases and a perfusion-limited exchange for inert gases. This can be explained by the ability of reactive, but not inert, gases to chemically bind with blood components (1) which buffers the local, blood partial-pressures of those gases (i.e. transmucosal reactive gas exchange does not affect P^a/v_g violating Equation 5). There, the local blood acts as a near infinite sink/reserve and gas exchange is rate limited by diffusion across the mucosal tissue (t) (i.e. the perfusion contribution as given by Equation 12 is negligible). This time-constant is better represented as: K^’m_g = (δP^m_g /δt)/(P^t_g-P^m_g) = C^mA^m (S^t_gD^t_g)/H^m; where C^m=N^mRT^m/V^m; A^m is the area of the tissue-air interface, H^m is the distance between tissue-air interface and capillary; S^t_g and D^t_g are the solubility and diffusivity of gas g in tissue, and P^t_g is approximated by the partial-pressure of gas g in mucosal tissue (21). Note that the ratio of time-constants measured in the same ear for gases characterized by diffusion-limited exchange is equal to the ratio of their respective S^t_gD^t_g product. Because D^t_g is not appreciably different for the physiological gases, that product is dominated by the effect of S^t_g which is not much different from S^b_g.; i.e. like perfusion-limited gases, the time-constant ratio for diffusion-limited gases is approximately equal to the solubility ratio for the paired gases.

Inclusion of these revisions in mathematical descriptions of ME pressure behavior improves the correspondence between prediction and experiment and explains a number of observations not accounted for by the more simple exchange model (10,11,13). However, the phase relationship between predicted and measured pressure change was distorted when the model was calibrated using K^m+/-_g values measured for positive ME-blood gradients and the data were acquired for situations with established negative ME-blood gradients (11,13). This observation suggests a directional asymmetry in the measured value of K^m+/-_g, a hypothesis that was supported by measurement of K^m+/-_N2O in past experiments that established either positive or negative ME-blood N₂O gradients (6-9,19). Importantly, those studies documented a linear relationship between the rate of ME pressure change (δP^m/δt) and extant gradient (P^a_N2O - P^m_N2O), a condition specified if the assumptions underlying the model equations are valid (See Methods).

In the present study, we estimated the K^m+/-_N2O for transmucosal exchange in both ears of 8 monkeys under conditions of induced positive and negative ME-blood N₂O pressure-gradients. The measured K^m+/-_N2O values were similar to those derived from the data for previous experiments that used modifications of these procedures (7-9,19). Because N₂O is an inert gas characterized by perfusion-limited transmucosal exchange, Equation 12 (K^m+/-_g=F^+/-_gRQ^mT^mS^b_g)/V^m) is strictly applicable. Paired left-right K^m+/-_N2O measures for both positive and negative ME-blood partial-pressure-gradients were highly correlated, as were the paired K^m+/-_N2O values measured for each ear in response to positive and negative ME-blood driving gradients. This is explicable by the lesser Q^m/V^m variance for the same animal when compared to that for the population. However, the measured time-constant for established positive ME-blood gradients was approximately 13 times greater than that for established negative ME-blood gradients. From Equation 12, this requires that F^+/-_N2O ≠ 1, since for a given ME, the ratio of the N₂O time-constant for the directional exchanges is equal to F⁺_N2O/F^-_N2O and, by symmetry of exchange 1/F^-_N2O =F⁺_N2O. Therefore, the time-constant ratio measured for a perfusion-limited gas at positive to negative ME-blood gradients is equal to (F⁺_g)². From the experimental data, (F⁺_N2O)² was estimated to be approximately 13, and thus F⁺_N2O approximately equals 3.6 (and F^-_N2O ≈ 0.28). As discussed above, experimental evidences suggest that the value of F⁺_g (and by symmetry F^-_g) is not dependent on the species of inert gas and, if true, the estimate derived for N₂O in the present study can be used to calibrate the directional time-constants for other inert gases whose transmucosal exchange is too slow to be measured in experiments (e.g. N₂).

The physiology represented by the value of F^+/-_g in the exchange equation for perfusion-limited gases is not readily apparent. Because this parameter is a ratio of pressure-gradients, we hypothesize that its value reflects the distributed, gas-species gradient across the ME mucosa, and consequently requires a multi-compartment mathematical model to describe the underlying physiology. We are currently exploring the development of a distributed model of transmucosal gas exchange that includes only the fine-structure geometry of the transmucosal exchange elements and the physiochemical properties of the relevant gases as inputs. It is expected that the exchange constants measured by experiment in existing models will be emergent quantities from these more basic parameters and that the physiology represented by the components (including F^+/-_g) of the lumped parameter time-constant will become evident when this model is completed.

None-the-less, the inclusion of F^+/-_g in mathematical descriptions of transmucosal inert gas exchange for a two-compartment exchange model is valid given that the quantity is contained within the standard equation for perfusion-limited exchange and inclusion of F^+/-_g in the lumped-parameter, time-constant yields results consistent with experiment. However, for reasons discussed above, the properties of F^+/-_g cannot be assigned ad hoc but need to be gleaned from experiment. Three properties of F^+/-_g are suggested by experimental evidences: 1) F^+/-_g is a constant for a given inert gas as evidenced by the linearity of the rate-pressure functions for transmucosal inert gas exchange, 2) F^+/-_g is independent of gas species as evidenced by it’s lack of contribution to the value of the time-constant ratio for paired inert gases, and 3) F^+/-_g ≠ 1 as evidenced by its dependence on gradient direction. Future experiments need to be done to determine the boundary conditions under which these properties remain valid.