Abstract
Objectives
To more efficiently determine the subcritical crack growth (SCG) parameters of dental ceramics, the effects of stressing rate and choice of statistical regression model on estimates of SCG parameters were assessed.
Methods
Two dental ceramic materials, a veneering material having a single critical flaw population (S) and a framework material having partially concurrent flaw populations (PC), were analyzed using constant stress-rate testing, or “dynamic fatigue”, with a variety of testing protocols. For each material, 150 rectangular beam specimens were prepared and tested in four-point flexure according to ISO6872 and ASTM1368. A full-factorial study was conducted on the following factors: material, stress rate assumed vs. calculated, number of stress rates, and statistical regression method.
Results
The proportion of specimens for which the statistical models over-estimated reliability was not significantly different based on regression method for Material S (P = 0.96, power = 94%) and was significantly different based on regression method for Material PC (P < 0.001). The standard method resulted in SCG parameters, n and ln B, of 35.9 and -11.1 MPa2s for Material S and 12.4 and 9.61 MPa2s for Material PC.
Significance
The method of calculation that uses only the median strength value at each stress rate provided the most robust SCG parameter estimates. Using only two stress rates resulted in fatigue parameters comparable to those estimated using four stress rates having the same range. The stress rate of each specimen can be assumed to be the target stress rate with negligible difference in SCG parameter estimates.
Keywords: dynamic fatigue, subcritical crack growth, statistics, reliability, fatigue test design, dentistry, ceramic, strength, Weibull distribution, critical flaw
1. Introduction
Ceramic components, such as dental prostheses, sometimes exhibit delayed catastrophic failure due to subcritical crack growth (SCG) [1, 2]. This crack growth can occur through simultaneous mechanisms of stress-corrosion and cyclic fatigue [3-5]. The lifetime of a component can be predicted if the stress distribution for the component and parameters characterizing the rate of SCG are known for each of the component materials in the service environment [6]. The SCG parameters for a given material can be deduced from experiments on standard geometry specimens [2, 7, 8]. When components are subject to a constant stress or are fabricated from materials that do not suffer cyclic fatigue, a static or dynamic fatigue test is sufficient to deduce the SCG parameters [4, 9].
The term “static fatigue” describes the experiment in which the induced stress is constant over time and the time to failure is the dependent variable [2]. To perform a static fatigue test for a material, measurements of failure time must be taken at several constant stress levels. In the static fatigue testing method, the time to failure for each specimen may take days or sometimes months to measure.
Constant stress-rate testing, also known as “dynamic fatigue”, is a technique to expedite determination of material SCG parameters [7, 8]. Constant stress-rate testing is the situation in which the induced stress is increased over time at a constant rate and the failure stress is the dependent variable. This method requires performing strength tests at several stress rates. For a material having fracture toughness (KIc) and flaw geometry (Y) independent of flaw size (a), failure stress (σf) decreases with decreasing stress rate, since flaws are given more time to grow before the critical stress intensity factor is reached. According to Equation 1, σf must decrease with increasing a when KIc and Y are constant [7].
| (1) |
Ritter derived the equation for strength of specimens tested under constant stress rate as [8]:
| (2) |
where σ̇ is the stress rate, and Si is the inert (moisture free) flexural strength. By performing regression of ln σf vs. ln σ̇, a linear model of best fit can be constructed and used to estimate the SCG parameters, n and B. These parameters can be used to estimate the lifetime (tf) under constant stress (σ) to be [8]:
| (3) |
Equation 3 shows that high values for both n and B represent greater resistance to stress-corrosion. However, B contains the fracture toughness; hence a high B value also represents greater fracture resistance in general [8]:
| (4) |
| (5) |
where ν is the velocity of subcritical crack growth, which is a function of the stress intensity factor (KI).
The dependence of strength on flaw distribution often leads to large variations in observed lifetime between specimens. This will cause an appreciable scatter in SCG parameter estimates. Since accurate estimates are necessary for accurate prediction of component lifetime, several authors have used Monte Carlo simulation to investigate the effects of the number of test specimens and range of stress rates employed on the accuracy and precision of estimates [10-12]. Ritter et al. found that the variability in estimating the fatigue parameters increased as the number of groups tested at different stress rates increased [12]. They also reported that if n is determined from strength measurements at two stress rates, then the statistical variability of n is quite sensitive to the stress-rate range, and the variability increased as the range of stress rates decreased [12]. In addition, variability of estimates was dependent on the total number of specimens but not the number of specimens per group. Salem and Weaver calculated the confidence intervals of fatigue parameter estimates using both a closed form solution (propagation of error) and Monte Carlo simulation [11]. They found that regression models using group mean values and median values were both adequate for estimating n, but because of the skewed distribution of B estimates, only median strength values were adequate for use in estimating B. Use of median strength values also provided a more conservative reliability model, since it resulted in lower values for B estimates [11]. McCool found that estimates of B have much greater variability than estimates of n [10]. He also reported that the number of specimens used to measure stress-corrosion has a greater influence on the variability of B estimates than does the number of specimens used to measure inert strength.
The present work is an extension of the investigations by Ritter et al., Salem and Weaver, and McCool. Contrary to the recommendations of Ritter et al., the ASTM1368 standard specifies that at least four stress rates should be used for dynamic fatigue testing [13]. This contradiction invites further investigation. The standard also specifies that, due to variation in specimen dimensions, the actual stress rate should be calculated for each specimen individually. However, some investigators may conserve effort by assuming that all specimens in a group experienced the same stress rate, the target stress rate. This would seem to be a minor assumption, but no data are yet available regarding the effect of this assumption on test results. In addition, there are three different regression methods that are commonly used: a method that uses all failure strength values (ASTM1368), a method that uses only median failure strength values [8], and a method that uses the ratios of all failure stresses to those of equally ranked specimens from the inert strength group [14]. It is unknown which of the above methods is least sensitive to irregularity in the distribution of strength data. In the present study, physical specimens made from two ceramics that are widely used in dental applications were used to:
determine the sensitivity of SCG parameter estimates to the number and range of stress rates,
determine whether assuming identical target stress rates for all the specimens in each group affects the accuracy of lifetime prediction, and
determine the most robust regression method to calculate SCG parameters.
Previous authors have used indentation-crack method, constant stress-rate testing, and cyclic loading to determine the SCG parameters of a variety of dental ceramics [15-30]. The ceramic materials used in this study were previously evaluated using fractographic methods to determine their critical flaw populations [27].
2. Materials and methods
This study was performed on two different dental ceramics that are widely used in fabricating all-ceramic dental fixed prostheses. A feldspathic porcelain (Vitadur Alpha; VITA Zahnfabrik, Bad Säckingen, Germany) was chosen to exemplify materials that are simple to characterize because a single type of critical flaw has been observed for this material (Material S) [27]. An alumina-zirconia-glass composite (In-Ceram® Zirconia; VITA Zahnfabrik) was chosen to exemplify materials that are difficult to characterize because its strength values were heavily skewed towards the lower end of the distribution, owing to two partially concurrent flaw populations (Material PC) [27]. Three hundred uniaxial flexure specimens (150 of each material) were fabricated to dimensions of 25 mm × 4 mm × 1.2 mm. All specimens were processed and treated according to the manufacturer's recommendations for fabricating an actual dental prosthesis.
Material S specimens were fabricated by mixing 0.5 g of ceramic powder (VITA Zahnfabrik) and 0.18 g of modeling liquid (VITA Zahnfabrik) to form a slurry. The slurry was poured into custom fabricated steel molds with dimensions of 25.50 mm × 4.75 mm × 2.00 mm. Then, the slurry was condensed in the molds using a mechanical vibrator (No. 1 A; Buffalo Dental, Syosset, NY, USA) followed by manual vibration to allow any trapped air to escape from the slurry. A firing cycle was performed using a dental porcelain furnace (Centurion Q200; Ney, Yucaipa, CA, USA) according to the manufacturer's instructions as follows: The specimens were dried at 600°C for 6 min, heated to 960°C at a rate of 60°C/min under full vacuum, held at 960°C for 1 min, and subsequently cooled for one minute before removing the specimens from the furnace. After completing the firing cycle, bench-cooling to room temperature was performed for all specimens. An additional firing cycle was performed as follows: The specimens were dried at 600°C for 6 min, heated to 950°C at a rate of 58°C/min under full vacuum, held at 950°C for 1 min under 1 atm pressure, and subsequently cooled for one minute before removing the specimens from the furnace. The second firing was used to simulate the processing step frequently used by dental technicians to make small corrections to the shape of a prosthesis. All specimens were ground to the final desired dimensions of 25 mm × 4 mm × 1.2 mm, and the tensile surfaces were polished using SiC abrasive papers with sequentially finer grit size (8″ Plain Back Silicon Carbide Discs; Allied High Tech Products, Rancho Dominguez, CA, USA). The polishing procedure was concluded by using a final grit size of 400, and the last polishing direction was performed along the long axis of the specimen. All the specimens were auto-glazed as follows: Each specimen was dried at 600°C for 4 min, heated to 920°C at a rate of 107°C/min, and held for 1 min at 920°C; this firing cycle was run under atmospheric pressure. Subsequently, all specimens were bench-cooled to room temperature.
A very thin (0.05 mm) adhesive tape (Scotch® Magic™ Tape; 3M, St. Paul, MN, USA) was placed on the compressive surface to secure the fractured segments of the specimen during the fracture test. The specimens were assigned randomly into five groups of 30 specimens each. One group of specimens was tested under an inert environment. The other specimens were tested while immersed in distilled water at 37°C. The inert strength specimens were heated at 140°C for 14 hours to remove any moisture from the specimens, and then they were placed in 140°C SAE 85W-140 oil (Super Tech; Wal-Mart Stores, Bentonville, AR, USA), and allowed to cool to 37°C in a desiccator to prevent atmospheric moisture from contacting the specimens. This should have prevented moisture from assisting crack growth during fracture.
Material PC specimens were fabricated to the dimensions of 25 mm × 4 mm × 1.2 mm. This was accomplished by cutting ceramic blocks (Zirconia ZB-80; VITA Zahnfabrik) into the desired shape and dimensions using a low-speed saw with a diamond cutting blade (Isomet; Buehler, Lake Bluff, IL, USA). The ceramic block was mounted on the cutting arm, which was adjusted by an attached micrometer to set the desired cut thickness. Zirconia ZB-80 blocks are porous; to fill the porosity a glass infiltration procedure was performed. This was performed by applying a coating of glass powder-water slurry (In-Ceram® Zirconia Glass Powder; VITA Zahnfabrik) to the ceramic specimens using a dental ceramic brush. The specimens were placed in a programmable vacuum porcelain furnace (Multimat® Touch & Press; Dentsply, York, PA, USA) to perform the glass infiltration firing cycle according to the manufacturer's recommendations as follows: All specimens were dried at 600°C for 1 min, heated to 1140°C at a rate of 20°C/min, and held at 1140°C for 40 min under full vacuum. After glass infiltration, the excess glass was removed using heatless coarse-grained SiC wheels (Mizzy Heatless® Wheels; Keystone, Cherry Hill, NJ, USA). Following this step, the Material PC specimens were treated exactly as the Material S specimens, and all the firing steps that were performed on the Material S specimens were also performed on the Material PC specimens, since in the clinical situation a veneer of Material S will be built on top of a core of Material PC, and accordingly, the core material will encounter all the firing cycles that the veneer encounters.
Four-point flexure testing was performed using a servohydraulic mechanical testing machine (Minibionix 858; MTS Systems Corporation, Eden Prairie, MN, USA) with a custom semi-articulating four-point flexure fixture having an outer span of 20 mm and an inner span of 10 mm. The target stress rates were attained using the mechanical testing machine in load-controlled mode. Equation 6 was used to determine the load rates necessary to reach the target stress rates with an assumed width and thickness.
| (6) |
where Ṗ is the load rate, σ̇ is the target stress rate, L is the outer (support) span of the test fixture, w is the specimen width, and t is the specimen thickness. Each group of the Material S specimens was fractured using one of four different target stress rates ranging on a logarithmic scale from 0.1 to 100 MPa/s. The fifth group was tested in inert environment (oil) with a target stress rate of 100 MPa/s. Different target stress rates, which ranged from 0.01 to 10 MPa/s, were used for the Material PC specimens, and a target stress rate of 10 MPa/s was used for the inert strength group. Slower stress rates were used for Material PC because pilot data showed a plateau in strength versus stress rate at faster stress rates. SCG parameters estimated from data on a strength plateau are not valid [13]. The width and thickness of each specimen were measured adjacent to the fracture surface to determine the flexural strength, σf, of each specimen according to the following equation:
| (7) |
where P is the maximum load recorded during testing. The actual stress rate, σ̇Actual, for each specimen was determined individually using the following equation:
| (8) |
where tf is the failure time determined from the four-point flexure test for each specimen.
Subsequent data analyses were performed to estimate the fatigue parameters, n and B, at the actual stress rates using three well known methods based on logarithmic transformation followed by linear regression. These methods are as follows: A method that uses all failure stress values as in Equation 9; median method, which uses only the median failure stress value from each group according to Equation 10; and homologous method, which uses the ratio of failure stresses of equally ranked specimens from the water and inert strength groups as in Equation 11.
| (9) |
| (10) |
| (11) |
where σ̄f is the median failure stress for each stress rate group,  is the corresponding stress rate, and Si is the inert strength of specimen with rank i. The flexural strengths accompanied with the corresponding stress rates were used to perform linear regression according to Equations 6-8, and the fatigue parameters were calculated. Equation 12 was used to calculate n as follows,
is the corresponding stress rate, and Si is the inert strength of specimen with rank i. The flexural strengths accompanied with the corresponding stress rates were used to perform linear regression according to Equations 6-8, and the fatigue parameters were calculated. Equation 12 was used to calculate n as follows,
| (12) |
and Equations 13-15 to calculate B for the all data points method, median points method, and homologous points method, respectively:
| (13) |
| (14) |
| (15) |
where S̄i is the median inert strength. In addition to actual stress rates, target stress rates were also used to perform the calculations again to determine the error that is introduced by the assumption of stress rate.
The proportion of specimens with failure stress values lower than the stress predicted by the reliability model was counted for each calculation method for each material. This was used as the basis to determine which model had the best fit for the data. The ideal case would be when 50% of the data points were located at lower stress than the model. The proportions of specimens with over-estimated reliability were compared by using a chi-square test (α = 0.05) to detect differences between calculation methods.
3. Results
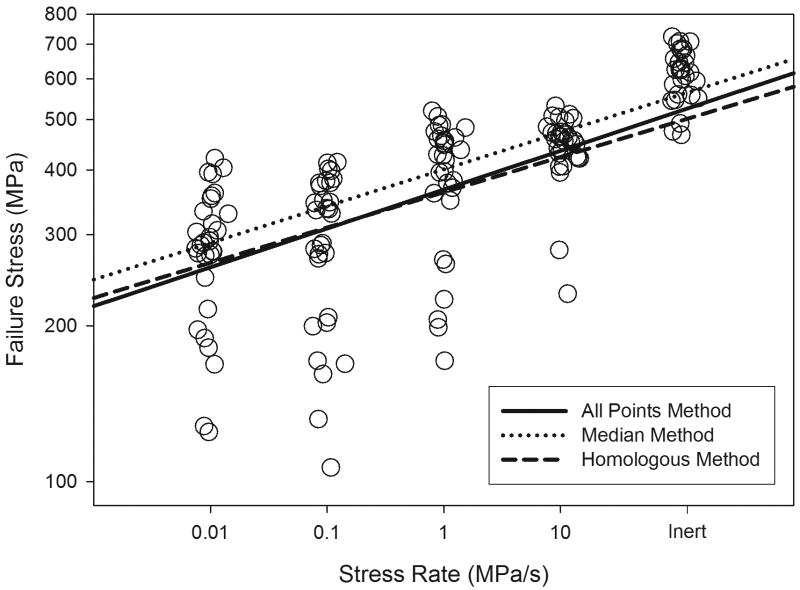
The estimates of SCG parameters, n and B, for Materials S and PC, resulting from each combination of calculation method and set of stress rates are summarized in Table 1. A reliability model was constructed from each pair of SCG parameters. Table 1 also lists the proportion of data points that were located at lower stress than predicted by each reliability model. The statistical model over-estimated the reliability of those specimens. For Material S, there was no significant difference in proportion of overestimated reliability between reliability models when using four stress rates (P = 0.96, power = 94%). However, there was a significant difference between reliability models for Material PC (P < 0.001). The difference between reliability models for Material PC was primarily associated with under estimation of the B parameter resulting from the homologous and all points calculation methods. Figure 1 illustrates the situation using data from Material PC specimens. The median calculation method was not sensitive to the skewed distribution of Material PC strength.
Table 1.
Summary of the estimated fatigue parameters of the Materials S and PC using different models and the proportion of the specimens failing at lower stress than predicted by each model.
| Material S | Material PC | |||||||
|---|---|---|---|---|---|---|---|---|
| Calculation Method | Stress Rate Groups | Stress Rate | Below Predicted (%) | n | ln B | Below Predicted (%) | n | ln B |
| All points | All four rates | Actual | 48.3 | 35.9 | -11.1 | 34.2 | 12.4 | 9.61 |
| Target | 48.3 | 35.5 | -10.8 | 34.2 | 12.4 | 9.61 | ||
| Two middle rates | Actual | 49.2 | 24.4 | -4.87 | 46.7 | 6.8 | 13.3 | |
| Target | 49.2 | 24.6 | -4.84 | 46.7 | 6.8 | 13.3 | ||
| Two extreme rates | Actual | 50.0 | 37.8 | -11.9 | 35.0 | 13.5 | 9.21 | |
| Target | 50.8 | 37.3 | -11.5 | 35.0 | 13.5 | 9.21 | ||
| Median points | All four rates | Actual | 46.7 | 38.4 | -12.7 | 54.2 | 13.1 | 10.4 |
| Target | 46.7 | 38.2 | -12.4 | 54.2 | 13.1 | 10.4 | ||
| Two middle rates | Actual | 45.0 | 23.6 | -4.86 | 57.5 | 8.2 | 13.6 | |
| Target | 45.0 | 23.7 | -4.79 | 57.5 | 8.2 | 13.6 | ||
| Two extreme rates | Actual | 53.3 | 41.1 | -13.3 | 46.7 | 14.0 | 9.61 | |
| Target | 53.3 | 40.9 | -13.1 | 46.7 | 14.0 | 9.61 | ||
| Homologous points | All four rates | Actual | 48.3 | 32.8 | -9.84 | 33.0 | 13.7 | 8.63 |
| Target | 47.5 | 32.6 | -9.59 | 33.0 | 13.7 | 8.63 | ||
| Two middle rates | Actual | 48.3 | 20.5 | -2.87 | 33.0 | 12.6 | 8.92 | |
| Target | 49.2 | 20.6 | -2.79 | 33.0 | 12.6 | 8.92 | ||
| Two extreme rates | Actual | 48.3 | 35.5 | -11.1 | 36.6 | 13.8 | 8.99 | |
| Target | 47.5 | 35.2 | -10.9 | 36.6 | 13.8 | 8.99 | ||
Figure 1.
Comparison of reliability models resulting from dynamic fatigue data analyzed using different calculation methods. All calculation methods used data from four stress rates with 30 specimens per group having multiple critical flaw populations.
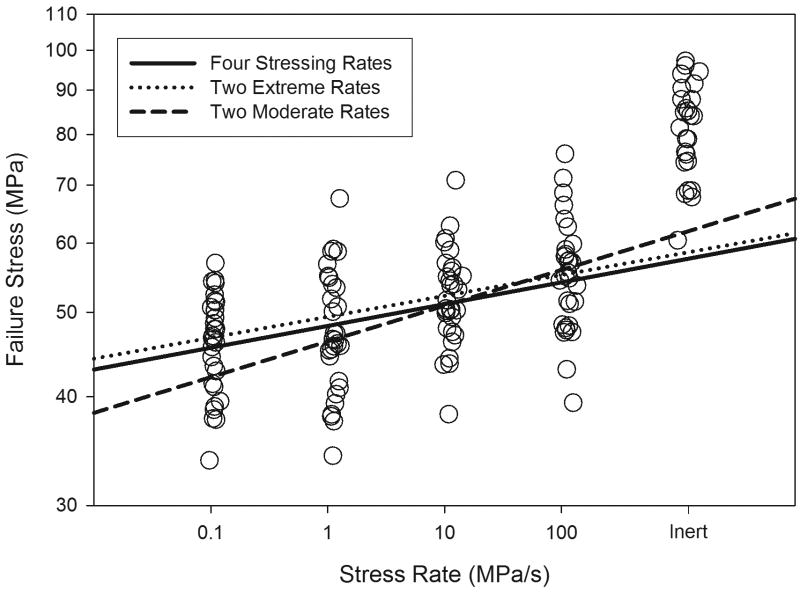
Although the choice of stress rates did not have a strong effect on the estimation of reliability for Material S, it did have a strong effect on SCG parameter estimates. The use of four stress rates ranging four orders of magnitude and the use of only two stress rates with maximum possible range resulted in similar estimates for n and B. However, use of two stress rates ranging two orders of magnitude resulted in different estimates. This is illustrated by differing slope and intercept in Figure 2 using data from Material S specimens. The intercept is related to the B parameter and the inert strength, but higher intercept values do not necessarily correspond to higher B values for small differences or no difference in inert strength (e.g., when comparing calculation methods for only one material) because the B parameter is also related to the difference between strength in an aqueous environment and inert strength (Equations 13-15). The B parameter estimate was generally lowest when two stress rates ranging four orders of magnitude (two extreme rates) were used for the calculation and was generally highest when two stress rates ranging two orders of magnitude (two middle rates) were used. This trend was evident regardless of calculation method (all points, median points, or homologous points) and material, except for the homologous points method used on Material PC. There was no consistent trend for the effect of calculation method on B parameter estimates across the two materials. The slope is related to the n parameter, where lower slope of the regression line corresponds to a higher n parameter estimate. The n parameter estimate was generally highest when two stress rates ranging four orders of magnitude were used and was generally lowest when two stress rates ranging two orders of magnitude were used. This trend was evident regardless of calculation method and material. Hence, there was a negative covariance between n and B parameter estimates (-25.1 for Material S and -4.15 for Material PC). There was no consistent trend for the effect of calculation method on n parameter estimates.
Figure 2.
Comparison of reliability models resulting from dynamic fatigue data gathered using different number and different span of stress rates. The models were calculated using the median rank method with 30 specimens per group have a single critical flaw population.
In both Figures 1 and 2 the data points representing the strength values of individual specimens are widely spread in the vertical direction, showing that the strongest specimen in each stress rate group had a much higher failure stress than the weakest specimen tested at the same target stress rate (ratio of 1.69 to 2.04 for Material S and 1.55 to 3.89 for Material PC). The median failure stress was slightly higher for faster target stress rates, which caused an upward trend in the data moving from left to right across the graphs. The data points have a small amount of spread in the horizontal direction within each target stress rate group because the loading method did not exactly achieve the target stress rate. The unintentional variation in stress rate (fastest/slowest ratio) ranged from 1.23 to 1.54 for Material S and from 1.69 to 1.93 for Material PC. There was only a weak correlation between variation in strength and unintentional variation in stress rate (R2 ≤ 0.11 for Material S and R2 ≤ 0.14 for Material PC). The assumption that specimens were tested at target stress rates instead of the actual rates had negligible effect on estimates of reliability and SCG parameters.
4. Discussion
The median calculation method was not sensitive to the skewed distribution of Material PC strength because the median strength of each group was unaffected by outliers. This finding agrees with the prediction of Salem and Weaver regarding the effect of a skewed distribution on mean versus median of B estimates [11]. This also supports the prediction of McCool that B estimates are more variable than n estimates [10]. Although the homologous and all points calculation methods provided less accurate estimates of reliability, they erred on the conservative side. In other words, components fabricated from Material PC would have a lower incidence of failure than predicted at a given service stress. However, the direction of error is influenced by the direction of skew in strength data. A strength distribution skewed towards the higher end, such as from proof-tested specimens, would result in a higher incidence of component failure than predicted. The median points calculation method seems to be the most robust method, so it may be better for use with confidence for a variety of data distributions, but additional studies should be conducted to compare the precision of SCG estimates determined using median points only versus the standard method.
The use of four stress rates ranging four orders of magnitude (as specified by ASTM1368) and the use of only two stress rates with maximum possible range (as recommended by Ritter et al.) resulted in similar estimates for n and B. However, use of two stress rates ranging two orders of magnitude resulted in different estimates. These results indicate, assuming that the log strength versus log stress rate fits a linear model, that the accuracy of SCG parameter estimates is affected by the range but not by the number of stress rates. Since Ritter et al. predict greater precision to result from the use of fewer stress rates, it seems advisable to use two stress rates with the maximum possible range instead of four stress rates. This strategy has the added benefit of conserving test specimens. However, testing a few specimens at an intermediate stress rate to verify linearity of the log-log relation is advisable.
The discrepancy in stress rates depends on variability in specimen dimensions, and the specimens used in this study had fairly well controlled dimensions of 1.22 ± 0.09 mm thickness and 3.98 ± 0.12 mm width (mean ± one standard deviation). For specimens meeting similar tolerance, it seems that the assumption of target stress rate is a safe one. Of course considering the speed of currently available personal computers, there is little need for such an assumption in order to simplify calculations, but this result should be reassuring for investigators working with incomplete data sets.
There was a large difference in SCG parameters for the two materials analyzed. Material PC had a much lower n compared to Material S, and Material S had a much lower B compared to Material PC, regardless of the method of estimation used. In practical terms, both n and B represent resistance to stress-corrosion cracking, and B also represents a general resistance to fracture because it contains the fracture toughness of the material (Equation 4), whereas n only describes the change in strength over time. However, n has a much stronger effect than B on SCG resistance because B describes a coefficient relation between stress and lifetime, whereas n describes a power law relation between stress and lifetime (Equation 3). In addition, it is common to observe a large variation in B estimates. For example, Monte Carlo simulations of soda-lime glass subjected to constant stress-rate testing predicted a 539% difference between the upper and lower bounds of the 95% confidence interval for B when 50 specimens were tested and 1442% difference when only 20 specimens were tested [10]. Therefore, when the trends in n values and B values are not consistent it is preferred to compare SCG resistance on the basis of the n values. Material PC had a lower n compared to Material S, so the strength of Material PC is more sensitive to the amount of time spent under load in an aqueous environment. Material PC had a higher inert strength than Material S, which is probably the reason that it had higher B, and this suggests that Material PC will have a higher strength than Material S in the short term even though the strength of Material PC will decrease at a faster rate over time. In fact, Equation 3 predicts that the median lifetime of specimens made of Material PC will be longer than the median lifetime of specimens made of Material S for stress levels higher than 14 MPa.
5. Conclusion
Within the limitations of this study, the following conclusions were drawn:
Using only two stress rates resulted in fatigue parameters comparable to those estimated using four stress rates having the same range.
The method of calculation that uses only the median strength value at each stress rate can be considered the most robust method.
The stress rate of each specimen can be assumed to be the target stress rate with negligible difference in SCG parameter estimates.
Acknowledgments
This study was supported by NIH-NIDCR grant DE013358 and King Saud University, Riyadh, Saudi Arabia. We gratefully acknowledge the donation of some of the materials by Mr. Bill Baker at Vident in Brea, CA, USA.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Paris P, Erdogan F. A critical analysis of crack propagation laws. J Basic Eng. 1963;85:528–34. [Google Scholar]
- 2.Wiederhorn SM. Subcritical crack growth in ceramics. In: Bradt RC, Hasselman DPH, Lange FF, editors. Fracture mechanics of ceramics. Vol. 2. New York, NY: Plenum Press; 1974. [Google Scholar]
- 3.Michalske T, Freiman S. A molecular interpretation of stress corrosion in silica. Nature. 1982;295:511–2. [Google Scholar]
- 4.Evans AG, Fuller ER. Crack propagation in ceramic materials under cyclic loading conditions. Metall Trans A. 1974;5:27–33. [Google Scholar]
- 5.Freiman SW, Wiederhorn SM, Mecholsky JJ., Jr Environmentally enhanced fracture of glass: A historical perspective. J Am Ceram Soc. 2009;92:1371–82. [Google Scholar]
- 6.Jadaan O, Nemeth N. Transient reliability of ceramic structures. Fatigue Fract Eng Mater Struct. 2001;24:475–87. [Google Scholar]
- 7.Evans AG, Wiederhorn SM. Crack propagation and failure prediction in silicon nitride at elevated temperature. J Mater Sci. 1974;9:270–8. [Google Scholar]
- 8.Ritter JE. Engineering design and fatigue failure of brittle materials. In: Lange FF, editor. Fracture mechanics of ceramics. New York, NY: Plenum Press; 1978. [Google Scholar]
- 9.Kawakubo T, Komeya K. Static and cyclic fatigue behavior of a sintered silicon nitride at room temperature. J Am Ceram Soc. 1987;70:400–5. [Google Scholar]
- 10.McCool JI. Statistical error in crack growth parameters deduced from dynamic fatigue tests. Int J Fatigue. 2004;26:1207–15. [Google Scholar]
- 11.Salem JA, Weaver AS. Estimation and simulation of slow crack growth parameters from constant stress rate data. In: White K, Bradt RC, Munz D, Sakai M, editors. Fracture mechanics of ceramics: active materials, nanoscale materials, composites, glass, and fundamentals. New York, NY: Springer; 2005. [Google Scholar]
- 12.Ritter JEJ, Bandyopadhyay N, Jakus K. Statistical reproducibility of the dynamic and static fatigue experiments. Am Ceram Soc Bull. 1981;60:798–806. [Google Scholar]
- 13.ASTM . C1368-06 Standard test method for determination of slow crack growth parameters of advanced ceramics by constant stress-rate flexural testing at ambient temperature. Philadelphia, PA: American Society for Testing and Materials; 2006. [Google Scholar]
- 14.Wilkins BJ. Engineering design and the probability of fatigue failure of ceramic materials. In: Lange FF, editor. Fracture mechanics of ceramics. New York, NY: Plenum Press; 1974. [Google Scholar]
- 15.Morena R, Beaudreau GM, Lockwood PE, Evans AL, Fairhurst CW. Fatigue of dental ceramics in a simulated oral environment. J Dent Res. 1986;65:993–7. doi: 10.1177/00220345860650071901. [DOI] [PubMed] [Google Scholar]
- 16.Anusavice KJ, Lee RB. Effect of firing temperature and water exposure on crack propagation in unglazed porcealain. J Dent Res. 1989;68:1075–81. doi: 10.1177/00220345890680060401. [DOI] [PubMed] [Google Scholar]
- 17.Fairhurst CW, Lockwood PE, Ringle RD, Twiggs SW. Dynamic fatigue of feldspathic porcelain. Dent Mater. 1993;9:269–73. doi: 10.1016/0109-5641(93)90073-y. [DOI] [PubMed] [Google Scholar]
- 18.Myers ML, Ergle JW, Fairhurst CW, Ringle RD. Fatigue characteristics of a high-strength porcelain. Int J Prosthodont. 1994;7:253–7. [PubMed] [Google Scholar]
- 19.Myers ML, Ergle JW, Fairhurst CW, Ringle RD. Fatigue failure parameters of IPS-Empress porcelain. Int J Prosthodont. 1994;7:549–53. [PubMed] [Google Scholar]
- 20.Twiggs SW, Fairhurst CW, Lockwood PE, Ringle RD. Cyclic fatigue of a model feldspathic porcelain. Dent Mater. 1995;11:273–6. doi: 10.1016/0109-5641(95)80062-X. [DOI] [PubMed] [Google Scholar]
- 21.Lohbauer U, Petschelt A, Greil P. Lifetime prediction of CAD/CAM dental ceramics. J Biomed Mater Res. 2002;63:780–5. doi: 10.1002/jbm.10468. [DOI] [PubMed] [Google Scholar]
- 22.Zhang Y, Lawn B. Long-term strength of ceramics for biomedical applications. J Biomed Mater Res B Appl Biomater. 2004;69:166–72. doi: 10.1002/jbm.b.20039. [DOI] [PubMed] [Google Scholar]
- 23.Zhang Y, Lawn BR, Rekow ED, Thompson VP. Effect of sandblasting on the long-term performance of dental ceramics. J Biomed Mater Res B Appl Biomater. 2004;15:381–6. doi: 10.1002/jbm.b.30097. [DOI] [PubMed] [Google Scholar]
- 24.Teixeira EC, Piascik JR, Stoner BR, Thompson JY. Dynamic fatigue and strength characterization of three ceramic materials. J Mater Sci Mater Med. 2007;18:1219–24. doi: 10.1007/s10856-007-0131-4. [DOI] [PubMed] [Google Scholar]
- 25.Lohbauer U, Krämer N, Petschelt A, Frankenberger R. Correlation of in vitro fatigue data and in vivo clinical performance of a glassceramic [sic] material. Dent Mater. 2008;24:39–44. doi: 10.1016/j.dental.2007.01.011. [DOI] [PubMed] [Google Scholar]
- 26.Mitov G, Lohbauer U, Rabbo MA, Petschelt A, Pospiech P. Investigations of subcritical crack propagation of the Empress 2 all-ceramic system. Dent Mater. 2008;24:267–73. doi: 10.1016/j.dental.2007.05.010. [DOI] [PubMed] [Google Scholar]
- 27.Taskonak B, Griggs JA, Mecholsky JJ, Yan JH. Analysis of subcritical crack growth in dental ceramics using fracture mechanics and fractography. Dent Mater. 2008;24:700–7. doi: 10.1016/j.dental.2007.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pinto MM, Cesar PF, Rosa V, Yoshimura HN. Influence of pH on slow crack growth of dental porcelains. Dent Mater. 2008;24:814–23. doi: 10.1016/j.dental.2007.10.001. [DOI] [PubMed] [Google Scholar]
- 29.Teixeira EC, Piascik JR, Stoner BR, Thompson JY. Dynamic fatigue behavior of dental porcelain modified by surface deposition of a YSZ thin film. J Prosthodont. 2008;17:527–31. doi: 10.1111/j.1532-849X.2008.00340.x. [DOI] [PubMed] [Google Scholar]
- 30.Pittayachawan P, McDonald A, Young A, Knowles JC. Flexural strength, fatigue life, and stress-induced phase transformation study of Y-TZP dental ceramic. J Biomed Mater Res B Appl Biomater. 2009;88:366–77. doi: 10.1002/jbm.b.31064. [DOI] [PubMed] [Google Scholar]