On the trail of Vikings with polarized skylight: experimental study of the atmospheric optical prerequisites allowing polarimetric navigation by Viking seafarers

Abstract

Between AD 900 and AD 1200 Vikings, being able to navigate skillfully across the open sea, were the dominant seafarers of the North Atlantic. When the Sun was shining, geographical north could be determined with a special sundial. However, how the Vikings could have navigated in cloudy or foggy situations, when the Sun's disc was unusable, is still not fully known. A hypothesis was formulated in 1967, which suggested that under foggy or cloudy conditions, Vikings might have been able to determine the azimuth direction of the Sun with the help of skylight polarization, just like some insects. This hypothesis has been widely accepted and is regularly cited by researchers, even though an experimental basis, so far, has not been forthcoming. According to this theory, the Vikings could have determined the direction of the skylight polarization with the help of an enigmatic birefringent crystal, functioning as a linearly polarizing filter. Such a crystal is referred to as ‘sunstone’ in one of the Viking's sagas, but its exact nature is unknown. Although accepted by many, the hypothesis of polarimetric navigation by Vikings also has numerous sceptics. In this paper, we summarize the results of our own celestial polarization measurements and psychophysical laboratory experiments, in which we studied the atmospheric optical prerequisites of possible sky-polarimetric navigation in Tunisia, Finland, Hungary and the high Arctic.

1. The viking sundial as a compass

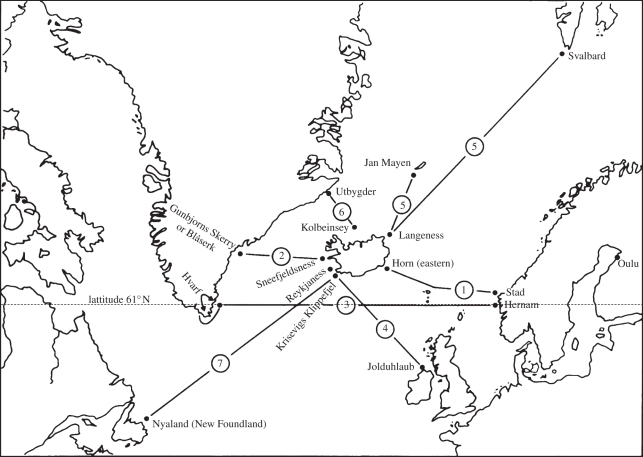
One of the most important Viking shipping routes between Norway and Greenland took them along latitude 61° N (figure 1). Archaeologists found a piece of stone and a fragment of a wooden disc (figure 2a), both featuring straight and hyperbolic carvings (figure 2b) [1]. It turned out that the two items had been parts of sundials used by the Vikings as a compass during their sea-crossings along latitude 61° N. A stick (the so-called gnomon) was mounted into the wooden disc perpendicular to the disc. If the disc was held horizontally at latitude 61° N during the sailing season of the Vikings (May to August) and the Sun was shining, then the tip of the shadow of the gnomon cast onto the disc followed the hyperbolic carving from sunrise through noon to sunset. Straight and hyperbolic carvings corresponded to the equinox and the summer solstice, respectively.

Figure 1.

The seven (1–7) main Viking sailing routes. Route 3 connected Hernam (nowadays the Norwegian Bergen) with Hvarf in South Greenland along latitude 61° N [1].

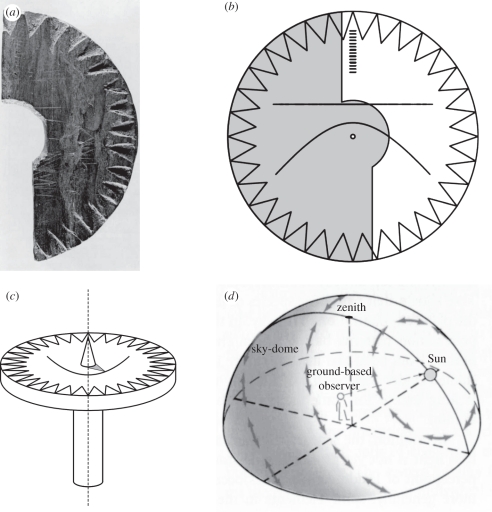
Figure 2.

(a) The wooden disc fragment (found in southern Greenland) onto which the Viking navigators scratched some hyperbolic curves [1]. (b) The reconstructed sundial used by the Vikings for navigation on the open sea. The left, grey part of the disc has not been found. (c) Three-dimensional drawing of the Viking sundial with a conical vertical gnomon and its shadow, the endpoint of which touches the hyperbola scratched into the horizontal wooden disc. (d) Sky-polarimetric navigation by Vikings can only function, if the direction of skylight polarization (symbolized by double-headed arrows) is perpendicular to the plane of scattering (determined by the Sun, the observer and the celestial point observed). This corresponds to Rayleigh's theory of first-order light scattering.

After carving the trajectories of the tip of the gnomon's shadow into the disc, the Vikings gained an instrument: the sundial. With it they could locate geographical north along latitude 61° N from May to August even on the high seas, provided the Sun was shining. All they needed to do was to hold the dial's disc horizontally into the Sun and rotate it around its vertical axis (coinciding with the axis of the gnomon) until the tip of the gnomon's shadow reached the corresponding carving on the dial. A notch on the disc then showed the geographical northern direction (figure 2b).

In a sailing competition across the Atlantic along latitude 61° N in recent years, the captains having a number of vessels were given replicas of the original Viking sundial and were asked to use these devices as compasses for a certain time during the competition. The result showed that it was possible to accurately navigate on the open ocean using only the Viking sundial, provided the Sun was shining [1]. This method of navigation is known as ‘solar Viking navigation’.

2. The hypothesis of sky-polarimetric navigation by vikings

As the Viking sundial can only be used when the Sun shines, the question arises as to how the Vikings could have navigated when the Sun was occluded by clouds or fog, a situation that can last for days along major parts of the North Atlantic sailing route of ancient Viking seafaring folk. At the end of the 1960s, the Danish archaeologist Ramskou [2] suggested that Vikings made use of polarized skylight when the Sun was behind clouds or fog:

• — First, the Viking navigator had to determine the direction of skylight polarization at two distinct points of the sky-dome by using a birefringent crystal (the sunstone) as a linear polarizer (figure 2d). Although it is not clear what the sunstone was made out of, it could have been cordierite or tourmaline, both common in Scandinavia. By rotating such a crystal to and fro and looking at the sky through it, the sky appears to brighten and fade periodically, because, with the exception of the polarizational neutral points [3], the skylight is partially linearly polarized. Looking through the birefringent crystal, the Viking navigator could calibrate the sunstone by adjusting it in such a way that a patch of the clear sky appears brightest. A line pointing to the true position of the Sun would then be scraped into the crystal. After such calibration, the direction of the Sun hidden by clouds can then be determined by looking at a clear patch of sky through the crystal and rotating the latter until the sky appears the brightest. The scratch on the sunstone shows the direction of the invisible Sun, if the direction of polarization of skylight corresponds to Rayleigh's theory of first-order light scattering, i.e. the direction of polarization of light from an arbitrary point of the clear sky is perpendicular to the plane of scattering determined by the observer, the Sun and the celestial point observed.

• — The Viking navigator could then estimate the intersection of the two great circles running through the two investigated celestial points parallel to the scratches on the crystals. If the pattern of the direction of polarization of skylight corresponded to Rayleigh's theory, then the point of intersection would give the position of the invisible Sun.

• — Finally, it would have been necessary to somehow imitate the rays of light from the invisible Sun to cast the imaginary shadow of the gnomon onto the dial. For example, an assistant could have held a burning torch so that the navigator would see it in the estimated direction of the invisible Sun. In this way, the Sun would be replaced by the torch, and the gnomon's shadow falling onto the dial. Another method could have involved a rotating thin tube (e.g. a piece of reed), attached to the tip of the gnomon. The navigator could have directed this tube into the estimated position of the invisible Sun, sliding a thin, straight stick (a straw, for example) into the tube; thus modelling the sunbeam through the gnomon's tip.

Ramskou [2] believed that by using this method, geographical north could be located even under cloudy or foggy conditions. Since this method is based on the pattern of the direction of skylight polarization, it is called ‘sky-polarimetric navigation by Vikings’. This theory of polarimetric Viking navigation is accepted and frequently cited, in spite of a total lack of experimental evidence. In one of the Viking sagas, the Sigurd legend, a reference to sky-polarimetric navigation by Vikings appears to have been made [2]: ‘The weather was very cloudy, it was snowing. Holy Olaf, the king sent out somebody to look around, but there was no clear point in the sky. Then he asked Sigurd, to tell him, where the Sun was. After Sigurd complied, he grabbed a sunstone, looked at the sky and saw from where the light came, from which he guessed the position of the invisible Sun. It turned out, that Sigurd was right’.

Further to this obscure Sigurd saga, there is another argument supporting sky-polarimetric navigation by Vikings: pilots of Scandinavian Airlines' DC-8 airplanes were using a polarimetric instrument to navigate with the help of the polarization of skylight when flying close to the North Pole. This instrument is Kollsman's sky compass, which was developed for the US Airforce in 1948 to navigate in twilight after sunset. The instrument was equipped with lenses, adjustment screws and scales and contained a linearly polarizing crystal. This sky compass was directed to the zenith, while the navigator was rotating the crystal around its vertical axis until the sky appeared brightest or darkest. The position of the Sun could then be estimated from the orientation of the crystal.

The third argument for sky-polarimetric navigation by Vikings is related with the discovery of Frisch [4], that honeybees (Apis mellifera) are sensitive to polarized light and use the direction of skylight polarization for navigation, when the Sun is hidden by clouds, but some clear regions of the sky are still visible. A similar capacity to detect polarization patterns and orient by means of sky polarization was later found in many other arthropod species [5].

The reason for the wide acceptance of the unproven hypothesis of sky-polarimetric navigation by Vikings is its elegance, appeal and lack of credible alternative. According to the widely accepted theory, the Vikings were able to navigate on the open sea with the help of sky polarization in all meteorological situations: under clear, partly cloudy, totally overcast and foggy skies. Since these claims were never tested, we decided to investigate whether the atmospheric optical prerequisites of sky-polarimetric navigation by Vikings are satisfied. Our aim was to measure the polarization pattern of clear, partly cloudy, totally overcast and foggy skies to determine which parts of the sky permit sky-polarimetric navigation by Vikings. In the following sections, we summarize the main results of our experimental studies [6–10].

3. Visual estimation of the sun position in cloudy and twilight skies

According to Roslund & Beckman [11], Vikings did not need to use sky-polarimetric navigation, because ‘Even when the Sun is hidden behind clouds, its location can often be found quite accurately for most navigational needs from the pattern of the Sun's illumination of clouds, from the bright lining of cloud tops and the crepuscular rays emanating from the Sun. On overcast days, careful observations of the sky may reveal the faint disk of the Sun if the cloud cover is not too dense. […] Nor does polarimetry give clues to the Sun's position when it is below the horizon that other methods do not. The arcs of dawn and twilight appear distinct enough for the naked eye to make out in which direction the Sun is’ [11, p. 4754].

However, the theory of sky-polarimetric navigation by Vikings cannot be dismissed by such qualitative counter-arguments. If the hypothesis that the position of the Sun behind clouds or under the horizon can quite accurately be estimated by the naked eye is correct, then the Vikings would not have to use the sky-polarimetric navigation method to locate the position of the invisible Sun.

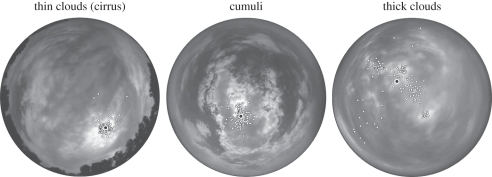
Barta et al. [6] investigated quantitatively if Roslund & Beckman [11] were right with their claim. We took photographs of several cloudy skies on the seashores of the island of Hailuoto and the city of Oulu in northern Finland through a 180° field-of-view fisheye lens. Thus, we could map the whole sky into a circular colour picture, in which the centre of the circle corresponded to the zenith and the perimeter to the horizon (figure 3). We took a second series of photographs of twilight skies, when the Sun was close to but below the sea horizon (figure 4).

Figure 3.

Three full-sky photographs (taken in Oulu, 65°0′ N, 25°26′ E) from 25 pictures of cloudy skies presented 12 times on a monitor to 18 test persons in the first psychophysical laboratory experiment. The task of the test persons was to guess the position of the Sun, hidden by clouds, with the naked eye. The centre and the perimeter of the circular pictures are the zenith and the horizon, respectively. The Sun positions estimated by the test persons are shown by tiny white dots with black perimeter, while the large black dots with white perimeter represent the average of these guessed solar positions.

Figure 4.

Three 180° field-of-view photographs (taken in Oulu, 65°0′ N, 25°26′ E) from the 15 pictures of twilight skies presented six times on a monitor to 18 test persons in the second psychophysical laboratory experiment. The task of the test persons was to guess the azimuth direction of the Sun below the sea horizon with the naked eye. The centre of the circular pictures points to the horizon, while the zenith and the nadir are the uppermost and lowermost points of the circle. The upper/lower halves of the pictures depict the sky/sea. The solar azimuth directions estimated by the test persons are shown by short vertical bars below the horizon. The long vertical bar above the horizon represents the average of these guessed azimuth directions, while their standard deviation is shown by the short vertical bars at the ends of the horizontal bar.

In our first psychophysical laboratory experiment, using a colour monitor, we showed 25 different cloudy sky photographs (figure 3) 12 times to 18 test persons in a dark room. In these photographs, the Sun was occluded by clouds, and the test persons' task was to visually estimate the position of the invisible Sun by using the computer's mouse. Our computer program stored the estimated Sun positions (ψ: zenith angle, φ: azimuth angle from an arbitrary reference azimuth direction) and calculated their averages (<ψ> and <φ>) and standard deviations (σ_‖, σ_⊥ and σ_φ) (table 1). In our second psychophysical laboratory experiment, we showed 15 different twilight sky photographs (figure 4) six times in a dark room on a colour monitor to 18 test persons. In these photographs, the Sun was under the sea horizon, and the test persons' task was to visually estimate the azimuth direction of the invisible Sun by using the mouse. As before, our computer program stored the estimated Sun azimuth directions (φ: azimuth angle from an arbitrary reference azimuth direction) and calculated their averages (<φ>) and standard deviations (σ_φ). The test persons were gents from Bremen, Budapest and Roskilde, aged between 23 and 45 years. Details of these experiments can be found in Barta et al. [6].

Table 1.

Definitions of the parameters used in this paper.

symbol of parameter	meaning
p	degree (%) of linear polarization of skylight
α	angle of polarization of skylight measured from the local meridian
ψ	zenith angle (angular distance from the zenith)
φ	azimuth angle from an arbitrary reference azimuth direction
<x>	mean of parameter x
≪x≫	average of the mean of parameter x
σ‖,σ⊥	standard deviations (along two orthogonal great circles crossing each other at the average Sun position) of the positions of the invisible Sun behind clouds located with the naked eye
σφ	standard deviation of the azimuth angle φ of the Sun
δmax	maximum angular distance between the estimated Sun positions
γmax	maximum angular distance between the estimated solar azimuth directions
max(δmax), max(γmax)	maximum values of δmax and γmax
θS	elevation angle of the Sun above the horizon
Δα = |αmeasured − αRayleigh|	difference between the measured (αmeasured) and the theoretical (αRayleigh) angles of polarization of skylight
NRayleigh	number of celestial points for which Δα < αthreshold = 5°
Nnon-Rayleigh	number of celestial points for which Δα > αthreshold = 5°
Noverexposed	number of celestial points for which the detector was overexposed
r = NRayleigh/N	proportion of the N examined points of the sky for which the direction of polarization differs from that of Rayleigh's theory by less than αthreshold = 5°
n = Nnon-Rayleigh/N	proportion of the N examined points of the sky for which the direction of polarization differs from that of Rayleigh's theory by more than αthreshold = 5°
o = Noverexposed/N	proportion of the overexposed celestial points
rred, rgreen, rblue	values of r in the red, green and blue parts of the spectrum
ɛ	the noisiness n of the celestial α-pattern
s	similarity of the celestial α-pattern to the theoretical (Rayleigh) α-pattern
d	dissimilarity of the celestial α-pattern in comparison with Rayleigh's theory

The standard deviations of the estimated solar positions in cloudy skies were between = 1.1° and 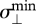= 1.4° (the Sun was almost visible through thin cirrus clouds) and 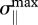= 20.2° and σ_⊥^max = 25.2° (the Sun was hidden by a large, thick cloud) depending on the degree of cloud cover. The maximum angular distance δ_max between the estimated Sun positions varied between 8.1° and 162.9° (electronic supplementary material, table S1). The averages of the standard deviations σ_‖, σ_⊥ and σ_φ and of the maximum angular distances δ_max for the 25 pictures were <σ_‖> =7.4°, <σ_⊥> = 11.9°, <σ_φ> =22.3° and <δ_max> =70.7°. Barta et al. [6] has also obtained data on locating the Sun when it was visible behind thin cirrus clouds (sky 2 in fig. 1 and table 1 of [6]). According to these data, the average inherent errors of the people tested in this psychophysical experiment were the following: σ_‖ = 1.1°, σ_⊥ = 1.4°, δ_max = 8.1° and σ_φ = 2.1°.

Depending on the solar elevation under the horizon and the degree of cloudiness, the standard deviations of the estimated Sun positions in the twilight pictures were between 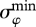= 0.6° (the Sun was still visible on the horizon) and 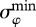= 2°, while the maximum angular distance between the estimated Sun azimuth directions γ_max varied between 2.1° (the Sun was above the horizon) and 99° (the Sun was below the horizon). The averages of σ_φ and γ_max for the 15 twilight pictures were <σ_φ> =11.4° and <γ_max> =37.3°. The averages of <σ_φ> and <γ_max> for the 18 test persons were ≪σ_φ≫ = 5.9° and ≪γ_max≫ = 14.5°. Data for locating the Sun when it was visible just on the horizon are also available (twilight sky 10 in fig. 2 and table 3 of [6]). The average inherent errors that people tested in this experiment made were: σ_φ = 0.6° and γ_max = 2.1°.

The averages of the standard deviations σ_‖, σ_⊥ and σ_φ and maximal angular distances δ_max and γ_max of the cloudy and twilight skies characterizing the accuracy of the visual estimation of the Sun position for all cloudy pictures (<σ_‖> = 7°, <σ_⊥> =12°, <σ_φ> = 22° and <δ_max> = 71°), for all twilight pictures (<σ_φ> = 11° and <γ_max> = 37°), and for all test persons (cloudy skies: ≪σ_‖≫ = 3°, ≪σ_⊥≫ = 8° and ≪δ_max≫ = 25°; twilight skies: ≪σ_φ≫ = 6° and ≪γ_max≫ = 15°) were quite high. The measured maximum values were 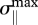= 20°, 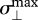= 25°, 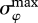= 80°, max(δ_max) = 163° for the cloudy skies, and 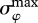= 42°, max(γ_max) = 99° for the twilight skies. These obviously high errors do not support the assumption that under cloudy or twilight skies the position of the invisible Sun can be estimated quite accurately by using the colour and intensity patterns of the sky.

Although these results underestimate the accuracy of the visual estimation of the Sun position by an experienced Viking navigator, the investigated counter-argument (that the position of the invisible Sun in cloudy skies could be estimated quite accurately, even by the naked eye, so that Viking navigators did not need polarizing crystals to determine the position of the Sun hidden) cannot be taken seriously as a valid criticism of the theory of sky-polarimetric navigation by Vikings. Our results disclaim only one counter-argument of the polarimetric Viking navigation and imply that Viking navigators might have needed some aid to navigate on open seas during cloudy or foggy weather conditions. Such an aid could, for example, have been the sky-polarimetric navigation method.

4. Proportion of clear and partly cloudy skies that can be used for sky-polarimetric navigation by vikings

The two atmospheric optical prerequisites of sky-polarimetric navigation by Vikings are the following:

• — The plane of the oscillation of skylight is perpendicular to the plane of scattering, i.e. the direction of polarization of skylight is the same as that predicted by Rayleigh's theory. The accuracy of sky-polarimetric navigation by Vikings is determined by that part of the sky, where the direction of polarization obeys first-order Rayleigh scattering.

• — The degree of linear polarization p of skylight is so high that the periodic brightening and darkening of the sky seen through a rotating sunstone (functioning as a polarizer) can be observed, and thus the direction of skylight polarization can be determined with sufficient accuracy.

The fulfilment of these conditions could not be examined earlier owing to the lack of wide field-of-view imaging polarimeters. We began to study this topic during an expedition to the Tunisian desert in 1999, when we investigated how similar polarization patterns of partly cloudy skies were to those of clear skies as a function of solar elevation angle θ_S above the horizon. This was important to understand the navigation of the desert ants, Cataglyphis bicolor based on the polarization of skylight [9]. Although earlier there had been several attempts to determine whether skylight polarization obeyed Rayleigh's theory, these studies were limited to a few directions of the sky owing to the usage of point-source polarimeters.

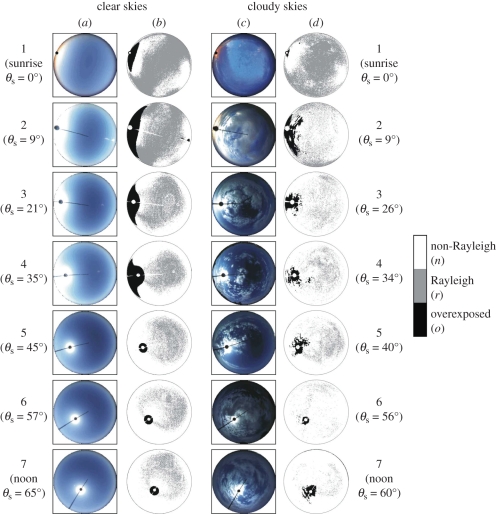
We computed the difference Δα = |α_measured − α_Rayleigh| between the measured and theoretical (Rayleigh) angles of polarization α_measured and α_Rayleigh of skylight for every celestial point by using the celestial pattern of the direction of polarization measured by 180° field-of-view imaging polarimetry at a given solar position and for a given spectral range (red, green and blue). Then we counted the number N_Rayleigh of celestial points for which Δα < α_threshold = 5°. From this we determined the ratio r = N_Rayleigh/N of the N = 150 000 examined points of the sky for which the direction of polarization differed from that of Rayleigh's theory by less than 5°. We also determined the number N_non-Rayleigh of points in the sky for which Δα > α_threshold = 5°. There were N_overexposed points in the sky near the Sun for which the detector was overexposed (here the polarization of skylight was unknown). We also calculated the n = N_non-Rayleigh/N and o = N_overexposed/N ratios. The relation among variables r, n and o are: r + n + o = 1. These calculations were performed for clear and partly cloudy skies measured in Tunisia as a function of the solar elevation θ_S (figure 5). The clouds in the pictures of cloudy skies were detected by a custom algorithm, thus we could also determine which parts of the sky followed Rayleigh's theory with an accuracy of α_threshold = 5° for both the clear and cloudy celestial regions. From our results [9,10] we concluded the following (e.g. figure 5 and electronic supplementary material, tables S2 and S3):

• — At a given solar elevation angle (θ_S) and in a given spectral range (central wavelength λ), the proportion r of the sky that is usable for sky-polarimetric navigation by Vikings is always higher for a clear sky than for a partly cloudy sky. Depending on θ_S and λ, for clear skies r varies between 13 and 70 per cent, while for partly cloudy skies r is between 4 and 69 per cent. If the Sun is near or on the horizon, then the r-values of partly cloudy skies are close to those of the clear skies.

• — The lower the solar elevation θ_S, the higher the ratio r of the sky that is appropriate for sky-polarimetric navigation by Vikings in connection with clear and partly cloudy skies, independent of the wavelength. For clear skies in the red spectral range (where the proportion o of the overexposed regions is smallest, i.e. where the accuracy of the measured r-values is highest) r increases from 19 to 65 per cent, while θ_S decreases from 65° (noon) to 0° (sunset/sunrise). For partly cloudy skies in the red spectral range r increases from 4 per cent to 56–65% while θ_S decreases from the highest solar elevation to zero.

• — In the case of high solar elevations for clear and partly cloudy skies r is highest in the blue and lowest in the red spectral range. For lower solar elevations r_green > r_red, but r_blue < r_green.

• — Sometimes in the cloudy regions of the sky relatively large areas (12–34%) of the celestial α-pattern follow Rayleigh's theory, and these areas increase with the decrease of solar elevation θ_S, independent of the wavelength.

Figure 5.

(a,c) 180° field-of-view colour photographs of Tunisian clear and partly cloudy skies as a function of the solar elevation angle θ_S from the horizon. The centre/perimeter of the circular pictures is the zenith/horizon, and the zenith angle ψ is proportional to the radius from the centre (ψ_zenith = 0°, ψ_horizon = 90°). (b,d) Maps of the proportion r of the sky that follows the pattern of the angle of polarization α_Rayleigh predicted by Rayleigh's theory of first-order scattering for clear skies in the red (650 nm), spectral range versus solar elevation angle θ_S. ‘Rayleigh’ points with Δα = |α_measured − α_Rayleigh| ≤ 5° are shaded in grey, ‘non-Rayleigh’ points with Δα > 5° are white, and overexposed points are black. Hence, the grey/white celestial regions are appropriate/inappropriate for sky-polarimetric navigation by Vikings, while nothing is known about the black areas. The radial bar in the circular pictures is the wire of the Sun occulter. The approximately hourly positions of the Sun are represented by dots or the disc of the Sun occulter. The numerical values of r, n and o in rows 1–7 of tables S2 and S3 in the electronic supplementary material were determined for these clear and partly cloudy skies.

If the α-pattern of the overexposed sky regions near the Sun were known, these regions would increase the ratio n of the sky inappropriate for sky-polarimetric navigation by Vikings, because these regions overlap with the surroundings of the neutral points [3], possessing a polarization pattern quite different from the Rayleigh pattern. That is why the r-values in the electronic supplementary material, tables S2 and S3 are only slightly different from the reality, in spite of the relatively high o-values.

Multiple scattering of the light in clouds can cause the direction of polarization of cloudlight to be different from that of skylight described by Rayleigh's theory based on first-order scattering. However, if clouds and the air layer beneath them are lit by direct sunlight, then it is highly probable that cloudlight (originating either directly from the cloud, or from the air column beneath it) reaches a ground-based observer after its first scattering by cloud particles or by the air column below the cloud. The lower the solar elevation θ_S, the greater the chance that the clouds and the air beneath them are lit by direct sunlight; thus, the lower θ_S, the higher the proportion r_cloudy of cloudy skies usable for sky-polarimetric navigation by Vikings. The value of r_cloudy can even reach the r-values of clear skies, if the Sun is on the horizon.

We conclude that for clear skies, the ratio r of the sky that follows Rayleigh's theory with an accuracy of α_threshold = 5° is high, depending on θ_S. This is particularly true for lower solar elevations (θ_S ≤ 13°), when 40% < r < 70%. Depending on the cloudiness and how the clouds are lit by sunlight, r decreases under cloudy conditions, but r can be surprisingly high, particularly for lower solar elevations (e.g. r_max = 69% for θ_S = 0°). Usually, large parts of the α-patterns of clear and partly cloudy skies quite accurately follow Rayleigh's theory, which is the base of the Viking's sky-polarimetric navigation.

5. The possibility of sky-polarimetric navigation by vikings in fog

Vikings sailing the North Atlantic (figure 1), must often have encountered poor visibility with fog so dense that even the Sun's disc would have been invisible to them, particularly with the Sun near the horizon. Could the Vikings have navigated by sky polarization under foggy weather conditions? Aboard the Swedish icebreaker ‘Oden’, Susanne Åkesson & Gábor Horváth crossed the Arctic Ocean as members of the Beringia 2005 six-week international expedition, organized by the Swedish Polar Research Secretariat in August and September 2005. They reached the North Pole on 12 September 2005. During this expedition they measured the polarization patterns of foggy or totally overcast Arctic skies, when the Sun's disc was not discernible [7] (figure 6 and electronic supplementary material, table S4).

Figure 6.

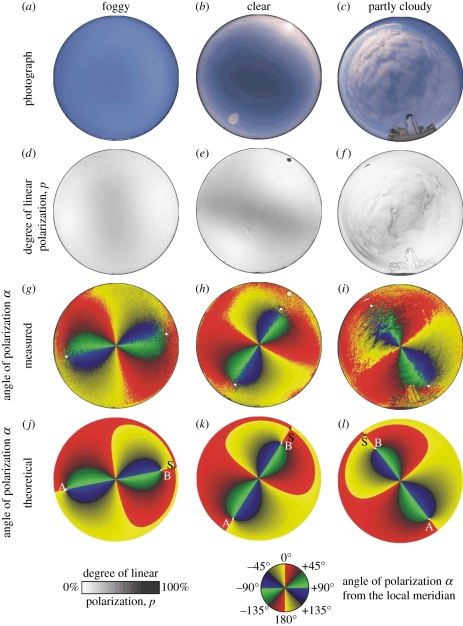
(a–c) 180° field-of-view photographs and (d–i) polarization patterns of Arctic foggy, clear and partly cloudy skies measured by full-sky imaging polarimetry in the blue (450 nm) part of the spectrum. (j–l) Patterns of the angle of polarization α (from the local meridian) calculated for the solar positions in patterns (a–i) on the basis of the Berry model, which can describe the polarization of the clear sky more accurately than the Rayleigh model [7]. In the α-patterns, white dots show the positions of the Sun (S), the Arago (A) and Babinet (B) neutral points.

In certain Arctic meteorological situations, the fog layer was lit by direct sunlight, because the Sun above the horizon was not occluded by clouds, but the Sun was invisible owing to the dense, sunlit fog. The averages of the degree of linear polarization p and the noisiness ɛ of the α-pattern of cloudy skies (p_cloudy = 10–25% and ɛ_cloudy = 4–15%) were between those of the clear (p_clear = 16–34% and ɛ_clear = 3–6%) and foggy (p_foggy = 4–15% and ɛ_foggy = 5–45%) skies. For the similarity s of the α-patterns of clear, partly cloudy and foggy skies to the theoretical α-patterns, we obtained s_clear = 65.8–70.7%, s_cloudy = 49.0–61.8% and s_foggy = 41.4–50.0%, while their minima and maxima were 45% ≤ s_clear ≤ 81%, 36% ≤ s_cloudy ≤ 72% and 19% ≤ s_foggy ≤ 71%, respectively. Thus, we see that if the fog layer is not too thick, then the α-pattern of the sunlit sky is very similar to the theoretical α-pattern. On the other hand, the relationships between the averages are the following: p_foggy < p_cloudy < p_clear, ɛ_clear < ɛ_cloudy < ɛ_foggy, s_foggy < s_cloudy < s_clear.

Our data from the Arctic and from Hungary ([7]; figure 6 and electronic supplementary material, table S4) allow us to conclude that if the fog is lit by direct sunlight, then the α-pattern of the foggy sky is quite similar to that of the clear sky. As a consequence, the first condition of the sky-polarimetric navigation by Vikings is met for foggy conditions nearly as well as for clear skies. On the other hand, the degrees of linear polarization p of foggy skies are often so low, that the second condition of polarimetric Viking navigation is usually not satisfied. Thus, the limiting factor of the sky-polarimetric navigation method is the degree of polarization, rather than the direction of polarization. Under partly cloudy conditions, both conditions of the Viking's sky-polarimetric navigation are generally satisfied.

6. Sky-polarimetric navigation by vikings under conditions of total overcast?

Vikings undoubtedly often had to sail under totally overcast conditions, perhaps for days on end and in the open water far away from land. For this reason, we also measured the polarization characteristics of light under totally overcast skies in the Arctic region and in Hungary [8] (figure 7 and electronic supplementary material, table S5), when the ground was covered by high-albedo snow and ice, and it was sometimes snowing or raining, allowing us to draw some conclusions about the composition of the clouds (ice or water). To our great surprise, the patterns of the direction of polarization under totally overcast skies were very similar to those of the clear skies (figures 5 and 7). We conclude that the first prerequisite of sky-polarimetric navigation by Vikings is met, even in totally overcast conditions, for (although very noisy: electronic supplementary material, table S5) large parts of the pattern of the direction of polarization of overcast skies exhibit the Rayleigh pattern. However, the degrees of linear polarization p of overcast skies are so low (electronic supplementary material, table S5) that it is very unlikely that Viking navigators were able to use the sky's polarization in totally overcast conditions, for if p is low, it is useless rotating the polarizing sunstone in front of the observer's eye. The periodic oscillation of the intensity of light from the totally overcast sky is undetectable or at best hardly visible. As a result, the direction of skylight polarization could be determined only very inaccurately.

Figure 7.

180° field-of-view photographs and patterns of the angle of polarization α (clockwise from the local meridian) of totally overcast skies measured by full-sky imaging polarimetry in the blue (450 nm) part of the spectrum on the Arctic Ocean (S1–S8) and in Hungary (S9–S15). The ground was covered by high-albedo white snow and ice, both in the Arctic and Hungary.

7. Further research

Our investigations [6–10] determined the meteorological situations under which the atmospheric optical prerequisites for sky-polarimetric navigation by Vikings are or are not satisfied. What remains to be measured in psychophysical laboratory experiments with a large number of probands are the:

• — error in determinations of the oscillation direction of partially linearly polarized light with different sunstones (e.g. birefringent cordierite, tourmalin or calcite crystals), functioning as linear polarizers, as a function of the degree of linear polarization (first step of the sky-polarimetric navigation by Vikings);

• — error of determining the position of the Sun hidden by clouds/fog with estimating the intersection of the two great circles passing through two arbitrary celestial points parallel to the local plane of oscillation of skylight (second step of the polarimetric Viking navigation);

• — error of determining the geographical northern direction with a Viking sundial, if the position of the Sun occluded by clouds/fog is known (third step of the sky-polarimetric navigation by Vikings).

Once these psychophysical experiments have provided us with data on the above-mentioned error functions, computer modelling should allow us to estimate the likelihood that in the chosen meteorological situation the geographical north could be determined with a certain amount of deviation by using the polarimetric Viking method. Finally, we ought to be able to answer the question in which meteorological situations the Vikings could have satisfactorily navigated by means of sky polarization.

Since the psychophysical experiments, outlined above, cannot be performed with Viking navigators, we plan to measure the error functions by using male German, Hungarian and Swedish students. These measurements are in progress.