Spatial and temporal signatures of fragility and threshold proximity in modelled semi-arid vegetation

Abstract

Understanding the behaviour of complex environmental systems, particularly as critical thresholds are approached, is vitally important in many contexts. Among these are the moisture-limited vegetation systems in semi-arid (SA) regions of the World, which support approximately 36 per cent of the human population, maintain considerable biodiversity and which are susceptible to rapid stress-induced collapse. Change in spatially self-organized vegetation patterning has previously been proposed as a means of identifying approaching thresholds in these systems. In this paper, a newly developed cellular automata model is used to explore spatial patterning and also the temporal dynamics of SA vegetation cover. Results show, for the first time, to my knowledge, in a cellular automata model, that ‘critical slowdown’ (a pronounced reduction in post-perturbation recovery rates) provides clear signals of system fragility as major thresholds are approached. A consequence of slowing recovery rates is the appearance of quasi-stable population states and increased potential for perturbation-induced multi-staged population collapse. The model also predicts a non-patterned cover where environmental stress levels are high, or where more moderate stress levels are accompanied by frequent perturbations. In the context of changing climatic and environmental pressures, these results provide observable indicators of fragility and threshold proximity in SA vegetation systems that have direct relevance to management policies.

1. Introduction

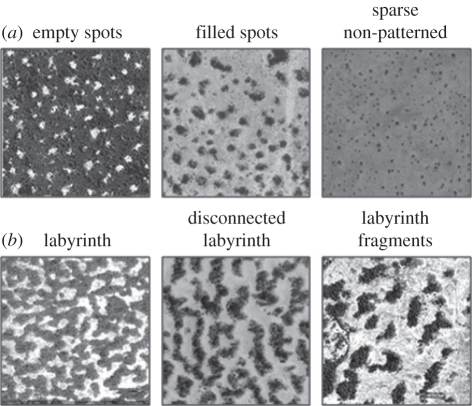
The loss of natural surface vegetation in semi-arid (SA) regions leads to a broad range of detrimental effects including enhanced sediment mobility and depletion of agricultural potential, deleterious hydrological and climatic effects on many scales, and reduction in global carbon sequestration [1]. SA regions are also important in supporting approximately 36 per cent of the World's human population and a highly diverse flora and fauna [1,2]. There is a pressing need to gauge the health status of vegetated SA landscapes and the likelihood of accelerated future die-off as relevant thresholds are crossed [2]. A potentially promising approach focuses on identifying modifications of the self-organized spatial patterning of SA vegetation in response to changes in environmental stress [3,4]. Many published reports document a variety of patterns in SA vegetation from locations in Africa, Australia, Middle East, North and South America [5]; examples are shown in figure 1. Empirical and theoretical data (e.g. [4,6–10]) suggest a short-range facilitative effect (on the scale of metres) encourages the growth/establishment of plants and is most likely a consequence of improved moisture availability owing to shading, reduced evaporation rates and increased water infiltration rates [3,10]. Conversely, competition for soil moisture occurs at larger radial distances, owing to networks of relatively shallow root systems and increased run-off rates potentially owing to surface crust formation [3,4,7,10,11]. This system is analogous to the activation-inhibition systems first described by Turing [12], where patterns emerge spontaneously as symmetry-breaking instabilities. Successful theoretical models have reproduced the characteristic self-organizing patterns (e.g. ‘spots’ and ‘labyrinths’) of natural SA vegetation by tuning the scale and strength of the competition and facilitation effects (e.g. [3,8]). Relevant features such as hysteresis and bistability over restricted parameter ranges have also been previously reported (e.g. [13]). A comprehensive review of efforts to model pattern formation is given by Borgogno et al. [5]. The possibility of using such patterns to assess levels of environmental stress, the state of health of vegetation systems and also to forewarn of imminent (threshold-related) transitions is a tantalizing practical application of such work [3]. Indeed, progress has been made in assessing threshold proximity through the analysis of spatial distribution properties in SA vegetation data [4] and in a range of model data, for lake eutrophication [14] and a more general spatial population dynamics model [15].

Figure 1.

Greyscale images of semi-arid (SA) vegetation in Chad, Mali and Republic of Niger, captured from GoogleEarth (v. 5.1). Dark shades are inferred vegetation and white/lighter shades are inferred bare sediment. In each image, North is vertical and each image covers approximately 300 × 300 m. From left to right, the image locations are (a) 13°11′29″ N, 1°15′09.07′ E (Republic of Niger); 11°52′09.52″ N, 15°59′42.7′ E (Chad); 16°02′11.89″ N, 0°48′51.95″ W (Mali); (b) 12°44′02.28″ N, 3°05′40.47′ E (Republic of Niger); 13°06′08.29″ N, 2°13′19.12″ E (Republic of Niger); 13°11′51.96″ N, 2°00′14.80″ E (Republic of Niger).

Limitations of pattern-based approaches in the present context are that much SA vegetation does not display strong patterning and also that pattern re-adjustment to changes in prevailing conditions may take a significant time. Additional indicators are therefore likely to be useful in making more general progress towards threshold prediction. The proximity of transitions is notoriously difficult to assess, both in modelled and in real natural systems [16,17]. Recent advances [16,18,19] have shown critical slowdown (CSD: an increase in the relaxation time of a system following a small perturbation) and/or increased signal variance, to be capable of identifying the approach of catastrophic thresholds in some systems (although the cautionary findings of Hastings & Wysham [20] show that this cannot be universally expected). Predicting when a given system will undergo rapid collapse can only be attempted when reliable forecasts of future forcing are available. In the absence of such forecasts, a pragmatic approach is to identify system states with enhanced susceptibility to collapse under the likely spectrum of future perturbations. Prior to this study it was unclear whether SA vegetation systems were expected to display CSD, and the associated effects, and more generally, how any such temporal dynamics may relate to the appearance of self-organizing spatial patterns.

The results described here are from a new cellular automata model, where cells relate to positions on an idealized surface that can accommodate individual plants. The model is used to investigate the interplay of spatial patterning and the temporal dynamics of population density under a range of different forcing conditions, with a focus on practical solutions to assessing system fragility.

2. Brief model description

Simulations were conducted using a probabilistic cellular automata model, with a square (two-dimensional) grid defining the modelled space, regularly tiled by square cells, with periodic boundaries. The approach taken is similar in essence to that of Thiery et al. [8], in that a defined neighbourhood is used to calculate local plant-interaction effects, although several new features are introduced (such as age-dependent interactions). The model was implemented in Matlab (v. 7.7.0, R2008b), using code written by the author and experiments were run on a grid of 250 × 250 cells (unless otherwise stated). Unoccupied cells are recorded as 0, occupied as 1 and time progresses discretely (each step being referred to as a model year). For the initial condition, the model grid is populated randomly with a density of P₀ (0–1) live cells with random ages between 1 and 50. The probability of survival for any given cell is governed by three factors: (i) response of the live cell to global ‘environmental stress’; (ii) the cell age; and (iii) the effects of local interaction from cells within a neighbourhood defined by five concentric shells. Within this neighbourhood, nearby occupied cells (in shells 1 and 2) provide a net facilitating effect, shell 3 is neutral and more distant occupied cells (in shells 4 and 5) exert net competition. The strength of (and sensitivity to) these neighbourhood influences is dependent on both the age of the cell in question and of the cells in its neighbourhood. Cells arbitrarily reach maturity at 25 years and the probability of survival decreases as age increases thereafter, such that survival beyond 60 years is highly improbable, even under favourable environmental conditions. The global ‘environmental stress’ parameter, α (which is common to all cells), is a lumped parameter that combines all relevant sources of abiotic environmental stress (e.g. moisture and nutrient availability). The term α denotes the external forcing factor for this model and as it is decreased, the probability of cell death increases and the population density on the grid naturally reduces (and vice versa). A full description of the model (including a description of α, justification for the various age dependencies and details on model initialization) is given in the electronic supplementary material.

3. Stable solutions

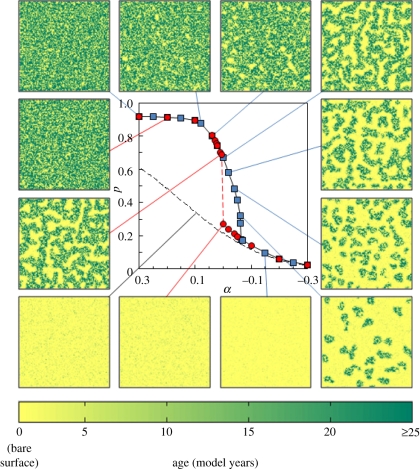
Under constant forcing conditions (α = constant), the model settles down over time from the initial condition to a stable solution, where no systematic trends or periodic oscillations are observed in the grid population density (p). For α > 0.2, the sensitivity to α is relatively low and the spatial coverage is dense (p > 0.9) and homogeneous. As α is decreased through the range 0.2 ≤ α ≤ −0.5 (with P₀ = 1), lower equilibrium populations are observed, in association with the spontaneous emergence of spatial patterning (figure 2): first, empty spots appear; these expand to bare patches and as α is reduced further, bare patches connect, forming distinctive labyrinth-type patterns; as α is further reduced, the labyrinth pattern fragments into isolated patches, then to isolated spots. A similar pattern progression towards isolated spots has been observed in other spatial models (e.g. [3,13]), with bare surface reached after the spotted pattern. A significant difference in the present model is that isolated spots are followed by a homogeneous and non-patterned state as stress is increased, with eventual full extinction (bare surface) reached when α < −0.5. Occupied cells shown in figure 2 are coloured darker with age, which has the advantage of not visually over-exaggerating the contribution of very young live cells (i.e. relatively small individual plants). Under ‘stable’ conditions, minor fluctuations (owing to the probabilistic nature of the model) promote a continuous slow adjustment of spatial patterning, but the pattern type is preserved, in the same sense that the population fluctuates around the mean value. Qualitatively, there is a good degree of correspondence between these stable solution results and the observed patterns shown in figure 1. However, the stable solutions are not unique over the full range of α and bistability is observed over a narrow α range (α₁ ≤ α≤ α₂, with α₁ = 0 and α₂ = −0.065), referred to as the ‘bistable region’ hereafter. Within the bistable region, it is the initial population that determines which solution is reached for any given α, and in figure 2 stable solutions with p₀ = 1 are shown as filled blue squares and those with p₀ = 0 are shown as filled red circles. Distinct spatial patterning occurs only in the upper limb and this is discussed further in §6.

Figure 2.

The central figure shows stable population density (p_eq) at different environmental stress levels (α), for two initial conditions: full cover (p₀ = 1, blue squares) and unoccupied (p₀ = 0, red squares). The dashed red line shows the transition to the upper stable state. The dashed black line shows stable p for the case where all neighbourhood scores are neglected (effectively the survival curve for lone cells). Examples of stable patterns are shown (100 × 100 cells in each case), representative of the progression of increasingly degraded patterns as α is reduced, plotted as yellow for bare ground, with darker shades representing older cells, to the level of full maturity at 25 years (see main text and electronic supplementary material for further details of age dependence).

The transition to bistability is an important aspect of system behaviour because of the associated potential for population collapse to a lower density state. Assessing the proximity of an approaching bifurcation point has clear practical relevance and is the focus of the following section.

4. Early warning indicators of bifurcation point

(a). Spatial patterning

As α is reduced towards the bifurcation point (α₁), there is a smooth transition in patterning, from open spots, which elongate to form the connected labyrinth pattern (figure 2). Once labyrinth patterns are established, critical transitions are possible within this model. This progression in patterns offers some possibility of gauging the proximity of the system to a bifurcation point, when it is relatively close. However, under conditions of fluctuating stress (i.e. temporal variability in α), re-adjustment of patterns over short time scales (discussed in §7) means interpretations based on single snapshots may be unreliable, and that pattern assessment over several years may be necessary to adequately gauge the system state.

(b). Critical slowdown

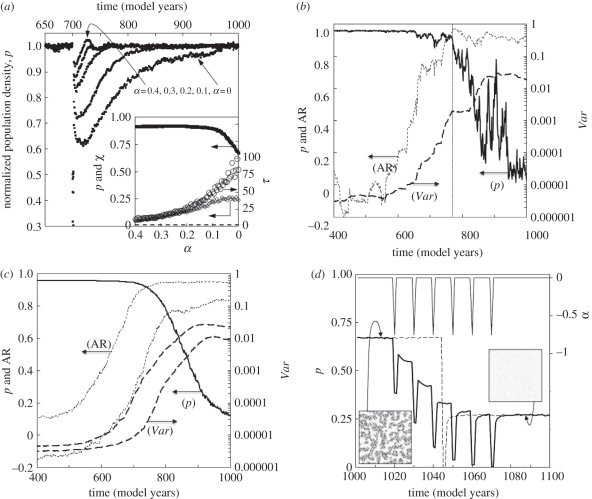
Observations of several other types of systems indicate that CSD has the potential for providing indication of threshold proximity (e.g. [19]; see §1). To the author's knowledge, the effects of CSD have not been previously investigated in SA vegetation data (observed or modelled), or in spatially defined cellular automata models. A key experiment therefore tested whether the current model undergoes CSD as the system is driven to the bifurcation point. Figure 3a shows example p time-series data where the model, run to equilibrium at constant α (0 ≤ α ≤ 0.4) was perturbed in year 700 by high stress (α = −1), causing immediate population reduction. From year 701 onwards, α is returned to the initial value and the population recovers back to the equilibrium level seen prior to the perturbation, p_eq (here, average p from years 680–699). The precise form of the recovery depends on the magnitude of the perturbation. The recovery time (τ) is defined as the period taken for p to reach 0.5p_eq and τ increases considerably as the bifurcation point is approached (inset to figure 3a). In principle therefore, CSD (as defined by the increase in τ) potentially provides a clear leading indicator of stress-induced population collapse. Further, CSD is apparent prior to the first appearance of persistent patterning (open patches) in vegetation cover at α ≅ 0.2.

Figure 3.

(a) Post-perturbation recovery. The model was run to equilibrium at α-values in the range 0 ≤ α ≤ 0.4; α remained constant throughout each experiment except for 1 year (year 700), where α was reduced to −1. Example p time-series data are shown, normalized to unity using mean p (years 680–699). The inset shows the dependence on α of pre-perturbation equilibrium population (p_eq), perturbation sensitivity (χ) and half-recovery time (τ) for the present model (open symbols) and the separate case where neighbourhood effects are neglected (dashed line) (discussed in main text). (b) An example p time series (1 of 100 similar runs) driven by α with a red noise distribution (and decreasing mean; see main text). The vertical line marks the threshold point, identified by eye. First-order autoregression coefficients (AR) and variance (Var) are also shown. Calculation of AR and Var requires stationary data and each p dataset was de-trended by subtracting a robust local regression, based on weighted linear least squares and a first-degree polynomial model, with a span of 75 years (using the rlowess Matlab function). A 100-year window was moved through the residual data, within which AR and Var were calculated (following Dakos et al. [19]) using the Yule–Walker method (the aryule Matlab function). (c) The 10th and 90th percentiles of the 100 Var and AR datasets described in (b), and the median p response. (d) The model was run with α = 0, reaching equilibrium at p = 0.67 in the first 1000 years (not shown). Repeated decadal-spaced perturbations of α = −0.75 (lasting 1 year) were administered between years 1010 and 1060. The α and p time series are shown by the solid lines. In a similar experiment, a single larger perturbation (α = −2) was administered at year 1045. The p response is shown by the dashed line. Plots of grids (100 × 100 cells) show the associated spatial patterning.

The idealized conditions of these experiments (figure 3a), where stable population densities are perturbed by single, short, relatively minor shocks, do not reflect the highly variable real-world stressors (e.g. rainfall variability) in SA systems. Under temporally variable (noisy) stress conditions, the effects of CSD are less visible in time-series data, but may, in principle, be identifiable through increases in both signal variance and in the first-order autoregression coefficient (here AR) in moving-window data [19]. The soil moisture store (a major source of stress in SA regions) serves to integrate the white noise of rainfall variability, resulting in a time series with red noise spectral properties [21,22]. Therefore, to simulate temporal variability in forcing, α-values were generated with red spectral properties using equation (4.1) (taken from [16]):

4.1

where α_t is the α-value at year t, k is the approximate period of the noise (years) (k = 5), is mean α (time-averaged), ω_α controls the levels of annual variability in α_t and ɛ is a random value drawn (each year) from a standard normal distribution (mean = 0, variance = 1). As an example, Hunt [23] reports the relative standard deviation of annual Sahel rainfall to be approximately 13 per cent. The integrating effect of soil hydrology reduces this variability [21,22] and ω_α = 0.1 was chosen for the present simulations, yielding σ_α ≈ 17%. This approach most likely provides adequate variability to assess the effects of CSD.

Figure 3b shows a typical time series of p, where was decreased linearly from +1.5 (low stress) to −0.5 (high stress) over 1000 model years. Following increasingly large oscillations in p, a relatively rapid collapse occurs from year 770. As the threshold (at year 770) is approached, Var increases by a factor of approximately 600, and AR increases from near zero to approximately 0.95. Figure 3c shows the 10th and 90th percentiles for each parameter from 100 similar runs, confirming that the increases observed are beyond the level of inter-run variability and thus statistically significant (the precise threshold point varies over a range of approx. 100 years, owing to the influence of noise, and this is reflected in the width of the percentile limits shown). Further experiments (data not shown) confirmed that CSD can be distinguished from potential ‘false-positives’, where increases in Var are driven by increases in σ_α, rather than being a consequence of reduction in (where α fluctuations are not sufficiently large, and negative, to cause significant decreases in mean p). In this case, AR values remain stable at approximately zero. The questions of why CSD occurs in the present model, and how it is linked to the spatial domain (patterning) are addressed in §6.

In principle then, monitoring for CSD provides considerable potential for gauging the proximity of bifurcation points in real SA systems. The practical difficulty of obtaining the required lengthy, high temporal resolution data series [17,19] of p may potentially be overcome by using combinations of high-resolution sampling for palaeoecological indicators (e.g. pollen), coupled with remotely sensed data where available, although these possibilities are yet to be explored.

The present section shows that the approach of the bistable region is ‘announced’ by spatial patterning and by the effects of CSD. The next section describes the fragility of the population in this lead-up to the bistable region and then the likelihood of population collapse once the bistable region is entered.

5. Population fragility

The fragility of the simulated population is a useful concept that can be defined in a number of ways. For example, sensitivity, χ, can be calculated as the change in population (Δp) owing to a change (a small one-year increase) in stress (a reduction in α, Δα): χ = Δp/Δα. In the present model, χ increases significantly with environmental stress towards the bifurcation point (inset to figure 3a). However, because the dependence of χ on α takes on a strong dependence on Δα within the bistable region, an additional evaluation of ecological resilience (sensu 16) is useful: the minimum perturbation (in α) necessary to switch p from a higher to a lower stable state.

Based on data shown in figure 2, the magnitude of perturbation in α required to force a transition to the lower stable population state, should be smaller under greater levels of background environmental stress. In separate experiments (data not shown), a 1-year reduction in environmental stress (from α to α_p, and defining α_↓ = α_p − α) necessary to cause this transition was found: α_↓ = −1.55 when α = 0 (connected labyrinth); α_↓ = −1.51 when α = −0.02 (fragmented labyrinth) and α_↓ = −1.45 when α = −0.05 (isolated spots). As expected, smaller perturbations are required under more stressful conditions. However, this simple picture of resilience can be taken further. The reduction in recovery rate described in §4b means that under some circumstances the return (post-perturbation) to stable equilibrium may take many thousands of model years (mechanisms discussed in §6). This slow recovery (large τ) results in highly persistent quasi-stable states (QS-states), where p is out of equilibrium with the background stress level and p remains effectively constant over decades to centuries. These QS-states have particular relevance for population resilience in cases where τ is large in comparison to the frequency at which perturbations occur. This is demonstrated in figure 3d, where perturbations are imposed on an equilibrium population stabilized at α = 0. As expected, a single relatively large perturbation (1 year with α_p = −2) drives the system to a low-p state, from which recovery is extremely slow (dashed line in figure 3d), even though the stress level is returned to the pre-shock level of α = 0. The existence of QS-states means that repeated smaller shocks (α_p = −1) have a similar effect. In this case, the population is unable to recover before the next perturbation arrives, and ‘ratchets’ down to the same low population-density QS-state (lower solid line in figure 3d). In the practical sense, both of these transitions to low-density states represent effectively irreversible shifts in system state (over time scales of hundreds of years), not driven by changes in mean stress, but by one or more perturbations. The point at which the system becomes susceptible to this multi-staged effect depends on τ and on the frequency/magnitude of the stress events. However, the probability of multi-stage collapse increases dramatically as the patterning becomes more degraded, and as such, patterning potentially provides an accurate guide to the fragility, and potential recovery rate, of the population. Why the recovery rate slows, allowing multi-stage collapse, and how is this connected to spatial patterning, is the focus of §6.

6. Recovery rates and the importance of spatial patterning

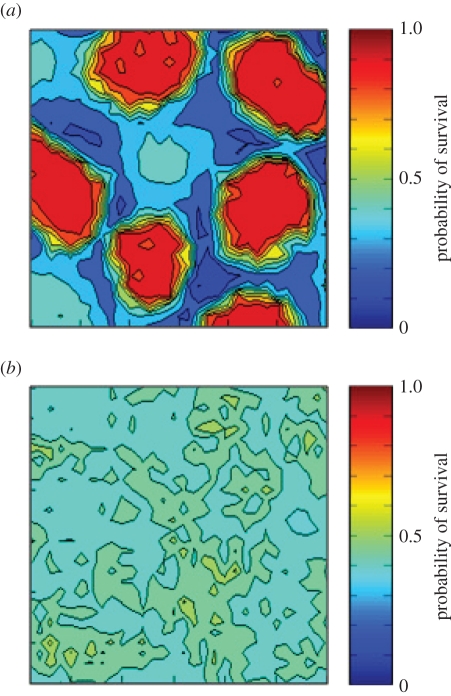
Populations in equilibrium at progressively lower values of α (as α → α₂; see §3) become increasingly sensitive to perturbations (here, sharp decreases) in α (figure 3a). Consequently, post-perturbation recovery proceeds from more degraded states (cf. figure 2). Recovery of p to the pre-perturbation equilibrium level (p_eq) requires the colonization of empty cells on the grid. At lower values of α (where α > α₂), the survival of isolated cells, not supported by facilitation, becomes less probable (relevant data shown in figure 2, for the case where all neighbourhood effects are set to zero, c_i = 0). As α is reduced, the survival of new ‘re-colonizing’ cells therefore depends increasingly on empty cell locations being favourable in terms of facilitation. Where patches exist, post-perturbation (whatever their form; cf. figure 2), the interior of these patches, and relatively thin ‘habitable’ regions bounding them, provide this facilitation. Conversely, the concentration of net competition further beyond the patch may actually result in harsher conditions in the inter-patch regions than would be the case for unpopulated bare ground (figure 4a, discussed below), depending on α. Under such circumstances, recovery only proceeds as the expansion of existing patches. The smaller and the more isolated the patches are over the entire grid (i.e. the bigger the perturbation and hence the more degraded the patterning), the smaller the bounding area providing adequate facilitation, and the lower the possible recovery rate. Similarly, lower α increases the dependence on facilitation by reducing the habitability of the inter-patch zones. Together, these factors explain the slower recovery rate both under conditions of lower α and for larger perturbations. Conversely, under progressively lower environmental stress (higher α), the sensitivity to perturbations is reduced and the probability of inter-patch survival increases, until ultimately no facilitation is required for individual cells to survive. Under these conditions, re-colonization is highly likely for all non-occupied cells and re-colonization of the grid progresses relatively quickly.

Figure 4.

Values for the survival probability of individual cells, plotted as contours, for populations stabilized in the upper and lower stable states at α = −0.05 (cf. figure 2). Each plot shows a 30 × 30 cell portion of the grid. (a) Upper stable state, p ≈ 0.42, p₀ = 0.92; (b) lower stable state, p ≈ 0.20, p₀ = 0. Further details in main text.

In the case where population recovery begins from below the lower equilibrium level (and α < α₁), individual cells throughout the grid have a similar and relatively low chance of survival. The chance of cells reaching maturity, and therefore providing stronger facilitation, remains relatively low, and the likelihood of several adjacent cells surviving long enough to form a coherent patch is effectively zero. Therefore, patches do not form, p remains relatively low and the age distribution peaks at low values. As α increases, the expected cell lifetime increases and this maturity brings greater facilitation; eventually, the probability of having adjacent long-surviving cells becomes large enough to allow small groupings to emerge. Once present, these small patches provide a self-sustaining (facilitating) environment that buffers patch members from environmental stress, allowing higher population density (locally) than would be the case were no neighbourhood effects included (dashed line in figure 2). This point marks the end of the lower limb of the bistable region and the transition to the higher p state. Following on from this, it is to be expected that no patterning or CSD should be observed if neighbourhood effects are removed. Model results do indeed show this to be the case and example data are shown in the inset to figure 3a, where recovery rate (τ) remains constant independent of α, and no patterning is observed in these or other similar simulations when neighbourhood (competition and facilitation) effects are set to zero (figure 2).

Figure 4 provides a demonstration of the spatial effects described above, plotting contours of calculated survival probability (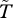, see electronic supplementary material) for two experiments, both with the population stabilized at α = −0.05. In the upper panel, the model was first run to equilibrium at α = 1 (for 200 years, yielding p ≈ 0.92), and α was then reduced to −0.05 and the model allowed to reach a new equilibrium in the isolated-spot state (cf. figure 1), with p ≈ 0.42. In the second case (lower panel), initial stabilization was at α = −1 (yielding p = 0), followed again by stabilization at the same α = −0.05, yielding a non-patterned stable state (cf. figure 1), with p ≈ 0.20. Contours of 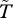show the strong facilitation effects of the patches, the harsh inter-patch conditions (figure 4a), and the relatively homogeneous and low survival probabilities of the lower-p state (figure 4b). We may speculate, based on these results, that the prevalence of sparse non-patterned vegetation in many SA regions of the World is consistent with either high background stress levels, or with more moderate stress levels coupled with frequent perturbations, sufficient to maintain the population on the lower limb of the bistable solutions (figures 2 and 3d).

Spatial effects therefore control the population recovery rate. The question of whether a population recovery, once underway, could be identified, is the focus of §7.

7. Transient solutions

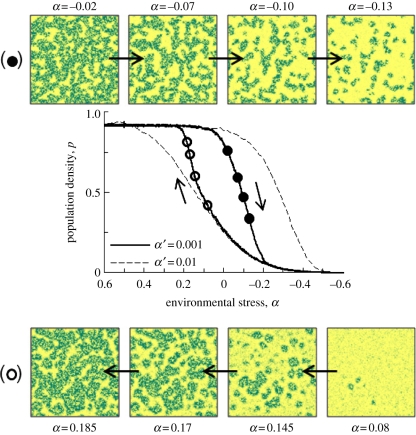
Figure 5 shows representative snapshots of model grids from simulations, where α was increased linearly from lower stress conditions (α = 0.5), to higher stress (α = −0.5), and then reduced back (linearly) to α = 0.5 over 2000 years (0.001 α yr⁻¹). The instantaneous population density (p, as shown) is hysteretic, not in equilibrium with α, and the lag in population re-adjustment depends on the rate of change in α (as shown). On the downward limb (decreasing α), transient patterns spontaneously emerge, which are qualitatively similar to the stable solutions shown in figure 2. However, on the upward limb, returning from the bare state as stress is reduced, a different set of emergent patterns is observed. Population increases first as homogeneous cover, and then within the bistability region, small patches emerge and expand, coalescing to form connected structures with corridors of bare surface, leading to isolated bare patches and ultimately ‘full’ coverage. This progression of expanding patches is the expected consequence of the processes described in §6. Further, multiple partial re-adjustments under fluctuating stress levels result in a rich variety of modelled patterns. Increasing α causes existing pattern elements to expand, while decreases promote shrinkage and the expansion of bare patches. Pattern re-adjustment therefore has much potential to record information on short-term fluctuations in stress and also the long-term trajectory of p. However, it is possible for qualitatively similar patterns to result from a range of different stress histories and accurate evaluations of system state, based on patterning, may therefore necessitate observations of patterning trends over time rather than assessments of single vegetation coverage ‘snapshots’.

Figure 5.

Transient solutions for population density (p) and representative examples of spatial patterning. The main part shows the hysteretic nature of the response and the dependence on the rate of change of α (α′, in units α per year). Arrows indicate the decline in p as α is decreased from 0.6, and the increase in p as α is increased from −0.6. The filled/open circles indicate the position on the descending/ascending limb of the plotted grids (100 × 100 cells in each case).

8. Conclusions

• — A wide range of spatial patterns is observed in the model results, from highly (self-) organized structures to homogeneous effectively random distributions. Pattern formation emerges spontaneously owing to the effects of net competition and facilitation, and the resultant patches provide self-sustaining environments that allow considerably higher levels of environmental stress to be tolerated than is the case for isolated plants (or, equivalently, the case where local effects are neglected).

• — Understanding the effects of patterning on plant survival shows why bistability must occur in this system and why the bifurcation point is announced by a slow-down in post-perturbation recovery rate, driven by spatially localized interactions and observed in population time series as increases in both variance and autocorrelation.

• — Rapid perturbation-induced population collapse is possible within the bistable region. Under higher levels of environmental stress, the reduction in recovery rates (and the associated change to more degraded patterning) significantly decreases the resilience of the population to repeated perturbations. The prevalence of sparse non-patterned vegetation cover is an expected consequence of highly stressed and/or frequently perturbed systems.

• — In areas where patterning persists, changes in transient patterns have potential to provide reliable indicators of the system state and trajectory.

• — The present results come from a model which is defined only in its spatial relationships. The ability of this model to produce meaningful time-series signatures suggests that looking for comparable signals in other spatially defined models/systems of different phenomena may be profitable.