Primate extinction risk and historical patterns of speciation and extinction in relation to body mass

Abstract

Body mass is thought to influence diversification rates, but previous studies have produced ambiguous results. We investigated patterns of diversification across 100 trees obtained from a new Bayesian inference of primate phylogeny that sampled trees in proportion to their posterior probabilities. First, we used simulations to assess the validity of previous studies that used linear models to investigate the links between IUCN Red List status and body mass. These analyses support the use of linear models for ordinal ranked data on threat status, and phylogenetic generalized linear models revealed a significant positive correlation between current extinction risk and body mass across our tree block. We then investigated historical patterns of speciation and extinction rates using a recently developed maximum-likelihood method. Specifically, we predicted that body mass correlates positively with extinction rate because larger bodied organisms reproduce more slowly, and body mass correlates negatively with speciation rate because smaller bodied organisms are better able to partition niche space. We failed to find evidence that extinction rates covary with body mass across primate phylogeny. Similarly, the speciation rate was generally unrelated to body mass, except in some tests that indicated an increase in the speciation rate with increasing body mass. Importantly, we discovered that our data violated a key assumption of sample randomness with respect to body mass. After correcting for this bias, we found no association between diversification rates and mass.

1. Introduction

Several studies have implicated body size as a risk factor for extinction in mammals [1–4]. Large body size is thought to correlate with higher extinction risk through a number of life-history covariates of increased body mass, such as longer generation times and smaller litters [2,5]. These factors should increase the time needed to recover from stochastic demographic reductions in population size, thus increasing the probability of extinction. To test this hypothesis, studies have quantified extinction risk among living species as a ranked variable derived from the IUCN Red List conservation status categories (www.iucnredlist.org; [1,2,4]). In mammals, Cardillo et al. [2] found that ‘intrinsic’ biological life-history traits influenced extinction risk only when species were greater than 3 kg in mass. Below 3 kg mass, the primary determinants of extinction risk were ‘extrinsic’ factors that are not genetically heritable, such as geographical range size and nearby human population density [2]. Studies also have failed to detect a consistent association between diversification rate and body mass across mammalian clades [5,6].

Understanding the predictors of present-day extinction risk, as reflected by the IUCN Red List, has clear relevance given the pressing need for primate conservation [7]. For example, the great apes are all large bodied and critically endangered (IUCN Red List). An important question is whether large-bodied primate species experience higher extinction rates irrespective of human activities. If so, then large-bodied primates may be especially vulnerable to anthropogenic drivers of extinction, such as reductions in habitat or climate change. It is possible to infer speciation and extinction rates from a dated phylogeny because higher rates of extinction relative to speciation should produce longer internal branches on a tree with an apparent burst of diversification close to the tips [8,9]. Recent advances provide a way to integrate the study of speciation and extinction that is dependent upon another trait [10], such as body mass. Previous studies have investigated patterns of diversification more generally in primates [6,11–15] using an older inference of primate phylogeny [16].

Using a newly inferred primate phylogeny that enabled us to incorporate phylogenetic uncertainty, we investigated the links between body mass, extinction risk and diversification rates. First, we tested for an association between body mass and present-day extinction risk categories obtained from the IUCN Red List. As with previous studies, we predicted that larger bodied primates are at greater risk of extinction [1,2,4]. In our analyses, we used methods that incorporate phylogenetic uncertainty, better model character evolution on the tree and test for spurious results arising from the ordinal (rather than integer) measurement of extinction threat categories.

Second, we predicted that primate lineages characterized by greater body mass have experienced higher extinction rates throughout evolutionary history. For this, we applied a new method to estimate extinction rates on a phylogenetic tree in relation to a biological characteristic [10], again running the test in a way that incorporated phylogenetic uncertainty.

Last, we turned our attention to speciation by predicting that lineages with smaller body mass have higher speciation rates. We made this prediction based on several studies showing a trend for smaller bodied mammalian clades to be more diverse, possibly because they experience vicariance events more frequently or they are able to partition the environment into more niches [1,2,5,6,17,18].

2. Methods

(a). Tree inference

As our hypotheses pertained to the order Primates as a whole, we needed a phylogeny that included as many species as possible. To this end, we used the trees available from the 10kTrees project, v. 1 (http://10ktrees.fas.harvard.edu/). The website provides extensive documentation on the tree inference, a graphical interface for downloading trees and a number of visualizations of the trees. Details regarding tree inference are available in Arnold et al. [19]. Our use of Bayesian tree inference enabled us to deal with phylogenetic uncertainty by running comparative tests on multiple trees saved from the Markov chain. Incorporating such topological and branch length uncertainty is important because the phylogeny used can affect the conclusions that are drawn from a comparative analysis [20,21].

We used two sets of trees from the Bayesian analysis: a sample of 100 trees distributed evenly along the post-burn-in Markov chain and a consensus tree of all nodes with clade credibility support greater than 0.5. We dated all trees prior to comparative analysis by using seven fossil calibration points employed by previous phylogenetic studies (table 1; [22–26]). We conducted molecular dating with the software r8s [27] using the penalized-likelihood algorithm with a smoothing parameter of 100, chosen because this value best recovered dates inferred from phylogenetic analyses of smaller taxonomic samples but with more extensive sequence data [23–25].

Table 1.

Fossil calibration ranges used to date molecular phylogenies. (n.a., not applicable.)

most recent common ancestor node	min. age (Ma)	max. age (Ma)	source
Homo-Pan	5	8	[57]
			[58]
			[59]
			[60]
Homo-Pongo	12.5	18	[61]
Papio-Theropithecus	3.5	6.5	[62]
extant Catarrhini	21.0	30.0	[63]
			[64]
Cebus-Saimiri	12.5	n.a.	[65]
Loris-Galago	38	42	[22]

(b). Body mass and IUCN Red List data

Body mass data were obtained from the work of Smith & Jungers [28]. We calculated the mean female body mass across study sites for our analysis. In this manner, we obtained body mass data on 160 species that could be matched to our phylogeny through translation via the taxonomy of Wilson & Reeder [29]. Analyses used the natural log of female body mass. We obtained IUCN conservation status for the species on our phylogeny from the IUCN Red List website (www.iucnredlist.org). From each IUCN category, we constructed an ordinal variable with higher ranks corresponding to greater extinction threat. Specifically, ranked from smallest to highest, we used the following categories of threat: least concern, near threatened, vulnerable, endangered and critically endangered. Six species labelled ‘data deficient’ in the IUCN Red List were removed from the analysis, reducing the sample size to 154 species. The highest rank was assigned to ‘critically endangered’ rather than ‘extinct in the wild’ because our study included only extant species as data points.

(c). Comparative analyses

We tested for an association between body size and IUCN extinction risk through a phylogenetic generalized least-squares (PGLS) model applied across our Bayesian tree block. This analysis of the primate data replicates previous independent contrasts analyses across mammals (e.g. [2,4]). However, PGLS implemented in the program BayesTraits [30] enabled us to incorporate Bayesian estimation of the branch-scaling parameter λ [31] across a tree block, which should improve upon contrasts-based approaches. In particular, we suspected that Brownian motion along the branch lengths in our block of 100 trees might not reflect evolutionary change in a character such as threat status. Brownian motion along branch lengths is an assumption of independent contrasts. The scaling parameter λ adjusts the internal branch lengths with a length multiplier such that the data meet the assumption of Brownian motion. By systematically searching through many possible values for λ, the program locates the value that makes the data most likely and thus best accommodates the assumption of Brownian motion. In primates, Purvis et al. [32] showed that IUCN rank alone exhibited λ = 0.77 that excluded both zero and one (95% CI 0.51–0.90). Thus, we considered it important to estimate λ in our PGLS, and especially to do so in a way that incorporates uncertainty in phylogenetic relationships and branch lengths.

The use of PGLS or independent contrasts treats IUCN extinction risk as a continuous variable [33,34]. Counter to this assumption, extinction risk codes in the IUCN Red List are not continuously varying. Instead, extinction risk is an ordinal variable in which ranks probably vary in the amount of difference in the actual underlying extinction risk [32]. For example, the true (quantitative) difference in extinction risk may differ between categories of near threatened and vulnerable, when compared with endangered and critically endangered. Treating ordinal variables as continuous can produce elevated type 1 error rates because such treatment applies arithmetic operations that do not preserve the variance structure of the original ordinal ranks [35,36]. The problem occurs specifically when the ordinal ranks are separated by unequal distances along the underlying continuous variable that they measure, a point acknowledged by Purvis et al. [32].

We used computer simulations to assess whether the treatment of IUCN threat categories as continuously varying may have introduced error into this study and previous studies [2,4,32]. Specifically, we tested whether treating threat status as continuously varying resulted in elevated type 1 error rates. We conducted 1000 simulations of two uncorrelated continuous characters on our consensus tree (function ‘sim.char’ in the R package ‘geiger’; [37,38]). Characters evolved randomly with a constant accumulation of variance (set at 1.0 per unit; branch length) and an initial state of zero. We then rescored one character from each pair into a set of ordinal ranks with the same number of species in each state as was observed for each corresponding IUCN threat status in our dataset. The lowest continuous values of the simulated character thus became rank ‘0’, while the highest became rank ‘4’, with other ranks derived from intermediate values and all in matching proportion to the observed frequency of each rank in the IUCN data. This rendered one character a true continuous distribution, such as body size, but the other character had been rescored into a set of ordinal ranks with different real distances between the means of each rank. We then conducted 1000 PGLS tests to test for a significant association of the two characters, one of which was ordinal and one continuous. Significant associations were counted as type 1 errors because the characters evolved independently during the simulations. An alternative approach to deal with ordinal IUCN data would be to include additional parameters that model the ordinal nature of the dependent variable. While this procedure in principle can be implemented [39], given the prominent prior research that treated IUCN as continuous, we preferred to use simulations to test this approach more generally. Additionally, ordinal data do not necessarily violate the assumptions of linear regression if the states are sufficiently evenly spaced [35].

To test for effects of body size on the actual speciation and extinction rates experienced by different lineages on the primate tree, we employed the ‘binary-state speciation and extinction’ (BiSSE) test [10], as implemented in the R package diversitree [40,41]. This procedure uses likelihood methods to test a six-parameter model of speciation, extinction and trait evolution. Following the procedure recommended in Maddison et al. [10], we constructed five- and six-parameter models to test body-size-dependent speciation and extinction rates, which we investigated separately. For each state of a binary character, BiSSE can model a rate of speciation, extinction and character state transitions. Thus, six rates are possible for the most complex BiSSE model. The five-parameter models constrained the speciation (or extinction) rates to be equal in the two body size categories, while the six-parameter models allowed speciation (or extinction) rates to vary for different body sizes. Because these models were nested, we assessed statistical significance using likelihood ratio tests.

To use BiSSE with our measures of body mass, we binned species into categories of ‘small’ and ‘large’ body mass. As it is not immediately clear what cut-off should be used for these categories, we initially tested our hypotheses with three different cut-offs derived from the primatological literature. The first break point, 500 g, reflects the point above which primate species are not strictly faunivorous (i.e. Kay's threshold) [42]. We thought this widely accepted energetic constraint might reflect the life-history variables that underlie previously observed associations between body mass and extinction risk. The second break point, 984 g, was the phylogenetic mean body mass at the root of the dated consensus tree, as inferred through squared change parsimony reconstruction [43] of log body mass values in Mesquite v. 2.6 [44]. The third break point of 3000 g came from a study of extinction risk across mammals [2], in which the authors found that biologically intrinsic life-history traits only influenced extinction risk above a body mass of 3000 g. We ran these analyses of the three a priori break points across the 100 dated trees from the Bayesian tree search.

To assess the sensitivity of our results to the break point used for binning species, we conducted an analysis with a sliding break point that divided the body mass data into small and large categories along 20 intervals of 0.2 log units of body mass. We quantified the precision of the sliding break point estimates by sampling the six-parameter model with a Markov chain Monte Carlo (MCMC) that we initialized with the maximum-likelihood estimates for parameter values (R package diversitree; [40,41]). We used only the dated consensus tree for the sliding break point analysis. We constructed 95 per cent credible intervals for parameter values by calculating the range of each parameter across the MCMC samples after excluding the largest and smallest 2.5 per cent of sampled values.

The implementation of BiSSE in diversitree allows one to specify the degree of species sampling employed in the study. Doing so is important because methods to test trait-dependent extinction are biased by incomplete sampling of the study group [8,41]. The diversitree package includes modified-likelihood equations to account for this bias [41]. Under the Wilson & Reeder [29] taxonomy, which served as the taxonomy for the present study, we sampled 42 per cent of extant primates. We used this value as our sampling percentage in all BiSSE analyses.

The BiSSE correction for incomplete sampling is statistically valid only when the species have been sampled randomly. Two issues are relevant here: random sampling of species from the phylogeny, and random sampling with respect to the character hypothesized to affect speciation and extinction rates.

To assess the randomness of our species sample with respect to phylogeny, we conducted a G-test of proportions of species from each genera within our observed sample ([45] R script by P. Hurd, http://www.psych.ualberta.ca/∼phurd/cruft/). The G-test uses maximum-likelihood techniques to assess whether an observed proportion of species within genera can be viewed as a random sample of species given their known frequencies from the complete taxonomy [29]. We conducted this test at the generic level because, based on our primate phylogeny [19], generic classifications reflect monophyletic clades.

To test whether sampling was random with respect to body mass, we calculated the deviation of the observed number of species sampled from a genus compared with the number expected to be sampled given the number of species in each genus in the complete taxonomy. Thus, a positive deviation indicated that more species were sampled from a genus than expected under random sampling, whereas a negative number indicated fewer were sampled than expected. We then conducted a PGLS test for an association between body mass and sampling deviation using our dated consensus tree to control for phylogenetic non-independence (R packages ape [46] and nlme [47]).

We then retested our hypothesis regarding speciation and body size using the diversification test of Freckleton et al. [15]. This test is simply a PGLS of a character trait as a dependent variable with the number of nodes from the tree root to each tip as the independent variable. If a particular character state, such as body size, is associated positively with diversification rates, then a positive association should exist between the character value and lineages that exhibit more nodes. The advantage of this test is that, because it is conducted through a PGLS framework, we were able to include the deviations from the randomly expected sampling as an independent variable; in other words, we could investigate the effects of body mass on diversification while controlling for body-mass-related biased sampling if it exists, even if not statistically significant in the above tests. Another advantage of this test is it treats body size as a continuous variable, whereas the use of BiSSE required us to bin body size into a set of binary categories. The disadvantage of the Freckleton et al. [15] test is that it investigates the association between net diversification rate and body size, rather than specifically investigating speciation and extinction separately (as in BiSSE). We used the dated consensus tree for this analysis.

3. Results

(a). Extinction risk and body mass

In our dataset, 68 species were categorized as ‘least concern’, nine as ‘near threatened’, 30 as ‘vulnerable’, 40 as ‘endangered’ and seven as ‘critically endangered’ (table S1, electronic supplementary material). We found a significant and positive association between IUCN extinction risk and body mass in a PGLS analysis across our dated Bayesian tree block (n = 154, β = 0.40, p = 0.004). Additionally, we found that λ differed from zero and one (λ = 0.78, 95% credible interval λ = 0.63–0.89). This indicates significant phylogenetic signal and thus highlights the importance of controlling for phylogeny, but further shows that a non-Brownian component may contribute to variation in residual values. In our 1000 simulations that tested the effect of ordinal ranking for IUCN, only 5 per cent of statistical tests were deemed significant at the 0.05 nominal level. Thus, the type 1 error rate was as expected.

(b). Extinction rate and body mass

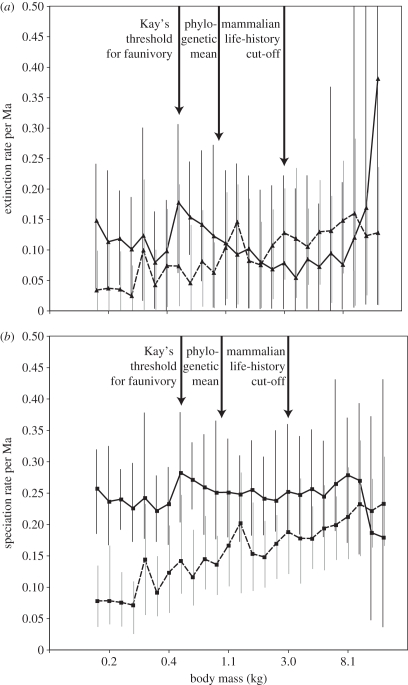
In our BiSSE analyses of 160 primate species, likelihood ratio tests supported no significant relationship between log body mass and historical extinction rate either at our a priori break points or in our sliding break point analysis (figure 1a). Similarly, across the 100 trees, extinction rates at the a priori break points were significantly different relative to body mass for only 1 of the 100 trees sampled from our tree block. This was true even though extinction rates were estimated to be different from zero in many cases (figure 1a). Several papers have indicated that methods for inferring trait-dependent extinction may suffer from low statistical power [10,11,18,48,49], a point to which we return in §4.

Figure 1.

Sliding break point analysis of body-mass-dependent speciation and extinction rates on the consensus tree. Solid lines connecting points show rates for species that have larger body mass than the given point on the body mass in the x-axis (black 95% credible interval bars), while dashed lines are for species with smaller body mass (grey 95% credible interval bars). Triangles in (a) show inferred extinction rates and squares in (b) show inferred speciation rates. Thick vertical arrows correspond to our three a priori hypotheses.

(c). Speciation rate and body mass

In contrast to the results from the extinction analysis, we found significant speciation rate differences at Kay's threshold a priori break point on our dated consensus phylogeny and across 95 of the 100 trees (for the consensus tree, p = 0.016). Differences in the speciation rate at the phylogenetic mean and 3 kg break points were not significant on the consensus tree or on any of the trees from the tree block. Importantly, the result for Kay's threshold was opposite to our prediction, with higher estimated speciation rates in larger bodied species (figure 1b). This pattern seemed to apply across most of the variation in primate body mass, but not at the largest body mass categories (figure 1b). However, MCMC sampling of the speciation estimates showed that 95 per cent credible intervals overlapped across most of the body mass sliding break points (figure 1b).

In testing for speciation and extinction rates, BiSSE also estimated two rates of transition (small to large and large to small) in all analyses. The transition rate estimates showed overlapping credible intervals across almost the entire range of sliding break points (figure S1, electronic supplementary material). This indicates rates of body size increase and decrease are generally equivalent regardless of the break point used to identify large and small species.

The BiSSE results are not compromised by non-random sampling of species in our dataset with respect to phylogeny. The G-test for independence showed that the observed sampling of species within genera was within the variation expected from random sampling of taxa (p = 0.147). However, the observed sample of species was biased towards greater sampling of species with larger body mass in a PGLS test (β = 0.80, p = 0.037). Thus, biased sampling towards species with larger body mass may have influenced the BiSSE results; specifically, the denser sampling of the larger species may have biased the test to estimate a higher rate of speciation because these lineages would have occurred more commonly on the tree representing the sample of species.

When we controlled for the observed sampling deviations from the random sampling expectation, our PGLS test of diversification effects on body size did not find any association between these variables (β = 0.00, p = 0.71). When we removed the sampling variable from the analysis, however, the PGLS obtained a trend more consistent with the results of the BiSSE analysis (β = 0.08, p = 0.081). Although this PGLS test cannot technically distinguish between body-mass-related speciation and extinction effects, we would expect to find a positive association between diversification and body mass if speciation rate correlates positively with body mass and extinction rates do not (as suggested by the above tests). Additionally, simulations by Freckleton et al. [15] showed that their test was more sensitive to speciation effects than to extinction effects. Thus, given the lower power of the test to detect an effect of extinction, any positive result would more probably result from speciation effects.

4. Discussion

We tested a series of predictions involving the links among body mass, phylogenetic diversification and current extinction risk in primates. With regard to current patterns of extinction, we found that larger bodied species experience higher extinction risk. This result replicates previous findings, but for the first time, to our knowledge, incorporates phylogenetic uncertainty and uses the scaling parameter λ to control for the non-Brownian distribution of variation in IUCN threat status categories [2–4]. We also tested, for the first time, whether the ordinal nature of IUCN threat status categories impacts the statistical performance of independent contrasts and PGLS analyses that use it as a dependent variable. Our 1000 phylogenetic simulations show the ordinal coding itself does not produce elevated Type 1 error in our primate dataset.

Despite finding a strong association between threat categories and body mass in primates, we failed to find evidence for an historical association between body mass and extinction rates. Instead, in a limited number of tests, we found that speciation rates may increase with body mass, which was opposite to our predictions. These analyses point to an association between larger body mass and higher speciation rate, which contrasts with most predictions, including ours, that speciation rates covary negatively with body mass (see also [50]). After controlling for biased sampling of species in a PGLS model, however, we found no association between the diversification rate—a function of speciation and extinction—and body mass.

Previous studies found that intrinsic biological variables can explain a substantial proportion of variation in risk status [1,2]. These previous statistical models found that high risk variables, including large body mass, high trophic level, small geographical range and slow life history, explain threat status to a substantial degree and independently of anthropogenic effects [1,2,51]. Thus, the present-day extinction risk status should be related to the historically experienced extinction rates of lineages.

We found it surprising that current patterns of extinction risk covaried with body mass in our study and previous studies, while estimates of extinction rates across primate phylogeny failed to show this effect. It could be that higher threat categories among large-bodied primates have resulted only from anthropogenic effects in the present. Alternatively, the tests may have failed to detect differences because available methods to estimate historical extinction rates suffer from low statistical power ([10], see also [11,18,48,49,52,53]). Using simulations, for example, Maddison et al. [10] showed that the power to detect variation in speciation rates is relatively high (power for speciation in simulations of 500 species was approx. 58%), when compared with the power of detecting variation in extinction rates (approx. 21%). Rabosky [53] recently showed that, in addition to low power, current methods cannot accurately estimate extinction rates when these rates vary across the tree. His analyses were conducted with complete sampling and phylogenetic information of every extant species. Given the fossil evidence for a plethora of extinct primate species, we agree with Rabosky [53] that future analyses should incorporate fossil information as a means to increase power and to estimate extinction rates more accurately (see also [51]).

Our study also offers a cautionary tale about the importance of testing the assumptions of methods for studying speciation and extinction rates. When using a new method to account for incomplete sampling of taxa, we found some support for an association between speciation and body mass. However, our data violated another assumption of these methods, namely that sampling of species is random with respect to body mass. When we controlled for non-random sampling, the association between diversification rates and body mass became non-significant. Thus, we offer a valuable empirical example of shortcomings to these methods that complement previous simulation studies and provide a procedure for investigating biased sampling for others to use in future studies. The potential effects of non-random sampling are a serious concern for previous studies of trait-dependent diversification [11,14,15,54].

We began this study with the prediction that populations of smaller bodied animals may speciate more quickly, as they experience vicariance events more frequently or they are able to better partition the environment into more niches [18]. Previous studies provided hints that the speciation rate could increase with body mass in primates, rather than showing a strict negative correlation with body mass. For example, Purvis et al. [11] found that the family Cercopithecidae (Old World monkeys) experienced larger speciation rates than did other primate lineages. While their study did not assess how speciation covaried with characteristics such as body mass, our results are consistent with their findings given that the cercopithecids are generally larger bodied than extant platyrrhine and strepsirrhine primates that more frequently fall below Kay's threshold. The cercopithecids are also typically smaller than the (relatively) species depauperate hominoids. These clade-specific patterns could be tested more rigorously with the new statistical software MEDUSA [55]. Our results are consistent with Freckleton et al.'s [15] findings of a significant correlation between body mass and diversification rate. The results imply that some degree of species selection on body mass may have occurred in primates, in that the influence of body mass on cladogenesis explains the distribution of body mass even after allowing for anagenic change as it is incorporated into the model (figure S1, electronic supplementary material; [10,11,56]).

In summary, we used new methods to incorporate phylogenetic uncertainty and to assess how body mass influences primate diversification. Our results add to a growing body of evidence that larger bodied animals are more susceptible to extinction. The lack of significance for historical patterns of extinction may indicate that methods to detect extinction rates from extant species are severely compromised in statistical power [10,11,18,48,49,53]. Intriguingly, we found some evidence that speciation rates appear to increase with body mass in primates (see also [50]). It will be interesting to see if similar patterns occur in other groups of vertebrates and, if so, how and why the effects of body size on speciation vary among clades.