Methods and Biostatistics: a concise guide for peer reviewers

Abstract

The purpose of the Materials and Methods section of a scientific manuscript is to provide information in sufficient detail, so that another scientist working in the same field of endeavor is able to repeat the experiments and reproduce the results. Authors are entitled to a justified decision on the publication or not of their work. Thus, reviewers need to assure the authors that they have studied, correctly interpreted and fairly judged their work. This can be done by writing a short introductory paragraph in their critique, mentioning the type of study, the subjects recruited, the time and places the study was conducted, the interventions, the outcome measures and the statistical tests. All these information should be found in the methods section. If the reviewer cannot find these information, he needs not to read the whole article. Reading through the abstract and the methods section, he can reject the article on good grounds. If the methods section is appropriate, then the whole article need to be further reviewed. In this manuscript we shall discuss several critical aspects of the methods and statistics from the reviewer's perspective to provide reviewers the knowledge basis to write the aforementioned introductory paragraph of their critique.

The Methods section of a scientific publication allows peer reviewers and readers to judge whether the appropriate materials, instrumentation and the best techniques, have been used, in order to obtain results¹. Peer reviewers should evaluate this section for adequacy and clarity of the description of the methodological processes including study design, laboratory and experimental procedures, ethical considerations, and quantitative or qualitative analyses. Limitations in study design, like the absence of a control group or confounding factors, reduce the validity of a study. It is important to describe the sample and sampling method so that its representativeness to the population, to which the results will be generalized, can be assessed. A frequent problem in both experimental and clinical analytical research is the use of a small sample size, resulting in a lack of statistical power, such that even in the case where true differences do exist between groups, these are not detected (Type β error)².

In 2004, Curran-Everett & Benos published a set of guidelines for authoring a scientific manuscript which have been both endorsed and advocated^3–8. Previous authors have also proposed certain approaches in order to thoroughly read a manuscript^1,9. Specific statement guidelines for reporting randomized clinical trials, observational studies and meta-analyses have also been published.

Authors are entitled to a justified decision on the publication or not of their work. Thus reviewers need to assure the authors that they have studied, correctly interpreted and fairly judged their work (Table 1). This can be done by writing a short introductory paragraph in their critique, mentioning the type of study, the subjects recruited, the time and places the study was conducted, the interventions, the outcome measures and the statistical tests (Table 2). All these information should be found in the methods section. If the reviewer cannot find these information, he needs not read the whole article. Reading through the abstract and the methods section, he can reject the article on good grounds. If the methods section is appropriate, then the whole article need to be further reviewed. In this manuscript we shall discuss several critical aspects of the methods and statistics from the reviewer's perspective to provide reviewers the knowledge basis to write the aforementioned introductory paragraph of their critique.

Table 1: Reviewers checklist on methodological aspects of the paper (Modified from Greenhalgh⁹).

Table 2: Reviewers checklist on statistical aspects of the paper (Modified from Greenhalgh⁹).

Methods

Reproducibility

The main reason for including a Methods & Patients (or Materials) section in a scientific paper is to allow for reproducibility. Reproducibility is one of the main principles of the scientific method, and refers to the ability of a test or experiment to be accurately reproduced, or replicated, by someone else working independently in the same field. The first piece of information that ought to be reported is the type of the study: is it an experimental study in animals? An in vitro study? A study involving human subjects? In the latter case, is it a case report, a case series, a case-control, a cohort or a randomized controlled trial? This information is better to be reported in the abstract to avoid any misinterpretations. The second important piece of information concerns the unit of analysis. The unit of analysis is the major entity that is being analyzed in the study. It is the 'what' or 'whom' that is being studied¹⁰. The unit of analysis can be populations of cells cultured in some medium, each animal, groups of animals, each patient or groups of patients. This is not to be confused with the unit of observation, which is the unit on which data are collected for (i.e. data on each animal). For example, a study may have a unit of observation at the individual animal level but may have the unit of analysis at the group of animals' level, drawing conclusions on group characteristics from data collected from each animal¹⁰.

Laboratory and experimental methods

Methods in biomedical science fall in four distinct categories¹. The first includes those methods which are familiar to every scientist and most doctors through their pregraduate training. The determination of the pH in a solution is such an example. Therefore, authors are not expected to report on the pH measurement methodology in the methods section. The second category includes those methods that are less common but have been well documented previously in the literature. An example is the quantification of p53 protein¹¹. In this case, the method should be mentioned in brief with the appropriate reference and an indication, when necessary, of the materials used for standardization of the method. In the case that commercially available kits where used, the trade name and manufacturers data should be reported. The third category includes methods that are relatively uncommon or that require specification of experimental conditions; these should be described in sufficient detail so that someone who wants to repeat your experiment can do so by referring to the original description of the method and to the specific modifications the authors used. Thus, such methods should write up as per follow: "The p53 was quantified using flow cytofluorometry, as described by Khochbin et al. with the following modifications." The fourth category includes methods that were developed by the researchers; these should be described in detail, with all reagents, conditions, and equipment precisely specified. Furthermore, critical points for the success of the experiment need to be emphasized.

A reviewer, who accepts the responsibility to review a manuscript, should be able to determine to which category the described methods fall and act accordingly, to ensure reproducibility.

Informed Consent, Ethics Committee approval

Any study that describes or analyses people or tissues from people, needs to report formal informed written consent of subjects or their parents, if they are minors¹. Alternatively, to determine unequivocally that such consent is not required, approval of a competent institutional ethics committee which is present at many institutions is required. If the researchers' institution does not have such a Committee, they should adhere to the guidelines reported in the World Medical Associations "Helsinki Declaration," which details the ethical principles for medical research that involves human subjects¹².

Types of Studies

It is imperative for the reviewer to be able to classify the clinical study he was presented for review: Case reports, case series, cross sectional, case control and cohort studies are the main types of observational studies, in order of increasing evidence quality. Controlled, quasi-randomized and randomized clinical trials are the main types of interventional studies, the last category being recognized as the prominent tool in clinical research^{2,13– 15}.

For case-control and cohort studies, which are observational, the Strengthening the Reporting of Observational Studies in Epidemiology (STROBE) Statement: Guidelines for Reporting Observational Studies have been published¹⁶. For clinical trials, the Consolidated Standards of Reporting Trials (CONSORT) has been published^17–18. These guidelines comprise a minimum set of recommendations for reporting studies, and offer a standard way for authors to prepare reports of their findings, facilitating their complete and transparent reporting, and aiding their critical appraisal and interpretation^16–18. These statements include guidance for reporting methods: study design, setting, participants, variables, data sources/measurement, bias, study size, definition of variables and statistical analysis. We elected not to discuss these guidelines; rather the reader is referred to them, for further study (References ^16–18).

The reviewer needs to be aware whether these guidelines are a prerequisite for publication in the journal. In this case, they ought to be used as checklists to ensure compliance. In the case they are not prerequisite for publication in the journal, understanding them helps the reviewer to more systematically review the manuscript.

Questionnaire Instruments: Validity and Reliability

Questionnaires need to have a clinically meaningful and scientifically robust conceptual and measurement model. Patient questionnaires that are not formally developed and tested may seem to pose clinically reasonable questions, but unless they are properly developed and psychometrically tested, it is not possible to be confident about their reliability (consistency and reproducibility) or validity (ability to measure the intented outcome)¹⁹. Furthermore, questionnaires are valuable and precise instruments, provided they are used in the populations they were designed for; otherwise, content validity is not assured²⁰. Information on any experimental, medical or physiological instruments used including validity (the extent to which an instrument measures what it purports to measure) and reliability (the extent to which an instrument provides consistent measurements) should be made available when possible². Validity is subdivided into four types. Each type addresses a specific methodological question:

1. Is there a relationship between cause and effect (Conclusion validity),

2. Is the relationship causal (Internal validity),

3. Can we generalize to the construct (Construct validity),

4. Can we generalize to other persons, places, times? (External validity)²¹.

Bias

Potential sources of bias and any efforts to address them need to be reported in the Methods section. Further discussion of these sources of bias, when appropriate, is better placed in the first paragraph of the Discussion section.

Biostatistics

In this section, the basic statistic knowledge for peer reviewers is reviewed. Most information is included in pre-graduate text books. However, we only provide essential information and emphasize on critical aspects of statistics that are important for peer-review.

Qualitative and Quantitative data

Qualitative data can be further divided into two distinct categories:

1. Unordered qualitative data (statistics: nominal variable), e.g. ventilatory support (none, non-invasive, intermittent positive-pressure ventilation, oscillatory) and

2. Ordered qualitative data (statistics: ordinal variable), e.g. severity of disease (mild, moderate and severe).

Quantitative data are numerical and can be further divided into the following two distinct categories:

1. Discrete quantitative data (statistics: ordinal variable), such as the number of days spent in hospital;

2. Continuous quantitative data (statistics: scale variable), such as blood pressure or haemoglobin concentrations.

Quantitative data need to be reported with a number of digits that is commensurate with scienti?c relevance⁸. Reviewers are expected to question over three decimal numbers when they appear either in results section or in tables. Tables are a useful way of describing both qualitative and grouped quantitative data and there are also many types of graph presentations that can provide a convenient summary. Qualitative data are commonly described using bar or pie charts, whereas quantitative data can be represented using histograms or box and whisker plots^22–24.

Summarizing data

The two most important elements of a dataset are its location (where on average the data lie) and its variability (the extent to which individual data values deviate from the location)²².

Location measures

• Mean: The mean is the most well known average value. It is calculated by summing all of the values in a dataset and dividing them by the total number of values.

• Median: The median is the central value when all observations are sorted in order. If there is an odd number of observations then it is simply the middle value; if there is an even number of observations then it is the average of the middle two.

• Mode: The mode is simply the most commonly occurring value in the data²³.

Variability measures

• Range: Range is the difference between the largest and smallest observation in the dataset.

• Standard deviation(SD): The standard deviation is a measure of the degree to which individual observations in a dataset deviate from the mean value. Broadly, it is the average deviation from the mean across all observations. It is calculated by squaring the difference of each individual observation from the mean (squaring is needed to remove any negative differences), adding them together, dividing by the total number of observations minus 1, and taking the square root of the result. The SD and 95% reference range describe variability within a sample and these quantities are best used when the objective is description of the sample itself²⁵.

• Variance: Another measure of variability that may be encountered is the variance. This is simply the square of the standard deviation²³.

• Standard Error of the Mean(SE): The SE and 95% confidence interval describe variability between samples, and therefore provide a measure of the precision of a population value estimated from a single sample. In other words, a 95% confidence interval provides a range of values within which the true population value of interest is likely to lie. These quantities are best used when the objective is estimation of the true values in the maternal population²⁵.

Standard deviation or standard error?

Guideline 5 by Curran-Everett & Benos states" "Report variability using a standard deviation." These statistics estimate different things: a standard deviation estimates the variability among individual observations in a sample, but a standard error of the mean estimates the theoretical variability among means of samples derived from the same population⁷. Many researchers report SE (as opposed to SD) merely for cosmetic reasons, despite the fact that they provide no valid estimate of data variability²⁶. The distinction between standard deviation and standard error of the mean is far more than cosmetic: it is an essential one. We provide a rationale for reporting in the definitions of each quantity immediately above: researchers should report SEs only when the maternal population and not the sample is concerned⁴.

Samples and Populations

It is seldom possible to obtain information from every individual in the population, however, and attention is more commonly restricted to a sample drawn from it. The question of how best to obtain such a sample is a subject worth a discussion on its own and is not covered here. Nevertheless, it is essential that any sample is as representative as possible of the population from which it is drawn, and the best means of obtaining such a sample is generally through random sampling²⁵. It is important to describe the sample and sampling method so that its representativeness to the population, to which the results will be generalized, can be assessed².

Normal Distribution

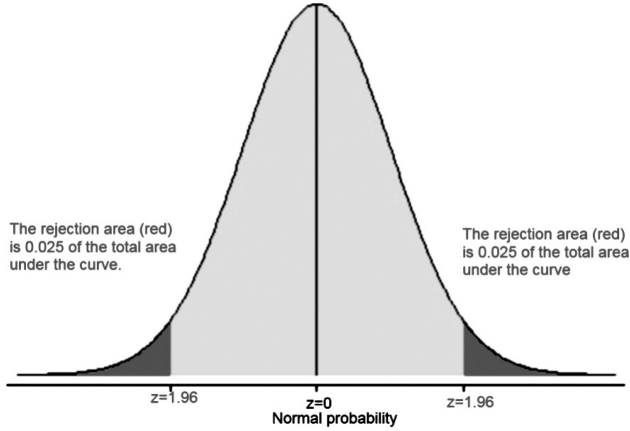
Quantitative clinical data follow a wide range of distributions. By far the most common of these is symmetrical and unimodal, with a single peak in the middle and equal tails at either side. This distinctive bell-shaped distribution is known as 'Normal' or 'Gaussian'²⁵. The properties of the Normal distribution lead to another useful measure of variability in a dataset. Rather than using the SD in isolation, the 95% reference range can be calculated as (mean – 1.96 SD) to (mean + 1.96 SD), provided that the data are (approximately) normally distributed (Figure 1)²⁵.

Figure 1: The normal distribution: P-values and confidence intervals. A z value of 1.96 (aka a distance of 1.96 SD from the mean) denotes both the 95% confidence intervals (the grey shaded area under the curve which equals the 0.95 of the total area under curve) and the alpha-value (the probability "p" level, the 0.05 of the total area under curve or the rejection area).

The Null Hypothesis

A typical analytical research question is most easily expressed in terms of there being some difference between groups. For example, 'In patients with severe trauma, does the intravenous administration of colloid solutions (as compared with crystalloid) reduce mortality?' To answer this question, the most appropriate study design would be a randomized controlled trial comparing trauma patients who receive intravenous colloid solutions with control patients who receive crystalloid solutions. The challenge then would be to interpret the results of that study. Even if there is no real effect of intravenous colloid fluid administration on mortality, sampling variation means that it is extremely unlikely that exactly the same proportion of patients in each group will die. Thus, any observed difference between the two groups may be due to the treatment or it may simply be a coincidence, in other words due to chance. The aim of hypothesis testing is to establish which of these explanations is most likely. Statistical analyses can never prove the truth of a hypothesis, but rather merely provide evidence to support or refute it. To do this, the research question is more formally expressed in terms of there being no difference. This is known as the null hypothesis. In the current example the null hypothesis would be expressed as, 'The administration of intravenous colloid solutions has no effect on mortality in trauma patients when compared to crystalloid solutions. In hypothesis testing any observed differences between two (or more) groups are interpreted within the context of this null hypothesis. More formally, hypothesis testing explores how likely it is that the observed difference would be seen by chance alone if the null hypothesis were true^27–28. This type of research, which incidentally is the standard practice, is known as "Reject- Support" research²⁹. The researcher favors to reject the null hypothesis. In the "Reject-Support" situation, a Type α error represents, a "false positive" for the researcher's theory. From the Editor's standpoint, such false positives are particularly undesirable. They result in much wasted effort, especially when the false positive is interesting from a theoretical standpoint, and as a result stimulates a substantial amount of research. Such follow-up research will probably not replicate the incorrect original work, a fact that will result in much confusion and frustration²⁹. Thus journal editors (and reviewers serving them good) will strive for low Type α error.

Reporting P-values

A broad range of statistical tests is available, suitable for any type of investigation. The end result of any statistical test is a P value. The 'P' stands for probability, and measures how likely it is that any observed difference between groups is due to chance, in other words, stated the probability of Type α error. In simple English, the P value is the probability of seeing the observed difference just by coincidence if the null hypothesis is true. Being a probability, P can take any value between 0 and 1. Values close to 0 indicate that the observed difference is unlikely to be coincidental, whereas a P value close to 1 suggests there is no difference between groups other than that due to random variation. The interpretation of a P value is not always straightforward and several important factors must be taken into account, as outlined below. Basically the P value measures the strength of evidence against the null hypothesis²⁸.

Most scientific publications include a number of p-values. Often, the methods through which those values were obtained are not reported or only partially reported. In addition, reviewers tend to reply to non significant values with a clichi like "If P is not <0.05 it's not significant" and reject or request revision on that ground²⁶. Curran-Everett & Benos state in their guidelines: "De?ne and justify a critical signi?cance level appropriate to the goals of the study"⁸. They further state "report uncertainty about scienti?c importance using a con?dence interval", report a precise P value. A precise P value does two things: it communicates more information with the same amount of ink, and it permits each reader to assess individually a statistical result" and "in the Abstract, report a con?dence interval and a precise P value for each main result"⁸.

P-values and confidence intervals

Although P values provide a measure of the strength of an association, there is a great deal of additional information to be obtained from confidence intervals. Recall the normal distribution and that a confidence interval gives a range of values (for 95% CIs, mean ±1.96 SD) within which it is likely that the true population value lies (Figure 1)²⁸.

When examining confidence intervals in a published medical report, reviewers should look at whether:

• the intervals contain a value that implies no change or no effect.

• the confidence intervals lie partly or entirely within a range of clinical indifference³⁰.

Statistical versus Medical Inference

Medical inference of any study requisites affirmative answer in two questions:

1. Has there been a change in any of the quantities measured and

2. Is the change large enough to be meaningful?

The first question is answered by hypothesis testing and the second by estimation. It is important to establish whether or not a change has occurred that cannot be accounted for by coincidence. However, hypothesis testing is largely an arti?cial construct. The more important issue is whether the magnitude and direction of the change have any clinical relevance³¹.

This point is made more trenchantly by Goodman³², when he refers to the P value fallacy. The author emphasizes that there is a clear distinction between statistical significance and scientific significance, with hypothesis testing pointing to the first, but only estimations revealing the latter³¹. The term "P…ing" refers to the habit of medical writers to provide a large number of p-values, which are of least or immaterial true scientific significance, although statistically significant. Goodman reported that statisticians, armed with an understanding of the limitations of traditional methods, interpret quantitative results, especially P values, very differently from how most non-statisticians do³². A P value is the probability that an observed effect is simply due to chance; it therefore provides a measure of the strength of an association. A P value does not provide any measure of the size of an effect, and cannot be used in isolation to inform clinical judgement. P values are affected both by the magnitude of the effect and by the size of the study from which they are derived, and should therefore be interpreted with caution. In particular, a large P value does not always indicate that there is no association and, similarly, a small P value does not necessarily signify an important clinical effect. Subdividing P values into 'significant' and 'non-significant' is poor statistical practice and should be avoided²⁸. Exact P values should always be presented, along with estimates of effect and associated confidence intervals^7–8,28.

The same apply for confidence intervals. It is correct to say that a confidence interval characterizes uncertainty about the true value of a parameter but incorrect to say that it provides an assessment of scientific importance⁶.

In a world where medical researchers have access to increasingly sophisticated statistical software, the statistical complexity of published research is increasing, and clinical practice is being driven by the empirical evidence base, a deeper understanding of statistics may have come to be too important to leave only to statisticians³².

Power

An increasingly occurring theme of reviewers' comments relates to the issue of sample size²⁶. Typically, the comments allude to sample sizes that are too low, even when a significant effect has been found! Reviewers are expected to question the statistical power of the findings only in those instances where a low sample size was employed and no significant treatment effect was observed²⁶.

Power is the probability of correctly identifying a difference between the two groups in the study sample when one genuinely exists in the populations from which the samples were drawn³³. The ideal study for the researcher is one in which the power is high. This means that the study has a high chance of detecting a difference between groups if one exists; consequently, if the study demonstrates no difference between groups the researcher can be reasonably confident in concluding that none exists in reality. The power of a study depends on several factors (see below), but as a general rule higher power is achieved by increasing the sample size³³. Thus researchers will strive for high power studies. In this case, with "too much power," trivial effects may become "highly significant"²⁹.

It is important to be aware of this because quite often studies are reported that are simply too small to have adequate power to detect the hypothesized effect. In other words, even when a difference exists in reality it may be that too few study subjects have been recruited (Type β error)⁹. In other words, an apparently null result that shows no difference between groups may simply be due to lack of statistical power, making it extremely unlikely that a true difference will be correctly identified³⁴.

Furthermore, many investigators stand accused of conducting unethical research because their studies were "underpowered". This is based on the idea that the projected scientific or clinical value of a study will be unacceptably low if it has low power, that is, if it has less than an 80% chance of producing p<0.05 under an assumed minimum important effect size. It could therefore be unethical to ask participants to accept the risks and discomforts of participation^33,35.

Statistical methods and software

Authors are expected to identify their use of statistical methods, and cite them using textbooks or review papers. Commercial software used for statistical analysis need to be cited separately⁸.

Comparison of means

The familiar t-test requires that certain assumptions are made regarding the format of the data. The one sample t-test requires that the data have an approximately Normal distribution, whereas the paired t-test requires that the distribution of the differences is approximately Normal. The unpaired t-test relies on the assumption that the data from the two samples are both normally distributed, and has the additional requirement that SDs from the two samples are approximately equal.

If assumptions of normality are violated, then appropriate transformation of the data may be used before performing any calculations. Transformations which commonly include square root, logarithmic and napierian may also be useful if the SDs are different in the unpaired case²⁴. However, it may not always be possible to get around these limitations; where this is the case, there are a series of alternative tests that can be used. Known as nonparametric tests, they require very few or very limited assumptions to be made about the format of the data, and can therefore be used in situations where classical methods, such as t-tests, may be inappropriate³⁶.

Non-parametric statistics

A nonparametric alternative to the unpaired t-test is given by the Wilcoxon rank sum test, which is also known as the Mann–Whitney test³⁷. Nonparametric methods may lack power as compared with more traditional approaches²⁴. This is a particular concern if the sample size is small or if the assumptions for the corresponding parametric method (e.g. Normality of the data) are true. Nonparametric methods are geared toward hypothesis testing rather than estimation of effects. It is often possible to obtain nonparametric estimates and associated confidence intervals, but this is not generally straightforward³⁷.

The normality explorations of a dataset should be reported in all cases that parametric tests are used. When this is not done, the likelihood that normality assumptions are not met, should be questioned by reviewers.

Correlation, regression, causation

Correlation is not concerned with the relationship between variables and makes no a priori assumption as to whether one variable is dependent on the other(s). It gives an estimate of the degree of association between the examined variables. Actually, correlation analysis tests for interdependence of the variables.

Consider two variables: crop yield and rainfall. These are measured independently, one by the weather station precipitation appliance and the other by mass scales. While correlation analysis would show a high degree of association between these two variables, regression analysis would be able to demonstrate the dependence of crop yield on rainfall. However, careless use of regression analysis could also demonstrate that rainfall is dependent on crop yield³⁸.

How we regard the relationship between rainfall and crop yield is important. In correlation, both variables are assumed to be variables with random error in them so both are treated on an equal footing and there is no distinction between them. In regression analysis, crop yield is the dependent variable and rainfall is the explanatory variable, according to the theoretical background. The distinction is that the dependent variable, crop yield has no random component, all values are derivative from this distribution³⁹.

Regression denotes dependence amongst variables within a model, still it cannot imply causation⁴⁰. For example, we previously reported that rainfall affects crop yield. However, this is a one-way relationnship: crop yield cannot affect rainfall. Thus, regression can also denote causation only if there is an established cause and effect theoretical association among variables. In short, a statistical relationship does not imply causation^39–40.

Relative risks and Odds ratios

The risk ratio, which it is often referred to as the relative risk measures the increased risk for developing a disease when having been exposed to a risk factor compared with not having been exposed to the risk factor. It is given by RR = risk for the exposed / risk for the unexposed^41–42.

The odds ratio is the measure of effect size, describing the strength of the association or dependence between two dichotomous variables. It is used as a descriptive statistic, and provides the basis for logistic regression. Logistic regression provides a useful way for modelling and quantifying the dependence of a dischtomous dependent variable on one or more independent variables, where the latter can be either categorical or continuous. A number of methods can be used to assess the goodness of fit of the resulting model^23,43–44.

When large samples are concerned, odds ratios and relative risks are practically the same. However, when the sample size is not large, the reviewer can expect the authors to state if they approximated relative risks through odds ratios and why was this done in the methods section.

Control for multiple comparisons

Curran-Everett & Benos report in their guidelines "Control for multiple comparisons"^7–8,23.

Study designs that involve problems of multiple comparisons are common in medical science³. Researchers are more likely to reject a true null hypothesis if they fail to use a multiple comparison procedure when they analyze a family of comparisons³. Specific statistical procedures have been developed to compensate for this effect, namely the Newman-Keuls procedure, the Bonferroni procedure and the Least Significant Difference (LSD) procedure. Each of these has its limitations. The Newman-Keuls and LSD procedures fail to control the family error rate, that is the probability that we reject at least one true null hypothesis in many experimental situations (Type α error). In contrast, the Bonferroni inequality procedure is overly conservative: it fails to detect some of the actual differences that exist within the family (type β error)²³.

Simpson's Paradox

In probability and statistics, Simpson's paradox (or else the Yule-Simpson effect, the reversal paradox or the amalgamation paradox) is an apparent paradox in which the successes of groups seem reversed when the groups are combined³⁰. This result is often encountered in medical science statistics, and occurs when frequency data are hastily given causal interpretation, the paradox disappears when causal relations are derived systematically, through formal analysis. This paradox is chiefly an issue of aggregated statistical analysis where separate -in real life- groups are analyzed together^45–46. The variable that should have been used to separate these groups is called a confounder^30,46.

Apart from the Simpsons paradox, which is a relatively advanced knowledge for a peer reviewer, simple confounders have been reported to exist even among the inclusion criteria of well designed multicenter clinical trials⁴⁷. For that, the reviewers need to thoroughly read the methods section. Of note, by manipulating Simpson's paradox in statistics, authors could publish their results in a way that a certain experimental modality or drug is favoured^30,46. If such issues origin queries to the reviewers, further consultation with the journal's biostatisticians may be justified.

Number needed to treat / harm

Number needed to treat (NNT) (or Number needed to harm (NNH) for adverse effects) is a way for expressing the effectiveness and safety of an intervention, which is truly meaningful for clinical practice. NNT is always computed with respect to two treatments A and B, with A typically being a drug and B being a placebo¹⁴. A defined endpoint has to be specified (for instance development of osteonecrosis of the jaws (ONJ) in cancer patients receiving denosumab)⁴⁸. If the probabilities pA and pB of this endpoint under treatments A and B, respectively, are known, then the NNT is computed as 1/(pB-pA). For example, in the FREEDOM trial⁴⁹, NNT was not reported. In the latter trial, NNT for vertebral, hip and non vertebral fractures was 20, 200 and 67 respectively. This means that in order to prevent a single vertebral fracture we have to prescribe denosumab to 20 patients. In order to prevent a single hip fracture, a clinicians would need to prescribe debosumab to 200 patients. Notably, the authors reported that "treatment with denosumab was associated with a significant 68% reduction in the risk of new vertebral fractures, 40% reduction in the risk of hip fractures and 20% reduction in the risk of vertebral fractures, when compared to placebo⁴⁹. It is evident that peer reviewers for the New England Journal of Medicine overlooked this important aspect. Another example, an NNH of 50 means if 50 patients are treated with denosumab, one would develop the adverse effect of ONJ⁴⁸. An NNT of 2 or 3 indicates that a treatment is quite effective (with one patient in 2 or 3 responding to the treatment). An NNT of 20 to 40 can still be considered clinically effective¹⁴. Often, multicenter RCTs published in well-known journals, fail to report on NNT^49–50. Reviewers should question the authors' intentions⁵⁰.

Discussion

It is common sense, that one cannot become an excellent reviewer only though reading a relevant manuscript. It would take reviewing a number of manuscripts before a reviewer would develop his "reviewer personality". Before that happening, he would probably break some or all of the guidelines reported in this manuscript. Reviewers sometimes base their judgments on cues that have only a weak relation to quality such as statistical significance, large sample size, complex procedures, socalled "negative" data, and obscure writing⁵¹. The reviewers also recommended rejection of the paper with non-significant findings three times as often as those with significant findings⁵¹. To compensate for this, specific guidelines have been proposed^7–8. The guidelines and suggestions reviewed herein, aim to stimulate further reading rather than be used as a checklist to evaluate the work of our colleagues. However, some form of checklist could be handy, for the reviewer to ensure he/ she keeps most aspects of scientific reporting in mind. Such lists are presented in Tables 1 and 2⁹. Their use should not be implemented in the review process, however they could be beneficial to the inexperienced reviewer, who has not yet developed his own "reviewer personality". We believe that authors too, need to refer to such guidance prior to undertaking a scientific writing endeavor. On the other hand, reviewers need not to use these guidelines as checklists when performing their duties, or else the inevitable will happen: a reviewer, not knowing a lot of statistics, but knowing the guidelines well, will reject a manuscript because the statistics are "wrong"⁶. And this is why such guidelines have been both advocated and attacked.

Another matter of concern is how strict should the reviewer be in regard with the journal he serves. Does a reviewer need to be as strict for a manuscript submitted to Hippokratia as he would be for a manuscript submitted to The New England Journal of Medicine? Apparently not: high citation rates, impact factors, and circulation rates, and low manuscript acceptance rates and indexing on Brandon/Hill Library List appear to be predictive of higher methodological quality scores for journal articles⁵². However, the basic principles remain the same and the reviewers should abstain from easily accepting manuscripts for publication. They need to bear in mind that they are the Editor's only quality regulators. If the impact of a journal is likely to go up, the reviewers would be responsible for that. Apart from quality issues, the reviewers are responsible for the suitability of a manuscript and its readability from the journals audience. More complex statistical methods, multivariate statistics and regression analysis may be too confusing for the inexperienced reader who will reject a well designed clinical trial in favor of a short case report in the last pages. Thus the reviewers need also to assure that published manuscripts are appropriate for the ability of the readers. Articles with too complex methodology or discussing too constricted fields of medical practice may be more suitable for more specialized journals, where they will likely draw more citations⁵³.

Other sources of inspiration for authors but also for reviewers²⁶ are the Consolidated Standards for Reporting Trials (CONSORT) statement (checklist criteria and a flow diagram for what should be included in reporting randomized control trials)¹⁷, the Strengthening the Reporting of Observational Studies in Epidemiology (STROBE) statement (guidelines for reporting observational studies)¹⁶, the MOOSE proposal (Guidelines for Meta-Analyses and Systematic Reviews of Observational Studies).

It is the reviewers' responsibility to ensure that the authors are both fair treated and they clearly understand the rational behind the rejection or the acceptance of their article.