Meta-analysis in medical research

Abstract

The objectives of this paper are to provide an introduction to meta-analysis and to discuss the rationale for this type of research and other general considerations. Methods used to produce a rigorous meta-analysis are highlighted and some aspects of presentation and interpretation of meta-analysis are discussed.

Meta-analysis is a quantitative, formal, epidemiological study design used to systematically assess previous research studies to derive conclusions about that body of research. Outcomes from a meta-analysis may include a more precise estimate of the effect of treatment or risk factor for disease, or other outcomes, than any individual study contributing to the pooled analysis. The examination of variability or heterogeneity in study results is also a critical outcome. The benefits of meta-analysis include a consolidated and quantitative review of a large, and often complex, sometimes apparently conflicting, body of literature. The specification of the outcome and hypotheses that are tested is critical to the conduct of meta-analyses, as is a sensitive literature search. A failure to identify the majority of existing studies can lead to erroneous conclusions; however, there are methods of examining data to identify the potential for studies to be missing; for example, by the use of funnel plots. Rigorously conducted meta-analyses are useful tools in evidence-based medicine. The need to integrate findings from many studies ensures that meta-analytic research is desirable and the large body of research now generated makes the conduct of this research feasible.

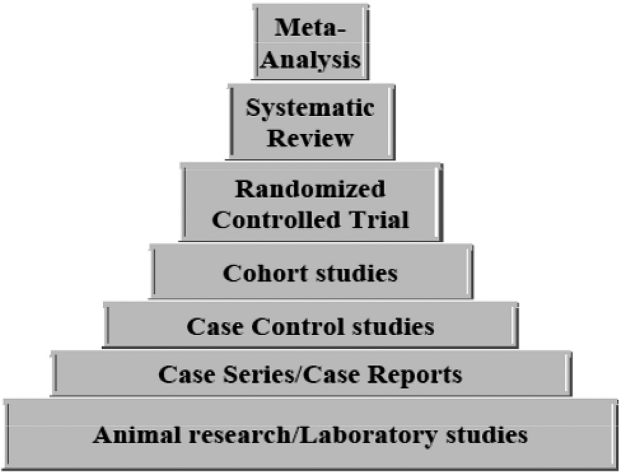
Important medical questions are typically studied more than once, often by different research teams in different locations. In many instances, the results of these multiple small studies of an issue are diverse and conflicting, which makes the clinical decision-making difficult. The need to arrive at decisions affecting clinical practise fostered the momentum toward "evidence-based medicine"^1–2. Evidence-based medicine may be defined as the systematic, quantitative, preferentially experimental approach to obtaining and using medical information. Therefore, meta-analysis, a statistical procedure that integrates the results of several independent studies, plays a central role in evidence-based medicine. In fact, in the hierarchy of evidence (Figure 1), where clinical evidence is ranked according to the strength of the freedom from various biases that beset medical research, meta-analyses are in the top. In contrast, animal research, laboratory studies, case series and case reports have little clinical value as proof, hence being in the bottom.

Figure 1: Hierarchy of evidence.

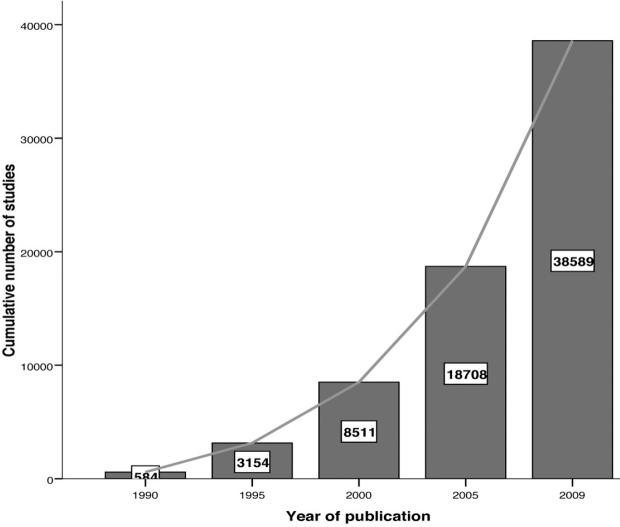
Meta-analysis did not begin to appear regularly in the medical literature until the late 1970s but since then a plethora of meta-analyses have emerged and the growth is exponential over time (Figure 2)³. Moreover, it has been shown that meta-analyses are the most frequently cited form of clinical research⁴. The merits and perils of the somewhat mysterious procedure of meta-analysis, however, continue to be debated in the medical community^{5– 8}. The objectives of this paper are to introduce meta-analysis and to discuss the rationale for this type of research and other general considerations.

Figure 2: Cumulative number of publications about metaanalysis over time, until 17 December 2009 (results from Medline search using text "meta-analysis").

Meta-Analysis and Systematic Review

Glass first defined meta-analysis in the social science literature as "The statistical analysis of a large collection of analysis results from individual studies for the purpose of integrating the findings"⁹. Meta-analysis is a quantitative, formal, epidemiological study design used to systematically assess the results of previous research to derive conclusions about that body of research. Typically, but not necessarily, the study is based on randomized, controlled clinical trials. Outcomes from a meta-analysis may include a more precise estimate of the effect of treatment or risk factor for disease, or other outcomes, than any individual study contributing to the pooled analysis. Identifying sources of variation in responses; that is, examining heterogeneity of a group of studies, and generalizability of responses can lead to more effective treatments or modifications of management. Examination of heterogeneity is perhaps the most important task in meta-analysis. The Cochrane collaboration has been a long-standing, rigorous, and innovative leader in developing methods in the field¹⁰. Major contributions include the development of protocols that provide structure for literature search methods, and new and extended analytic and diagnostic methods for evaluating the output of meta-analyses. Use of the methods outlined in the handbook should provide a consistent approach to the conduct of meta-analysis. Moreover, a useful guide to improve reporting of systematic reviews and meta-analyses is the PRISMA (Preferred Reporting Items for Systematic reviews and Meta-analyses) statement that replaced the QUOROM (QUality Of Reporting of Meta-analyses) statement^11–13.

Meta-analyses are a subset of systematic review. A systematic review attempts to collate empirical evidence that fits prespecified eligibility criteria to answer a specific research question. The key characteristics of a systematic review are a clearly stated set of objectives with predefined eligibility criteria for studies; an explicit, reproducible methodology; a systematic search that attempts to identify all studies that meet the eligibility criteria; an assessment of the validity of the findings of the included studies (e.g., through the assessment of risk of bias); and a systematic presentation and synthesis of the attributes and findings from the studies used. Systematic methods are used to minimize bias, thus providing more reliable findings from which conclusions can be drawn and decisions made than traditional review methods^14,15. Systematic reviews need not contain a meta-analysisthere are times when it is not appropriate or possible; however, many systematic reviews contain meta-analyses¹⁶.

The inclusion of observational medical studies in meta-analyses led to considerable debate over the validity of meta-analytical approaches, as there was necessarily a concern that the observational studies were likely to be subject to unidentified sources of confounding and risk modification¹⁷. Pooling such findings may not lead to more certain outcomes. Moreover, an empirical study showed that in meta-analyses were both randomized and non-randomized was included, nonrandomized studies tended to show larger treatment effects¹⁸.

Meta-analyses are conducted to assess the strength of evidence present on a disease and treatment. One aim is to determine whether an effect exists; another aim is to determine whether the effect is positive or negative and, ideally, to obtain a single summary estimate of the effect. The results of a meta-analysis can improve precision of estimates of effect, answer questions not posed by the individual studies, settle controversies arising from apparently conflicting studies, and generate new hypotheses. In particular, the examination of heterogeneity is vital to the development of new hypotheses.

Individual or Aggregated Data

The majority of meta-analyses are based on a series of studies to produce a point estimate of an effect and measures of the precision of that estimate. However, methods have been developed for the meta-analyses to be conducted on data obtained from original trials^19,20. This approach may be considered the "gold standard" in metaanalysis because it offers advantages over analyses using aggregated data, including a greater ability to validate the quality of data and to conduct appropriate statistical analysis. Further, it is easier to explore differences in effect across subgroups within the study population than with aggregated data. The use of standardized individual-level information may help to avoid the problems encountered in meta-analyses of prognostic factors^21,22. It is the best way to obtain a more global picture of the natural history and predictors of risk for major outcomes, such as in scleroderma^23–26.This approach relies on cooperation between researchers who conducted the relevant studies. Researchers who are aware of the potential to contribute or conduct these studies will provide and obtain additional benefits by careful maintenance of original databases and making these available for future studies.

Literature Search

A sound meta-analysis is characterized by a thorough and disciplined literature search. A clear definition of hypotheses to be investigated provides the framework for such an investigation. According to the PRISMA statement, an explicit statement of questions being addressed with reference to participants, interventions, comparisons, outcomes and study design (PICOS) should be provided^11,12. It is important to obtain all relevant studies, because loss of studies can lead to bias in the study. Typically, published papers and abstracts are identified by a computerized literature search of electronic databases that can include PubMed (www.ncbi.nlm.nih.gov./entrez/query.fcgi), ScienceDirect (www.sciencedirect.com), Scirus (www.scirus.com/srsapp ), ISI Web of Knowledge (http://www.isiwebofknowledge.com), Google Scholar (http://scholar.google.com) and CENTRAL (Cochrane Central Register of Controlled Trials, http://www.mrw.interscience.wiley.com/cochrane/cochrane_clcentral_articles_fs.htm). PRISMA statement recommends that a full electronic search strategy for at least one major database to be presented¹². Database searches should be augmented with hand searches of library resources for relevant papers, books, abstracts, and conference proceedings. Crosschecking of references, citations in review papers, and communication with scientists who have been working in the relevant field are important methods used to provide a comprehensive search. Communication with pharmaceutical companies manufacturing and distributing test products can be appropriate for studies examining the use of pharmaceutical interventions.

It is not feasible to find absolutely every relevant study on a subject. Some or even many studies may not be published, and those that are might not be indexed in computer-searchable databases. Useful sources for unpublished trials are the clinical trials registers, such as the National Library of Medicine's ClinicalTrials.gov Website. The reviews should attempt to be sensitive; that is, find as many studies as possible, to minimize bias and be efficient. It may be appropriate to frame a hypothesis that considers the time over which a study is conducted or to target a particular subpopulation. The decision whether to include unpublished studies is difficult. Although language of publication can provide a difficulty, it is important to overcome this difficulty, provided that the populations studied are relevant to the hypothesis being tested.

Inclusion or Exclusion Criteria and Potential for Bias

Studies are chosen for meta-analysis based on inclusion criteria. If there is more than one hypothesis to be tested, separate selection criteria should be defined for each hypothesis. Inclusion criteria are ideally defined at the stage of initial development of the study protocol. The rationale for the criteria for study selection used should be clearly stated.

One important potential source of bias in meta-analysis is the loss of trials and subjects. Ideally, all randomized subjects in all studies satisfy all of the trial selection criteria, comply with all the trial procedures, and provide complete data. Under these conditions, an "intention-totreat" analysis is straightforward to implement; that is, statistical analysis is conducted on all subjects that are enrolled in a study rather than those that complete all stages of study considered desirable. Some empirical studies had shown that certain methodological characteristics, such as poor concealment of treatment allocation or no blinding in studies exaggerate treatment effects²⁷. Therefore, it is important to critically appraise the quality of studies in order to assess the risk of bias.

The study design, including details of the method of randomization of subjects to treatment groups, criteria for eligibility in the study, blinding, method of assessing the outcome, and handling of protocol deviations are important features defining study quality. When studies are excluded from a meta-analysis, reasons for exclusion should be provided for each excluded study. Usually, more than one assessor decides independently which studies to include or exclude, together with a well-defined checklist and a procedure that is followed when the assessors disagree. Two people familiar with the study topic perform the quality assessment for each study, independently. This is followed by a consensus meeting to discuss the studies excluded or included. Practically, the blinding of reviewers from details of a study such as authorship and journal source is difficult.

Before assessing study quality, a quality assessment protocol and data forms should be developed. The goal of this process is to reduce the risk of bias in the estimate of effect. Quality scores that summarize multiple components into a single number exist but are misleading and unhelpful²⁸. Rather, investigators should use individual components of quality assessment and describe trials that do not meet the specified quality standards and probably assess the effect on the overall results by excluding them, as part of the sensitivity analyses.

Further, not all studies are completed, because of protocol failure, treatment failure, or other factors. Nonetheless, missing subjects and studies can provide important evidence. It is desirable to obtain data from all relevant randomized trials, so that the most appropriate analysis can be undertaken. Previous studies have discussed the significance of missing trials to the interpretation of intervention studies in medicine^29,30. Journal editors and reviewers need to be aware of the existing bias toward publishing positive findings and ensure that papers that publish negative or even failed trials be published, as long as these meet the quality guidelines for publication.

There are occasions when authors of the selected papers have chosen different outcome criteria for their main analysis. In practice, it may be necessary to revise the inclusion criteria for a meta-analysis after reviewing all of the studies found through the search strategy. Variation in studies reflects the type of study design used, type and application of experimental and control therapies, whether or not the study was published, and, if published, subjected to peer review, and the definition used for the outcome of interest. There are no standardized criteria for inclusion of studies in meta-analysis. Universal criteria are not appropriate, however, because meta-analysis can be applied to a broad spectrum of topics. Published data in journal papers should also be cross-checked with conference papers to avoid repetition in presented data.

Clearly, unpublished studies are not found by searching the literature. It is possible that published studies are systemically different from unpublished studies; for example, positive trial findings may be more likely to be published. Therefore, a meta-analysis based on literature search results alone may lead to publication bias.

Efforts to minimize this potential bias include working from the references in published studies, searching computerized databases of unpublished material, and investigating other sources of information including conference proceedings, graduate dissertations and clinical trial registers.

Statistical analysis

The most common measures of effect used for dichotomous data are the risk ratio (also called relative risk) and the odds ratio. The dominant method used for continuous data are standardized mean difference (SMD) estimation. Methods used in meta-analysis for post hoc analysis of findings are relatively specific to meta-analysis and include heterogeneity analysis, sensitivity analysis, and evaluation of publication bias.

All methods used should allow for the weighting of studies. The concept of weighting reflects the value of the evidence of any particular study. Usually, studies are weighted according to the inverse of their variance³¹. It is important to recognize that smaller studies, therefore, usually contribute less to the estimates of overall effect. However, well-conducted studies with tight control of measurement variation and sources of confounding contribute more to estimates of overall effect than a study of identical size less well conducted.

One of the foremost decisions to be made when conducting a meta-analysis is whether to use a fixed-effects or a random-effects model. A fixed-effects model is based on the assumption that the sole source of variation in observed outcomes is that occurring within the study; that is, the effect expected from each study is the same. Consequently, it is assumed that the models are homogeneous; there are no differences in the underlying study population, no differences in subject selection criteria, and treatments are applied the same way³². Fixed-effect methods used for dichotomous data include most often the Mantel-Haenzel method³³ and the Peto method ³⁴(only for odds ratios).

Random-effects models have an underlying assumption that a distribution of effects exists, resulting in heterogeneity among study results, known as τ2. Consequently, as software has improved, random-effects models that require greater computing power have become more frequently conducted. This is desirable because the strong assumption that the effect of interest is the same in all studies is frequently untenable. Moreover, the fixed effects model is not appropriate when statistical heterogeneity (τ2) is present in the results of studies in the meta-analysis. In the random-effects model, studies are weighted with the inverse of their variance and the heterogeneity parameter. Therefore, it is usually a more conservative approach with wider confidence intervals than the fixed-effects model where the studies are weighted only with the inverse of their variance. The most commonly used random-effects method is the DerSimonian and Laird method³⁵. Furthermore, it is suggested that comparing the fixed-effects and random-effect models developed as this process can yield insights to the data³⁶.

Heterogeneity

Arguably, the greatest benefit of conducting metaanalysis is to examine sources of heterogeneity, if present, among studies. If heterogeneity is present, the summary measure must be interpreted with caution ³⁷. When heterogeneity is present, one should question whether and how to generalize the results. Understanding sources of heterogeneity will lead to more effective targeting of prevention and treatment strategies and will result in new research topics being identified. Part of the strategy in conducting a meta-analysis is to identify factors that may be significant determinants of subpopulation analysis or covariates that may be appropriate to explore in all studies.

To understand the nature of variability in studies, it is important to distinguish between different sources of heterogeneity. Variability in the participants, interventions, and outcomes studied has been described as clinical diversity, and variability in study design and risk of bias has been described as methodological diversity¹⁰. Variability in the intervention effects being evaluated among the different studies is known as statistical heterogeneity and is a consequence of clinical or methodological diversity, or both, among the studies. Statistical heterogeneity manifests itself in the observed intervention effects varying by more than the differences expected among studies that would be attributable to random error alone. Usually, in the literature, statistical heterogeneity is simply referred to as heterogeneity.

Clinical variation will cause heterogeneity if the intervention effect is modified by the factors that vary across studies; most obviously, the specific interventions or participant characteristics that are often reflected in different levels of risk in the control group when the outcome is dichotomous. In other words, the true intervention effect will differ for different studies. Differences between studies in terms of methods used, such as use of blinding or differences between studies in the definition or measurement of outcomes, may lead to differences in observed effects. Significant statistical heterogeneity arising from differences in methods used or differences in outcome assessments suggests that the studies are not all estimating the same effect, but does not necessarily suggest that the true intervention effect varies. In particular, heterogeneity associated solely with methodological diversity indicates that studies suffer from different degrees of bias. Empirical evidence suggests that some aspects of design can affect the result of clinical trials, although this may not always be the case.

The scope of a meta-analysis will largely determine the extent to which studies included in a review are diverse. Meta-analysis should be conducted when a group of studies is sufficiently homogeneous in terms of subjects involved, interventions, and outcomes to provide a meaningful summary. However, it is often appropriate to take a broader perspective in a meta-analysis than in a single clinical trial. Combining studies that differ substantially in design and other factors can yield a meaningless summary result, but the evaluation of reasons for the heterogeneity among studies can be very insightful. It may be argued that these studies are of intrinsic interest on their own, even though it is not appropriate to produce a single summary estimate of effect.

Variation among k trials is usually assessed using Cochran's Q statistic, a chi-squared (χ²) test of heterogeneity with k-1 degrees of freedom. This test has relatively poor power to detect heterogeneity among small numbers of trials; consequently, an α-level of 0.10 is used to test hypotheses^38,39.

Heterogeneity of results among trials is better quantified using the inconsistency index I ², which describes the percentage of total variation across studies⁴⁰. Uncertainty intervals for I ² (dependent on Q and k) are calculated using the method described by Higgins and Thompson⁴¹. Negative values of I ² are put equal to zero, consequently I ² lies between 0 and 100%. A value >75% may be considered substantial heterogeneity⁴¹. This statistic is less influenced by the number of trials compared with other methods used to estimate the heterogeneity and provides a logical and readily interpretable metric but it still can be unstable when only a few studies are combined⁴².

Given that there are several potential sources of heterogeneity in the data, several steps should be considered in the investigation of the causes. Although random-effects models are appropriate, it may be still very desirable to examine the data to identify sources of heterogeneity and to take steps to produce models that have a lower level of heterogeneity, if appropriate. Further, if the studies examined are highly heterogeneous, it may be not appropriate to present an overall summary estimate, even when random effects models are used. As Petiti notes⁴³, statistical analysis alone will not make contradictory studies agree; critically, however, one should use common sense in decision-making. Despite heterogeneity in responses, if all studies had a positive point direction and the pooled confidence interval did not include zero, it would not be logical to conclude that there was not a positive effect, provided that sufficient studies and subject numbers were present. The appropriateness of the point estimate of the effect is much more in question.

Some of the ways to investigate the reasons for heterogeneity; are subgroup analysis and meta-regression. The subgroup analysis approach, a variation on those described above, groups categories of subjects (e.g., by age, sex) to compare effect sizes. The meta-regression approach uses regression analysis to determine the influence of selected variables (the independent variables) on the effect size (the dependent variable). In a meta-regresregression, studies are regarded as if they were individual patients, but their effects are properly weighted to account for their different variances⁴⁴.

Sensitivity analyses have also been used to examine the effects of studies identified as being aberrant concerning conduct or result, or being highly influential in the analysis. Recently, another method has been proposed that reduces the weight of studies that are outliers in meta-analyses⁴⁵. All of these methods for examining heterogeneity have merit, and the variety of methods available reflects the importance of this activity.

Presentation of results

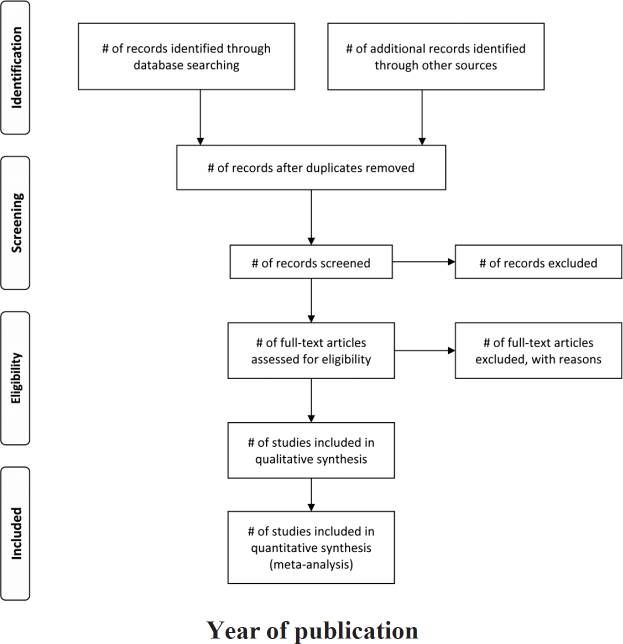
A useful graph, presented in the PRISMA statement¹¹, is the four-phase flow diagram (Figure 3).

Figure 3: PRISMA 2009 Flow Diagram (From Moher D, Liberati A, Tetzlaff J, Altman DG; PRISMA Group. Preferred reporting items for systematic reviews and meta-analyses: the PRISMA statement. J Clin Epidemiol 2009;62:1006-12, For more information, visit www.prisma-statement.org).

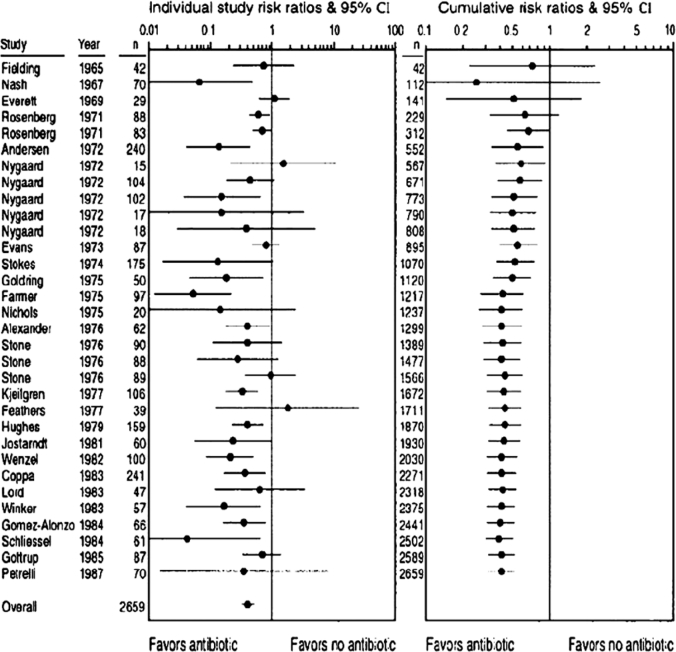
This flow-diagram depicts the flow of information through the different phases of a systematic review or meta-analysis. It maps out the number of records identified, included and excluded, and the reasons for exclusions. The results of meta-analyses are often presented in a forest plot, where each study is shown with its effect size and the corresponding 95% confidence interval (Figure 4).

Figure 4: Forest plots of the meta-analysis addressing the use of antibiotic prophylaxis compared with no treatment in colon surgery. The outcome is would infection and 32 studies were included in the meta-analysis. Risk ratio <1 favors use of prophylactic antibiotics, whereas risk ratio > 1 suggests that no treatment is better. Left panel, Studies displayed chronologically by year of publication, n represents study size. Each study is represented by a filled circle (denoting its risk ratio estimate) and the horizontal line denotes the corresponding 95% confidence interval. Studies that intersect the vertical line of unity (RR=1), indicate no difference between the antibiotic group and the control group. Pooled results from all studies are shown at bottom with the random-effect model. Right panel,Cumulative meta-analysis of same studies with random-effects model, where the summary risk ratio is re-estimated each time a study is added over time. It reveals that antibiotic prophylaxis efficacy could have been identified as early as 1971 after 5 studies involving about 300 patients (n in this panel represents cumulative number of patients from included studies). (From Ioannidis JP, Lau J. State of the evidence: current status and prospects of metaanalysis in infectious diseases. Clin Infect Dis 1999;29:117885).

The pooled effect and 95% confidence interval is shown in the bottom in the same line with "Overall". In the right panel of Figure 4, the cumulative meta-analysis is graphically displayed, where data are entered successively, typically in the order of their chronological appearance^46,47. Such cumulative meta-analysis can retrospectively identify the point in time when a treatment effect first reached conventional levels of significance. Cumulative meta-analysis is a compelling way to examine trends in the evolution of the summary-effect size, and to assess the impact of a specific study on the overall conclusions⁴⁶. The figure shows that many studies were performed long after cumulative meta-analysis would have shown a significant beneficial effect of antibiotic prophylaxis in colon surgery.

Biases in meta-analysis

Although the intent of a meta-analysis is to find and assess all studies meeting the inclusion criteria, it is not always possible to obtain these. A critical concern is the papers that may have been missed. There is good reason to be concerned about this potential loss because studies with significant, positive results (positive studies) are more likely to be published and, in the case of interventions with a commercial value, to be promoted, than studies with non-significant or "negative" results (negative studies). Studies that produce a positive result, especially large studies, are more likely to have been published and, conversely, there has been a reluctance to publish small studies that have non-significant results. Further, publication bias is not solely the responsibility of editorial policy as there is reluctance among researchers to publish results that were either uninteresting or are not randomized⁴⁸. There are, however, problems with simply including all studies that have failed to meet peer-review standards. All methods of retrospectively dealing with bias in studies are imperfect.

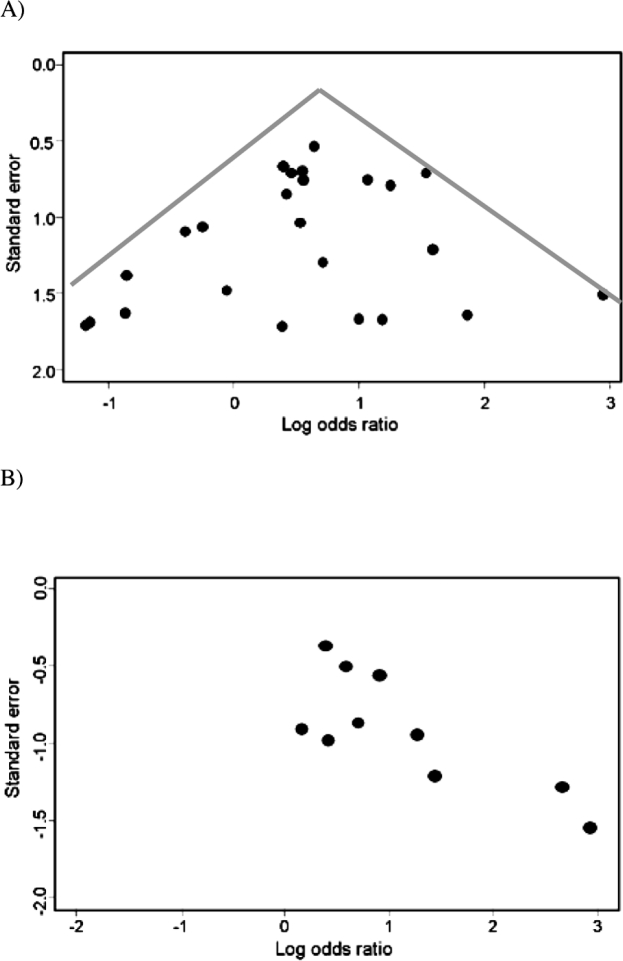
It is important to examine the results of each meta-analysis for evidence of publication bias. An estimation of likely size of the publication bias in the review and an approach to dealing with the bias is inherent to the conduct of many meta-analyses. Several methods have been developed to provide an assessment of publication bias; the most commonly used is the funnel plot. The funnel plot provides a graphical evaluation of the potential for bias and was developed by Light and Pillemer⁴⁹ and discussed in detail by Egger and colleagues^50,51. A funnel plot is a scatterplot of treatment effect against a measure of study size. If publication bias is not present, the plot is expected to have a symmetric inverted funnel shape, as shown in Figure 5A.

Figure 5: A) Symmetrical funnel plot. B) Asymmetrical funnel plot, the small negative studies in the bottom left corner is missing.

In a study in which there is no publication bias, larger studies (i.e., have lower standard error) tend to cluster closely to the point estimate. As studies become less precise, such as in smaller trials (i.e., have a higher standard error), the results of the studies can be expected to be more variable and are scattered to both sides of the more precise larger studies. Figure 5A shows that the smaller, less precise studies are, indeed, scattered to both sides of the point estimate of effect and that these seem to be symmetrical, as an inverted funnel-plot, showing no evidence of publication bias. In contrast to Figure 5A, Figure 5B shows evidence of publication bias. There is evidence of the possibility that studies using smaller numbers of subjects and showing an decrease in effect size (lower odds ratio) were not published.

Asymmetry of funnel plots is not solely attributable to publication bias, but may also result from clinical heterogeneity among studies. Sources of clinical heterogeneity include differences in control or exposure of subjects to confounders or effect modifiers, or methodological heterogeneity between studies; for example, a failure to conceal treatment allocation. There are several statistical tests for detecting funnel plot asymmetry; for example, Eggers linear regression test⁵⁰, and Begg's rank correlation test⁵² but these do not have considerable power and are rarely used. However, the funnel plot is not without problems. If high precision studies really are different than low precision studies with respect to effect size (e.g., due different populations examined) a funnel plot may give a wrong impression of publication bias⁵³. The appearance of the funnel plot plot can change quite dramatically depending on the scale on the y-axis - whether it is the inverse square error or the trial size⁵⁴.

Other types of biases in meta-analysis include the time lag bias, selective reporting bias and the language bias. The time lag bias arises from the published studies, when those with striking results are published earlier than those with non-significant findings⁵⁵. Moreover, it has been shown that positive studies with high early accrual of patients are published sooner than negative trials with low early accrual⁵⁶. However, missing studies, either due to publication bias or time-lag bias may increasingly be identified from trials registries.

The selective reporting bias exists when published articles have incomplete or inadequate reporting. Empirical studies have shown that this bias is widespread and of considerable importance when published studies were compared with their study protocols^29,30. Furthermore, recent evidence suggests that selective reporting might be an issue in safety outcomes and the reporting of harms in clinical trials is still suboptimal⁵⁷. Therefore, it might not be possible to use quantitative objective evidence for harms in performing meta-analyses and making therapeutic decisions.

Excluding clinical trials reported in languages other than English from meta-analyses may introduce the language bias and reduce the precision of combined estimates of treatment effects. Trials with statistically significant results have been shown to be published in English⁵⁸. In contrast, a later more extensive investigation showed that trials published in languages other than English tend to be of lower quality and produce more favourable treatment effects than trials published in English and concluded that excluding non-English language trials has generally only modest effects on summary treatment effect estimates but the effect is difficult to predict for individual meta-analyses⁵⁹.

Evolution of meta-analyses

The classical meta-analysis compares two treatments while network meta-analysis (or multiple treatment metaanalysis) can provide estimates of treatment efficacy of multiple treatment regimens, even when direct comparisons are unavailable by indirect comparisons⁶⁰. An example of a network analysis would be the following. An initial trial compares drug A to drug B. A different trial studying the same patient population compares drug B to drug C. Assume that drug A is found to be superior to drug B in the first trial. Assume drug B is found to be equivalent to drug C in a second trial. Network analysis then, allows one to potentially say statistically that drug A is also superior to drug C for this particular patient population. (Since drug A is better than drug B, and drug B is equivalent to drug C, then drug A is also better to drug C even though it was not directly tested against drug C.)

Meta-analysis can also be used to summarize the performance of diagnostic and prognostic tests. However, studies that evaluate the accuracy of tests have a unique design requiring different criteria to appropriately assess the quality of studies and the potential for bias. Additionally, each study reports a pair of related summary statistics (for example, sensitivity and specificity) rather than a single statistic (such as a risk ratio) and hence requires different statistical methods to pool the results of the studies⁶¹. Various techniques to summarize results from diagnostic and prognostic test results have been proposed^62–64. Furthermore, there are many methodologies for advanced meta-analysis that have been developed to address specific concerns, such as multivariate meta-analysis^65–67, and special types of meta-analysis in genetics⁶⁸ but will not be discussed here.

Meta-analysis is no longer a novelty in medicine. Numerous meta-analyses have been conducted for the same medical topic by different researchers. Recently, there is a trend to combine the results of different meta-analyses, known as a meta-epidemiological study, to assess the risk of bias^79,70.

Conclusions

The traditional basis of medical practice has been changed by the use of randomized, blinded, multicenter clinical trials and meta-analysis, leading to the widely used term "evidence-based medicine". Leaders in initiating this change have been the Cochrane Collaboration who have produced guidelines for conducting systematic reviews and meta-analyses¹⁰ and recently the PRISMA statement, a helpful resource to improve reporting of systematic reviews and meta-analyses has been released¹¹. Moreover, standards by which to conduct and report meta-analyses of observational studies have been published to improve the quality of reporting⁷¹.

Meta-analysis of randomized clinical trials is not an infallible tool, however, and several examples exist of meta-analyses which were later contradicted by single large randomized controlled trials, and of meta-analyses addressing the same issue which have reached opposite conclusions⁷². A recent example, was the controversy between a meta-analysis of 42 studies⁷³ and the subsequent publication of the large-scale trial (RECORD trial) that did not support the cardiovascular risk of rosiglitazone⁷⁴. However, the reason for this controversy was explained by the numerous methodological flaws found both in the meta-analysis and the large clinical trial⁷⁵.

No single study, whether meta-analytic or not, will provide the definitive understanding of responses to treatment, diagnostic tests, or risk factors influencing disease. Despite this limitation, meta-analytic approaches have demonstrable benefits in addressing the limitations of study size, can include diverse populations, provide the opportunity to evaluate new hypotheses, and are more valuable than any single study contributing to the analysis. The conduct of the studies is critical to the value of a meta-analysis and the methods used need to be as rigorous as any other study conducted.