Abstract
We present a fully automatic lung lobe segmentation algorithm that is effective in high resolution computed tomography (CT) datasets in the presence of confounding factors such as incomplete fissures (anatomical structures indicating lobe boundaries), advanced disease states, high body mass index (BMI), and low-dose scanning protocols. In contrast to other algorithms that leverage segmentations of auxiliary structures (esp. vessels and airways), we rely only upon image features indicating fissure locations. We employ a particle system that samples the image domain and provides a set of candidate fissure locations. We follow this stage with maximum a posteriori (MAP) estimation to eliminate poor candidates and then perform a post-processing operation to remove remaining noise particles. We then fit a thin plate spline (TPS) interpolating surface to the fissure particles to form the final lung lobe segmentation. Results indicate that our algorithm performs comparably to pulmonologist-generated lung lobe segmentations on a set of challenging cases.
1 Introduction
Anatomically, the lungs consist of distinct lobes: the left lung is divided into upper and lower lobes, while the right lung is divided into upper, middle, and lower lobes. Each lobe has airway, vascular, and lymphatic supplies that are more or less independent of those supplies to other lobes. Fissures (left oblique, right oblique, and right horizontal) define the boundaries between the lobes and present as 3D surfaces that have greater attenuation (i.e. are brighter) than the surrounding lung parenchyma in CT datasets.
Several pulmonary diseases preferentially affect specific lobes: tuberculosis and silicosis tend to affect the upper lobes while interstitial pulmonary fibrosis tends to occur in the lower lobes [1]. In the case of chronic obstructive pulmonary disease (especially emphysema), there are ongoing efforts to produce clinically relevant disease subtypes for better diagnosis and patient management. Performing lobe-based quantitative analysis can assist such efforts, especially in the context of epidemiological studies. Additionally, lobe specific measurements can help determine whether patients are good candidates for procedures such as lung volume reduction surgery [2]. These issues motivate the need for automatic and reliable lobe segmentation algorithms.
Advanced disease states (e.g. emphysema), atelectasis, and certain imaging protocols (low-dose, and expiratory acquisitions) can make it difficult to detect fissures in certain regions, and so-called incomplete fissures are not uncommon [3]. In [4] the authors address the issue of missing fissures. They use contextual information drawn from segmentations of the lung, fissure, and bronchial tree in conjunction with a multi-atlas selection mechanism to segment datasets that exhibit incomplete fissures. In a similar vein [5] does not rely on the presence of fissures but instead rely on the absence of vessels in the vicinity of the fissures (leveraging the dedicated blood supplies to each lobe). [1] uses vascular and airway tree segmentations to provide contextual clues for fissure locations. These approaches, however, rely on reliable segmentations of auxiliary structures (although [4] do not require such structures to be segmented, segmentation accuracy diminishes when they are not used in the presence of missing fissures). [6] has shown that by selecting a small set of points along each of the three fissures, thin plate spline (TPS) interpolation is sufficient to accurately delineate the major lobes. However, the points in this study were manually selected. We build on this work and automatically identify fissure locations by adopting and extending the particle system for ridge surface extraction previously described by [7]. Other fissure identification and enhancement schemes have been proposed, namely [8]. We choose the particle approach because it is a fast and flexible way in which to sample likely fissure locations from the image data, and it fits seamlessly into the TPS surface fitting stage.
Following particle convergence, maximum a posteriori (MAP) estimation is used to both estimate the parameters of a smoothly fit TPS surface and to classify the particles as being members of either fissure or non-fissure classes. Making the assumption that fissures are locally planar, a post-processing stage is used to reject any remaining non-fissure points. We then use the methodology described in [6] to acquire the final lung lobe segmentation.
The paper is outlined as follows. In section 2 we describe the steps in our approach: lung segmentation, particles based sampling, MAP estimation, post-processing, and TPS fitting. In section 3 we describe the data used in our study and report the results of our algorithm on these datasets as compared to pulmonologist-established ground truth. In section 4 we discuss our results and draw conclusions about our methodology.
2 Methods
In this section we describe our approach to lobe segmentation. We begin by performing lung segmentation, which produces a labeling of the left and right lungs. Lung segmentation algorithms have been described elsewhere ([6],[9]), so we do not discuss this step here. Below we briefly review the method described by [6], by which interpolating surfaces are fit through a sparse set of points to define lobe boundaries. Next we discuss the sampling method used to identify candidate fissure points, which is based on [7] specialized for ridge features. Following this we describe the MAP estimation that enables the elimination of non-fissure points from the sampling stage. Finally, we present a post-processing stage that eliminates remaining noise points. The final set of points is then used to define the lobe boundaries as in [6].
Thin Plate Spline Interpolation
Our goal is to identify a set of points along each fissure through which a TPS surface can be fit that accurately captures the lobe boundaries. [6] suggested that a small set of such points is sufficient to identify these surfaces. The TPS interpolating surface is the minimally curved surface that passes through all the selected points. The equation is given by
| (1) |
where U(r) = r2 log r is the radial basis function. The coefficient vector, a = (a1, a2, a3), and the weight vector, w = (w1, …, wn) are determined from the n identified fissure points, P, such that the height function’s bending energy is minimized [10]. In the procedure we will outline below, a TPS surface is fit independently for each of the three fissures of interest.
Particles Sampling
Once the lung field is segmented we rescale the intensity from [−1024HU,−200HU] to [0, 216] to maximize contrast and then compute a sampling of features that include the fissures. We adopt a particle system for feature extraction described by [7]. As the fissure surface between lung lobes has higher radio-opacity than the lobes themselves, the fissure can be isolated as a ridge surface, defined by [11] as the loci of points where the gradient of the image is orthogonal to the minor eigenvector of the Hessian. For the particle system, a smooth image domain is computed by cubic B-Spline interpolation, and the particles are constrained to lie within ridge surfaces by a Newton optimization that maximizes the image intensity, restricted to motion along the Hessian minor eigenvector e3 (with corresponding negative eigenvalue λ3).
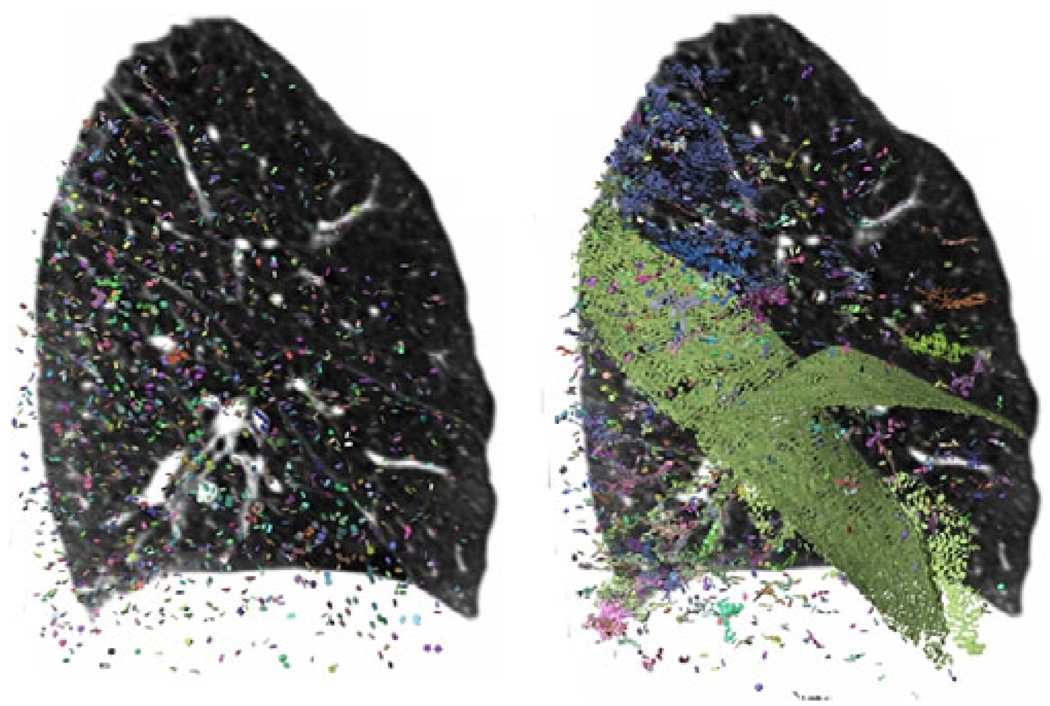
The iterative solution of the particle system involves adding, moving, or removing particles to minimize the collective energy of the system, which is the sum of energy from all pair-wise particle interactions, governed by a single rotationally symmetric potential ϕ(r) around each point. As described in [7], having a small negative well in ϕ(r) allows the particle system’s population control to be formulated in the same energy minimization that moves particles into a uniform close-packing onto ridge surfaces. Particles are also removed when the local image properties suggest that they are no longer within a well-defined ridge surface, for which we adopted two heuristics. First, ridge surface strength −λ3 (how concave-down the image is, cutting across the fissure) had to satisfy −λ3 > 4, 000, an empirically determined threshold that depends linearly on image contrast. Second, the mode of the Hessian eigenvalues γ1 (the third standardized moment of the three eigenvalues) had to satisfy γ1 < −0.3; a perfect ridge surface might have Hessian eigenvalues {0,0,-1} ⇒ γ1 = −1. The system is initialized by seeding 6, 000 particles randomly throughout the lung field, and then run for 100 iterations. Due to the population control mechanism, the final number of particles ranges from 15, 000 to 20, 000 depending on the case. We select parameters for the particle system that tend to make it very sensitive at the price of specificity. That is, we attempt to find a dense sampling of true fissure locations and permit a great deal of other locations that locally behave like ridge surfaces to be detected. Figure 1 illustrates the sampling procedure.
Fig. 1.
Sagittal CT slice (right lung) and glyphs illustrating particles-based image sampling. The system is initialized with a random distribution of particles (left image). Upon convergence, the fissures are well sampled (pale green glyphs in right image). Additional, non-fissure locations that locally behave like ridges are also detected.
MAP Estimation
After point selection, we use MAP estimation to separate true fissure particles from noise. We formulate the problem as follows. Let S = {p1, … , pn} be the set of n particle points detected in our image where each particle point, p, is given by (x, e3), x being the spatial location, (x, y, z), of the particle and e3 being the Hessian eigenvector in the direction normal to the local planar image feature at x. We seek the parameters, Θ, of a probability distribution that best explains the subset of particles, D ⊂ S, that lie on the true fissure (note that these steps are carried out for each of the three fissures). We assume the elements of D are independent and identically distributed (i.i.d.) random variables. The parameters, Θ = (z1, … , zl), that we seek are the heights of l control points (we use l = 10) of a “smoothed” TPS surface that is loosely fit to our data, and it is with respect to this surface that the probability that a particle point is a fissure point (p(p|ω), where ω is the class of true fissure particles) is defined. We will refer to this surface as STPS and denote it as fs. It is important to distinguish between the STPS surface and the TPS surface that will be fit through our final set of fissure points. (The construction of the STPS surface will be described below). We represent the class-conditional probability distribution given a specific choice of Θ as
| (2) |
where N represents the normal distribution. Here h indicates the height difference in the z-direction between the particle and the STPS surface: z – fs (x, y), and θ is the angle formed between the particle’s eigenvector, e3, and the surface’s normal vector at (x, y). The intuitive description of this distribution is that if a particle is far away from the surface and/or not parallel in orientation with respect to the surface normal, it is unlikely to be a fissure particle. Note that we assume independence between h and θ.
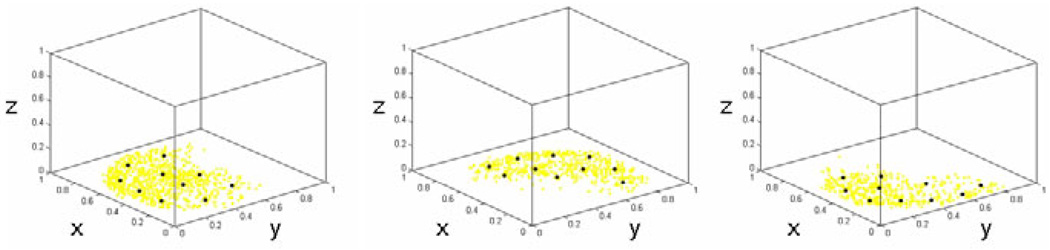
To construct the STPS, we use a parameterization scheme that enables MAP estimation. Each parameter is a control point in our domain (the X-Y plane). By selecting a dispersed set of control points we can fit a surface to the data by controling their heights (z-values). For each fissure, a different set of control points is needed, and the representation needs to be coordinate frame agnostic. We begin by generating manually segmented CT datasets following [6]: two pulmonologists manually select points on each of the three fissures to segment the lobes. We then map the manually selected points to a common coordinate frame by applying the transform needed to map the corresponding lung’s bounding box to the unit cube (via scaling and translating); this is done independently for the left and right lung. Once all the points are in the unit cube’s coordinate frame, we project their coordinates onto the X-Y plane, which serves as the domain for the STPS function. Note that our approach to placing all points in the same coordinated frame is in lieu of a more elaborate registration scheme. Given that the datasets were acquired with similar patient position (head-first, supine scans) this scheme is sufficient for our purposes. Once all the manually selected points across all the training datasets are projected on the unit cube’sX-Y plane, we have a good idea of where the control points need to be for each fissure STPS. Performing simple k-means clustering then allows us to choose a small set of points that will then be used for subsequent MAP estimation. Figure 2 illustrates the control point selection within the unit cube.
Fig. 2.
STPS control points for each of the three fissures: right oblique (left), left oblique (middle), and right horizontal (right). Yellow indicates the pulmonologist-selected points on the training scans, mapped to the unit cube and projected onto the X-Y plane. Black indicates the ten control points used for our MAP estimation.
After the control points are chosen, priors for each fissure, p(Θ) are constructed. This is done by determining the parameter vectors for each of the three fissures across all the training datasets. We compute the z-value at each control point using the TPS surface for each fissure in our training set. Thus, for a given fissure the parameter vector can be represented as Θ = (z1, …, z10). All of this is done within the unit cube, and it is done idependently for each fissure. Once we have our population of parameter vectors, we compute the mean and covariance matrix and represent the priors with a multivariate normal distribution.
With all these terms defined, we can now represent the function we wish to maximize as ln p(D|Θ) + lnp(Θ) where
| (3) |
is the likelihood of Θ given our data.
This is the standard MAP formalism, but we note that this mechanism assumes that all of our data, p, are drawn from the same distribution. In our case this is not true given that we initially compute the likelihood function across all data points in S. However, we perform an iterative search for Θ using a gradient descent optimizer (applied to the negative of the log likelihood), and at the end of each convergence we prune away the most unlikely candidate points and then continue the search for Θ. For the pruning step we evaluate the probability of each point, p(p|ω,Θ), and cast away a percentage of the points least likely to be fissure points (we use 30% for our experiments). This “enriches” our dataset over several iterations, increasing the ratio of true fissure particles to non fissure particles until what remains is very close to D, the set of true fissure points.
Post-Processing
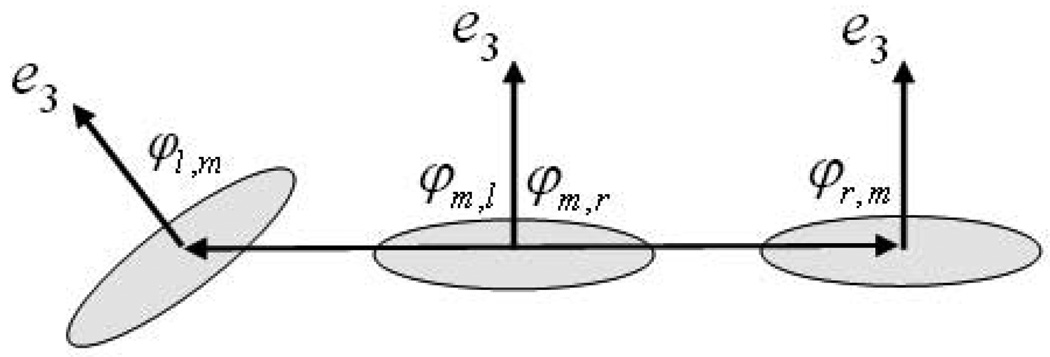
After the MAP estimation stage, we are left with a set of particles along the given fissure of interest. However, some non-fissure particles survive owing to their high probability of being fissure particles as measured by our likelihood function. In order to eliminate these, we perform a final post-processing stage. We make the assumption that fissures are locally planar structures and construct connected components in the following manner. For each remaining particle we compute the vector between its position, p, and the positions of every other particle. If the magnitude of this vector is above a threshold (chosen to be 5mm in our study), no direct connection is said to exist between them. If the particles are in close proximity to one another, we compute the angle formed between the vector that connects them and each of their eigenvectors, e3. If the angles are sufficiently different than right angles (we use a tolerance of 20°), we assume that they represent different planar structures, and we do not form a connection between them. This is illustrated in the figure below. After all possible connections are made, small connected components are rejected, and we are left with our final set of points through which we compute the TPS that represents the lobe boundaries as in [6].
3 Results
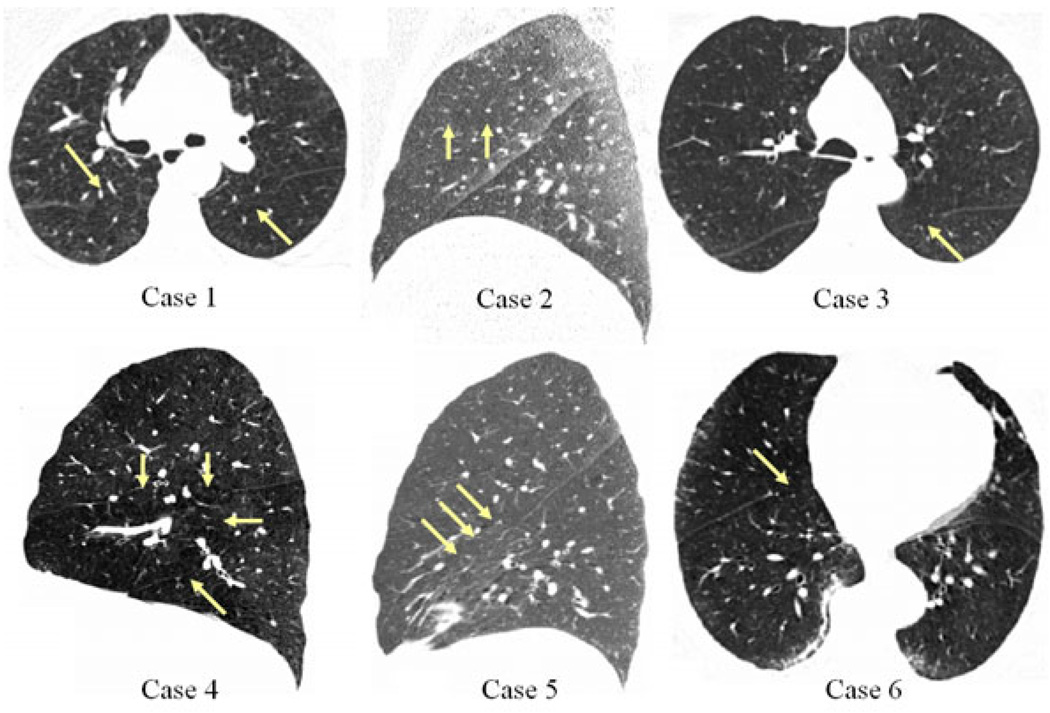
Here we provide results on a set of challenging cases. For our study we have chosen cases that exhibit incomplete fissures (as determined by pulmonologists and defined as the absence of clearly visible fissure delineating adjacent lobes) and a range of other factors which make the lobe segmentation task difficult (expiratory acquisitions, low dose, high body mass index (BMI), disease presence). The scans have in-plane spacing ranging from 0.52mm to 0.74mm and z-spacing ranging from 0.625mm to 0.75mm. More case details are presented in figure 1.
Table 1 shows the results of our algorithm on the test cases, and figure 5 illustrates an output segmentationmask superimposed on a slice of the CT image from which it was derived. We compared our algorithm’s performance to segmentations produced by two pulmonologists (readers 1 and 2), and we additionally compared the readers to each other. To measure segmentation agreement, we computed the average Euclidean distance between the fissures in question. As can be seen, the algorithm performs comparably to the pulmonologists.
Table 1.
Algorithm performance comparison to pulmonologist segmentations. Units are in mm. LO = left obliuqe, RO = right oblique, RH = right horizontal. Note also comparison between readers 1 and 2.
| Reader 1 vs. Alg. | Reader 2 vs. Alg. | Reader 1 vs. Reader 2 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| LO | RO | RH | LO | RO | RH | LO | RO | RH | |
| Case 1 | 1.63 ± 1.56 | 0.86 ± 0.96 | 2.95 ± 2.67 | 1.82 ± 1.90 | 2.12 ± 2.01 | 3.54 ± 5.78 | 2.75 ± 2.72 | 2.58 ± 2.36 | 4.08 ± 3.69 |
| Case 2 | 3.39 ± 3.19 | 2.34 ± 3.05 | 1.21 ± 1.33 | 1.68 ± 1.69 | 2.83 ± 3.63 | 1.02 ± 1.03 | 2.75 ± 2.59 | 1.10 ± 1.32 | 0.80 ± 0.70 |
| Case 3 | 2.11 ± 2.57 | 1.81 ± 2.08 | 1.08 ± 2.96 | 2.38 ± 2.57 | 1.29 ± 1.30 | 1.25 ± 1.43 | 1.32 ± 1.23 | 1.29 ± 1.24 | 0.66 ± 0.81 |
| Case 4 | 1.82 ± 1.97 | 4.35 ± 4.65 | 1.87 ± 2.38 | 1.84 ± 1.70 | 6.07 ± 6.99 | 2.93 ± 5.72 | 2.83 ± 2.69 | 2.68 ± 2.72 | 2.39 ± 2.15 |
| Case 5 | 0.82 ± 0.92 | 1.50 ± 1.50 | 2.92 ± 2.57 | 1.28 ± 1.71 | 1.37 ± 1.43 | 4.68 ± 4.95 | 1.44 ± 1.54 | 0.81 ± 0.82 | 6.44 ± 8.14 |
| Case 6 | 1.04 ± 1.28 | 2.52 ± 2.87 | 1.35 ± 1.27 | 1.69 ± 1.76 | 2.29 ± 2.28 | 4.27 ± 3.99 | 0.99 ± 1.07 | 4.01 ± 3.75 | 4.32 ± 7.73 |
| Average | 1.80 ± 1.92 | 2.23 ± 2.52 | 1.90 ± 2.20 | 1.78 ± 1.89 | 2.66 ± 2.94 | 2.95 ± 3.82 | 2.01 ± 1.97 | 2.08 ± 2.04 | 3.12 ± 3.87 |
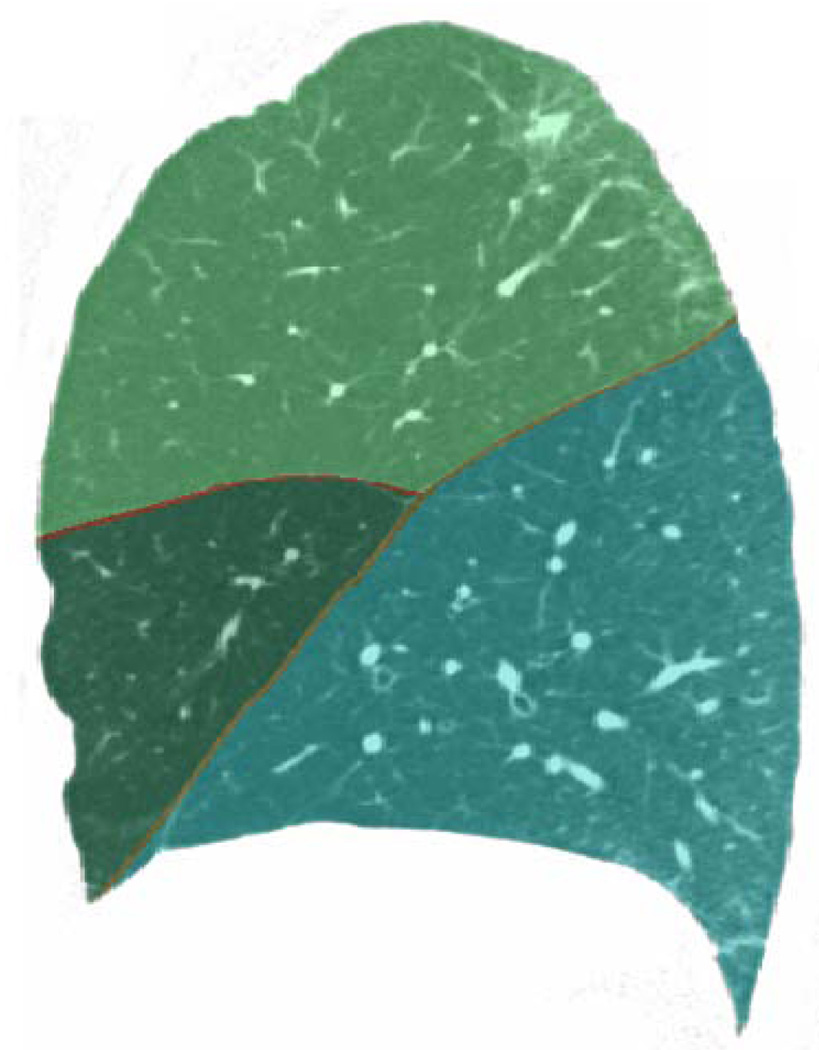
Fig. 5.
Sagittal view of right lung (case 3) with algorithm output displayed semi-transparently. Note agreement between segmented boundaries and fissure locations, visible just below the red boundary lines.
4 Discussion and Conclusion
The algorithm execution time was on the order of 30–45 minutes, although we did not attempt to measure this exactly. This was a proof of concept study, and we made no attempt to optimize the algorithm. The most time consuming stage is the MAP estimation, which involves a series of fitting and pruning stages. The fitting stage uses gradient descent to find the optimal heights of our (10) control points. It may be possible to generate equally good results with many fewer control points; we did not investigate this. Reducing the dimensionality of the search space would improve execution time. We also continued the fitting-pruning until we were left with a user-specified fraction of the original number of points. Post-processing was then applied. The fraction that we used was arbitrarily chosen, but terminating the fitting-pruning earlier would reduce execution time and may not adversely affect results.
In summary, we present a fully automatic method for lung lobe segmentation that performs very well on challenging cases. Whereas other methods tend to rely on segmentations of auxiliary structures (vessels, airways) to augment algorithm performance, we only rely on existing fissure image features, even though they may be scarce. We do not deny that other structures can provide contextual clues for fissure localization, but generating segmentations of these structures, especially for patients with advanced disease, presents its own challenges. Furthermore, we believe that obtaining these structures is not necessary and that sufficient fissure information is directly obtainable provided these image features are carefully selected.
Fig. 3.
Connected components analysis. The middle particle, m, is considered connected to the right particle, r, given their proximity and orientation (φm,r ≈ φr,m ≈ π/2), but the leftmost particle, l, and the middle particle would not be connected, given their discrepancy in orientation (φl,m > π/2).
Fig. 4.
CT slices of the datasets used in this study. Arrows indicate partial fissures. Case 1: low dose, expiratory scan, severe emphysema; Case 2: low dose, expiratory scan, high BMI, right horizontal fissure nearly absent (feature directly below arrows appears as fissure in this slice); Case 3: low dose, expiratory scan, moderate emphysema; Case 4: inspiratory scan, moderate emphysema; Case 5: low dose, expiratory scan, marked fissure aberration; Case 6: inspiratory scan, high BMI, mild diffuse interstitial abnormalities.
Footnotes
This work was supported by NIH grants U01-HL089897, U01-HL089856, K23HL08935301A1, R01MH074794, P41RR013218, Harvard Catalyst (NIH UL1 RR 025758-02), and the Parker B. Francis Foundation.
References
- 1.Ukil S, Reinhardt J. Anatomy-guided lung lobe segmentation in x-ray ct images. IEEE Transactions on Medical Imaging. 2009;28:202–214. doi: 10.1109/TMI.2008.929101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.National Emphysema Treatment Trial Research Group. A randomized trial comparing lung-volume reduction surgery with medical therapy for severe emphysema. N. Engl. J. Med. 2003;348:2059–2073. doi: 10.1056/NEJMoa030287. [DOI] [PubMed] [Google Scholar]
- 3.Aziz M, Ashizawa K, Nagaoki K, Hayashi K. High resolution CT anatomy of the pulmonary fissures. Journal Thoracic Imaging. 2004;19:186–191. doi: 10.1097/01.rti.0000131590.74658.24. [DOI] [PubMed] [Google Scholar]
- 4.van Rikxoort E, Prokop M, de Hoop B, Viergever M, Pluim J, van Ginneken B. Automatic segmentation of the pulmonary lobes from fissures, airways, and lung borders: Evaluation of robustness against missing data. In: Yang G-Z, Hawkes D, Rueckert D, Noble A, Taylor C, editors. MICCAI 2009, Part I. LNCS. vol. 5761. Springer: Heidelberg; 2009. pp. 263–271. [DOI] [PubMed] [Google Scholar]
- 5.Kuhnigk J, Dicken V, Zidowitz S, Bornemann L, Kuemmerlen B, Krass S, Peitgen H, Yuval S, Jend H, Rau W, Achenbach T. New tools for computer assistance in thoracic ct part 1. functional analysis of lungs, lung lobes and bronchopulmonary segments. Radiographics. 2005;25:525–536. doi: 10.1148/rg.252045070. [DOI] [PubMed] [Google Scholar]
- 6.Ross J, San José Estépar R, Díaz A, Westin C, Kikinis R, Silverman E, Washko G. Lung extraction, lobe segmentation and hierarchical region assessment for quantitative analysis on high resolution computed tomography images. In: Yang G-Z, Hawkes D, Rueckert D, Noble A, Taylor C, editors. MICCAI 2009, Part II. LNCS. vol. 5762. Springer: Heidelberg; 2009. pp. 690–698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kindlmann G, Estépar SJ, Smith R, Westin SC. Sampling and visualizing creases with scale-space particles. IEEE Transactions on Visualization and Computer Graphics. 2009;15:1415–1424. doi: 10.1109/TVCG.2009.177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.van Rikxoort E, van Ginneken B, Klik M, Prokop M. Supervised enhancement filters: application to fissure detection in chest ct scans. IEEE Transactions on Medical Imaging. 2008;27:1–10. doi: 10.1109/TMI.2007.900447. [DOI] [PubMed] [Google Scholar]
- 9.Hu S, Hoffman E, Reinhardt J. Automatic lung segmentation for accurate quantitation of volumetric x-ray CT images. IEEE Transactions on Medical Imaging. 2001;20:490–498. doi: 10.1109/42.929615. [DOI] [PubMed] [Google Scholar]
- 10.Bookstein F. Principal warps: thin-plate splines and the decomposition of deformations. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1989;11 [Google Scholar]
- 11.Eberly D. Ridges in Image and Data Analysis. Dordrecht: Kluwer Academic Publishers; 1996. [Google Scholar]