Skip to main content
PMC home page
Journal of Cerebral Blood Flow & Metabolism logoLink to Journal of Cerebral Blood Flow & Metabolism
. 2010 Jul 14;31(1):371–383. doi: 10.1038/jcbfm.2010.112

Optimized data preprocessing for multivariate analysis applied to 99mTc-ECD SPECT data sets of Alzheimer's patients and asymptomatic controls

Dorit Merhof 1,*, Pawel J Markiewicz 2, Günther Platsch 3, Jerome Declerck 4, Markus Weih 5, Johannes Kornhuber 5, Torsten Kuwert 6, Julian C Matthews 7, Karl Herholz 2
PMCID: PMC3049460  PMID: 20628401

Abstract

Multivariate image analysis has shown potential for classification between Alzheimer's disease (AD) patients and healthy controls with a high-diagnostic performance. As image analysis of positron emission tomography (PET) and single photon emission computed tomography (SPECT) data critically depends on appropriate data preprocessing, the focus of this work is to investigate the impact of data preprocessing on the outcome of the analysis, and to identify an optimal data preprocessing method. In this work, technetium-99methylcysteinatedimer (99mTc-ECD) SPECT data sets of 28 AD patients and 28 asymptomatic controls were used for the analysis. For a series of different data preprocessing methods, which includes methods for spatial normalization, smoothing, and intensity normalization, multivariate image analysis based on principal component analysis (PCA) and Fisher discriminant analysis (FDA) was applied. Bootstrap resampling was used to investigate the robustness of the analysis and the classification accuracy, depending on the data preprocessing method. Depending on the combination of preprocessing methods, significant differences regarding the classification accuracy were observed. For 99mTc-ECD SPECT data, the optimal data preprocessing method in terms of robustness and classification accuracy is based on affine registration, smoothing with a Gaussian of 12 mm full width half maximum, and intensity normalization based on the 25% brightest voxels within the whole-brain region.

Keywords: Alzheimer's disease (AD), intensity normalization, multivariate analysis, principal component analysis (PCA), single photon emission computed tomography (SPECT), spatial normalization

Introduction

With increasing life expectancy in developed countries, there is a corresponding increase in the frequency of diseases typically associated with old age, in particular dementia. Alzheimer's disease (AD) is the most prevalent type of dementia, followed by vascular or multiinfarct dementia. The socioeconomic impact of dementia is extraordinarily large, with considerable effort being made to understand the pathophysiologic mechanisms of AD to further the development of effective treatment strategies for the disease.

Pathologic studies show that neurodegeneration in AD begins in the entorhinal cortex, progressing to the hippocampus, the limbic system, and neocortical regions (Braak and Braak, 1991; Hyman et al, 1984). The AD is characterized by accumulations of amyloid plaques and neurofibrillary tangles (Dickson, 2003; Taylor et al, 2002), which promote oxidative stress and inammation (Pratico et al, 2002) and thus exert direct and indirect neurotoxic effects.

Neuroimaging has identified a wide range of biomarkers that can differentiate AD patients from asymptomatic controls, such as reduced cerebral blood flow (Johnson et al, 1987; Holman et al, 1992; Powers et al, 1992), reduced glucose metabolism (Mielke et al, 1996; Burdette et al, 1996; Herholz et al, 2002), and deposition of amyloid plaques and neurofibrillary tangles (Selkoe, 2001; Petrella et al, 2003; Engler et al, 2006). Imaging agents frequently used in the analysis of dementia are 18F-2-fluoro-2-deoxy--glucose to assess metabolic changes, and technetium-99methylcysteinatedimer (99mTc-ECD) or technetium-99m-hexamethyl-propyleneamine oxime for analyzing the perfusion pattern in the brain.

In recent research, multivariate image analysis techniques have received increasing attention (Fripp et al, 2008; Habeck et al, 2008; Markiewicz et al, 2009). As opposed to univariate analysis, multivariate analysis takes into account statistical relationships between all voxels simultaneously. It has a potentially greater statistical power compared with univariate techniques, which are forced to use very strict and often too conservative corrections for voxel-wise multiple comparisons. Multivariate analysis is therefore much better suited for prospective application of results obtained from the analysis of a group of data sets to entirely new images, and provides superior diagnostic performance (Habeck et al, 2008).

In this work, multivariate analysis of single photon emission computed tomography (SPECT) data sets of AD patients and asymptomatic controls is performed. As previous comparisons of positron emission tomography (PET) with SPECT showed only a modest advantage of PET (Mielke et al, 1994), optimizing the analysis of SPECT for broader clinical use is worthwhile to bring it close to 18F-2-fluoro-2-deoxy--glucose PET at a substantially less cost. Whereas previous work focuses on the methodology of multivariate analysis for detecting dementia (Fripp et al, 2008; Habeck et al, 2008; Markiewicz et al, 2009), this work primarily investigates different data preprocessing methods to obtain optimal performance of the classification. Data preprocessing comprising registration, smoothing, and intensity normalization has an important function in most applications involving PET or SPECT data:

  • Registration is required to align the data sets, which is an important step for any kind of voxel-by-voxel-based image analysis.

  • Smoothing effectively reduces differences in the data, which cannot be compensated for by registration alone, such as intrapatient variations in gyri and pathology, and the resolution of the reconstruction of scans. Another reason for smoothing is the reduction of noise.

  • Intensity values of the data sets may vary significantly, depending on the individual physiology of the patient (e.g., injected dose, body mass, washout rate, metabolic rate). These factors are not relevant in the study of the disease, and need to be eliminated using intensity normalization, to obtain meaningful statistical comparisons during multivariate analysis.

The choice of preprocessing methods potentially has a crucial impact on the classification accuracy and robustness, and therefore on the interpretation of the results. For this reason, different data preprocessing methods commonly used for processing PET and SPECT data sets are investigated in detail in this work, and the robustness and accuracy of multivariate analysis, depending on the data preprocessing method, is investigated. Although the analysis presented in this work is based on 99mTc-ECD SPECT data, the same methodology could be applied to technetium-99m-hexamethyl-propyleneamine oxime SPECT and 18F-2-fluoro-2-deoxy--glucose PET data sets.

Materials and methods

Image Data

Patient population

The 99mTc-ECD SPECT data sets used in this work comprise 28 patients with mild-to-medium AD (17 females, 11 males), with an age group between 52 and 81 years (mean±s.d.: 67.4±7.5), as well as 28 asymptomatic controls (21 females, 7 males) with an age group between 50 and 78 years (mean±s.d.: 61.6±8.0). The data sets were acquired between 2003 and 2008 at the Clinic of Nuclear Medicine, University of Erlangen-Nuremberg, Erlangen, Germany.

Acquisition parameters

Injection of 20 mCi (740 MBq) of 99mTc-labeled ECD was performed on subjects under resting conditions. The patients were lying with eyes closed in a quiet, dark, or dimly lit environment from at least 10 minutes prior until 5 minutes after injection. For image acquisition, the patients were positioned supine in the scanner, with their arms down. The head was placed naturally so that the patients felt comfortable and motion could be minimized during the acquisition. The image data were acquired on a Siemens MultiSPECT3 scanner 30 minutes after injection of the tracer, with a scan duration of 30 minutes at most. The field of view of the image contained the entire brain and the cerebellum. The projection data were processed with filtered back projection, and Chang attenuation correction was applied.

Criteria for asymptomatic controls and Alzheimer's disease patients

The asymptomatic data sets originate from patients who were referred to the Clinic of Nuclear Medicine for brain perfusion SPECT for diagnostic purposes, but the results of the scans were normal. Further clinical investigations showed no evidence of any diseases, which would lead to an altered brain perfusion pattern. Computed tomography or magnetic resonance was performed between 4 weeks before and 4 weeks after the SPECT examination and there were no clinical events between magnetic resonance/computed tomography and SPECT.

The AD data sets originate from daily clinical routine and were not collected as part of a prospective dementia study. For this reason, no neuropsychologic measure is available for these patients. All dementia patients were referred to the Clinic of Nuclear Medicine with questions related to diagnostic findings. The data sets underwent a semiquantitative analysis based on Neurological Statistical Image Analysis Software (NEUROSTAT) (Minoshima et al, 1994, 1995c), and reading by a nuclear medicine physician with expert knowledge in dementia diagnosis. The patients included in the AD population comprise mild and medium AD cases with uptake patterns typical of dementia of AD type.

Image Preprocessing

In this section, the registration, smoothing, and intensity normalization methods that are used in this work are presented. For data preprocessing, any combination of preprocessing methods listed below was investigated.

Registration reference

One of the conditions for a voxel-based analysis is that a one-to-one correspondence for each brain voxel must be obtained for all data sets, that is, all brains can be represented in a common coordinate system. For this reason, the brain scans are transformed into a reference coordinate system, which is based on the Montreal Neurological Institute single subject brain. This reference coordinate system is widely used, for example, as the standard coordinate system for the templates used in the SPM package (Friston et al, 2007).

Because of the absence of anatomical data, a registration reference is needed, which makes it possible to directly register the SPECT data sets to the reference coordinate system. The registration reference is constructed using the average of a number of functional scans, which have previously been transformed into the Montreal Neurological Institute coordinate system. The reason for using functional scans rather than anatomical scans is that registration performance is generally better when both scans are of the same modality and tracer (Meyer et al, 1999). As there is no clear anatomical definition in the functional scan, variations will be better captured using a structural rather than an anatomical registration reference. For deformable registration in particular, there may be more local bias in the normalization if anatomical scans are used as reference, which would result in a local bias in the normalization.

Registration

To register the SPECT scan of a subject to the registration reference, a rigid registration is performed first (translation and rotation only).

In a second step, either an affine or deformable registration is performed: affine registration allows translation, rotation, scaling, and shearing of the data set with respect to the registration reference, and compensates for most of the differences in size and shapes between brains. Several large-scale studies have shown the value of affine registration for the purposes of AD assessment, both in PET and SPECT (Herholz et al, 2002; Bradley et al, 2002).

Alternatively, a fully automated deformable registration is used in the second step. The deformable fine alignment is based on Gaussian radial basis functions (Arad et al, 1994), and uses mutual information (Wells et al, 1996) as a similarity measure and a classic gradient descent as an optimization scheme (Rueckert et al, 1998). The control points for the transformation (which are the centers of the Gaussian radial basis functions) are placed on a regular grid, which covers the brain volume, three along the inferior–superior direction, three left–right, and four anterior–posterior, with a sigma for the Gaussian of 30 mm. Deformable registration offers more degrees of freedom thus providing more flexibility. However, deformable warping may also overfit the data, introducing errors that may impact the principal component analysis (PCA) analysis.

Typically, the registration method would be accurate down to the resolution of the image itself (i.e., about 1 cm for SPECT images). To compensate for a potential misalignment, an equivalent amount of smoothing needs to be applied in the next step.

Smoothing

Individual voxels in the reconstructed data usually represent very few counts that have actually been measured. Consequently, intensity values of individual voxels are subject to exceedingly large noise. To normalize the cross-correlation between voxels, equalize resolution differences among scanners, compensate for inaccuracies of registration, and compensate for anatomical differences, substantial smoothing before statistical analysis is required. Although smoothing leads to loss of spatial information, this step is necessary to compute meaningful statistics (Worsley et al, 1998).

Once registration is complete, smoothing is applied to the voxel intensity values before intensity normalization. Smoothing is commonly based on a Gaussian filter with typical filter widths between 6 and 12 mm. In this work, a standard isotropic Gaussian filter is used with full width half maximum (FWHM) of either 8 or 12 mm. The latter value is widely accepted to provide adequate performance from an experimental point of view (Herholz et al, 2002; Ishii et al, 2001; Matsuda et al, 2002).

Intensity normalization

Intensity values of the data sets may vary arbitrarily, depending on factors such as injected dose and systemic tracer elimination. These factors are not relevant in the study of the disease and would only introduce unnecessary variance, which is not desirable. For this reason, the images need to be intensity normalized, to obtain meaningful statistical comparisons during PCA and Fisher discriminant analysis (FDA) analysis.

The normalization of intensity values is achieved by globally scaling the entire scan to a new reference range using a linear transformation. However, the choice of a proper reference region to scale each SPECT data set is not straightforward: results obtained from an intensity normalized scan may be misleading if there is a physiologically relevant or disease-related change in the reference region. Therefore, the reference region has to be chosen carefully, either on the assumption that a particular region is not affected by the disease, or that a combination of regions provides sufficiently low bias in the normalization.

A number of strategies for intensity normalization have been reported in the literature. Various studies have chosen the pons (Minoshima et al, 1995a), the thalamus (Bartenstein et al, 1997; Minoshima et al, 1995b), the cerebellum (Ishii et al, 1997, 2001; Soonawala et al, 2002), or the whole brain (Herholz et al, 2002) as reference region. However, some of these regions are small, which makes them very sensitive to noise and registration errors. This problem becomes even more evident in ageing brains and in brains where dementia is present, because of the ventricular enlargement observed in these cases. A small translation or scaling of the reference region may greatly affect the intensity normalization. For these reasons, there is no consensus in the literature as to which anatomical region is an appropriate choice.

Even though the pons alone seems to be too small to be identified reliably by automated spatial registration, its use as reference region is desirable because of the relative sparing in AD. For this reason, one of the regions considered for intensity normalization in this work is the brainstem, which consists of the midbrain, the pons, and the medulla oblongata. The second region being considered is the cerebellum, which is often used as a reference in studies of AD, assuming that it is spared by any major pathological involvement. A very popular region for intensity normalization is the ‘whole-brain' area, which is the third method investigated in this work. The whole-brain region is based on the automated anatomical labeling segmentation (Tzourio-Mazoyer et al, 2002) of the Montreal Neurological Institute single subject brain. It comprises the cerebrum as well as the cerebellum and was generated by fusing all automated anatomical labeling label regions and filling remaining gaps. The fourth and fifth regions considered for intensity normalization are the pons and the thalamus.

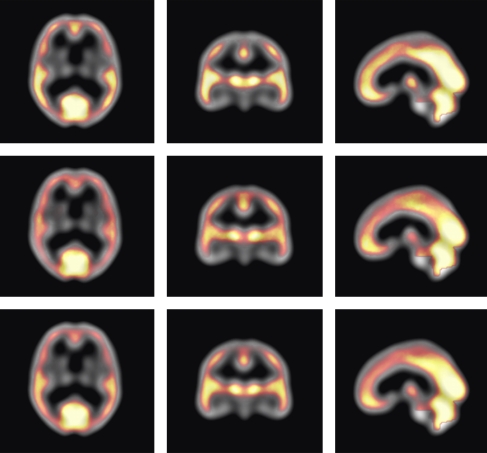
The respective regions used for intensity normalization are predefined on the registration reference and are transferred to an individual SPECT data set after registration. To compensate for any residual registration errors and minor abnormalities within the respective reference region, the mean value of the 25% brightest voxels within the region is computed and used as the constant in the intensity normalization step. For the whole-brain area, the voxels effectively used for intensity normalization are shown in Figure 1.

Figure 1.

Figure 1

Open in a new tab

Base image (grayscale colormap): registration reference. Overlay image (colormap ranging from red to white): voxels with top 25% intensities within the whole-brain region. The color indicates how often a voxel is used across all data sets. Voxels in the occipital lobe and the cerebellum are most frequently among the voxels used for intensity normalization (upper row: all Alzheimer's disease (AD) data sets; middle row: all asymptomatic control data sets; and lower row: both AD and control data sets). The color reproduction of this figure is available on the html full text version of the manuscript.

Computational framework for data preprocessing

The framework for data preprocessing and analysis was implemented in MATLAB, Version 7.5.0.342 (The MathWorks Inc., Natick, MA, USA; http://www.mathworks.com). It automatically applies different preprocessing methods (i.e., any combination of registration, smoothing, and intensity normalization approaches) on the initial set of data. For each preprocessing method, the analysis described in the following sections is performed.

Principal Component Analysis

The PCA (Pearson, 1901) is a multivariate analysis method that aims at revealing the trends in the data by representing the data in a dimensionally lower space. The first PC accounts for as much of the variability in the data as possible by a single component, and each succeeding component accounts for as much as possible of the remaining variability. The PCA thus projects high-dimensional data onto a lower dimensional space represented by a subset of PCs, which can be more easily explored to analyze the underlying structure of the data. Even though each data set can exactly be represented as a linear combination of all principal components, data analysis usually only retains a few principal components to focus on the main variations of the data and to take advantage of the dimensionality reduction effect obtained by PCA, considering the remaining PCs as noise or atypical variations.

The PCs are computed as follows (Markiewicz et al, 2009): the n × m data matrix X comprises all m data sets, whereas each column of X represents one data set (i.e., contains the n voxels of the whole-brain region of this particular data set). The PCs are computed as the eigenvectors of the covariance matrix XXT using singular value decomposition. However, as an individual data set may be used multiple times in a bootstrap sample (see section ‘Bootstrap Resampling'), the singular value decomposition may become numerically unstable. In these cases, a more stable but slightly slower method for calculating the PCs called nonlinear iterative partial least squares (Wold, 1966, 1975) is used.

Fisher Discriminant Analysis

Although PCA allows the identification of components, which are suited for representing the whole population (i.e., asymptomatic controls and AD patients), there is no reason to assume that each component on its own should be useful for discriminating between both groups. As PCA seeks for directions that are efficient for representing the data, a discriminant analysis is needed in a second step, which seeks directions that are efficient for differentiating between groups.

The goal of FDA is to identify a discrimination vector w such that projecting each data set onto this vector provides the best possible separation between both groups. To obtain a good separation of the projected data, it is desirable that the difference between the means of each class is large relative to some measure of the variation in each class. For this reason, the criterion function J that is maximized in FDA (Duda et al, 2001)

graphic file with name jcbfm2010112e1.jpg

is based on the between-class scatter matrix SB and the within-class scatter matrix Sw

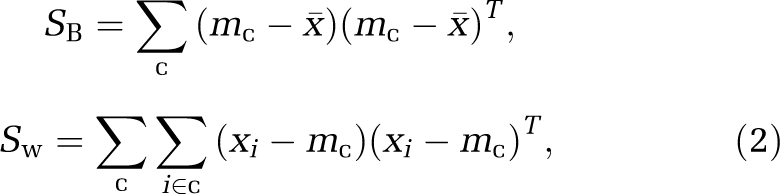graphic file with name jcbfm2010112e2.jpg

where x̄ is the mean image vector across subjects, c represents the classes to be separated, and mc are the class means.

In mathematical physics, equation (1) is well known as the generalized Rayleigh quotient. It can be shown that the solution w that optimizes J is (Duda et al, 2001)

graphic file with name jcbfm2010112e3.jpg

whereas m1 and m2 indicate the n-dimensional sample means of the two populations. However, because of the small number of data sets compared with the dimensionality of the images, an FDA analysis directly on the original data would result in a singular within-class scatter matrix, which cannot be inverted as required in equation (3). Therefore, the FDA is applied to the PC scores resulting from projecting the original data onto the PCs of the PCA subspace used for the analysis (Swets and Weng, 1996; Markiewicz et al, 2009), rather than the original data.

Bootstrap Resampling

In statistics, resampling techniques are used to validate models and to assess their statistical accuracy by using random subsets (bootstrapping, cross-validation) (Efron and Tibshirani, 1993). Following the analysis used in Markiewicz et al (2009), 0.632 bootstrap resampling with stratification is applied to evaluate the robustness and the predictive accuracy of the PCA and FDA approach, given different methods of data preprocessing. For a total number of 500 replications, 28 asymptomatic controls and 28 AD patients are randomly drawn from each group, resulting in a new bootstrap sample per replication. For each bootstrap sample, PCA is performed, as well as FDA for different numbers of PCs. Bootstrap resampling followed by PCA and FDA is performed for each individual data preprocessing method, and statistical results are calculated (see section ‘Measures for Evaluation') to evaluate the different data preprocessing methods.

Measures for Evaluation

The following statistical measures are calculated for each preprocessing method to assess the accuracy and robustness of classification (more details are provided in Markiewicz et al (2009)).

Classification accuracy

The accuracy of classifying AD and controls correctly in the context of 0.632 bootstrap sampling is estimated as follows: for both the data sets, which are not part of the bootstrap sample as well as for the full set of data (i.e., the training set), the classification accuracy is calculated. The accuracy of individual bootstrap samples is typically based on fewer training instances (on average 63.2% of the bootstrap subjects are from the original training set, whereas the remaining 36.8% are used for testing), and is therefore lower. For this reason, a trade-off between the accuracy of the training set and the accuracy of individual bootstrap samples is provided by combining both constituent parts, to obtain the 0.632 bootstrap classification accuracy:

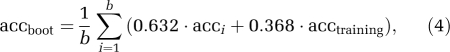graphic file with name jcbfm2010112e4.jpg

where b is the number of bootstrap replications, acci is the accuracy of the individual bootstrap sample that corresponds to replication i, and acctraining is the accuracy of the training set (Efron and Tibshirani, 1993). To provide a more accurate estimate of acctraining, again bootstrap resampling based on 200 iterations is applied, whereas the same instances used in the bootstrap sample are also used for calculating the accuracy, which is averaged across all samples.

Angle between principal component analysis subspaces

For each bootstrap replication, the angle between the PCA subspace based on the whole sample, and the PCA subspace based on the bootstrap sample is computed. For this purpose, pairs of vectors from both subspaces and corresponding angles are identified as follows (Golub and Van Loan, 1996): the first principal angle is the smallest angle between any pair of vectors originating from both PCA subspaces. To identify the second principal angle, only vectors in each subspace are considered, which are orthogonal to the vector that was used to define the first principal angle, and so forth. The angle between both PCA subspaces is then defined as the largest principal angle of all computed principal angles (Golub and Van Loan, 1996). The smaller the largest principal angle between two PCA subspaces, the closer and more similar are the PCA subspaces, which can be considered as a sign of robustness.

Angle between Fisher discriminant analysis vectors

For each bootstrap replication, the angle between the FDA vector based on the whole sample and the FDA vector based on the bootstrap sample is calculated for different numbers of PCs. For an increasing number of PCs, the angle is expected to increase, as the PCA and FDA analysis adapts to features specific of the sample, rather than features that differentiate between both classes, which indicates a decrease of robustness.

Results

To address the question whether data preprocessing methods impact the classification accuracy and robustness of PCA/FDA analysis, and to compare the performance of different preprocessing methods, a comprehensive results analysis is provided in this section.

Classification Accuracy

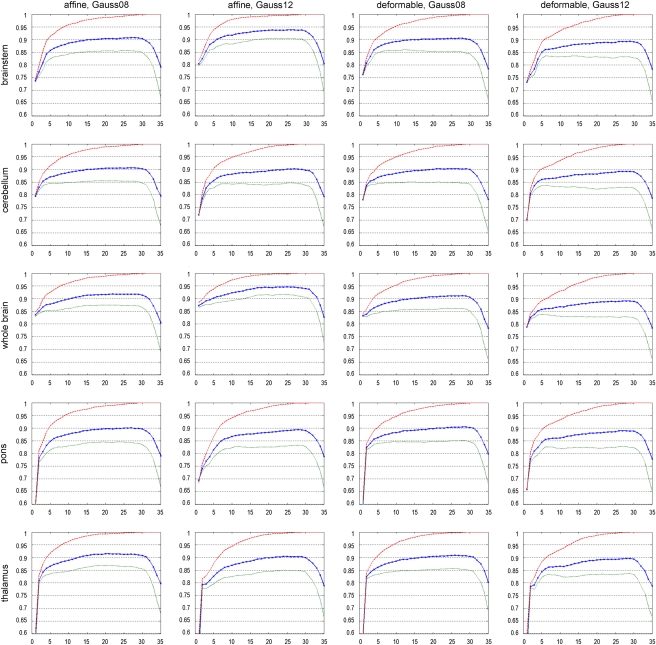
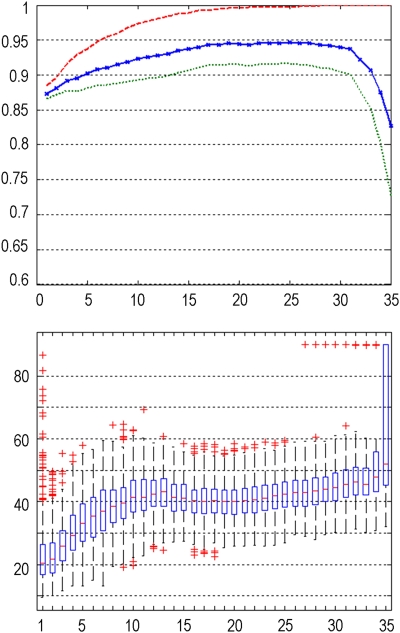
The predicted classification accuracy provides insight into the future performance of different data preprocessing methods. In Figure 2, the classification accuracy of different data preprocessing methods depending on the number of PCs used for the analysis is shown. The red (dashed) curve indicates the classification accuracy obtained for 500 bootstrap iterations, with the chosen instances in the bootstrap sample being used for training and testing, providing the training accuracy used in the 0.632 bootstrap predictive accuracy estimation. The green (dotted) curve represents the accuracy achieved on average for all the samples generated in 500 bootstrap replications (chosen instances in a bootstrap sample are used for training with the remaining instances being used for estimating the accuracy). The blue (solid with crosses) curve represents the final accuracy for the bootstrap 0.632 estimator (with the correction in equation (4) applied). Table 1 summarizes the classification accuracy results for three PCs across different data preprocessing methods.

Figure 2.

Figure 2

Open in a new tab

Classification accuracy of the training set (red, dashed), for individual bootstrap samples (averaged) (green, dotted), and for the bootstrap 0.632 estimator (corrected, averaged) (blue, solid with crosses), depending on the number of principal components (PCs) included into the analysis. In each plot, the horizontal axis denotes the number of PCs included into the analysis, and the vertical axis denotes the respective classification accuracy. The color reproduction of this figure is available on the html full text version of the manuscript.

Table 1. Accuracy for different preprocessing methods.

  Affine, Gauss08 Affine, Gauss12 Deformable, Gauss08 Deformable, Gauss12
Brainstem 0.81 0.86 0.83 0.79
Cerebellum 0.85 0.82 0.85 0.84
Whole brain 0.86 0.89 0.86 0.84
Pons 0.81 0.77 0.84 0.81
Thalamus 0.84 0.80 0.84 0.79
Open in a new tab

The accuracy is estimated using 500 bootstrap replications and the first three principal components included in the discrimination analysis.

The accuracy curves in each plot follow a characteristic scheme: with increasing number of PCs incorporated into the analysis, the accuracy increases as well, as discriminative features for separating both classes are better captured. However, from a certain number of PCs onwards, the accuracy drops again, as PCs are included into the analysis, which represent individual bootstrap samples only (with repeated instances in the bootstrap sample), rather than the whole data set.

Angles Between Principal Component Analysis Subspaces and Fisher Discriminant Analysis Vectors

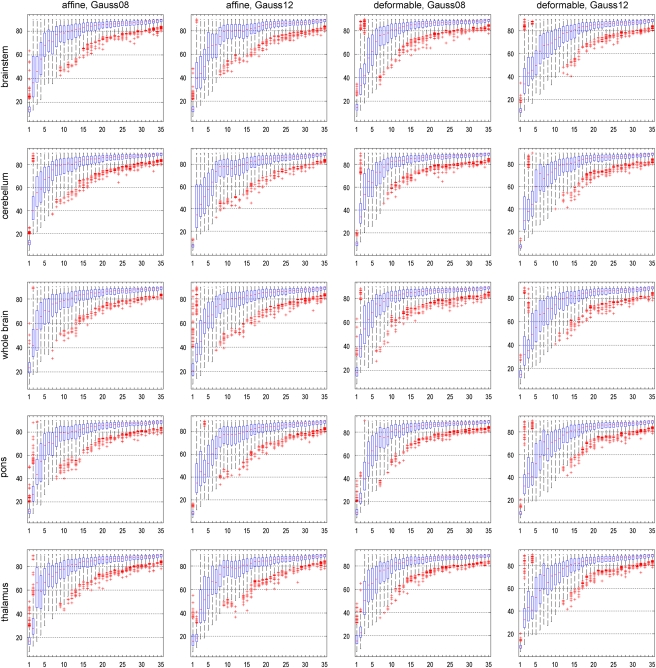
The robustness of a PCA subspace is indicated by the sampling distribution of the angle between PCA subspaces, a small angle and a narrow distribution being a sign of robustness. Figure 3 shows for each data preprocessing method, the sampling distribution of the angle between PCA subspaces for 500 bootstrap replications, depending on the number of PCs. In general, with the increasing number of PCs spanning the PCA subspace, the robustness of the subspace decreases for any preprocessing method.

Figure 3.

Figure 3

Open in a new tab

For different data preprocessing methods: sampling distribution of the angle between principal component analysis (PCA) subspaces for 500 bootstrap replications, depending on the number of PCs. Robustness is indicated by a small angle between PCA subspaces, and a comparatively narrow distribution. In each boxplot, the horizontal axis denotes the number of PCs included into the analysis, and the vertical axis denotes the angle between PCA subspaces.

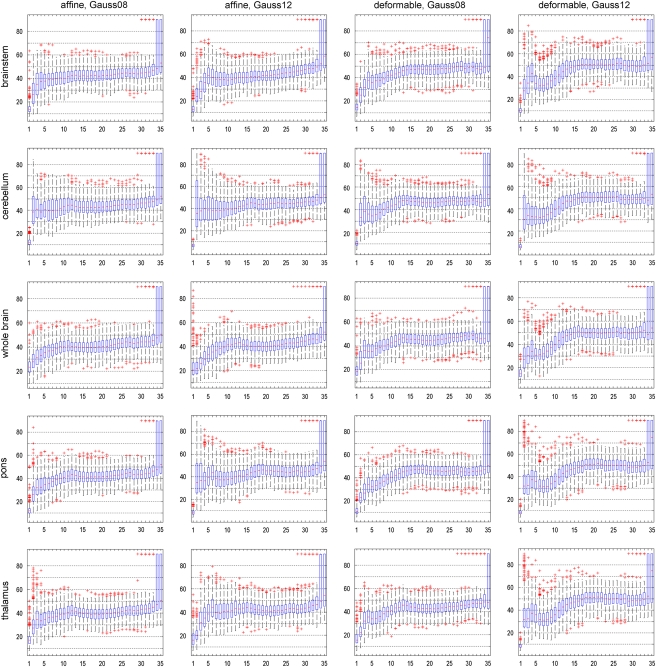
A similar behavior can be observed for the angle between FDA vectors, as outlined in Figure 4. Again, robustness is indicated by a small angle between FDA vectors, and a comparatively narrow distribution. For an increasing number of PCs, the angle between FDA vectors deteriorates, indicating a decrease of robustness of the analysis.

Figure 4.

Figure 4

Open in a new tab

For different data preprocessing methods: sampling distribution of the angle between Fisher discriminant analysis (FDA) vectors for 500 bootstrap replications, depending on the number of principal components (PCs). Robustness is indicated by a small angle between FDA vectors, and a comparatively narrow distribution. In each boxplot, the horizontal axis denotes the number of PCs included into the analysis, and the vertical axis denotes the angle between FDA vectors.

Interestingly, distinct differences of robustness can be observed between different preprocessing methods (both for the angle between PCA subspaces as well as the angle between FDA vectors). According to Figure 4, intensity normalization according to the cerebellum results in very unrobust results, with large angles and high variability already for low numbers of PCs. The results for the pons seem to suggest a lack of robustness when 12 mm smoothing is used, but notably better with 8 mm smoothing. The registration methods, affine and deformable, result in very similar distributions with no clear preference for either method. Affine registration with a Gaussian filter of 12 mm FWHM and intensity normalization based on the whole-brain region, which provides the best classification accuracy (see section ‘Classification Accuracy'), also provides noticeably good results for both robustness analyses.

By combining these results with the accuracy analysis in section ‘Classification Accuracy,' it can be observed that the increase of accuracy for an increasing number of PCs occurs at the cost of robustness as indicated by the analysis of angles between FDA vectors and PCA subspaces. This is also illustrated in Figure 5, which provides a direct comparison between accuracy and robustness (as parameterized by the angle between the FDA vectors), and shows the inverse relationship between both. These results show that a small number of PCs provides a good trade-off between robust analysis and high accuracy, given an optimized preprocessing method. Tables 2 and 3 summarize the results for the angle between PCA subspaces (Table 2) and the angle between FDA vectors (Table 3) for the first three PCs across different data preprocessing methods.

Figure 5.

Figure 5

Open in a new tab

Direct comparison of the classification accuracy (upper image) and the angle between Fisher discriminant analysis (FDA) vectors (lower image) clearly shows the trade-off relationship between both (exemplarily, data preprocessing using whole-brain intensity normalization, affine registration, and Gaussian smoothing, with a full width half maximum (FWHM) of 12 mm was used). In both plots, the horizontal axis denotes the number of principal components (PCs) included into the analysis, and the vertical axis denotes the respective classification accuracy (upper plot) and the angle between FDA vectors (lower plot), respectively.

Table 2. Median angle between PCA subspaces for different data preprocessing methods.

  Affine, Gauss08 Affine, Gauss12 Deformable, Gauss08 Deformable, Gauss12
Brainstem 46° 43° 42° 43°
Cerebellum 55° 44° 54° 38°
Whole brain 55° 45° 55° 35°
Pons 44° 45° 40° 43°
Thalamus 66° 43° 50° 43°
Open in a new tab

PCA, principal component analysis.

The angle is estimated using 500 bootstrap replications and the first three PCs included in the discrimination analysis.

Table 3. Median angle for different data preprocessing methods.

  Affine, Gauss08 Affine, Gauss12 Deformable, Gauss08 Deformable, Gauss12
Brainstem 35° 28° 32° 34°
Cerebellum 41° 38° 39° 34°
Whole brain 31° 26° 36° 30°
Pons 45° 32° 32° 34°
Thalamus 35° 31° 32° 32°
Open in a new tab

The angle is estimated using 500 bootstrap replications and the first three principal components included in the discrimination analysis.

Visualization of Principal Components and Discriminant Vector

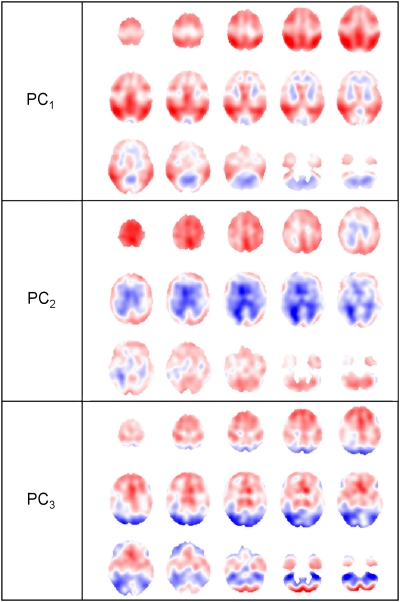
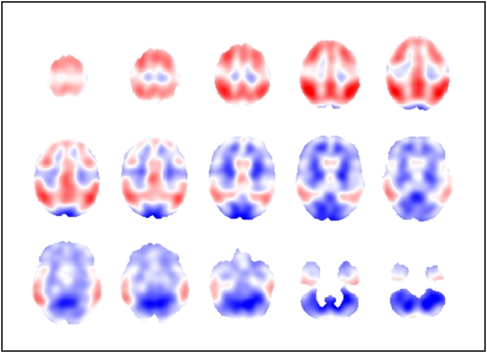
The PCs as well as the discrimination image can be regarded as three-dimensional data sets and can be visualized accordingly. Axial slices of the first three PCs are shown in Figure 6, for data preprocessing based on affine registration, Gaussian smoothing with an FWHM of 12 mm, and intensity normalization based on the whole-brain region. The discriminant image for this particular preprocessing method and FDA based on three PCs is provided in Figure 7.

Figure 6.

Figure 6

Open in a new tab

Axial slices (every fourth slice from slice 72 to 16) of first, second, and third principal component (PC), for data preprocessing based on affine registration, Gaussian smoothing with a full width half maximum (FWHM) of 12 mm, and intensity normalization according to the whole-brain region.

Figure 7.

Figure 7

Open in a new tab

Axial slices (every fourth slice from slice 72 to 16) of discriminant image based on three principal components (PCs), for data preprocessing based on affine registration, Gaussian smoothing with a full width half maximum (FWHM) of 12 mm, and intensity normalization according to the whole-brain region.

The first PC image shows patterns, which are typical for dementia of AD type, with more intense colors (blue, red), indicating a higher contribution to the discrimination. Areas of high hypo-metabolism (red) are to be found in the temporal, parietal, and frontal lobes, as expected in AD patients. The second PC image shows areas of high discrimination (blue) in the vicinity of the ventricles, which could be attributed to the widening of ventricles in dementia, a shape variation not corrected by registration.

The discriminant image shows areas of high hypo-metabolism (red) in the temporal, parietal, and frontal lobes. The central region and the occipital lobes are not affected and only show very small values (white, light blue, and red), which are patterns typically seen in real AD patient images. The dark blue regions particularly in the cerebellum are due to the use of global normalization where relatively preserved areas once intensity normalized can increase in AD patients.

Discussion

In this work, the impact of data preprocessing methods on the robustness and accuracy of multivariate image analysis of 99mTc-ECD SPECT data in AD patients and asymptomatic controls is investigated. To provide more reliable results, bootstrap resampling is applied to assess the robustness of classification.

A limitation that needs to be acknowledged is the fact that no neuropsychologic measure is available as the data sets originate from daily clinical routine and were not collected as part of a prospective dementia study. For this reason, the accuracy and robustness measures reported in this work are based on visual reading by an expert nuclear medicine physician as ground truth, that is, the system has been optimized to achieve classification results that are comparable to visual reading by a medical expert.

The data preprocessing methods for registration, smoothing, and intensity normalization investigated in this work are commonly used in the literature. The classification accuracy given by bootstrap 0.632 provides evidence with respect to the best performing set of preprocessing methods, with a clear preference for affine registration, Gaussian smoothing with an FWHM of 12 mm, and intensity normalization according to the whole-brain region. This particular combination of methods seems to harmonize very well and provides excellent classification accuracy, already for low numbers of PCs. The robustness of PCA/FDA analysis assessed by the angle between PCA subspaces and between FDA vectors generally decreases with increasing number of PCs spanning the subspace.

By adding more PCs into the discriminative model, the loadings of the resulting discriminative pattern become significantly more variable, although the classification accuracy is to some degree insensitive to this unrobustness of the pattern and maintains high levels. This can be explained by the fact that bootstrap resampling assumes that the given sample size is well representative of the populations (ADs and healthy controls). However, this is not applicable to most studies where only a limited number of recruited and scanned subjects is available. When using a discriminative pattern trained on a small sample, and validated on a larger and independent sample (i.e., from different medical centers), the robustness of the pattern will have a significant role resulting in lower actual accuracy compared with the accuracy predicted based on the smaller sample. For this reason, the analysis of robustness gives better insight into the future performance of a given discriminant analysis, especially if it is based on a small sample size. Therefore, a small number of PCs providing a higher robustness is preferable for the analysis, which is in accordance with results for PET data published previously (Markiewicz et al, 2009). A more detailed analysis of the robustness results shows that intensity normalization according to the cerebellum is relatively unrobust, compared with the other intensity normalization methods. The brainstem and the whole-brain reference region, however, perform similarly well in terms of robustness, with no clear preference for either region. However, to achieve an equivalent accuracy of classification using brainstem intensity normalization, more PCs need to be included into the analysis, which in turn results in less robustness, that is, the robustness of brainstem is worse than whole-brain intensity normalization if classification accuracy is approximately equivalent. Affine registration with a Gaussian filter of 12 mm FWHM and intensity normalization based on the whole-brain region, which provides the best classification accuracy, also provides noticeably good results for both robustness analyses, and seems to be a preferred combination of methods.

In general, the performance of a reference region used for intensity normalization not only depends on the uniformity of tracer uptake in this specific region, but also on the quality of registration. If the registration does not provide sufficient alignment between the patient data set and the registration template, the reference region defined on the template does not appropriately match the patient data set, resulting in a poor intensity normalization. This effect is one possible explanation for the poor accuracy values obtained for the pons and the thalamus (especially for a low number of PCs).

The method of using the mean value of only the brightest 25% of voxels of the reference region provides reliable intensity normalization, and allows for correct intensity normalization even if a slight misregistration between patient data set and registration reference is present. If the whole-brain region is used as reference region, this approach ensures that the regions affected by AD (consequently showing decreased uptake) do not compromise the intensity normalization. However, it should be noted that for patients with grossly abnormal uptake within the whole-brain region (for instance as a result of stroke, or in patients with very severe dementia), this approach may not be able to entirely compensate abnormalities, hence resulting in an error introduced into the scaling factor applied to the voxel intensities. However, such cases will appear as clearly abnormal by inspection of the uptake image, and are not the cases that are targeted with the multivariate analysis applied in this work.

The visualization of slice images of the discriminant image for the best performing preprocessing method shows patterns typically expected in dementia of AD type, with high values in the temporal, parietal, and frontal lobes, indicating a higher contribution to the discrimination. The slice images of the first two PCs can also be interpreted in terms of contribution to dementia, with the first PC showing patterns of AD, and the second PC showing changes, which could be due to the widening of the ventricles in AD patients. However, these interpretations should be regarded with caution. The PCA seeks the directions of greatest variation in the data, which could just as well represent anatomical variability within the population, rather than changes that can be attributed to dementia.

Conclusion

The results presented in this work illustrate that different data preprocessing methods have a significant impact on the accuracy and robustness of multivariate image analysis in 99mTc-ECD SPECT data. Among the preprocessing methods investigated in this work, the best performing method could be identified, which is based on affine registration, Gaussian smoothing with an FWHM of 12 mm, and intensity normalization according to the 25% brightest voxels within the whole-brain region. In current literature, the effect of data preprocessing on the outcome of image analysis and adjustments for optimizing the results are often not investigated in detail. However, this aspect greatly affects the analysis and becomes even more important if very slight deviations from normal need to be detected, as in early AD cases. Overall, this work contributes to a more robust and accurate classification of AD patients and asymptotic controls based on multivariate image analysis.

The authors declare no conflict of interest.

References

  1. Arad N, Dyn N, Reisfeld D, Yehezkel Y. Image warping by radial basis functions: applications to facial expressions. CVGIP-Graph Model Im. 1994;56:161–172. [Google Scholar]
  2. Bartenstein P, Minoshima S, Hirsch C, Buch K, Willoch F, Moesch D, Schad D, Schwaiger M, Kurz A. Quantitative assessment of cerebral blood flow in patients with Alzheimer's disease by SPECT. J Nucl Med. 1997;38:1095–1101. [PubMed] [Google Scholar]
  3. Braak H, Braak E. Neuropathological stageing of Alzheimer-related changes. Acta Neuropathol. 1991;82:239–259. doi: 10.1007/BF00308809. [DOI] [PubMed] [Google Scholar]
  4. Bradley K, O'Sullivan V, Soper N, Nagy Z, King E, Smith A, Shepstone B. Cerebral perfusion SPET correlated with Braak pathological stage in Alzheimer's disease. Brain. 2002;125 (Part 8:1772–1781. doi: 10.1093/brain/awf185. [DOI] [PubMed] [Google Scholar]
  5. Burdette J, Minoshima S, Borght TV, Tran D, Kuhl D. Alzheimer disease: improved visual interpretation of PET images by using threedimensional stereotaxic surface projections. Radiology. 1996;198:837–843. doi: 10.1148/radiology.198.3.8628880. [DOI] [PubMed] [Google Scholar]
  6. Dickson D. Neurodegeneration: The Molecular Pathology of Dementia and Movement Disorders. Blackwell Publishing Ltd: Boston, MA, USA; 2003. [Google Scholar]
  7. Duda R, Hart P, Stork D. Pattern Classification. John Wiley & Sons, Inc: New York, NY, USA; 2001. [Google Scholar]
  8. Efron B, Tibshirani R.1993An Introduction to the BootstrapVol. 43.Chapman & Hall/CRC: Boca Raton, FL, USA [Google Scholar]
  9. Engler H, Forsberg A, Almkvist O, Blomquist G, Larsson E, Savitcheva I, Wall A, Ringheim A, Langstroem B, Nordberg A. Two-year followup of amyloid deposition in patients with Alzheimer's disease. Brain. 2006;129 (Part 11:2856–2866. doi: 10.1093/brain/awl178. [DOI] [PubMed] [Google Scholar]
  10. Fripp J, Bourgeat P, Acosta O, Raniga P, Modat M, Pike K, Jones G, O'Keefe G, Masters C, Ames D, Ellis K, Maruff P, Currie J, Villemagne V, Rowe C, Salvado O, Ourselin S. Appearance modeling of 11C PiB PET images: characterizing amyloid deposition in Alzheimer's disease, mild cognitive impairment and healthy aging. Neuroimage. 2008;43:430–439. doi: 10.1016/j.neuroimage.2008.07.053. [DOI] [PubMed] [Google Scholar]
  11. Friston K, Ashburner J, Kiebel S, Nichols T, Penny W. Statistical Parametric Mapping: The Analysis of Functional Brain Images. Academic Press: London, UK; 2007. [Google Scholar]
  12. Golub G, Van Loan C. The Johns Hopkins University Press: Baltimore, MD, USA; 1996. Matrix computations (Johns Hopkins Studies in Mathematical Sciences) [Google Scholar]
  13. Habeck C, Foster N, Perneczky R, Kurz A, Alexopoulos P, Koeppe R, Drzezga A, Stern Y. Multivariate and univariate neuroimaging biomarkers of Alzheimer's disease. Neuroimage. 2008;40:1503–1515. doi: 10.1016/j.neuroimage.2008.01.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Herholz K, Salmon E, Perani D, Baron J, Holthoff V, Frlich L, Schönknecht P, Ito K, Mielke R, Kalbe E, Zündorf G, Delbeuck X, Pelati O, Anchisi D, Fazio F, Kerrouche N, Desgranges B, Eustache F, Beuthien-Baumann B, Menzel C, Schroeder J, Kato T, Arahata Y, Henze M, Heiss W. Discrimination between Alzheimer dementia and controls by automated analysis of multicenter FDG PET. Neuroimage. 2002;17:302–316. doi: 10.1006/nimg.2002.1208. [DOI] [PubMed] [Google Scholar]
  15. Holman B, Johnson K, Gerada B, Carvalho P, Satlin A. The scintigraphic appearance of Alzheimer's disease: a prospective study using technetium-99m-HMPAO SPECT. J Nucl Med. 1992;33:181–185. [PubMed] [Google Scholar]
  16. Hyman B, Hoesen GV, Damasio A, Barnes C. Alzheimer's disease: cell-specific pathology isolates the hippocampal formation. Science. 1984;225:1168–1170. doi: 10.1126/science.6474172. [DOI] [PubMed] [Google Scholar]
  17. Ishii K, Sasaki M, Kitagaki H, Yamaji S, Sakamoto S, Matsuda K, Mori E. Reduction of cerebellar glucose metabolism in advanced Alzheimer's disease. J Nucl Med. 1997;38:925–928. [PubMed] [Google Scholar]
  18. Ishii K, Willoch F, Minoshima S, Drzezga A, Ficaro E, Cross D, Kuhl D, Schwaiger M. Statistical brain mapping of 18F-FDG PET in Alzheimer's disease: validation of anatomic standardization for atrophied brains. J Nucl Med. 2001;42:548–557. [PubMed] [Google Scholar]
  19. Johnson K, Mueller S, Walshe T, English R, Holman B. Cerebral perfusion imaging in Alzheimer's disease. Use of single photon emission computed tomography and iofetamine hydrochloride I 123. Arch Neurol. 1987;44:165–168. doi: 10.1001/archneur.1987.00520140035014. [DOI] [PubMed] [Google Scholar]
  20. Markiewicz P, Matthews J, Declerck J, Herholz K. Robustness of multivariate image analysis assessed by resampling techniques and applied to FDG-PET scans of patients with Alzheimer's disease. Neuroimage. 2009;46:472–485. doi: 10.1016/j.neuroimage.2009.01.020. [DOI] [PubMed] [Google Scholar]
  21. Matsuda H, Kitayama N, Ohnishi T, Asada T, Nakano S, Sakamoto S, Imabayashi E, Katoh A. Longitudinal evaluation of both morphologic and functional changes in the same individuals with Alzheimer's disease. J Nucl Med. 2002;43:304–311. [PubMed] [Google Scholar]
  22. Meyer J, Gunn R, Myers R, Grasby P. Assessment of spatial normalization of PET ligand images using ligand-specific templates. Neuroimage. 1999;9:545–553. doi: 10.1006/nimg.1999.0431. [DOI] [PubMed] [Google Scholar]
  23. Mielke R, Pietrzyk U, Jacobs A, Fink G, Ichimiya A, Kessler J, Herholz K, Heiss W. HMPAO SPET and FDG PET in Alzheimer's disease and vascular dementia: comparison of perfusion and metabolic pattern. Eur J Nucl Med. 1994;21:1041–1043. doi: 10.1007/BF00181059. [DOI] [PubMed] [Google Scholar]
  24. Mielke R, Schroeder R, Fink G, Kessler J, Herholz K, Heiss W. Regional cerebral glucose metabolism and postmortem pathology in Alzheimer's disease. Acta Neuropathol. 1996;91:174–179. doi: 10.1007/s004010050410. [DOI] [PubMed] [Google Scholar]
  25. Minoshima S, Frey K, Foster N, Kuhl D. Preserved pontine glucose metabolism in Alzheimer disease: a reference region for functional brain image (PET) analysis. J Comput Assist Tomogr. 1995a;19:541–547. doi: 10.1097/00004728-199507000-00006. [DOI] [PubMed] [Google Scholar]
  26. Minoshima S, Frey K, Koeppe R, Foster N, Kuhl D. Alzheimer's disease using three-dimensional stereotactic surface projections of fluorine-18-FDG PET. J Nucl Med. 1995b;36:1238–1248. [PubMed] [Google Scholar]
  27. Minoshima S, Frey K, Koeppe R, Foster NL, Kuhl DE. A diagnostic approach in Alzheimers disease using three-dimensional stereotactic surface projections of fluorine-18-FDG PET. J Nucl Med. 1995c;36:1238–1248. [PubMed] [Google Scholar]
  28. Minoshima S, Koeppe R, Frey K, Kuhl D. Anatomic standardization: linear scaling and nonlinear warping of functional brain images. J Nucl Med. 1994;35:1528–1537. [PubMed] [Google Scholar]
  29. Pearson K. On lines and planes of closest fit to systems of points in space. Philos Mag. 1901;2:559–572. [Google Scholar]
  30. Petrella J, Coleman R, Doraiswamy P. Neuroimaging and early diagnosis of Alzheimer disease: a look to the future. Radiology. 2003;226:315–336. doi: 10.1148/radiol.2262011600. [DOI] [PubMed] [Google Scholar]
  31. Powers W, Perlmutter J, Videen T, Herscovitch P, Grieth L, Royal H, Siegel B, Morris J, Berg L. Blinded clinical evaluation of positron emission tomography for diagnosis of probable Alzheimer's disease. Neurology. 1992;42:765–770. doi: 10.1212/wnl.42.4.765. [DOI] [PubMed] [Google Scholar]
  32. Pratico D, Clark C, Liun F, Rokach J, Lee V, Trojanowski J. Increase of brain oxidative stress in mild cognitive impairment: a possible predictor of Alzheimer disease. Arch Neurol. 2002;59:972–976. doi: 10.1001/archneur.59.6.972. [DOI] [PubMed] [Google Scholar]
  33. Rueckert D, Hayes C, Studholme C, Summers PE, Leach MO, Hawkes DJ.1998Non-rigid registration of breast MR images using mutual informationInternational Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI)1144–1152.Cambridge, MA, USA [Google Scholar]
  34. Selkoe D. Alzheimer's disease: genotypes, phenotypes, and treatments. Physiol Rev. 2001;81:741–766. doi: 10.1152/physrev.2001.81.2.741. [DOI] [PubMed] [Google Scholar]
  35. Soonawala D, Amin T, Ebmeier K, Steele J, Dougall N, Best J, Migneco O, Nobili F, Scheidhauer K. Statistical parametric mapping of (99m)Tc-HMPAO-SPECT images for the diagnosis of Alzheimer's disease: normalizing to cerebellar tracer uptake. Neuroimage. 2002;17:1193–1202. doi: 10.1006/nimg.2002.1259. [DOI] [PubMed] [Google Scholar]
  36. Swets D, Weng J. Using discriminant eigenfeatures for image retrieval. IEEE Trans Pattern Anal Mach Intell. 1996;18:831–836. [Google Scholar]
  37. Taylor J, Hardy J, Fischbeck K. Toxic proteins in neurodegenerative disease. Science. 2002;296:1991–1995. doi: 10.1126/science.1067122. [DOI] [PubMed] [Google Scholar]
  38. Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, Joliot M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. NeuroImage. 2002;15:273–289. doi: 10.1006/nimg.2001.0978. [DOI] [PubMed] [Google Scholar]
  39. Wells W, Viola P, Atsumi H, Nakajima S, Kikinis R. Multi-modal volume registration by maximization of mutual information. IEEE Trans Med Imaging. 1996;1:35–52. doi: 10.1016/s1361-8415(01)80004-9. [DOI] [PubMed] [Google Scholar]
  40. Wold H.1966Estimation of principal components and related models by iterative least squares Multivariate Analysis(Krishnaiah PR, ed),Academic Press: New York, NY, USA [Google Scholar]
  41. Wold H.1975Path models with latent variables: the NIPALS approach Quantitative Sociology: International Perspectives on Mathematical and Statistical Model Building(Blalock HM et al, eds), Academic Press: New York, NY, USA [Google Scholar]
  42. Worsley K, Marrett S, Neelin P, Evans A. Searching scale space for activation in PET images. Human Brain Mapping. 1998;4:74–90. doi: 10.1002/(SICI)1097-0193(1996)4:1<74::AID-HBM5>3.0.CO;2-M. [DOI] [PubMed] [Google Scholar]

Articles from Journal of Cerebral Blood Flow & Metabolism are provided here courtesy of SAGE Publications

RESOURCES