Regression models for patient-reported measures having ordered categories recorded on multiple occasions

Abstract

Objectives

The article reviews proportional and partial proportional odds regression for ordered categorical outcomes, such as patient-reported measures, that are frequently used in clinical research in dentistry.

Methods

The proportional odds regression model for ordinal data is a generalization of ordinary logistic regression for dichotomous responses. When the proportional odds assumption holds for some but not all of the covariates, the lesser known partial proportional odds model is shown to provide a useful extension.

Results

The ordinal data models are illustrated for the analysis of repeated ordinal outcomes to determine whether the burden associated with sensory alteration following a bilateral sagittal split osteotomy procedure differed for those patients who were given opening exercises only following surgery and those who received sensory retraining exercises in conjunction with standard opening exercises.

Conclusions

Proportional and partial proportional odds models are broadly applicable to the analysis of cross-sectional and longitudinal ordinal data in dental research.

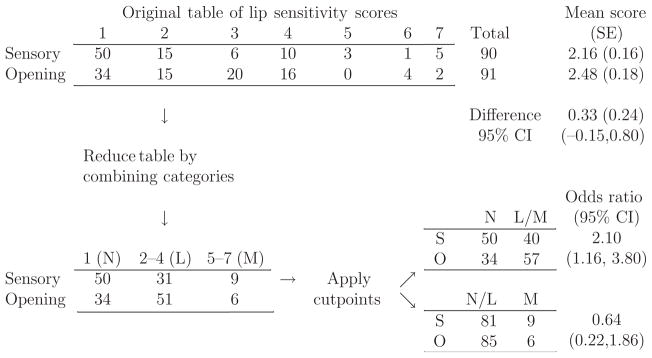
Outcomes having ordered categories are common in dental research. Consider, for example, frequency count data (Fig. 1) from a randomized, parallel-group, controlled clinical trial to determine whether the burden associated with sensory alteration following a bilateral sagittal split osteotomy (BSSO) procedure differed for those patients who were given opening exercises only following surgery and those who received sensory retraining exercises in conjunction with standard opening exercises (1). Patients were asked to rate ‘loss of lip sensitivity’ using a seven-point integer scale where a value of 1 equals ‘no problem’ and 7 is “serious problem”. Intermediate values between 1 and 7 were not descriptively identified; even if descriptors such as ‘slight problem’ and ‘moderate problem’ had been attached to them, imposing an interval scale to the responses would be inappropriate and could give distorted data analysis results. In other words, the actual distance between values is unknown, and one cannot say, for example, that the difference between 1 and 2 in terms of increased severity is the same as the distance between 6 and 7. It is understood, rather, that the numeric values only convey that a score of 7 represents greater severity of problems than a score of 6, which, in turn, indicates greater severity than a score of 5, and so on. In the common schema for the classification of variable types, lip sensitivity is an ordinal variable.

Fig. 1.

Observed frequency counts of patient replies to ‘My lips feel less sensitive to touch’ at the 6-month follow-up visit in a randomized, parallel-group, controlled clinical trial measuring sensory alteration following a bilateral sagittal split osteotomy procedure. The first row provides counts for the group given sensory (S) re-training exercises; the second row provides counts for the group receiving opening (O) exercises only. The scale ranges from a value of 1 (‘no problem’ or ‘N’) to a value of 7 (‘serious problem’) with unspecified descriptors for intermediate values. Created categories are (L) for little problem and (M) for moderate problem.

Researchers often inappropriately apply statistical methods for continuous data to ordinal data. However, just because a mean score can be computed for an ordinal variable based on the numeric values assigned to distinguish its categories does not imply there is any real meaning to the average scores so obtained. Indeed, one could calculate a 95% confidence interval for the difference in means scores, or apply a two sample t-test, in an attempt to determine whether there are any significant differences in problem severity between the two treatment groups. For the data in Fig. 1, the common large-sample 95% confidence interval for the difference in mean integer scores contains a value of zero, suggesting there is no difference between treatments. Furthermore, the t-statistic (not shown) is 1.36, not statistically significant (P-value = 0.18; 179 degrees of freedom, or d.f.). These misleading results are based on the erroneous assumption of an interval scale, imposing interpretations on the scores for lip sensitivity that lack adequate justification.

Rather, the data in Fig. 1 have an ordinal scale, for which statistical methods with appropriate assumptions are required (2). Hypothesis testing procedures based on ranks instead of integer scores are often appropriate as they assume ordering of the categories, while assuming distances between response categories are unknown. For example, the Wilcoxon rank sum test’s chi-square (with 1 d.f.) value of 4.52 corresponds to a large sample P-value of 0.034, leading to a different conclusion than that provided by the t-test. In this analysis, the set of 181 integer scores from the combined treatment groups are ranked from smallest to largest, and, using mid-ranks for ties, the result is that the average rank for opening exercises only is significantly larger than the average rank for sensory retraining. In other words, sensory retraining significantly reduces the extent of problems relative to opening exercises only. Unlike the analysis comparing mean integer scores, the analysis based on ranks is defensible as minimal assumptions are required. Furthermore, the results based on rank scores are consistent with the general observation that a larger percentage of participants in the sensory training group (n = 50, 56%) reported ‘no problems’ compared to subjects in the opening exercises only group (n = 34, 37%). Also, as expected, the Wilcoxon rank sum test is more robust than the t-test to the impact of the relatively few individuals who reported a score of 7 for ‘serious problems’. This simple example illustrates that inappropriate application of statistical analysis methods based on continuous data may lead to incorrect results when applied to ordinal data.

While nonparametric rank tests for ordinal data are useful in an initial stage of analysis, for example to establish treatment efficacy in a clinical trial, dental researchers often have the goal to quantify the effects of multiple explanatory variables in a regression modeling framework. Even in the case of a single explanatory factor such as treatment in Fig. 1, the structure of the relationship between factor and response may be too complex to be adequately captured as a difference of means (i.e., t-test) or a comparison of medians (i.e., Wilcoxon test). A modeling framework for ordinal responses based on odds ratios offers a high degree of flexibility and interpretability. In this paper, we discuss multivariable modeling approaches for ordinal data that are extensions of logistic regression for dichotomous responses.

Logistic regression models for ordinal response data require that the number of categories not be large (3). Usually, the ordinal response variable will have a small number of categories (e.g., three or four); when categories are numerous, it is often reasonable to combine them in a way that achieves a manageable and moderately small number (e.g., seven or less). When cross-classified data, such as presented in the 2 by 7 frequency table in Fig. 1, contain zero cells or cells with small counts, commonly used large-sample statistical procedures (e.g., Pearson chi-square test) may not be applicable. As the counts for lip sensitivity are small for categories 5, 6, and 7, these may be combined without much loss of information. We also observe that a value of 1 indicating ‘no problem’ represents a qualitatively different experience of lip sensitivity loss than all other categories where some problems are indicated, so that this category corresponding to the first column in the table should not be combined with any other. Finally, it seems reasonable to combine categories 2, 3, and 4 as these are adjacent categories with increasing levels of severity but without individual descriptors. These data reductions result in the 2 by 3 table in the lower left part of Fig. 1. For ease of interpretation, we apply the descriptors ‘little severity’ to the combined category 2–4 and ‘moderate severity’ to the combined category 5–7. While these descriptors are somewhat arbitrary, an approach based on dichotomizing the response variable as 1 for ‘no problem’ versus 2–7 for ‘some problem’ would have resulted in a substantial loss of information. Conversely, while there are other defensible data reductions (e.g., creating combined categories 1 versus 2–3 versus 4–7 would give qualitatively similar confidence intervals to those in Fig. 1), those resulting in more than three categories would be difficult to manage in a multivariable regression analysis for ordinal data.

The regression modeling approach discussed in this article treats an ordinal response variable as a generalization of dichotomous data as shown in the bottom half of Fig. 1. This is achieved by applying all possible cutpoints to the ordinal variable to obtain a series of two by two tables such that only consecutively adjacent categories are grouped to form the dichotomies. From the reduced 2 by 3 table in Fig. 1, we may combine either the first two columns (N with L) or the last two columns (L with M), obtaining the pair of 2 by 2 tables shown in the lower right portion of the figure. The goal here is not further data reduction with attendant information loss, but rather to address whether there is a significant relationship between treatment group and severity of lip sensitivity problems, and if so, to determine whether the relationship differs for the two tables produced by different cutpoints.

The data in Fig. 1 suggest the answer is ‘yes’ to both questions. Specifically, we find that the odds of having ‘no problem’ versus ‘little’ or ‘moderate’ problems is an estimated 2.10 times higher for the group that received sensory retraining exercises than in the group that received opening exercises only. The fact that the corresponding large-sample 95% confidence interval (4) does not contain one indicates that sensory retraining results in a significantly better outcome with regard to lip sensitivity loss than treatment restricted to standard opening exercises. Interestingly, for the cutpoint contrasting ‘no problem’ or ‘little problem’ versus ‘moderate problem’, the relationship between treatment and outcome, though not statistically significant, is in the opposite direction, i.e., the odds ratio of 0.64 is <1, indicating that sensory retraining may lead to greater levels of moderate problems from lip sensitivity loss than treatment based on standard opening exercises only. Such variations in odds ratio estimates by cutpoint, if statistically substantiated, would be missed by a single summary statistic based on differences of mean or median scores, or an odds ratio taking an assumed common value for the two tables.

This paper reviews multivariable regression analysis of ordinal data for both cross-sectional and longitudinal data, thereby extending consideration of such research questions to account for covariates. In particular, we consider a common extension to ordinal outcomes of ordinary logistic regression for dichotomous responses known as the proportional odds regression model (PORM), as well as a lesser known extension of that model called the partial proportional odds regression model (PPORM). When two odds ratio estimates, as in Fig. 1, are statistically indistinguishable, a PORM would estimate a single odds ratio to represent an average association that summarizes the relationships in both tables. The proportional odds assumption corresponding to a single odds ratio implies that the mechanism by which predictive factors relate to the odds of no problem versus any problem is similar to that predicting no or little problem versus moderate problem. However, when the odds ratios produced by applying different cutpoints to an ordinal outcome vary, as is illustrated in Fig. 1, a PPORM is applicable. In such a case, interpretations depend upon cutpoint. The preliminary confidence interval results of Fig. 1 suggest that the two treatments can be distinguished by the odds of having any problem, but may not be distinguishable relative to moderate problem versus little or no problem.

The next section describes the study data from the sensory retraining clinical trial and the structure of statistical models for the analysis of cross-sectional and longitudinal ordinal data. The section that follows reports results of an analysis of the sensory retraining data using longitudinal PORM and PPORM. The closing discussion section considers special issues in the choice of model type. Statistical and implementation details are described elsewhere (13).

Methods

Sensory retraining following orthognathic surgery clinical trial

This paper presents an analysis of 184 subjects that were enrolled in a randomized, parallel-group, controlled clinical trial to determine whether the burden associated with sensory alteration following a BSSO procedure differed for those patients who were given opening exercises only following surgery and those who received sensory retraining exercises in conjunction with standard opening exercises. Subjects were included if they had either mandibular surgery only or if both jaws were operated on. Two patients from an earlier analysis (5) are not included because they represent protocol violations, having had maxillary surgery only. Data were collected on five ordinal outcomes prior to surgery and at 1, 3, and 6 months following surgery. Among five items linked to the hypothesized effect of sensory retraining on altered sensory signals from the trigeminal nerve following BSSO and subsequent motor function, three items are considered in this paper: (i) Unusual feelings in my face or mouth; (ii) Numbness in facial area or around mouth; and (iii) Loss of lip sensitivity (e.g., using a straw, kissing) (1). For each item, subjects reported the magnitude of the problem during the past 2 weeks on a scale from 1 for ‘no problem’ to 7 for ‘serious problem’. The earlier analysis found no evidence that sensory retraining impacted two outcomes relating to painful altered sensations on the face or in the mouth (5).

The analysis in this paper seeks new insights relative to the original analysis based upon a score aggregated over all outcomes and visits that found no significant difference between treatments (5). Supplementary analyses based on repeated-measures proportional odds models for the individual items identified some statistically significant treatment differences for some of the items at some visits. Those analyses modeled the three time points simultaneously, estimating model parameters by the method of generalized estimating equations (GEE), commonly used in the analysis of repeated-measures categorical data to account for intrasubject correlation of response variables (6–8).

This paper extends these earlier analyses by fitting models that relax the proportional odds assumption in an attempt to reach a more informed conclusion on the potential benefits of sensory retraining following a BSSO procedure, adjusting for baseline response, number of jaws operated on (one or two), and genioplasty (yes, no).

Because of sparse data, categories are combined as in an earlier analysis (4) to create ordinal variables with three categories for the level of problems or interference in daily life: a value of 1 for no problem, 2 for little and 3 for moderate to severe. As in Fig. 1, and to simplify interpretations throughout the paper, we henceforth refer to the last category as ‘moderate’, dropping the term ‘severe’. Only six subjects have incomplete outcomes, with the 3- and/or 6-month visits missing.

Ordinal regression models for cross-sectional data

Suppose O_i is a variable taking one of c possible ordered values for a subject indexed by i; for simplicity, the i subscript is dropped for the remainder of this section. For the sensory retraining data, c = 3; specifically, O is classified as 1 = no problem; 2 = little problem; or 3 = moderate problem. Following Fig. 1, we create two binary response variables from O; first, let Y₁ = 1 if O = 1 and Y₁ = 0 if O = 2 or O = 3, and second, let Y₂ = 1 if O = 1 or O = 2 and Y₂ = 0 if O = 3. Next, we define the probability of having no problem θ₁ = Pr(Y₁ = 1) = Pr(O ≤ 1) and the probability of having no problem or little problem θ₂ = Pr(Y₂ = 1) = Pr(O ≤ 2). Therefore, the odds of having no problem relative to some problem is θ₁/(1−θ₁), whereas the odds of having no or little problem relative to moderate problem is θ₂/(1−θ₂). While ‘odds’ refers to binary data, θ₁ and θ₂ are cumulative probabilities because the binary responses Y₁ or Y₂ on which they are based are formed by applying cutpoints, resulting in combined categories, to an underlying ordinal variable. Thus, a cumulative odds logistic regression model for the ordinal response O is given by

$$log[{\theta }_{\text{h}}/(1-{\theta }_{\text{h}})]={\beta }_{0\text{h}}+\text{x}{\beta }_1+(\text{z}\times \text{x}){\beta }_2\text{h}=1,2;$$ (1)

where h indexes the cutpoint specifying the model for either Y₁ or Y₂; x = 1 for sensory retraining and x=0 for opening exercises only; and z is a dummy variable for the cutpoint applied to the ordinal response, i.e., z = 0 if h = 1, and z = 1 if h = 2.

Equation 1, the cumulative odds logistic regression model for a single covariate in compact form, can be expanded to reveal a model for each log odds, or logit. The log odds of no problem relative to some problem (i.e., logit h = 1) is

$$log[{\theta }_1/(1-{\theta }_1)]={\beta }_{01}+\text{x}{\beta }_1$$ (2)

and the log odds of no problem or little problem relative to moderate problem (i.e., logit h = 2) is

$$log[{\theta }_2/(1-{\theta }_2)]={\beta }_{02}+\text{x}({\beta }_1+{\beta }_2)$$ (3)

Note that β_0h is the intercept for the h-th logit, h = 1,2; β₁ is the difference in the log odds (i.e., β₁ is the log odds ratio) of no problem relative to some problem for sensory retraining versus opening exercises only; and β₂ is the incremental difference, relative to the first log odds (h = 1), of the effect of the sensory retraining on the second log odds (h = 2). In terms of the data in the lower right part of Fig. 1, this is a saturated model, i.e., it places no restrictions on the data. As such, separate ordinary logistic regression fits for binary response data can be made to Eqs. (2) and (3); their respective maximum likelihood estimates reproduce the observed odds ratios in Fig. 1, exp(β̂₁) = 2.10 and exp(β̂₁ + β̂₂) = 0.64.

Simultaneous estimation of the regression coefficients in model Eq. 1 is employed when there is structure (i.e., restrictions) placed on the relationship of treatment and outcome. In particular, assuming β₂ = 0 gives the PORM (4, 9) compactly written as

$$log[{\theta }_{\text{h}}/(1-{\theta }_{\text{h}})]={\beta }_{0\text{h}}+\text{x}{\beta }_1\text{h}=1,2.$$ (4)

where exp(β₁) is the odds ratio corresponding to both cutpoints, e.g., for both tables in Fig. 1. In a data analysis, interpretations based on the PORM have to be sufficiently general to apply to both cutpoints, yet still be descriptive: β₁ in Eq. 4 is the difference in the log odds of having less problem relative to more problem for sensory retraining versus opening exercises only. This concise and generic language incorporates the comparison of both no problem versus some problem and no or little problem versus moderate problem.

Estimation of the PORM parameters β₀₁,β₀₂, and β₁ in Eq. 4, or the PPORM parameters in Eq. 1, is typically by the method of maximum likelihood (9, 10), although estimation can be performed with an approximation approach using software for dichotomous response logistic regression (11). The estimate of the common odds ratio exp(β₁) from Eq. 4 for the data in Fig. 1 is 1.75, a value between 2.10 and 0.64 that averages these seemingly divergent effects. In practice, one typically performs a statistical test of the proportional odds assumption by comparing nested models in Eqs. (1) and (4). If the hypothesis H₀: β₂ = 0 is rejected, the PPORM is selected, otherwise the PORM is chosen. Alternatively, an analysis based on a PPORM is sometimes prespecified; considerations for such preplanned analyses are treated in the discussion section.

One attractive property of the PORM is that the proportional odds assumption can reduce considerably the number of regression coefficients that need to be estimated in more complex models, those with multiple covariates and/or more than three categories to the ordinal response. For example, if the data in Fig. 1 had been reduced to a table with four columns (instead of three columns denoted ‘N’, ‘L’, and ‘M’), the model would assume a common value for the three resulting odds ratios obtained by applying all possible cutpoints. In general, for c ordinal response categories, there will be c − 1 cutpoint-specific odds ratios that are assumed to be equal under the PORM. The proportional odds assumption could be applied selectively to a subset of covariates in an expanded multivariable model giving the PPORM (10) as described in the next section.

Models for longitudinal ordinal data

Equation 1 may be extended to allow multiple time points. Let O_it be the ordinal response for the i-th subject at time t = 1,…,T_i, where T_i ≤ T, such that data are collected up to T fixed time points, but the actual number of observations per subject T_i may vary, to account for dropout or missed visits. For the sensory retraining data, the outcome O_it is classified as 1 = no problem; 2 = little problem; or 3 = moderate problem. Define the probabilities θ_it1 = Pr(O_it ≤ 1) and θ_it2 = Pr(O_it ≤ 2). Interest is in modeling θ_it1/(1−θ_it1) and θ_it2/(1−θ_it2), the cumulative odds at time t of no problem relative to some level of problem and no or little problem relative to moderate problem, respectively. For the sensory retraining data, T = 3, and a longitudinal cumulative odds logistic regression model is

$$\begin{array}{l}log[{\theta }_{\text{ith}}/(1-{\theta }_{\text{ith}})]={\beta }_{0\text{h}}+x_{\text{it}}^{\prime }{\beta }_1+(\text{z}\times {\text{w}}_{\text{it}}^{\prime }){\beta }_2\\ \text{h}=1,2;\text{t}=1,2,3,\end{array}$$ (5)

where x_it is a vector of possibly time-dependent covariates (e.g., treatment, number of jaws operated on, genioplasty, baseline response, time, and time × treatment), w_it is a vector consisting of some of the covariates in x_it, or all of them (i.e., w_it = x_it); and z is defined as in Eq. 1. Again, β_0h is the intercept for the h-th logit; β₁ is a vector whose elements contain the effects of individual covariate components of x_it on the log odds of no relative to some problem (i.e., h = 1); and β₂ is a vector of incremental differences, relative to the first log odds (h = 1), of the effect of the covariates w_it on the second log odds of no or little problem relative to moderate problem (h = 2).

Equation 5 encompasses both PPORM and PORM. In particular, for T = 3, the longitudinal PORM obtained by setting β₂ = 0 is

$$log[{\theta }_{\text{ith}}/(1-{\theta }_{\text{ith}})]={\beta }_{0\text{h}}+{\text{x}}_{\text{it}}^{\prime }{\beta }_1\text{h}=1,2;\text{t}=1,2,3;$$ (6)

when T = 1, it reduces to the PORM in Eq. 4 for a univariate outcome. The proportional odds assumption of the longitudinal PORM is assessed by testing H₀: β₂ = 0, in this instance, through comparison of models in Eqs. (5) and (6). These models are estimated by GEE (12,13).

Note that the PPORM in Eq. 5 includes w_it that is a subset of x_it so that the proportional odds assumption holds for some covariates (i.e., those in x_it but excluded from w_it), but not for others. Specifically, when β_2j ≠ 0, inclusion of a covariate-by-cutpoint interaction term allows the effect of a covariate (indexed by j) to vary across logits. Equations (5) and (6) generalize to c > 3 ordinal outcome categories by including c − 2 dummy variables (replacing z) to distinguish the c − 1 odds. For c = 2, both these models reduce to the logistic regression model (e.g., Eq. 2) that specifies the probability structure of a dichotomous outcome (e.g., no problem versus some problem) over time.

Results

Table 1 shows frequencies of subjects reporting no, little, or moderate problem levels relating to altered sensations following orthognathic surgery. Immediately prior to surgery (baseline), there are few problems with sensation. One month after surgery, nearly one-half of subjects report moderate problem levels with numbness, and between a fifth and a third report moderate problem levels with unusual feelings or loss of lip sensitivity. As follow-up progresses, subjects have a decreasing likelihood to report moderate problem levels with altered sensation, and an increasing likelihood to report no problem. Subjects receiving sensory retraining exercises are more likely to report no problem at 3 and 6 months than subjects receiving standard opening exercises only.

Table 1.

Number (and percentage) of patients reporting no (N), little (L), or moderate (M) difficulty or problem level with altered sensations experienced in preceding 2 weeks. The first row provides counts and percentages for sensory retraining exercises; the second row provides counts and percentages for opening exercises only

	Unusual feelings			Numbness			Loss of lip sensitivity
	N	L	M	N	L	M	N	L	M
Baseline	80 (88%)	9 (10%)	2 (2%)	86 (95%)	4 (4%)	1 (1%)	83 (91%)	8 (9%)	0 (0%)
	84 (90%)	9 (10%)	0 (0%)	89 (96%)	4 (4%)	0 (7%)	88 (95%)	3 (3%)	2 (2%)
1 month	15 (16%)	48 (53%)	28 (31%)	4 (4%)	38 (42%)	49 (54%)	19 (21%)	41 (45%)	31 (34%)
	21 (23%)	51 (55%)	21 (23%)	6 (6%)	42 (45%)	45 (48%)	20 (22%)	44 (47%)	29 (31%)
3 months	38 (43%)	42 (47%)	9 (10%)	17 (19%)	55 (62%)	17 (19%)	34 (38%)	41 (46%)	14 (16%)
	27 (30%)	53 (58%)	11 (12%)	10 (11%)	59 (64%)	23 (25%)	29 (32%)	45 (49%)	17 (19%)
6 months	52 (58%)	33 (37%)	5 (6%)	33 (37%)	45 (50%)	12 (13%)	50 (56%)	31 (34%)	9 (10%)
	46 (51%)	43 (47%)	2 (2%)	20 (22%)	63 (69%)	8 (9%)	34 (37%)	51 (56%)	6 (7%)

The unadjusted odds ratios (Table 2) comparing sensory retraining to opening exercises for each of the three outcomes suggest discordance between the cutpoints (h = 1,2), particularly at 6 months. As noted in the introduction, the 6-month odds ratio for no problem versus some (i.e., little or moderate) problem regarding lip sensitivity is 2.10, using data from Table 1. Thus, subjects receiving sensory retraining have an estimated 2.10 (95% CI 1.16, 3.80) times higher odds of having no burden associated with decreased lip sensitivity at 6-month follow-up compared to subjects receiving standard opening exercises while the estimated 6-month odds ratio for no or little problem versus moderate problem regarding lip sensitivity is 0.64 (95% CI: 0.22,1.86). Interestingly, there is a fair degree of consistency of effect sizes across the three outcomes.

Table 2.

Cumulative odds ratios estimates (95% confidence intervals) for less severe problems ^a for the comparison of sensory retraining to opening exercises only

	Unusual feelings		Numbness		Loss of lip sensitivity
	N vs L/M	N/L vs M	N vs L/M	N/L vs M	N vs L/M	N/L vs M
Unadjusted b
1 Month	0.68 (0.33,1.41)	0.66 (0.34,1.27)	0.67 (0.18,2.44)	0.80 (0.45,1.43)	0.96 (0.47,1.95)	0.88 (0.47,1.63)
3 Months	1.77 (0.95,3.27)	1.22 (0.48,3.11)	1.94 (0.83,4.50)	1.41 (0.70,2.87)	1.32 (0.72,2.44)	1.23 (0.57,2.68)
6 Months	1.34 (0.74,2.41)	0.38 (0.07,2.02)	2.06 (1.07,3.96)	0.63 (0.24,1.61)	2.10 (1.16,3.80)	0.64 (0.22,1.86)
Proportional odds regression c
1 Month	0.60 (0.50,0.72)	0.60 (0.50,0.72)	0.79 (0.67,0.93)	0.79 (0.67,0.93)	0.93 (0.79,1.09)	0.93 (0.79,1.09)
3 Months	1.53 (1.30,1.81)	1.53 (1.30,1.81)	1.61 (1.35,1.93)	1.61 (1.35,1.93)	1.29 (1.10,1.52)	1.29 (1.10,1.52)
6 Months	1.15 (0.97,1.36)	1.15 (0.97,1.36)	1.45 (1.22,1.73)	1.45 (1.22,1.73)	1.66 (1.43,1.94)	1.66 (1.43,1.94)
Partial proportional odds regression
1 Month	0.65 (0.31,1.36)	0.62 (0.31,1.24)	0.63 (0.17,2.32)	0.73 (0.40,1.31)	0.93 (0.46,1.89)	0.83 (0.44,1.56)
3 Months	1.75 (0.95,3.24)	1.18 (0.45,3.14)	2.00 (0.87,4.64)	1.36 (0.65,2.83)	1.39 (0.74,2.60)	1.24 (0.56,2.74)
6 Months	1.29 (0.71,2.33)	0.37 (0.06,2.18)	2.11 (1.09,4.06)	0.59 (0.22,1.56)	2.19 (1.21,3.96)	0.60 (0.20,1.86)

^aResponse categories are N = ‘no problem’, L = ‘little problem’, M = ‘moderate problem’.

^bConfidence intervals are given by the exponentiated 95% confidence interval bounds for log odds ratio (Agresti, 2002) (4).

^cThe results are based on model Eq. (1) with β₂ = 0 fitted to three collapsed categories of the response variable. Analogous results presented in Table 6 of Phillips et al. (2007) (5) are based on a model fitted to a response defined by the seven uncollapsed categories.

The unadjusted odds ratios do not, however, account for covariates. To adjust for the effects of covariates, the PORM in Eq. 6 is fit separately for each outcome variable using explanatory variables ${\text{x}}_{\text{it}}^{\prime }=({\text{x}}_{\text{it}1},{\text{x}}_{\text{it}2},\dots ,{\text{x}}_{\text{it}8})$ where x_it1, x_it2 and x_it3 are 0/1 indicator variables with ‘1’ indicating sensory retraining, one jaw operated on, and genioplasty performed, respectively; x_it4 is the baseline response, x_it5 and x_it6 are indicators for the 3- and 6-month follow-up exams, respectively; and x_it7 = x_it1 × x_it5 and x_it8 = x_it1 × x_it6 are terms for visit by treatment interactions.

Table 2 presents odds ratio estimates based upon the longitudinal PORM, which are computed from the regression coefficients reported in Table 3. Adjusting for number of jaws operated on and genioplasty, subjects receiving sensory retraining have an estimated exp(β̂₁₁ + β̂₁₈) = exp(−0.07+ 0.58) = 1.66 (95% CI: 1.43, 1.94) times higher odds of having less burden (versus more burden) associated with lip sensitivity at 6-month follow-up compared to subjects receiving standard opening exercises. This estimate provides the effect of sensory retraining on both the odds of no relative to some problem and the odds of no problem or little problem relative to moderate problem. There are also statistically significant positive effects of sensory retraining exercises on lip sensitivity loss at the 3-month follow-up visit, on numbness at the 3- and 6-month follow-up visits, and on unusual feelings at the 3-month follow-up visit. The effect of sensory retraining on numbness at 6-month follow-up was nearly statistically significant at the 0.05 significance level.

Table 3.

Generalized estimating equations (GEE) parameter estimates (empirical standard errors) for cumulative logit models^a for loss of lip sensitivity for the comparison of sensory retraining to opening exercises only

	Proportional odds model		Partial proportional odds model
	est (SE)	P-value	est (SE)	P-value
Intercept 1 (β01)	−1.23 (0.46)	0.007	−1.08 (0.49)	0.027
Intercept 2 (β02)	1.05 (0.47)	0.024	0.84 (0.48)	0.082
Treatment (β11)	−0.07 (0.29)	0.802	−0.07 (0.36)	0.851
One jaw operated on (β12)	0.52 (0.22)	0.020	0.54 (0.23)	0.018
Genioplasty (β13)	0.13 (0.24)	0.590	−0.11 (0.26)	0.666
Baseline response (β14)	−0.51 (0.32)	0.105	−0.48 (0.33)	0.152
Visit 2 (3 months) (β15)	0.70 (0.20)	0.001	0.51 (0.25)	0.046
Visit 3 (6 months) (β16)	1.13 (0.23)	< 0.001	0.79 (0.31)	0.010
Visit 2 × treatment (β17)	0.33 (0.30)	0.276	0.40 (0.39)	0.306
Visit 3 × treatment (β18)	0.58 (0.35)	0.098	0.85 (0.44)	0.056
Cutpoint by covariate interactions
Treatment (β21)	–	–	−0.12 (0.39)	0.765
Genioplasty (β23)	–	–	0.78 (0.33)	0.017
Visit 2 (β25)	–	–	0.16 (0.31)	0.611
Visit 3 (β26)	–	–	1.12 (0.52)	0.029
Visit 2 × treatment (β27)	–	–	0.00 (0.48)	0.999
Visit 3 × treatment (β28)	–	–	−1.17 (0.67)	0.080

^aEstimation uses multinomial GEE with unstructured correlation matrix fitted with authors’ SAS macro. Similar results using an approximation approach based on logistic regression for dichotomous outcomes may be obtained as described by Stokes et al. (2000) (11) and Preisser et al. (2010) (13).

The appropriateness of the proportional odds assumption for these analyses can be assessed based on the fact that the PORM is nested within the PPORM. By specifying w_it = x_it in Eq. 5, asymptotically chi-square distributed ( ${\chi }_8^2$; i.e., with 8 d.f.) empirical score tests (14) of the proportional odds assumption H₀: β₂ = 0 were not statistically significant, providing insufficient evidence to reject proportional odds: lip sensitivity ${\chi }_8^2=13.12$, p = 0.11; numbness ${\chi }_8^2=11.07$, p = 0.20; unusual feelings ${\chi }_8^2=6.43$, p = 0.60. In other words, even though the cutpoint-specific unadjusted odds ratios from the PPORM, also reported in Table 2, appear widely disparate, their variability is sufficiently large such that one cannot statistically distinguish the effect of sensory retraining on the odds of having no problem relative to some problem, from the odds of having no problem or little problem relative to moderate problem. In conclusion, there is insufficient evidence to reject the assumption of proportional odds, and, thus, basing inferences on Eq. 6 is not contradicted.

Although hypothesis tests did not reject the proportional odds assumption for any outcome measure, for the sake of exposition, we consider inference for the sensory retraining study based on the PPORM. Further, one may consider that the nonsignificance of the tests may be because of lack of statistical power to identify the discrepant odds ratios, such as those suggested by the observed data of Fig. 1. We have noted that Table 2 reveals that at 3- and 6-month follow-up visits, the unadjusted odds ratio for no problem relative to little or moderate problem appears to be greater than the unadjusted odds ratio for no problem or little problem relative to moderate problem, and this pattern holds for all three outcomes. These cutpoint-specific odds ratios are allowed to vary by retaining in Eq. 5 the cutpoint-specific interaction with treatment; the model is simplified by omitting selected nonsignificant covariate-by-cutpoint interactions. Preliminary analysis indicated that the covariates number of jaws operated on and baseline response had nonsignificant interactions with cutpoint. Therefore, the final PPORM used x_it defined above and ${\text{w}}_{\text{it}}^{\prime }=({\text{w}}_{\text{it}1},{\text{w}}_{\text{it}3},{\text{w}}_{\text{it}5},{\text{w}}_{\text{it}6},{\text{w}}_{\text{it}7},{\text{w}}_{\text{it}8})$, where w_itj = x_itj, for the j-th covariate. Estimated regression coefficients for the PORM and PPORM are shown in Table 3 while detailed explication of the computations involved for this application are described elsewhere (13).

Table 2 shows that the results of the PPORM applied for each outcome gives odds ratio estimates and confidence intervals that are very close in magnitude to the unadjusted odds ratios. The PPORM estimated odds ratios for no problem versus some problem reveal statistically significant differences among treatments at 6 months for numbness and lip sensitivity whereas, unlike in the PORM analysis, there is no significant effect of the odds ratio for no or little problem versus moderate problem. For example, subjects receiving sensory retraining have an estimated exp(β̂₁₁ + β̂₁₈) = 2.19 (95% CI: 1.16, 3.80) times higher odds of having no problem versus some problem with lip sensitivity at 6-month follow-up compared to subjects receiving standard opening exercises, while the corresponding estimated odds ratio for comparing no or little problem versus moderate problem is 0.60 (95% CI: 0.20, 1.86). In contrast to these cutpoint-specific odds ratio estimates provided by the PPORM, the PORM effectively computes a weighted average of the two odds ratios, potentially masking the strength of the PPORM odds ratio for no problem versus some problem. It is of further interest to note that the PPORM did not indicate any statistically significant treatment effects at 3-month follow-up (note all confidence intervals contain 1), in contrast to the PORM that found differences at this visit for all three outcomes. In sum, the PPORM gives results that are qualitatively different than those based on the PORM.

Discussion

This paper reviewed statistical methods for the regression analysis of repeated ordinal outcomes and applied them to a clinical trial to assess the impact of sensory retraining exercises relative to standard opening exercises only on reducing the severity of problems associated with altered sensation following a BSSO procedure. Whereas both the PORM and PPORM analyses provided strong statistical support that sensory retraining reduces the burden associated with altered sensation, the inferred timing and extent of the beneficial effects of sensory retraining differed substantively between the two analyses. In particular, the PORM identified a larger number of statistically significant effects of sensory retaining relative to standard opening exercises than the PPORM, most noticeably at the 3-month visit. Correspondingly, the PPORM had wider confidence intervals than the PORM, whereas the latter pooled information across cutpoints providing increased precision in estimates.

Generally, inference should be based on the PORM when the proportional odds assumption is not rejected. Thus, the longitudinal PORM analysis, similar to an analysis reported earlier (5) is preferred for the sensory retraining data. This standard modeling strategy tends to limit the occurrence of spurious findings of statistical significance because of multiple hypothesis testing, as might arise with increased frequency in the context of an analysis based on the PPORM. Notwithstanding, given the disparate results obtained with PORM versus PPORM, a substantial degree of doubt exists about the final form of the model for the sensory retraining data. Whether the PORM is the correct model cannot be known. One possible explanation for the failure to reject the proportional odds assumption is that the sample size was not sufficiently large to provide adequate statistical power for its rejection.

When the proportional odds assumption is rejected by statistical testing, the PPORM, or other alternative such as the generalized logits model (4), should be used. The consequences of inappropriately applying a PORM may be substantial, as measured by a comparison of estimates from the PPORM and the incorrect PORM.

Various strategies exist to address the issue of model uncertainty for cumulative logistic regression models for ordinal data. The obvious, but potentially cost-prohibitive, solution is to design studies with large enough sample sizes to have a high degree of power to statistically discriminate between the PORM and PPORM in the analysis stage. For confirmatory clinical trials, another strategy may be employed in the planning stage of a study through the a priori specification of the statistical analysis plan; indeed, specifying the statistical analysis before the data are collected is standard practice for clinical trials subject to regulatory guidelines. As has been stated, a common strategy would declare the primary statistical analysis for an ordinal outcome to be based on the PORM, and only if the proportional odds assumption were rejected, would analysis proceed with the PPORM.

A different analysis planning strategy, not employed in the sensory retraining study, would be to declare a priori that primary interest is in the dichotomous outcome related to prevalence of the disease or condition (e.g., no problems versus any problems), whereas odds ratios related to disease severity and based on the other cutpoints are declared to be secondary endpoints. In such a scenario, the PPORM could be declared as the primary modeling approach, its use not predicated upon rejection of the proportional odds assumption. With this approach, greater emphasis may be placed on one dichotomy of the responses rather than assuming that all dichotomies are equally important. For example, if outcome levels include ‘no problem’ representing the absence of condition, the greatest emphasis among all possible dichotomies might be placed on whether an individual has the condition irrespective of severity.

In conclusion, when the assumption of a common odds ratio is not justified on statistical grounds owing to formal rejection with hypothesis testing, or on substantive reasons owing to asymmetric importance given a priori to the respective outcome categories, partial proportional odds models are useful alternatives for the analysis of univariate and longitudinal ordinal data. There are other approaches for the regression analysis of longitudinal ordinal data, including models for odds ratios constructed from continuation ratios or adjacent categories (4), random effects models, transition models, and Bayesian methods (15,16).