Habituation Reveals Fundamental Chromatic Mechanisms in Striate Cortex of Macaque

Abstract

Prolonged viewing of a chromatically modulated stimulus usually leads to changes in its appearance, and that of similar stimuli. These aftereffects of habituation have been thought to reflect the activity of two populations of neurons in visual cortex that have particular importance in color vision, one sensitive to red–green modulation, the other to blue–yellow, but they have not been identified. We show here, in recordings from macaque primary visual cortex (V1), that prolonged exposure to chromatic modulation reveals two fundamental mechanisms with distinctive chromatic signatures that match those of the mechanisms identified by perceptual observations. In nearly all neurons, these mechanisms contribute to both excitation and to regulatory gain controls, and as a result their habituation can have paradoxical effects on response. The mechanisms must be located near the input layers of V1, before their distinct chromatic signatures diffuse. Our observations suggest that the fundamental mechanisms do not give rise to two distinct L–M and S chromatic pathways. Rather, the mechanisms are better understood as stages in the elaboration of chromatic tuning, expressed in varying proportions in all cells in V1 (and beyond), and made accessible to physiological and perceptual investigation only through habituation.

Introduction

Models of human color vision generally have emphasized the special status of three postreceptoral mechanisms, one sensitive to luminance variations and driven by the signals from cone photoreceptors acting together and two others that are sensitive to purely chromatic (“red–green” and “blue–yellow”) variations, and driven by opposed signals from cones of different types. The chromatic signatures of these mechanism have been most clearly delineated by studies that used habituation to chromatic modulation [contrast adaptation (Krauskopf et al., 1982)] to reveal a red–green mechanism that receives opposed inputs from L and M cones and a blue–yellow mechanism that receives inputs from S cones opposed to a sum of inputs from L and M cones. Although these mechanisms are well defined psychophysically, they remain elusive physiologically.

Single-unit recordings in primate have revealed the existence of chromatically opponent neurons in the lateral geniculate nucleus (LGN) (De Valois et al., 1966; Wiesel and Hubel, 1966; Gouras, 1971; Derrington et al., 1984) and primary visual cortex (V1) (Gouras, 1974; Livingstone and Hubel, 1984; Thorell et al., 1984; Lennie et al., 1990). In LGN, the chromatic preferences of S+ (blue-on) cells and P-cells are mostly well aligned with the blue–yellow and red–green dimensions, respectively (Derrington et al., 1984; Tailby et al., 2008), but these cell types are little affected by habituation (Solomon et al., 2004b; Tailby et al., 2008). Although recent physiological work (Tailby et al., 2008) shows some susceptibility to habituation in S− (blue-off) neurons in LGN, this is unlikely to account for much of what is observed psychophysically.

Neurons in striate cortex are usually susceptible to habituation (Ohzawa et al., 1985), making it a potential locus of the fundamental mechanisms. The chromatic preferences of neurons there are broadly distributed throughout the isoluminant plane (Lennie et al., 1990; Wachtler et al., 2003; Johnson et al., 2004; Solomon and Lennie, 2005; Conway and Livingstone, 2006; Horwitz et al., 2007), reminiscent of the higher order color mechanisms inferred psychophysically (Krauskopf et al., 1986; Webster and Mollon, 1994). This suggests that the fundamental mechanisms characterized psychophysically might be established early in V1, at or near the interface with LGN inputs, and that their signals are combined with variable weights before being expressed in the broadly distributed chromatic signatures of most V1 neurons. We sought to expose these mechanisms through habituation to chromatic modulation.

We measured the chromatic preferences of V1 neurons before and during habituation to stimuli modulated along several directions in color space. In many neurons, habituation revealed inputs from mechanisms tuned to one or both of the fundamental chromatic directions. The distinctive properties of these mechanisms become evident only under particular conditions (habituation to prolonged stimulation) and are then expressed through subsequent stages of cortical processing.

Materials and Methods

Visual stimulus and experimental procedure.

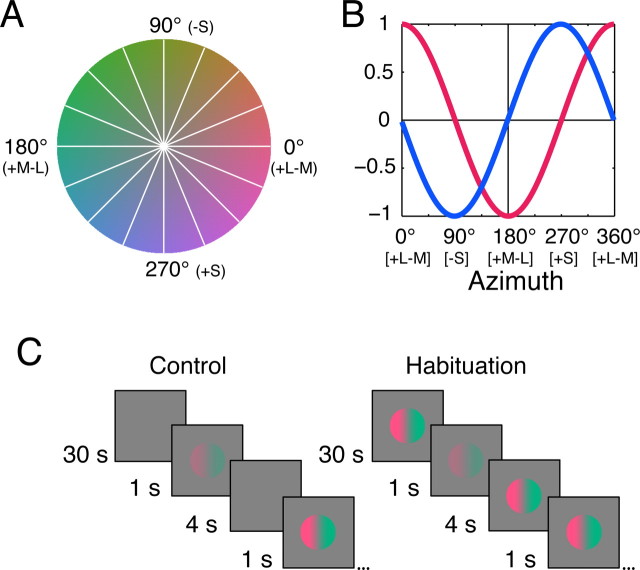
The preparation, methods for recording, and the generation and delivery of visual stimuli are fully described by Solomon and Lennie (2005). Single-unit recordings were made from V1 in 17 anesthetized, paralyzed male Macaca fascicularis. All procedures conformed to the guidelines approved by the New York University Animal Welfare Committee. Stimuli were spatially uniform fields modulated in time, or drifting sinusoidal gratings, presented as circular patches of the diameter optimum for the receptive field. The remainder of the screen was held at the mean luminance of ∼50 cd/m² (CIE 1931 x, y ∼ 0.30, 0.32). All stimuli were produced by spatiotemporal modulation through this point. These modulations can be represented in a three-dimensional color space described previously (Derrington et al., 1984; Lennie et al., 1990), calibrated using the Smith and Pokorny (1975) cone fundamentals and the 2° Judd-Voss CIE 1931 modified color matching functions (Brainard, 1996). Stimuli were restricted to a plane within which chromaticity varies without change in luminance, defined by an axis along which L- and M-cone signals are modulated in opposition and an axis along which only S-cone signals are modulated. Within this plane, color direction is specified by azimuth, where 0° represents +L–M modulation and 270° represents +S modulation (Fig. 1A). Normal to this plane is the achromatic axis along which the signals from the three cone classes vary in proportion.

Figure 1.

Sensitivity of the fundamental mechanisms to color modulations. A, The isoluminant plane of the color space used in our experiments. This plane contains stimuli that vary in chromaticity without change in luminance, and is defined by two orthogonal axes: the L–M-axis (0–180°), along which signals arising in the L and M cones vary in opposition; and the S-axis (90–270°), along which only signals of the S cone are modulated. All stimuli were defined as modulations along vectors through the origin of this space. The white lines show the eight test vectors sampled. B, Responses of the two putative fundamental mechanisms as a function of the direction of stimulus modulation in the space shown in A. The L–M mechanism opposes the inputs of L and M cones and thus responds best to L–M modulation and is blind to modulation along the S-axis. The S mechanism (which opposes inputs from S cones to a combination of inputs from L and M cones) responds best to S modulation and is blind to L–M modulation. For both mechanisms, response amplitude varies sinusoidally with direction of modulation. C, Schematic of habituation procedure. Responses to test probes (drifting gratings or temporally modulated uniform fields) were measured at intervals during control conditions (left) and during habituation (right) to unit contrast modulation. Habituation began with 30 s exposure to high-contrast modulation and was maintained with 4 s of modulation between each probe.

For the analyses presented here, we define the maximum attainable modulation along the L–M-axis and the S-axis as a contrast of 1.0. Along the L–M-axis, a stimulus of contrast 1.0 produced cone contrasts of 0.08 for the L cones, 0.15 for the M cones, and 0.001 for the S cones. Along the S-axis, a stimulus of contrast 1.0 produced cone contrasts of 0.85 for the S cones and <0.002 for the L and M cones.

Through preliminary measurements on each neuron, we established its spatial, temporal, and chromatic tuning. Then with stimuli of the preferred orientation, spatial frequency, temporal frequency (usually 5 Hz), and color direction, we measured responses at several contrasts to establish its contrast–response function. From this, we identified the minimum contrast to which the cell responded (C_min), and a contrast at the upper end of its linear contrast–response range (C_max). To determine the effect of habituation on the contrast–response function, we presented test stimuli at contrasts between C_min and 0.9; to determine the effect of habituation on azimuth tuning, we measured responses to test stimuli presented at contrast C_max along eight vectors within the isoluminant plane (Fig. 1A). In both cases, responses were obtained before, during, and after recovery from habituation to modulation along a single color vector. The spatial and temporal configuration of the habituating stimulus always matched that of the test stimulus.

In making measurements before and after recovery from habituation, each test stimulus was presented for 1 s, with 4 s of blank screen between presentations. These runs were preceded by ∼5 min of exposure to a blank screen. In making measurements during habituation, each test stimulus was presented for 1 s, separated by 4 s habituation, after an initial habituating period of 30 s (Fig. 1C). We usually obtained responses to 10 presentations of each test stimulus. Measurements made before habituation and after recovery from it were generally in very close agreement, and for each cell we combined these for comparison with measurements obtained in the habituated state. We refer to these combined measurements as “control” runs. Data from six neurons were discarded because the prehabituation and posthabituation runs did not match. To avoid contaminating the analysis of the steady-state response, the first 150 ms of response was always discarded from the analysis. For averaging responses across cells, we first normalized the responses for each cell to the maximum obtained in the control runs. We used as the response the amplitude of the modulated component if it exceeded the elevation in mean firing rate for the preferred stimulus; otherwise, we used the mean firing rate.

Model of chromatic response.

Our model supposes two fundamental chromatic mechanisms, whose preferred color directions are aligned respectively with the L–M- and S-axes of the color space of Figure 1. Following Solomon and Lennie (2005), we call these I_LM and I_S. These chromatic mechanisms are fatigable by habituation. Their outputs are the source of excitation to subsequent mechanisms that control the response of the neuron: a linear receptive field (LRF) (denoted S_(θ)) and a contrast gain control (N_(θ)) that normalizes the response of the neuron to chromatic modulation (Solomon and Lennie, 2005). The linear receptive field sums the signals from the fundamental mechanisms with weights that determine its preferred color direction. The squared signals of the fundamental mechanisms drive the gain control with weights that determine its preferred color direction. The LRF and the gain control need not attach the same weights to inputs from the I_LM and I_S mechanisms.

We need to consider the effect of habituation on both the linear receptive field and the gain control because loss of excitation to them will affect the neuron in opposite ways: reducing excitation to the LRF makes the neuron less responsive, but reducing excitation to the gain control makes the neuron more responsive. The balance of these opposing influences will determine the overall effect of habituation on signal generation. Beyond its effect in desensitizing the fundamental chromatic mechanisms, we suppose that habituation also acts directly to weaken the response-generating mechanism of the neuron (Carandini and Ferster, 1997; Sanchez-Vives et al., 2000) in a response-dependent way. We refer to this as “response adaptation.”

The responses of the I_LM and the I_S mechanisms to a stimulus within the isoluminant plane are the cosine and the sine of the stimulus azimuth (θ), respectively (Fig. 1B). Note that all modulations used here were within the isoluminant plane so we substitute θ, stimulus azimuth, for the λ used throughout Solomon and Lennie (2005). The response of the LRF is determined by its preferred azimuth, φ, which defines the weights the LRF attaches to each of the fundamental mechanisms as follows:

where c is contrast. For the current analyses, which are concerned only with the effect of habituation on response amplitude, we ignore response phase.

The gain controlling signal from the normalization pool is constructed in a similar way. The weighted responses of the fundamental mechanisms are squared before summation in the pool, with the preferred azimuth of the pool (ϑ) defining the weight attached to each mechanism as follows:

Combining the response of the LRF and that of the normalization pool gives us the response of the neuron, the “generator signal,” before spike generation as follows:

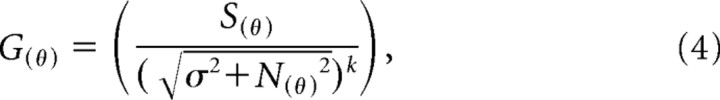where σ determines the strength of the normalizing signal. The denominator of this equation is not usually raised to an additional power (Carandini et al., 1997; Solomon and Lennie, 2005); in the following analyses, we set k to be 2. Functionally, this means that the effect of habituation on the fundamental mechanisms is expressed more strongly in the gain control than in the linear receptive field. As we show in Results, this is important for capturing the diversity of effects observed in V1.

We relate this generator signal to spiking responses by adding an offset hyperpolarization (V_t), half-wave rectification, a gain term (R_max), and an exponent (n) as follows:

In the control state, V_t is set to 0; response adaptation brought about by habituation causes a change in V_t (Carandini and Ferster, 1997; Sanchez-Vives et al., 2000), and our fitting procedure estimates that.

We assume that an habituating stimulus desensitizes the fundamental chromatic mechanisms in proportion to its projection onto each. In the case of the I_LM mechanism, this is represented by the following expression, which is then substituted for I_LM in Equations 2 and 3 as follows:

where ρ is the response of the I_LM mechanism to the habituating azimuth; A_LM is the susceptibility of the I_LM mechanism to habituation and can range from 0 to 1. A similar expression can be written for the I_S mechanism.

The set of parameters that minimized the reduced χ² error between the model and the data were found using “lsqnonlin” in the MatLab environment (version 7; Mathworks, Natick, MA). For each cell, the control and all habituated conditions were fit simultaneously: the parameters φ, R_max, n, σ, ϑ, A_LM, and A_S were held fixed across all conditions, and separate values of V_t were derived for each habituation condition. The model was fit to the control condition along with one habituation condition in 12 cells (16 data points; 8 parameters; median percent variance explained, 90.0%), two habituation conditions in 29 cells (24 data points; 9 parameters; median percent variance explained, 93.1%), three habituation conditions in 30 cells (32 data points; 10 parameters; median percent variance explained, 93.5%), and four habituation conditions in 8 cells (40 data points; 11 parameters; median percent variance explained, 91.6%). None of the neurons characterized here was contained in the data set of Solomon and Lennie (2005).

Results

Psychophysical observations that most clearly demonstrate the existence of two fundamental chromatic mechanisms have revealed these mechanisms by desensitizing them with prolonged exposure to modulation of chromaticity through a white point (Krauskopf et al., 1982). We wanted to know whether neurons could be similarly desensitized by isoluminant modulation, and whether any such desensitization was chromatically selective. We conducted experiments only on those V1 neurons that responded robustly (>10 imp/s) to, though did not necessarily prefer, purely chromatic modulation of visual stimuli. This criterion excluded 363 of 442 neurons initially screened. Of the remaining 79 neurons, 44 expressed strong color opponency [group C of Solomon and Lennie (2005)], 31 expressed weak opponency (group B), and 4 preferred essentially achromatic stimuli (group A); the distribution of their preferred directions within the isoluminant plane was nearly uniform. All neurons had receptive fields within 5° of the fovea (mean eccentricity, ∼2.5°).

Chromatic modulation habituates neurons in V1

In what follows, we refer to the set of measurements made during prolonged exposure as “habituated” measurements and the average of the other sets made before habituation and after recovery as “control” measurements.

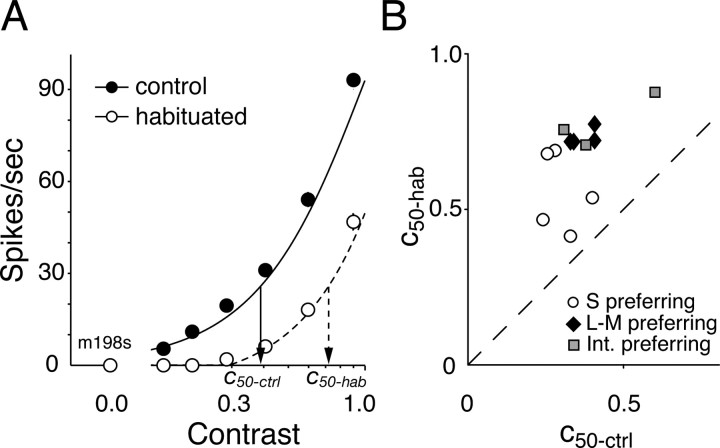
Figure 2A shows contrast–response curves for one cell obtained in the control (filled symbols) and habituated (open symbols) states. The continuous and dashed lines show the best-fitting solution of the model described in Materials and Methods (Eqs. 1–6). For this cell and all others on which similar measurements were made, the principal effect of habituation was to shift the contrast–response function rightward on a semilogarithmic plot (equivalent to a reduction in contrast sensitivity).

Figure 2.

A, Contrast–response functions from a representative cell, measured during control conditions (filled symbols) and during habituation (open symbols) to unit contrast modulation. The probe and the habituating stimulus were modulated in the preferred color direction (45°). In this and all subsequent figures, the vertical bars show ±1 SEM. Responses were fit with the model described in Materials and Methods. The arrows identify contrasts in the control (c_50-ctrl) and habituated (c_50-hab) states that evoke one-half of the maximum response in the habituated state. B, Impact of habituation on contrast sensitivity of cells of different types: c_50-ctrl is plotted against c_50-hab. We take the ratio of these contrasts as a measure of the change in contrast sensitivity.

We therefore quantified the effect of habituation on the contrast sensitivity by calculating, from the model fits, the ratio of the contrasts required in the habituated (c_50-hab) and control (c_50-ctrl) states to evoke a response equal to one-half of the maximum response observed in the habituated state. Figure 2B shows this. Habituation to the preferred stimulus reduced contrast sensitivity on average by a factor of 2.0 (see legend of Fig. 2B).

Habituation in V1 exposes two fundamental chromatic mechanisms

To explore the selectivity of habituation, we measured chromatic tuning by recording responses to stimuli modulated along eight directions in the isoluminant plane during control conditions and during habituation to particular color directions. Every cell was habituated along the L–M-axis (0–180°) and the S-axis (90–270°), along its preferred azimuth, and along an additional azimuth intermediate to the principal axes, if time permitted. The contrast of all test stimuli was set to C_max (see Materials and Methods).

Before considering results from real neurons, it is helpful to examine how the model behaves under different habituation conditions. Figure 3 illustrates the behavior of its different stages.

Figure 3.

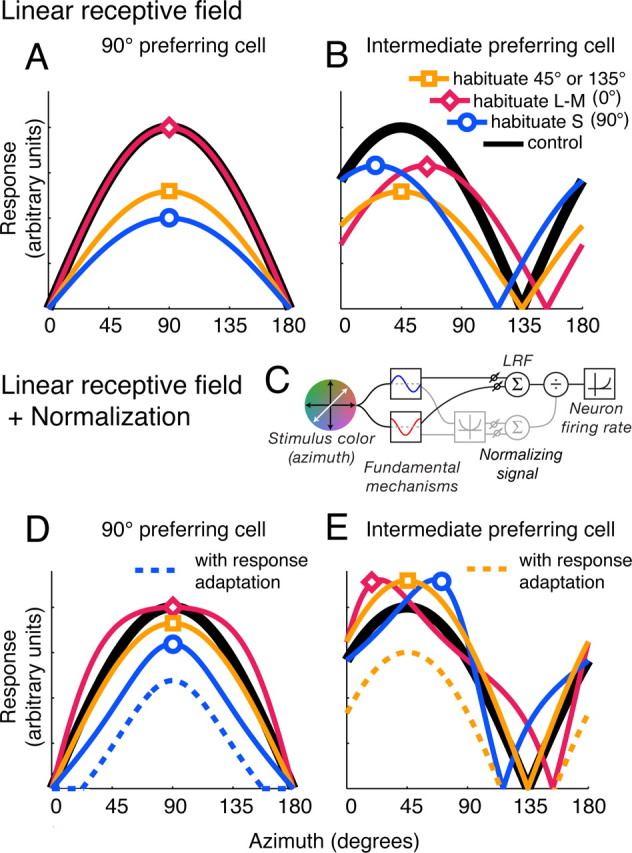
The effect of habituation on model V1 neurons. Each panel shows how the response of a different model neuron varied with direction of modulation in the control condition (black curve), and during habituation along S (blue curve), L–M (magenta curve), or an intermediate color direction (45 or 135°; orange curve). In this and similar figures, the sign of the response (increase or decrease in discharge) is ignored, and all responses are plotted as positive values. A, B, Model incorporating linear receptive field only. The neuron in A receives input only from the S mechanism; the neuron in B sums inputs from both the L–M and S mechanisms. C, Diagram showing the components of the model outlined in the text. The stimulus is filtered separately through the two fundamental mechanisms: the sum of their weighted linear outputs drives the LRF; the sum of their squared weighted outputs drives a chromatic gain control (normalizing signal) that acts divisively on the response of the LRF. The resulting signal is then transformed into firing rate via an instantaneous nonlinear function. D, E, Model neurons incorporating linear receptive field and normalization (see Materials and Methods). D, S-preferring cell with normalization from both the L–M and the S mechanisms. E, Intermediate-preferring cell with normalization from both the L–M and the S mechanisms. The dashed curves show the additional effect of response adaptation, demonstrated for habituation to the preferred direction. Other conventions are as in A and B.

We consider first an instantiation in which the gain control is too weak to influence the response of the neuron (σ is large). Under these simplified circumstances, the behavior of a cell is fully described by its linear receptive field. The full range of behaviors exhibited by this “LRF-only” form of the model can be seen by examining the potential impact of habituation on two types of LRF, one that prefers a fundamental (L–M or S) color direction and one that prefers an intermediate color direction. For a cell tuned to one of the fundamental directions, the strongest desensitization is caused by habituation to that direction. Habituation to an intermediate direction will reduce responses less, because the fundamental mechanism is less sensitive to the habituating stimulus; habituation to the orthogonal fundamental direction will have no effect at all (Fig. 3A). For a cell tuned to an intermediate direction, and thus drawing on both fundamental mechanisms, habituation along one of the fundamental axes should deform the curve by shifting its peak away from the habituating direction (Fig. 3B). This is because habituation reduces the sensitivity of the fundamental mechanism tuned to the habituation direction and leaves the sensitivity of the orthogonal fundamental mechanism unaffected, effectively shifting the relative weight of input in favor of the orthogonal fundamental mechanism. A particularly interesting prediction of the LRF-only form of model is that, in a cell tuned to an intermediate chromatic direction, habituation to chromatic modulation along its null direction, which will drive the cell negligibly or not at all, should nonetheless affect its sensitivity; in the special case of a cell that draws balanced input from both mechanisms, it should be just as effective as habituation to modulation along the preferred direction (Fig. 3B). This is because the habituating stimulus drives (and hence habituates) both fundamental mechanisms, even though it elicits no response from the cell.

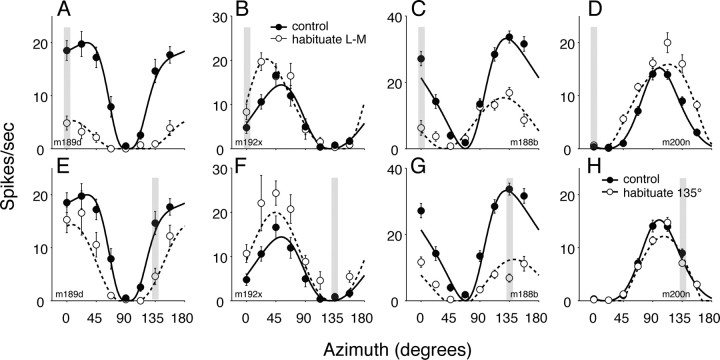
Figure 4A–D shows the effects of habituation along the L–M-axis on the chromatic properties of four V1 neurons with different preferred color directions.

Figure 4.

Impact of habituation on chromatic tuning of V1 neurons. A–D, Responses of four neurons to modulation along color directions in the isoluminant plane during control conditions (filled symbols) and during habituation (open symbols) to L–M modulation (indicated by the shaded bar at azimuth 0°). The smooth/dashed lines show predictions of the best fitting model. E–H, Responses of the same four neurons during control conditions (filled symbols) and during habituation (open symbols) to modulation along an azimuth of 135° (indicated by the shaded bar at azimuth 135°). The smooth/dashed lines show predictions of the best fitting model. The model parameters for the cells shown are as follows: m189d, θ = 2.8°, R_max = 19.9, n = 3.58, A_LM = 0.67, A_S = 0.0, ϑ = 20.2°, σ = 0.58, V_{t (0°)} = 0.017, V_{t (135°)} = 0.012; m192x, θ = 39.0°, R_max = 14.42, n = 2.45, A_LM = 0.25, A_S = 0.12, ϑ = 41.3°, σ = 0.003, V_{t (0°)} = 0.076, V_{t (135°)} = 0.0; m188b, θ = 157.7°, R_max = 33.2, n = 2.0, A_LM = 0.70, A_S = 0.59, ϑ = 17.3°, σ = 1.14, V_{t (0°)} = 0.0, V_{t (135°)} = 0.056; and m200n, θ = 108.3°, R_max = 15.2, n = 2.32, A_LM = 0.34, A_S = 0.00, ϑ = 38.7°, σ = 0.047, V_{t (0°)} = 0.0, V_{t (135°)} = 0.222.

In some neurons (Fig. 4A,C), habituation to L–M modulation reduced the responses broadly in the manner expected from a weakening of the L–M input to the LRF, but in others (Fig. 4B,D) the habituation had a paradoxical effect: it reliably elevated the responses to modulation along a broad range of directions. For the neuron in Figure 4B, the preferred color direction shifted toward that of the habituating stimulus; for the neuron that preferred S cone modulation (Fig. 4D), it broadened the tuning curve.

Figures 4E–H show the effects of habituation along an intermediate direction (135°) on the chromatic properties of the same four neurons. The LRF-only form of the model predicts that this habituation should reduce responsiveness in all neurons, regardless of preferred color direction, because it will desensitize both the L–M and the S mechanisms. For the neurons tuned to the L–M-axis (Fig. 4E) and the S-axis (Fig. 4H), habituation did depress sensitivity symmetrically about the preferred axis of the neuron. This was also the case for the neuron tuned to the habituating direction (Fig. 4G), but for the neuron tuned to an azimuth of 45° (Fig. 4F), and which was unresponsive to the habituating modulation, habituation substantially augmented the responses to modulations along all directions.

Contribution of normalization signals to responses during habituation

The enhancement of response seen in Figure 4, B, D and F, is unintelligible within the framework of the LRF-only model outlined above. However, a simple extension of this model, in which the fundamental mechanisms also feed a suppressive (normalizing) signal, captures the complexity of the data shown here. Consider the responses of the S-preferring cell shown in Figure 4D. If the LRF of this cell draws principally on the S mechanism, and the output of the LRF is regulated by a suppressive signal that receives input from the L–M mechanism, then habituation to L–M will have a negligible effect on the LRF, but it will reduce the sensitivity of the L–M fundamental mechanism, and consequently the strength of the normalizing signal along all directions to which the L–M mechanism responds. This “releases” the response of the LRF (which is driven by the S mechanism) along these directions, resulting in a broadening of the tuning curve of the neuron without effect on its peak sensitivity. This behavior is shown in Figure 3D for a model neuron in which the LRF is driven exclusively by one fundamental mechanism, and the normalizing signal draws input from both mechanisms.

Habituation of a normalizing signal can similarly account for the facilitation effects seen in the V1 neuron that prefers an intermediate color direction (Fig. 4B,F). Habituation to the preferred or the null direction (Fig. 4F) of an intermediate preferring cell will decrease the sensitivity of both fundamental mechanisms. This reduces their input to both the LRF and the normalization pool, but the squaring of the signals in the normalization pool (see Materials and Methods) causes a disproportionate reduction in its gain controlling capacity. As a result, the effects of reducing the drive to the LRF are undone by the greater reduction in the normalizing signal, giving rise to response facilitation. This paradoxical effect is also evident after habituation confined to either of the fundamental mechanisms (Fig. 4B), and causes the peak of the curve to shift toward the habituating direction. These behaviors are those seen in Figure 3E for a model neuron in which both the LRF and the normalization pool draws equally on both fundamental mechanisms. Thus, depending on the strength of the normalizing signal, habituation along the fundamental directions can repel (Fig. 3B), attract (Fig. 3E), or leave unchanged the chromatic preference of a neuron tuned to an intermediate direction.

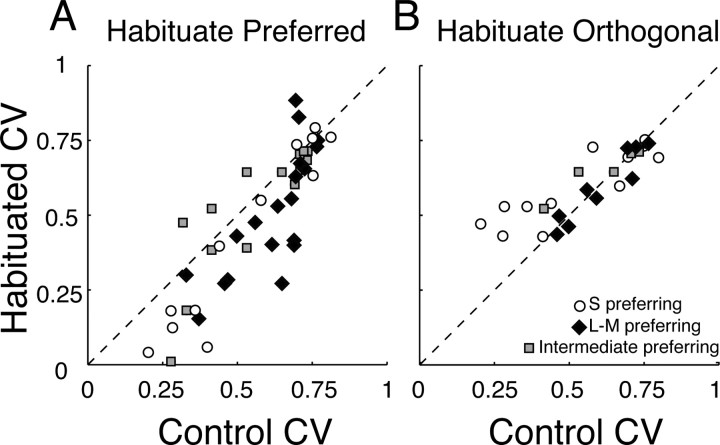
Contribution of response adaptation to response during habituation

Habituation to modulation along the preferred direction of a neuron did not generally bring about a proportional reduction in the response of a neuron to all stimuli. Instead, it reduced the responses to weak stimuli disproportionately, thus narrowing the chromatic tuning of the cell (Fig. 4A). The breadth of chromatic tuning, and the change in it brought about by habituation, can be captured by computing a measure of circular variance (Batschelet, 1981). Figure 5A shows the distributions of this statistic measured during control conditions and during habituation along the preferred color direction of each neuron; habituation generally reduced the circular variance and hence the tuning bandwidth. Figure 5B shows comparable distributions when the habituating modulations lay along the null directions of the cells. Habituation increased the circular variance among cells that preferred S-cone modulation (particularly those in group C), but had no effect on others.

Figure 5.

Habituation changes the color-tuning width of V1 cells. A, Scatterplot of the circular variance (CV) during control conditions and during habituation to the preferred color direction. On average, habituation reduces CV to 0.71 of that in the control condition. B, Scatterplot of CV during control conditions and during habituation to the azimuth orthogonal to that preferred.

The narrowing of chromatic tuning caused by habituation to the preferred direction is reminiscent of an activity-dependent hyperpolarization of the membrane potential (Carandini and Ferster, 1997; Sanchez-Vives et al., 2000). In our model, we included a final stage at which sensitivity can be lost after the normalizing signal acts on the signal from the LRF. This causes a narrowing of the tuning curve, essentially by submerging its tails (Fig. 3D,E), and will be greatest when the neuron is habituated to its preferred stimulus. The upshot is that response adaptation can countermand the increased responsiveness that might otherwise result from habituation of the normalizing signal (such as is shown in Fig. 3E).

We fit this full model to each of the cells in our data set. In fitting the data, we required that a single set of parameters account for behavior under all the habituation conditions studied. This is an important constraint: the model is capable of giving rise to varied behaviors, but only by varying the values of its parameters. These values are well constrained for any one cell.

Our model provides a comprehensive and quantitatively satisfactory account of a wide range of behaviors. The smooth curves of Figure 4 show best fitting results of the model characterized in Figure 3 (see Materials and Methods). It explained a median 92.6% (SD, 11%) of the variance in our measurements on 79 neurons. For only four neurons (three complex, one simple) did it account for <75% of the variance. Model fits show that, on average, habituation to stimulus modulation along the L–M- and S-axes reduced the sensitivities of the corresponding mechanisms by 43 and 39%, respectively. The complex effects of habituation are explained by the reduced strength of the normalizing signal, and by adaptation of a mechanism that operates after signal combination (response adaptation). We need fatigable normalization and response adaptation to account for the broadening of tuning in S-preferring cells after habituation to L–M modulation (Figs. 4D, 5B), the attractive shifts in preferred direction among cells tuned to intermediate directions after habituation along a fundamental axis (Fig. 4B), the enhancement of response in the same cells after habituation along the null direction (Fig. 4F), and the narrowing of tuning after habituation along the preferred direction (Figs. 4A, 5A). We used the Akaike information criterion (Motulsky and Christopoulos, 2004) to assess the level of complexity of the model that most parsimoniously accounted for the effects of habituation. With normalization omitted, fits were worse for 66 of 79 cells; with response adaptation omitted, fits were worse for 62 of the cells.

Among neurons for which normalization was substantial, the distribution of the chromatic signatures of the LRFs was not distinguishable from uniform (p > 0.05, χ² test; df = 5; bin width, 30°), but the chromatic signatures of the normalization pools were clustered around 45° (mean angle, 44.7°; circular variance, 0.03). This indicates that, regardless of the direction preferred by the LRF, the normalization pool draws on both the L–M and S mechanisms in a way that makes it equally sensitive to modulation along all directions in the isoluminant plane.

The magnitude of the response adaptation term was largest for stimuli that drove the cells well, and can account for the habituation-induced reduction in circular variance shown in Figure 5A.

We also confirmed the special status of the L–M- and S-cone axes by comparing the quality of the fits returned by the model based on these axes with variations of it in which the fundamental mechanisms were aligned with different pairs of azimuths, specifically the following: (0, 22.5°), (0, 45°), (0, 67.5°), (0, 112.5°), (0, 135°), (0, 157.5°), and (45, 135°). The best model fits were obtained when the fundamental mechanisms were aligned to the L–M- and the S-cone axes. The means (±SEMs) of the log transform of reduced χ² statistics returned by the different models, in the order listed above, were 0.777 (±0.062), 0.722 (±0.058), 0.674 (±0.052), 0.712 (±0.06), 0.769 (±0.064), 0.815 (±0.061), and 0.74 (±0.063), compared with 0.658 (±0.051) when the mechanisms were aligned to the L–M- and S-axes.

Overall effect of habituation

Depending on the relative strengths of the signals in the linear receptive field and in the normalization pool, the model gives rise to quite different effects of habituation (for example, whether habituation shifts the tuning toward or away from the habituating direction). Over the population of neurons, there are some dominant trends. Figure 6 summarizes these. Each panel represents a different pairing of direction of habituating modulation and preferred chromatic direction: along a row, the habituating stimuli had the same color direction; within a column, the cells share the same preferred azimuth (for details, see legend of Fig. 6). Each panel shows, for the group of cells that were tuned to the direction associated with the column, the population average tuning curve obtained during control conditions (filled circles) and during (open circles) habituation along the direction identified by the shaded bar. The responses of each cell were normalized to its peak control response before being included in the population average (see Materials and Methods).

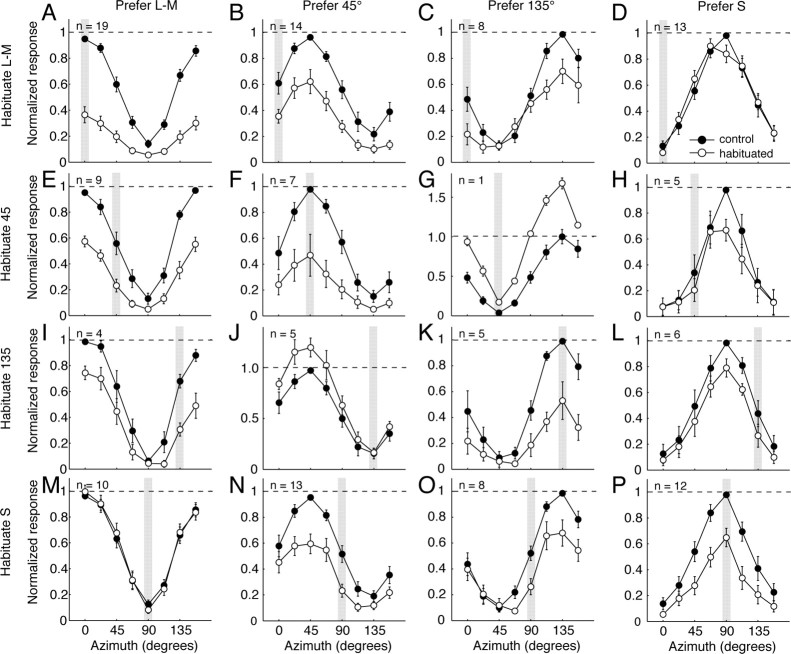
Figure 6.

Population average color-tuning functions of different groups of V1 neurons during control conditions and during habituation to different color directions. Neurons are grouped in columns by their preferred azimuths in the control condition, and into rows by the azimuth of the habituating stimulus. The first column contains neurons with preferred color directions between −15 and +15°; the second column contains neurons preferring directions between 30 and 60°; the third column contains neurons preferring directions between 120 and 150°; the last column contains neurons preferring directions between 75 and 105°. In each panel, the shaded bar shows the habituated azimuth. The filled circles show normalized responses during the control condition; the open circles show the normalized responses during habituation (see Materials and Methods). An individual neuron can be represented in more than one row. The figure shows measurements made on 60 neurons altogether.

For cells that preferred a fundamental axis (leftmost and rightmost columns), habituation caused a general reduction of response. The strength of habituation was reduced with increasing separation between the preferred azimuth and habituated azimuth. Habituation to pure S modulation had no effect on responses of L–M-preferring cells (Fig. 6M); habituation to pure L–M modulation had no effect on the peak response of S-preferring cells (Fig. 6D), though it did broaden the tuning curve. The asymmetry reflects the greater susceptibility of the L–M mechanism to habituation, and the tendency for normalization to be slightly stronger in S-preferring cells than in L–M-preferring cells.

For cells tuned to intermediate azimuths (center columns), habituation to the preferred stimulus also caused a general reduction of response (Fig. 6F,K). Habituation along the null direction (Fig. 6G,J) increased the responsiveness along all color directions, as we noted previously (Fig. 4F). Habituating these cells to modulation along the fundamental axes usually caused changes in chromatic tuning. Among both 45 and 135° preferring cells, pure S habituation caused the largest reductions in response along the S-axis (Fig. 6N,O). Pure L–M habituation affected these two groups differently: responses along the L–M-axis were reduced in both groups, but responses to pure S modulation were undiminished in cells tuned to 135° (Fig. 6C), while being substantially reduced in those tuned to 45° (Fig. 6B). Neurons tuned to 45° behave as if the major effect of habituation occurs after combination of signals from the S and L–M mechanisms. We return to this in Discussion.

Absent the influence of the contrast gain control, we would expect the underlying loss of sensitivity in the L–M or S mechanism to shift the preferred color direction away from that habituated direction. This is not pronounced in Figure 6, because the averaged responses reflect the behavior of cells in which habituation causes both repulsive and attractive shifts (the direction depending on the strength of the contrast gain control, as described above).

Discussion

Our measurements show that responses of neurons in striate cortex are changed by prolonged exposure to purely chromatic modulation, and that the changes in response can be explained by a loss of sensitivity in two fundamental chromatic mechanisms (one that prefers L–M modulation, and another that prefers S modulation) that provide inputs to a V1 neuron, and an additional loss of sensitivity in the response-generating mechanism of the neuron. A wide range of behaviors, some paradoxical, can be explained by supposing that the fundamental chromatic mechanisms provide inputs both to the linear receptive field and to a nonlinear gain control that regulates the contrast sensitivity of a neuron.

Nature and locus of fundamental mechanisms

The fundamental mechanisms should not be thought of as defining distinct L–M and S-[L+M] chromatic pathways through cortex. Rather, the fundamental mechanisms are better conceived as early stages in the elaboration of chromatic tuning in cortex, stages whose properties are exposed (and made accessible to physiological and perceptual investigation) only through the habituation caused by prolonged stimulation. Their signals are drawn on in varying proportions by cells in all cortical layers, giving rise to the broad range of chromatic signatures found in V1.

Our analysis of the laminar placement of cells in V1 [51 characterized here, plus another 283 from data sets reported previously (Solomon et al., 2004a; Solomon and Lennie, 2005; Webb et al., 2005)] shows that moderately and strongly color-preferring cells [groups B and C of Solomon and Lennie (2005)], which have preferred azimuths distributed throughout the isoluminant plane, are encountered in cortical layers 2 through 6 (Lennie et al., 1990; Johnson et al., 2001). The strongly color-preferring cells aligned close to (within ±22.5°) the L–M-axis were proportionally most common in layers 4cβ and 6, those aligned close to the S-axis in layer 4a. It therefore seems likely that the fatigable L–M and S mechanisms are already present in the input layers of V1, and that their influence is propagated broadly in the upper and lower layers.

It is unclear whether the locus of the S mechanism is exclusively cortical, or emerges precortically and is augmented in cortex. We have shown elsewhere that at least two populations of LGN neurons carry S cone signals; they have different chromatic signatures and are affected differently by habituation (Tailby et al., 2008). S+ cells have chromatic signatures that are closely aligned with the S-axis, and are only weakly desensitized by habituation. S− cells have chromatic signatures broadly distributed around an intermediate color direction (∼70° azimuth) and reveal desensitization of an S-cone-specific signal. Thus, the fatigable S mechanism we study in cortical neurons must arise in cortex if it is driven by input from S+ cells. If cortical neurons receive inputs from S− cells in LGN, some component of the fatigable mechanism probably originates in the retina.

Habituation in cells that prefer an azimuth of 45° is distinctive: habituation to L–M or S reduces responses across all azimuths, with habituation to S also producing some additional loss around the S-axis. This result is intelligible if these cells receive their principal input from S− cells in LGN (which have a similar chromatic preference), rather than from the fundamental L–M and S mechanisms. Response adaptation in these cortical cells would cause response to drop for modulation along all color directions. The chromatic specificity seen during habituation to S-cone modulation, but not during L–M modulation, is also seen in S− cells in the LGN (Tailby et al., 2008).

Neither the retina nor the LGN can be the locus of the L–M mechanism: P-cells, which provide the opponent L–M input to cortex, are not desensitized by prolonged chromatic modulation (Derrington et al., 1984; Tailby et al., 2008). The L–M mechanism therefore probably arises at the geniculocortical synapse (Chance et al., 1998), or among layer IV neurons. Were the loss of sensitivity caused by depression of the geniculocortical synapse, we would expect to be able to induce it through prolonged exposure to achromatic modulation. This is a powerful stimulus to LGN neurons (and consequently their terminals in cortex). In 15 color-preferring V1 neurons, we measured contrast–response relationships for the preferred chromatic stimulus, during control conditions and during habituation to a full contrast achromatic grating of optimal configuration, a potent stimulus to the P-cells that provide the primary L–M drive to cortical neurons. Seven neurons showed some loss of sensitivity, but even among that group the loss was considerably smaller than that brought about by prolonged chromatic modulation that would have been a less effective stimulus to LGN neurons. Were synaptic depression at work, we might also have expected L–M modulation of a spatially uniform field (a strong stimulus in parvocellular LGN) to desensitize cortical neurons that strongly preferred achromatic gratings. We explored this in 44 neurons but found no effect. We therefore think it likely that the desensitization that reveals the fundamental L–M mechanism occurs beyond the geniculocortical synapse.

Relationship to psychophysics

The chromatic signatures of the fundamental mechanisms match well those of the “cardinal” mechanisms inferred from psychophysical observations (Krauskopf et al., 1982): one that is maximally sensitive to L–M modulation and the other maximally sensitive to S modulation. Our measurements and our modeling show that habituation can also give rise to response adaptation (Carandini and Ferster, 1997; Sanchez-Vives et al., 2000). For a given neuron, this is most pronounced after habituation to the stimulus that drives it best (in the case of a chromatic stimulus, modulation along its preferred color direction). Chromatic preferences are broadly distributed among cortical neurons, so over the population as a whole response adaptation will cause the greatest loss of sensitivity in neurons tuned to the direction of the habituating modulation. This is of considerable interest in the context of psychophysical observations (Krauskopf et al., 1982, 1986; Webster and Mollon, 1994) that reveal, in addition to the cardinal mechanisms, innumerable less prominent mechanisms tuned along different directions in color space. These characteristics of what have been called “higher order” mechanisms (Krauskopf et al., 1986) are consistent with their arising in response adaptation in neurons that receive input from the fundamental mechanisms.

Habituation could lead to an increase in the response of a neuron to test stimuli, a finding that has no counterpart in psychophysical observations. This happens only at higher contrasts that normally engage the contrast gain control, and would not be expected at contrasts in the threshold range.