Conformationally Constrained Macrocyclic Diporphyrin-Fullerene Artificial Photosynthetic Reaction Center

Abstract

Photosynthetic reaction centers convert excitation energy from absorbed sunlight into chemical potential energy in the form of a charge-separated state. The rates of the electron transfer reactions necessary to achieve long-lived, high-energy charge-separated states with high quantum yields are determined in part by precise control of the electronic coupling among the chromophores, donors and acceptors, and of the reaction energetics. Successful artificial photosynthetic reaction centers for solar energy conversion have similar requirements. Control of electronic coupling in particular necessitates chemical linkages between active component moieties that both mediate coupling and restrict conformational mobility so that only spatial arrangements that promote favorable coupling are populated. Toward this end, we report the synthesis, structure and photochemical properties of an artificial reaction center containing two porphyrin electron donor moieties and a fullerene electron acceptor in a macrocyclic arrangement involving a ring of 42 atoms. The two porphyrins are closely spaced, in an arrangement reminiscent of that of the special pair in bacterial reaction centers. The molecule is produced by an unusual cyclization reaction that yields mainly a product with C₂ symmetry and trans-2 disubstitution at the fullerene. The macrocycle maintains a rigid, highly-constrained structure that was determined by UV-vis spectroscopy, NMR, mass spectrometry, and molecular modeling at the semi-empirical PM6 and DFT (B3LYP/6-31G**) levels. Transient absorption results for the macrocycle in 2-methyltetrahydrofuran reveal photoinduced electron transfer from the porphyrin first excited singlet state to the fullerene to form a P^•+-C₆₀^•−-P charge separated state with a time constant of 1.1 ps. Photoinduced electron transfer to the fullerene excited singlet state to form the same charge-separated state has a time constant of 15 ps. The charge-separated state is formed with a quantum yield of essentially unity and has a lifetime of 2.7 ns. The ultrafast charge separation coupled with charge recombination that is over 2000 times slower is consistent with a very rigid molecular structure having a small reorganization energy for electron transfer, relative to related porphyrin-fullerene molecules.

Introduction

In photosynthetic reaction centers, excited chlorophyll resulting from absorption of sunlight donates an electron to a nearby acceptor chlorophyll, beginning an electron transfer cascade that ultimately moves an electron through a series of acceptors to a quinone. Although there is substantial thermodynamic driving force for recombination of the final charge-separated state to the ground state with degradation of the stored energy to heat, recombination is slow because the electronic coupling between the initial chlorophyll, which now bears a positive charge, and the reduced quinone is weak due to the large spatial separation of the moieties. The reaction center is able to generate this final charge-separated state with a quantum yield of essentially unity in spite of the weak coupling because the final state is achieved via a series of short-range, fast, and therefore efficient electron transfer steps between adjacent donor-acceptor moieties. The high quantum yield requires that the electron coupling interaction in each donor-acceptor pair be optimized, and this in turn requires a rigid structure in which donor-acceptor separations and orientations are highly constrained. This constraint is provided by the protein matrix, which can also tune the driving force, coupling, and reorganization energies of the system.

Many artificial reaction centers consisting of porphyrin or related chromophores chemically joined to electron donor or acceptor moieties have been reported. Some of these rival natural reaction centers in their ability to generate long-lived, high-energy charge-separated states in high yield.^1–5 Artificial reaction centers that feature porphyrins as excited state electron donors and fullerenes as acceptors have proven especially successful, due in part to favorable energetics, low reorganization energies for electron transfer, and low sensitivity of the porphyrin and fullerene radical ions to solvent stabilization.^6–17 Most of these constructs feature a single chemical linkage joining the porphyrin and fullerene, and electron transfer between the two moieties is usually mediated by through-bond superexchange interactions involving this linkage. Some of these linkages are relatively rigid, and this rigidity restricts the conformations, and therefore the possible values of the electronic coupling between the initial excited state and the charge-separated state. This is important, because a range of coupling values in a “floppy” molecule ensures that in some conformations electron transfer will not occur at an optimal rate, can enhance the rate of undesirable charge recombination, and complicates measurement, analysis and interpretation of the electron transfer rates. In virtually all molecules featuring a single linkage between the porphyrin and fullerene moieties, rotation around bonds occurs, and this can change donor-acceptor separations, angles, and coupling.

If the porphyrin and fullerene are joined in a cyclic arrangement, this can in principle further constrain the relative motions of the two moieties by limiting rotations about bonds. Several porphyrin-fullerene systems linked in this way have been reported,^18–27 although the degree of conformational flexibility in the molecules varies. In most cases, these cyclic molecules involve functionalization of the C₆₀ moiety in two locations. Multiple substitution of a fullerene can generate a plethora of isomeric forms. For example, bis-addition to a fullerene using the commonly employed 1,3-dipolar cycloaddition of azomethine ylides (Prato reaction) can result in 8 different regioisomeric adducts, even for an unsubstituted N-alkylpyrrolidine ring.^28–30 By using two reactive groups joined by a carefully designed covalent linkage to carry out the addition reactions, the number of isomers resulting from bis-addition can be significantly constrained.^31–39 In the cyclic porphyrin-fullerene systems mentioned above, such strategies were employed to yield regioisomerically pure products.

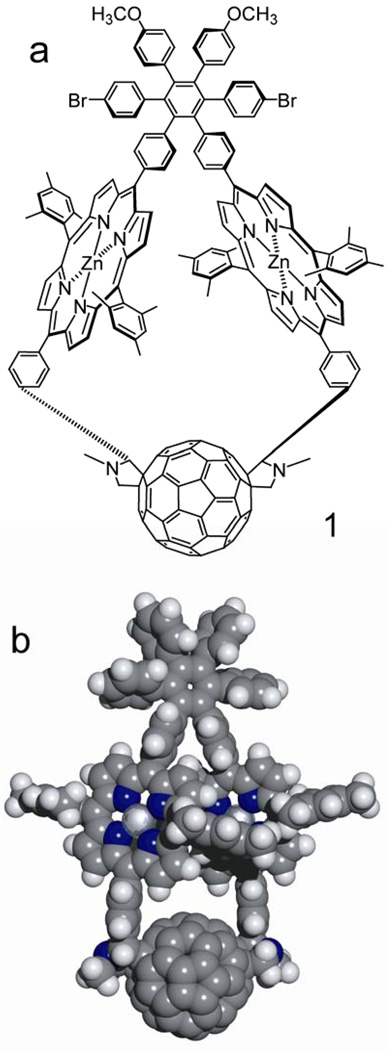
Here we report diporphyrin-fullerene triad 1, in which the three photochemically active moieties are linked in a strained, highly conformationally restricted macrocycle containing 42 atoms in the ring (Figure 1). This large macrocycle was formed in an unusual single-pot reaction process from precursor 5 (Figure 2) and C₆₀. Two linkages to the fullerene are formed in this reaction even though the resulting structure contains significant strain that deforms the porphyrin macrocycles. A major product of the reaction has the trans-2 structure at the fullerene and identical configurations (RR or SS) at the stereocenters on the pyrrolidine rings. Rotation about the bonds within the macrocycle is highly restricted, at least on the NMR time scale, and the porphyrins assume a tilted, partially overlapping conformation, resulting in overall C₂ symmetry for the molecule. The arrangement is reminiscent of that of the special pair of chlorophylls in bacterial reaction centers. Below, we discuss the synthesis, structure determination, and photochemistry of these macrocycles, and propose a mechanism for their formation.

Figure 1.

(a) Structure of triad 1. One of the two enantiomers is shown. (b) Space-filling model of triad 1 based on PM6 semi-empirical calculations. The bromine and methoxy groups have been replaced by hydrogen atoms to simplify calculations. The molecule has trans-2 regiochemistry at the fullerene, the RR-configuration at the stereocenters on the pyrrolidine rings, and overall C₂-symmetry.

Figure 2.

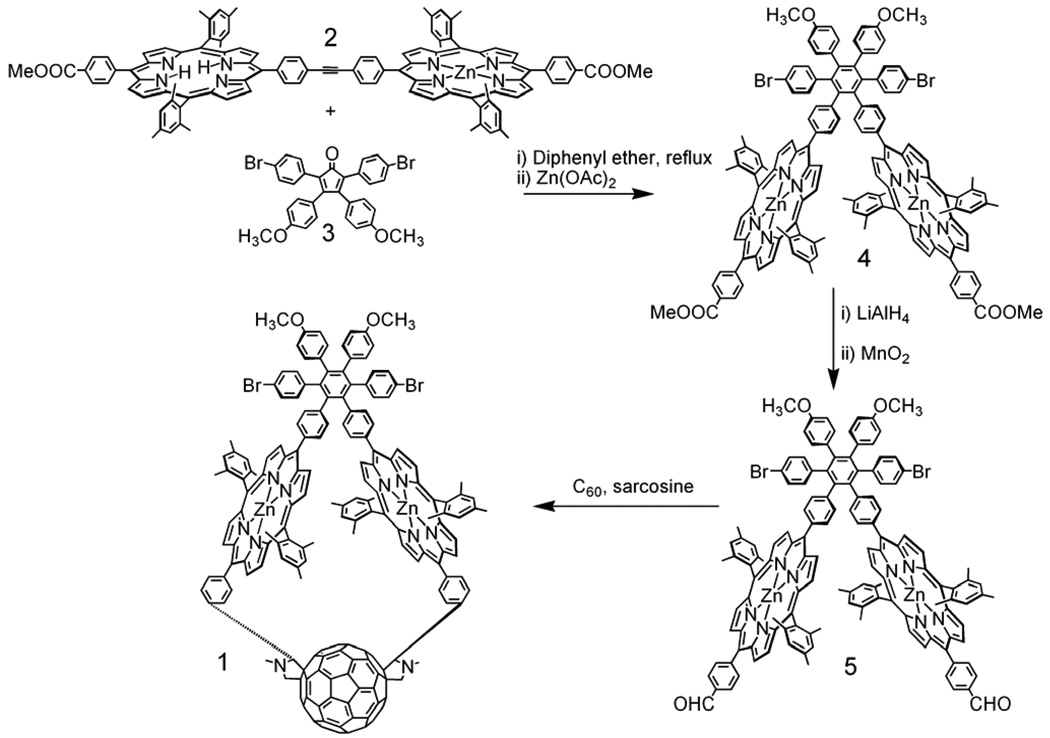
Final steps in the synthesis of triad 1. Details are given in the Supporting Information.

Results

Synthesis

Major aspects of the synthetic route to 1 are shown in Figure 2. Porphyrin dyad 2 was prepared by coupling a suitable porphyrin having a meso-(4-iodophenyl) group and a phenylacetylene-bearing porphyrin using a palladium reagent. Tetra-arylcyclopentadienone 3 was prepared by the base-catalyzed condensation of 1,3-bis(4-bromophenyl)propanone and 4,4’-dimethoxybenzil. Diels-Alder reaction of 2 with 3 and elimination of carbon monoxide, followed by metalation with zinc acetate, gave porphyrin dyad 4. The methyl ester groups of 4 were reduced to alcohols with lithium aluminum hydride and then oxidized to aldehydes with manganese dioxide to give 5. A double Prato-type 1,3-dipolar cycloaddition of C₆₀ and the azomethine ylides formed from N-methylglycine and the aldehydes of 5 gave 1 with a yield of 20%, as well as the non-macrocyclic tetrad bearing a fullerene on each porphyrin (40%) and small amounts of macrocyclic triads with different regiochemistry and/or stereochemistry at the stereocenters that were not studied further. Details of the synthesis and characterization of all new compounds are given in the Supporting Information.

Structure

In the final cyclization reaction that produces 1 (Figure 2) the coupling between C₆₀ and the ylide intermediates formed from the porphyrin aldehyde group and sarcosine must be sequential. That is, first one ylide reacts with C₆₀ in solution and then the second ylide attacks the already-linked fullerene moiety. This reaction course leads to many possibilities for isomerism in the final product:

1. Two Prato-type reactions with C₆₀ that lead to unsubstituted N-alkylpyrrolidine rings give 8 possible regioisomeric substitution patterns on the fullerene. Three of these are chiral, existing in two enantiomeric forms.

2. For each constitutional isomer mentioned above, each phenyl substituent on the pyrrolidine rings may be attached to either of two different carbon atoms, leading to additional isomers.

3. Each pyrrolidine ring carbon that bears a phenyl ring is a stereocenter; the configuration at each center may be R or S.

4. As can be seen in Figure 1b, the porphyrin macrocycles of the triad are tilted relative to the plane of the central benzene ring in the hexaphenylbenzene, yielding another element of chirality. As discussed in more detail later, conformational interconversion between the two helicities does not occur, or is slow on the NMR time scale.

A number of lines of evidence allow other possible isomers to be ruled out, and permit assignment of the structure as shown in Figure 1b. The most important considerations are:

1. UV-vis spectroscopy reveals that the molecule has trans-2 regiochemistry at the fullerene, eliminating structures with the 7 other regiochemistries and establishing that the molecule is chiral.

2. NMR spectroscopy indicates that the molecule has a C₂ symmetry axis. Thus, the molecule belongs to symmetry point group C₂. This reduces the number of possible isomers to 4 pairs of enantiomers.

3. Molecular modeling using the PM6 semi-empirical method and DFT calculations at the B3LYP/6-31G** level indicate that of the 4 possible structures, the one shown in Figure 1b is the most stable. Modeling also suggests that the transition state for formation of the triad shown is of lowest energy.

Below, these lines of evidence are explicated.

UV-vis spectroscopy

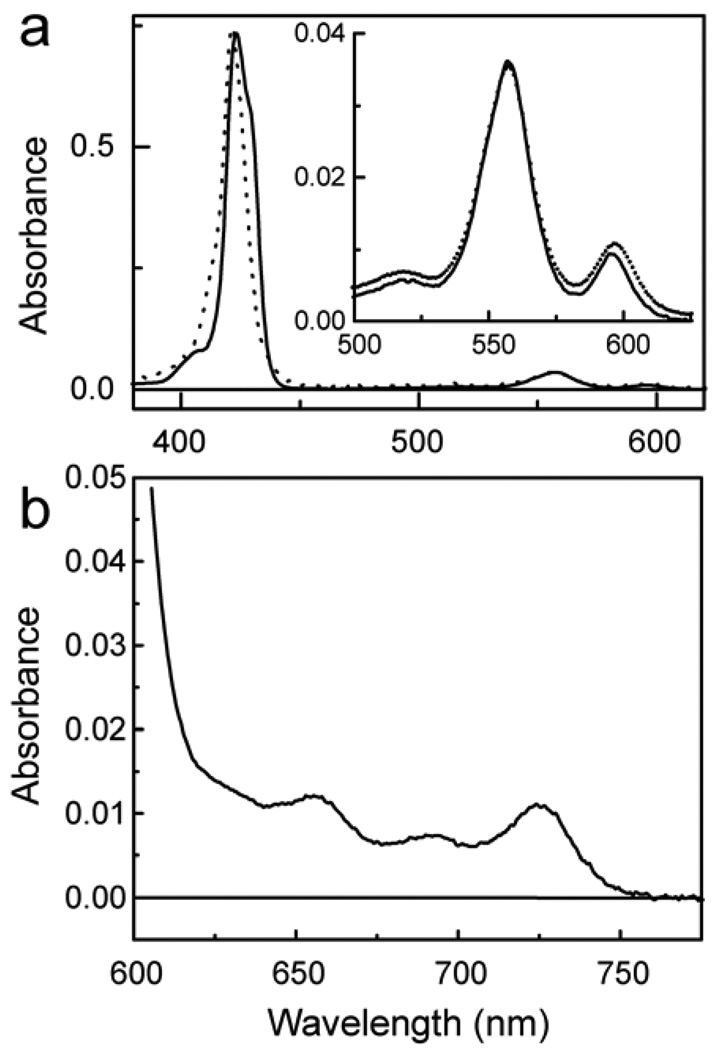
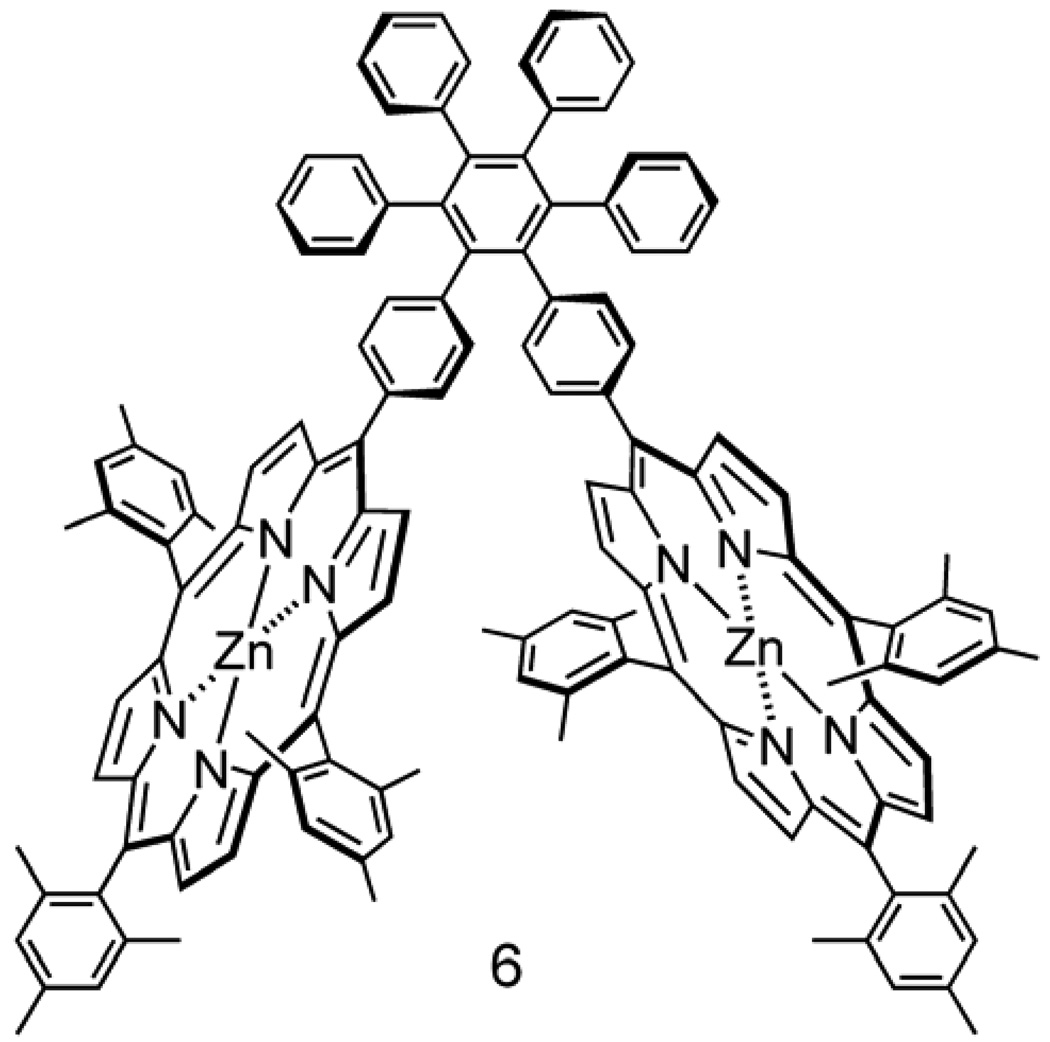
Figure 3 shows the absorption spectra of triad 1 and model porphyrin 6 (Figure 4) in 2-methyltetrahydrofuran solution. Triad 1 shows maxima at ~412 (sh), 422, 517, 557, 597, 656, 693 and 727 nm. The bands below 600 nm are characteristic of zinc tetra-arylporphyrins, and are found in model porphyrin dyad 6 at 407 (sh), 423, ~428 (sh), 518, 557 and 598 nm. The Soret band of dyad 6 is broader than that of a single porphyrin due to excitonic interactions between the two cyclic tetrapyrroles. The Soret band in triad 1 is also broad, is shifted to shorter wavelengths relative to that of 6, and has a different shape. These differences between the Soret bands of 6 and 1 are ascribed to differences in the excitonic interactions between the porphyrins in the twisted arrangement shown in Figure 1b and those in the dyad 6. The porphyrin rings in the triad are somewhat distorted from planarity due to strain introduced by the macrocyclic ring, and this may also contribute to the spectral changes.

Figure 3.

(a) Absorption spectra in 2-methyltetrahydrofuran of triad 1 (dotted) and model porphyrin dyad 6 (solid). The inset shows the Q-band region at a higher concentration. (b) Absorption spectrum in 2-methyltetrahydrofuran of triad 1 showing the long-wavelength fullerene absorption bands. These establish the trans-2 substitution pattern,²⁹ which is also consistent with the nmr results.

Figure 4.

Structure of model zinc porphyrin dyad 6.

The fullerene moiety absorbs throughout the UV and visible regions, out to about 750 nm. The fullerene absorption pattern at long wavelengths displays maxima at 656, 693 and 727 nm (Figure 3b). Prato and coworkers²⁹ have synthesized and characterized the eight possible regioisomeric bis-fulleropyrrolidines, and found that they each has a distinctive UV-vis absorption spectrum. The pattern observed for triad 1 (Figure 3b) is consistent only with trans-2 substitution,^29,30 and allows unambiguous assignment of this regiochemistry to the triad. The trans-2 regiochemistry requires that the highest symmetry possible for the triad is point group C₂, and that 1 is a chiral molecule that exists in two enantiomeric forms. As discussed later, this is consistent with ¹H-NMR results for 1.

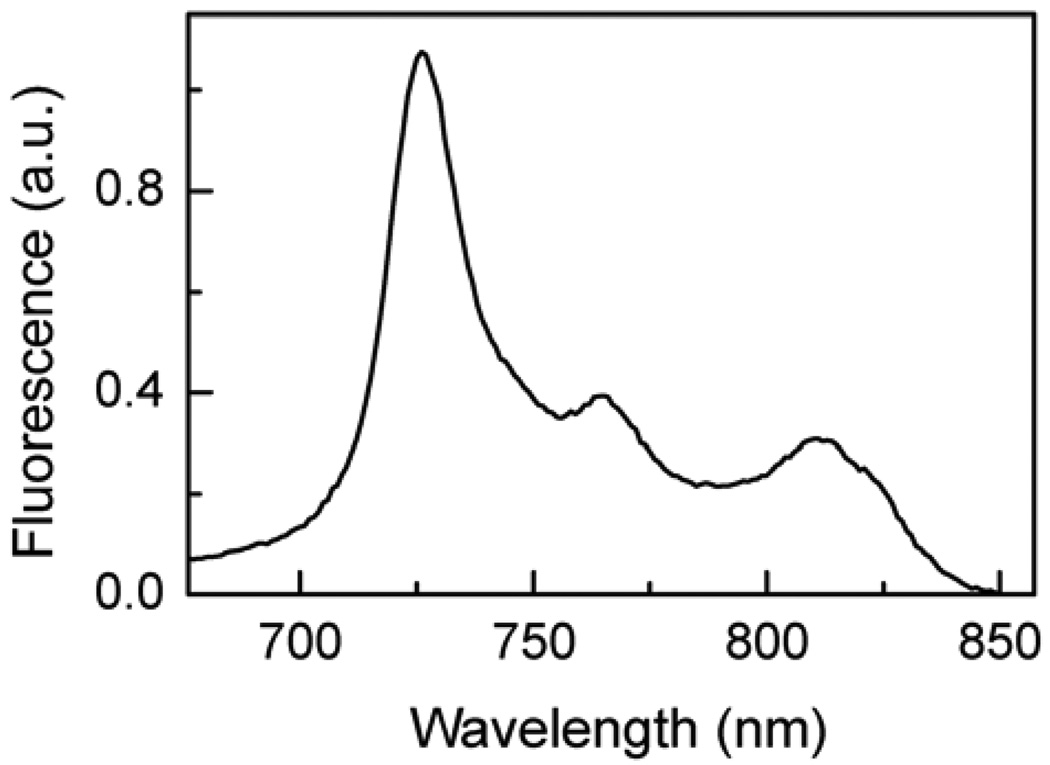
The fluorescence emission spectrum of triad 1 in cyclohexane solution is shown in Figure 5. Maxima are found at 726, 765 and 812 nm, and the emission is characteristic of the fullerene component of the triad. Zinc porphyrins similar to model compound 6 emit with maxima around 600 and 650 nm. Such emissions were not significant in the spectrum of 1, signaling that the porphyrin first excited singlet state is strongly quenched by the attached fullerene (vide infra). When 1 is dissolved in a more polar solvent, 2-methyltetrahydrofuran, no significant emission from either porphyrin or fullerene is observed. The quenching of emission from both types of chromophores in 2-methyltetrahydrofuran is consistent with photoinduced electron transfer from both kinds of first excited singlet states by photoinduced electron transfer. This possibility is discussed in more detail in the section on transient spectroscopy.

Figure 5.

Fluorescence emission spectrum of triad 1 in cyclohexane. Excitation was at 420 nm. Extremely weak zinc porphyrin fluorescence was observed at ~600 and 650 nm.

NMR spectroscopy

The ¹H-NMR spectrum of 1 obtained at 500 MHz was assigned completely using a combination of chemical shift, COSY, NOESY, TOCSY, and HMBC experiments. The assignments are reported in the Supplementary Information. Importantly, the spectra were only consistent with a molecule having a C₂ symmetry axis bisecting the two central bonds of the central ring of the hexaphenylbenzene and containing the C₂ axis of the trans-2 substituted fullerene moiety. Only half as many proton resonances were observed as would be expected for a molecule without the C₂ axis. This is true even for the protons of the fulleropyrrolidine ring and the attached aryl groups. This is the part of the molecule where the effects of fullerene addition in a non-symmetrical fashion would be most apparent. The fact that the large number of proton resonances observed for 1 are all consistent with a C₂ axis makes it highly unlikely that the number of signals is due instead to accidental overlap of every one of the resonances. The finding of the C₂ axis coupled with the trans-2 regiochemistry prove that 1 belongs to point group C₂ and is chiral.

The NMR spectrum of 1 has some other interesting and unusual features. In precursor diporphyrin 5, all four porphyrin meso-mesityl rings would feature isochronous ¹H-NMR resonances (have identical chemical shifts for corresponding protons) if rotations about all single bonds were rapid on the NMR time scale. However, this is not the case. For example, the mesityl methyl resonances appear as four singlets at 2.66 ppm (6H), 2.09 ppm (6H), 1.86 ppm (12H), and 1.33 ppm (12H). A similar doubling of resonances is seen for the aromatic protons of the mesityl rings. In accord with molecular mechanics (MM+) modeling, this doubling of resonances is due to the congested stereochemistry of the molecule. The two porphyrin macrocycles cannot have their planes perpendicular to that of the central hexaphenylbenzene ring. There is strong hindrance to coplanarity of the six peripheral rings of the hexaphenylbenzene, and they lie at angles close to 90° to the central ring.^40–42 The energy barrier to rotation of one of the phenyl rings by 180° is ~17 kcal/mol.⁴² Likewise, the meso-aryl rings on the porphyrins lie at steep angles to the plane of the porphyrin macrocycle, and the barrier to coplanarity is on the order of 16 – 18 kcal/mol.^43–45 The rotational barrier for the mesityl rings, which feature o-methyl groups, is significantly higher.⁴⁶ If a porphyrin of 5 were to have a conformation perpendicular to the central ring of the hexaphenylbenzene, the ring linking it to the hexaphenylbenzene core would have to approach coplanarity with the central hexaphenylbenzene ring and/or the porphyrin macrocycle, and this is energetically highly unfavorable. Molecular modeling also shows some steric interference if the two porphyrins are coplanar with each other and the central ring of the hexaphenylbenzene. Thus, the molecule assumes a twisted, C₂ conformation, with the planes of the porphyrin macrocycles making equal angles to the plane of the central hexaphenylbenzene ring greater than 0 but less than 90°. If the porphyrins of 5 were locked in this twisted conformation, one would expect 6 resonances for the mesityl methyl groups, each integrating for six protons. This is not observed.

However, modeling suggests a low barrier for the two porphyrins to pass one another via an idealized transition state in which the two porphyrin rings and the hexaphenylbenzene central ring are all coplanar. This would not require rotation through high-energy conformations about the bonds linking the porphyrins to the hexaphenylbenzene. If the low-energy motion were to occur and the molecule assume a “time averaged” planar conformation on the NMR time scale, one would expect the NMR spectrum to feature four mesityl methyl resonances in the ratio of 6:6:12:12, exactly as observed. Consistent behavior is expected, and observed, for the two aromatic protons on each mesityl ring. Thus, the NMR evidence supports this behavior for 5.

In triad 1, the situation is quite different. The mesityl methyl resonances now appear with six different chemical shifts, each corresponding to six protons, at 2.68, 2.32, 1.77, 1.55, 0.86 and −3.47 ppm. The aromatic protons of the mesityl rings appear as singlets at 7.44, 7.24, 6.39 and 4.02 ppm, each of which integrates for 2 protons. Clearly, the rotational averaging that reduced the number of resonances observed for 5 is no longer occurring in 1. The spectra are now consistent with a conformation in which the two porphyrin rings are locked in a twisted, C₂ conformation on the NMR time scale, as shown in Figure 1b. The porphyrin rings are not only forced into this twisted conformation, but also rather tightly jammed together, with relatively strong π-π interactions between portions of the macrocycles. This close approach is what gives rise to the excitonic interactions in the Soret band mentioned above. It also means that two of the mesityl methyl groups ortho to the porphyrin macrocycle are forced into the face of the companion porphyrin (Figure 1b). This puts these groups into the strongly shielding region above the plane of the macrocycle. Consequently, the porphyrin aromatic ring current causes these protons to resonate at −3.47 ppm, which is upfield even of the central protons on nitrogen in a free base porphyrin. Related upfield shifts are found for two of the mesityl aromatic protons, which fall at 4.07 ppm, which is more than 3 ppm upfield of their usual position.

Theoretical modeling

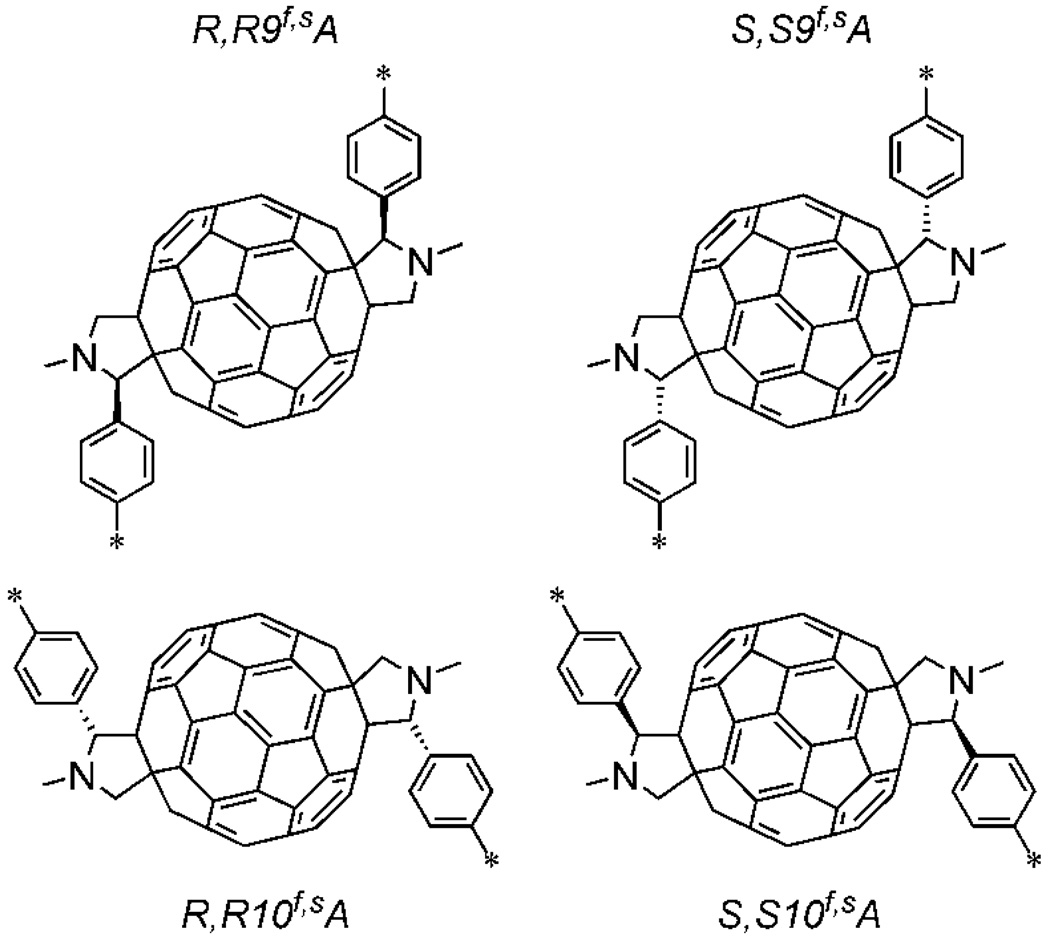
The UV-vis and NMR evidence discussed above reduce the plethora of isomers theoretically obtainable from the reaction of 5 with fullerene to four sets of enantiomers. None of the other possibilities possess the requisite overall C₂ symmetry. The substituted fullerene portions of these isomers are shown diagrammatically in Figure 6. In these representations, the C₂ axis lies perpendicular to the figure and bisects the bond fusing the two 6-membered rings at the center of the fullerene. The asterisks indicate the points of attachment of these fragments to the two porphyrin meso-positions in 1. The stereochemistry is designated by a shorthand for ease of discussion. For example, the structure in the upper left is designated “R,R9^f,sA,” where “R,R” indicates the configurations of the two stereocenters on the pyrrolidine rings, “9” indicates the minimum number of carbon-carbon bonds separating these stereocenters, and “^f,sA” indicates the helicity of the trans-2 isomer in the nomenclature system reviewed by Thilgen and Diederich.⁴⁷ Note that there are also four enantiomeric structures that are not shown. For example, S,S9^f,sC indicates the structure enantiomeric to R,R9^f,sA. The final element of stereoisomerism in the triad, i.e. the twist, or helicity of the tilted porphyrin rings (Figure 1b) is enforced by the elements of chirality of the fragments shown in Figure 6.

Figure 6.

Potential isomeric partial structures of 1 in the region of the fullerene. The asterisks indicate the points of attachment to the two porphyrin meso-positions. As explained in the text, 1 is found to have the R,R9^f,sA structure. Each fragment has C₂ symmetry, and in the drawings, the C₂ axis lies perpendicular to the figure, and passes through the center of the bond fusing the two 6-membered rings at the center of the fullerene. These structures are chiral, and as a result, each has an enantiomer (e.g. S,S9^f,sC). Triad 1 was prepared in racemic form.

As mentioned above, the formation of 1 via the Prato reaction must occur stepwise. First, one aldehyde group of 5 reacts with sarcosine to form the very reactive ylide intermediate, and this intermediate reacts with a bond fusing two 6-membered rings on the C₆₀ to form the first pyrrolidine ring. Then, the remaining aldehyde, on the second porphyrin, is converted to the ylide, which attacks another fullerene bond. Applying the Hammond postulate to this second reaction, we make the assumption that of the four possible C₂ product molecules indicated by the structures represented in Figure 6, the one that forms most readily and is therefore observed will be the most stable. Theoretical calculations were employed to investigate the stability of the four possible products.

The initial calculations were simplified by using the free base form of the triad and replacing the bromine and methoxy groups with hydrogen atoms, as it was judged that these changes would have little effect on the overall structure. First, the four isomeric free base triads formed from the four structures in Figure 6 were optimized at the PM6 level in the C₂ point group. The heats of formation were: R,R9^f,sA, 1308.40 kcal/mol; S,S9^f,sA, 1352.74 kcal/mol; R,R10^f,sA, 1327.44 kcal/mol and S,S10^f,sA, 1346.04 kcal/mol. Furthermore, structure optimization without the C₂ symmetry constraint showed that only R,R9^f,sA and R,R10^f,sA isomers are stable in the C₂ point group. Clearly, the isomer with the R,R9^f,sA structure, which corresponds to the stereochemistry shown in Figure 1b, is significantly more stable than the other three. Because the accuracy of PM6 is in general <4.4 kcal/mol for calculations of this type,⁴⁸ we conclude that the molecule prepared most likely has the indicated stereochemistry. Visual inspection indicates that this isomer also has significantly less distortion of the porphyrin rings than the others, suggesting less strain.

To bolster our conclusion, single point density functional calculations at the C₂ PM6-optimized geometries were performed at the B3LYP/6-31G** level. The B3LYP ground state energies are: R,R9^f,sA, −8083.7670 Hartrees; S,S9^f,sA, −8083.6856 Hartrees; R,R10^f,sA, −8083.741766 Hartrees and SS10^f,sA, −8083.69375 Hartrees. Again, the R,R9^f,sA energy is the lowest. If we set the R,R9^f,sA energy to zero, then relative strain energies of the other structures are: SS9^f,sA, +51 kcal/mol; R,R10^f,sA, +15.8 kcal/mol and S,S10^f,sA, +46 kcal/mol. Again, these are substantially larger than the expected error limits (~0.4 kcal/mol) for this method.⁴⁹

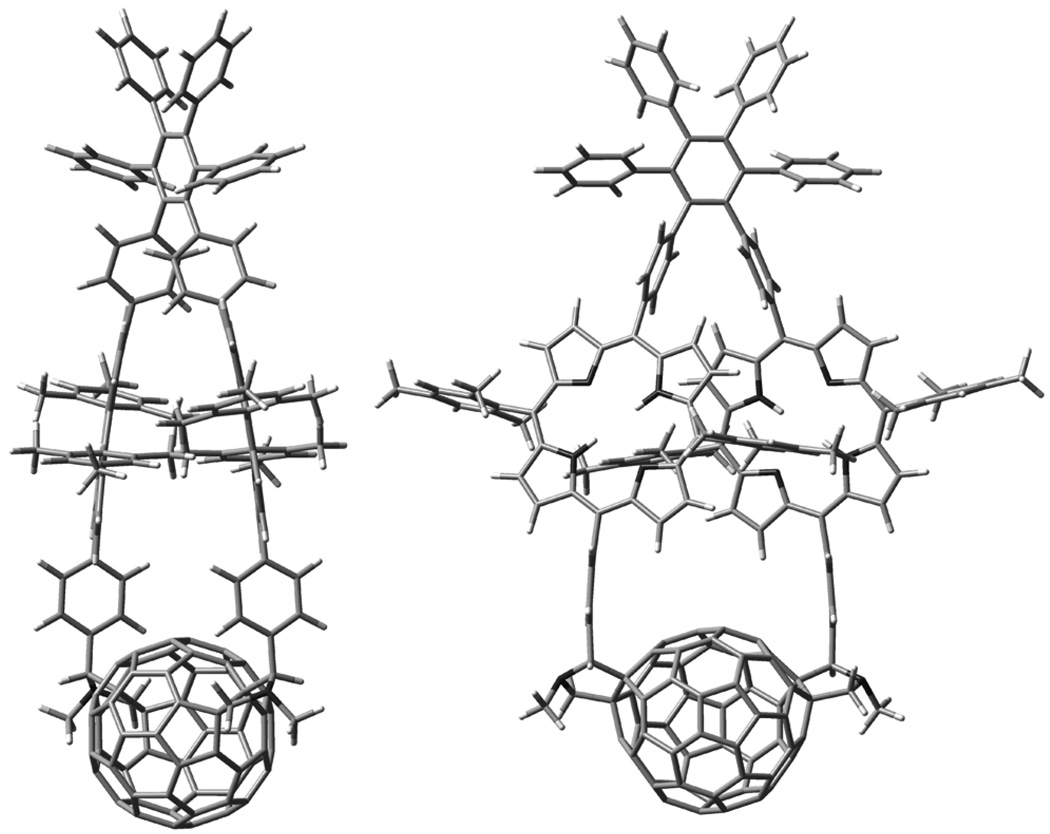
Figure 7 shows two views of the energy-minimized structure of the model for triad 1. The porphyrin rings are twisted into a helical conformation relative to the plane of the central ring of the hexaphenylbenzene, in accord with the NMR results. The porphyrin macrocycles approach one another closely (as expected based on the Soret band spectral shifts), and the macrocycles are slightly dished towards one another (bowl shaped) due to the strain imposed by closing the large ring. The mesityl groups on the “inside” of the structure closely contact the neighboring porphyrin, consistent with the large shielding observed in the NMR spectra for some of the mesityl methyl protons. The dipole moment was 2.0 Debye at the B3LYP/6-31G(d,p) level (1.4 Debye at the PM6 level). The dipole is oriented along the C₂ axis, and points from the hexaphenylbenzene towards the fullerene. The HOMO is localized fully on the porphyrins, whereas the LUMO is centered on the fullerene moiety.

Figure 7.

Two views of the energy-minimized structure of the free base model for triad 1. Note that strain in the large macrocyclic ring results in bending of the planes of the two porphyrins and the linkages joining them to the hexaphenylbenzene and the fullerene. Also note that one mesityl ring on each porphyrin is forced into the face of the companion porphyrin.

The central protons of the porphyrins in the model were then replaced with two zinc atoms, and the structure of triad 1 was calculated. The resulting structure is that shown in Figure 1b. Note that the overall structure changes very little upon introduction of zinc. The heat of formation is 1287.1 kcal/mol at the PM6 level and 11639.838 Hartrees at the B3LYP/6-31G** level. The corresponding dipole moments are 1.74 and 1.63 Debye.

An alternative approach was also used to estimate the relative energies of the transition states for formation of the four products based on the structures in Figure 6. Molecular mechanics (MM+) energy-minimized models of the intermediate product in the formation of the triad from 5, e.g. the molecule with a fulleropyrrolidine attached to one porphyrin phenyl ring and an aldehyde group on the other, were constructed for each of the four possibilities. The distance of closest approach between the aldehyde carbon and its future position in the second fulleropyrrolidine was measured for each possibility. The distances obtained were: R,R9^f,sA, 14.9 Å; S,S9^f,sA, 24.6 Å; R,R10^f,sA, 21.7 Å and S,S10^f,sA, 20.2 Å. Thus, the reactive ylide that forms from the second aldehyde group is significantly closer to the position where its carbon atom will be found in the final product for the model based on R,R9^f,sA than for any of the other three. This is consistent with a scenario wherein the molecule must distort in order for the final addition to occur, and the addition which occurs most readily is that which requires the least motion away from equilibrium, and thus the least energy input.

All the above lines of evidence consistently point to structures and conformations for 1 analogous to those shown in Figure 7 and Figure 1b.

Electrochemistry

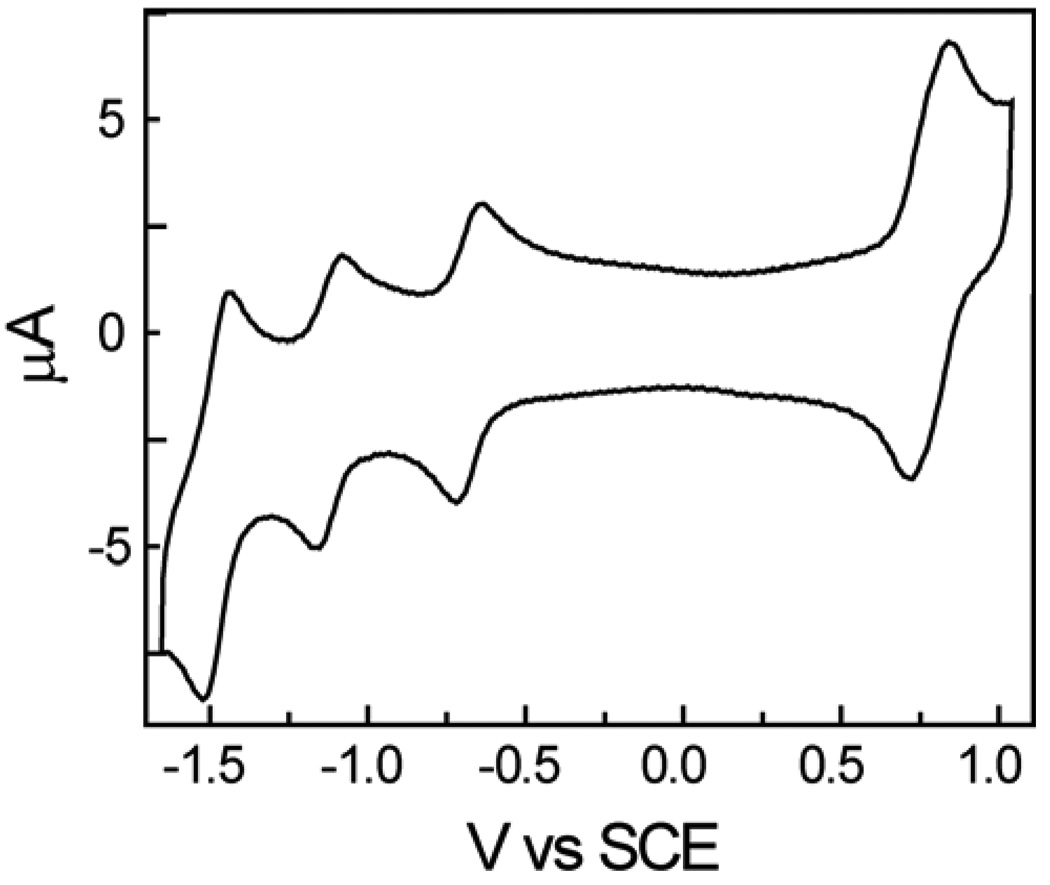
Triad 1 was designed to function as an artificial photosynthetic reaction center in which a porphyrin excited state donates an electron to the fullerene to form a P^•+-C₆₀^•−-P charge-separated state. The redox behavior of 1 was investigated in order to obtain information concerning the energetics of the electron transfer reaction. Cyclic voltammetric studies of 1 in benzonitrile solution containing 0.1 M tetra-n-butylammonium hexafluorophosphate were carried out using a glassy carbon working electrode, a platinum counter electrode, and a Ag/AgNO₃ (0.1 M) reference electrode. Ferrocene was used as an internal redox reference material. A typical voltammogram is shown in Figure 8. Reversible oxidation waves were observed at 0.78 and 1.21 (not shown) V vs. SCE. Reversible reductions were found at −0.68 and −1.12 V, and at more negative potentials. The two oxidation potentials are assigned to the first and second oxidations of the zinc porphyrins. The first oxidation potential is essentially identical to that reported for tetramesitylporphyrin,⁵⁰ and so the distortion of the porphyrin rings in 1 has little effect. The first two reductions are ascribed to the fullerene moiety. The bis-substituted fullerene is about 100 mV more difficult to reduce than the corresponding mono-adduct. ⁵¹ These data permit estimation of the energy of a P^•+-C₆₀^•−-P state at 1.46 eV above the ground state. The energy of the zinc porphyrin first excited singlet state of 1 is estimated at 2.06 eV, based on model compounds. The driving force for photoinduced electron transfer from this state to form P^•+-C₆₀^•−-P is therefore about 600 meV. The absorption and emission data for the fullerene component of 1 presented earlier allow estimation of the energy of its first excited singlet state at 1.71 eV, and this in turn leads to a thermodynamic driving force for photoinduced electron transfer to this state to form P^•+-C₆₀^•−-P of 250 meV.

Figure 8.

Cyclic voltammogram of 4 in benzonitrile containing 0.1 M tetra-n-butylammonium hexafluorophosphate. The conditions are explained in the text. This voltammogram was obtained at a scan rate of 100 mV/s.

Transient spectroscopy

Transient spectroscopy was used to investigate the fate of excitation energy in triad 1. The fluorescence quenching mentioned earlier was further studied by transient measurements using the single photon timing method. In 2-methyltetrahydrofuran, The zinc porphyrins in dyad 6 have a first excited singlet state lifetime of 2.2 ns. In the same solvent, all fluorescence from both fullerene and porphyrin moieties of 1 is quenched to <10 ps. When dissolved in cyclohexane and excited at 420 nm, triad 1 shows an exponential decay of ~7 ps at 650 nm where the zinc porphyrin emits,⁵¹ and 990 ps at 725 nm where the fullerene emits (χ² = 1.15).⁵² A model for the fullerene component of 1 is not available, but the 990 ps lifetime is similar to the lifetime of 1.3 ns found for a related but monosubstituted fullerene,⁵² suggesting that in cyclohexane there is little or no quenching of the fullerene first excited singlet state.

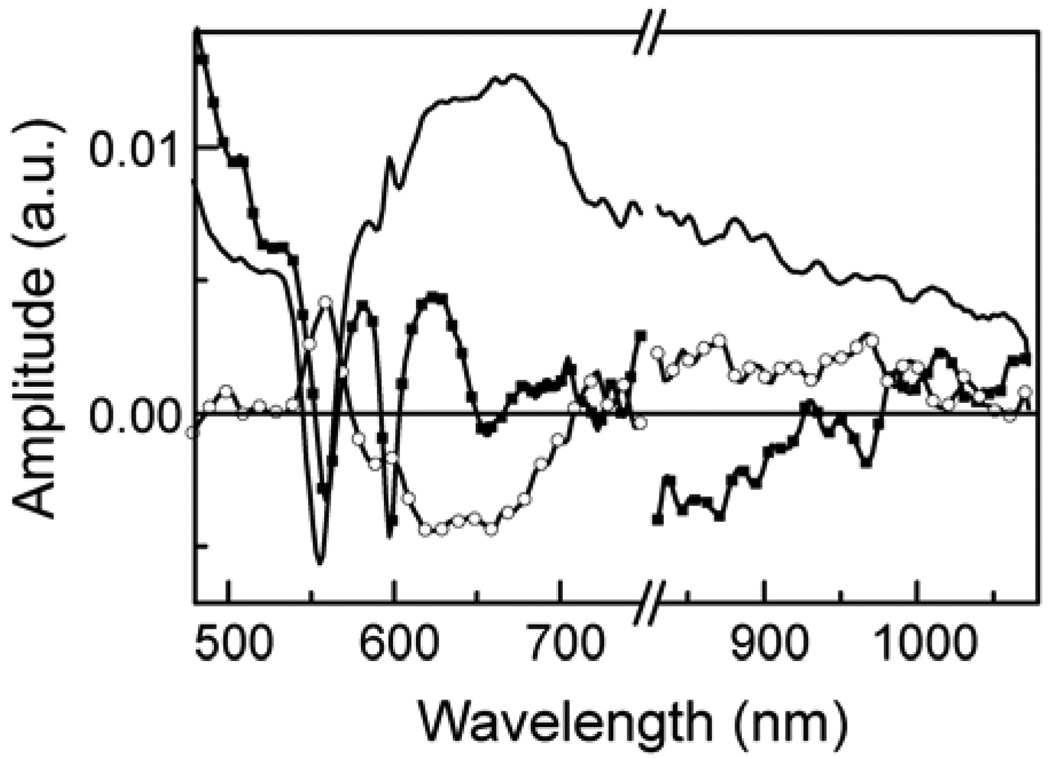
Additional information was obtained from transient absorption measurements. Figure 9 shows the transient absorption decay-associated spectra (DAS) of 1 in 2-methyltetrahydrofuran with excitation from a 600 nm, ~100 fs laser pulse. The spectra were obtained by fitting the data to three exponential functions. The DAS show the absorptions associated with the three lifetimes, and in general do not represent spectra of individual chemical species. The time constants obtained were 1.1 ps, 7.8 ps (fixed in the analysis (vide infra), and 2.7 ns. The 1.1 ps spectrum is associated with the decay of the zinc porphyrin first excited singlet state (bleaching of the Q-band absorptions and decay of stimulated emission in the 600 and 650 nm regions) and formation of the P^•+-C₆₀^•−-P charge-separated state, which shows both Q-band bleach and broad absorbance at wavelengths around 600 nm and longer. The 2.7 ns transient is characteristic of P^•+-C₆₀^•−-P, with induced absorption of the zinc porphyrin radical cation having a poorly-defined maximum around 650 nm, and indicates decay of that state to the ground state. The absorption of the fullerene radical anion at 900 nm is broad and weak,²⁷ and not well defined in these spectra. The 7.8 ps transient has features compatible with decay of the fullerene first excited singlet state (positive amplitude above 700 nm) and rise of P^•+-C₆₀^•−-P, but is rather featureless.

Figure 9.

Transient absorption decay associated spectra of triad 1 in 2-methyltetrahydrofuran with excitation at 600 nm. The data were fitted as three exponentials with time constants of 1.1 ps (squares), 7.8 ps (fixed in the analysis, circles) and 2.7 ns (solid line). Data were taken over two wavelength regions, as indicated by the break in the horizontal axis. The vertical axis represents the relative amplitude of the transient absorption signal associated with the relevant time constant.

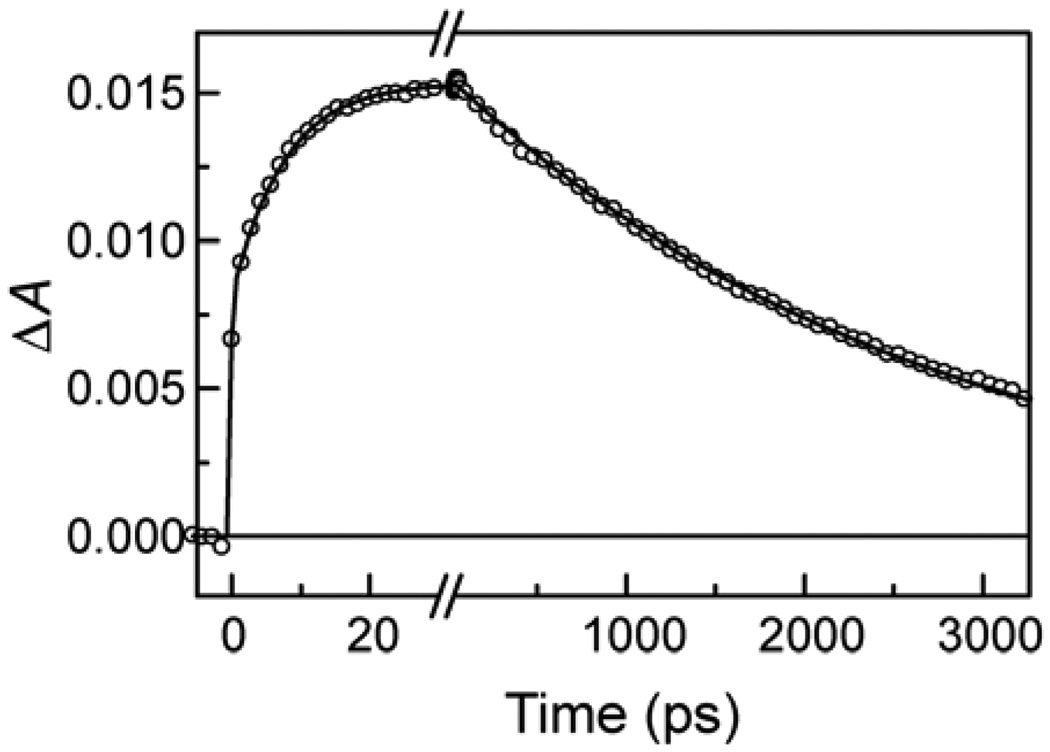
In order to further probe the photochemistry of ¹C₆₀, a similar transient absorption experiment in 2-methyltetrahydrofuran was carried out with excitation at 725 nm, where only the fullerene component of the triad absorbs. The resulting transients at 650 nm are shown in Figure 10. After the prompt formation of ¹C₆₀ absorbance with the laser pulse, there is a growth of absorbance at 650 with a time constant of 7.8 ps that is characteristic of the porphyrin radical cation of P^•+-C₆₀^•−-P. On a longer time scale, this transient decays with a time constant of 2.7 ns.

Figure 10.

Transient absorption kinetics at 650 nm for triad 1 in 2-methyltetrahydrofuran following excitation at 725 nm with a ~100 fs laser pulse. The solid line represents an exponential fit with time constants of 7.8 ±0.2 ps and 2.69 ns ±10 ps.

Taken together, the transient emission and absorption results demonstrate that in 2-methyltetrahydrofuran, P^•+-C₆₀^•−-P is formed from ¹P-C₆₀-P in 1.1 ps and from P-¹C₆₀-P with a time constant of 7.8 ps, and decays with a lifetime of 2.7 ns.

Photoinduced electron transfer

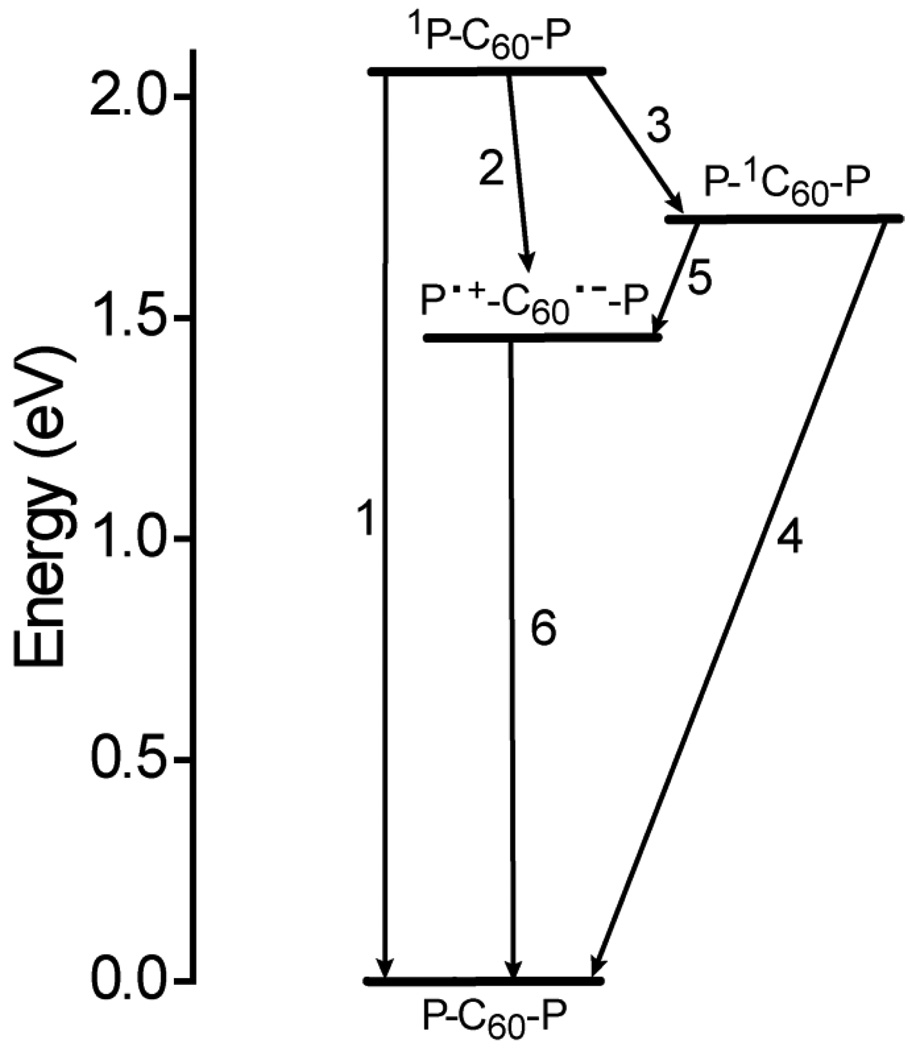
The information reported above allows an understanding of the photoinduced electron transfer behavior of 1. This can be discussed in terms of Figure 11, which shows the high-energy states of the triad produced following excitation with light and their relevant interconversion pathways in 2-methyltetrahydrofuran. In the Figure, the energies of the various states are estimated from the spectroscopic and electrochemical results given above. Excitation of either porphyrin moiety in 2-methyltetrahydrofuran gives the first excited singlet state, which can decay by the usual photophysical processes (relax to the ground or triplet state or fluoresce) with a time constant of 2.2 ns, based on results for model compound 6. This process is step 1 in the Figure, and the associated rate constant k₁ = 4.6 × 10⁸ s⁻¹. Competing with step 1 is photoinduced electron transfer to the fullerene (step 2) to yield P^•+-C₆₀^•−-P. The rate constant k₂ may be determined from eq. 1, where τ_s is the measured lifetime of the porphyrin first excited singlet state (1.1 ps): k₂ = 9.1 × 10¹¹ s⁻¹.

$$1/{\tau }_s=k_1+k_2$$ (1)

The quantum yield of P^•+-C₆₀^•−-P formed by this pathway is 1.0. The charge-separated state decays to the ground state (step 6) with a time constant of 2.7 ns (k₆ = 3.7 × 10⁸ s⁻¹). No residual absorption characteristic of triplet states, formed by charge recombination, was observed.

Figure 11.

Energetics of triad 1. The horizontal bars represent different states of the molecule, and the arrows the relevant interconversion pathways. The energies were estimated from spectroscopic and cyclic voltammetric data, as explained in the text, and are relevant in relatively polar solvents such as 2-methyltetrahydrofuran. In cyclohexane, the energy of P^•+-C₆₀^•−-P is higher because of loss of stabilization of the ions by solvent dipoles.

Illumination of the triad at wavelengths <750 nm excites not only the porphyrins, but also the fullerene moiety. The transient results in 2-methyltetrahydrofuran show that the fullerene first excited singlet state decays in 7.8 ps, forming P^•+-C₆₀^•−-P (step 5 in Figure 11). Using an equation similar to eq. 1 and taking the lifetime of P-¹C₆₀-P as 990 ps in the absence of photoinduced electron transfer (based on the results in cyclohexane), a rate constant of 1.3 × 10¹¹ s⁻¹ may be calculated. Because there are two porphyrin moieties quenching the fullerene excited state, the rate constant for electron transfer from a single porphyrin to the fullerene excited state, k₅, equals 6.5 × 10¹⁰ s⁻¹. The quantum yield of P^•+-C₆₀^•−-P by this route is 1.0. Thus, all light absorbed by the triad leads to formation of P^•+-C₆₀^•−-P with an overall quantum yield of unity.

The situation in cyclohexane is different. In this solvent, the fluorescence decay results show that the fullerene excited singlet state undergoes little or no quenching by photoinduced electron transfer. This is ascribed mainly to the fact that the energy of P^•+-C₆₀^•−-P in the non-polar solvent increases due to loss of stabilization by the solvent dipoles, and the driving force for photoinduced electron transfer in cyclohexane is too small to allow it to occur at a significant rate. It is probable that the energy of P^•+-C₆₀^•−-P increases to a value above the energy of the fullerene first excited singlet state, making any electron transfer endergonic. This energetic ordering has been observed in other porphyrin-fullerene systems.^6,53,54

The porphyrin first excited singlet states, however, are quenched to ~7 ps in cyclohexane. In principle, this quenching could be either photoinduced electron transfer to the fullerene or singlet-singlet energy transfer to that moiety (step 3 in Figure 11). Calculations using the Förster theory^55,56 of singlet energy transfer, a porphyrin-fullerene separation of 12 Å (based on the PM6 model), and assuming an average mutual orientation of the transition dipoles (κ² = 0.67) yields a time constant for singlet-singlet energy transfer of 91 ps, which is much longer than the observed lifetime of the porphyrin excited state. In addition, no rise time for the fullerene first excited singlet state was observed. These considerations suggest that the quenching of ¹P-C₆₀-P in cyclohexane is due to photoinduced electron transfer.

Discussion

Formation of the triad

The UV-vis and NMR results and the theoretical calculations discussed above allow us to assign the structure of the cyclic triad to that shown in Figure 1b. The many other possible isomers may be ruled out on spectroscopic or energetic grounds. But why does the triad form in the first place? The yield of the non-cyclic diporphyrin difullerene tetrad from the Prato reaction is only about twice that of triad 1. As discussed above, the fulleropyrrolidine rings in 1 must be formed sequentially, with one ylide intermediate reacting first with C₆₀, followed by reaction of the ylide formed from the second aldehyde to yield the macrocycle. Molecular mechanics models (MM+) show that the intermediate mono-adduct is a relatively rigid structure. Facile rotation that significantly changes the distance between the fullerene and the second ylide can only occur around one bond – that joining the porphyrin meso-aryl ring to the pyrrolidine ring. Such rotation can bring the fullerene no closer than ~15 Å to its final position in the triad. Although attractive interactions between the two porphyrins that might not be reflected in such models could in principle bring the two porphyrin reaction sites closer together, the NMR data given above do not support such an attraction. The NMR data show that the two porphyrin moieties of dyad 5 are able to freely rotate through the plane of the hexaphenylbenzene central ring on the NMR time scale, but such rotation is precluded in triad 1. In addition, two of the mesityl methyl groups in 1 are highly shielded in the NMR spectrum, indicating that the two porphyrins are forced together. This is not observed in the spectrum of 5. Thus, the large-scale bending motions of the two porphyrins linked to the hexaphenylbenzene that are required in order to allow formation of the second pyrrolidine ring must occur transiently during the reactions. The relatively high yield of the triad can be ascribed to the high reactivity of the azomethine ylide after its formation from the porphyrin aldehyde group and sarcosine. When suitable large-scale distortions of the molecule occur, the ylide reacts extremely rapidly and irreversibly with the fullerene 6,6-bond to form the large, strained macrocycle.

Photoinduced electron transfer

The transient data show that the rigid, cyclic conformation of 1 holds the fullerene in a position that is highly favorable for photoinduced electron transfer. This results in a very short time constant (1.1 ps) for electron transfer from the porphyrin first excited singlet state to the fullerene in 2-methyltetrahydrofuran, yielding P^•+-C₆₀^•−-P. This conformation also favors photoinduced electron transfer in P-¹C₆₀-P (τ = 15 ps) to give P^•+-C₆₀^•−-P. The time constant for this process is larger than that for ¹P-C₆₀-P because the thermodynamic driving force is less by 350 meV, and the reaction lies in the normal region of the Marcus electron transfer rate constant vs. free energy change relationship.⁵⁷

Charge recombination of P^•+-C₆₀^•−-P is relatively slow (2.7 ns), given the favorable geometric relationship. This is typical of porphyrin-fullerene systems, where reorganization energies are small, and charge recombination lies in the inverted region of the Marcus relationship.^{14,19,51,52,54,58,59}

It is interesting to compare the electron transfer results for triad 1 with those for a related zinc porphyrin-fullerene dyad⁵¹ featuring a single pyrrolidine link, as opposed to two such linkages in 1. This compound is much less rigid than 1, and rotations about single bonds in the porphyrin-fullerene linkage are expected to be facile. In the model dyad, the thermodynamic driving force for formation of the P^•+-C₆₀^•− state from the porphyrin first excited singlet state is 0.050 eV larger than in 1, but the rate constant for photoinduced electron transfer is 6.7 × 10¹¹ s⁻¹, as opposed to 9.1 × 10¹¹ s⁻¹ for the triad. For charge recombination of P^•+-C₆₀^•− to the ground state, the driving force in the model dyad is 1.41 eV (vs. 1.46 eV in the triad), and the corresponding rate constant is 1.5 × 10⁹ s⁻¹ (vs. 3.7 × 10⁸ s⁻¹ in the triad). Thus in the triad, charge separation is 1.4 times faster than in the dyad, even though the driving force is less. Charge recombination, on the other hand, is 4.1 times slower in the triad, and the driving force in the inverted region of the Marcus rate constant vs. free energy relationship is larger.

The differences between these molecules can be understood in terms of Marcus theory by postulating a smaller reorganization energy for the triad than for the dyad. The compact, rigid structure in the triad, where one face of each porphyrin macrocycle is forced close to that of the other and the fullerene is rigidly held near both porphyrins, is expected to reduce the solvent reorganization energy because of reduced exposure of the donor and acceptor to the solvent environment. The more rigid, constrained structure would also be expected to reduce the internal reorganization energy. Marcus theory predicts that the reduced reorganization energy in the triad would increase the rate of photoinduced electron transfer for a given value of driving force in the normal region of the electron transfer rate vs. free energy change relationship. In the triad, this increase is larger than the decrease in rate due to the decrease in driving force measured electrochemically, and any additional decrease due to loss of stabilization of the radical ions by solvent in the more compact structure.

The difference in charge recombination rates for the two molecules is about three times larger than the difference in charge separation rates. Several factors contribute to the reduced recombination rate. Because charge recombination occurs in the inverted region of the relationship, a decrease in reorganization energy slows the recombination rate. This is augmented by the increase in driving force for recombination as measured electrochemically, and by any additional increase in driving force due to reduced solvent stabilization in the compact macrocyclic structure. The increased driving force moves recombination further into the Marcus inverted region. The very rigid nature of the triad may also impede charge recombination by preventing the radical ions from approaching one another more closely after they are formed, which could increase the electronic coupling interaction between them.

As mentioned in the Introduction, there are several other examples of photoinduced electron transfer in zinc porphyrin-fullerene molecules where the donor and acceptor are joined in a cyclic structure with two covalent linkages to the fullerene. These vary greatly in the nature of the linkages, and consequently in the rate constants for electron transfer. However, there are two such molecules that display photoinduced charge separation in tetrahydrofuran with time constants of <10 ps. One has a time constant for charge separation of 2 ps and a time constant for recombination of 134 ps.²⁷ The second shows charge separation in 6.7 ps and charge recombination in 385 ps.^20,60 The charge recombination times are substantially shorter than the 2.7 ns observed for triad 1. This difference may be ascribed at least in part to the low reorganization energy for electron transfer in 1 as discussed above and the rigid structure which prevents the ions in the charge separated state from approaching one another and thereby increasing the coupling for the charge recombination reaction.

Conclusions

The unusual double Prato reaction of C₆₀ and dialdehyde 5 yields a macrocyclic diporphyrin-fullerene triad that displays very rapid photoinduced electron transfer from both the porphyrin and the fullerene first excited singlet states to yield a relatively long lived charge separated state. Thus, the triad performs as an artificial photosynthetic reaction center. The relatively rigid molecular structure enforced by the strained, 42-atom macrocycle ensures that the porphyrins and fullerene are always in a conformation favorable for electron transfer, and reduces the reorganization energies for charge separation and recombination, even relative to their already-low values in singly-linked porphyrin-fullerene artificial reaction centers. As a result, photoinduced charge separation in the triad is over 2000 times faster than charge recombination. Having two porphyrin moieties per fullerene acceptor essentially doubles the absorption cross section for photoinduced electron transfer. It also provides two electron-donor moieties to donate to the fullerene excited singlet state, thus helping ensure a high quantum yield of charge separation from that state even though the driving force for electron transfer is relatively small. The use of a hexaphenylbenzene architecture to establish a rigid framework for the triad also provides four additional aryl rings on the hexaphenylbenzene that could be used to attach antenna moieties or other auxiliary components to the artificial reaction center, yielding an antenna-reaction center complex. The hexaphenylbenzene system has been used to incorporate different antenna species in related molecules, and these show quantitative energy transfer to the porphyrin chromophores.^9,14,61,62