Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2011 Mar 8.
Published in final edited form as: Child Neuropsychol. 2009 Sep;15(5):417–424. doi: 10.1080/09297040802603661

HIGHER ORDER FACTOR STRUCTURE OF THE WISC-IV IN A CLINICAL NEUROPSYCHOLOGICAL SAMPLE

Doug Bodin 1, Dustin A Pardini 2, Thomas G Burns 3, Abigail B Stevens 3
PMCID: PMC3049991  NIHMSID: NIHMS248687  PMID: 19132580

Abstract

A confirmatory factor analysis was conducted examining the higher order factor structure of the WISC-IV scores for 344 children who participated in neuropsychological evaluations at a large children’s hospital. The WISC-IV factor structure mirrored that of the standardization sample. The second order general intelligence factor (g) accounted for the largest proportion of variance in the first-order latent factors and in the individual subtests, especially for the working memory index. The first-order processing speed factor exhibited the most unique variance beyond the influence of g. The results suggest that clinicians should not ignore the contribution of g when interpreting the first-order factors.

Keywords: Neuropsychological assessment, Pediatric neuropsychology, Child assessment, Factor analysis, WISC-IV

The Wechsler Intelligence Scale for Children-Fourth Edition (WISC-IV) is the most recent version of the Wechsler Intelligence Scale for Children (Wechsler, 2003a). Prior studies have investigated the factor structure of previous versions in the Wechsler series. Kaufman’s original factor analysis of the WISC-R standardization sample (Kaufman, 1975) identified three factors: Verbal Comprehension, Perceptual Organization, and Freedom from Distractibility. Subsequent factor analytic studies of the WISC-R in a variety of clinical samples (Donders, 1993; Hodges, 1982; Tingstrom & Pfeiffer, 1988) confirmed this three-factor structure; although several of these authors urged caution when interpreting the third (freedom from distractibility) factor because of relatively weak factor loadings. With the emergence of a new subtest (symbol search) on the WISC-III, a four-factor model was supported in several factor analytic studies using the standardization sample (Blaha & Wallbrown, 1996; Keith & Witta, 1997) and using clinical samples (Donders & Warschausky, 1996; Grice, Krohn, & Logerquist, 1999; Tupa, Wright, & Fristad, 1997). Burton et al. (2001) identified a five-factor structure using confirmatory factor analysis on the WISC-III in a clinical sample that was cross-validated using the standardization sample; however, this five-factor model was contingent on the administration of the supplemental subtests.

Published studies investigating the factor structure of the fourth edition of this popular instrument are relatively scarce. Watkins (2006) conducted an orthogonal higher order structural analysis on the 10 core subtests of the WISC-IV standardization sample and found support for the four-factor structure described in the WISC-IV technical manual (Wechsler, 2003b). However, the general factor (g) accounted for the greatest amount of variance. Watkins, Wilson, Kotz, Carbone, and Babula (2006) conducted a factor analysis with the 10 core WISC-IV subtests using a sample of 432 children referred for special education services and found support for the first-order four-factor solution; although the perceptual reasoning and working memory factors accounted for very little total variance. These authors also found that the general factor (g) explained the greatest amount of variance and they discouraged interpreting first-order factors over the second-order (general intelligence) factor. Keith, Fine, Taub, Reynolds, and Kranzler (2006) reanalyzed the WISC-IV standardization sample, using both core and supplemental subtests. While a higher order four-factor model fit the data well, some results suggested that a five-factor solution may provide a better fit to the data. However, the specification of this five-factor structure was contingent on administering all 15 subtests of the WISC-IV and included several cross-loadings across first-order factors.

The Standards for Educational and Psychological Testing (American Educational Research Association [AERA], 1999) discuss the importance of establishing the validity of constructs that instruments are designed to measure in populations for which the measure is designed to be used. Therefore, investigating the construct validity of the WISC-IV index scores in clinical populations is important. Children with neurological impairment may exhibit different patterns of performance than non-neurologically impaired children on the individual tasks comprising each factor, which may result in a different factor structure. Investigating the higher order factor structure of the WISC-IV is also important given the emphasis placed on the four index scores in abandoning the Verbal and Performance IQ model used in previous versions (Wechsler, 2003b). Another important issue is to examine the extent to which the four first-order factors of the WISC-IV contain unique variance beyond the influence of the higher order general intelligence factor g (Watkins et al., 2006). Therefore, the present study sought to investigate the higher order factor structure of the core WISC-IV subtests in a pediatric neuropsychological sample.

METHODS

The current sample consisted of 344 children ranging in age from 6 to 16 years who participated in an administration of the WISC-IV as part of a comprehensive neuropsychological evaluation at a large pediatric hospital in the southeastern United States. Data was collected by completing a chart review of all patients who were seen for a neuropsychological evaluation, including the WISC-IV, in 2005. The majority of the WISC-IV administrations were conducted by a master’s level technician, with a smaller percentage of administrations conducted by either a licensed psychologist or supervised trainee. Demographic information and each participant’s scores from the WISC-IV core subtests were included as variables in subsequent analyses.

Sixty percent of the current sample (n = 217) were males. The mean age was 10.5 years with a range of 6 years, 0 months to 16 years, 11 months. The diagnostic breakdown (i.e., primary diagnosis) of the current sample was as follows: attention deficit/hyperactivity disorder (ADHD, 20%), epilepsy (18%), learning disability (14%), traumatic brain injury (9%), cerebral palsy (4%), meningitis/encephalitis (3%), spina bifida (2%), in-utero/perinatal conditions (1%), other medical conditions (29%). This breakdown of presenting diagnoses is similar to that found in a study of hospital neuropsychology referral patterns conducted at three Midwestern children’s hospitals (Yeates, Ris, & Taylor, 1995).

Confirmatory factor analysis was conducted using maximum likelihood estimation in Mplus 4.2 (Muthén & Muthén, 1998–2004). Confirmatory factor analysis was chosen because it is considered the appropriate technique for establishing construct validity and allows investigators to examine competing models using established psychometric criteria (Floyd & Widaman, 1995). Based on theoretical and empirical work with previous versions of the WISC, four alternative models were specified: (a) a one-factor baseline model; (b) a two-factor model separating subtests measuring verbal and nonverbal abilities; (c) a three-factor model separating subtests measuring verbal abilities, perceptual abilities, and working memory/processing speed; and (d) the four-factor model separating subtests measuring verbal, perceptual, processing speed, and working memory abilities. For the multiple factor models, each first-order factor was specified to load on a single second-order factor representing general intelligence (g). For each successive nested model, chi-square difference testing was used to determine if the more complex model resulted in a significant increase in model fit. For the best-fitting model, the proportion of variance in each of the 10 subtests attributable to the second-order factor g, the first-order factors, and unique influences (i.e., subtest specific and error variance) were calculated. Indirect loadings of each of the subtests on the second-order factor g were calculated by taking the product of the subtest loading on the first factor with the first-order factor loading on the second-order factor (Keith et al., 2006; Keith & Witta, 1997). The absolute fit of the models was examined using the normed chi square (χ2/df), the comparative fit index (CFI), the Tucker-Lewis index (TLI), the root mean square error of approximation (RMSEA), and the standardized root mean square residual (SRMR). Indicators of good model fit include normed chi-square values below 2 (Bollen, 1989), CFI and TLI values greater than .95, RMSEA values below .06, and SRMR values below .08 (Hu & Bentler, 1998, 1999).

We also compared the best fitting higher order factor model to a correlated factor model to determine which model provided a more parsimonious fit to the data. For this comparison, several fit measures that value parsimony (i.e., simpler models are preferred) were used to determine the preferred model, including the parsimonious CFI (PCFI), parsimonious normed fit index (PNFI), and the Bayesian information criteria (BIC). The model with the highest values on the PCFI and PNFI and lowest value on the BIC is considered more parsimonious.

RESULTS AND DISCUSSION

Table 1 presents the data for the specified factor models. Chi-square difference tests and global fit indices indicated that the higher order four-factor model provided a better fit to the data than the single-, two-, or three-factor models. All global fit indices for the higher order four-factor model were indicative of a reasonably good fitting model. Moreover, examination of the PCFI, PNFI, and BIC values indicated that the higher order four-factor model provided a more parsimonious fit to the data than a correlated four-factor model. As a result, the higher order four-factor model was selected as the preferred model for the WISC-IV subtests in this sample.

Table 1.

Fit Statistics for Alternative Factor Models of the WISC-IV in a Neuropsychology Clinic Sample (N = 344)

Alternative Models χ2 df Δχ2 χ2/df CFI TLI RMSEA SRMR PCFI PNFI BIC
1. Single-factor 274.89 35 – 7.85 0.87 0.84 0.14 0.07 0.68 0.67 16433.65
2. Higher order two-factor 205.28 34 69.60*** 6.04 0.91 0.88 0.12 0.06 0.69 0.67 16369.89
3. Higher order three-factor 135.17 32 70.11*** 4.22 0.95 0.92 0.10 0.05 0.67 0.66 16311.46
4. Higher order four-factor 63.93 31 71.25*** 2.06 0.98 0.98 0.06 0.03 0.68 0.67 16246.06
5. Correlated four-factor 53.27 29 – 1.84 0.99 0.98 0.05 0.02 0.64 0.63 16247.09
Open in a new tab

Note. df = degrees of freedom; CFI = comparative fit index; TLI = Tucker-Lewis index; RMSEA = root mean square error of approximation; SRMR = standardized root mean square residual; PCFI = parsimonious comparative fit index; PNFI = parsimonious normed fit index; BIC = Bayesian information criteria.

***

p < .001.

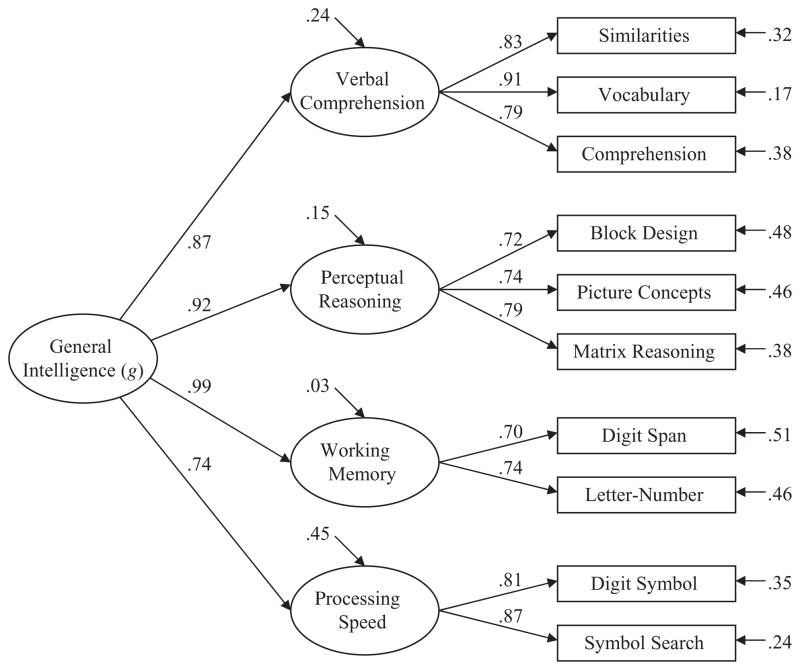
Figure 1 shows that the standardized loadings for the higher order four-factor model were high and statistically significant for all first-order factors, Bs=.70 – .91, ps < .001, as well as for the second-order factor, Bs = .74 – .99, ps < .001. The WISC-IV general intelligence factor accounted for 55% of the processing speed (PS) factor, 76% of the verbal comprehension (VC) factor, 85% of the perceptual reasoning (PR) factor, and 97% of the working memory (WM) factor. Composite reliabilities for the first-order factors were: VC = .88, PR = .79, WM = .68, PS = .83. At the subtest level (see Table 2), the WM factor explained only 1% of the variance in each of the two subtests making up the factor after accounting for the indirect influence of g. In contrast, the PS factor accounted for 29% to 34% of the variance in its two subtests after accounting for the indirect influence of g. For each WISC-IV subtest, the proportion of variance accounted for by the indirect influence of g (i.e., 36%–63%) was higher than the proportion of variance uniquely accounted for by the first-order factors (i.e., 1%–34%). Similarly, the general intelligence factor indirectly accounted for the largest proportion of both total (48.3%) and common variance (77.2%) across all subtests.

Figure 1.

Figure 1

Open in a new tab

Higher order four-factor structure of the WISC-IV in a neuropsychology clinic sample (N = 344). The four columns of values depicted in the figure represent (from right to left): unique/error variances for the WISC-IV subtests, standardized first-order factor loadings, first-order factor residual variances, and standardized second-order factor loadings.

Table 2.

Decomposition of Variance for the Higher Order Four-Factor Model of the WISC-IV in a Neuropsy-chology Clinic Sample (N = 344)

Subtests g
 VC
 PR
 WM
 PS
 h2 u2
B var B var B var B var B var
Similarities 0.72 52 0.41 17 0.68 0.32
Vocabulary 0.79 63 0.45 20 0.83 0.17
Comprehension 0.69 47 0.39 15 0.62 0.38
Block Design 0.67 44 0.28 8 0.52 0.48
Picture Concepts 0.68 46 0.28 8 0.55 0.46
Matrix Reasoning 0.73 53 0.30 9 0.62 0.38
Digit Span 0.69 48 0.11 1 0.49 0.51
Letter-Number 0.73 53 0.11 1 0.54 0.46
Digit Symbol Coding 0.60 36 0.54 29 0.65 0.35
Symbol Search 0.65 42 0.59 34 0.76 0.24
% Total Var 48.3 5.2 2.5 0.2 6.4 62.6 37.4
% Common Var 77.2 8.3 4.0 0.4 10.2
Open in a new tab

Note. Loadings and variances for first-order factors are after accounting for the indirect effects of the higher order general intelligence factor. g = general intelligence factor; VC = verbal comprehension factor; PR = perceptual reasoning factor; WM = working memory factor; PS = processing speed factor; B = loading of the subtest on the factor; var = percent variance explained in the subtest; h2 = communality; u2 = uniqueness.

These findings indicate that the factor structure of the WISC-IV, as described in the WISC-IV technical manual (Wechsler, 2003b), can be replicated in a neuropsychological sample. Consistent with previous research (Watkins, 2006; Watkins et al., 2006), the WISC-IV general intelligence factor (g) accounted for the majority of variance in the first-order latent factors (between 55% and 97%). Also consistent with previous studies, the PR (2.5%) and WM (0.2%) factors accounted for the smallest percentage of total variance compared to the other two factors. At the subtest level, the general intelligence factor explained a higher proportion of variance than the first-order factors. This was especially true for the WM subtests, for which only 1% of the variance was explained by the WM factor.

The PS factor explained a relatively high amount of variance in the subtests making up that factor (29% for coding and 34% for symbol search). This is consistent with previous studies of the WISC-III PS index, which found that this factor is less dependent on g than the other factors (Calhoun & Mayes, 2005). The relative independence of PS may be a function of the high demands for graphomotor skills inherent in these subtests, relative to other WISC-IV subtests. In neurologically compromised samples, this is important given the fact that processing speed and graphomotor skills are often impaired in these populations, especially in the case of traumatic brain injury (Donders & Warschausky, 1997). Given the unique variance seen for the PS subtests, and the sensitivity of these measures to neurological dysfunction (Yeates & Donders, 2005), the current results provide strong support for the construct validity of the PS index in pediatric neuropsychological populations.

The current results will likely continue the debate regarding the WM factor. Colom, Rebollo, Palacios, Juan-Espinosa, and Kyllonen (2004) found that WM (using measures of working memory not found on the WISC-IV) is a latent factor that is almost completely predicted by g. Our results are consistent with this finding. This is not surprising given the fact that the concept of working memory has been described to involve an individual’s capacity and efficiency of cognitive ability (Colom et al., 2004; Jensen, 1998). There is also some controversy regarding the composition of the PR index on the WISC-IV, especially in regards to the picture concepts subtest, which did not have strong loadings on the PR factor in the standardization sample (Wechsler, 2003b). However, in the current sample, the three PR subtests had similar loadings onto the PR factor, after accounting for the indirect effects of g. The PR index was designed to measure fluid reasoning over visual spatial skills (Yeates & Donders, 2005). As a result, it has been suggested that the PR index may be less sensitive to brain impairment than similar factors on previous versions of the WISC (Yeates & Donders, 2005). The present results reveal that the variance in the PR factor subtests is largely explained by g. As a result, performance on each of the PR subtests may not be strongly influenced by neurological impairment.

This study is not without limitations. First, because the study was retrospective and accomplished through a chart review, several important pieces of demographic data, such as race and socioeconomic status, were not available. In addition, only the core subtests were included in the confirmatory factor analysis. As a result, we were unable to describe the factor structure of all 15 subtests. Given the limited scope of this study, we were also unable to address the clinical validity of the WISC-IV factor scores by examining correlations between the factor scores and performance on tests of other neuropsychological domains, such as memory, executive functioning, and academic achievement.

One of the most important limitations of the current study is the heterogeneous nature of the sample, which consisted of children with a variety of medical and neurodevelopmental diagnoses. The use of heterogeneous clinical samples in establishing construct validity of assessment instruments has been criticized because the differences in neuropathological processes across different neurological disorders may mask any unique cognitive distinctions inherit in a specific measure (Delis, Jacobson, Bondi, Hamilton, & Salmon, 2003). For example, children with epilepsy may exhibit different patterns of performance on the WISC-IV than children with traumatic brain injuries, because of differences in underlying neuropathology, and this unique pattern of performance may not be evident in factor analytic studies that combine these two distinct groups into one clinical sample. As a result, this heterogeneity limits conclusions regarding the potential effects of specific neuropathological processes on WISC-IV performance patterns.

Evaluating the higher order factor structure of popular psychological instruments such as the WISC-IV is informative from theoretical and practical perspectives. The current results suggest that the second-order g factor accounts for most of the variance in the WISC-IV first-order latent factors and in the individual subtests. This is consistent with recent research indicating that full scale intelligence quotient (FSIQ) on the WISC-IV is a robust predictor of reading and math achievement in clinical and normative samples even in the presence of significant variability across index scores (Watkins, Glutting, & Lei, 2007). These results suggest that clinicians should not ignore the contribution of g when interpreting the WISC-IV factor scores, especially in the case of the working memory index. This point was also made by Watkins (2006) and Watkins et al. (2006). That said, certain WISC-IV factors (i.e., processing speed) are likely to require considerable interpretative attention in neuropsychological samples.

The Wechsler series of intelligence tests have been criticized for not being guided by theoretical models (Keith et al., 2006). The current results support the notion that the hierarchical nature of intelligence should be acknowledged in both test design and interpretation. Future factor analytic studies of the WISC-IV in clinical samples are necessary. Replication of the current results with larger samples is needed to determine if the current results are merely sample specific and open to subjective interpretation. In addition, a larger sample would allow for separate factor analyses across different clinical populations. A larger sample would also enable replication of the factor structure across the four age groups examined in the original WISC-IV factor analysis studies. Finally, future studies examining the predictive utility of the WISC-IV full scale and index scores in relation to important clinical outcomes would be informative.

Footnotes

A preliminary version of this paper was presented as a poster at the annual meeting of the American Association of Clinical Neuropsychology in Philadelphia, PA, June 2006.

References

  1. American Educational Research Association. Standards for educational and psychological testing. Washington, DC: American Psychological Association; 1999. [Google Scholar]
  2. Blaha J, Wallbrown FH. Hierarchical factor structure of the Wechsler Intelligence Scale for Children-III. Psychological Assessment. 1996;8(2):214–218. [Google Scholar]
  3. Bollen KA. Structural equations with latent variables. New York: John Wiley & Sons; 1989. [Google Scholar]
  4. Burton DB, Sepehri A, Hecht F, VandenBroek A, Ryan JJ, Drabman R. A confirmatory factor analysis of the WISC-III in a clinical sample with cross-validation in the standardization sample. Child Neuropsychology. 2001;7(2):104–116. doi: 10.1076/chin.7.2.104.3130. [DOI] [PubMed] [Google Scholar]
  5. Calhoun SL, Mayes SD. Processing speed in children with clinical disorders. Psychology in the Schools. 2005;42:333–343. [Google Scholar]
  6. Colom R, Rebollo I, Palacios A, Juan-Espinosa M, Kyllonen PC. Working memory is (almost) perfectly predicted by g. Intelligence. 2004;32:277–296. [Google Scholar]
  7. Delis DC, Jacobson M, Bondi MW, Hamilton JM, Salmon DP. The myth of testing construct validity using factor analysis or correlations with normal or mixed clinical populations: Lessons from memory assessment. Journal of the International Neuropsychological Society. 2003;9:936–946. doi: 10.1017/S1355617703960139. [DOI] [PubMed] [Google Scholar]
  8. Donders J. Factor structure of the WISC-R in children with traumatic brain injury. Journal of Clinical Psychology. 1993;49(2):255–260. doi: 10.1002/1097-4679(199303)49:2<255::aid-jclp2270490220>3.0.co;2-q. [DOI] [PubMed] [Google Scholar]
  9. Donders J, Warschausky S. A structural equation analysis of the WISC-III in children with traumatic head injury. Child Neuropsychology. 1996;2(3):185–192. [Google Scholar]
  10. Donders J, Warschausky S. WISC-III factor score patterns after traumatic head injury in children. Child Neuropsychology. 1997;3(1):71–78. [Google Scholar]
  11. Floyd FJ, Widaman KF. Factor analysis in the development and refinement of clinical assessment instruments. Psychological Assessment. 1995;7:286–299. [Google Scholar]
  12. Grice JW, Krohn EJ, Logerquist S. Cross-validation of the WISC III factor structure in two samples of children with learning disabilities. Journal of Psychoeducational Assessment. 1999;17:236–248. [Google Scholar]
  13. Hodges K. Factor structure of the WISC-R for a psychiatric sample. Journal of Consulting and Clinical Psychology. 1982;50:141–142. doi: 10.1037//0022-006x.50.1.141. [DOI] [PubMed] [Google Scholar]
  14. Hu L, Bentler PM. Fit indices in covariance structure modeling: Sensitivity to underparameterized model misspecification. Psychological Methods. 1998;3:424–453. [Google Scholar]
  15. Hu L, Bentler PM. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling. 1999;6:1–55. [Google Scholar]
  16. Jensen A. The g factor. Westport: Praeger; 1998. [Google Scholar]
  17. Kaufman AS. Factor analysis of the WISC-R at 11 age levels between 6.5 and 16.5 years. Journal of Consulting and Clinical Psychology. 1975;43:135–147. doi: 10.1037//0022-006x.43.5.661. [DOI] [PubMed] [Google Scholar]
  18. Keith TZ, Fine JG, Taub GE, Reynolds MR, Kranzler JH. Higher order, multi-sample, confirmatory factor analysis of the Wechsler Intelligence Scale for Children-Fourth Edition: What does it measure? School Psychology Quarterly. 2006;35(1):108–127. [Google Scholar]
  19. Keith TZ, Witta EL. Hierarchical and cross-age confirmatory factor analysis of the WISC-III: What does it measure? School Psychology Quarterly. 1997;12(2):89–107. [Google Scholar]
  20. Muthén LK, Muthén BO. Mplus user’s guide. 3. Los Angeles, CA: Muthén & Muthén; 1998–2004. [Google Scholar]
  21. Tingstrom DH, Pfeiffer SI. WISC-R factor structure in a referred pediatric population. Journal of Clinical Psychology. 1988;44:799–802. doi: 10.1002/1097-4679(198809)44:5<799::aid-jclp2270440524>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
  22. Tupa DJ, Wright MO, Fristad MA. Confirmatory factor analysis of the WISC-III with child psychiatric inpatients. Psychological Assessment. 1997;9(3):302–306. [Google Scholar]
  23. Watkins MW. Orthogonal higher-order structure of the Wechsler Intelligence Scale for Children-Fourth Edition. Psychological Assessment. 2006;18(1):123–125. doi: 10.1037/1040-3590.18.1.123. [DOI] [PubMed] [Google Scholar]
  24. Watkins MW, Glutting JJ, Lei P. Validity of the full-scale IQ when there is significant variability among WISC-III and WIC-IV factor scores. Applied Neuropsychology. 2007;14:13–20. [Google Scholar]
  25. Watkins MW, Wilson SM, Kotz KM, Carbone MC, Babula T. Factor structure of the Wechsler Intelligence Scale for Children-Fourth Edition among referred students. Educational and Psychological Measurement. 2006;66(6):975–983. [Google Scholar]
  26. Wechsler D. Wechsler Intelligence Scale for Children. 4. San Antonio, TX: Psychological Corporation; 2003a. [Google Scholar]
  27. Wechsler D. Technical and interpretive manual. 4. San Antonio, TX: Psychological Corporation; 2003b. Wechsler Intelligence Scale for Children. [Google Scholar]
  28. Yeates KO, Donders J. The WISC-IV and neuropsychological assessment. In: Prifitera A, Saklosfske DH, Weiss LG, editors. WISC-IV clinical use and interpretation: Scientist-Practitioner perspectives (Practical resources for the mental health professional) Burlington, MA: Academic Press; 2005. pp. 415–434. [Google Scholar]
  29. Yeates KO, Ris MD, Taylor HG. Hospital referral patterns in pediatric neuropsychology. Child Neuropsychology. 1995;1(1):56–62. [Google Scholar]

RESOURCES